1 Introduction

Time delays are important aspect of many systems whether they are natural (e.g., biological or ecological), or part of some technological process (electrical or mechanical). In other situations, it may be appropriate for the delay to depend on the solution of the governing differential equation. We call such a delay a state-dependent delay. Functional differential equations with state-dependent delays (sd-FDEs) arise in various applications, in particular, in mathematical ecology and bio-economics [1–4], in classical electrodynamics [5], in models of commodity price fluctuations [6], and in models of blood cell productions [7]. In this paper, we consider state-dependent delay in van der Pol equations at the current time only, although delays that depend on the solution at previous times may also be considered. Furthermore, we restrict attention only to ordinary differential equation models and do not attempt to include spatial effects. Our aim was to construct expressions for periodic solutions which bifurcate from the steady states in such models and to infer their stability from the sub/supercriticality of the bifurcation.

The van der Pol oscillator is an oscillator with nonlinear damping governed by the second-order differential equation

$$\begin{aligned} \ddot{x}-\varepsilon (1-x^2)\dot{x}+x=0. \end{aligned}$$
(1)

This model was originally proposed by Balthasar van der Pol [8]. The van der Pol equation, which was later extensively studied as a host of a rich class of dynamical behavior, including relaxation oscillations, quasi-periodicity, elementary bifurcations, and chaos, plays an important role in electronics and mathematics dynamical systems. Recently, the van der Pol equations with time delay have been studied by many researchers. Atay [9], Zhang and Guo  [11], and Wei and Jiang [12] have studied the behavior of the limit cycle of the van der Pol equations of the form

$$\begin{aligned} \ddot{x}-\varepsilon (1-x^2)\dot{x}+x=\varepsilon kx(t-\tau ), \end{aligned}$$
(2)

where \(x\) is a dynamical variable and \(\varepsilon >0\) is a parameter indicating the nonlinearity and the strength of the damping. In this paper, however, we consider the van der Pol equation with state-dependent delay

$$\begin{aligned} \ddot{ x}-\varepsilon (1-x^2)\dot{x}+x=\varepsilon kx(t-\tau (x(t))). \end{aligned}$$
(3)

It is easy to see that system (3) is more general than system (2). Most practical implementations of feedback have inherent delays, the presence of which results in an infinite-dimensional system, thus complicating the analysis.

Hopf bifurcation is the birth of a limit cycle from an equilibrium in dynamical systems, when the equilibrium changes stability via a pair of purely imaginary eigenvalues. The bifurcation can be supercritical or subcritical, resulting in stable or unstable (within an invariant two-dimensional manifold) limit cycle, respectively. A local Hopf bifurcation theory for sd-FDEs was developed by Eichmann [13] with the help of the Fredholm alternative Theorem. Hu and Wu [14] develop a local and global Hopf bifurcation theory for sd-FDEs by using the homotopy invariance property of the \(\mathbb {S}^1\)-equivariant degree to relate the Hopf bifurcation problem of sd-FDEs to the change of stability of stationary states of the corresponding system of auxiliary equations obtained through formal linearization. Very recently, Sieber [15] extended the Hopf bifurcation theorem by Eichmann [13] by showing that periodic boundary-value problems for delay differential equations are locally equivalent to finite-dimensional algebraic systems of equations. In [13–15], however, there is no result on the Hopf bifurcation direction. Our goal in this paper is to apply the perturbation procedure to describe the occurrence of local Hopf bifurcation from a stationary state, and the bifurcation direction for such a class of sd-FDEs as (3). In comparison, our results here provide a tool and framework to study the Hopf bifurcation problem and, in particular, local bifurcation of periodic solutions of differential equations with state-dependent delay. For an autonomous planar vector field, index theory can be used to show that: Inside the region enclosed by a periodic orbit, there must be at least one equilibrium (see, for example [16]). For such sd-FDEs as (3), however, we shall see that there may be no equilibrium inside the region enclosed by a periodic orbit.

2 Hopf bifurcation analysis

The local stability of steady-state solutions of sd-FDEs was studied in [17, 18]. It was shown, under natural assumptions on the right-hand side of the equation and on the delay function \(\tau \), that generically the behavior of the state-dependent delay \(\tau \) except for its value \(\tau \) has no effect on the stability and that a local linearization is valid by treating \(\tau \) as a constant at the steady state. Hence, to study the local stability of a steady state of (3), we linearize (3) at \(x=0\) by treating \(\tau =\tau (0)\). The resulting linear equation is a constant delay differential equation,

$$\begin{aligned} \ddot{ x}-\varepsilon \dot{x}+x=\varepsilon kx(t-r), \end{aligned}$$
(4)

where \(r=\tau (0)\). Thus, the characteristic equation is given by

$$\begin{aligned} \lambda ^2-\varepsilon \lambda -k\varepsilon e^{-\lambda r}+1=0. \end{aligned}$$
(5)

We know that \(\pm \mathrm{i}\omega \) (\(\omega >0\)) are a pair of purely imaginary roots of (5) if and only if \(\omega \) satisfies

$$\begin{aligned} \left\{ \begin{array}{l} 1-\omega ^2=\varepsilon k\cos (r\omega ) , \\ \omega =k \sin (r\omega ). \end{array}\right. \end{aligned}$$
(6)

Hence, the Hopf bifurcation surface is given by

$$\begin{aligned}&\mathcal {H}=\{(\varepsilon ,r,k): 1-\omega ^2=\varepsilon k\cos (r\omega ),\\&\quad \quad \quad \omega =k\sin (r\omega ), \omega >0\}. \end{aligned}$$

Then, it follows from (6) that \(\omega \) satisfies

$$\begin{aligned} \frac{\varepsilon \omega }{1-\omega ^2}=\tan (r\omega ). \end{aligned}$$
(7)

Let \(\{\xi _n\}^\infty _{n=1}\) be the monotonic increasing sequence of the positive solutions of \(x=\tan x\), and

$$\begin{aligned} \begin{aligned} r_n^*&=\sqrt{2+\xi _n^2}, \quad \varepsilon _n^*=\frac{2}{\sqrt{2+\xi _n^2}},\\ \omega _n^*&=\frac{\xi _n}{\sqrt{2+\xi _n^2}}, \quad k_n^*=\frac{\xi _n}{\sqrt{2+\xi _n^2}\sin \xi _n}. \end{aligned} \end{aligned}$$
(8)

Some version of the following result has appeared in Guo and Wu [10] and Zhang and Guo [11], we include the proof for the completeness of the presentation.

Lemma 1

At and only at \((\varepsilon ,r,k)\in \mathcal {H}\backslash \{(\varepsilon _n^*,r_n^*,k_n^*)\}^\infty _{n=1}\), Eq. (5) has a pair of simple purely imaginary solutions \(\pm \mathrm{i}\omega \), where \(\omega \) is a solution to (6). Moreover, at and only at \((\varepsilon ,r,k)=(\varepsilon ^*_n,r^*_n,k^*_n)\) for some \(n\in \mathbb {N}^+\), Eq. (5) has a pair of double purely imaginary solutions \(\pm \mathrm{i}\omega ^*_n\).

Proof

If \(\mathrm{i}\omega \) is not simple, then we have

$$\begin{aligned} \frac{\mathrm{d}}{\mathrm{d}\lambda }(\lambda ^2-\varepsilon \lambda +1-\varepsilon k {\mathrm {e}}^{-\lambda r})\mid _{\lambda =\mathrm{i}\omega }=0, \end{aligned}$$

that is

$$\begin{aligned} 2\mathrm{i}\omega -\varepsilon +r\varepsilon k(\mathrm {\cos }\omega r-\mathrm{i}\mathrm {\sin }\omega r)=0. \end{aligned}$$

Separating the real and imaginary parts, we obtain

$$\begin{aligned} \begin{aligned}&1=r k\mathrm {\cos }\omega r,\\&2\omega =r\varepsilon k\mathrm {\sin }\omega r. \end{aligned} \end{aligned}$$
(9)

It follows from (6) and (9) that

$$\begin{aligned} \begin{aligned}&r\varepsilon =2,\\&r(1-\omega ^2)=\varepsilon ,\\&r\omega =\xi , \end{aligned} \end{aligned}$$
(10)

where \(x=\xi >0\) is a solution to the equation \(x={{{\tan }}}x\). Then, it follows from (10) that \((\varepsilon ,r,k)=(\varepsilon ^*_n,r^*_n,k^*_n)\) for some \(n\in \mathbb {N}^+\). The proof is completed. \(\square \)

In what follows, we fix \((\varepsilon ,k)\in \mathbb {R}^2\) and regard \(r\) as a bifurcation parameter. It follows from (6) that

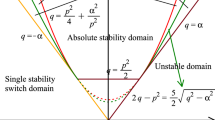
$$\begin{aligned} \omega ^4+(\varepsilon ^2-2)\omega ^2+1-\varepsilon ^2k^2=0. \end{aligned}$$
(11)

The number of positive solutions to (11) may be zero, one, or two, which is determined by the signs of \((\varepsilon ^2+4k^2-4)\) and \((\varepsilon |k|-1)\). In fact, the curves \(\varepsilon ^2+4k^2=4\) and \(\varepsilon |k|=1\) divide the right half \((\varepsilon ,k)\)-plane into six regions (See Fig. 1):

$$\begin{aligned} D_1&= \left\{ (\varepsilon ,k)\in \mathbb {R}^+\times \mathbb {R}:\,\,\varepsilon ^2+4k^2<4\right\} ,\\ D^+_2&= \left\{ (\varepsilon ,k)\in \mathbb {R}^+\times \mathbb {R}:\,\, \varepsilon k>1\right\} ,\\ D^-_2&= \left\{ (\varepsilon ,k)\in \mathbb {R}^+\times \mathbb {R}:\,\, \varepsilon k<-1\right\} ,\\ D^+_3&= \left\{ (\varepsilon ,k)\in \mathbb {R}^+\times \mathbb {R}:\,\,\sqrt{1-\frac{\varepsilon ^2}{4}}<k<\frac{1}{\varepsilon },\, \varepsilon <\sqrt{2}\right\} \!,\\ D^-_3&= \left\{ (\varepsilon ,k)\in \mathbb {R}^+\times \mathbb {R}:\,\sqrt{1-\frac{\varepsilon ^2}{4}}\!<-k\!<\!\frac{1}{\varepsilon },\, \varepsilon \!<\!\sqrt{2}\right\} \!,\\ D_4&= \left\{ (\varepsilon ,k)\in \mathbb {R}^+\times \mathbb {R}:\,\,\varepsilon ^2+4k^2>4,\right. \\&\quad \left. \varepsilon |k|<1,\, \varepsilon >\sqrt{2}\right\} \!. \end{aligned}$$
Fig. 1
figure 1

Curves \(\varepsilon ^2+4k^2=4\) and \(\varepsilon |k|=1\) and regions \(D_1\), \(D^{\pm }_2\), \(D^{\pm }_3\), and \(D_4\)

Full size image

More precisely, Eq. (11) has two positive solutions \(\omega =\omega _{\pm }(\varepsilon ,k)\) when \((\varepsilon ,k)\in D^+_3\cup D^-_3\), has exactly one positive solution \(\omega =\omega _{+}(\varepsilon ,k)\) when \((\varepsilon ,k)\in D^+_2\cup D^-_2\), and has no positive solution when \((\varepsilon ,k)\in D_1\cup D_4\), where

$$\begin{aligned} \omega _{\pm }(\varepsilon ,k)=\sqrt{1-\frac{\varepsilon ^2}{2}\pm \varepsilon \sqrt{k^2-1+\frac{\varepsilon ^2}{4}}}. \end{aligned}$$

Thus, the Hopf bifurcation values of \(r\) are given as follows:

$$\begin{aligned}&r_j^+(\varepsilon ,k)\\&\qquad \!=\left\{ \begin{array}{ll}\frac{1}{\omega _+(\varepsilon ,k)}\left( 2\pi -\arcsin \frac{\omega _+(\varepsilon ,k)}{\mid k\mid }+2j\pi \right) &{}\quad {\mathrm {if}}\, k\le -1,\\ \frac{1}{\omega _+(\varepsilon ,k)}\left( \pi +\arcsin \frac{\omega _+(\varepsilon ,k)}{\mid k\mid }+2j\pi \right) &{}\quad {\mathrm {if}}\, -1\le k<0,\\ \frac{1}{\omega _+(\varepsilon ,k)}\left( \arcsin \frac{\omega _+(\varepsilon ,k)}{\mid k\mid }+2j\pi \right) &{}\quad {\mathrm {if}}\, 0<k\le 1,\\ \frac{1}{\omega _+(\varepsilon ,k)}\left( \pi -\arcsin \frac{\omega _+(\varepsilon ,k)}{\mid k\mid }+2j\pi \right) &{}\quad {\mathrm {if}}\, k>1,\end{array}\right. \\ \end{aligned}$$
$$\begin{aligned}&r_j^-(\varepsilon ,k)\\&\qquad =\left\{ \begin{array}{ll}\frac{1}{\omega _-(\varepsilon ,k)}\left( \pi +\arcsin \frac{\omega _-(\varepsilon ,k)}{\mid k\mid }+2j\pi \right) &{}\quad {\mathrm {if}}\, k<0,\\ \frac{1}{\omega _-(\varepsilon ,k)}\left( \arcsin \frac{\omega _-(\varepsilon ,k)}{\mid k\mid }+2j\pi \right) &{}\quad {\mathrm {if}}\, k>0, \end{array}\right. \end{aligned}$$

for \(j\in \mathbb {N}_0:=\{0,1,2,\ldots \}\). In summary, we have the following conclusions.

Lemma 2

  1. (i)

    For any fixed \((\varepsilon ,k)\in D^+_3\)(\(D^-_3\)), the characteristic equation (5) with \(r=r_j^+(\varepsilon ,k)\) (respectively, \(r=r_j^-(\varepsilon ,k)\)) has a pair of simple imaginary roots \(\pm {\mathrm {i}} \omega _{+}(\varepsilon ,k)\) (respectively, \(\pm {\mathrm {i}} \omega _{-}(\varepsilon ,k)\)), \(j\in \mathbb {N}_0\).

  2. (ii)

    For any fixed \((\varepsilon ,k)\in D^+_2\cup D^-_2\), the characteristic equation (5) with \(r=r_j^+(\varepsilon ,k)\) has a pair of simple imaginary roots \(\pm {\mathrm {i}} \omega _{+}(\varepsilon ,k)\), \(j\in \mathbb {N}_0\).

Lemma 3

  1. (i)

    For any fixed \((\varepsilon ,k)\in D_1\cup D^+_2\cup D^-_2\cup D_4\) and \(r\ge 0\), the characteristic equation (5) has at least one solution \(\lambda \) satisfying \({\mathrm {Re}}\lambda >0\). Furthermore, for any fixed \((\varepsilon ,k)\in D^+_2\cup D^-_2\), system (3) undergoes Hopf bifurcation at the origin near \(\tau (0)=r^+_{j}(\varepsilon ,k)\), \(j\in \mathbb {N}_0\).

  2. (ii)

    For any fixed \((\varepsilon ,k)\in D^+_3\), there exists a nonnegative integer \(m\) such that (5) has a pair of roots with positive real parts when \(r^+_{j-1}(\varepsilon ,k)<r<r^-_j(\varepsilon ,k)\), \(j=0,1,2,\ldots ,m\) with \(r^+_{-1}(\varepsilon ,k)=0\), and all roots of (5) have negative real parts when \(r^-_{j}(\varepsilon ,k)<r<r^+_j(\varepsilon ,k)\), and (5) has at least a pair of roots with positive real parts when \(r>r_m^+(\varepsilon ,k)\). Furthermore, system (3) undergoes Hopf bifurcation at the origin near \(\tau (0)=r^\pm _{j}(\varepsilon ,k)\), \(j\in \mathbb {N}_0\).

Cooke and Huang [17] have shown that generically the behavior of the state-dependent delay (except the value of the delay) near an equilibrium has no effect on the stability and that the local linearization method can be applied by treating the delay \(\tau (\cdot )\) as a constant value at the equilibrium. Thus, in order to investigate the local stability of the steady state of (3), it suffices to discuss the existence of solutions with positive real parts for the characteristic equation (5). In view of Lemma 3, we have the following result.

Theorem 1

The equilibrium point \(x=0\) of (3) is asymptotically stable when \((\varepsilon ,k)\in D^+_3\) and \(\tau (0)\in \cup ^m_{j=0}(r^-_{j}(\varepsilon ,k),r^+_j(\varepsilon ,k))\) and is unstable when either \((\varepsilon ,k)\in D_1\cup D^+_2\cup D^-_2\cup D_4\) and \(\tau (0)\ge 0\) or \((\varepsilon ,k)\in D^+_3\) and \(\tau (0)\in \cup ^m_{j=0}(r^{+}_{j-1}(\varepsilon ,k),r^-_j(\varepsilon ,k))\cup (\tau ^+_m(\varepsilon ,k),+\infty )\).

Theorem 1 does not present the local stability of the equilibrium \(x=0\) in the case where \((\varepsilon ,k)\in D^-_3\), because it is hard to determine the order of critical values \(\{r^{\pm }_j(\varepsilon ,k)\}^{\infty }_{j=0}\) of \(\tau (0)\). Lemmas 1 and 2 implies that Eq. (3) with the delay function \(\tau (\cdot )\) frozen at the steady state \(x=0\) undergoes a Hopf bifurcation as \((\varepsilon ,\tau (0),k)\) passes through the points in \(\mathcal {H}\backslash \{(\varepsilon _n^*,r_n^*,k_n^*)\}^\infty _{n=1}\), or equivalently, points \((\varepsilon ,r_j^{\pm }(\varepsilon ,k),k)\), \(j\in \mathbb {N}_0\). In the subsequent section, we shall fix \((\varepsilon ,k)\) and construct the bifurcating periodic solution of the nonlinear equation (3) for \(\tau (0)\) near \(r^+_j(\varepsilon ,k)\) or \(r^-_j(\varepsilon ,k)\), \(j\in \mathbb {N}_0\). These bifurcating periodic solutions have frequency \(\omega \) close to the linearized frequency \(\omega _{+}(\varepsilon ,k)\) or \(\omega _{-}(\varepsilon ,k)\).

3 Perturbation expansion

For convenience, let \((r_0,\omega _0)=(r^+_j(\varepsilon ,k),\omega _{+}(\varepsilon ,k))\) if \((\varepsilon ,k)\in D_2^{\pm }\cup D_3^{\pm }\) or \((r_0,\omega _0)=(r^+_j(\varepsilon ,k),\omega _{+}(\varepsilon ,k))\) if \((\varepsilon ,k)\in D_1\), \(j\in \mathbb {N}_0\). To construct the bifurcating periodic solution of the nonlinear equation (3), we assume that they have frequency \(\omega \) close to the linearized frequency \(\omega =\omega _0\). To introduce \(\omega \) into the equation, we set \(s=\omega t\). Letting \(u(s)=x(s/\omega )\), the equation becomes

$$\begin{aligned} \omega ^2u''-\varepsilon \omega (1-u^2)u'+u=\varepsilon ku(s-\omega \tau (u(s))), \end{aligned}$$
(12)

Let \(\mathcal {C}_{2\pi }\) (respectively, \(\mathcal {C}^j_{2\pi }\)) be the set of continuous (respectively, \(j\) times differentiable) one-dimensional \(2\pi \)-periodic mappings. If we denote

$$\begin{aligned} \Vert u\Vert _0=\max _{s\in [0,2\pi ]}\{|u(s)|\} \end{aligned}$$

for \(u\in \mathcal {C}_{2\pi }\), and \(\Vert u\Vert _j=\max \{\Vert u\Vert _0,\Vert u'\Vert _0,\ldots , \Vert u^{(j)}\Vert _0\} \) for \(u\in \mathcal {C}^j_{2\pi }\), then \(\mathcal {C}_{2\pi }\) and \(\mathcal {C}^j_{2\pi }\) are Banach spaces when they are endowed with the norms \(\Vert \cdot \Vert _0\) and \(\Vert \cdot \Vert _j\), respectively. We introduce the inner product \(\langle \cdot ,\cdot \rangle \): \(\mathcal {C}_{2\pi }\times \mathcal {C}_{2\pi }\rightarrow \mathbb {R}\) defined by

$$\begin{aligned} \langle v,u\rangle =\frac{1}{2\pi }\int ^{2\pi }_0\overline{v}^T(t)u(t)\mathrm{d}t, \end{aligned}$$

for \(u,v\in \mathcal {C}_{2\pi }\).

We now expand \(u(s)\) about the steady state \(u(s)\equiv 0\), \(\omega \) about the linearized frequency \(\omega _0\), and also \(\tau (0)\), in terms of a small parameter \(\eta \) by writing

$$\begin{aligned}&u(s)\sim \displaystyle {\sum _{i=1}^{\infty }}\eta ^iu_i(s),\nonumber \\&\omega \sim \omega _0+\displaystyle {\sum _{i=1}^{\infty }}\eta ^i\omega _i,\\&\tau (0)\sim r_0+\displaystyle {\sum _{i=1}^{\infty }}\eta ^i\tau _i(0).\nonumber \end{aligned}$$
(13)

Substituting (13) into (12) and collecting powers of \(\eta \), if we define the linear operator \(\fancyscript{L}\): \(C^2_{\omega }\rightarrow C_{\omega }\) as

$$\begin{aligned} (\fancyscript{L}u)(s)=\omega ^2_0u''(s)-\varepsilon \omega _0u'(s)+u(s)-\varepsilon ku(s-\omega _0r_0), \end{aligned}$$
(14)

then the first three equations are

$$\begin{aligned} (\fancyscript{L}u_1)(s)=0, \end{aligned}$$
(15)
$$\begin{aligned} (\fancyscript{L}u_2)(s)&= -\,2\omega _0\omega _1u''_1(s)+\varepsilon \omega _1u'_1(s)\nonumber \\&-\,\varepsilon k u'_1(s-\omega _0r_0)[\omega _1r_0+\omega _0\tau _1(0)\nonumber \\&+\,\omega _0\tau '(0)u_1(s)], \end{aligned}$$
(16)
$$\begin{aligned} (\fancyscript{L}u_3)(s)&= -\,2\omega _0\omega _1u''_2(s)-2\omega _0\omega _2u''_1(s)-\omega _1^2u_1''(s)\nonumber \\&+\,\varepsilon \omega _1u'_2(s)+\varepsilon \omega _2u'_1(s)-\varepsilon \omega _0u^2_1(s)u'_1(s)\nonumber \\&-\,\varepsilon ku'_2(s-\omega _0r_0)\left[ \omega _1r_0+\omega _0\tau _1(0)\right. \nonumber \\&\left. +\,\omega _0\tau '(0)u_1(s)\right] \nonumber \\&+\,\frac{1}{2}\varepsilon ku''_1(s-\omega _0r_0)\left[ \omega _1r_0+\omega _0\tau _1(0)\right. \nonumber \\&\left. +\,\omega _0\tau '(0)u_1(s)\right] ^2\nonumber \\&-\,\varepsilon ku'_1(s-\omega _0r_0)\left[ \omega _0\tau '(0)u_2(s)\right. \nonumber \\&+\,\frac{1}{2}\omega _0\tau ''(0)u^2_1(s) +\,\omega _1\tau '(0)u_1(s)\nonumber \\&\left. +\,\omega _2r_0+\omega _0\tau _2(0)+\omega _1\tau _1(0)\right] . \end{aligned}$$
(17)

Recall that (15) now has two linearly independent solutions, namely \(\sin s\) and \(\cos s\). For simplicity, we take (without loss of generality)

$$\begin{aligned} u_1(s)=A\cos s. \end{aligned}$$
(18)

The adjiont \(\fancyscript{L}^*\) of linear operator of \(\fancyscript{L}\) is given by

$$\begin{aligned} (\fancyscript{L}^*u)(s)&= \omega ^2_0u''(s)+\varepsilon \omega _0u'(s)\nonumber \\&+\,u(s)-\varepsilon ku(s+\omega _0r_0), \end{aligned}$$
(19)

the kernel of which is spanned by

$$\begin{aligned} \psi _1(s)=\sin (s),\quad \psi _2(s)=\cos (s). \end{aligned}$$

Note that, although the adjoint equation \(\fancyscript{L}^*u\) appears to involve an advanced term, the adjoint equation is only posed in a space of periodic functions, so we do not need to worry about the issue of well posedness.

Substituting (18) into (16), we have

$$\begin{aligned} (\fancyscript{L}u_2)(s)&= 2A\omega _0\omega _1\cos s-A\varepsilon \omega _1\sin s\nonumber \\&+A\varepsilon k \sin (s-\omega _0r_0)[\omega _1r_0+\omega _0\tau _1(0)\nonumber \\&+A\omega _0\tau '(0)\cos s]. \end{aligned}$$
(20)

Now, applying the Fredholm orthogonality condition to (20), we have

$$\begin{aligned} \begin{aligned}&2A\omega _0\omega _1+A\varepsilon k\left[ \omega _1r_0+\omega _0\tau _1(0)\right] \sin (r_0\omega _0)=0,\\&A\varepsilon \omega _1+A\varepsilon k\left[ \omega _1r_0+\omega _0\tau _1(0)\right] \cos (r_0\omega _0)=0. \end{aligned}\nonumber \\ \end{aligned}$$
(21)

This implies that

$$\begin{aligned} \tau _1(0)=0,\quad \omega _1=0. \end{aligned}$$

Equation (20) now reduces to

$$\begin{aligned} (\fancyscript{L}u_2)(s)=A^2\omega _0\tau '(0)\varepsilon k \sin (s-\omega _0r_0)\cos s. \end{aligned}$$
(22)

which can be solved for \(u_2(s)\) to give

$$\begin{aligned} u_2(s)=A^2[R_0+R_1\sin (2s)+R_2\cos (2s)], \end{aligned}$$
(23)

where

$$\begin{aligned} R_1=\frac{bc-ad}{a^2+b^2},\quad R_2=\frac{ac+bd}{a^2+b^2},\quad R_0=\frac{d}{1-\varepsilon k}, \end{aligned}$$

and

$$\begin{aligned} a&= 2\varepsilon \omega _0-\varepsilon k\sin (2\omega _0r_0),\\ b&= 1-4\omega _0^2-\varepsilon k\cos (2\omega _0r_0),\\ c&= \frac{1}{2}\omega _0\tau '(0)\varepsilon k\cos (\omega _0r_0),\\ d&= -\frac{1}{2}\omega _0\tau '(0)\varepsilon k\sin (\omega _0r_0). \end{aligned}$$

Substituting (18) and (23) into our final equation (17) and applying the Fredholm orthogonality condition as before results in

$$\begin{aligned} 0&= \omega _0\omega _2A\!-\!\frac{\omega _0\tau '(0)\varepsilon kA^3}{4} \cos (\omega _0r_0)\left( \frac{3}{4}\omega _0\tau '(0)\!+\!R_1\right) \\&-\frac{\varepsilon kA}{2}\sin (\omega _0r_0) \left( \omega _2r_0+\omega _0\tau _2+\omega _0\tau '(0)R_0A^2\right. \\&\left. +\frac{\omega _0\tau ''(0)A^2}{4} -\frac{\omega _0\tau '(0)R_2A^2}{2}\right) \\&-\frac{1}{2}\varepsilon k\omega _0\tau '(0)A^3(R_1\cos (2\omega _0r_0)+R_2\sin (2\omega _0r_0)),\\ 0&= \frac{\varepsilon \omega _0 A^3}{8}-\frac{\varepsilon \omega _2 A}{2}-\frac{\omega _0\tau '(0)\varepsilon kA^3}{4}\sin (\omega _0r_0)\\&\!\times \! \left( \frac{1}{4}\omega _0\tau '(0)+R_1\right) \!+\!\frac{\varepsilon kA}{2}\cos (\omega _0r_0) \left( \omega _2r_0\!+\!\omega _0\tau _2\right. \\&\left. +\,\omega _0\tau '(0)R_0A^2+\frac{\omega _0\tau ''(0)A^2}{4} -\frac{\omega _0\tau '(0)R_2A^2}{2}\right) \\&-\,\frac{1}{2}\varepsilon k\omega _0\tau '(0)A^3\left( R_1\sin (2\omega _0r_0)-R_2\cos (2\omega _0r_0)\right) , \end{aligned}$$

which solve to give

$$\begin{aligned}&\omega _2=-\frac{\varepsilon \omega _0e+\left( 1-\omega _0^2\right) f}{\varepsilon ^2-2+2\omega _0^2}A^2,\\&\tau _2(0)=\frac{\left( \varepsilon r_0\omega _0-2\omega _0\right) e+\left( r_0-r_0\omega _0^2-\varepsilon \right) f}{\omega _0\left( \varepsilon ^2-2+2\omega _0^2\right) }A^2, \end{aligned}$$

where

$$\begin{aligned} e&= \left( \frac{2-2\omega _0^2}{k}+\frac{\epsilon }{2}\right) \omega _0\tau '(0)R_1\\&+\left( \frac{1-\omega _0^2}{2}+\frac{2\epsilon \omega _0^2}{k}-\epsilon k\right) \tau '(0)R_2 -\frac{\epsilon }{4}\\&+\frac{\tau '(0)^2}{8}\epsilon \omega _0^2-(1-\omega _0^2)\left( \tau '(0)R_0+\frac{\tau ''(0)}{4}\right) ,\\ f&= \left( \frac{1-\omega _0^2}{2}-\frac{2\epsilon \omega _0^2}{k}+\epsilon k\right) \tau '(0)R_1\\&+\left( \frac{2-2\omega _0^2}{k}-\frac{\epsilon }{2}\right) \omega _0\tau '(0)R_2\\&+\frac{3\tau '(0)^2}{8}\omega _0(1-\omega _0^2)+\epsilon \omega _0\left( \tau '(0)R_0+\frac{\tau ''(0)}{4}\right) ,\\ \end{aligned}$$

Up to \(\hbox {O}(\eta ^2) \), we therefore have

$$\begin{aligned} \omega =\omega _0+\eta ^2\omega _2,\quad \tau =r_0+\eta ^2\tau _2(0), \end{aligned}$$
(24)

and have

$$\begin{aligned} u(s)=A\eta \cos s+A^2\eta ^2[R_0+R_1\cos 2s+R_2\cos 2s] \end{aligned}$$
(25)

as the solution to (12). Then, we have the following theorem.

Theorem 2

The Hopf bifurcation occurs as \(\tau \) crosses \(r_0\) to the right (subcritical Hopf bifurcation) if \(\tau _2(0)>0\) and to the left (supercritical Hopf bifurcation) if \(\tau _2(0)<0\). Moreover, the period of the bifurcating periodic solutions is greater than (respectively, smaller than) \(\frac{2\pi }{\omega _0}\) if \(\omega _2\) is negative (respectively, positive).

It is easy to see that \(\tau _2(0)\) is highly dependent on the values of \(\tau (0)\), \(\tau '(0)\), \(\tau ''(0)\), and \(\omega _0\). Thus, we can regard \(\tau _2(0)\) as the function of \(r_0\), \(\omega _0\), \(\tau '(0)\), and \(\tau ''(0)\). This is to say,

$$\begin{aligned} \tau _2(0)=\varUpsilon (r_0,\omega _0,\tau '(0),\tau ''(0)). \end{aligned}$$

In addition, it is a standard result (see, for example [19, 20]) that for classical Hopf bifurcations, subcritical bifurcating periodic solutions are unstable, while supercritical bifurcating periodic solutions have the same stability as the trivial solution had before the bifurcation. Thus, by Theorem 1, we have the following result.

Theorem 3

  1. (i)

    System (3) with \((\varepsilon ,k)\in D^+_2\cup D^-_2\) undergoes Hopf bifurcation at the origin near \(\tau (0)=r^+_j(\varepsilon ,k)\), \(j\in \mathbb {N}_0\). More precisely, if \(\varUpsilon (\tau ^+_j(\varepsilon ,k),\omega _0,\tau '(0),\tau ''(0))>0\) (respectively, \(<0\)), then a branch of small-amplitude periodic solutions exists only for \(\tau (0)>r^+_j(\varepsilon ,k)\) (respectively, \(\tau (0)<r^+_j(\varepsilon ,k)\)) and is unstable.

  1. (ii)

    System (3) with \((\varepsilon ,k)\in D^+_3\) undergoes Hopf bifurcation at the origin near \(\tau (0)=r^+_j(\varepsilon ,k)\) and \(\tau (0)=r^-_j(\varepsilon ,k)\), \(j\in \mathbb {N}_0\). More precisely,

    1. (a)

      If \(\varUpsilon (\tau ^{\pm }_j(\varepsilon ,k),\omega _0,\tau '(0),\tau ''(0))>0\) (respectively, \(<0\)) then a branch of small-amplitude periodic solutions exists only for \(\tau (0)>r^{\pm }_j(\varepsilon ,k)\) (respectively, \(\tau (0)<r^+_j(\varepsilon ,k)\)).

    2. (b)

      The bifurcating periodic solutions near \(\tau (0)=r^{\pm }_j(\varepsilon ,k)\) (\(j>m\)) are unstable, where \(m\) is given in Lemma 3;

    3. (c)

      Necessary and sufficient conditions for the existence of stable small-amplitude periodic solutions of (3) near \(\tau (0)=\tau ^{+}_j\) (respectively, \(\tau (0)=\tau ^{-}_j\)) for some \(j\in \{0,1,2,\ldots , m\}\) are \(\varUpsilon (\tau ^+_j,\omega _0,\tau '(0),\tau ''(0))>0\) (respectively, \(<\)0).

  2. (iii)

    System (3) with \((\varepsilon ,k)\in D^-_3\) undergoes Hopf bifurcation at the origin near \(\tau (0)=r^+_j(\varepsilon ,k)\) and \(\tau (0)=r^-_j(\varepsilon ,k)\), \(j\in \mathbb {N}_0\). More precisely, if \(\varUpsilon (\tau ^{\pm }_j(\varepsilon ,k),\omega _0,\tau '(0),\tau ''(0))>0\) (respectively, \(<0\)) then a branch of small-amplitude periodic solutions exists only for \(\tau (0)>r^{\pm }_j(\varepsilon ,k)\) (respectively, \(\tau (0)<r^+_j(\varepsilon ,k)\)).

4 Illustrating examples

4.1 Constant delay

Equation (2) is a special case of (3), i.e., (3) with a constant delay \(\tau (x)\equiv \tau \). In this subsection, we investigate the Hopf bifurcating periodic solution of (2) for \(\tau \) near \(r_0\), where \(r_0=r^+_j(\varepsilon ,k)\) when \((\varepsilon ,k)\in D^+_2\cup D^-_2\cup D^+_3\cup D^-_3\), or \(r_0=r^\pm _j(\varepsilon ,k)\) when \((\varepsilon ,k)\in D^+_3\cup D^-_3\), for some \(j\in \mathbb {N}_0\). Obviously, then, we have \(\tau '(0)=0\) and

$$\begin{aligned} \omega _2=\frac{\varepsilon ^2\omega _0A^2}{4(\varepsilon ^2-2+2\omega _0^2)}, \quad \tau _2(0)=\frac{\varepsilon (2-\varepsilon r_0)A^2}{4(\varepsilon ^2-2+2\omega _0^2)}, \end{aligned}$$

where \(\omega _0=\omega _+(\varepsilon ,k)\) (respectively, \(\omega _-(\varepsilon ,k)\)) if \(r_0=r^+_j(\varepsilon ,k)\) (respectively, \(r^-_j(\varepsilon ,k)\)), \(j\in \mathbb {N}_0\). Obviously, \({\mathrm {sgn}}\{\tau _2(0)\}={\mathrm {sgn}}\{(2-\varepsilon r_0)(\varepsilon ^2-2+2\omega _0^2)\}\).

We next present some numerical results of system (2) with \((\varepsilon ,k)=(0.01,80)\). Namely, we consider the following system to verify the analytical predictions obtained in the previous discussion

$$\begin{aligned} \left\{ \begin{array}{ll} \dot{u} &{}= v,\\ \dot{v} &{}=-u+0.01(1-u^2)v+0.8u(t-\tau ). \end{array} \right. \end{aligned}$$
(26)

It follows from the previous section that

$$\begin{aligned} \omega _+(0.01,80)=1.3416,\quad \omega _-(0.01,80)=0.4473, \end{aligned}$$

and that \(r^{-}_0(0.01,80)=0.0125\), \(r^{+}_0(0.01,80)=2.3292\), \(r^{-}_1(0.01,80)=14.0617\), \(r^{+}_1(0.01,80)=7.0125\), \(r^{+}_{15}(0.01,80)=72.5795\). Notice that \((\varepsilon ,k)=(0.01,80)\in D^+_3\), then it follows from Lemma 3 and Theorem 1 that we obtain

Corollary 1

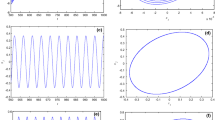
The equilibrium point \((u,v)=(0,0)\) of system (26) is asymptotically stable for \(\tau \in (0.0125,2.3292)\) and is unstable for all \(\tau \in [0,0.0125)\cup (2.3293,\infty )\), which is shown in Fig. 2.

Fig. 2
figure 2

Numerical simulations of system (26) with \(\tau =2\). a The equilibrium point \((u,v)=(0,0)\) is asymptotically stable; b the phase portrait of the asymptotically stable equilibrium

Full size image

It follows from Lemma 3 that system (26) undergoes Hopf bifurcation at the equilibrium point \((u,v)=(0,0)\) as \(\tau \) crosses \(r^+_j\) and \(r^-_j\), where \(r^{\pm }_j=r^{\pm }_j(0.01,80)\), \(j=0,1,2,\ldots \) Moreover, it is easy to see that

$$\begin{aligned} \left\{ \begin{array}{ll} \omega _2<0 &{}\quad \text{ if }\,\, (\varepsilon ,\omega _0,r_0)\!\in \! \left\{ \left( 0.01,0.4473,r^-_j\right) :\,j\!\in \! \mathbb {N}_0\right\} ,\\ \omega _2>0 &{}\quad \text{ if }\,\, (\varepsilon ,\omega _0,r_0)\!\in \! \left\{ \left( 0.01,1.3416,r^+_j\right) :\,j\!\in \! \mathbb {N}_0\right\} , \end{array}\right. \end{aligned}$$

and

$$\begin{aligned} \left\{ \begin{array}{ll} \tau _2(0) < 0 &{}\quad \text{ if }\,\, (\varepsilon ,\omega _0,r_0)\\ &{}\quad \in \left\{ \left( 0.01,0.4473,r^-_j\right) :\,0 \le j \le 14\right\} ,\\ \tau _2(0) > 0 &{}\quad \text{ if }\,\, (\varepsilon ,\omega _0,r_0)\\ &{}\quad \in \left\{ \left( 0.01,1.3416,r^+_j\right) :\, 0 \le j \le 42\right\} . \end{array}\right. \end{aligned}$$

In view of Theorem 2, we have

Corollary 2

At the equilibrium point \((u,v)=(0,0)\) of system (26), Hopf bifurcation occurs as \(\tau \) crosses each of \(r^{+}_{j}\) (\(0\le j\le 42\)) and \(r^{-}_{s}\) (\(s\ge 15\)) to the right, and crosses each of \(r^{-}_{j}\) (\(0\le j\le 14\)) and \(r^{+}_{s}\) (\(s\ge 43\)) to the left. Moreover, the period of periodic solutions bifurcated from \((u,v,\tau )=(0,0,r^+_j)\) (respectively, \((u,v,\tau )=(0,0,r^-_j)\)) is less than \(\frac{2\pi }{\omega _{+}}\) (respectively, greater than \(\frac{2\pi }{\omega _{-}}\)).

In view of Theorem 3, we have

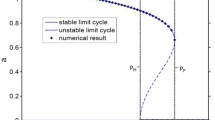
Corollary 3

For system (26), only the arising periodic solutions at \(\tau =r^+_0\) are stable, all the arising periodic solutions at \(\tau =r^+_j\) and \(\tau =r^-_s\) (\(j\in \mathbb {N}^+\) and \(s\in \mathbb {N}_0\)) are unstable.

Numerical simulations of system (26) with \(\tau =10\), \(\tau =80\), \(\tau =0.008,\tau =0.01\), and \(\tau =0.02\) are shown in Fig. 3 and 4.

Fig. 3
figure 3

Numerical simulations of system (26) with a \(\tau =10\) and b \(\tau =80\)

Full size image
Fig. 4
figure 4

Numerical simulations of (28) with a \(\tau \) = 0008, b \(\tau \) = 001, c \(\tau \) = 002

Full size image

4.2 Linear delay

For a linear delay \(\tau (x)=\alpha x+\beta \), where \(\tau (0)=\beta \) and \(|\beta -r_0|\ll 1\), then

$$\begin{aligned} \tau _2(0)=\frac{(\varepsilon r_0\omega _0-2\omega _0)e+(r_0-r_0\omega _0^2-\varepsilon )f}{\omega _0(\varepsilon ^2-2+2\omega _0^2)}A^2, \end{aligned}$$

where

$$\begin{aligned} e&= -(1-\omega _0^2)\alpha R_0+\left( \frac{2-2\omega _0^2}{k}+\frac{\varepsilon }{2}\right) \omega _0\alpha R_1\\&+\,\left( \frac{1-\omega _0^2}{2}+\frac{2\varepsilon \omega _0^2}{k}-\varepsilon k\right) \alpha R_2-\frac{\varepsilon }{4}+\frac{\alpha ^2}{8}\varepsilon \omega _0^2,\\ f&= \varepsilon \omega _0\alpha R_0+\left( \frac{1-\omega _0^2}{2}-\frac{2\varepsilon \omega _0^2}{k}+\varepsilon k\right) \alpha R_1\\&+\,\left( \frac{2-2\omega _0^2}{k}-\frac{\varepsilon }{2}\right) \omega _0\alpha R_2+\frac{3\alpha ^2}{8}\omega _0(1-\omega _0^2). \end{aligned}$$

We now present some numerical results of system (3) with \((\varepsilon ,k)=(0.01,80)\) and \(\tau (x)=2 x+\beta \). Namely, we consider the following model to verify the analytical predictions obtained in the previous discussion

$$\begin{aligned} \left\{ \begin{array}{l} \dot{u} = v,\\ \dot{v} =-u+0.01(1-u^2)v+0.8u(t-2 u(t)-\beta ). \end{array}\right. \end{aligned}$$
(27)

As stated in the previous subsection, some critical values of \(\beta \) are \(r^{-}_0=0.0125\), \(r^{+}_0=2.3292\), \(r^{-}_1=14.0617\), \(r^{+}_1=7.0125\), \(r^{+}_{15}=72.5795\), and the critical frequencies are \(\omega _+=1.3416\) and \(\omega _-=0.4473\). Numerical simulations of system (27) with \(\beta =2.3\), \(13\), \(13.5\), \(14\), \(20\), \(40\), \(50\), \(60\), \(70\), \(80\), \(90\), and \(100\), respectively, are shown in Figs. 5, 6, and 7. Most importantly, we see from Fig. 5 that the equilibrium point \((u,v)=(0,0)\) is not inside the region enclosed by a periodic orbit. This is different from the classical theory of planar dynamical systems.

Fig. 5
figure 5

Numerical simulations of (27) with a \(\beta =20\), b \(\beta =40\), c \(\beta =50\), d \(\beta =60\)

Full size image
Fig. 6
figure 6

Numerical simulations of (27) with a \(\beta =70\), b \(\beta =80\), c \(\beta =90\), d \(\beta =100\)

Full size image
Fig. 7
figure 7

Numerical simulations of  (27) with a \(\beta \) = 70, b \(\beta \) = 80, c \(\beta \) = 90, d \(\beta \) = 100

Full size image

4.3 Exponential delay

For a linear delay \(\tau (x)=\beta \exp (\alpha x)\),where \(\tau (0)=\beta \) and \(|\beta -r_0|\ll 1\), then

$$\begin{aligned} \tau _2(0)=\frac{(\varepsilon r_0\omega _0-2\omega _0)e+(r_0-r_0\omega _0^2-\varepsilon )f}{\omega _0(\varepsilon ^2-2+2\omega _0^2)}A^2, \end{aligned}$$

where

$$\begin{aligned} e&= \left( \frac{2-2\omega _0^2}{k}+\frac{\varepsilon }{2}\right) \omega _0\alpha \beta R_1\\&+\, \left( \frac{1-\omega _0^2}{2}+\frac{2\varepsilon \omega _0^2}{k}-\varepsilon k\right) \alpha \beta R_2-\frac{\varepsilon }{4}\\&+\,\frac{\alpha ^2\beta ^2}{8}\varepsilon \omega _0^2-(1-\omega _0^2)\alpha \beta \left( R_0+\frac{\alpha }{4}\right) ,\\ f&= \left( \frac{1-\omega _0^2}{2}-\frac{2\varepsilon \omega _0^2}{k}+\varepsilon k\right) \alpha \beta R_1\\&+ \left( \frac{2-2\omega _0^2}{k}-\frac{\varepsilon }{2}\right) \omega _0\alpha \beta R_2\\&+\,\frac{3\alpha ^2\beta ^2}{8}\omega _0(1-\omega _0^2)+\varepsilon \omega _0\alpha \left( R_0+\frac{\alpha }{4}\right) . \end{aligned}$$

We now present some numerical results of system (3) with \((\varepsilon ,k)=(0.01,80)\) and \(\tau (x)=\beta \exp (2x)\). Namely, we consider the following model to verify the analytical predictions obtained in the previous discussion

$$\begin{aligned} \left\{ \begin{array}{l} \dot{u} = v,\\ \dot{v} =-u+0.01(1-u^2)v+0.8u(t\!-\!\beta \exp (2u(t))). \end{array}\right. \end{aligned}$$
(28)

As stated in the previous subsection, some critical values of \(\beta \) are \(r^{-}_0=0.0125\), \(r^{+}_0=2.3292\), \(r^{-}_1=14.0617\), \(r^{+}_1=7.0125\), \(r^{+}_{15}=72.5795\), and the critical frequencies are \(\omega _+=1.3416\) and \(\omega _-=0.4473\). Numerical simulations of system (28) with \(\beta =0.06\), \(0.4\), \(3.5\), \(5\), \(10\), \(30\), \(50\), \(150\), \(280\), \(305\), respectively, are shown in Figs. 8 and 9.

Fig. 8
figure 8

Numerical simulations of (28) with a \(\beta \) =  006, b \(\beta \) =  04, c \(\beta \) =  35, d \(\beta \) =5

Full size image
Fig. 9
figure 9

Numerical simulations of (28) with a \(\beta \)  = 10, b \(\beta \)  = 30, \(\beta \) = 50, d \(\beta \)  = 150, e \(\beta \)  = 280, f \(\beta \)  = 30

Full size image

5 Conclusions

In this paper, we present a detailed study of Hopf bifurcation in the van der Pol equation with state-dependant delayed feedback. In studying the stability of equilibrium states, it has been shown [17] that the linear stability of an equilibrium can be analyzed by simply replacing the varying delay \(\tau \) by its value at the equilibrium. This is to say, the linear stability does not depend upon any other properties of the delay function \(\tau \). In this paper, however, we show that both the bifurcation direction and the stability of the bifurcating periodic solutions are strongly dependent on the precise form of the delay function \(\tau \). In fact, they are determined by the value of the delay function and its first two derivatives at the equilibrium. For any given delay function, it is possible to determine the parameter space for which periodic solutions near the steady states exist and to divide this into stable and unstable regions.

Obviously, there is a question that is worthy of further investigation. Liao et al. [21] investigated the linear stability and standard Hopf bifurcation for a van der Pol equation with a distributed time delay. By using the symmetric bifurcation theory of delay differential equations combined with representation theory of Lie groups, Song [22] investigated the spatio-temporal patterns of Hopf bifurcating periodic oscillations in a pair of van der Pol oscillators with delayed velocity coupling. Using the center manifold reduction technique, normal form theory, and symmetric bifurcation theory, Zang et al. [23] investigated the dynamics of a system of van der Pol–Duffing oscillators with delay coupling. Algaba et al. [24, 25] employed the normal form analysis to investigate high codimension bifurcations in a modified van der Pol-Duffing electronic circuit. Using the method of averaging to reduce the problem to the study of a slow flow in three dimensions, Wirkus and Rand [26] studied the dynamics of a pair of van der Pol oscillators where the coupling is chosen to be through the damping terms but not of diffusive type. Edelman and Gendelman [27] investigated the dynamical behavior in a system of two van der Pol oscillators coupled by non-dispersive elastic rod. In this paper, we only consider a single van der Pol oscillator with state-dependent delayed feedback. It is interesting to generalize our results in this paper to systems of van der Pol oscillators with state-dependent delayed coupling.