1 Introduction

All types of vegetables as well as crops are our main source of food but the land for planting those resources is limited. So we do not have the liberty to destroy even a single mole of food. But in nature many small insects, weeds, and animals are involved in maximum loss of the production of those invaluable crops. Further there are also so many fungi, bacteria, viruses etc. which cause harm by parasitizing the livestock of trees and plants. So it is easy to understand why the control of the pest is one of the biggest world wide problems. Most of the current pest control methods focused on chemical insecticides. According to Uboh et al. [1], the application of chemical insecticides is an attempt to control pest directly at low cost. However, research works have shown that these chemicals have many environmental effects that include chemical resides in crops and in the agricultural ecosystems. However, effective control of these pests can be obtained through the use of living organisms, making them less abundant.

It has been observed that there are so many animals and birds whose food are those pests but these creatures can not hamper the agriculture. Hence these populations can be used as one of the biological controls for the pest. Use of predator populations for the purpose of removing pest can be found in the research work [2–8] and references therein. Further the pest may be affected due to the infection of some viral or bacterial diseases. For an example baculovirus usually grows in plants and these virus has not any direct effect on the production of crops but they can be involved to reduce the pest population. When a baculovirus enters in the crop’s body it is not only causes its death but also make other pest infected during the contact with the infected pest (see [9–12]). Interactions among crop, pest, infection and the predator of pests were also studied in [13–15]. In their work, Anderson and May [16, 17] discussed the interactions between host and parasites. Tan and Chen [18] described the control of pest by introducing infected pest. Wang and Song [19] also used mathematical models to control a pest population by infected pests. Thus infection to the pest population is one of the ways which can be successfully used to eliminate them from agriculture. Further there are some theoretical works on prey–predator models with disease in the prey populations (see [20–27] and references therein) and these works are also very helpful to describe the dynamics of pest and its natural enemy. Some more theoretical works on pest control problem can also be formed in Wang et al. [28], Wang and Chen [29], Guo and Chen [30] and references there in.

In southern portion of India, both of coconut and oil palm trees are two of the most economically beneficial agricultural trees. But both trees are being heavily affected by the insect Oryctes rhinoceros. Central Plantation Crops Research Institute (CPCRI) found a virus namely BaculoVirus Oryctes (BVO) which can be used to destroy those pest populations (Gopal et al. [31]). So this BVO can be treated as one of the biological controls of the pest Oryctes rhinoceros. Hence it can be concluded that simultaneous use of pesticide control, the infection for the pest, and the use of biological predator population would be mostly effective strategy to control pest. But it is evident that the viral infection which spread within the pest also can be spread among the predators. On the other hand if the pest population is the only source of food to the predator then pest control may reduce the predator and even predator population may go extinct. So there must be an alternative source of food to the conserve the predator population.

Alternative source of food to the predator population in a prey–predator system plays an important role (see [32–36] etc.). However, to control pest, the effect of alternative food draws more attention than the ordinary predator–prey dynamics in the context of biological conservation. Alternative source of food must be given to the natural enemy of the pest for both the conservation of the predator and reduction of the pest. Srinivasu et al. [35] considered the use of alternative food as parallel source of food to the predator and it can choose either prey or that additional food. In our work, we are also interested to consider the influence of the alternative food to the predator population and here we want to consider both of pest and the alternative food as a double way to consume food i.e., a predator can consumes food from pest and the alternative source simultaneously.

Now we construct our mathematical model on the basis of the following assumptions:

(A1) At any time t, the pest populations are divided into two classes namely the susceptible pest S(t) and the infected pest I(t). Hence S(t)+I(t) is the total biomass of prey populations. Also let us assume that P(t) is the total biomass of the predator populations.

(A2) Between the two classes of pest, the susceptible pest population S is only able to reproduce following logistic law of growth with intrinsic growth rate r and environmental carrying capacity K. Therefore the change of biomass of S can be written as the following differential equation:

$$ \frac{dS}{dt} = r S \biggl(1-\frac{S+\eta I}{K} \biggr). $$
(1)

Here η is the impact of a predator individual on the per capita growth rate of a pest individual relative to the impact of a pest individual on its own per capita growth rate (see [19, 37, 38]).

(A3) Disease spread within the susceptible pest due to their direct contact with the infected pest and let α be the force of infection. The predator population consumes both the susceptible as well as infected pest but the infected pests are much more vulnerable to the predator as they are weak and so easy to catch whereas some handling time is required for the predation of the susceptible pests (see Kar et al. [8]). So we assume that the predator predates susceptible pests at a rate with Holling type II functional response βS/(a+S) where β is the maximum capturing rate and a is the half saturation constant, and infected pests with Holling type I functional response γI where γ is the maximum capturing rate. Further we assume that the death rate of infected pest is σ. Therefore the rate of change of susceptible and infected pest can be separated as follows:

$$ \begin{aligned} \frac{dS}{dt} &= r S \biggl(1- \frac{S+\eta I}{K} \biggr)-\alpha S I-\frac {\beta S P}{a+S}, \\ \frac{dI}{dt}&= \alpha S I-\gamma I P-\sigma I. \end{aligned} $$
(2)

(A4) Let l and m be the respective contributions of predator populations from the susceptible pest and infected pest. Further we assume that there is a negative effect nγI(n≥0) to the biomass of predator populations due to the infection from the infected pests. Also the natural death rate of the predator is μ and it has density dependent mortality rate δ. Therefore the rate of change for the predator population is as follows:

$$ \frac{dP}{dt} = \frac{l \beta S P}{a+S}+(m-n)\gamma I P -\mu P-\delta P^2. $$
(3)

(A5) The predator population is supplied some alternative source of food and the growth rate due to this food is d (see [32]). Thus the final differential equation for the predator population is as follows:

$$\begin{aligned} \frac{dP}{dt} =& \frac{l \beta S P}{a+S}+(m-n)\gamma I P +d \biggl(1- \frac{S+\eta I}{K} \biggr)P \\ &{}-\mu P-\delta P^2. \end{aligned}$$
(4)

Combining all of above assumptions we construct our final eco-epidemic system as follows:

$$ \begin{aligned} &\frac{dS}{dt} = r S \biggl(1- \frac{S+\eta I}{K} \biggr)-\alpha S I-\frac {\beta S P}{a+S}, \\ &\frac{dI}{dt}= \alpha S I-\gamma I P-\sigma I, \\ &\frac{dP}{dt}= \frac{l \beta S P}{a+S}+(m-n)\gamma I P +d \biggl(1- \frac {S+\eta I}{K} \biggr)P\\ &\hphantom{\frac{dP}{dt}=} {}-\mu P-\delta P^2, \end{aligned} $$
(5)

subject to the initial conditions

$$ S(0)\geq0,\qquad I(0)\geq0,\qquad P(0) \geq0. $$
(6)

The rest of the paper is organized as follows. In Sect. 2, we describe the dynamical behavior of the system theoretically and numerical illustrations are given in Sect. 3. In Sect. 4, we formulate and solve an optimal control problem with the help of time dependent pesticide control. Using the Runge–Kutta fourth order procedure we solve the optimal control problem numerically in Sect. 5. Finally, Sect. 6 presents the main conclusions and discusses their implications.

2 Dynamical behavior of the system

2.1 Boundedness of the system

The system (5) is uniformly bounded. Mathematical details are given in Appendix A.

2.2 Equilibria of the system

The system has the following equilibria:

  1. (i)

    The trivial equilibrium E 0(0,0,0).

  2. (ii)

    The boundary equilibrium E 1(K,0,0).

  3. (iii)

    The pest free equilibrium E 2(0,0,P 0), where P 0=(d−μ)/δ. This equilibrium is feasible if d>μ i.e., if the growth rate of predator population due to the alternative source of food is greater than their natural death rate and reduces to the trivial equilibrium E 0 if d≤μ.

  4. (iv)

    The infection free equilibrium E 3(S 1,0,P 1), where S 1 is the positive root of the following equation:

    $$ S^3+l_1S^2+l_2S+l_3=0, $$
    (7)

    with

    $$\begin{aligned} &{l_1=\frac{2ar \delta- d\beta-Kr\delta}{r\delta},}\\ &{l_2=\frac{a r\delta-a(d\beta+2Kr\delta)+\beta K(d+l\beta-\mu)}{r \delta},}\\ &{l_3=-\frac{aK(ar\delta+\beta\mu-d \beta)}{r \delta}} \end{aligned}$$

    and \(P_{1}=\frac{r}{\beta}(1-\frac{S_{1}}{K})(a+S_{1})\).

    Now the sufficient condition for which there is a positive root of (7) is a>K+(dβ)/(rδ). Moreover if Eq. (7) has no positive solution for S then the equilibrium E 3 reduces to the equilibrium E 2 provided d>μ.

  5. (v)

    The predator free equilibrium E 4(S 2,I 2,0), where S 2=σ/α and I 2=r(αK−σ)/(α(Kα+rη)). This equilibrium is feasible if σ<αK, otherwise this equilibrium reduces to the boundary equilibrium E 1(K,0,0).

  6. (vi)

    Lastly the interior equilibrium E ∗(S ∗,I ∗,P ∗), whose feasibility criterion is given in Appendix B.

2.3 Stability and bifurcation around different equilibria

2.3.1 Local stability

In the following theorem we draw conclusions regarding the asymptotic behavior of the trajectories of the system (5).

Theorem 2.1

The system (5) has the following behavior at different equilibria:

  1. (i)

    The trivial equilibrium E 0 is always unstable.

  2. (ii)

    The boundary equilibrium E 1(K,0,0) is locally asymptotically stable if σ>Kα and μ>Klβ/(a+K).

  3. (iii)

    The pest free equilibrium E 2(0,0,P 0) is locally asymptotically stable if d>μ+arδ/β.

  4. (iv)

    The infection free equilibrium E 3(S 1,0,P 1) is locally asymptotically stable if σ+γP 1>αS 1 and (a+S 1)2{μK+(2r+d)S 1}+P 1 K{a(β+2aδ)+2δS 1(2a+S 1)}>(a+S 1)K{(d+r)(a+S 1)+lβS 1}.

  5. (v)

    The predator free equilibrium E 4(S 2,I 2,0) is locally asymptotically stable if (αrηK)/(2rη+αK)<σ<αK and I 2<I 21/I 22, where I 21=aα{dσ+(μ−d)αK}+σ{αKμ+dσ−αK(d+lβ)} and I 22=α(aα+σ){(m−n)γK−dη}.

Next we study the behavior of the system around its interior equilibrium E ∗, where all the three classes of populations coexist. We have the following result concerning the existence and local stability of the interior equilibrium depending on the value of the parameter α:

  1. (i)

    There is a value of α, say, α max such that E ∗ does not exist for α>α max.

  2. (ii)

    The system is locally asymptotically stable at E ∗ when α∈(0,α cr) and unstable for α∈(α cr,α max].

  3. (iii)

    The system undergoes a Hopf bifurcation at E ∗ for α=α cr.

Detailed mathematical calculations of the above results are given in Appendix B.

2.3.2 Transcritical bifurcation

Theorem 2.2

The system (5) undergoes through a transcritical bifurcation around E 4(S 2,I 2,0) at σ=Kα provided the following three conditions are satisfied: (a) I 2<I 21/I 22, (b) \(\sigma>\frac{\alpha r \eta K}{2r \eta+\alpha K}\) and (c) \(\mu>\frac{K l \beta}{a+K}\).

Proof

The parametric conditions given in (a) and (b) along with σ<Kα are the sufficient conditions for the system (5) to be locally asymptotically stable around E 4. Again the parametric conditions given in (c) along with σ>Kα are the sufficient conditions for the system (5) to be locally asymptotically stable around E 1(K,0,0). Therefore we may conclude that a change of stability occurs through a bifurcation from equilibrium E 4 to E 1 for σ=Kα provided all the three parametric conditions (a), (b) and (c) hold. This type of bifurcation which occurs at E 4 for σ=Kα is known as a transcritical bifurcation (detailed mathematical works are given in Guckenheimer and Holmes [39], Kar and Mandol [40]). □

Note

The biological interpretation which follows from the above theorem is that, if the death rate of the infected pest is greater than the maximum possible recruitment of the infected pest at the carrying capacity of the susceptible pest then the equilibrium E 4 becomes infeasible and it reduces to the equilibrium E 1(K,0,0) provided all the three parametric conditions (a)–(c) are satisfied.

2.3.3 Global stability

First we give the sufficient condition for the equilibrium E 2 to be globally asymptotically stable as it is the most important equilibrium from economic point of view.

Theorem 2.3

The system is globally asymptotically stable around its pest free equilibrium if F min≥0, where

$$F_{\min}=\inf_{P}\bigl\{F(P)\bigr\} $$

and

$$\begin{aligned} F(P) =&\biggl\{(P-P_0)^2- \frac{1}{\delta K} \bigl(r K C_{11} \mu_{21}\\ &{}+dP_0 (\mu_{21}+\eta \mu_{22} ) \bigr)\biggr\}. \end{aligned}$$

Proof

To prove the global stability of the system around E 2, let us construct the Lyapunov function as follows:

$$ V_2(S,I,P)=A_1 S+B_1 I+C_1\int_{P_0}^P \frac{P-P_0}{P}\,dP, $$
(8)

where A 1, B 1, C 1 are positive constants to be determined in the subsequent steps.

Now taking the time derivative of (8), we have

$$\begin{aligned} \frac{dV_2}{dt} =&-C_1 \delta(P-P_0)^2\\ &{}+C_1 \biggl( \frac{l\beta S}{a+s} +(m-n)\gamma I-\frac{d}{K}(S+\eta I) \biggr)\\ &{}\times (P-P_0) +A_1 \biggl[rS \biggl(1-\frac{S+\eta I}{K} \biggr)\\ &{}-\alpha S I - \frac{\beta S P}{a+S} \biggr] +B_1 (\alpha S I -\gamma I P- \sigma I ). \end{aligned}$$

The above equation reduces to

$$\begin{aligned} \frac{dV_2}{dt} \le&\alpha(B_1-A_1) SI + \gamma \bigl((m-n)C_1-B_1 \bigr) I P \\ &{}+ (C_1 l-A_1 )\frac{\beta S P}{a+S}-\frac{S+\eta I}{K} \bigl(C_1d(P_0-P) \\ &{}-A_1rS \bigr) +ArS-B\sigma I -C_1\delta(P-P_0)^2. \end{aligned}$$

Now taking A 1=B 1=1 and C 1= min {1/(m−n),1/l}=1/C 11, (provided m>n) we have from the above inequality,

$$\begin{aligned} \frac{dV_2}{dt} \le&\frac{S+\eta I}{K} \biggl(\frac{d (P_0-P)}{C_{11}}-rS \biggr) +(rS-\sigma I) \\ &{}-\frac{\delta}{C_{11}} (P-P_0)^2. \end{aligned}$$
(9)

From (9) it is clear that dV 2/dt≤0 if

$$\begin{aligned} F(P) =&(P-P_0)^2 \\ &{}- \frac{1}{\delta K} \bigl(r K C_{11} \mu_{21}+dP_0 (\mu_{21}+\eta \mu_{22} ) \bigr) \\ \ge&0, \end{aligned}$$
(10)

i.e. if F min≥0. Hence the theorem. □

To describe the global dynamics of system (5) around the interior equilibrium E ∗, we state and prove the following theorem.

Theorem 2.4

The sufficient conditions for the system (5) to be globally asymptotically stable around its interior equilibrium E ∗ are (i) F 1(0) and F 2(0) are nonnegative and (ii) Kγn>dη+Kγn where

$$\begin{aligned} &{F_1(S)=\frac{r}{K}+\frac{C^*d}{2K}-\frac{\beta (2P^*+alC^*)}{2(a+S)(a+S^*)},}\\ &{F_2(S)=\delta+\frac{C^*d}{2K}-\frac{a\beta l C^*}{2(a+S)(a+S^*)}} \end{aligned}$$

with C ∗=Kγ/(α(Kγ(m−n)−dη)).

Proof

To show the globally asymptotic stability of the system around E ∗, let us construct a Lyapunov function as follows:

$$\begin{aligned} V(S,I,P) =&A\int_{S^*}^S \frac{S-S^*}{S}\,dS+B\int_{I^*}^I \frac{I-I^*}{I}\,dI \\ &{}+C\int_{P^*}^P \frac{P-P^*}{P}\,dP, \end{aligned}$$
(11)

where A, B, C are positive constants to be determined in the subsequent steps. Now taking the time derivative of (11) we get

$$\frac{dV}{dt}=A\frac{S-S^*}{S}\frac{dS}{dt}+B\frac{I-I^*}{I}\frac{dI}{dt}+C\frac{P-P^*}{P}\frac{dP}{dt}, $$

which on simplification gives

$$\begin{aligned} \frac{dV}{dt} =&-A \biggl(\frac{r}{K}-\frac{\beta P^*}{(a+S)(a+S^*)} \biggr) \bigl(S-S^*\bigr)^2\\ &{}-\delta \bigl(P-P^* \bigr)^2 - \biggl( \frac{Ar\eta}{K}+A\alpha-\alpha B \biggr)\\ &{}\times \bigl(S-S^*\bigr) \bigl(I-I^*\bigr)- \biggl(B\gamma -C(m-n)\gamma\\ &{}+\frac{Cd\eta}{K} \biggr) \bigl(I-I^*\bigr) \bigl(P-P^*\bigr)\\ &{} + \biggl[\frac{Cal\beta}{(a+S)(a+S^*)}-\frac{A\beta}{a+S}-\frac {Cd}{K} \biggr]\\ &{}\times \bigl(S-S^*\bigr) \bigl(P-P^*\bigr). \end{aligned}$$

Now let us choose B=1/α, A=K/(rη+αK)=A ∗ and C=Kγ/(α(Kγ(m−n)−dη))=C ∗ and take Kγn>dη+Kγn so that C ∗ would be positive. For these values of A, B, C and using arithmetic mean always greater than or equal to the value with the geometric mean, we have from the above equation,

$$ \frac{dV}{dt} \le-A F_1(S) \bigl(S-S^* \bigr)^2- F_2(S) \bigl(P-P^*\bigr)^2. $$
(12)

From (12) it is clear that if both of F 1(0) and F 2(0) are nonnegative then dV/dt would never be positive. Therefore, if the above conditions hold then the system (5) is globally asymptotically stable around its interior equilibrium E ∗. Hence the theorem. □

2.4 System with d=0

When d=0 i.e. when there is no alternative source of food to the predator population then the system (5) reduces to the following form:

$$ \begin{aligned} \frac{dS}{dt} &= r S \biggl(1- \frac{S+\eta I}{K} \biggr)-\alpha S I-\frac {\beta S P}{a+S}, \\ \frac{dI}{dt}&= \alpha S I-\gamma I P-\sigma I, \\ \frac{dP}{dt}&= \frac{l \beta S P}{a+S}+(m-n)\gamma I P -\mu P-\delta P^2, \end{aligned} $$
(13)

subject to the initial conditions

$$ S(0)\geq0,\quad I(0)\geq0,\quad P(0)\geq0. $$
(14)

Now it is easy to derive that except the pest free equilibrium E 2(0,0,(d−μ)/δ) the system (13) has the same equilibria and same nature as that of (5). If there is no alternative source of food then the main difference compare to the original system (5) is that in this case there would be no pest free equilibrium i.e. our original system confirms that predator populations are able to survive even in the absence of pests. Further during the process of controlling the pests, the predator also decreases due to the lack of food and even may not survive. So to protect those biological predators it is necessary to provide alternative source of food to them.

3 Numerical simulation and its discussion

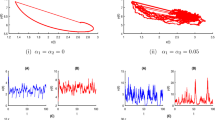
In this section we give some simulation works for the validation of our analytical results. For this purpose we take: r=2.1, η=1, K=50, β=0.36, a=0.21, γ=0.5, σ=0.15, l=0.5, m=0.3, n=0.15, d=0.6, μ=0.21, δ=0.11. Using this set of parameters, we get a critical value α cr=0.4041 such that for α<α cr, the system is locally asymptotically stable around the interior equilibrium E ∗ and there is another critical value α max=4.1305 such that for α∈[α cr,α max] the system (5) is unstable around E ∗ and is locally asymptotically stable around the pest free equilibrium E 2. Again for α>α max, the interior equilibrium does not exist and in this case the system is locally asymptotically stable around E 2. In Fig. 1, it is shown that the system (5) is asymptotically stable around interior equilibrium E ∗ for α<α cr. Now for α=0.3 with the above parameter set we see that the system is globally asymptotically stable around E ∗. In Fig. 2, we plot the phase portrait of the system (5) to show the global asymptotic stability around E ∗. In Figs. 3, 4, 5, and 6 it is shown that the system is unstable as α passes through α cr through a Hopf bifurcation.

Fig. 1
figure 1

Solution curve of the system around E ∗ for α=0.3<α cr

Full size image
Fig. 2
figure 2

Solution curve of the system (5) for α=0.3<α cr

Full size image
Fig. 3
figure 3

Oscillatory behavior for susceptible pest around E ∗ for α=0.5>α cr

Full size image
Fig. 4
figure 4

Oscillatory behavior for infected pest around E ∗ for α=0.5>α cr

Full size image
Fig. 5
figure 5

Oscillatory behavior for predator population around E ∗ for α=0.5>α cr

Full size image
Fig. 6
figure 6

Phase portrait of the system for α=0.5>α cr showing the oscillatory behavior of the system around E ∗

Full size image

In Fig. 7, it is shown that the system has asymptotic stable nature around the pest free equilibrium E 2 when the infection rate α∈[α cr,α max]and in Fig. 8, it is shown that if α>α max then the interior equilibrium does not exist but the system has stable behavior around E 2. However, it is quite difficult task to get theoretically the explicit values of both α cr and α max.

Fig. 7
figure 7

System is asymptotically stable around E 2 for α=0.5>α cr

Full size image
Fig. 8
figure 8

System has infeasible interior equilibrium E ∗ and asymptotic stable nature at E 2 for α=4.5>α max

Full size image

The above two figures (Figs. 7–8) clearly indicate that the system is locally asymptotically stable around E 2 for α>α cr and the interior equilibrium E ∗ is not feasible for α>α max.

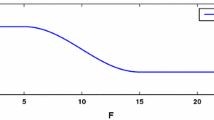
Next we examine the influence of the parameter α, the force of infection to the pest and their predators. In Fig. 9, we draw the effective changes of the biomass of both the classes of pests and predator as the force of infection varies. From the figure it is observed that as the force of infection increases, initially the susceptible pests reduces but the infected pest increases and then after a threshold value of α it reduces. Initially the predator population increases very fast as the force of infection increases and then it starts to decrease slowly due to unavailability of its main source of food (pest). After a certain value of the force of infection, the system would be pest free but even then there may be a predator in the system due to the presence of an alternative source of food.

Fig. 9
figure 9

Change of biomass of pest and their predator as the force of infection increases

Full size image

It is also clear from the Fig. 9, that for the above said parameter set, when α≥5, the system (5) would be pest free forever and if the force of infection increases more, then it has no effect on the system since then the predator is entirely depends on the alternative source of food. Further since the system becomes pest free, it cannot grow unless it has emigrated from other source.

Now we study the influence of the parameter n to the system (5). In Fig. 10, we give the changes of biomass of both types of the pest as well as their predator with respect to the parameter n, associated with the effect of infection for the predator. It is seen that both the susceptible pest and predator decreases but the infected pest increases with n. These phenomena happen due to the lower number of predator population, infected pest are increased due to low predation and susceptible to decrease due to higher infectious pests present in the system. But the predator population decreases as n increases and somewhere around n=0.526 predator population vanishes and after that system would be predator free although the system is not pest free. In Fig. 11 we represent the effect of infected pest on the predator population for different values of m and n.

Fig. 10
figure 10

Change of biomass of pest and their predator as n varies

Full size image
Fig. 11
figure 11

Change of biomass of predator with respect to the change of biomass of I for different m and n respectively

Full size image

In Fig. 12, we present the biomass of both the classes of pests and their predator as the parameter d changes for fixed α=0.3. For this α=0.3 both the population coexist in the system but the predator population increases as d increases. Now if the rate of infection becomes high, the pest population may go extinct as d increases although predator populations always exists in the system. In Fig. 13, it is shown that for α=5, the predator population increases up to d≤0.45 and thereafter it decreases slightly since for d=0.45 and α=5 the system would be pest free. But if d increases much (d≥0.52) then the predator population again started increasing due to availability of a sufficient amount of alternative food.

Fig. 12
figure 12

Change of biomass of pest and their predator as d varies

Full size image
Fig. 13
figure 13

Change of biomass of predator as d varies for α=5

Full size image

4 Formulation and application of optimal control problem

Throughout the previous sections we have described the dynamical behaviors of the system using only the biological control of pest, namely, the predator and infected pest. But it is not always possible to control the pest by using only such type of controls. So we need some other control measures. In this situation application of pesticides (both chemical and herbal) are very useful. In their recent works Ghosh and Bhattacharya [4], Kar et al. [8] also used pesticide controls to reduce the quantity of pest.

In this regard we modify our system (5) on the basis of the assumption that u be the quantity of pesticide controls that are used to the system and both the susceptible as well as infected pests are reduced by the amount of ϵ 1 uS and ϵ 2 uI, respectively. Here we assume that the pesticide control is more effective to the infected one than the susceptible one and so we take two different death rates namely ϵ 1 and ϵ 2 and generally the latter one is greater than the former. Further since the pesticide is in general some type of poisons, it affects, more or less, to the all creatures of the system and hence the predator population also be affected which is not considered in the work of Kar et al. [8]. We assume that due to the pesticide control u, the density of the predator population diminishes at a rate ϵ 3. Therefore the system (5) modified as follows:

$$ \begin{aligned} &\frac{dS}{dt} = r S \biggl(1- \frac{S+\eta I}{K} \biggr)-\alpha S I-\frac {\beta S P}{a+S}-\epsilon_1 u S, \\ &\frac{dI}{dt}= \alpha S I-\gamma I P-\sigma I-\epsilon_2 u I, \\ &\frac{dP}{dt}= \frac{l \beta S P}{a+S}+(m-n)\gamma I P +d \biggl(1- \frac {S+\eta I}{K} \biggr)P\\ &\hphantom{\frac{dP}{dt}=} {}-\mu P-\delta P^2-\epsilon_3 u P, \end{aligned} $$
(15)

subject to the initial conditions

$$ S(0)\geq0,\qquad I(0)\geq0,\qquad P(0)\geq0. $$
(16)

Furthermore this pesticide control u should be time dependent as it is used according to the necessity. Though in this section our primary objective is to reduce the quantity of pest by using pesticide, we have to keep in mind its harmful effect on the environment as well as its cost. Moreover, if it is used more, it may make the crops poisonous. Also some pesticides are so poisonous that its deadly effects would remain present to the crops for a long time even after the finish of the application and thus it directly affects the human body. So, to make the control of pests more economically and socially viable, it is required to use a proper mixture of pesticide and biological control. We should minimize the square of the applying pesticide so that we are able to minimize not only the application cost for the pesticide control but also the side effects of it (see Joshi et al. [41]).

Thus we form the objective functional of our optimal control problem as follows:

$$ J (S,I,P,u )=\min_{u}\int _0^{t_1}\; \bigl(v_{1}S+v_{2}I+v_{3}u^{2} \bigr)\,dt $$
(17)

subject to the system of differential equations (15) along with the initial conditions (16).

The objective functional J is a continuously differentiable function of state variables S,I,P and control variable u. With the help of Pontryagin’s maximum principle (Pontryagin et al. [42]), we get the necessary criteria to determine a positive value of the control for which the J is optimized. If this feasible control exists then it is known to be the optimal control (for further details see Clark [43], Lenhart and Workman [44] etc.).

Now our object is to find a control u ∗ such that

$$ J\bigl(u^{*}\bigr)=\min_{u\in\varOmega}J(u), $$
(18)

where Ω={u:is measurable and 0≤u(t)≤1 for t∈[0,t 1]} is the set for the controls. Here all the three weight factors v 1, v 2, and v 3 balance out the relative importance of the three terms in the objective functional and are known as the passive constants (for details see Bodine et al. [45]). However, v 1, v 2 are the weights taken corresponding to the susceptible and infected pest, respectively, and v 3 is associated with the square of the pesticide control. The square of the control parameter is taken to remove the harmful side effect of the pesticide (see Joshi [41], Kar and Batabyal [46, 47] etc.). According to the articles [46, 47], we may conclude that the nonnegative bounded solutions of the optimal control problem exists and to solve it we form the Lagrangian of our problem as follows:

$$ L (S,I,P,u )=v_{1}S+v_{2}I+v_{3}u^{2}. $$
(19)

To minimize the Lagrangian L let us now form the Hamiltonian of the problem as:

$$ H=L+\varPsi_{1}\frac{dS}{dt}+ \varPsi_{2}\frac{dI}{dt}+\varPsi_{3}\frac{dP}{dt}, $$
(20)

where Ψ i (t) for i=1,2,3 are known as the adjoint variables or the costate variables and they can be determined by solving the following system of differential equations:

$$\begin{aligned} &{\dot{\varPsi}_1 =- \frac{\partial H}{\partial S} =-v_{1}+ \biggl[\alpha I -r\biggl(1- \frac{2S+\eta I}{K}\biggr)} \\ &{\hphantom{\dot{\varPsi}_1 =} {}+\frac{a\beta P}{(a+S)^{2}}+\epsilon_{1} u \biggr] \varPsi_{1}- \alpha I \varPsi_{2}} \\ &{\hphantom{\dot{\varPsi}_1 =} {}+ \biggl(\frac{dP}{K}- \frac{l a \beta P}{(a+S)^{2}} \biggr)\varPsi_3,} \\ &{\dot{\varPsi}_2 =-\frac{\partial H}{\partial I} =-v_{2}+ \biggl( \alpha+\frac{r\eta}{K} \biggr)S \varPsi_{1}} \\ &{\hphantom{\dot{\varPsi}_2 =} {}+ (\gamma P -\alpha S + \sigma+\epsilon_2 u ) \varPsi_{2}}\\ &{\hphantom{\dot{\varPsi}_2 =} {}+ \biggl( \frac{d \eta}{K}-(m-n)\gamma \biggr) P \varPsi_{3},} \\ &{\dot{\varPsi}_3 =-\frac{\partial H}{\partial P} =\frac{\beta S}{a+S} \varPsi_{1}+\gamma I \varPsi_{2}} \\ &{\hphantom{\dot{\varPsi}_3 =} {}+ \biggl[\mu+2\delta P+ \epsilon_3 u-\frac{l\beta S}{a+S}-(m-n)\gamma I} \\ &{\hphantom{\dot{\varPsi}_3 =} {} -d \biggl(1- \frac{S+\eta I}{K} \biggr) \biggr]\varPsi_{3},} \end{aligned}$$
(21)

satisfying the transversality conditions

$$ \varPsi_{i}(t_{1})=0,\quad i=1,2,3. $$
(22)

We assume that \(\hat{S}\), \(\hat{I}\), \(\hat{P}\) are the optimum value of S, I, P respectively. Also let \(\hat{\varPsi}_{1}\), \(\hat{\varPsi}_{2}\), \(\hat{\varPsi}_{3}\) be the solutions of the system (21).

Now following the results in Lukes [48] and Chakraborty et al. [49], we state and prove the following theorem.

Theorem 4.1

There is an optimal control u ∗(t) for t∈[0,t 1] such that

$$J\bigl(S(t), I(t), u^{*}(t)\bigr)= \min_{u} J\bigl(S(t), I(t),u(t)\bigr) $$

subject to the system of differential equations (15).

Proof

Here the control variable u(t) is convex since all the state and control variables are non negative. Furthermore the control space Θ is also closed and convex. Hence the optimal control is bounded and therefore the existence of an optimal control u ∗(t), which minimizes (17) for t∈[0,t 1] is established.

With the help of Pontryagin’s Maximum Principle (see Pontryagin et al. [42]) and Theorem 4.1, we are now ready to state and prove the following theorem. □

Theorem 4.2

The optimal control u ∗ which minimizes J over the region Θ is given by

$$u^{*}=\max \bigl\{0,\min(\bar{u},1) \bigr\} $$

where \(\bar{u}=(\varPsi_{1}\epsilon_{1}S+\varPsi_{2}\epsilon_{2}I +\varPsi_{3} \epsilon_{3} P)/(vV_{3})\).

Proof

According to the optimality condition we have ∂H/∂u=0 and it gives us u=(Ψ 1 ϵ 1 S+Ψ 2 ϵ 2 I+Ψ 3 ϵ 3 P)/(2v 3). It is obvious that this control u should be bounded; respective upper and lower bounds are 1 and 0. This means that u=0, whenever \(\bar{u} \le0\) whereas u=1 whenever \(\bar{u} \ge1\) and in the rest period of time \(u=\bar{u}\). Combining these results we have the theorem. □

5 Numerical simulations for the optimal control problem

Since our problem is not based on a case study, for the simulation purposes, we take a simulated set of parameters as P 1={r,η,K,α,β,a,ϵ 1,γ,σ,ϵ 2,l,m,n,d,μ,δ,ϵ 3}={2.1,1,50,0.3,0.36,0.21,1,0.5,0.15,2,0.5,0.3,0.15,0.84,0.21,0.11,0.01}. Furthermore since in this problem our aim is to minimize pest, so we take both the weights v 1 and v 2 as 1. Also we take v 3 as 0.1 unit as it associated with the cost for killing a single pest which will be very low. We apply this control in 100 units of time that may be either in days or in weeks or even in months. Thus we set t 1 as 100. Next we take the initial guess for the susceptible pest, infected pest and predator as 5, 3, and 2, respectively.

Now we solve the optimal control problem numerically using Runge–Kutta fourth order iterative method. For the state variables, first we solve the system (15) by forward Runge-Kutta fourth order procedure and then using those state values we solve the system (21) by using backward fourth order Runge–Kutta procedure (see [44, 50–53] etc.). In Fig. 14, we represent the solution curves of the three state variables both in the presence and absence of the control. It is observed that the application of optimal control reduces a quite larger number of pests than in the absence of the control. Again from the figure it is easy to see that the predator population also much affected due to the use of the pesticide control. This is occurring as the application of pesticide control reduces the pest population significantly and the predator population primarily depends on pest for their food. Thus we may conclude that application of the optimal pesticide control not only reduces the number of pest population but also reduces the predator populations.

Fig. 14
figure 14

Variation of state variables both in the presence and absence of control

Full size image

Figure 15 represents the variation of optimal control and in Fig. 16, we draw the variation of adjoint variables in the presence control. From Fig. 15, it is observed that the control would be optimal if it is used at its highest level for almost first 95 units of time.

Fig. 15
figure 15

Variation of the optimal control

Full size image
Fig. 16
figure 16

Variation of adjoint variables in the presence of control

Full size image

Figure 17 is obtained by increasing 40 % value of d when the optimal control is applied. This is done as the application of control reduces pest and hence reduces predator, so for biological conservation it is necessary to supply more additional food to predator.

Fig. 17
figure 17

Variation of state variables (when control is applied then amount of alternative food is 40 % greater than the without control case)

Full size image

6 Discussion and conclusions

In recent agro-ecosystems, pest control is a world wide problem because of the increasing human population. In addition today there is no proper method for controlling pest population. Therefore effective pest control strategy has a high impact on society. In this paper we make systematic approach for controlling pest population by using combination of three possible ways namely (i) effective use of predator population, (ii) release of infection among the pest population and (iii) use of chemical or herbal pesticide. Our mathematical model is a predator–prey type system with three state variables namely the susceptible pest S, the infected pest I, and the biological predator to the pest P. Moreover we consider that there is an alternative source of food to the predator species to protect themselves when the availability of the pest population would be very less or negligible. It is shown that if the growth rate of the predator due to the alternative source of food is greater than the natural death rate of the predator then the predator population never goes extinct. This ensures that it is possible to protect the predator population by providing appropriate additional food.

It has been shown that the system (5) is always uniformly bounded and therefore all the solutions entirely lie in the positive region. We make a systematic analysis of the dynamics of the system by examining the nature of the system around all its six feasible equilibria. The boundary equilibrium E 1(K,0,0) is locally asymptotically stable depending on the value of the environmental carrying capacity K, infection rate α and the death rate of infected σ. Also it is interesting to observe that the sufficient condition for the predator free equilibrium E 4(S 2,I 2,0) to be feasible is that the boundary equilibrium E 1 is unstable (see Sect. 2). Also the infection free equilibrium E 3(S 1,0,P 1) may be conditionally feasible as well as locally asymptotically stable and as S 1 increases this equilibrium reduces to the boundary equilibrium E 1(K,0,0), through a possible transcritical bifurcation. We have also discussed the existence and stability criteria of the interior equilibrium E ∗. It is shown that the higher infection rate makes the interior equilibrium unstable and the pest free equilibrium locally asymptotically stable. Further increase of infection rate may make the system pest free.

From an economical point of view, E 2(0,0,P 0) is the most important equilibrium since if the system (5) goes to this equilibrium then the system becomes pest free but the biological predator remains in the system. It is established that if the maximum growth of the predator due to the alternative food is greater than the natural death rate of the predator plus a threshold quantity then the system becomes locally asymptotically stable around the pest free equilibrium E 2 and thus the system would be pest free. Another interesting observation is that the present system contains no equilibrium of the form (0,I,P) although the system has both types of pest free equilibrium E 2(0,0,P 0) and the infection free equilibrium E 3(S 1,0,P 1). This phenomenon is occurring in the system due to the facts that infectious pests have neither reproduction power nor recovery. Therefore if the susceptible pest goes extinct then the infectious pests also go extinct and thus the system becomes pest free. Thus to make the system pest free it is sufficient to make the system free from the susceptible pest.

In this paper the additional food is assumed to be either non reproducing prey or some food source. We only assume that the predator is capable of reproducing by consuming either of the available food, and we discuss about the quantity of food only when relevant to understanding model or predict. The role of additional food is very much important in relevance to pest control because it is not only help to protect predator population when the pest population is not sufficient, but also it helps to reduce pest population if it is huge amount. It occurs since manipulating non-target prey can influence the predator in a way that increases target predation and eventually controls the prey populations. But from the point of view of biological conservation of the predator, when there is a sufficient amount of pest then additional food does not have so much importance in the system. In these context we do claim that the model and its prediction both are important from the biological point of view.

In agro-ecosystem though the use of pesticide is, however, a good process to remove the pest, its application cost and environmental lost should be taken into account. In this point of view we form an optimal control problem including all those items. As it is expected, optimal use of pesticide control reduces the pest as well as predator population. But it is seen that if the amount of alternative food is increased by 40 % then application of optimal control increases biomass of predator populations compared to the no control cases although the pest population decreases. Thus it is a measure that to protect the predator population the amount of alternative food should be increased when the pesticide control is applied optimally (see Fig. 17).

In the present problem we include the cost for the deadly effects of the pesticide in optimal control problem. More use of poisonous pesticides not only pollutes the environment but also the causes of several diseases like skin problems, health problems etc. But there are several eco-friendly herbal pesticides which should be used in place of the harmful chemical insecticides. Thus there must be a proper balance between the chemical and herbal pesticides in order to reduce cost and the environmental loss.

The numeric analysis deprives us of the possibility of drawing conclusions on a general level, however, a thorough analysis clearly indicates that the interactions between pest and its predator do matter when the provision of additional food to the predator and use of pesticide control is considered. All the simulation works in this present article are considered from a qualitative, rather than a quantitative point of view. However, numerous scenarios which cover the breath of the biological feasible parameter space are conducted. This study offers insight into the possible management strategies that involve manipulation of supply level of additional food to predators.