1 Introduction

The typical feature of chaotic systems is that a very small change in the initial conditions leads to very large differences in the system states. Since Pecora and Carroll completed the pioneering work about synchronization between two chaotic systems [1, 2], Chaos synchronization has been driven a lot of attention and studied extensively in a variety of research fields during the last two decades. A variety of approaches have been developed for the synchronization of chaotic systems, such as complete synchronization [3], phase synchronization [4, 5], anti-synchronization [6], partial synchronization [7], generalized synchronization [8], lag synchronization [9, 10], Q-S synchronization [11] and projective synchronization [12–14], etc.

However, most of researchers mainly focused on the previous drive-response synchronization schemes within one driven system and one response system model, did not consider three or more chaotic systems. Recently, an active backstepping design has proposed to achieve combination synchronization between two drive systems and one response system [15, 16]. To the best of authors’ knowledge, however, research on the synchronization problem among three or more chaotic systems is still open and remains challenging.

Motivated by the above discussions, synchronization between combination of two drive systems and combination of two response systems in drive-response synchronization model is investigated in this paper, which can be seen combination–combination synchronization. Four identical Lü systems and four different chaotic systems (Lorenz system, Rössler system, Chen’s system and Lü system) are realized by adaptive control, respectively. Numerical simulations are discussed to show the effectiveness and feasibility of the proposed method.

The organization of this work is organized as follows. Section 2 shows a scheme of combination–combination synchronization. In Sect. 3, the synchronization among four identical Lü systems is realized by our control design. In Sect. 4, we investigate the synchronization among four different chaotic systems. Finally, concluding remarks are given in Sect. 5.

2 The scheme of combination–combination synchronization

In the section, we firstly design the scheme of combination–combination synchronization in our drive–response synchronization scheme with two drive systems and two response systems. The two drive systems are, respectively, given as follows:

(1)
(2)

and the two response systems are, respectively, described as follows:

(3)
(4)

where x 1=(x 11,x 12,…,x 1n ), x 2=(x 21,x 22,…,x 2n ), y 1=(y 11,y 12,…,y 1n ) and y 2=(y 21,y 22,…,y 2n ) are the state vectors of systems (1), (2), (3) and (4), respectively; f 1, f 2, g 1, g 2: R n→R n are four continuous vector functions, u, u ∗: R n×R n×R n×R n→R n are two controllers of the response systems (3) and (4) which will be designed, respectively.

Definition 1

If there exist four constant matrices A, B, C, D∈R n and C≠0 or D≠0 such that

$$ \lim_{t\rightarrow\infty}\|Ax_1+Bx_2-Cy_1-Dy_2 \|=0, $$
(5)

the drive systems (1) and (2) are realized combination-combination synchronization with the response systems (3) and (4), where ∥⋅∥ represents the matrix norm.

Remark 1

The constant matrices A, B, C, D are called the scaling matrices. In addition, A, B, C, D can be extended to functional matrices of state variables x 1, x 2, y 1 and y 2.

Remark 2

If C=0 or D=0, then combination–combination synchronization problem will be reduced to the combination synchronization problem.

Remark 3

If A=0, C=I, D=0 or A=C=0, D=I or B=0, C=I, D=0 or B=C=0, D=I, then the combination synchronization problem will be reduced to the projective synchronization, where I is a n×n identity matrix.

Remark 4

If A=0, C=−I, D=0 or A=C=0, D=−I or B=0, C=−I, D=0 or B=C=0, D=−I, then the combination synchronization problem will be reduced to the projective anti-synchronization.

Remark 5

If the scaling matrix A=B=C=0 or A=B=D=0, then the combination synchronization will be turned into a chaos control problem.

Remark 6

Definition 1 shows that the combination of drive systems and response systems can be extended to three or more chaotic systems. In addition, drive systems and response systems of the combination can be identical or different.

3 Synchronization among four identical chaotic systems

In this section, we can realize combination-combination synchronization among four identical Lü systems. The two Lü systems are, respectively, given as the drive systems as follows:

(6)
(7)

where the Lü systems exhibits a chaotic attractor at parameters a 1=a 2=36, b 1=b 2=3 and c 1=c 2=20, and the two Lü systems are, respectively, described as the response systems as follows:

(8)
(9)

where u 1, u 2, u 3, \(u_{1}^{*}\), \(u_{2}^{*}\) and \(u_{3}^{*}\) are controllers to be designed.

For the convenience of our discussions, we assume \(A=\operatorname {diag}(\alpha_{1}, \alpha_{2}, \alpha_{3})\), \(B=\operatorname {diag}(\beta_{1}, \beta_{2}, \beta_{3})\), \(C=\operatorname {diag}(\gamma_{1}, \gamma_{2}, \gamma_{3})\), \(D=\operatorname {diag}(\delta_{1}, \delta_{2}, \delta_{3})\) in our synchronization scheme. We get the error system as follows:

$$ \begin{cases} e_{1}=\alpha_1x_{11}+\beta_1x_{21}-\gamma_1y_{11}-\delta_1y_{21},\\[3pt] e_{2}=\alpha_2x_{12}+\beta_2x_{22}-\gamma_2y_{12}-\delta_2y_{22},\\[3pt] e_{3}=\alpha_3x_{13}+\beta_3x_{23}-\gamma_3y_{13}-\delta_3y_{23}.\\ \end{cases} $$
(10)

Denote

$$ \begin{cases} U_1=\gamma_1{u}_1+\delta_1{u}_1^{*},\\[3pt] U_2=\gamma_2{u}_2+\delta_2{u}_2^{*},\\[3pt] U_3=\gamma_3{u}_3+\delta_3{u}_3^{*}.\\ \end{cases} $$
(11)

Theorem 1

If the combination control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} U_1&=&\alpha_1x_{11}+\beta_1x_{21}-\gamma_1y_{11}-\delta_1y_{21}+a_1(\alpha_2x_{12}\\[5pt] &&{}+\beta_2x_{22}-\gamma_2y_{12}-\delta_2y_{22})+\alpha_1a_1(x_{12}-x_{11})\\[5pt] &&{}+\beta_1a_2(x_{22}-x_{21})-\gamma_1a_3(y_{12}-y_{11})\\[5pt] &&{}-\delta_1a_4(y_{22}-y_{21}),\\[5pt] U_2&=&\alpha_2x_{12}+\beta_2x_{22}-\gamma_2y_{12}-\delta_2y_{22}-a_1(\alpha_3x_{13}\\[5pt] &&{}+\beta_3x_{23}-\gamma_3y_{13}-\delta_3y_{23})-a_1(\alpha_1x_{11}\\[5pt] &&{}+\beta_1x_{21}-\gamma_1y_{11}-\delta_1y_{21})+\alpha_2(c_1x_{11}\\[5pt] &&{}-x_{11}x_{13})+\beta_2(c_2x_{21}-x_{21}x_{23})-\gamma_2(c_3y_{11}\\[5pt] &&{}-y_{11}y_{13})-\delta_2(c_3y_{11}-y_{11}y_{13}),\\[5pt] U_3&=&\alpha_3x_{13}+\beta_3x_{23}-\gamma_3y_{13}-\delta_3y_{23}+a_1(\alpha_2x_{12}\\[5pt] &&{}+\beta_2x_{22}-\gamma_2y_{12}-\delta_2y_{22})+\alpha_3(x_{11}x_{12}\\[5pt] &&{}-c_1x_{13})+\beta_3(x_{21}x_{22}-b_2x_{23})-\gamma_3(y_{11}y_{12}\\[5pt] &&{}-b_3y_{13})-\delta_3(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(12)

then the drive systems (6) and (7) will achieve combination–combination synchronization with the response systems (8) and (9).

Proof

It is easy to see from (10) that the error dynamics system can be obtained as follows:

$$ \left \{ \begin{array}{@{}lll} \dot{e}_{1}&=&\alpha_1a_1(x_{12}-x_{11})+\beta_1a_2(x_{22}-x_{21})\\[5pt] &&{}-\gamma_1[a_3(y_{12}-y_{11})+u_1]\\[5pt] &&{}-\delta_1[a_4(y_{22}-y_{21})+u_1^{*}],\\[5pt] \dot{e}_{2}&=&\alpha_2(c_1x_{11}-x_{11}x_{13})+\beta_2(c_2x_{21}-x_{21}x_{23})\\[5pt] &&{}-\gamma_2(c_3y_{11}-y_{11}y_{13}+u_2)\\[5pt] &&{}-\delta_2(c_4y_{21}-y_{21}y_{23}+u_2^{*}),\\[5pt] \dot{e}_{3}&=&\alpha_3(x_{11}x_{12}-c_1x_{13})+\beta_3(x_{21}x_{22}-b_2x_{23})\\[5pt] &&{}-\gamma_3(y_{11}y_{12}-b_3y_{13}+u_3)\\[5pt] &&{}-\delta_3(y_{21}y_{22}-b_4y_{23}+u_3^{*}).\\ \end{array} \right . $$
(13)

Choose a candidate Lyapunov function as follows:

$$ V(e_1,e_2,e_3)=\frac{1}{2} \bigl(e_1^2+e_2^2+e_3^2 \bigr). $$
(14)

Then

(15)

Substitute (12) into (15),

(16)

Since \(\dot{V} \leq0\) as t→+∞, according to the Lyapunov theorem, we know e i →0 (i=1,2,3), which means that the drive systems (6) and (7) will achieve combination-combination synchronization with the response systems (8) and (9). □

The following corollaries are easily obtained from Theorem 1, and their proofs are similar to Theorem 1, so the processes will be omitted here.

Corollary 1

(i) Assume δ 1=δ 2=δ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1&=&\frac{1}{\gamma_1}[(\alpha_1x_{11}+\beta_1x_{21}-\gamma_1y_{11})+a_1(\alpha_2x_{12}\\[7pt] &&{}+\beta_2x_{22}-\gamma_2y_{12})+\alpha_1a_1(x_{12}-x_{11})\\[7pt] &&{}+\beta_1a_2(x_{22}-x_{21})]-a_3(y_{12}-y_{11}),\\[7pt] {u}_2&=&\frac{1}{\gamma_2}[(\alpha_2x_{12}+\beta_2x_{22}-\gamma_2y_{12})-a_1(\alpha_3x_{13}\\[7pt] &&{}+\beta_3x_{23}-\gamma_3y_{13})-a_1(\alpha_1x_{11}+\beta_1x_{21}\\[7pt] &&{}-\gamma_1y_{11})+\alpha_2(c_1x_{11}-x_{11}x_{13})+\beta_2(c_2x_{21}\\[7pt] &&{}-x_{21}x_{23})]-(c_3y_{11}-y_{11}y_{13}),\\[7pt] {u}_3&=&\frac{1}{\gamma_3}[\alpha_3x_{13}+\beta_3x_{23}-\gamma_3y_{13}+a_1(\alpha_2x_{12}\\[7pt] &&{}+\beta_2x_{22}-\gamma_2y_{12})+\alpha_3(x_{11}x_{12}-c_1x_{13})\\[7pt] &&{}-\beta_3(x_{21}x_{22}-b_2x_{23})]-(y_{11}y_{12}-b_3y_{13}), \end{array} \right . $$
(17)

then the drive systems (6) and (7) will achieve combination synchronization with the response system (8).

(ii) Assume γ 1=γ 2=γ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1^{*}&=&\frac{1}{\delta_1}[(\alpha_1x_{11}+\beta_1x_{21}-\delta_1y_{21})\\[7pt] &&{}+a_1(\alpha_2x_{12}+\beta_2x_{22}-\delta_2y_{22})\\[7pt] &&{}+\alpha_1a_1(x_{12}-x_{11}) +\beta_1a_2(x_{22}-x_{21})]\\[7pt] &&{}-a_4(y_{22}-y_{21}),\\[7pt] {u}_2^{*}&=&\frac{1}{\delta_2}[(\alpha_2x_{12}+\beta_2x_{22}-\delta_2y_{22})-a_1(\alpha_3x_{13}\\[7pt] &&{}+\beta_3x_{23}-\delta_3y_{23})-a_1(\alpha_1x_{11}+\beta_1x_{21}\\[7pt] &&{}-\delta_1y_{21})+\alpha_2(c_1x_{11}-x_{11}x_{13})\\[7pt] &&{}+\beta_2(c_2x_{21}-x_{21}x_{23})]\\[7pt] &&{}-(c_3y_{11}-y_{11}y_{13}),\\[7pt] {u}_3^{*}&=&\frac{1}{\delta_3}[\alpha_3x_{13}+\beta_3x_{23}-\delta_3y_{23}+a_1(\alpha_2x_{12}\\[7pt] &&{}+\beta_2x_{22}-\delta_2y_{22})+\alpha_3(x_{11}x_{12}-c_1x_{13})\\[7pt] &&{}+\beta_3(x_{21}x_{22}-b_2x_{23})]\\[7pt] &&{}-(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(18)

then the drive systems (6) and (7) will achieve combination synchronization with the response system (9).

Corollary 2

(i) Assume β 1=β 2=β 3=0, γ 1=γ 2=γ 3=1 and δ 1=δ 2=δ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1&=&(\alpha_1x_{11}-y_{11})+a_1(\alpha_2x_{12}-y_{12})\\[6pt] &&{}+\alpha_1a_1(x_{12}-x_{11})-a_3(y_{12}-y_{11}),\\[6pt] {u}_2&=&(\alpha_2x_{12}-y_{12})-a_1(\alpha_3x_{13}-y_{13})\\[6pt] &&{}-a_1(\alpha_1x_{11}-y_{11})+\alpha_2(c_1x_{11}-x_{11}x_{13})\\[6pt] &&{}-(c_3y_{11}-y_{11}y_{13}),\\[6pt] {u}_3&=&\alpha_3x_{13}-y_{13}+a_1(\alpha_2x_{12}-y_{12})\\[6pt] &&{}+\alpha_3(x_{11}x_{12}-c_1x_{13})\\[6pt] &&{}-(y_{11}y_{12}-b_3y_{13}), \end{array} \right . $$
(19)

then the drive system (6) will achieve the projective synchronization with the response system (8).

(ii) Assume α 1=α 2=α 3=0, γ 1=γ 2=γ 3=1 and δ 1=δ 2=δ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1&=&(\beta_1x_{21}-y_{11})+a_1(\beta_2x_{22}-y_{12})-x_{11})\\[5pt] &&{}+\beta_1a_2(x_{22}-x_{21})-a_3(y_{12}-y_{11}),\\[5pt] {u}_2&=&(\beta_2x_{22}-y_{12})-a_1(\beta_3x_{23}-y_{13})\\[5pt] &&{}-a_1(\beta_1x_{21}-y_{11})+\beta_2(c_2x_{21}-x_{21}x_{23})\\[5pt] &&{}-(c_3y_{11}-y_{11}y_{13}),\\[5pt] {u}_3&=&\beta_3x_{23}-y_{13}+a_1(\beta_2x_{22}-y_{12})-\beta_3(x_{21}x_{22}\\[5pt] &&{}-b_2x_{23})-(y_{11}y_{12}-b_3y_{13}), \end{array} \right . $$
(20)

then the drive system (7) will achieve the projective synchronization with the response system (8).

(iii) Assume β 1=β 2=β 3=0, γ 1=γ 2=γ 3=0 and δ 1=δ 2=δ 3=1, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1^{*}&=&\alpha_1x_{11}-y_{21}+a_1(\alpha_2x_{12}-y_{22})\\[5pt] &&{}+\alpha_1a_1(x_{12}-x_{11})-a_4(y_{22}-y_{21}),\\[5pt] {u}_2^{*}&=&\alpha_2x_{12}-y_{22}-a_1(\alpha_3x_{13}-y_{23})\\[5pt] &&{}-a_1(\alpha_1x_{11}-y_{21})+\alpha_2(c_1x_{11}-x_{11}x_{13})\\[5pt] &&{}-(c_3y_{11}-y_{11}y_{13}),\\[5pt] {u}_3^{*}&=&\alpha_3x_{13}-y_{23}+a_1(\alpha_2x_{12}-y_{22})+\alpha_3(x_{11}x_{12}\\[5pt] &&{}-c_1x_{13})-(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(21)

then the drive system (6) will achieve the projective synchronization with the response system (9).

(iv) Assume α 1=α 2=α 3=0, γ 1=γ 2=γ 3=0 and δ 1=δ 2=δ 3=1, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1^{*}&=&\beta_1x_{21}-y_{21}+a_1(\beta_2x_{22}-y_{22})\\[5pt] &&{}+\beta_1a_2(x_{22}-x_{21})-a_4(y_{22}-y_{21}),\\[5pt] {u}_2^{*}&=&\beta_2x_{22}-y_{22}-a_1(\beta_3x_{23}-y_{23})\\[5pt] &&{}-a_1(\beta_1x_{21}-y_{21})+\beta_2(c_2x_{21}-x_{21}x_{23})\\[5pt] &&{}-(c_3y_{11}-y_{11}y_{13}),\\[5pt] {u}_3^{*}&=&\beta_3x_{23}-y_{23}+a_1(\beta_2x_{22}-y_{22})+\beta_3(x_{21}x_{22}\\[5pt] &&{}-b_2x_{23})-(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(22)

then the drive system (7) will achieve the projective synchronization with the response system (9).

Corollary 3

(i) Suppose α 1=α 2=α 3=0, β 1=β 2=β 3=0, γ 1=γ 2=γ 3=1 and δ 1=δ 2=δ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1&=&-y_{11}-a_1y_{12}+a_1(x_{12}-x_{11})\\[6pt] &&{}-a_3(y_{12}-y_{11}),\\[6pt] {u}_2&=&-y_{12}+a_1y_{13}+a_1y_{11}-(c_3y_{11}-y_{11}y_{13}),\\[6pt] {u}_3&=&-y_{13}-a_1y_{12}-(y_{11}y_{12}-b_3y_{13}), \end{array} \right . $$
(23)

then the equilibrium point (0,0,0) of the response system (8) is asymptotically stable.

(ii) Suppose α 1=α 2=α 3=0, β 1=β 2=β 3=0, γ 1=γ 2=γ 3=0 and δ 1=δ 2=δ 3=1, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}l} {u}_1^{*}=-y_{21}-a_1y_{22}-a_4(y_{22}-y_{21}),\\[6pt] {u}_2^{*}=-y_{22}+a_1y_{23}+a_1y_{21}-(c_3y_{11}-y_{11}y_{13}),\\[6pt] {u}_3^{*}=-y_{23}-a_1y_{22}-(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(24)

then the equilibrium point (0,0,0) of the response system (9) is asymptotically stable.

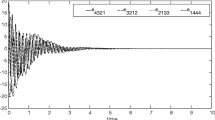
Numerical experiments are given to demonstrate our results. Fourth-order Runge–Kutta method is used with time step size 0.001. In the simulation process, we assume α 1=α 2=α 3=1, β 1=β 2=β 3=1, γ 1=γ 2=γ 3=1 and δ 1=δ 2=δ 3=1, and the initial states for the drive systems and response systems are arbitrarily given by (x 11,x 12,x 13)=(0.5,1,1.5), (x 21,x 22,x 23) = (1,1,2), (y 11,y 12,y 13) = (−4,5,−6) and (y 21,y 22,y 23)=(−5,25,1). The corresponding numerical results are shown in Fig. 1–4. Figure 1 displays time response of the synchronization error e=(e 1,e 2,e 3)T. The error vector converges to zero which implies that systems (6), (7) and (8), (9) have achieved combination–combination synchronization. Figures 2, 3 and 4 depict the time response of the states x 11+x 21 and y 11+y 21, x 12+x 22 and y 12+y 22, x 13+x 23 and y 13+y 23 of the drive systems (6), (7) and the response systems (8), (9), respectively.

Fig. 1
figure 1

Synchronization errors e 1,e 2,e 3 between drive systems (6), (7) and response systems (8), (9)

Full size image
Fig. 2
figure 2

Response for states x 11+x 21 and y 11+y 21 between drive systems (6), (7) and response systems (8), (9)

Full size image
Fig. 3
figure 3

Response for states x 12+x 22 and y 12+y 22 between drive systems (6), (7) and the response systems (8), (9)

Full size image
Fig. 4
figure 4

Response for states x 13+x 23 and y 13+y 23 between drive systems (6), (7) and response systems (8), (9)

Full size image

4 Synchronization among four different chaotic systems

In this section, we can realize the combination–combination synchronization among four different chaotic systems. The Lorenz system and Rössler system are, respectively, described as the drive systems as follows:

(25)
(26)

where the Lorenz system and Rössler system exhibit chaotic behavior at parameters a 1=10, b 1=28, c 1=2.667 and a 2=0.2, b 2=0.2, c 2=5.7, respectively, and Chen’s system and Lü system are given, respectively, as the response systems as follows:

(27)
(28)

where the Chen system and Lü system exhibit chaotic behavior at parameters a 3=35, b 3=3, c 3=28 and a 4=36, b 4=3, c 4=20, respectively, u 1, u 2, u 3, \(u_{1}^{*}\), \(u_{2}^{*}\) and \(u_{3}^{*}\) are controllers to be designed.

For the convenience of our discussions, we assume \(A=\operatorname {diag}(\alpha_{1}, \alpha_{2}, \alpha_{3})\), \(B=\operatorname {diag}(\beta_{1}, \beta_{2}, \beta_{3})\), \(C=\operatorname {diag}(\gamma_{1}, \gamma_{2}, \gamma_{3})\), \(D=\operatorname {diag}(\delta_{1}, \delta_{2}, \delta_{3})\) in our synchronization scheme. We can have the error system as follows:

$$ \left \{ \begin{array}{@{}l} e_{1}=\alpha_1x_{11}+\beta_1x_{21}-\gamma_1y_{11}-\delta_1y_{21},\\[7pt] e_{2}=\alpha_2x_{12}+\beta_2x_{22}-\gamma_2y_{12}-\delta_2y_{22},\\[7pt] e_{3}=\alpha_3x_{13}+\beta_3x_{23}-\gamma_3y_{13}-\delta_3y_{23}. \end{array} \right . $$
(29)

Denote

$$ \left \{ \begin{array}{@{}l} U_1=\gamma_1{u}_1+\delta_1{u}_1^{*},\\[7pt] U_2=\gamma_2{u}_2+\delta_2{u}_2^{*},\\[7pt] U_3=\gamma_3{u}_3+\delta_3{u}_3^{*}. \end{array} \right . $$
(30)

Theorem 2

If the control laws combination are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} U_1&=&(\alpha_1x_{11}+\beta_1x_{21}-\gamma_1y_{11}-\delta_1y_{21})-a_1(\alpha_2x_{12}\\[6pt] &&{}+\beta_2x_{22}-\gamma_2y_{12}-\delta_2y_{22})+\alpha_1a_1(x_{12}-x_{11})\\[6pt] &&{}+\beta_1(-x_{22}-x_{23})-\gamma_1a_3(y_{12}-y_{11})\\[6pt] &&{}-\delta_1a_4(y_{22}-y_{21}),\\[6pt] U_2&=&(\alpha_2x_{12}+\beta_2x_{22}-\gamma_2y_{12}-\delta_2y_{22})+a_1(\alpha_1x_{11}\\[6pt] &&{}+\beta_1x_{21}-\gamma_1y_{11}-\delta_1y_{21})-a_4(\alpha_3x_{13}\\[6pt] &&{}+\beta_3x_{23}-\gamma_3y_{13}-\delta_3y_{23})+\alpha_2(b_1x_{11}-x_{12}\\[6pt] &&{}-x_{11}x_{13})+\beta_2(x_{21}+a_2x_{22})\\[6pt] &&{}-\gamma_2[(c_3-a_3)y_{11}+c_3y_{12}-y_{11}y_{13}]\\[6pt] &&{}-\delta_2(c_4y_{21}-y_{21}y_{23}),\\[6pt] U_3&=&\alpha_3x_{13}+\beta_3x_{23}-\gamma_3y_{13}-\delta_3y_{23}+a_4(\alpha_2x_{12}\\[6pt] &&{}+\beta_2x_{22}-\gamma_2y_{12}-\delta_2y_{22})+\alpha_3(x_{11}x_{12}\\[6pt] &&{}-c_1x_{13})+\beta_3[b_2+x_{23}(x_{22}-c_2)]\\[6pt] &&{}-\gamma_3(y_{11}y_{12}-b_3y_{13}) -\delta_3(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(31)

then the drive systems (25) and (26) will achieve combination–combination synchronization with the response systems (27) and (28).

Proof

It is easy to see from (29) that the error dynamics system can be obtained as follows:

$$ \left \{ \begin{array}{@{}lll} \dot{e}_{1}&=&\alpha_1a_1(x_{12}-x_{11})+\beta_1a_2(x_{22}-x_{21})\\[6pt] &&{}-\gamma_1[a_3(y_{12}-y_{11})+u_1]\\[6pt] &&{}-\delta_1[a_4(y_{22}-y_{21})+u_1^{*}],\\[6pt] \dot{e}_{2}&=&\alpha_2(c_1x_{11}-x_{11}x_{13})+\beta_2(c_2x_{21}-x_{21}x_{23})\\[6pt] &&{}-\gamma_2(c_3y_{11}-y_{11}y_{13}+u_2)-\delta_2(c_4y_{21}\\[6pt] &&{}-y_{21}y_{23}+u_2^{*}),\\[6pt] \dot{e}_{3}&=&\alpha_3(x_{11}x_{12}-c_1x_{13})+\beta_3(x_{21}x_{22}-b_2x_{23})\\[6pt] &&{}-\gamma_3(y_{11}y_{12}-b_3y_{13}+u_3)-\delta_3(y_{21}y_{22}\\[6pt] &&{}-b_4y_{23}+u_3^{*}). \end{array} \right . $$
(32)

Choose a candidate Lyapunov function as follows:

$$ V(e_1,e_2,e_3)=\frac{1}{2} \bigl(e_1^2+e_2^2+e_3^2 \bigr). $$
(33)

Then

(34)

Substitute (31) into (34),

(35)

Since \(\dot{V} \leq0\) as t→+∞, according to the Lyapunov theorem, we know e i →0 (i=1,2,3), which means that the drive systems (25) and (26) will achieve combination–combination synchronization with the response systems (27) and (28). □

The following corollaries are easily obtained from Theorem 2, and their proofs are similar to Theorem 2, so the processes will be omitted here.

Corollary 4

(i) Assume δ 1=δ 2=δ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1&=&\frac{1}{\gamma_1}[(\alpha_1x_{11}+\beta_1x_{21}-\gamma_1y_{11}-\delta_1y_{21})\\[5pt] &&{}-a_1(\alpha_2x_{12}+\beta_2x_{22}-\gamma_2y_{12})+\alpha_1a_1(x_{12}\\[5pt] &&{}-x_{11})+\beta_1(-x_{22}-x_{23})]-a_3(y_{12}-y_{11}),\\[5pt] {u}_2&=&\frac{1}{\gamma_2}[(\alpha_2x_{12}+\beta_2x_{22}-\gamma_2y_{12})+a_1(\alpha_1x_{11}\\[5pt] &&{}+\beta_1x_{21}-\gamma_1y_{11})-a_4(\alpha_3x_{13}+\beta_3x_{23}\\[5pt] &&{}-\gamma_3y_{13})+\alpha_2(b_1x_{11}-x_{12}-x_{11}x_{13})\\[5pt] &&{}+\beta_2(x_{21}+a_2x_{22})]-[(c_3-a_3)y_{11}\\[5pt] &&{}+c_3y_{12}-y_{11}y_{13}],\\[5pt] {u}_3&=&\frac{1}{\gamma_3}\{\alpha_3x_{13}+\beta_3x_{23}-\gamma_3y_{13}+a_4(\alpha_2x_{12}\\[5pt] &&{}+\beta_2x_{22}-\gamma_2y_{12})+\alpha_3(x_{11}x_{12}-c_1x_{13})\\[5pt] &&{}+\beta_3[b_2+x_{23}(x_{22}-c_2)]\}\\[5pt] &&{}-(y_{11}y_{12}-b_3y_{13}), \end{array} \right . $$
(36)

then the drive systems (25) and (26) will achieve combination synchronization with the response system (27).

(ii) Assume γ 1=γ 2=γ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1^{*}&=&\frac{1}{\delta_1}[(\alpha_1x_{11}+\beta_1x_{21}-\delta_1y_{21})-a_1(\alpha_2x_{12}\\[7pt] &&{}+\beta_2x_{22}-\delta_2y_{22})+\alpha_1a_1(x_{12}-x_{11})\\[7pt] &&{}+\beta_1(-x_{22}-x_{23})]-a_4(y_{22}-y_{21}),\\[7pt] {u}_2^{*}&=&\frac{1}{\delta_2}[(\alpha_2x_{12}+\beta_2x_{22}-\delta_2y_{22})+a_1(\alpha_1x_{11}\\[7pt] &&{}+\beta_1x_{21}-\delta_1y_{21})-a_4(\alpha_3x_{13}+\beta_3x_{23}\\[7pt] &&{}-\delta_3y_{23})+\alpha_2(b_1x_{11}-x_{12}-x_{11}x_{13})\\[7pt] &&{}+\beta_2(x_{21}+a_2x_{22})]-(c_4y_{21}-y_{21}y_{23}),\\[7pt] {u}_3^{*}&=&\frac{1}{\delta_3}\{\alpha_3x_{13}+\beta_3x_{23}-\delta_3y_{23}+a_4(\alpha_2x_{12}\\[7pt] &&{}+\beta_2x_{22}-\delta_2y_{22})+\alpha_3(x_{11}x_{12}-c_1x_{13})\\[7pt] &&{}+\beta_3[b_2+x_{23}(x_{22}-c_2)]\}\\[7pt] &&{}-(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(37)

then the drive systems (25) and (26) will achieve combination synchronization with the response system (28).

Corollary 5

(i) Assume β 1=β 2=β 3=0, γ 1=γ 2=γ 3=1 and δ 1=δ 2=δ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1&=&\alpha_1x_{11}-y_{11}-\delta_1y_{21}-a_1(\alpha_2x_{12}-y_{12})\\[6pt] &&{}+\alpha_1a_1(x_{12}-x_{11})-a_3(y_{12}-y_{11}),\\[6pt] {u}_2&=&\alpha_2x_{12}-y_{12}+a_1(\alpha_1x_{11}-y_{11})-a_4(\alpha_3x_{13}\\[6pt] &&{}-y_{13})+\alpha_2(b_1x_{11}-x_{12}-x_{11}x_{13})\\[6pt] &&{}-[(c_3-a_3)y_{11}+c_3y_{12}-y_{11}y_{13}],\\[6pt] {u}_3&=&\alpha_3x_{13}-y_{13}+a_4(\alpha_2x_{12}-y_{12})\\[6pt] &&{}+\alpha_3(x_{11}x_{12}-c_1x_{13})-(y_{11}y_{12}-b_3y_{13}), \end{array} \right . $$
(38)

then the drive system (25) will achieve the projective synchronization with the response system (27).

(ii) Assume α 1=α 2=α 3=0, γ 1=γ 2=γ 3=1 and δ 1=δ 2=δ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1&=&(\beta_1x_{21}-y_{11}-\delta_1y_{21})-a_1(\beta_2x_{22}-y_{12})\\[5pt] &&{}+\beta_1(-x_{22}-x_{23})-a_3(y_{12}-y_{11}),\\[5pt] {u}_2&=&(\beta_2x_{22}-y_{12})+a_1(\beta_1x_{21}-y_{11})\\[5pt] &&{}-a_4(\beta_3x_{23}-y_{13})+\beta_2(x_{21}+a_2x_{22})\\[5pt] &&{}-[(c_3-a_3)y_{11}+c_3y_{12}-y_{11}y_{13}],\\[5pt] {u}_3&=&\beta_3x_{23}-y_{13}+a_4(\beta_2x_{22}-y_{12})+\beta_3[b_2\\[5pt] &&{}+x_{23}(x_{22}-c_2)]-(y_{11}y_{12}-b_3y_{13}), \end{array} \right . $$
(39)

then the drive system (26) will achieve the projective synchronization with the response system (27).

(iii) Assume β 1=β 2=β 3=0, γ 1=γ 2=γ 3=0 and δ 1=δ 2=δ 3=1, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1^{*}&=&(\alpha_1x_{11}-a_1(\alpha_2x_{12}-y_{22})\\[5pt] &&{}+\alpha_1a_1(x_{12}-a_4(y_{22}-y_{21}),\\[5pt] {u}_2^{*}&=&(\alpha_2x_{12}-y_{22})+a_1(\alpha_1x_{11}-y_{11})\\[5pt] &&{}-a_4(\alpha_3x_{13}-y_{23})+\alpha_2(b_1x_{11}-x_{12}\\[5pt] &&{}-x_{11}x_{13})-(c_4y_{21}-y_{21}y_{23}),\\[5pt] {u}_3^{*}&=&\alpha_3x_{13}-y_{23}+a_4(\alpha_2x_{12}-y_{22})\\[5pt] &&{}+\alpha_3(x_{11}x_{12}-c_1x_{13})-(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(40)

then the drive system (25) will achieve the projective synchronization with the response system (28).

(iv) Assume α 1=α 2=α 3=0, γ 1=γ 2=γ 3=0 and δ 1=δ 2=δ 3=1, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1^{*}&=&(\beta_1x_{21}-y_{21})-a_1(\beta_2x_{22}-y_{22})\\[5pt] &&{}+\beta_1(-x_{22}-x_{23})-a_4(y_{22}-y_{21}),\\[5pt] {u}_2^{*}&=&(\beta_2x_{22}-y_{22})+a_1(\beta_1x_{21}-y_{21})\\[5pt] &&{}-a_4(\beta_3x_{23}-y_{23})+\beta_2(x_{21}+a_2x_{22})\\[5pt] &&{}-(c_4y_{21}-y_{21}y_{23}),\\[5pt] {u}_3^{*}&=&\beta_3x_{23}-y_{23}+a_4(\beta_2x_{22}-y_{22})\\[5pt] &&{}+\beta_3[b_2+x_{23}(x_{22}-c_2)]\\[5pt] &&{}-(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(41)

then the drive system (26) will achieve the projective synchronization with the response system (28).

Corollary 6

(i) Suppose α 1=α 2=α 3=0, β 1=β 2=β 3=0, γ 1=γ 2=γ 3=1 and δ 1=δ 2=δ 3=0, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}lll} {u}_1&=&-y_{11}-\delta_1y_{21}+a_1y_{12}-a_3(y_{12}-y_{11}),\\[5pt] {u}_2&=&-y_{12}-a_1y_{11}+a_4y_{13}-[(c_3-a_3)y_{11}\\[5pt] &&{}+c_3y_{12}-y_{11}y_{13}],\\[5pt] {u}_3&=&-y_{13}-a_4y_{12}-(y_{11}y_{12}-b_3y_{13}), \end{array} \right . $$
(42)

then the equilibrium point (0,0,0) of the response system (27) is asymptotically stable.

(ii) Suppose α 1=α 2=α 3=0, β 1=β 2=β 3=0, γ 1=γ 2=γ 3=0 and δ 1=δ 2=δ 3=1, if the control laws are chosen as follows:

$$ \left \{ \begin{array}{@{}l} {u}_1^{*}=-y_{21}+a_1y_{22}-a_4(y_{22}-y_{21}),\\[5pt] {u}_2^{*}=-y_{22}-a_1y_{21}+a_4y_{23}-(c_4y_{21}-y_{21}y_{23}),\\[5pt] {u}_3^{*}=-y_{23}-a_4y_{22}-(y_{21}y_{22}-b_4y_{23}), \end{array} \right . $$
(43)

then the equilibrium point (0,0,0) of the response system (28) is asymptotically stable.

Numerical experiments are given to illustrate our results. Fourth-order Runge–Kutta method is used with time step size 0.001. In the simulation process, we assume α 1=α 2=α 3=1, β 1=β 2=β 3=1, γ 1=γ 2=γ 3=1 and δ 1=δ 2=δ 3=1, and the initial states for the drive systems and response systems are arbitrarily given by (x 11,x 12,x 13)=(0.5,1,1.5), (x 21,x 22,x 23) = (1,1,2), (y 11,y 12,y 13) = (−4,5,−6) and (y 21,y 22,y 23)=(−5,25,1). The corresponding numerical results are shown in Figs. 5–8. Figure 5 displays the time response of synchronization error e=(e 1,e 2,e 3)T. The error vector converges to zero which implies that systems (25), (26) and (27), (28) have achieved combination–combination synchronization. Figures 6, 7 and 8 depict the time response of the states x 11+x 21 and y 11+y 21, x 12+x 22 and y 12+y 22, x 13+x 23 and y 13+y 23 of the drive systems (25), (26) and the response systems (27), (28), respectively.

Fig. 5
figure 5

Synchronization errors e 1,e 2,e 3 between drive systems (25), (26) and response systems (27), (28)

Full size image
Fig. 6
figure 6

Response for states x 11+x 21 and y 11+y 21 between drive systems (25), (26) and response systems (27), (28)

Full size image
Fig. 7
figure 7

Response for states x 12+x 22 and y 12+y 22 between drive systems (25), (26) and response systems (27), (28)

Full size image
Fig. 8
figure 8

Response for states x 13+x 23 and y 13+y 23 between drive systems (25), (26) and response systems (27), (28)

Full size image

5 Conclusion

In this paper, we propose a new type of synchronization with two drive systems and two response systems, which can be seen this synchronization as combination-combination synchronization. Based on Lyapunov stability theorem and adaptive control, some sufficient conditions for combination–combination synchronization of four identical or different chaotic systems are obtained. Numerical simulations are shown to verify the feasibility and effectiveness of the proposed control technique.

Although the combination synchronization of chaotic system has more advantages than synchronization between one drive system and one response system, it appears that one response system may be a disadvantage. Combination–combination synchronization is designed to overcome the trouble of combination synchronization. Most of the previous proposed adaptive synchronization are included as its special items. The combination of all the chaotic systems is regarded as the drive or response systems, such that we can design a universal combination drive systems and response systems model and a universal adaptive controller. According to our actual requirements, we choose the corresponding system or systems combination, the corresponding parameter values are given to the drive systems and response systems to realize synchronization. Too much time and energy are saved for our future every application. If synchronization can be controlled intelligently at will, then it may be possible to attain vastly better performance for secure communication and information processing.