1 Introduction

Synchronization of chaotic systems has been intensively investigated over the past two decades and lots of theoretical results have been obtained [1,2,3,4,5]. The potential interdisciplinary applications in physics, biological systems, electrical engineering, information processing, communication theory and many other fields have been extensively explored in the literature on chaos synchronization [6,7,8,9,10]. Due to the diverse nature of the chaotic systems, many types of synchronization methods have been proposed and investigated in the past years such as complete synchronization [11,12,13], antisynchronization [14, 15], projective synchronization [16,17,18], lag synchronization [19,20,21], phase synchronization [22, 23], reduced order synchronization [24, 25], increased order synchronization [26, 27], etc. Moreover, to achieve chaos synchronization, various methods have been developed and widely studied including active control method [28, 29], adaptive control method [30, 31], sliding mode control [32, 33], active backstepping method [34, 35].

Most of the work in chaos synchronization, upto now, has been restricted to the synchronization studies between one drive system–one response system model. The synchronization problem among three or more chaotic systems is still a relatively unexplored area of research and deserves investigation. In the recent years, new ideas have been initiated in the study of chaos synchronization wherein three or more chaotic systems are involved. Synchronization schemes such as combination synchronization [36,37,38,39], combination–combination synchronization [40,41,42,43], compound synchronization [44, 45], double compound synchronization [46], compound–combination synchronization [47, 48] etc. have recently been presented. In addition to their own intrinsic interest, these schemes are significant in enhancing the security of information transmitted via chaotic signals because of the complexity which they bring in transmitted signal.

Recently, Sun et al introduced the scheme of compound synchronization among four chaotic systems in [44]. In this method, the drive system is divided into two categories: Scaling drive system and base drive system. The scaling drive system scales the signals of two base drive systems, generating resultant signals. Then the response system is synchronized with the resultant signals. This scheme of compound synchronization is an extension and improvement of the existing synchronization schemes in the literature. In the existing literature on compound synchronization, the corresponding state variables of the drive systems have been combined to form a resultant signal which is in turn synchronized with the corresponding state variable of the response system.

Multiswitching synchronization was first proposed by Ucar et al in [49]. In the multiswitching synchronization scheme, different states of the drive system are synchronized with different state of the response system. Thus, a wide range of possible synchronization directions exist for multiswitching synchronization schemes. The relevance of this kind of synchronization schemes to information security makes them a very interesting topic to be explored. A few studies of this kind have been reported in the literature [50,51,52]. Almost the entire reported work in multiswitching synchronization relates to single drive and single response system. Only recently, multiswitching combination synchronization scheme involving multiple chaotic drive and response systems has been reported [53,54,55,56]. Nevertheless, the diverse possibilities of multiswitching synchronization have not been investigated yet with regards to compound synchronization involving three drive systems.

Motivated by the above discussions, in this paper, we present a new multiswitching compound antisynchronization (MSCoAS) scheme, wherein three drive chaotic systems are multiswitched in various manner to form a resultant signal which is then antisynchronized with some state variable of a single response chaotic system. To the best of our knowledge, multiswitching synchronization study involving four chaotic systems has not been reported before. Using Lyapunov stability theory and nonlinear controllers we propose sufficient condition for achieving MSCoAS. Numerical simulations have been performed to illustrate and verify the effectiveness of the proposed method. The main contributions of this study are: (a) The multiswitching scheme is extended to three drive and one response system and generalized for a class of chaotic systems. (b) The transmitted resultant compound signal is very complex and will thus provide improved performances for secure communication and information processing. (c) Suitable controllers are constructed which, in special cases, adjust themselves accordingly to achieve novel modified function projective antisynchronization where the scaling factor is a chaotic system.

The paper is organized as follows. In §2 the formulation of MSCoAS is stated. In §3, three Lorenz multidrive chaotic systems are compound antisynchronized with Lorenz response chaotic system in multiswitched compound manner. Numerical simulations are performed to validate the scheme in §4. Finally, the conclusions are given in §5.

2 Formulation of multiswitching compound antisynchronization problem

In this section, we formulate the scheme of MSCoAS of chaotic systems. We need three chaotic drive systems and one response system. Let the scaling drive system be described by

$$\begin{aligned} \dot{x}=f_1(x) \end{aligned}$$
(1)

and the base drive systems be given by

$$\begin{aligned} \dot{y}&=f_2(y), \end{aligned}$$
(2)
$$\begin{aligned} \dot{z}&=f_3(z). \end{aligned}$$
(3)

The response system is given by

$$\begin{aligned} \dot{w}=g(w)+u. \end{aligned}$$
(4)

Here \(x=(x_{1}, x_{2}, x_{3}, ..., x_{n})^T\), \(y=(y_{1}, y_{2}, y_{3}, ..., y_{n})^T\), \(z=(z_{1}, z_{2}, z_{3}, ..., z_{n})^T\), and \(w=(w_{1}, w_{2}, w_{3}, ..., w_{n})^T\) are state vectors of systems (1)–(4) respectively; \(f_1=(f_{11}, f_{12}, f_{13}, ..., f_{1n})^T\), \(f_2=(f_{21}, f_{22}, f_{23}, ..., f_{2n})^T\), \(f_3=(f_{31}, f_{32}, f_{33}, ..., f_{3n})^T\), and \(g=(g_{1}, g_{2}, g_{3}, ..., g_{n})^T\) are four continuous vector functions, \(u=(u_1, u_2, ..., u_n)^T: R^n \times R^n \times R^n \times R^n \rightarrow R^n\) are controllers to be designed for the response system (4). To solve the compound antisynchronization problem the error is defined as \(e=AX(BY+CZ)+DW\).

DEFINITION 1

If there exist four constant diagonal matrices \(A, B, C, D \in R^{n \times n}\) and \(D \ne 0\) such that

$$\begin{aligned} \lim _{t \rightarrow \infty } \Vert e \Vert = \lim _{t \rightarrow \infty } \Vert AX(BY+CZ)+DW \Vert = 0, \end{aligned}$$
(5)

where \(\Vert \cdot \Vert \) is the matrix norm, then the drive systems (1)–(3) are said to be in compound antisynchronization with the response system (4). Here we assume \(X=\mathrm {diag}(x_{1}, x_{2}, x_{3}, ..., x_{n})\), \(Y=\mathrm {diag}(y_{1}, y_{2}, y_{3}, ..., y_{n})\), \(Z=\mathrm {diag}(z_{1}, z_{2}, z_{3}, ..., z_{n})\), and \(W=\mathrm {diag}(w_{1}, w_{2}, w_{3}, ..., w_{n})\). The constant matrices \(A, \, B, \, C, \, D\) are called the scaling matrices, drive system (1) is called the scaling drive system and drive systems (2) and (3) are called the base drive systems.

Remark 1

In Definition 1 the state vectors \(x=(x_{1}, x_{2}, x_{3}, ..., x_{n})^T\), \(y=(y_{1}, y_{2}, y_{3}, ..., y_{n})^T\), \(z=(z_{1}, z_{2}, z_{3}, ..., z_{n})^T\), and \(w=(w_{1}, w_{2}, w_{3}, ..., w_{n})^T\) are designed as four diagonal matrices \(X=\mathrm {diag}(x_{1}, x_{2}, x_{3}, ..., x_{n})\), \(Y=\mathrm {diag}(y_{1}, y_{2}, y_{3}, ..., y_{n})\), \(Z=\mathrm {diag}(z_{1}, z_{2}, z_{3}, ..., z_{n})\) and \(W=\mathrm {diag}(w_{1}, w_{2}, w_{3}, ..., w_{n})\) respectively. Observe that by this definition error is obtained as a diagonal matrix

$$\begin{aligned} e= & {} \mathrm {diag}(e_{1}, e_{2}, e_{3}, ..., e_{n})\nonumber \\= & {} AX(BY+CZ)+DW. \end{aligned}$$
(6)

Remark 2

If \(A=\mathrm {diag}(\alpha _1, \alpha _2, \alpha _3, ..., \alpha _n)\), \(B=\mathrm {diag} (\beta _1, \beta _2, \beta _3, ..., \beta _n)\), \(C=\mathrm {diag}(\gamma _1, \gamma _2, \gamma _3, ..., \gamma _n)\), and \(D=\mathrm {diag}(\delta _1, \delta _2, \delta _3, ..., \delta _n)\) then eq. (5) is equivalent to saying that compound antisynchronization is achieved between systems (1) and (4) when

$$\begin{aligned} \lim _{t \rightarrow \infty } e_l=\lim _{t \rightarrow \infty } [\alpha _ix_i(\beta _jy_j+\gamma _kz_k)+\delta _lw_l ]=0, \end{aligned}$$
(7)

where \(e=\mathrm {diag}(e_1, e_2, e_3, ..., e_n)\) and \(l = 1, 2, ..., n\).

Remark 3

Let us rewrite the components of e as

$$\begin{aligned} e_{l_{(ijkl)}} = \alpha _ix_i(\beta _jy_j+\gamma _kz_k)+\delta _lw_l, \end{aligned}$$
(8)

where \(e=(e_{1_{(ijkl)}}, e_{2_{(ijkl)}}, e_{3_{(ijkl)}}, ..., e_{n_{(ijkl)}})^T\), \(i, j, k, l = 1, 2, ..., n\) and the subscript (ijkl) denotes the ith component of x, jth component of y, kth component of z, and lth component of w. In relation to Definition 1, the indices (ijkl) of the error states \(e_{l_{(ijkl)}}\) are strictly chosen to satisfy \(i = j = k = l \,(i,j,k,l = 1,2,...,n)\).

DEFINITION 2

If the indices of the error states in (7) are redefined such that \(i=j=k \ne l\) or \(i=j=l \ne k\) or \(i=k=l \ne j\) or \(j=k=l \ne i\); or \(i=j \ne k=l\) or \(i=k \ne j=l\) or \(i=l \ne j=k\); or \(i=j \ne k \ne l\) or \(i=k \ne j \ne l\) or \(i=l \ne k \ne j\) or \(i \ne j=k \ne l\) or \(i \ne j \ne k=l\) or \(i \ne k \ne j=l\); or \(i \ne j \ne k \ne l\) and

$$\begin{aligned} \lim _{t \rightarrow \infty } e=\lim _{t \rightarrow \infty } \Vert AX(BY+CZ)+DW \Vert = 0, \end{aligned}$$
(9)

where \(i, j, k, l = 1, 2, ..., n\), then the drive systems (1)–(3) are said to be in multiswitching compound antisynchronization with the response system (4).

Remark 4

If \(A\ne 0\), \(B=0\) or \(C=0\), and \(D\ne 0\) then the MSCoAS will be turned into a novel type of switched modified function projective antisynchronization where the scaling factor is a chaotic system. Thus, the compound of two drive systems can synchronize a response system in multiswitching manner.

3 Synchronization theory

In this section, we achieve multiswitching compound antisynchronization among three chaotic drive systems (1)–(3) and one chaotic response system (4). Let the control functions be defined as

$$\begin{aligned} u_l=-\frac{1}{\delta _l}\phi _l-g_l-\frac{1}{\delta _l}Ke, \quad {i, j, k, l=1, 2, ..., n}, \end{aligned}$$
(10)

where

$$\begin{aligned} \phi _l= & {} \alpha _1f_{1i}(\beta _jy_j+\gamma _kz_k)+\alpha _ix_i(\beta _jf_{2j}+\gamma _kf_{3k}), \nonumber \\&{l, j, k, l =1, 2, ..., n} \end{aligned}$$
(11)

and \(K=(K_1, K_2, K_3, ..., K_n)\) is the gain matrix controlling the rate of convergence and \(f_{1i}\), \(f_{2j}\), and \(f_{3k}\), are the ith, jth, and kth components of \(f_1\), \(f_2\), and \(f_3\) respectively.

Theorem 1

If the control functions are chosen as given in (10) then the drive systems (1)–(3) achieve multiswitching compound antisynchronization with the response system (4).

Proof

Using (8) the error dynamical system can be written as

$$\begin{aligned} \dot{e}_{l_{(ijkl)}}= & {} \,\alpha _i\dot{x}_i(\beta _jy_j+\gamma _kz_k)+\alpha _ix_i(\beta _j\dot{y}_j+\gamma _k\dot{z}_k)\nonumber \\&+\delta _lw_l, \quad {\,i,j, k, l=1, 2, ..., n}\nonumber \\= & {} \,\alpha _if_{1i}(\beta _jy_j+\gamma _kz_k)+\alpha _ix_i(\beta _jf_{2j}+\gamma _kf_{3k})\nonumber \\&+\delta _l(g_l+u_l), \end{aligned}$$
(12)

where the indices (ijkl) satisfy one of the generic conditions given in Definition 2.

Let the Lyapunov function be defined as

$$\begin{aligned} V=\,&\frac{1}{2}e^Te\\ =\,&\frac{1}{2} \sum _{l=1}^{n} (e_{l_{(ijkl)}})^2 . \end{aligned}$$

The derivative \(\dot{V}\) is obtained as

$$\begin{aligned} \dot{V}=\sum _{l=1}^{n} e_{l_{(ijkl)}}\dot{e}_{l_{(ijkl)}}. \end{aligned}$$
(13)

Using (12) in the above equation we get

$$\begin{aligned} \dot{V}=\,&\sum _{l=1}^{n} e_{l_{(ijkl)}}[\alpha _if_{1i}(\beta _jy_j+\gamma _kz_k)\\&+\alpha _ix_i(\beta _jf_{2j}+\gamma _kf_{3k})+\delta _l(g_l+u_l)].\\ \end{aligned}$$

Using (10) in the above equation, we choose the gain matrix K in such a way that we get

$$\begin{aligned} \dot{V}=\,&\sum _{l=1}^{n} e_{l_{(ijkl)}}(-K_le_{l_{(ijkl)}})\\ =\,&\sum _{l=1}^{n} -K_l(e_{l_{(ijkl)}})^2. \end{aligned}$$

Thus, we see that \(\dot{V}\) is negative definite. Using Lyapunov stability theory, we get \(\lim _{t \rightarrow \infty } \Vert e \Vert =0\). This means that the drive systems (1)–(3) achieve multiswitching compound antisynchronization with response system (4).\(\square \)

The following corollaries are easily obtained from Theorem 1 and their proofs are omitted here.

COROLLARY 1

If \(A\ne 0\), \(B=0\), and \(C\ne 0\), \(i, j, k, l= 1, 2, ..., n\), and the control function is chosen as

$$\begin{aligned} u_l= & {} -\frac{\alpha _i\gamma _k}{\delta _l}[f_{1i}z_k+x_if_{3k}]\\&-g_l-\frac{1}{\delta _l}Ke, \quad {i, j, k, l=1, 2, ..., n} \end{aligned}$$

then the drive systems (1) and (3) achieve switched modified function projective antisynchronization with the response system (4).

COROLLARY 2

If \(A\ne 0\), \(B\ne 0\), and \(C=0\), \(i, j, k, l= 1, 2, ..., n\), and the control function is chosen as

$$\begin{aligned} u_l=\,&-\frac{\alpha _i\beta _j}{\delta _l}[f_{1i}y_j+x_if_{2j}]-g_l-\frac{1}{\delta _l}Ke,\nonumber \\&{i, j, k, l=1, 2, ..., n}\nonumber \end{aligned}$$

then the drive systems (1) and (2) achieve switched modified function projective antisynchronization with the response system (4).

COROLLARY 3

If \(A=0\), and \(B=C=0\), \(i, j, k, l= 1, 2, ..., n\), and the control function is chosen as

$$\begin{aligned} u_l=-g_l-Ke, \quad {l=1, 2, ..., n} \end{aligned}$$

then the equilibirium point (0, 0, ..., 0) of the response system (4) is asymptotically stable.

4 Computational results and numerical simulations

In this section, we achieve multiswitching compound antisynchronization among four identical Lorenz chaotic systems. The scaling drive Lorenz system is represented by

$$\begin{aligned} \left\{ \begin{aligned} \dot{x}_{1}&=a_1(x_2-x_1),\\ \dot{x}_{2}&=b_1x_1-x_1x_3-x_2,\\ \dot{x}_{3}&=x_1x_2-c_1x_3,\\ \end{aligned} \right. \end{aligned}$$
(14)

and the two base drive systems are represented as follows:

$$\begin{aligned}&\left\{ \begin{aligned} \dot{y}_{1}&=a_2(y_2-y_1),\\ \dot{y}_{2}&=b_2y_1-y_1y_3-y_2,\\ \dot{y}_{3}&=y_1y_2-c_2y_3,\\ \end{aligned} \right. \end{aligned}$$
(15)
$$\begin{aligned}&\left\{ \begin{aligned} \dot{z}_{1}&=a_3(z_2-z_1),\\ \dot{z}_{2}&=b_3z_1-z_1z_3-z_2,\\ \dot{z}_{3}&=z_1z_2-c_3z_3.\\ \end{aligned} \right. \end{aligned}$$
(16)

The Lorenz response system is described as

$$\begin{aligned} \left\{ \begin{aligned} \dot{w}_{1}&=a_4(w_2-w_1)+u_1,\\ \dot{w}_{2}&=b_4w_1-w_1w_3-w_2+u_2,\\ \dot{w}_{3}&=w_1w_2-c_4w_3+u_3,\\ \end{aligned} \right. \end{aligned}$$
(17)

where \(u_1\), \(u_2\), and \(u_3\) are the controllers to be designed. In our synchronization scheme, we assume \(A=\mathrm {diag}\,(\alpha _1, \alpha _2, \alpha _3)\), \(B=\mathrm {diag}(\beta _1, \beta _2, \beta _3)\), \(C=\mathrm {diag}(\gamma _1, \gamma _2, \gamma _3)\), and \(D=\mathrm {diag}\,(\delta _1, \delta _2, \delta _3)\). The notations \(\alpha _i, \beta _j, \gamma _k, \delta _l\, (i, j, k, l= 1,2,3)\) representing the scaling factors are set for the convenience of discussion and may assume different or same values in applications.

Various switching combinations exist for defining the error states for the drive–response systems (14)–(17). In this paper, we present results for one randomly selected error space vector combination formed out of several switching possibilities. Let us define the error \(e=(e_{1_{(2231)}}, e_{2_{(3132)}}, e_{3_{(1323)}})\) where

$$\begin{aligned} \left\{ \begin{aligned} e_{1_{(2231)}}&= \alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1,\\ e_{2_{(3132)}}&= \alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2,\\ e_{3_{(1323)}}&= \alpha _1x_1(\beta _3y_3+\gamma _2z_2) + \delta _3w_3. \end{aligned} \right. \end{aligned}$$
(18)

We refer eq. (18) as Switch 1 for simplicity. For Switch 1, the error dynamical system is given as follows:

$$\begin{aligned} \left\{ \begin{aligned} \dot{e}_{1_{(2231)}}&= \alpha _2\dot{x}_2(\beta _2y_2+\gamma _3z_3) +\alpha _2x_2(\beta _2\dot{y}_2+\gamma _3\dot{z}_3)\\ {}&\quad + \delta _1\dot{w}_1,\\ \dot{e}_{2_{(3132)}}&= \alpha _3\dot{x}_3(\beta _1y_1+\gamma _3z_3) +\alpha _3x_3(\beta _1\dot{y}_1+\gamma _3\dot{z}_3)\\ {}&\quad +\delta _2\dot{w}_2,\\ \dot{e}_{3_{(1323)}}&= \alpha _1\dot{x}_1(\beta _3y_3+\gamma _2z_2) +\alpha _1x_1(\beta _3\dot{y}_3+\gamma _2\dot{z}_2)\\ {}&\quad +\delta _3\dot{w}_3. \end{aligned} \right. \end{aligned}$$
(19)

Combining with eqs (14)–(17) the error system (19) is transformed into the following form:

$$\begin{aligned} \left\{ \begin{aligned} \dot{e}_{1_{(2231)}} =\,&\alpha _2(b_1x_1-x_1x_3-x_2)(\beta _2y_2+\gamma _3z_3)\\&+\alpha _2x_2(\beta _2(b_2y_1-y_1y_3-y_2)\\&+\gamma _3(z_1z_2-c_3z_3))+\delta _1(a_4(w_2-w_1))\\&+\delta _1u_1,\\ \dot{e}_{2_{(3132)}} =\,&\alpha _3(x_1x_2-c_1x_3)(\beta _1y_1+\gamma _3z_3)\\&+\alpha _3x_3(\beta _1a_2(y_2-y_1)+\gamma _3(z_1z_2-c_3z_3))\\&+\delta _2(b_4w_1-w_1w_3-w_2)+\delta _2u_2,\\ \dot{e}_{3_{(1323)}} =\,&\alpha _1a_1(x_2-x_1)(\beta _3y_3+\gamma _2z_2)\\&+\alpha _1x_1(\beta _3(y_1y_2-c_2y_3)\\&+\gamma _2(b_3z_1-z_1z_3-z_2))\\ {}&+ \delta _3(w_1w_2-c_4w_3)+\delta _3u_3.\\ \end{aligned} \right. \end{aligned}$$
(20)

Theorem 2

If the control functions \(u_1\), \(u_2\), and \(u_3\) are chosen such that

$$\begin{aligned} \left\{ \begin{aligned} u_1 =\,&-\frac{1}{\delta _1}\phi _1 - a_4(w_2-w_1)\\ {}&-\frac{1}{\delta _1}[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\\&+\frac{a_1}{\delta _1}[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2]\\ {}&-\frac{a_2}{\delta _1}[\alpha _1x_1(\beta _3y_3+\gamma _2z_2) + \delta _3w_3],\\ u_2 =\,&-\frac{1}{\delta _2}\phi _2 - (b_4w_1-w_1w_3-w_2)\\&-\frac{1}{\delta _2}[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2]\\&-\frac{a_1}{\delta _2}[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\\&+\frac{a_3}{\delta _2}[\alpha _1x_1(\beta _3y_3+\gamma _2z_2) + \delta _3w_3],\\ u_3 =\,&-\frac{1}{\delta _3}\phi _3 - (w_1w_2-c_4w_3)\\&-\frac{1}{\delta _3}[\alpha _1x_1(\beta _3y_3+\gamma _2z_2) + \delta _3w_3]\\&+\frac{a_2}{\delta _3}[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\\ {}&-\frac{a_3}{\delta _3}[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2],\\ \end{aligned} \right. \end{aligned}$$
(21)

then the drive systems (14)–(16) will achieve multiswitching compound antisynchronization with the response system (17) where

$$\begin{aligned} \left\{ \begin{aligned} \phi _1 =\,&\alpha _2(b_1x_1-x_1x_3-x_2)(\beta _2y_2+\gamma _3z_3)\\&+\alpha _2x_2(\beta _2(b_2y_1-y_1y_3-y_2)\\&+\gamma _3(z_1z_2-c_3z_3)),\\ \phi _2 =\,&\alpha _3(x_1x_2-c_1x_3)(\beta _1y_1+\gamma _3z_3)\\&+\alpha _3x_3(\beta _1a_2(y_2-y_1)+\gamma _3(z_1z_2-c_3z_3)),\\ \phi _3 =\,&\alpha _1a_1(x_2-x_1)(\beta _3y_3+\gamma _2z_2)\\&+\alpha _1x_1(\beta _3(y_1y_2-c_2y_3)\\&+\gamma _2(b_3z_1-z_1z_3-z_2)).\\ \end{aligned} \right. \end{aligned}$$
(22)
Fig. 1
figure 1

3D phase plot of compound of multidrive Lorenz system.

Full size image

Proof

For simplicity, we rewrite system (20) as

$$\begin{aligned} \left\{ \begin{aligned} \dot{E}_{1}&= \phi _1 + \delta _1(a_4(w_2-w_1))+\delta _1u_1,\\ \dot{E}_{2}&= \phi _2 + \delta _2(b_4w_1-w_1w_3-w_2)+\delta _2u_2,\\ \dot{E}_{3}&= \phi _3 + \delta _3(w_1w_2-c_4w_3)+\delta _3u_3, \end{aligned} \right. \end{aligned}$$
(23)

where \(E_1=e_{1_{(2231)}}, E_2=e_{2_{(3132)}}\), and \(E_3=e_{3_{(1323)}}\) and \(\phi _1, \phi _2\), and \(\phi _3\) are as given in eq. (22). Consider the Lyapunov function in the form of

$$\begin{aligned} V(E(t))= \frac{1}{2}({E_1}^{\!\!2}+{E_2}^{\!\!2}+{E_3}^{\!\!2}). \end{aligned}$$
(24)

The derivative of V along the trajectories of (23) is obtained as

$$\begin{aligned} \begin{aligned} \dot{V}(E(t)) =\,&E_1\dot{E_1}+E_2\dot{E_2}+E_3\dot{E_3}\\ =\,&E_1( \phi _1 + \delta _1(a_4(w_2-w_1))+\delta _1u_1)\\&+E_2(\phi _2 + \delta _2(b_4w_1-w_1w_3\\&-w_2)+ \delta _2u_2)\\&+ E_3(\phi _3 + \delta _3(w_1w_2-c_4w_3)+\delta _3u_3). \end{aligned} \end{aligned}$$
(25)

Substituting the values of \(u_1\), \(u_2\), and \(u_3\) in (25), we get

$$\begin{aligned} \dot{V}(E(t))= & {} E_1\left\{ \phi _1 + \delta _1a_4(w_2-w_1)\right. \\&+\delta _1\left\{ -\frac{1}{\delta _1}\phi _1- a_4(w_2-w_1)\right. \\&-\frac{1}{\delta _1}[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\\&+\frac{a_1}{\delta _1}[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2]\\&\left. \left. -\frac{a_2}{\delta _1}[\alpha _1x_1(\beta _1y_1+\gamma _2z_2) + \delta _3w_3]\right\} \right\} \\&+E_2\left\{ \phi _2 + \delta _2(b_4w_1-w_1w_3-w_2)\right. \\&+\delta _2\left\{ -\frac{1}{\delta _2}\phi _2 - (b_4w_1-w_1w_3-w_2)\right. \\&-\frac{1}{\delta _2}[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2]\\&-\frac{a_1}{\delta _2}[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\\&\left. \left. +\frac{a_3}{\delta _2}[\alpha _1x_1(\beta _1y_1+\gamma _2z_2) + \delta _3w_3]\right\} \right\} \\&+E_3\left\{ \phi _3 + \delta _3(w_1w_2-c_4w_3)\right. \\&+\delta _3\left\{ -\frac{1}{\delta _3}\phi _3 - (w_1w_2-c_4w_3)\right. \\&-\frac{1}{\delta _3}[\alpha _1x_1(\beta _1y_1+\gamma _2z_2) + \delta _3w_3]\\&+\frac{a_2}{\delta _3}[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\\&\left. \left. -\frac{a_3}{\delta _3}[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2]\right\} \right\} .\\ \end{aligned}$$

This can be written as

$$\begin{aligned} \begin{aligned} \dot{V}(E(t)) =\,&E_1\left\{ -[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\right. \\ {}&+a_1[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2]\\&\left. -\,a_2[\alpha _1x_1(\beta _1y_1+\gamma _2z_2) + \delta _3w_3]\right\} \\ {}&+E_2\left\{ -[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2]\right. \\&-a_1[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\\ {}&\left. +\,a_3[\alpha _1x_1(\beta _1y_1+\gamma _2z_2) + \delta _3w_3]\right\} \\&+E_3\left\{ -[\alpha _1x_1(\beta _1y_1+\gamma _2z_2) + \delta _3w_3]\right. \\ {}&+a_2[\alpha _2x_2(\beta _2y_2+\gamma _3z_3) + \delta _1w_1]\\&\left. -\,a_3[\alpha _3x_3(\beta _1y_1+\gamma _3z_3) + \delta _2w_2]\right\} . \end{aligned} \end{aligned}$$

This can be further rewritten as

$$\begin{aligned} \begin{aligned} \dot{V}(E(t)) =\,&E_1(-E_1+ a_1E_2 -a_2E_3 )\nonumber \\&+E_2(-E_2-a_1E_1+a_3E_3)\nonumber \\&+E_3(-E_3+a_2E_1-a_3E_2)\nonumber \\ =\,&-{E_1}^{\!\!2}-{E_2}^{\!\!2}-{E_3}^{\!\!2}\nonumber \\ =\,&-E^TE,\nonumber \end{aligned} \end{aligned}$$

where \(E^T=(E_1, E_2, E_3)^T\). Thus, we see that \(\dot{V}(E(t))\) is negative definite. According to Lyapunov stability theory, we know \(E_i\rightarrow 0 \,(i=1, 2, 3)\), that is, \(\lim _{t \rightarrow \infty } \Vert E \Vert = 0\), which means that the drive systems (14)–(16) will achieve multiswitching compound antisynchronization with the response system (17). \(\square \)

Remark 5

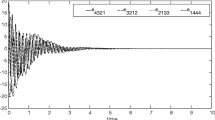
In many previous studies, one common problem on the compound of multiple drive system is that the compound signal often is asymptotically stable or emanative. This is not desirable as the dynamic evolution of the signal obtained by compound of multidrive system is either too easy or completely useless for transmitting information signals. However, in our work, the resulting compound system is still chaotic and the dynamic evolution is more abundant and complex as can be seen in figure 1. This can be utilized to attain improved performances for secure communication and information processing in the future.

Remark 6

In Theorem 2, the designed control inputs \(u_1\), \(u_2\), and \(u_3\) are highly nonlinear in nature due to the high nonlinearity present in the structural design of the drive system signals where the resultant signal of the sum of two drive systems is being scaled by signals of the scaling drive system. To design a less complicated control input for achieving desired multiswitching compound antisynchronization will be the topic of our future research.

The following corollaries can be easily obtained from Theorem 2, but their proofs are omitted here for brevity. Suppose \(A\ne 0\), \(B=0\), and \(C\ne 0\), then we have the following corollary:

COROLLARY 4

If the control functions \(u_1\), \(u_2\), and \(u_3\) are chosen such that

$$\begin{aligned} u_1 =\,&-\frac{\alpha _2\gamma _3}{\delta _1}[(b_1x_1-x_1x_3-x_2)z_3\\ {}&+x_2(z_1z_2-c_3z_3)] \\&-a_4(w_2-w_1)- \frac{1}{\delta _1}[\alpha _2\gamma _3x_2z_3 + \delta _1w_1]\\&+\frac{a_1}{\delta _1}[\alpha _3\gamma _3x_3 z_3 + \delta _2w_2]\\&-\frac{a_2}{\delta _1}[\alpha _1\gamma _2x_1 z_2 +\delta _3w_3],\\ u_2 =\,&-\frac{\alpha _3\gamma _3}{\delta _2}[(x_1x_2-c_1x_3)z_3 +x_3(z_1z_2-c_3z_3)] \\&-(b_4w_1-w_1w_3-w_2)\\&-\frac{1}{\delta _2}[\alpha _3\gamma _3x_3z_3 + \delta _2w_2]\\&- \frac{a_1}{\delta _2}[\alpha _2\gamma _3x_2 z_3 + \delta _1w_1]\\&+\frac{a_3}{\delta _2}[\alpha _1\gamma _2x_1 z_2 + \delta _3w_3],\\ u_3 =\,&-\frac{\alpha _1\gamma _2}{\delta _3}[a_1(x_2-x_1)z_2 +x_1(b_3z_1-z_1z_3-z_2)]\\&-(w_1w_2-c_4w_3)-\frac{1}{\delta _3}[\alpha _1\gamma _2x_1z_2 + \delta _3w_3]\\&+\frac{a_2}{\delta _3}[\alpha _2\gamma _3x_2z_3 + \delta _1w_1]\\&-\frac{a_3}{\delta _3}[\alpha _3\gamma _3x_3z_3 + \delta _2w_2], \end{aligned}$$

then the drive systems (14) and (16) will achieve a novel type of switched modified function projective antisynchronization with response system (17).

Suppose \(A\ne 0\), \(B\ne 0\), and \(C=0\), then we have the following corollary:

COROLLARY 5

If the control functions \(u_1\), \(u_2\), and \(u_3\) are chosen such that

$$\begin{aligned} u_1 =\,&-\frac{\alpha _2\beta _2}{\delta _1}[(b_1x_1-x_1x_3-x_2)y_2 \\&+x_2(b_2y_1-y_1y_3-y_2)]\\&-a_4(w_2-w_1)- \frac{1}{\delta _1}[\alpha _2\beta _2x_2y_2 + \delta _1w_1]\\&+\frac{a_1}{\delta _1}[\alpha _3\beta _1x_3y_1 + \delta _2w_2]\\&-\frac{a_2}{\delta _1}[\alpha _1\beta _3x_1y_3 + \delta _3w_3],\\ u_2 =\,&-\frac{\alpha _3\beta _1}{\delta _2}[(x_1x_2-c_1x_3)y_1 +a_2x_3(y_2-y_1)]\\&-(b_4w_1-w_1w_3-w_2)\\&-\frac{1}{\delta _2}[\alpha _3\beta _1x_3y_1 + \delta _2w_2]\\&-\frac{a_1}{\delta _2}[\alpha _2 \beta _2 x_2 y_2 +\delta _1w_1]\\&+\frac{a_3}{\delta _2}[\alpha _1\beta _3x_1y_3 + \delta _3w_3],\\ u_3 =\,&-\frac{\alpha _1\beta _3}{\delta _3}[a_1(x_2-x_1)y_3 +x_1(y_1y_2-c_2y_3)]\\&-(w_1w_2-c_4w_3)-\frac{1}{\delta _3}[\alpha _1\beta _3x_1y_3 + \delta _3w_3]\\&+\frac{a_2}{\delta _3}[\alpha _2\beta _2x_2y_2 + \delta _1w_1]\\&-\frac{a_3}{\delta _3}[\alpha _3\beta _1x_3y_1 + \delta _2w_2], \end{aligned}$$

then the drive systems (14) and (15) will achieve a novel type of switched modified function projective antisynchronization with response system (17).

Fig. 2
figure 2

Response for states \(x_2(y_2+z_3)\) and \(w_1\) for the drive systems (14)–(16) and the response system (17).

Full size image
Fig. 3
figure 3

Response for states \(x_3(y_1+z_3)\) and \(w_2\) for the drive systems (14)–(16) and the response system (17).

Full size image
Fig. 4
figure 4

Response for states \(x_1(y_3+z_2)\) and \(w_3\) for the drive systems (14)–(16) and the response system (17).

Full size image
Fig. 5
figure 5

Synchronization errors \(e_{1_{(2231)}}\), \(e_{2_{(3132)}}\), and \(e_{3_{(1323)}}\) between the drive systems (14)–(16) and the response system (17).

Full size image
Fig. 6
figure 6

Time response of the controllers used to achieve compound antisynchronization between the drive systems (14)–(16) and the response system (17).

Full size image
Fig. 7
figure 7

Ratios between the controllers \(u_1\), \(u_2\) and \(u_3\) and the uncontrolled response system signals \(w_1\), \(w_2\), and \(w_3\).

Full size image
Fig. 8
figure 8

Ratios between the controllers \(u_1\), \(u_2\) and \(u_3\) and the drive system signals \(x_2(y_2+z_3)\), \(x_3(y_1+z_3)\), and \(x_1(y_3+z_2)\).

Full size image

Suppose \(A=0\) or \(B=C=0\), then we have the following corollary:

COROLLARY 6

If the control functions \(u_1\), \(u_2\), and \(u_3\) are chosen such that

$$\begin{aligned} u_1&= a_4(w_1-w_2)-w_1+\frac{a_1}{\delta _1}\delta _2w_2 - \frac{a_2}{\delta _1}\delta _3w_3,\\ u_2&= (w_1w_3+w_2-b_4w_1) -w_2- \frac{a_1}{\delta _2}\delta _1w_1\\&\quad + \frac{a_3}{\delta _2}\delta _3w_3,\\ u_3&= (c_4w_3-w_1w_2)-w_3+ \frac{a_2}{\delta _3}\delta _1w_1- \frac{a_3}{\delta _3}\delta _2w_2, \end{aligned}$$

then the equilibrium point (0, 0, 0) of the response system (17) is asymptotically stable.

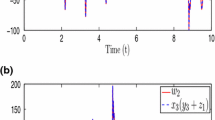
To demonstrate the effectiveness of our proposed method we perform numerical simulations in MATLAB using fourth-order Runge–Kutta method and give the results for Switch 1. In the simulation process we assume \(\alpha _1=\alpha _2=\alpha _3=1\), \(\beta _1=\beta _2=\beta _3=1\), \(\gamma _1=\gamma _2=\gamma _3=1\), and \(\delta _1=\delta _2=\delta _3=1\). Note that \(\delta _i\) is the scaling factor of the response system, and its value is set to unity to ensure that only the response system antisynchronizes with compound of multidrive system, while \(\alpha _i, \beta _j, \text {and } \gamma _k\) may take any values. The system parameters of Lorenz system are taken as \(a_1=a_2=a_3=a_4=10\), \(b_1=b_2=b_3=b_4=28\), and \(c_1=c_2=c_3=c_4=8/3\) and initial states of the chaotic drive and response system are given by \((x_1(0), x_2(0), x_3(0)){=}(0, 1, 0.5)\), \((y_1(0), y_2(0), y_3(0)){=}(0.1, 0, 1.5)\), \((z_1(0), z_2(0), z_3(0)){=}(1, 0.5, 1)\) and \((w_1(0), w_2(0), w_3(0))=(4, -2, 3)\). Figure 1 shows that the switched compound drive system remains chaotic. The time response of the synchronized states \(w_1, w_2\), and \(w_3\) of the response system with states \(x_2(y_2+z_3)\), \(x_3(y_1+z_3)\), and \(x_1(y_3+z_2)\) of the drive systems (14)–(16) respectively is illustrated in figures 2, 3, 4. Figure 5 displays the time response of synchronization errors \(e_{1_{(2231)}}\), \(e_{2_{(3132)}}\), and \(e_{3_{(1323)}}\). Figures 2–5 show that the drive systems (14)–(16) achieve multiswitching compound antisynchronization successfully with the response system (17). Figure 6 shows the time response of the controllers used in Theorem 2 and figures 7 and 8 display the ratios of the controllers with the corresponding uncontrolled response system signal and compound drive system signal respectively.

5 Conclusions

In this paper, we have introduced a new type of synchronization involving four chaotic systems, namely MSCoAS. Using Lyapunov stability theory some sufficient conditions are obtained for achieving MSCoAS of four chaotic systems. In this new synchronization scheme, the state variables involved in the compound of multidrive system are multiswitched in various ways to antisynchronize with different state variables of the response system. The main advantages of the proposed scheme can be summarized as:

(i) For synchronization achieved in this manner, the possible combinations for error space vectors in which synchronization may take place is very large due to multiswitching. In the context of secure communication applications [44, 45], this scheme will provide better resistance and antiattack ability than normal synchronization schemes as it would be very difficult for the intruder to predetermine the combination in which synchronization would occur.

(ii) The proposed scheme theoretically guarantees good control performance.

(iii) The proposed scheme will be helpful in synchronizing multiple chaotic systems and producing complex resultant signals which will further strengthen the security of the transmitted signals.

(iv) A novel type of switched modified function projective synchronization is obtained as a special case of MSCoAS.

The main disadvantage of the obtained results lies in the highly nonlinear nature of the designed controller. Numerical simulations are performed using Lorenz system to demonstrate the validity and effectiveness of our proposed scheme. The presented scheme MSCoAS may form the basis of various other synchronization studies in future. Using fractional chaotic systems as the drive and the response systems, or utilizing function scaling factors or considering the chaotic system with parameter uncertainty are some interesting directions for future work.