1 Introduction

Compared to most other methods of chaos control and synchronization, the main advantages of impulsive method are that [1–3]: (1) it allows the control and synchronization of a chaotic system by using only small control impulses at discrete instants; (2) it provides an efficient technology to deal with systems which cannot endure continuous disturbance; (3) since only impulses at discrete instants are needed, it is more efficient, secure, and thus useful in many applications, especially for secure communication [4, 5]. In addition, there exist many examples of impulsive control systems in practice, such as the population control system of insects, some chemical reactors, financial systems [6], and neural networks [7].

Because of the above facts, many impulsive control and synchronization methods for a chaotic system have been presented. In [8], robustness of the continuous differential system was used to explain the mechanics of impulsive synchronization. Yang et al. used the theory of comparison system and impulsive differential equations to study the stabilization and synchronization of Lorenz system in [9] and [10], respectively. Sun et al. presented a new comparison theorem for asymptotic stability of impulsive differential system [11], which was used to study the synchronization of Lorenz system [12] and the control of chaotic Rössler system [13]. Some sufficient conditions for asymptotic stability of impulsive system are given in [14], and the results have been used to stable and synchronize Lorenz [15] and unified chaotic system [16]. Based on linear matrix inequality, the impulsive synchronization of chaotic system was investigated in [17]. In [18], Iton et al. studied the impulsive control for synchronization of some continuous systems under the assumption that the synchronization errors are sufficiently small. Hu et al. researched the projective synchronization of Lorenz system via impulsive control in [19]. Zhang et al. investigated the problem of impulsive lag synchronization for a class of nonlinear discrete chaotic systems [20]. The impulsive synchronization with parametric mismatch was studied in [21, 22]. Itoh et al. presented some experimental results on impulsive synchronization of chaotic circuits in [23], which suggests that various applications of impulsive control and synchronization of chaotic system are feasible. Some other research results can be found in [24–26]. However, few of the above mentioned methods consider the case where both control gains and impulsive intervals are variable.

Hyperchaotic phenomenon has been observed and analyzed in some models [27–30], and some synchronization methods of the hyperchaotic system without impulsive technology have been presented [31, 32]. Unified hyperchaotic system, which was presented by the authors in a previous paper [33], contains the hyperchaotic Lorenz system and the hyperchaotic Chen system as two dual systems at the two extremes of its parameter spectrum. The system is hyperchaotic over almost the whole parameter range, and can realize continued transition from the hyperchaotic Lorenz system to the hyperchaotic Chen system. Its dynamic behavior is more complex than other chaotic and hyperchaotic systems. Therefore, in the field of secure communication, the control and synchronization of this system probably has more significance than other chaotic (hyperchaotic) systems.

In this paper, based on the Lyapunov stability theory and the comparison theorem, we propose an impulsive law with variable control gains and impulsive intervals to achieve the control and synchronization of the unified hyperchaotic system. The rest of the paper is organized as follows. We review some basic theory in Sect. 2. The impulsive control and synchronization theorems of the system are investigated in Sects. 3 and 4, respectively. Section 5 gives numerical simulations. Conclusions and acknowledgements are given in the final section.

2 Basic theory of impulsive differential equations

Let a general system be in the form of \(\dot{\boldsymbol{x}} = \boldsymbol{f}(t,\boldsymbol {x})\), where f:R +×R n↦R n is continuous, x∈R n is the state variable. Discrete set {τ i } of time instants satisfies 0<τ 1<τ 2<⋯<τ i <τ i+1<⋯,τ i →∞ as i→∞.

\(U(i,\boldsymbol{x})=\Delta\boldsymbol{x} \mid_{t=\tau_{i}}\triangleq\boldsymbol{x}(\tau _{i}^{+})-\boldsymbol{x}(\tau_{i}^{-})\) is the state variable at instant τ i , then an impulsive differential system in which impulses occur at fixed times is described by

$$ \begin{array} {@{}l} \dot{\boldsymbol{x}} = \boldsymbol{f}(t,\boldsymbol{x}),\quad t\neq\tau_{i}, \\[2mm] \Delta\boldsymbol{x}=U(i,\boldsymbol{x}),\quad t=\tau_{i}, \\[2mm] \boldsymbol{x}\bigl(t_{0}^{+}\bigr)=\boldsymbol{x}(t_{0}), \quad t_{0}\geq0,\ i=1,2,\ldots. \end{array} $$
(1)

Equation (1) is also called impulsive differential equation. To make the paper self-contained, we recall the following definitions and theorems [6].

Definition 1

Let V:R +×R n↦R +, then V is said to belong to class \(\mathcal{V}_{0}\) if

  1. 1.

    V is continuous in (τ i−1,τ i ]×R n and for each x∈R n, \(i=1,2,\ldots,\lim_{(t,\boldsymbol{y}) \to(\tau_{i}^{+},\boldsymbol {x})}V(t,\boldsymbol{y})=V(\tau_{i}^{+},\boldsymbol{x})\) exists;

  2. 2.

    V is locally Lipschitzian in x.

Definition 2

For (t,x)∈(τ i−1,τ i ]×R n, we define \(D^{+}V(t,\boldsymbol{x})\triangleq \limsup_{h\to0}\frac{1}{h}[V(t+h,\boldsymbol {x}+h\boldsymbol{f}(t,\boldsymbol{x}))-V(t,\boldsymbol{x})]\).

Definition 3

(Comparison system)

Let \(V\in\mathcal{V}_{0}\) and assume that

$$ \begin{array} {@{}l} D^{+}V(t, \boldsymbol{x})\leq g\bigl(t,V(t,\boldsymbol{x})\bigr),\quad t\neq \tau_{i}, \\[2mm] V\bigl(t,\boldsymbol {x}+U(i,\boldsymbol{x})\bigr)\leq\psi_{i} \bigl(V(t,\boldsymbol{x})\bigr),\quad t=\tau_{i}, \end{array} $$
(2)

where g:R +×R +↦R is continuous and ψ i :R +↦R + is nondecreasing. Then the following system

$$ \begin{array} {@{}l} \dot{\omega}=g(t,\omega),\quad t \neq\tau_{i}, \\[2mm] \omega\bigl(\tau_{i}^{+}\bigr)=\psi_{i}\bigl( \omega(\tau_{i})\bigr),\qquad\omega\bigl(t_{0}^{+} \bigr)=\omega_{0}\geq0, \end{array} $$
(3)

is the comparing system of Eq. (1).

Definition 4

A function α is said to belong to class \(\mathcal{K}\) if \(\alpha \in\mathcal{C}[\boldsymbol{R}_{+},\boldsymbol{R}_{+}]\), α(0)=0 and α(x) is strictly increasing in x.

Let S ρ ={x∈R n∣∥x∥<ρ}, where ∥⋅∥ denotes the Euclidean norm on R n. Assume that f(t,0)=0, U(i,0)=0 and g(t,0)=0 for all i. Then the following comparing theorems offer sufficient conditions for stability criteria.

Theorem 1

[6]

Assume that the following three conditions are satisfied,

  1. 1.

    V:R +×S ρ ↦R +, ρ>0, \(V\in\mathcal{V}_{0}\), D + V(t,x)≤g(t,V(t,x)), t≠τ i .

  2. 2.

    There exists a ρ 0>0 such that \(\boldsymbol{x}\in S_{\rho _{0}}\) implies that \(\boldsymbol{x}+U(i,\boldsymbol{x})\in S_{\rho_{0}}\) for all i, and V(t,x+U(i,x))≤ψ i (V(t,x)), t=τ i , \(\boldsymbol{x}\in S_{\rho_{0}}\).

  3. 3.

    β(∥x∥)≤V(t,x)≤α(∥x∥) on R +×S ρ , where \(\alpha,\beta\in\mathcal{K}\).

Then the stability properties of the trivial solution ω=0 of Eq. (3) imply the corresponding stability properties of the trivial solution x=0 of Eq. (1).

Theorem 2

[6]

Let \(g(t,\omega)=\dot{\zeta}(t)\omega\), \(\zeta\in \mathcal{C}^{1}[\boldsymbol{R}_{+},\boldsymbol{R}_{+}]\), ψ i (ω)=d i ω, d i ≥0 for all i, then the origin of system (1) is asymptotically stable if conditions

$$ \zeta(\tau_{i+1})+\ln(\gamma d_{i})\leq\zeta(\tau_{i}),\quad\mathit{for\ all}\ i,\ \mathit{where}\ \gamma>1, $$
(4)

and \(\dot{\zeta}(t)\geq0\) are satisfied.

3 Impulsive control of unified hyperchaotic system

The unified hyperchaotic system presented by authors [33] recently is described by

$$ \begin{array}{@{}l} \dot{x} = (26a + 10)(y - x),\\[2mm] \dot{y} = (28 - 44a)x - xz + (29a - 1)y - v, \\[2mm] \dot{z} = xy - (8 + a)z / 3,\\[2mm] \dot{v} = 0.1(1 - a)yz + ax + r, \end{array} $$
(5)

where a∈[0,1]. System (5) unified the hyperchaotic Lorenz system (when a=0) and the hyperchaotic Chen system (when a=1). Furthermore, when −0.7<r<0.7, system (5) is hyperchaotic for almost all parameter a in [0,1] and realizes the entire transition spectrum from one to the other.

Let x=(x,y,z,v)T. By decomposing the linear and nonlinear parts, the unified system (5) can be rewritten as

$$ \dot{\boldsymbol{x}} = A\boldsymbol{x}+\boldsymbol{\phi}(\boldsymbol{x}), $$
(6)

where

The impulsive control of the unified hyperchaotic system is then given by

$$ \left\{ \begin{array}{@{}l@{\quad}l} \dot{\boldsymbol{x}} = A\boldsymbol{x}+\boldsymbol{\phi}(\boldsymbol{x}), & t\neq\tau_{i}, \\[2mm] \Delta\boldsymbol{x}=B_{i}\boldsymbol{x},& t=\tau_{i}, \end{array} \right. $$
(7)

where τ i ,i=1,2,… denotes the moment when impulsive control occurs, B i is the control gain matrix. Chaotic (hyperchaotic) signals are bounded, so there exists a positive number M such that |y|≤M for all t. We use I to represent identity matrix. Then we have the following stability theorem for the impulsive control system (7).

Theorem 3

Let d i be the largest eigenvalue of \((I+B_{i}^{T})(I+B_{i})\), B i is Hermitian, the spectral radius of I+B i , ρ(I+B i )≤1, d=max{d i }. And let λ max(a) be the largest eigenvalue of \(\frac{1}{2}(A+A^{T})\) in a∈[0,1]. If

(8)

then the origin of the impulsive controlled unified hyperchaotic system (7) is asymptotically stable.

Proof

Construct the Lyapunov function \(V(t,\boldsymbol{x})=\frac {1}{2}\boldsymbol{x}^{T}\boldsymbol{x}\), for t≠τ i . The time derivative of V(t,x) along the solution of Eq. (7) is

(9)

So condition 1 of Theorem 1 is satisfied with g(t,ω)=(2λ max(a)+0.1(1−a)M)ω.

Since I+B i is symmetric, by employing Euclidean norm, we have ρ(I+B i )=∥I+B i ∥. Then for any ρ 0>0 and \(\boldsymbol{x}\in S_{\rho _{0}}\), we have ∥x+U(i,x)∥=∥x+B i x∥≤∥I+B i ∥∥x∥=ρ(I+B i )∥x∥≤∥x∥. Consequently, \(\boldsymbol{x}+B_{i}\boldsymbol{x}\in S_{\rho_{0}}\). For t=τ i , we have

(10)

So condition 2 of Theorem 1 is satisfied with ψ i (ω)=dω. Obviously, condition 3 of Theorem 1 is also satisfied. Hence, the asymptotic stability of the system (7) is implied by that of the following comparison system

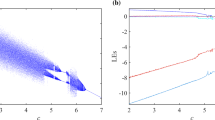
$$ \begin{array} {@{}l} \dot{\omega}=\bigl(2 \lambda_{\max}(a)+0.1M(1-a)\bigr)\omega,\quad t\neq\tau_{i}, \\[2mm] \omega\bigl(\tau_{i}^{+}\bigr)=d\omega(\tau_{i}), \qquad \omega \bigl(t_{0}^{+}\bigr)=\omega_{0}\geq0. \end{array} $$
(11)

From (8), we have \(\int_{\tau_{i}}^{\tau_{i+1}}(2\lambda_{\max}(a)+0.1M(1-a))\,dt+\ln (\xi d)\leq0\), ξ>1, for all i. It can be seen from Fig. 1 that λ(a)>0, where λ(a) is the largest eigenvalue of \(\frac {1}{2}(A+A^{T})\) at a. So λ max(a)=max{λ(a)}>0 and \(\dot{\zeta}(t)=2\lambda_{\max}(a)+0.1(1-a)M>0\). From Theorem 2, we can know that the trivial solution of Eq. (7) is asymptotically stable.

Fig. 1
figure 1

The value of λ(a)

Full size image

 □

Remark 1

{τ i } is said to be equidistant if there exists a constant δ>0 such that τ i+1−τ i =δ,i=1,2,…. Then (8) can be rewritten as

$$ \bigl(2\lambda_{\max}(a)+0.1(1-a)M\bigr)\leq- \frac{1}{\delta}\ln(\xi d),\quad \xi>1. $$
(12)

Furthermore, we can obtain an estimate of the upper bound of \(\delta ,\delta_{\max}=-\frac{\ln(\xi d)}{2\lambda_{\max}(a)+0.1(1-a)M}\). Here, d i and d should satisfy 0<d,d i <1.

4 Impulsive synchronization of unified hyperchaotic system

The impulsive synchronization of unified hyperchaotic system will be studied in this section. In order to synchronize system (6) (the driving system) via impulses, we design the following response (or driven) system:

$$ \left\{ \begin{array}{@{}l@{\quad}l} \dot{\tilde{\boldsymbol{x}}} = A\tilde{\boldsymbol{x}}+ \boldsymbol{\phi}(\tilde{\boldsymbol{x}}), & t\neq\tau_{i}, \\[2mm] \Delta\tilde{\boldsymbol{x}}=-P_{i}\boldsymbol{e}, & t=\tau_{i}, \end{array} \right. $$
(13)

where \(\tilde{\boldsymbol{x}}=(\tilde{x},\tilde{y},\tilde{z},\tilde{v})^{T}\) is the state variables of the response system, P i is a 4×4 control gain matrix, \(\boldsymbol{e}=(e_{1},e_{2},e_{2})^{T}=(x-\tilde {x},y-\tilde{y},z-\tilde{z},v-\tilde{v})^{T}\) is the synchronization error.

Let \(\boldsymbol{\varphi}(\boldsymbol{x},\tilde{\boldsymbol{x}})=\boldsymbol{\phi}(\boldsymbol{x})-\boldsymbol{\phi}(\boldsymbol {\tilde{x}})=(0,-xz+\tilde{x}\tilde{z}, xy-\tilde{x}\tilde {y},0.1(1-a)(yz-\tilde{y}\tilde{z}))^{T}\). Then the error system of the impulsive synchronization is given by

$$ \left\{ \begin{array}{@{}l@{\quad}l} \dot{\boldsymbol{e}} = A\boldsymbol{e}+\boldsymbol{\varphi}(\boldsymbol{x},\tilde{\boldsymbol{x}}), & t\neq\tau_{i}, \\[2mm] \Delta\boldsymbol{e}=P_{i}\boldsymbol{e}, & t=\tau_{i}. \end{array} \right. $$
(14)

For the stability of the origin of error system (14), we have the following theorem.

Theorem 4

Let d i be the largest eigenvalue of \((I+P_{i}^{T})(I+P_{i})\), P i is Hermitian, the spectral radius of I+P i , ρ(I+P i )≤1, d=max{d i }. And let λ max(a) be the largest eigenvalue of \(\frac{1}{2}(A+A^{T})\) in a∈[0,1], If

(15)

Then the origin of the error system (14) is asymptotically stable.

Proof

It is easy to know that the state variables of system (13) are bounded. We assume that \(N=\max\{ |y|,|z|,|\tilde{z}|,|\tilde{v}|\}\). Let \(V(t,\boldsymbol{e})=\frac{1}{2}\boldsymbol {e}^{T}\boldsymbol{e}\). The time derivative of V(t,e) along the solution of Eq. (14) is

(16)

Hence, condition 1 of the theorem is satisfied with g(t,ω)=(2λ max(a)+2N+0.3(1−a)N)ω. The remaining part of the proof is the same as the corresponding proof of Theorem 3. □

Remark 2

If {τ i } is equidistant, the estimate of the upper bound of impulsive interval is

$$\delta_{\max}= -\frac{\ln(\xi d)}{2\lambda _{\max}(a)+2N+0.3(1-a)N}, $$

0<d, d i <1.

5 Numerical simulations results

In order to show how the impulsive control and synchronization method works, we present some simulation results in this section. For simplicity, we assume {τ i } is equidistant, and τ i+1−τ i =δ.

5.1 Impulsive control

In this simulation, we take the control gain matrix B i =B, and \(B=\operatorname{diag}(k,-0.8,-0.8,-0.8)\) (\(\operatorname{diag}\) stands for the diagonal matrix with the column vector on its diagonal). So B is Hermitian. From Theorem 3, we can obtain that −2≤k≤0. Then we have

$$d=\left\{ \begin{array}{@{}l@{\quad}l} (k+1)^2, & (k+1)^2\geq0.04, \\[1mm] 0.04, & \mathrm{otherwise}, \end{array} \right. $$

and the estimates of bounds of stable regions are given by

$$0\leq \delta\leq \left\{ \begin{array}{@{}l@{\quad}l} -\frac{\ln(\xi)+\ln(k+1)^{2}}{2\lambda_{\max}(a)+0.1(1-a)M}, & (k+1)^2\geq0.04, \\[2mm] -\frac{\ln(\xi)+\ln(0.04)}{2\lambda_{\max}(a)+0.1(1-a)M}, & \mathrm{otherwise}, \end{array} \right. $$

where M=28.9255. By computing, we obtain λ max(a)=29.5263.

When r=0.2, Fig. 2(a) shows the stable region for different ξs versus a∈[0,1] and k∈[−2,0]. To verify the performance of the impulsive control method, we choose a=0.84 and r=0.2, the stable region is shown in Fig. 2(b). In Figs. 2(a) and (b), the region under the curved surface(curve) of ξ is the stable region.

Fig. 2
figure 2

The impulsive control of unified hyperchaotic system: (a) stable region for ξ=1,2,10 (from the top down) versus a and k; (b) stable region when a=0.84; (c) stable results; (d) unstable results (Color figure online)

Full size image

Figure 2(c) shows the stable results within the stable region with k=−1.6, δ=0.015, and ξ=1. It can be seen from Fig. 2(c) that the system asymptotically approaches the origin. Figure 2(d) shows the unstable results with k=−1.6, δ=0.15, and ξ=1. The 4 lines in Fig. 2(c) and (d) show the evolution of x,y,z, and v, respectively.

Remark 3

In simulation, we find that some δ above the curved surface (curve) also make the system stable. There are two reasons for this. First, the upper bound given in theorem is sufficient but not necessary. Second, we enlarged the denominator of the upper bound in the proof process of Theorem 3. However, the stable region under the curved surface (curve) need less time to achieve control than that above the curved surface (curve), which may have some practical significance.

5.2 Impulsive synchronization

Here, we take the control gain matrix P i =P, and \(P=\operatorname{diag}(k,-0.8,-0.8,-0.8)\), −2≤k≤0. So P is Hermitian. Then we have

$$d= \left\{ \begin{array}{@{}l@{\quad}l} (k+1)^2, & (k+1)^2\geq0.04, \\[1mm] 0.04, & \mathrm{otherwise}, \end{array} \right. $$

and the estimates of bounds of stable regions are given by

$$0\leq \delta\leq \left\{ \begin{array}{@{}l} -\frac{\ln(\xi)+\ln(k+1)^{2}}{2\lambda_{\max}(a)+2N+0.3(1-a)N},\\[2mm] \quad (k+1)^2\geq0.04, \\[2mm] -\frac{\ln(\xi)+\ln(0.04)}{2\lambda_{\max}(a)+2N+0.3(1-a)N},\quad \mathrm{otherwise}, \end{array} \right. $$

where N=50.0015. By computing, we obtain λ max(a)=29.5263.

The initial conditions are given by (x(0),y(0),z(0),v(0))=(5,2,7,5) and \((\tilde{x}(0),\tilde{y}(0),\tilde{z}(0),\tilde{v}(0))=(2,4,6,8)\). We take r=0.2. Figure 3(a) shows the stable region for different ξs in a∈[0,1] and k∈[−2,0]. To verify the performance of the impulsive control method, we choose a=0.84 and r=0.2, the stable region is shown in Fig. 3(b).

Fig. 3
figure 3

The impulsive synchronization of unified hyperchaotic system: (a) stable region for ξ=1,2,6 (from the top down) versus a and k; (b) stable region when a=0.84; (c) stable synchronization results; (d) when δ is too large, synchronization cannot be achieved (Color figure online)

Full size image

Figure 3(c) shows the synchronization results for k=−0.6, δ=0.01, and ξ=1. it can be seen from Fig. 3(c) that the synchronization is achieved rapidly. Figure 3(d) shows that the impulsive synchronization is unstable when k=−1.2, δ=0.1, and ξ=1. The 4 lines in Figs. 3(c) and (d) show the evolution of e 1,e 2,e 3, and e 4, respectively.

6 Conclusions

In this paper, we studied the control and synchronization of a new unified hyperchaotic system. The control gains and impulsive intervals are both variable. The conditions for global asymptotic stability were derived, and the upper bound of impulsive interval is given. The results presented in this paper may be useful for designing a communication system with a high security level.