Hopf bifurcations in a predator-prey system of population allelopathy with a discrete delay and a distributed delay

Abstract

A delayed Lotka–Volterra predator-prey system of population allelopathy with discrete delay and distributed maturation delay for the predator population described by an integral with a strong delay kernel is considered. By linearizing the system at the positive equilibrium and analyzing the associated characteristic equation, the asymptotic stability of the positive equilibrium is investigated and Hopf bifurcations are demonstrated. Furthermore, the direction of Hopf bifurcation and the stability of the bifurcating periodic solutions are determined by the normal form theory and the center manifold theorem for functional differential equations. Finally, some numerical simulations are carried out for illustrating the theoretical results.

1 Introduction

In recent years, a large number of population models, especially the Lotka–Volterra predator-prey models modeled by ordinary differential equations (ODEs), have been proposed and studied extensively since the pioneering theoretical works by Lotka [1] and Volterra [2]. With the modification of Brelot [3], the model has the form

$$ \left \{ \begin{array}{rcl} \dot{x}(t) &=& x(t)[r_{1} - a_{11}x(t) \\[5pt] && - a_{12}\int^{t}_{-\infty}F(t -s)y(s)\,ds],\\[5pt] \dot{y}(t) &=& y(t)[-r_{2} + a_{21}\int^{t}_{-\infty}G(t -s)x(s)\,ds\\[5pt] && - a_{22}y(t)], \end{array} \right . $$

(1)

where r _i >0, a _ij >0, (i,j=1,2) and $\int_{0}^{\infty}F(s)\,ds=1$, $\int_{0}^{\infty}G(s)\,ds=1$.

Systems such as (1) with various delay kernels and delayed intraspecific competitions have been investigated extensively by many researchers; see [4–13]. When F(s)=δ(s−τ) (τ≥0) and G(s)=δ(s−η) (η≥0), namely, system (1) has two different discrete delays, He [14] and Lu and Wang [15] investigated the stability of the positive equilibrium of the system, and they found that the positive equilibrium is globally asymptotically stable for any values of delays τ and η when the coefficients of the system satisfy the condition a ₁₁ a ₂₂−a ₁₂ a ₂₁>0. In addition, under the condition that η>0, by considering η as the bifurcation parameter and using the linearization method, Faria [5] investigated the stability of the positive equilibrium of system (1) and the Hopf bifurcation of nonconstant periodic solutions near the positive equilibrium, and the normal form of Hopf bifurcations was also given by using the normal form theory and the center manifold theorem developed by Faria and Magalhes [16]. Following Faria [5], some researchers pay attention to stage-structured population models. For the predator-prey system, see [17–21]. For the study of system (1) with delayed intraspecific competitions, one can refer to [7, 10, 11, 22].

When one of F(s) and G(s) is taken as the Dirac delta function δ(s−τ), then system (1) has two different styles delay, discrete delay and distributed delay. These types of models have been considered in [8, 23, 25]. For example, assume that F(s)=δ(s−τ) (τ≥0), then system (1) is reduced to the following Lotka–Volterra two-species predator-prey system with a discrete delay and a distributed delay:

$$ \left \{ \begin{array}{rcl} \dot{x}(t) &=& x(t)[r_{1} - a_{11}x(t) - a_{12}y(t-\tau)],\\[5pt] \dot{y}(t) &=& y(t)[-r_{2} + a_{21}\int^{t}_{-\infty}G(t -s)x(s)\,ds\\[5pt] & & - a_{22}y(t)], \end{array} \right . $$

(2)

where the nonnegative constant τ can be interpreted as the hunting delay of the predator population. The delay kernel function G(s) may take the so-called “weak” generic kernel function G(s)=αe ^−αs (α>0) and “strong” generic kernel function G(s)=α ² se ^−αs (α>0), where the “weak” generic kernel implies that the importance of events in the past simply decreases exponentially the further one looks into the past while the “strong” generic kernel implies that a particular time in the past is more important than any other [24]. When G(s) takes the “weak” generic kernel function and the “strong” generic kernel function G(s)=α ² se ^−αs (α>0), Song and Yuan [8] and Zhang, Yan, and Cui [25] separately investigated the stability of the positive equilibrium of system (2) and Hopf bifurcations of nonconstant periodic solutions by using the linearization method and regarding the discrete hunting delay τ as the bifurcation parameter; by using the normal form theory and the center manifold reduction for FDEs [26, 27], Song and Yuan [8] and Zhang, Yan, and Cui [25] also studied the direction of the Hopf bifurcations and the stability of bifurcated periodic solutions occurring through Hopf bifurcations.

In the real nature world, some species may produce substances which are toxic or stimulatory to the others while they themselves do not experience any reciprocal effects. For example, some species of poisonous snake release toxic substance to control prey during the process of prey. The production of toxic substance by the predator species will not be instantaneous, but mediated by some time lag [6, 28–30]. From this viewpoint and to reflect the nature fact actively, we have modified the model of (2); therefore, by considering that one specie produces a substance toxic to the other during the process of prey, but only when the other is present. Then the system (2) can be written as

$$ \left \{ \begin{array}{rcl} \dot{x}(t) &=& x(t)[k_{1} - \alpha_{1}x(t) - \beta_{12}y(t)\\ [5pt] && -\gamma_{1}x(t)y(t-\tau)],\\ [5pt] \dot{y}(t) &=& y(t)[-k_{2} +\alpha_{2}\int^{t}_{-\infty}G(t -s)x(s)\,ds\\ [5pt] && - \beta_{21}y(t)], \end{array} \right . $$

(3)

where G(s)=α ² se ^−αs (α>0), k _i >0, α _i >0, β _ij >0, γ _i >0 (i,j=1,2). We have investigated the bifurcation behavior on time delay of this modified dynamical system (3). It has also been observed that time delay can drive the competitive system to sustained oscillations, as shown by Hopf bifurcation analysis and limit cycle stability. Hence, interaction between the time delay effect produced by delayed toxin and other distributed delay can regulate the densities of different competing species in the aquatic ecosystem, thus influencing seasonal succession, blooms and pulses. To the best of our knowledge, no such attempts have been taken to include interaction between the time delay effect produced by delayed toxin and other distributed delay in a predator-prey system. Therefore, this research might be helpful to the study of predator-prey model and related problem in biological system.

This paper is organized as follows. In Sect. 2, by linearizing the resulting four-dimensional system at the positive equilibrium and analyzing the associated characteristic equation, it is found that under suitable conditions on the parameters the positive equilibrium is asymptotically stable when the delay is less than a certain critical value and unstable when the delay is greater than this critical value. Meanwhile, according to the Hopf bifurcation theorem for functional differential equations (FDEs), we find that the system can also undergo a Hopf bifurcation of nonconstant periodic solution at the positive equilibrium when the delay crosses through a sequence of critical values. In Sect. 3, to determine the direction of the Hopf bifurcations and the stability of bifurcated periodic solutions occurring through Hopf bifurcations, an explicit algorithm is given by applying the normal form theory and the center manifold reduction for FDEs developed by Hassard, Kazarinoff and Wan [31]. To verify our theoretical predictions, some numerical simulations are also included in Sect. 4.

2 Stability of equilibria and existence of Hopf bifurcations

The equilibrium points of system (3) for τ=0 are as follows:

where

$$x^{*}=\frac{-l_{1}+s}{2\alpha_{2}\gamma_{1}}, $$

$$y^{*}=\frac{-l_{2}+s}{2\beta_{21}\gamma_{1}} $$

and

$$l_{1}= \alpha_{1}\beta_{21}+\alpha_{2} \beta_{12}-\gamma_{1}k_{2}, $$

$$l_{2}= \alpha_{1}\beta_{21}+\alpha_{2} \beta_{12}+\gamma_{1}k_{2}, $$

$$\mbox{\fontsize{9.4}{10.5}\selectfont $\displaystyle s= \sqrt{(\alpha_{1}\beta_{21}+\alpha_{2}\beta_{12}-\gamma_{1}k_{2})^{2} +4\alpha_{2}\gamma_{1}(\beta_{12}k_{2}+\beta_{21}k_{1})}$.} $$

E(x ^∗,y ^∗) is a unique positive equilibrium when the condition

$$ (\mathrm{H1})\quad k_{1}\alpha_{2}-k_{2} \alpha_{1}>0 $$

holds. Throughout this section, we always assume that the condition (H1) holds.

Clearly, the characteristic equation of the linearized system of system (3) at the equilibrium E ₀(0,0) is (λ−k ₁)(λ+k ₂)=0, which has two real roots, k ₁>0, −k ₂<0. Therefore, the equilibrium E ₀(0,0) is unstable and is a saddle point of system (3). The characteristic equation of linearized system of system (3) at the equilibrium $E_{1}(0,-\frac{k_{2}}{\beta_{21}})$ is $(\lambda-k_{2})(\lambda-\frac{\beta_{12}k_{2} +\beta_{21}k_{1}}{\beta_{21}})=0$, which has two real roots, k ₂>0, $\frac{\beta_{12}k_{2}+\beta_{21}k_{1}}{\beta_{21}}>0$. Therefore, the equilibrium $E_{1}(0,-\frac{k_{2}}{\beta_{21}})$ is an unstable node of system (3). The characteristic equation at the equilibrium $E_{2}(\frac{k_{1}}{\alpha_{1}},0)$ resulting from the linear system (3) has the form

$$ (\lambda+k_{1}) \biggl(\lambda-\frac{\alpha_{2}k_{1}-\alpha_{1}k_{2}}{\alpha_{1} } \biggr)=0. $$

(4)

Under the condition (H1), Eq. (4) has a negative real root −k ₁ and a positive real root $\frac{\alpha_{2}k_{1}-\alpha_{1}k_{2}}{\alpha_{1}}$. Therefore, the equilibrium $E_{2}(\frac{k_{1}}{\alpha_{1}},0)$ is unstable and is also a saddle point of system (3) when the condition (H1) is satisfied.

In what follows, we investigate the stability of the positive equilibrium E(x ^∗,y ^∗) of system (3). To this end, we define the new variables u(t) and v(t) by

$$u(t)=\int^{t}_{-\infty}\alpha^{2}(t-s)e^{-\alpha(t-s)}x(s) \,ds $$

and

$$v(t)=\int^{t}_{-\infty}\alpha e^{-\alpha(t-s)}x(s)\,ds. $$

Then according to the law of solving the derivative for an integral with parameterized variables, one can observe that

$$ \left \{ \begin{array}{rcl} \dot{u}(t) &=& \alpha v(t)-\alpha u(t),\\[5pt] \dot{v}(t) &=& \alpha x(t)-\alpha v(t). \end{array} \right . $$

(5)

By means of (5), system (3) can be transformed into the following four-dimensional system of FDEs with a discrete delay:

(6)

and the equilibrium E(x ^∗,y ^∗) of system (3) is transformed into the equilibrium E ^∗(x ^∗,y ^∗,x ^∗,x ^∗) of system (6). Thus, the stability study of equilibrium E(x ^∗,y ^∗) of system (3) is equivalent to the stability study of equilibrium E ^∗(x ^∗,y ^∗,x ^∗,x ^∗) of system (6).

Under the assumption (H1), let x ₁(t)=x(t)−x ^∗, x ₂(t)=y(t)−y ^∗, x ₃(t)=u(t)−x ^∗, x ₄(t)=v(t)−x ^∗. Then system (6) is equivalent to the following four-dimensional system:

(7)

where

and the positive equilibrium E ^∗(x ^∗,y ^∗,x ^∗,x ^∗) of system (6) is transformed into the zero equilibrium (0,0,0,0) of system (7). It is easy to see that the characteristic equation of the linearized system of system (7) at the zero equilibrium (0,0,0,0) is

$$ \lambda^{4}+a_{3}\lambda^{3}+a_{2} \lambda^{2}+a_{1}\lambda +a_{0}+b_{0}e^{-\lambda\tau}=0, $$

(8)

where

(9)

It is well known that the stability of the zero equilibrium (0,0,0,0) of system (7) is determined by the real parts of the roots of Eq. (8). If all roots of Eq. (8) locate the left-half complex plane, then the zero equilibrium (0,0,0,0) of system (7) is asymptotically stable. If Eq. (8) has a root with positive real part, then the zero solution is unstable. Therefore, to study the stability of the zero equilibrium (0,0,0,0) of system (7), an important problem is to investigate the distribution of roots in the complex plane of the characteristic equation (8).

For Eq. (8), according to the Routh–Hurwitz criterion, we have the following result.

Lemma 2.1

If b ₀ and positive constants a _k (k=0,1,2,3) defined by (9) satisfy the condition:

$$(\mathrm{H2})\quad a_{1}a_{2}a_{3}-a_{1}^{2}>(a_{0}+b_{0})a_{3}^{2}, $$

then all roots of Eq. (8) have negative real parts when τ=0, and hence the zero equilibrium (0,0,0,0) of system (7) with τ=0 is asymptotically stable.

Next, we consider the effects of a positive delay τ on the stability of the zero equilibrium (0,0,0,0) of system (7). Since the roots of the characteristic equation (8) depend continuously on τ, a change of τ must lead to a change of the roots of Eq. (8). If there is a critical value of τ such that a certain root of (8) has zero real part, then at this critical value the stability of the zero equilibrium (0,0,0,0) of system (7) will switch, and under certain conditions a family of small amplitude periodic solutions can bifurcate from the zero equilibrium (0,0,0,0); that is, a Hopf bifurcation occurs at the zero equilibrium (0,0,0,0).

Now, we look for the conditions under which the characteristic equation (8) has a pair of purely imaginary roots, see [32]. Clearly, iω(ω>0) is a root of Eq. (8) if and only if ω satisfies the following equation:

Separating the real and imaginary parts of the above equation yields the following equations:

$$ \left \{ \begin{array}{rcl} \omega^{4}-a_{2}\omega^{2}+a_{0} &=& -b_{0}\cos\omega\tau,\\[5pt] -a_{3}\omega^{3}+a_{1}\omega&=& b_{0}\sin\omega\tau. \end{array} \right . $$

(10)

Adding up the squares of the corresponding sides of the above equations yields the following algebra equation with respect to ω:

(11)

Let z=ω ², and denote

(12)

Then Eq. (11) can be denoted simply as the following equation:

$$ z^{4}+az^{3}+bz^{2}+cz+d=0. $$

(13)

If Eq. (13) has positive real roots, then the characteristic equation (8) has a pair of purely imaginary roots at the associated critical value of τ; otherwise, (8) has no purely imaginary root.

From the definition of b ₀, a _k (k=0,1,2,3), we have

(14)

In order to study the bifurcation of system (3), Eq. (13) should have at least a positive real root. Therefore, we suppose

Let h(z)=z ⁴+az ³+bz ²+cz+d=0. Then $\dot {h}(z)=4z^{3}+3az^{2}+2bz+c$. Noticing that a>0, b>0 and the condition (H3), therefore, $\dot{h}(z)>0$ on (0,+∞), and hence h(z) is strictly monotonically increasing on (0,+∞). Thus, h(z) has a unique positive root if d<0 and h(z) has no positive root when d>0.

Now, suppose that d<0 and that the unique positive root of h(z) is denoted by z ₀. Then the unique positive root of Eq. (11) is $\omega_{0}=\sqrt{z_{0}}$. From the first equation of (10), we know that the value of τ associated with ω ₀ should satisfy

$$ \cos\omega_{0}\tau=\frac{a_{2}\omega_{0}^{2}- \omega_{0}^{4}-a_{0}}{b_{0}}. $$

(15)

If we define

(16)

then when τ=τ _j (j=0,1,2,3,…), Eq. (8) has a pair of purely imaginary roots ±iω ₀.

Let λ(τ)=α(τ)+iω(τ) be a root of Eq. (8) near τ=τ _j satisfying α(τ _j )=0 and ω(τ _j )=ω ₀. For this pair of conjugate complex roots, we have the following result.

Lemma 2.2

$$\frac{d\alpha(\tau)}{d\tau}\biggl|_{\tau=\tau_{j}}>0,\quad (j=0,1,2,3,\ldots). $$

Proof

It is similar to the proof of Lemma 2.2 in [25].

From the above discussion and the Hopf bifurcation theorem of FDEs [26, 31], we can obtain the following results on the stability of the zero equilibrium of system (7), that is, the stability of the positive equilibrium E(x ^∗,y ^∗) of system (3). □

Theorem 2.3

Suppose that the coefficients k _i , α _i (i=1,2) in system (3) satisfy the condition (H1). Let α>0, (H2) and (H3) hold. Then the following results hold.

• (i) If d≥0, then the positive equilibrium E(x ^∗,y ^∗) of system (3) is absolutely stable, that is, asymptotically stable for any values of τ≥0.

• (ii) If d<0, then E(x ^∗,y ^∗) is asymptotically stable when 0≤τ<τ ₀ and unstable when τ>τ ₀. In addition when τ crosses through each τ _j (j=0,1,2,3,…), system (3) can undergo a Hopf bifurcation at the positive equilibrium E(x ^∗,y ^∗), that is, a family of nonconstant periodic solutions can bifurcate from the positive equilibrium E(x ^∗,y ^∗) when τ crosses through each critical value τ _j (j=0,1,2,3,…).

3 Properties of Hopf bifurcations

In the previous section, we studied mainly the stability of the positive equilibrium E(x ^∗,y ^∗) of system (3) and the existence of Hopf bifurcations at the positive equilibrium E(x ^∗,y ^∗).

In this section, we shall study the properties of the Hopf bifurcations obtained by Theorem 2.3 and the stability of bifurcated periodic solutions occurring through Hopf bifurcations by using the normal form theory and the center manifold reduction for retarded functional differential equations (RFDEs) due to Hassard, Kazarinoff and Wan [31]. To guarantee the existence of the above Hopf bifurcations, throughout this section, we always assume that the conditions (H1), (H2), and (H3) hold and that d<0. Under these conditions, for fixed j∈{0,1,2,3,…}, let τ=τ _j +μ; then μ=0 is the Hopf bifurcation value of system (3) at the positive equilibrium E(x ^∗,y ^∗). Since system (3) is equivalent to system (7), in the following discussion we shall consider mainly system (7).

In system (7), let $\bar{x}_{k}(t)=x_{k}(\tau t)$ and drop the bars for simplicity of notation. Then system (7) can be rewritten as a system of RFDEs in C([−1,0],R ⁴) of the form

$$ \left \{ \begin{array}{rcl} \dot{x_{1}} &=& (\tau_{j}+\mu)[M x_{1}(t)+N x_{2}(t)+Q x_{2}(t-1)\\[5pt] && +a_{11}x_{1}^{2}(t)+a_{12}x_{1}(t)x_{2}(t)\\ [5pt] & & +a_{13}x_{1}(t)x_{2}(t-1)+a_{14}x_{1}^{2}(t)x_{2}(t-1)],\\[5pt] \dot{x_{2}} &=& (\tau_{j}+\mu)[Dx_{2}(t)+Ex_{3}(t)+b_{11}x_{2}^{2}(t)\\ [5pt] & & +b_{12}x_{2}(t)x_{3}(t)],\\ [5pt] \dot{x_{3}} &=& (\tau_{j}+\mu)[-\alpha x_{3}(t)+\alpha x_{4}(t)],\\ [5pt] \dot{x_{4}} &=& (\tau_{j}+\mu)[\alpha x_{1}(t)-\alpha x_{4}(t)]. \end{array} \right . $$

(17)

Define the linear operator L(μ):C→R ⁴ and the nonlinear operator f(⋅,μ):C→R ⁴ by

(18)

and

(19)

respectively, where ϕ=(ϕ ₁,ϕ ₂,ϕ ₃,ϕ ₄)^T∈C, and let x=(x ₁,x ₂,x ₃,x ₄).

By the Riesz representation theorem, there exists a 4×4 matrix function η(θ,μ), −1≤θ≤0, whose elements are of bounded variation such that

$$L_{\mu}\phi=\int^{0}_{-1}\,d\eta(\theta, \mu)\phi(\theta) \quad \mbox{for } \phi\in C\bigl([-1,0],R^{4}\bigr). $$

In fact, we can choose

$$ \eta(\theta,\mu)=(\tau_{j}+\mu)\eta_{0} \delta(\theta) -(\tau_{j}+\mu)\eta_{-1}\delta(\theta+1), $$

(20)

where

For ϕ∈C ¹([−1,0],R ⁴), define

$$ A(\mu)\phi=\left \{ \begin{array}{l@{\quad}l} \frac{d\phi(\theta)}{d\theta}, & \theta\in[-1,0), \\[5pt] \int^{0}_{-1}\,d\eta(\mu,\theta)\phi(\theta), & \theta=0, \end{array} \right . $$

(21)

and

$$ R(\mu)\phi= \left \{ \begin{array}{l@{\quad}l} 0, & \theta\in[-1,0), \\ [5pt] f(\mu,\phi), & \theta=0. \end{array} \right . $$

(22)

Then system (17) is equivalent to

$$ \dot{x}_{t}=A(\mu)x_{t}+R(\mu)x_{t}. $$

(23)

For ψ∈C ¹([0,1],(R ⁴)^∗), define

$$ A^{*}\psi=\left \{ \begin{array}{l@{\quad}l} -\frac{d\psi(s)}{ds}, & s\in(0,1], \\[5pt] \int^{0}_{-1}\,d\eta(t,0)\psi(-t), & s=0, \end{array} \right . $$

(24)

and a bilinear inner product

(25)

where η(θ)=η(θ,0). Then A(0) and A ^∗ are adjoint operators. In addition, from Sect. 2, we know that ±iω ₀ τ _j are eigenvalues of A(0). Thus, they are also eigenvalues of A ^∗. Let q(θ) be the eigenvector of A(0) corresponding to iω ₀ τ _j and q ^∗(s) is the eigenvector of A ^∗ corresponding to −iω ₀ τ _j .

Let $q(\theta)=(1,v_{1},v_{2},v_{3})e^{i\omega_{0}\tau_{j}\theta}$ and $q^{*}(s)=G(1,\allowbreak v_{1}^{*},v_{2}^{*},v_{3}^{*})e^{i\omega_{0}\tau_{j}s}$. From the above discussion, it is easy to know that

that is,

and

Thus, we can easily obtain

Since

We may choose $\bar{G}$ as

$$ G=\frac{1}{1+\bar{v}_{1}v_{1}^{*}+\bar{v}_{2}v_{2}^{*}+\bar{v}_{3}v_{3}^{*} +\tau_{j}e^{i\omega_{0}\tau_{j}}Q\bar{v}_{1}}, $$

(26)

which assures that 〈q ^∗(s),q(θ)〉=1.

By using the same notations as in [31], we first compute the coordinates to describe the center manifold C ₀ at μ=0. Let x _t be the solution of Eq. (17) when μ=0. Define

$$ z(t)=\bigl\langle q^{*},x_{t}\bigr\rangle, \quad W(t, \theta)=x_{t}(\theta)-2\Re\bigl\{z(t)q(\theta )\bigr\}. $$

(27)

On the center manifold C ₀, we have $W(t,\theta)=W(z(t), \bar{z}(t),\theta)$ where

(28)

z and $\bar{z}$ are local coordinates for center manifold C ₀ in the direction of q ^∗ and $\bar{q^{*}}$. Note that W is real if x _t is real. We consider only real solutions. For solution x _t ∈C ₀ of (17), since μ=0,

(29)

that is,

$$ \dot{z}(t)=i\omega_{0}\tau_{j}z(t)+g(z, \bar{z}), $$

(30)

where

$$ g(z,\bar{z})=g_{20}\frac{z^{2}}{2}+g_{11}z \bar{z}+g_{02}\frac{\bar{z}^{2}}{2} +g_{21}\frac{z^{2}\bar{z}}{2}+ \cdots. $$

(31)

Then it follows from (27) that

(32)

It follows together with (19) that

Comparing the coefficients with (31), we obtain

Since there are W ₂₀(θ) and W ₁₁(θ) in g ₂₁, we still need to compute them.

From (23) and (27), we have

(33)

where

$$ H(z,\bar{z},\theta)=H_{20}(\theta)\frac{z^{2}}{2}+H_{11}( \theta)z\bar{z} +H_{02}(\theta)\frac{\bar{z}^{2}}{2}+\cdots. $$

(34)

Substituting the corresponding series into (33) and comparing the coefficients, we obtain

(35)

From (33), we know that for θ∈[−1,0),

(36)

Comparing the coefficients with (34) gives that

$$ H_{20}(\theta)=-g_{20}q(\theta)- \bar{g}_{02}\bar{q}(\theta) $$

(37)

and

$$ H_{11}(\theta)=-g_{11}q(\theta)- \bar{g}_{11}\bar{q}(\theta). $$

(38)

From (35) and (37), we get

$$\dot{W}_{20}(\theta)=2i\omega_{0}\tau_{j}W_{20}( \theta) +g_{20}q(\theta)+\bar{g}_{02}\bar{q}(\theta). $$

Note that $q(\theta) = q(0)e^{i\omega_{0}\tau_{j}\theta}$, hence we obtain

(39)

Similarly, from (35) and (38), we have

$$\dot{W}_{11}(\theta)=g_{11}q(\theta)+\bar{g}_{11} \bar{q}(\theta) $$

and

(40)

In what follows, we shall seek appropriate E ₁ and E ₂ in (39) and (40), respectively. It follows from the definition of A and (35) that

$$ \int_{-1}^{0}\,d\eta( \theta)W_{20}(\theta)=2i\omega_{0}\tau_{j}W_{20}(0)-H_{20}(0) $$

(41)

and

$$ \int_{-1}^{0}\,d\eta( \theta)W_{11}(\theta)=-H_{11}(0), $$

(42)

where η(θ)=η(0,θ). From (33), we have

(43)

and

(44)

Substituting (39) and (43) into (41), we obtain

(45)

From the definition of A, we have

$$\int_{-1}^{0}e^{2i\omega_{0}\tau_{j}\theta}\,d\eta(\theta) =A( \mu)e^{2i\omega_{0}\tau_{j}\theta} =L_{\mu}\bigl(e^{2i\omega_{0}\tau_{j}\theta}\bigr). $$

Therefore, when μ=0, we have

Therefore,

(46)

where λ=iω ₀. Similarly, substituting (39) and (44) into (42), we get

(47)

It follows from (39), (40), (46), and (47) that g ₂₁ can be expressed. Thus, we can compute the following values:

(48)

which determine the quantities of bifurcating periodic solutions at the critical value τ _j . Specifically, μ ₂ determines the directions of the Hopf bifurcation: if μ ₂>0 (μ ₂<0), then the Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solutions exist for τ>τ _j (τ<τ _j ); β ₂ determines the stability of the bifurcating periodic solutions: the bifurcating periodic solutions in the center manifold are stable (unstable) if β ₂<0 (β ₂>0); and T ₂ determines the period of the bifurcating periodic solutions: the period increase (decrease) if T ₂>0 (T ₂<0). Further, it follows from Lemma 2.2 and (48) that the following results about the direction of the Hopf bifurcations hold.

Theorem 3.1

Suppose that (H ₁),(H ₂),(H ₃) hold and d<0. If ℜ(c ₁(0))<0 (ℜ(c ₁(0))>0), then system (3) can undergo a supercritical (subcritical) Hopf bifurcation at the positive equilibrium E(x ^∗,y ^∗) when τ crosses through the critical values τ _j . In addition, the bifurcated periodic solutions occurring through Hopf bifurcations are orbitally asymptotically stable on the center manifold if ℜ(c ₁(0))<0 and unstable if ℜ(c ₁(0))>0.

4 Numerical simulations

In this section, we give some numerical simulations for a special case of system (3) to support our analytical results obtained in Sects. 2 and 3. As an example, we consider system (3) with the coefficients k ₁=2,α ₁=1,β ₁₂=1,γ ₁=2.6,k ₂=1,α ₂=1.2,β ₂₁=1, that is,

(49)

Obviously, k ₂ α ₁<k ₁ α ₂; therefore, system (49) has a unique positive equilibrium E(1.04678,0.25613). In addition, a _k (k=0,1,2,3) and b ₀ given by (9) become b ₀=0.87564α ², a ₀=0.76839α ², a ₁=0.89332α+2.00000α ², a ₂=α ²+4.00000α+0.44666, a ₃=2α+2.00000. Therefore,

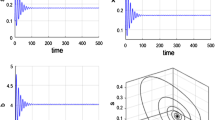
for any α>0. This shows that condition (H2) holds, and from Lemma 2.1 we know that the positive equilibrium E(1.04678,0.25613) of system (49) is asymptotically stable when τ=0 (see Fig. 1).

Fig. 1

The numerical approximations of system (49) when τ=0 and α=1. The positive equilibrium E(1.04678,0.25613) is asymptotically stable

On the other hand, since $d=a_{0}^{2}-b_{0}^{2}= -0.17631\alpha^{4}$, the positive equilibrium E(1.04678,0.25613) of system (49) is conditionally stable. In this case, if we take α=1, then a,b,c,d defined by (14) are a=5.10668, b=8.05636, c=0.00093, d=−0.17631, then (13) becomes

(50)

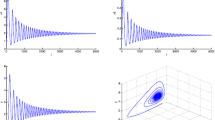
By means of the software Maple14, one can find that the unique approximately positive solution of system (50) is z ₀≈0.14150, and hence ω ₀≈0.37619. Thus, the τ _j (j=0,1,2,…) defined by (16) are τ _j =4.22951+16.70308j (j=0,1,2,…). From Theorem 2.3, we know that the positive equilibrium E(1.04678,0.25613) of system (49) is asymptotically stable when 0≤τ<τ ₀=4.22951 and unstable when τ>τ ₀=4.22951, and system (49) can also undergo a Hopf bifurcation at the positive equilibrium E(1.04678,0.25613) when τ crosses through the critical values τ _j =4.22951+16.70308j (j=0,1,2,…), i.e., a family of periodic solutions bifurcate from E(1.04678,0.25613) (see Figs. 2 and 3).

Fig. 2

The numerical approximations of system (49) when τ=4 and α=1. The positive equilibrium E(1.04678,0.25613) is asymptotically stable

Fig. 3

The numerical approximations of system (49) when τ=4.5 and α=1. The positive equilibrium E(1.04678,0.25613) is unstable and a stable periodic solution bifurcates from E