The Hopf bifurcation and stability of delayed predator–prey system

Abstract

In this paper, a mathematical model consisting of three populations with discrete time delays is considered. By analyzing the corresponding characteristic equations, the local stability of each of the feasible equilibria of the system is addressed and the existence of Hopf bifurcations at the coexistence equilibrium is established. The direction of the Hopf bifurcations and the stability of the bifurcating periodic solutions are analyzed using the theory of normal form and center manifold. Discussion with some numerical simulation examples is given to support the theoretical results.

1 Introduction

Over the last decade, the dynamic behavior of predator–prey systems has received much attention from many applied mathematicians and ecologists. Many theoreticians and experimentalists have investigated the stability of such systems when time delays are incorporated into the models. Time delay may have very complicated impact on the dynamic behavior of the system such as the periodic structure, and bifurcation. For references, see El Foutayeni and Khaladi (2016), Akkocaoglu et al. (2013), Çelik (2008, 2009, 2011), Chen (2007), Xuedi et al. (2015), Fowler and Ruxton (2002), Gause (1934), Gopalsamy (1980) and Hadjiavgousti and Ichtiaroglou (2008).

In El Foutayeni and Khaladi (2016), authors have considered a delayed ratio-dependent predator–prey system with stage structure for the predator,

$$\begin{aligned} \left\{ \begin{array}{l} \dot{x}_{1}\left( t\right) =r_{1}x_{1}\left( 1-x_{1}/K\right) -c_{12}x_{1}x_{2}-a_{13}x_{1}y, \\ \dot{x}_{2}\left( t\right) =r_{2}x_{2}\left( 1-x_{2}/K\right) -c_{21}x_{1}x_{2}-a_{23}x_{2}y, \\ \dot{y}=-\mathrm{{d}}y+\delta _{1}x_{1}y+\delta _{2}x_{2}y-\alpha _{1}x_{1}(t-\tau _{1})y-\alpha _{2}x_{2}(t-\tau _{2})y, \end{array} \right. \end{aligned}$$

(1)

where $x_{1}(t)$, $x_{2}(t)$ and y(t) be the density of fish populations at time t. Let $r_{1}$ and $r_{2}$ be the growth coefficients of the first and second populations, respectively, and K be the environmental carrying capacity, which is common for both the preys. Let $c_{ij}$ be the coefficient of competition between the population i and population j. Let $a_{ij}$ be the predation rate coefficient. Let d be the natural death rate of the third population, $\delta _{1}$ and $\delta _{2}$ be the maximum predator conversion rates. Let $\tau _{1}$, $\tau _{2}$ be the discrete time lags in the mortality of predator by two preys $x_{1}(t)$, $x_{2}(t)$, respectively.

In Sarkar et al. (2006), the authors have studied the equilibrium points and their stability properties: they have obtained conditions for the existence of different equilibria and discussed their stabilities in the cases: non-delay model, single delay model, and multiple delays model.

The purpose of the present paper is to study system (1) in view of bifurcation. The study of the stability of the system (1) is based on the detailed analysis of the distribution of the characteristic equation associated to this system. First, we investigate the stability of the fixed point and the existence of the Hopf bifurcations, and then we move to determine the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions.

This paper is organized as following. In Sect. 2, we analyze the distribution of the characteristic equation associated with the system (1) using the method of Ruan and Wei (2001, 2003), and then we get the existence of the local Hopf bifurcation. We note that the phenomenon of stability switch exist when the time delay varies. In Sect. 3, based on the normal form theory and center manifold argument presented in Hassard et al. (1981), we determine the direction and stability of periodic solutions bifurcating from the Hopf bifurcation. Finally, we discuss and illustrate the results found based on some numerical simulation examples.

2 Local stability of the interior equilibrium point and Hopf bifurcation

Following El Foutayeni and Khaladi (2016), we confirm that the system (1) has seven equilibrium points. But this system has a unique positive equilibrium point $P^{*}(x_{1}^{*},x_{2}^{*},y^{*}),$ where

$$\begin{aligned} \begin{array}{l} x_{1}^{*}=\frac{K\left( a_{23}r_{1}-a_{13}r_{2}\right) \left( \delta _{2}-\alpha _{2}\right) +d\left( a_{13}r_{2}-c_{12}a_{23}K\right) }{\left( a_{13}r_{2}-c_{12}a_{23}K\right) \left( \delta _{1}-\alpha _{1}\right) +\left( a_{23}r_{1}-a_{13}r_{2}\right) \left( \delta _{2}-\alpha _{2}\right) }, \\ \\ x_{2}^{*}=\frac{K\left( a_{13}r_{2}-a_{23}r_{1}\right) \left( \delta _{1}-\alpha _{1}\right) +d\left( a_{23}r_{1}-c_{21}a_{13}K\right) }{\left( a_{13}r_{2}-c_{12}a_{23}K\right) \left( \delta _{1}-\alpha _{1}\right) +\left( a_{23}r_{1}-a_{13}r_{2}\right) \left( \delta _{2}-\alpha _{2}\right) }, \\ \\ y^{*}=\frac{r_{1}\left( K-x_{1}^{*}\right) -c_{21}x_{2}^{*}}{ a_{13}K}. \end{array} \end{aligned}$$

We analyze the local stability of the positive interior equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ using the linear transformation $z_{1}\left( t\right) =x_{1}\left( t\right) -x_{1}^{*},$ $z_{2}\left( t\right) =x_{2}\left( t\right) -x_{2}^{*}$ and $z_{3}\left( t\right) =y\left( t\right) -y^{*}$ where $z_{1}\ll 1,$ $z_{2}\ll 1$ and $z_{3}\ll 1$ for which the system (1) can be written as

$$\begin{aligned} \left\{ \begin{array}{l} \dot{z}_{1}\left( t\right) =-\frac{r_{1}}{K}x_{1}^{*}z_{1}-c_{12}x_{1}^{*}z_{2}-a_{13}x_{1}^{*}z_{3}-\frac{r_{1}}{K} z_{1}^{2}-c_{12}z_{1}z_{2}-a_{13}z_{1}z_{3}, \\ \dot{z}_{2}\left( t\right) =-\frac{r_{2}}{K}x_{2}^{*}z_{2}-c_{21}x_{2}^{*}z_{1}-a_{23}x_{2}^{*}z_{3}-\frac{r_{2}}{K} z_{2}^{2}-c_{21}z_{1}z_{2}-a_{23}z_{2}z_{3}, \\ \dot{z}_{3}\left( t\right) =\left( \delta _{1}z_{1}+\delta _{2}z_{2}\right) y^{*}-\left[ \alpha _{1}z_{1}(t-\tau _{1})+\alpha _{2}z_{2}(t-\tau _{2}) \right] y^{*} \\ \qquad \qquad +(\delta _{1}z_{1}+\delta _{2}z_{2})z_{3}-\left[ \alpha _{1}z_{1}(t-\tau _{1})+\alpha _{2}z_{2}(t-\tau _{2})\right] z_{3}. \end{array} \right. \end{aligned}$$

(2)

Therefore, the corresponding characteristic equation of system (2) is given by

$$\begin{aligned} \lambda ^{3}+m_{2}\lambda ^{2}+m_{1}\lambda +m_{0}+\left( n_{1}\lambda +n_{0}\right) e^{-\lambda \tau _{1}}+\left( p_{1}\lambda +p_{0}\right) e^{-\lambda \tau _{2}}=0, \end{aligned}$$

(3)

where

$$\begin{aligned} \left\{ \begin{array}{l} m_{2}=\left( r_{1}x_{1}^{*}+r_{2}x_{2}^{*}\right) /K, \\ m_{1}=x_{1}^{*}x_{2}^{*}\left( r_{1}r_{2}/K^{2}-c_{12}c_{21}\right) +\left( a_{13}\delta _{1}x_{1}^{*}+a_{23}\delta _{2}x_{2}^{*}\right) , \\ m_{0}=x_{1}^{*}x_{2}^{*}y^{*}\left[ \left( a_{13}r_{2}/K-c_{12}a_{23}\right) \delta _{1}+\left( a_{23}r_{1}/K-c_{21}a_{13}\right) \delta _{2}\right] , \\ n_{1}=-a_{13}\alpha _{1}x_{1}^{*}y^{*}, \\ n_{0}=-\alpha _{1}x_{1}^{*}x_{2}^{*}y^{*}\left( a_{13}r_{2}/K-c_{12}a_{23}\right) , \\ p_{1}=-a_{23}\alpha _{2}x_{2}^{*}y^{*}, \\ p_{0}=-\alpha _{2}x_{1}^{*}x_{2}^{*}y^{*}\left( a_{23}r_{1}/K-c_{21}a_{13}\right) . \end{array} \right. \end{aligned}$$

Now we study the distribution of roots of the transcendental Eq. (3) using the Corollary 2.4 of Ruan and Wei (2003). The system (1) has two time delays $\left( \tau _{1}\text { and }\tau _{2}\right)$, then we have the following cases.

Case 1: $\tau _{1}=0$ and $\tau _{2}=0$

The characteristic Eq. (3) becomes

$$\begin{aligned} \lambda ^{3}+m_{2}\lambda ^{2}+(m_{1}+n_{1}+p_{1})\lambda +m_{0}+n_{0}+p_{0}=0. \end{aligned}$$

(4)

It is clear that $m_{2}>0$, $(m_{1}+n_{1}+p_{1})>0$ and $\left( m_{0}+n_{0}+p_{0}\right) >0$. Therefore, by Routh–Hurwitz criterion, we can confirm that all roots of (4) have negative real parts under the following condition:

$$\begin{aligned} (H1)\text { }m_{2}(m_{1}+n_{1}+p_{1})>m_{0}+n_{0}+p_{0}. \end{aligned}$$

To be specific, the equilibrium interior point $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ is locally asymptotically stable when the condition (H1) satisfies.

Case 2: $\tau _{1}>0$ and $\tau _{2}=0$

The Eq. (3) becomes

$$\begin{aligned} \lambda ^{3}+m_{2}\lambda ^{2}+\left( m_{1}+p_{1}\right) \lambda +m_{0}+p_{0}+\left( n_{1}\lambda +n_{0}\right) e^{-\lambda \tau _{1}}=0. \end{aligned}$$

(5)

Suppose iw ($w>0$) being a root of Eq. (5). Separating the real and imaginary parts gives

$$\begin{aligned} \left\{ \begin{array}{l} n_{0}\sin w\tau _{1}-n_{1}w\cos w\tau _{1}=-w^{3}+(m_{1}+p_{1})w, \\ n_{0}\cos w\tau _{1}+n_{1}w\sin w\tau _{1}=m_{2}w+(m_{0}+p_{0}) \end{array} \right. \end{aligned}$$

(6)

which leads to

$$\begin{aligned} w^{6}+b_{22}w^{4}+b_{21}w^{2}+b_{20}=0, \end{aligned}$$

(7)

where $b_{22}=m_{2}^{2}-2(m_{1}+p_{1}),$ $b_{21}=(m_{1}+p_{1})^{2}-2m_{2}(m_{0}+p_{0})-n_{1}^{2}$ and $b_{20}=(m_{0}+p_{0})^{2}-n_{0}^{2}.$

On substituting $v=w^{2},$ then Eq. (7) becomes

$$\begin{aligned} v^{3}+b_{22}v^{2}+b_{21}v+b_{20}=0. \end{aligned}$$

(8)

Let

$$\begin{aligned} g(v)=v^{3}+b_{22}v^{2}+b_{21}v+b_{20} \end{aligned}$$

(9)

We have $g(0)=b_{20},$ $\lim _{v\rightarrow \infty }g(v)=+\infty$, and

$$\begin{aligned} g^{^{\prime }}(v)=3v^{2}+2b_{22}v+b_{21}. \end{aligned}$$

(10)

The discussion about the roots of Eq. (10) [is similar to that in Song and Wei (2004)] leads to the following lemma.

Lemma 1

For the polynomial Eq. (8), we have the following results:

• (i) Eq. (8) has at least one positive root if $\left( H21\right) \ b_{20}<0$.

• (ii) Eq. (8) has no positive roots if $\left( H22\right)$ $b_{20}\ge 0$, and $\Delta =b_{22}^{2}-3b_{21}\le 0$.

• (iii) Eq. (8) has positive roots if $\left( H23\right) \ b_{20}\ge 0$, and $\Delta =b_{22}^{2}-3b_{21}>0,$ $v_{1}^{*}=\left( -b_{22}+\sqrt{ \Delta }\right) /3>0,$ $g(v_{1}^{*})\le 0$.

Without loss of generality, we suppose that Eq. (8) has tree positive roots, denoted as $v_{1}$, $v_{2}$ and $v_{3}$, respectively. Therefore, Eq. (7) has three positive roots $w_{k}=\sqrt{v_{k}}$, $k=1,2,3.$ The corresponding critical value of time delay $\tau _{1k}^{\left( j\right) }$ is

$$\begin{aligned} \tau _{1k}^{(j)}=\frac{1}{w_{k}}\arccos \left( \frac{ A_{24}w_{k}^{4}+A_{22}w_{k}^{2}+A_{20}}{B_{22}w_{k}^{2}+B_{20}}\right) + \frac{2j\pi }{w_{k}},{ \ \ }k=1,2,3;\text { }j=0,1,2,\ldots , \end{aligned}$$

where

$$\begin{aligned} A_{20}= & {} -\left( m_{0}+p_{0}\right) n_{0},\text { }A_{22}=m_{2}n_{0}-\left( m_{1}+p_{1}\right) n_{1},\text { }A_{24}=n_{1}, \\ B_{20}= & {} n_{0}^{2},\text { }B_{22}=n_{1}^{2}. \end{aligned}$$

Then $\pm \, iw_{k}$ is a pair of purely imaginary roots of Eq. (3) with $\tau _{1}=\tau _{1k}^{(j)}$, $\tau _{2}=0$.

Following the Hopf bifurcation theorem (Hassard et al. 1981), we must verify the transversality condition. Differentiating Eq. (5) with respect to $\tau _{1}$, and noticing that $\lambda$ is a function of $\tau _{1}$, it follows that

$$\begin{aligned} \left( \frac{d\lambda }{d\tau _{1}}\right) ^{-1}=\frac{(3\lambda ^{2}+m_{2}\lambda +m_{1}+p_{1})e^{\lambda \tau _{1}}}{\lambda (n_{1}\lambda +n_{0})}+\frac{n_{1}}{\lambda (n_{1}\lambda +n_{0})}-\frac{\tau _{1}}{ \lambda }. \end{aligned}$$

(11)

Thus,

$$\begin{aligned} \alpha ^{^{\prime }}\left( \tau _{k}^{(j)}\right) ^{-1}={\text {Re}}\left( \frac{d\lambda }{d\tau _{1}}\right) ^{-1} = {\text {Re}}\left[ \frac{ (3\lambda ^{2}+m_{2}\lambda +m_{1}+p_{1})e^{\lambda \tau _{1}}}{\lambda (n_{1}\lambda +n_{0})}\right] + {\text {Re}}\left[ \frac{n_{1}}{\lambda (n_{1}\lambda +n_{0})}\right] . \end{aligned}$$

Notice that sign$\left\{ \frac{d{\text {Re}}\lambda }{d\tau _{1}}\right\} _{\lambda =iw_{k}}= \,\,$sign$\left\{ {\text {Re}}\left( \frac{d\lambda }{d\tau _{1}} \right) ^{-1}\right\} _{\lambda =iw_{k}}$.

Then sign$\left\{ \frac{d{\text {Re}}\lambda }{d\tau _{1}}\right\} _{\lambda =iw_{k}} = \left( 3w_{k}^{6}+2b_{22}w_{k}^{4}+b_{21}w_{k}^{2}\right) /\Lambda =g ^{^{\prime }}\left( v_{k}^{2}\right) /\Lambda .$

Therefore, $\left\{ \frac{d{\text {Re}}\lambda }{d\tau _{1}}\right\} \ne 0$ if $\left( H24\right)$$g^{^{^{\prime }}}\left( v_{k}^{2}\right) \ne 0.$

Summarizing the above analysis, we can assure existence of the stability interval. Let I be the stability interval. Then, we have the following results.

Theorem 1

• (i) The positive equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ is asymptotically stable for all $\tau _{1}\ge 0,$ if (H22) holds.

• (ii) The positive equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ is asymptotically stable for all $\tau _{1}\in I$, if (H23) or (H21) and (H24) holds.

• (iii) The system (2) undergoes a Hopf bifurcation at the equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ when $\tau _{1}=\tau _{1k}^{(j)}$ $(j=0,1,2,...),$ if all conditions as stated in (ii) hold.

Case 3: $\tau _{1}=0$ , $\tau _{2}>0$

The analysis is the same as case 2, we have the following results.

Theorem 2

• (i) The positive equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ is asymptotically stable for all $\tau _{2}\ge 0$.

• (ii) The positive equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ is asymptotically stable for all $\tau _{2}\in I.$

• (iii) The system (2) undergoes a Hopf bifurcation at the equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ when $\tau _{2}=\tau _{2k}^{(j)}$ $(j=0,1,2,...),$ where $\tau _{2k}^{(j)}$ represents the minimum critical value of time delay $\tau _{2}$ for the occurrence of Hopf bifurcation when $\tau _{1}=0.$

Case 4: $\tau _{1}=\tau _{2}=\tau \ne 0$

The calculation is very similar to case 2, we have the following results.

Theorem 3

• (i) The positive equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ is asymptotically stable for all $\tau \in I.$

• (ii) The system (2) undergoes a Hopf bifurcation at the equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ when $\tau =\tau _{k},$ where $\tau _{k}$ represents the minimum critical value of time delay $\tau$ for the occurrence of Hopf bifurcation.

Case 5: $\tau _{2}>0,\tau _{1}\in I$ and $\tau _{1}\ne \tau _{2}$

We suppose that $i\omega (\omega >0)$ is the root of Eq. (3), then we get

$$\begin{aligned} \left\{ \begin{array}{l} -\omega ^{3}+m_{1}\omega +n_{1}\omega \cos \omega \tau _{1}-n_{0}\sin \omega \tau _{1}=p_{0}\sin \omega \tau _{1}-p_{1}\omega \cos \omega \tau _{2}, \\ m_{2}\omega ^{2}-m_{0}-n_{0}\cos \omega \tau _{1}-n_{1}\sin \omega \tau _{1}=p_{1}\omega \sin \omega \tau _{2}+p_{0}\cos \omega \tau _{1}, \end{array} \right. \end{aligned}$$

(12)

From Eq. (12), we can obtain

$$\begin{aligned}{}[\omega ^{4}+E_{1}\omega ^{2}+E_{2}]\omega ^{2}+E_{3}+[F_{1}\omega ^{2}+F_{2}]\omega \sin \omega \tau _{1}+[G_{1}\omega ^{4}+G_{2}\omega ^{2}+G_{3}]\cos \omega \tau _{1}=0, \end{aligned}$$

(13)

where

$$\begin{aligned} E_{1}= & {} m_{2}^{2}-2m_{1},\text { } E_{2}=m_{1}^{2}-2m_{0}m_{2}+n_{1}^{2}-p_{1}^{2}\text {, } E_{3}=m_{1}^{2}-2m_{0}m_{2}+n_{1}^{2}-p_{1}^{2}\text {,} \\ F_{1}= & {} 2n_{0}-2n_{1}m_{2}\text {, }F_{2}=2n_{1}m_{0}-2n_{0}m_{1}\text {,} \\ G_{1}= & {} -2n_{1},\text { }G_{2}=2n_{1}m_{1}-2n_{0}m_{2}\text {, } G_{3}=m_{0}n_{0}. \end{aligned}$$

We assume that: (H51) Eq. (13) has at least finite positive root. Without loss of generality, we suppose that Eq. (13) has N positive roots, denoted by $\omega _{i}$, ($i=1,2,....,N$). Notice Eq. (12), we get $\tau _{2i}^{(j)}$, $i=1,2,...,N$ ; $j=0,1,2,...$

Let $\ \tau _{2}^{0}=\tau _{2i_{0}}^{(0)}=min\{\tau _{2i}^{(0)}\}$, $\omega _{0}=\omega _{i0},$ and $\lambda (\tau _{2})=\alpha (\tau _{2})+i\omega (\tau _{2})$ be the root of Eq. (3) satisfying $\alpha (\tau _{2i}^{(j)})=0$ , $\omega (\tau _{2i}^{(j)})=\omega _{i}$. By computation, we obtain

$$\begin{aligned} \left\{ {\text {Re}}\left( \frac{d\lambda }{d\tau _{1}}\right) ^{-1}\right\} _{\lambda =i\omega _{i}}=\frac{p_{1}^{2}\omega _{0}^{4}+p_{0}^{2}\omega _{0}^{2}}{\Delta }, \end{aligned}$$

where $\Delta =L_{1}\sin \omega _{0}(\tau _{1}^{*}+\tau _{2}^{0})+L_{2}\cos \omega _{0}(\tau _{1}^{*}+\tau _{2}^{0})+L_{3}\sin \omega _{0}\tau _{2}^{0}+L_{4}\cos \omega _{0}\tau _{2}^{0}-p_{1}\omega _{0}^{2},$

$L_{1}=n_{1}p_{1}\tau _{1}^{*}\omega _{0}^{3}-n_{0}p_{0}\tau _{1}^{*}\omega _{0}+n_{1}p_{0}\omega _{0},$ $L_{2}=(n_{0}p_{1}\tau _{1}^{*}+n_{1}p_{0}\tau _{1}^{*}-n_{1}p_{1})\omega _{0}^{2},$

$L_{3}=p_{0}(n_{1}\omega _{0}+3\omega _{0}^{3})+2m_{2}n_{1}\omega _{0}^{3},$ $L_{4}=2m_{2}p_{0}\omega _{0}^{2}-n_{1}\omega _{0}(m_{1}\omega _{0}+3\omega _{0}^{3}).$

According to the analysis above, if $\Big \{ {\text {Re}}\left( \frac{d\lambda }{d\tau _{1}}\right) ^{-1}\Big \} _{\lambda =i\omega _{i}}\ne 0,$ then we have the following results.

Theorem 4

• (i) The positive equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ is asymptotically stable for all $\tau _{1}\in I.$

• (ii) If the condition (H51) is hold and $\Big \{ {\text {Re}}\left( \frac{d\lambda }{d\tau _{1}}\right) ^{-1}\Big \} _{\lambda =i\omega _{i}}\ne 0$, then system (2) undergoes a Hopf bifurcation at the equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$, when $\tau _{2}=\tau _{2}^{0}.$

Case 6: $\tau _{1}>0,\tau _{2}\in I$ and $\tau _{1}\ne \tau _{2}$

We consider (3) with $\tau _{2}$ in its stable interval, and $\tau _{1}$ is regarded as a parameter. The analysis is very similar to case 5, we can obtain the following theorem.

Theorem 5

• (i) The positive equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$ is asymptotically stable for all $\tau _{2}\in I.$

• (ii) The system (2) undergoes a Hopf bifurcation at the equilibrium $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})$, when $\tau _{1}=\tau _{1}^{0},$ where $\tau _{1}^{0}$ represents the minimum critical value of time delay $\tau _{1}$ for the occurrence of Hopf bifurcation when $\tau _{2}$ $\in I$.

3 Stability and direction of the Hopf bifurcation

In Sect. 2, we have shown that the system (2) undergoes Hopf bifurcation when $\tau _{2}=\tau _{2}^{0}$. In this section, we shall study the direction of Hopf bifurcation and the stability of bifurcating periodic solutions of system (2) when $\tau _{2}=\tau _{2}^{0},$ based on the normal form theory and center manifold theorem (Hassard et al. 1981).

Without loss of generality, we assume that $\tau _{2}^{0}>\tau _{1}^{*}$.

Letting $\tau _{2}=\tau _{2}^{0}+\eta$, $\varphi _{t}(\theta )=\varphi (t+\theta )\in C$ and $L_{\eta }:C\rightarrow \mathbb {R}^{3}$, denote $F: \mathbb {R}\times C\rightarrow \mathbb {R}^{3}$. Therefore, the system (2) can be written as a functional differential equation (FDE) in $C=C([-\tau _{1}^{*},0],\mathbb {R}^{3})$

$$\begin{aligned} \dot{\varphi }(t)=L_{\eta }(\varphi _{t})+f(\eta ,\varphi _{t}), \end{aligned}$$

(14)

where

$$\begin{aligned} L_{\mu }\chi =M_{1}\chi (0)+M_{2}\chi (-\tau _{1}^{*})+M_{3}\chi (-\tau _{2}^{0}), \end{aligned}$$

and

$$\begin{aligned} M_{1}=\left( \begin{array}{c@{\quad }c@{\quad }c} -\frac{r_{1}}{K}x_{1}^{*} &{} -c_{12}x_{1}^{*} &{} -a_{13}x_{1}^{*} \\ -c_{21}x_{2}^{*} &{} -\frac{r_{2}}{K}x_{2}^{*} &{} -a_{23}x_{2}^{*} \\ \delta _{1}y^{*} &{} \delta _{1}y^{*} &{} 0 \end{array} \right) ,\text { }M_{2}=\left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ -\alpha _{1}y^{*} &{} 0 &{} 0 \end{array} \right) , \end{aligned}$$

$$\begin{aligned} \text { }M_{3}=\left( \begin{array}{c@{\quad }c@{\quad }c} 0 &{} 0 &{} 0 \\ 0 &{} 0 &{} 0 \\ 0 &{} -\alpha _{2}y^{*} &{} 0 \end{array} \right) ,\text { }\chi (t)=\left( \chi _{1}(t),\chi _{2}(t),\chi _{3}(t)\right) ^{T} \end{aligned}$$

and

Then, by the Riesz representation theorem, there exists a $3\times 3$ matrix function $g(\theta ,\eta )$ of bounded variation for $\theta \in [-\tau _{1}^{*},0],$ such that

$$\begin{aligned} L_{\eta }\chi =\int \limits _{-\tau _{1}^{*}}^{0}\mathrm{d}g(\theta ,\eta )\chi (\theta ),\quad \text { }\forall \chi \in C. \end{aligned}$$

In fact, one can choose

$$\begin{aligned} g(\theta ,\eta )=\left\{ \begin{array}{ll} M_{1}+M_{2},&{} \quad \theta =0, \\ M_{3},&{} \quad \theta \in [-\tau _{2}^{0},0), \\ -M_{2}\delta (\theta +\tau _{1}^{*}),&{} \quad \theta \in [-\tau _{1}^{*},-\tau _{2}^{0}), \end{array} \right. \end{aligned}$$

where $\delta (\theta )= {\left\{ \begin{array}{ll} \begin{array}{ll} 0,&{}{ \ }\theta \ne 0 \\ 1,&{}{ \ }\theta =0 \end{array}. \end{array}\right. }$

For $\chi \in C^{1}([-\tau _{1}^{*},0],\mathbb {R}^{3})$, we define $M(\eta )\chi$ and $R(\eta )\chi$ as

$$\begin{aligned} M(\eta )\chi =\left\{ \begin{array}{ll} \frac{d\chi (\theta )}{d\theta }, &{}\quad \theta \in [-\tau _{1}^{*},0) \\ \int _{-\tau _{1}^{*}}^{0}dg(\xi ,\eta )\chi (\xi ),&{}\quad \theta =0 \end{array}, \right. \quad \mathrm{and }\quad R(\eta )\chi =\left\{ \begin{array}{ll} 0,&{}\quad { \ }\theta \in [-\tau _{1}^{*},0), \\ f(\eta ,\chi ),&{}\quad { \ }\theta =0. \end{array} \right. \end{aligned}$$

Hence, the system (14) can be written as the following operator equation:

$$\begin{aligned} \dot{\varphi }_{t}=M(\eta )\varphi _{t}+R(\eta )\varphi _{t}. \end{aligned}$$

For $\psi \in C^{1}([0,1],(\mathbb {R}^{3})^{*})$, where $(\mathbb {R} ^{3})^{*}$ is the three-dimensional space of row vectors. We define the adjoint operator $M^{*}$of M(0) as

$$\begin{aligned} M^{*}\chi =\left\{ \begin{array}{l} -\frac{d\chi (s)}{ds},s\in (0,\tau _{1}^{*}], \\ \int _{-\tau _{1}^{*}}^{0}dg^{T}(t,\theta )\chi (-t),s=0, \end{array} \right. \end{aligned}$$

For $\chi \in C^{1}([-\tau _{1}^{*},0],\mathbb {R}^{3})$ and $\psi \in C^{1}([0,1],(\mathbb {R}^{3})^{*})$, using the bilinear form

$$\begin{aligned} \langle \psi ,\chi \rangle =\bar{\psi }^{T}(0)\chi (0)-\int _{-\tau _{1}^{*}}^{0}\int _{\xi =0}^{0}\bar{\psi }^{T}(\xi -\theta )\mathrm{d}g(\theta )\chi (\xi )d\xi . \end{aligned}$$

(15)

In Sect. 2, we have shown that $\pm i\omega _{0}$ are eigenvalues of M(0). Hence, they are eigenvalues of $M^{*}$.

Suppose that $\rho (\theta )=\rho (0)e^{i\omega _{0}\theta }$ is an eigenvector of M(0) corresponding to the eigenvalue $i\omega _{0}$. Therefore, $M(0)=i\omega _{0}\rho (\theta )$. When $\theta =0$, we can get

$$\begin{aligned} \left[ i\omega _{0}I-\int _{-\tau _{1}^{*}}^{0}dg(\theta )e^{i\omega _{0}} \right] \rho (0)=0, \end{aligned}$$

which yields $\rho (0)=(1,e_{1},e_{2})^{T}$, where

$$\begin{aligned} e_{1}= & {} \frac{(i\omega _{0}K+r_{1}x_{1}^{*})a_{23}x_{2}^{*}-c_{21}a_{13}Kx_{1}^{*}x_{2}^{*}}{(i\omega _{0}K+r_{2}x_{2}^{*})a_{13}x_{1}^{*}-c_{12}a_{23}Kx_{1}^{*}x_{2}^{*}}, \\&\\ e_{2}= & {} \frac{c_{12}c_{21}K^{2}x_{1}^{*}x_{2}^{*}-(i\omega _{0}K+r_{1}x_{1}^{*})(r_{2}x_{2}^{*}+i\omega _{0}K)}{(i\omega _{0}K+r_{2}x_{2}^{*})a_{13}Kx_{1}^{*}-c_{12}a_{23}K^{2}x_{1}^{*}x_{2}^{*}}. \end{aligned}$$

Similarly, it can be verified that $\rho ^{*}(s)=D(1,e_{1}^{*},e_{2}^{*})e^{i\omega _{0}s}$ is the eigenvector of $M^{*}$ corresponding to $-i\omega _{0}$, with

$$\begin{aligned} e_{1}^{*}= & {} \frac{(r_{1}x_{1}^{*}-i\omega _{0}K)a_{23}x_{2}^{*}-c_{21}a_{13}Kx_{1}^{*}x_{2}^{*}}{(r_{2}x_{2}^{*}-i\omega _{0}K)a_{13}x_{1}^{*}-c_{12}a_{23}Kx_{1}^{*}x_{2}^{*}}, \\&\\ e_{2}^{*}= & {} \frac{c_{12}c_{21}K^{2}x_{1}^{*}x_{2}^{*}-(r_{1}x_{1}^{*}-i\omega _{0}K)(r_{2}x_{2}^{*}-i\omega _{0}K)}{ (i\omega _{0}K+r_{2}x_{2}^{*})a_{13}kx_{1}^{*}-c_{12}a_{23}K^{2}x_{1}^{*}x_{2}^{*}}. \end{aligned}$$

Then, from (15), we obtain

$$\begin{aligned} \langle {\rho }^{*}{(s),\rho (0)}\rangle= & {} \bar{D}{(1, \bar{e}_{1}^{*},\bar{e}_{2}^{*})(1,e_{1},e_{2})}^{T} \\&{-}\int _{-\tau _{1}^{*}}^{0}\int _{\xi =0}^{\theta }{(1, \bar{e}_{1}^{*},\bar{e}_{2}^{*})e}^{-i\omega _{0}(\xi -\theta )} {\mathrm{d}g(\theta )(1,e_{1},e_{2})}^{T}{e}^{i\omega _{0}\xi }{d\xi } \\= & {} 1+e{_{1}\bar{e}_{1}^{*}}+e{_{2}\bar{e}_{2}^{*}} -\int _{-\tau _{1}^{*}}^{0}{(1,\bar{e}_{1}^{*},\bar{e} _{2}^{*})}\theta e^{i\omega _{0}\theta }dg(\theta )({1,e_{1},e_{2})}^{T} \\= & {} 1+e{_{1}\bar{e}_{1}^{*}}+e{_{2}\bar{e}_{2}^{*}} -\int _{-\tau _{1}^{*}}^{0}{(1,\bar{e}_{1}^{*},\bar{e} _{2}^{*})}\theta e^{i\omega _{0}\theta }dg(\theta )({1,e_{1},e_{2})}^{T} \\= & {} 1+e{_{1}\bar{e}_{1}^{*}}+e{_{2}\bar{e}_{2}^{*}} +\tau _{1}^{*}\alpha _{1}{\bar{e}_{2}^{*}y}^{*}e^{-i\omega _{0}\tau _{1}^{*}}+\tau _{2}^{0}\alpha _{1}e{_{1} \bar{e}_{2}^{*}y}^{*}e^{-i\omega _{0}\tau _{2}^{0}}. \end{aligned}$$

Then, we can choose $\overline{D}$ as

$$\begin{aligned} \overline{D}=\frac{1}{1+e{_{1}\bar{e}_{1}^{*}}+e{_{2} \bar{e}_{2}^{*}}+\tau _{1}^{*}\alpha _{1}{\bar{e}_{2}^{*}y }^{*}e^{-i\omega _{0}\tau _{1}^{*}}+\tau _{2}^{0}\alpha _{1}e{_{1}\bar{e}_{2}^{*}y}^{*}e^{-i\omega _{0}\tau _{2}^{0}}}, \end{aligned}$$

such that $\left<\rho ^{*},\rho \right>=1.$

We can obtain the coefficients used in determining the direction of Hopf bifurcation and the stability of the bifurcation periodic solutions using the algorithms in Hassard et al. (1981) and using a similar calculation process in Song and Wei (2004)

$$\begin{aligned} g_{20}= & {} 2\overline{D}\left[ -\frac{r_{1}}{K}-c_{12}e_{1}-a_{13}e_{2}- {\bar{e}_{1}^{*}}(c_{21}e_{1}+\frac{r_{2}}{K} e_{1}^{2}+a_{23}e_{1}e_{2})\right] \\&+2\overline{D}\left[ {\bar{e}_{2}^{*}}(\delta _{1}e_{2}+\delta _{2}e_{1}e_{2}-\alpha _{1}e_{2}e^{-i\omega _{0}\tau _{1}^{*}}-\alpha _{2}e_{1}e_{2}e^{-i\omega _{0}\tau _{2}^{0}})\right] \end{aligned}$$

$$\begin{aligned} g_{11}= & {} \overline{D}\{-\frac{2r_{1}}{K}-c_{12}(e_{1}+{\bar{e} _{1}^{*}})-a_{13}(e_{2}+{\bar{e}_{2}^{*}}) \\&-\,{\bar{e}_{1}^{*}}[a_{23}(e_{1}+{\bar{e}_{1}^{*}})+2 \frac{r_{2}}{K}e_{1}{\bar{e}_{1}^{*}}+a_{23}(e_{1}{\bar{e} _{2}^{*}+\bar{e}_{1}^{*}}e_{2})] \\&+\,{\bar{e}_{2}^{*}}[\delta _{1}(e_{2}+{\bar{e}_{2}^{*} })\delta _{2}(e_{1}{\bar{e}_{2}^{*}+\bar{e}_{1}^{*}} e_{2})-\alpha _{1}(e_{2}e^{i\omega _{0}\tau _{1}^{*}}+{\bar{e} _{2}^{*}}e^{-i\omega _{0}\tau _{1}^{*}}) \\&-\,\alpha _{2}({\bar{e}_{1}^{*}}e_{2}e^{i\omega _{0}\tau _{2}^{0}}+e_{1}{\bar{e}_{2}^{*}}e^{-i\omega _{0}\tau _{2}^{0}})]\} \end{aligned}$$

$$\begin{aligned} g_{02}= & {} 2\overline{D}\left[ -\frac{r_{1}}{K}-c_{12}{\bar{e} _{1}^{*}}-a_{13}{\bar{e}_{2}^{*}}-{\bar{e}_{1}^{*}} (c_{21}{\bar{e}_{1}^{*}}+\frac{r_{2}}{k}{\bar{e}_{1}^{*2}}+a_{23}{\bar{e}_{1}^{*}\bar{e}_{2}^{*}})\right] \\&+\,2\overline{D}{\bar{e}_{2}^{*}}(\delta _{1}{\bar{e} _{2}^{*}}+\delta _{2}{\bar{e}_{1}^{*}\bar{e}_{2}^{*}} -\alpha _{1}{\bar{e}_{2}^{*}}e^{-i\omega _{0}\tau _{1}^{*}}-\alpha _{2}{\bar{e}_{1}^{*}\bar{e}_{2}^{*}}e^{-i\omega _{0}\tau _{2}^{0}}) \end{aligned}$$

and

$$\begin{aligned} g_{21}= & {} \overline{D}\Bigg \{-\frac{r_{1}}{K}\left[ 4W_{11}^{(1)}(0)+2W_{20}^{(1)}(0)\right] -{\bar{e}_{1}^{*}}\frac{ r_{2}}{K}\left[ 4W_{11}^{(2)}(0)+2W_{20}^{(2)}(0)\right] \\&-\,c_{12}\left[ 2W_{11}^{(2)}(0)+W_{20}^{(2)}(0)+2e{_{1}} W_{11}^{(1)}(0)+{\bar{e}_{1}}W_{20}^{(1)}(0)\right] \\&-\,a_{13}\left[ 2W_{11}^{(3)}(0)+W_{20}^{(3)}(0)+2e{_{2}} W_{11}^{(1)}(0)+{\bar{e}_{2}}W_{20}^{(1)}(0)\right] \\&+\,{\bar{e}_{1}^{*}}c_{21}\left[ 2W_{11}^{(2)}(0)+W_{20}^{(2)}(0)+2e{_{1}}W_{11}^{(1)}(0)+{\bar{e}_{1}}W_{20}^{(1)}(0)\right] \\&+\,{\bar{e}_{1}^{*}}c_{21}\left[ 2e{_{1}}W_{11}^{(3)}(0)+ {\bar{e}_{1}}W_{20}^{(3)}(0)+2e{_{2}}W_{11}^{(2)}(0)+{\bar{e}_{2}}W_{20}^{(2)}(0)\right] \\&+\,{\bar{e}_{2}^{*}}\delta _{1}\left[ 2W_{11}^{(3)}(0)+W_{20}^{(3)}(0)+2e{_{2}}W_{11}^{(1)}(0)+{\bar{e}_{2}}W_{20}^{(1)}(0)\right] \\&+\,{\bar{e}_{2}^{*}}\delta _{2}\left[ 2e{_{1}} W_{11}^{(3)}(0)+{\bar{e}_{1}}W_{20}^{(3)}(0)+2e{_{2}} W_{11}^{(2)}(0)+{\bar{e}_{2}}W_{20}^{(2)}(0)\right] \\&-\,{\bar{e}_{2}^{*}}\alpha _{1}\left[ 2e^{-i\omega _{0}\tau _{1}^{*}}W_{11}^{(3)}(0)+e^{i\omega _{0}\tau _{1}^{*}}W_{20}^{(3)}(0)+2e{_{2}}W_{11}^{(1)}\left( -\frac{\tau _{1}^{*}}{\tau _{2}^{0}}\right) \right] \\&-\,{\bar{e}_{2}^{*}}\alpha _{1}{\bar{e}_{2}}W_{20}^{(1)}\left( - \frac{\tau _{1}^{*}}{\tau _{2}^{0}}\right) -{\bar{e}_{2}^{*}}\alpha _{2}{\bar{e}_{2}}W_{20}^{(2)}(-1) \\&\phantom {\left\{ -\frac{r_{1}}{K}\left[ 4W_{11}^{(1)}(0)+2W_{20}^{(1)}(0)\right] -{\bar{e}_{1}^{*}}\frac{ r_{2}}{K}\left[ 4W_{11}^{(2)}(0)+2W_{20}^{(2)}(0)\right] \right. }-\,{\bar{e}_{2}^{*}}\alpha _{2}\left[ 2ae^{-i\omega _{0}\tau _{1}^{*}}W_{11}^{(3)}(0)+\overline{a}e^{i\omega _{0}\tau _{1}^{*}}W_{20}^{(3)}(0)+2e{_{2}}W_{11}^{(2)}(-1)\right] \Bigg \}. \end{aligned}$$

However,

$$\begin{aligned} W_{20}(\theta )= & {} \frac{ig_{20}}{\omega _{0}}\rho (\theta )e^{i\omega _{0}\theta }+\frac{i\overline{g}_{20}}{3\omega _{0}}\bar{\rho }(\theta )e^{-i\omega _{0}\theta }+V_{1}e^{2i\omega _{0}\theta }, \\ W_{11}(\theta )= & {} -\frac{ig_{11}}{\omega _{0}}\bar{\rho }(\theta )e^{i\omega _{0}\theta }+\frac{i\overline{g}_{11}}{\omega _{0}}\bar{\rho }(\theta )e^{-i\omega _{0}\theta }+V_{2}, \end{aligned}$$

Fig. 1

The interior equilibrium point is stable when $\tau _{1}=7$ and $\tau _{2}=0,$ with the initial condition (0.1, 0.1, 4)

Fig. 2

The interior equilibrium point is stable when$\tau _{1}=13$ and $\tau _{2}=0,$ with the initial condition (0.1, 0.1, 4)

Fig. 3

The interior equilibrium point is stable when $\tau _{1}=6$ and $\tau _{2}=5,$ with the initial condition (0.1, 0.1, 4)

Fig. 4

The interior equilibrium point is stable when $\tau _{1}=15$ and $\tau _{2}=8,$ with the initial condition (0.1, 0.1, 4)

where $V_{1}=(V_{1}^{(1)},V_{1}^{(2)},V_{1}^{(3)})\in \mathbb {R}^{3}$ and $V_{2}=(V_{2}^{(1)},V_{2}^{(2)},V_{2}^{(3)})\in \mathbb {R}^{3}$ are the constant vectors and they are determined by the following equations, respectively,

$$\begin{aligned} \left( \begin{array}{ccc} 2i\omega _{0}+\frac{r_{1}x_{1}^{*}}{K} &{} {c}_{12}{x} _{1}^{*} &{} {a}_{13}{x}_{1}^{*} \\ {c}_{21}{x}_{2}^{*} &{} {2i\omega }_{0}{+} \frac{r_{2}x_{2}^{*}}{K} &{} {a}_{23}{x}_{2}^{*} \\ {-\delta }_{1}{y}^{*}{+\alpha }_{1}{y}^{*}{e}^{-2i\omega _{0}\tau _{1}^{*}} &{} {-\delta }_{2}{y}^{*}{+\alpha }_{2}{y}^{*}{e}^{-2i\omega _{0}\tau _{2}^{0}} &{} {2i\omega }_{0} \end{array} \right) {V}_{1}{=2}\left( \begin{array}{l} N_{1} \\ N_{2} \\ N_{3} \end{array} \right) \end{aligned}$$

$$\begin{aligned} \left( \begin{array}{ccc} \frac{r_{1}x_{1}^{*}}{k} &{} {c}_{12}{x}_{1}^{*} &{} {a}_{13}{x}_{1}^{*} \\ {c}_{21}{x}_{2}^{*} &{} \frac{r_{2}x_{2}^{*}}{k} &{} {a}_{23}{x}_{2}^{*} \\ {(\alpha }_{1}{-\delta }_{1}{)y}^{*} &{} {(\alpha }_{2}{-\delta }_{2}{)y}^{*} &{} {0} \end{array} \right) {V}_{2}{=}\left( \begin{array}{l} P_{1} \\ P_{2} \\ P_{3} \end{array} \right) \end{aligned}$$

with

$$\begin{aligned} N_{1}= & {} {-}\frac{r_{1}}{K}{-c_{12}e_{1}-a}_{13}{e}_{2} \\ N_{2}= & {} {-}\frac{r_{2}}{K}{e_{1}^{2}-c_{21}e_{1}-a}_{23}e_{1} {e}_{2} \\ N_{3}= & {} {\delta }_{1}{e}_{2}{+\delta }_{2}e_{1}{e} _{2}{-\alpha }_{1}{e}_{2}{e}^{-i\omega _{0}\tau _{1}^{*}}{-\alpha }_{2}{e}_{1}{e}_{2}{e} ^{-i\omega _{0}\tau _{2}^{0}} \\ P_{1}= & {} {-}\frac{2r_{1}}{K}{-c_{12}(e_{1}+\bar{e}_{1})-a}_{13} {(e_{2}+\bar{e}_{2})} \\ P_{2}= & {} {-}\frac{2r_{2}}{K}{e_{1}\bar{e}_{1}-c_{21}(e_{1}+\bar{e} _{1})-a}_{23}{(e_{1}\bar{e}_{2}+e_{2}\bar{e}_{1})} \\ P_{3}= & {} {\delta }_{1}{(e_{2}+\bar{e}_{2})+\delta }_{2}{(e_{1}\bar{e}_{2}+e_{2}\bar{e}_{1})-\alpha }_{1}{(e_{2}e}^{-i\omega _{0}\tau _{1}^{*}}{+\bar{e}_{2}e}^{-i\omega _{0}\tau _{1}^{*}} {)} \\&{-\alpha }_{2}{(e_{2}\bar{e}_{1}e} ^{i\omega _{0}\tau _{2}^{0}}{+\alpha }_{2}{e_{1}\bar{e}_{2}e} ^{-i\omega _{0}\tau _{2}^{0}}{)}. \end{aligned}$$

Then, we can express $g_{21}$ by the parameters.

One can see that each $g_{ij}$ can be expressed by the parameters. Thus, we can compute the following results:

$$\begin{aligned} \begin{array}{l} C_{1}(0)=\frac{i}{2\omega _{0}}(g_{11}g_{20}-2|g_{11}|^{2}-\frac{|g_{02}|^{2} }{3})+\frac{g_{21}}{2}, \\ \\ \eta _{2}=-\frac{Re(C_{1}(0))}{Re(\lambda ^{\prime }(\tau _{_{2}}^{0}))},\quad { }\beta _{2}=2Re(C_{1}(0)), \\ \\ T_{2}=-\frac{Im(C_{1}(0))+\mu _{2}Im(\lambda ^{\prime }(\tau _{2}^{0}))}{ \omega _{0}}. \end{array} \end{aligned}$$

(16)

Based on the discussions above, we have the following result.

Theorem 6

For system (2),

• (i) the direction of Hopf bifurcation is determined by the sign of $\eta _{2}$ : if $\eta _{2}>0$ $(\eta _{2}<0),$ then the Hopf bifurcation is supercritical (subcritical) and the bifurcating periodic solutions exist for $\tau _{2}>\tau _{2}^{0}$ $(\tau _{2}<\tau _{2}^{0})$.

• (ii) The stability of the bifurcating periodic solution is determined by the sign of $\beta _{2}$: the bifurcations periodic solutions are orbitally asymptotically stable (unstable) if $\tau _{2}>\tau _{2}^{0}$ $(\tau _{2}<\tau _{2}^{0})$. The period of the bifurcation periodic solutions is determined by the sign of $T_{2}$ : if $T_{2}>0$ $(T_{2}<0)$, the bifurcating periodic solutions increase (decrease).

4 Numerical simulations and discussion

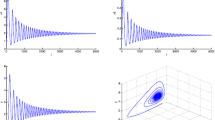
In this section, we will discuss the effect of single and multiple delays on the dynamics of the system (1). To achieve this goal, we take the parameter values as $r_{1}=2.5$, $r_{2}=2.3,$ $c_{12}=0.01,$ $c_{21}=0.03,$ $a_{13}=0.6,$ $a_{23}=0.55,$ $K=30,\ d=0.1,$ $\delta _{1}=0.4,$ $\delta _{2}=0.3,$ $\alpha _{1}=0.05,$ $\alpha _{2}=0.06$ (as the literature Sarkar et al. 2006). In this case, the positive interior equilibrium is $P^{*}(x_{1}^{*},x_{2}^{*},y^{*})=(0.15231,0.21301,4.1345)$. Using the parameter values above, we can confirm that the first condition (H1) is hold. When $\tau _{2}=0,$ we find that Eq. (7) has two positive roots $w_{1}=0.5278,$ $w_{2}=0.4190.$ Using these parameters in Eq. (6)  we get $\tau _{11}^{\left( j\right) }=7.0371+11.9045j>0$ and $\tau _{12}^{\left( j\right) }=11.6274+12.7969j>0$ $(j=0,1,...).$ When $\tau _{1}=\tau _{11}^{\left( j\right) }$ or $\tau _{1}=\tau _{12}^{\left( j\right) };$ then Eq. (4) has pure imaginary roots. Furthermore, we can note that $\alpha ^{^{\prime }}\left( \tau _{11}^{\left( j\right) }\right) >0$ and $\alpha ^{^{\prime }}\left( \tau _{12}^{\left( j\right) }\right) <0.$ When $\tau _{1}\in [0,7.0371)\cup (11.6247,18.9416)\cup \ldots \cup (114.0010,114.1776),$ by theorem 1,  the stability switches exist and the equilibrium $P^{*}$ is asymptotically stable. See Figs. 1 and 2.

When $\tau _{1}=6.02\in [0,7.0371),$ we get $\tau _{2}^{0}=5.5695.$ For $\tau _{2}\in [0,5.5695),$ by theorem 4,  the interior equilibrium $P^{*}$ is asymptotically stable. Moreover, using (16), we get $C_{1}(0)=-0.9734-1.0325i,$ $\beta _{2}=-1.9468<0$, $\eta _{2}=13.5851>0.$ When $\tau _{2}>\tau _{2}^{0}=5.5695,$ by theorem 6, the bifurcating periodic solution is orbitally asymptotically stable, and the direction of the Hopf bifurcation is supercritical.

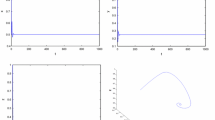
When $\tau _{1}=15.02\in (11.6274,18.9416),$ we get $\tau _{2}^{0}=8.8025.$ For $\tau _{2}\in [0,8.8025),$ by theorem 4,  the interior equilibrium $P^{*}$ is asymptotically stable. Furthermore, we get $C_{1}(0)=-1.4622-0.0365i,$ $\beta _{2}=-2.9244<0$, $\eta _{2}=22.9389>0.$ When $\tau _{2}>\tau _{2}^{0}=8.8025,$ by theorem 6,  the bifurcating periodic solution is orbitally asymptotically stable, and the direction of the hopf bifurcation is supercritical. See Figs. 3 and 4.

5 Conclusion

In this paper, we have analyzed a mathematical model consisting of three populations with discrete time delays. We have studied the stability behavior of the system around the interior equilibrium point for six cases. In the case of $\tau _{1}=\tau _{2}=0$ (system without delays), we find out that the interior equilibrium is asymptotically stable. In the case of $\tau _{2}=0$ ($\tau _{1}=0$),  we observe that the interior equilibrium is asymptotically stable when $\tau _{1}$ ($\tau _{2}$) varies. In the case of $\tau _{1}$ ($\tau _{2}$) in a stability interval I and $\tau _{2}>0$ ($\tau _{1}>0$),  we find that the system undergoes a Hopf bifurcation at the interior equilibrium. In this case, we have investigated the direction of the Hopf bifurcation and the stability of the bifurcating periodic solutions.