1 Introduction

Image encryption algorithms or schemes have been extensively studied in recent years. The main reason is that our digital information must be protected to avoid being copied, read, and held up by the illegal authorization in public places. Many methods [1–4], including the data encryption standard (DES), Fourier transform, chaos, and wave transmission, have been proposed for the encryption of digital images.

Due to the features of sensitive to the initial condition, pseudorandomness, and ergodicity, the algorithms based on chaotic systems show the promising results and high efficiency [5–10]. The structure of permutation followed by diffusion has been widely adopted. As the duplicated scanning effort can be reduced and the encryption can be accelerated, the authors of [5] combined the two separate stages and suggest a fast efficient method for image encryption. Gao and Chen [6] proposed a total shuffling algorithm considering the pixel position permutation to frustrate the strong correlation in the original plain image. To solve the problem of small key space, a coupled nonlinear chaotic map was suggested in [7]. Patidar et al. [9] investigated the algorithm of substitution and permutation for color RGB images using standard map, where the 3D matrix is converted to a new 2D matrix by column. Three-dimensional or high-dimensional chaotic systems were further studied in [8, 10] to enlarge the key space for resisting the brute-force attack. Further, time-delayed systems were studied in [11, 12]; a suitable controller was chosen to keep corresponding chaotic state suggested by Banerjee [11], the numerical results showed the good effectiveness. Ghosh [12] considered the chaos synchronization for time-delayed dynamical systems when the delay is not constant.

However, some chaos-based cryptographic schemes have been successfully cryptanalyzed [13, 14]. Alvarez and Li [13] pointed out that chaotic maps with a nonuniform distribution are weak and are not suitable cryptographic purposes. From the statistical analysis on the plaintext, the approach suggested in [15] possesses a low security and is breakable. In [14], Cokal and Solak demonstrated that the secret keys can be revealed using chosen- and known-plaintext attacks due to the simple XORing operation of the plain image and the pseudorandom sequence generated by Chen’s chaotic system. Thus, the encryption algorithm [8] was broken.

To resist statistical analyses, chosen- and known-plaintext attacks, we suggest a novel chaotic image encryption in which two generalized Arnold maps are used to generate the pseudorandom sequences. The whole algorithm is divided into three parts, i.e., circular permutation, positive diffusion, and opposite diffusion. The rest of the paper is organized as follows. In Sect. 2, the proposed encryption scheme, especially the encryption steps, is described in detail. Simulations results are presented in Sect. 3 to show the efficiency and the validity of the algorithm. In Sect. 4, common security analyses are demonstrated. Finally, conclusions are drawn in the last section.

2 Image encryption scheme

2.1 Generalized Arnold map

The discrete generalized Arnold map can be expressed as

$$ \left ( \begin{array}{c}x_{n+1} \\y_{n+1}\end{array} \right )= \left (\begin{array}{c@{\quad}c}1 & a \\b & 1+ab\end{array} \right ) \left ( \begin{array}{c}x_{n} \\y_{n}\end{array}\right ) \operatorname{mod}1$$
(1)

where a and b are real numbers, x i ,y i ∈[0,1). The largest Lyapunov characteristic exponent of the map (1) is \(\lambda=1+\frac{ab+\sqrt {a^{2}b^{2}+4ab}}{2}>1\), which means that the map is always chaotic for any a>0, b>0. More on the generalized Arnold map can be found in [16].

2.2 Pseudo-random sequence

Suppose that the plain-image is denoted as I m×n . The generalized Arnold map is iterated to obtain two pseudorandom sequences P11×mn and P21×mn with the initial conditions and parameters a 1, b 1, x 0, y 0, and a 2, b 2, \(\bar{x}_{0}\), \(\bar{y}_{0}\) in (1). The first p and q Arnold map outputs are ignored in generating P11×mn and P21×mn , respectively.

(2)
(3)

The two chaotic sequences P11×mn and P21×mn are formed by real numbers with values between 0 and 1. They are used in both the circular permutation and the diffusion stages.

2.3 Circular permutation

To reduce the high correlation between adjacent pixels in the plain-image, a permutation process is usually adopted. Instead of using two-dimensional chaotic map for permutation, we propose to use a circular shuffling with both row and column relocations. For column relocation, the pseudorandom sequence with n elements is selected after the rth element of P11×mn , where 1≤r≤mn−n. Then we obtain \(\{\mu_{i}\}_{i=1}^{n}\) (0≤μ i ≤m−1) by converting the pseudo-random real numbers to integers using the formula

$$\mu=\mathit{floor}\bigl(\bigl[P1(1,r+1:r+n)\times10^{14}\bigr]\operatorname{mod}(m)\bigr)$$
(4)

The function floor(x) rounds x to the nearest integer toward minus infinity.

The same method is used for row relocation. The pseudorandom sequence \(\{\nu_{j}\}_{j=1}^{m}\) (0≤ν i ≤n−1) is obtained from P2 with the control parameter t (1≤t≤mn−m) as

$$\nu=\mathit{floor}\bigl(\bigl[P2(1,t+1:t+m)\times10^{14}\bigr]\operatorname{mod}(n)\bigr)$$
(5)

There are four directions, i.e., (left, up), (left, down), (right, up), and (right, down), for performing the permutation, as shown in Table 1. The first element denotes the shift direction along the row while the second one determines the move direction in the column. For example, the first case (0, 0) means that the ith row is shifted ν i pixels toward left with i=1,2,…,m while the jth column is moved up μ j pixels where j=1,2,…,n. The effect of two rounds of permutations are shown in Fig. 1. A sorting operation is required to obtain the index sequence in [16] and so more time is required. However, this is not required in our scheme and the permutation time is reduced.

Fig. 1
figure 1

Permutation for Lena image: (a) traditional Arnold map (b) generalized Arnold map [16] (c) traditional row and column method (d) the proposed circular permutation

Full size image
Table 1 Circle permutation directions
Full size table

2.4 Diffusion function

The main goal of the diffusion function is to change the gray values of the image pixels to confuse the relationship between the plain-image and the cipher-image. An efficient encryption algorithm should satisfy the requirement that a tiny change in any pixel spreads out to almost all pixels in the whole image. First, the two-dimensional permutated image is converted to a one-dimensional vector φ 1×mn by scanning from left to right and then from top to bottom. To make the keystream depend on the permutated image, the following forward diffusion is carried out:

$$ f_{i}=f_{i-1}+\varphi_{i}+\alpha\times a_{i},\quad i=1,2,\ldots,mn$$
(6)

where

$$a_{i}=\left \{ \begin{array}{l@{\quad}l}P1(2i-1), & \operatorname{mod}(f_{i-1},2)=0 \\P1(2i), & \operatorname{mod}(f_{i-1},2)=1\end{array} \right .$$

f i and f i−1 denote the current and the former encrypted pixels, respectively, f 0 can be considered as a constant, and α is a new control parameter.

To make the influence of every pixel equal, the diffusion is performed again in the reverse direction [16] using the following formula:

(7)

where

$$b_{i}=\left \{ \begin{array}{l@{\quad}l}P2(2i-1), & \operatorname{mod}(e_{i+1},2)=0 \\P2(2i), & \operatorname{mod}(e_{i+1},2)=1\end{array} \right .$$

e mn+1 can be considered as a constant and β is another control parameter. Finally, the encrypted image is generated after the diffusions (6) and (7) in two directions.

2.5 Encryption steps

The whole encryption process is composed of five steps, as shown in Fig. 2:

  1. step 1

    Read the plain-image and store the pixel values in the matrix I m×n .

  2. step 2

    Iterate (1) using the chosen initial conditions and parameters a 1, b 1, x 0, y 0, a 2, b 2, \(\bar{x}_{0}\), \(\bar{y}_{0}\), p, q, r, and t to generate μ and ν.

  3. step 3

    Perform the circular permutation on I to obtain F. Then arrange it into φ by scanning from left to right and top to bottom.

  4. step 4

    Carry out the diffusion processes (6) and (7) on f with parameters α and β, respectively, to obtain e.

  5. step 5

    Output the cipher image E after rearrange e into a matrix of size m×n.

Fig. 2
figure 2

Block diagram

Full size image

2.6 Decryption steps

The decryption process is just a reverse of the above encryption steps. As the operations are similar, the computation complexity in this part is roughly the same as that in encryption:

  1. step 1

    Read the cipher-image and denote it as E m×n . Then arrange it into a vector e 1×mn .

  2. step 2

    Perform the inverse diffusions with parameters β and α for (7) and (6), respectively:

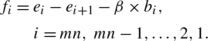    (8)
    (9)
  3. step 3

    Iterate (1) from the initial conditions a 1, b 1, x 0, y 0, a 2, b 2, \(\bar{x}_{0}\), \(\bar{y}_{0}\), p, q, r, and t, to obtain μ and ν.

  4. step 4

    Rearrange φ into a matrix of m×n. Then perform the reverse circular permutation by column and row, respectively, to reconstruct the original plain-image I.

3 Experiments

The proposed algorithm is implemented using Matlab 6.5 on the Windows XP platform using a personal computer with an Intel(R) Core(TM) 2, 2.00 GHz CPU. A 256×256 8-bit Cameraman image shown in Fig. 3(a) is chosen as the test image. Figure 3(b) shows the corresponding cipher-image after applied only one round of our encryption algorithm. The initial parameters are randomly set to x 0=0.434, y 0=0.506, a 1=33, b 1=20, p=100, \(\bar{x}_{0}=0.811\), \(\bar{y}_{0}=0.223\), a 2=57, b 2=42, q=120, r=80, t=90, α=6, and β=21.

Fig. 3
figure 3

Cameraman test image: (a) plain-image; (b) cipher-image; (c) decrypted image with 10−14 change in the key x 0; (d) decrypted image with 10−14 change in the key \(\bar{x}_{0}\); (e) encrypted image with 10−14 change in the key y 0; (f) difference between (b) and (e); (g) decrypted image with p=101, (h) decrypted image with β=20; (i) correctly decrypted image

Full size image

We also test our algorithm using other test images such as Lena, Rice, and Grass. They all show that the proposed scheme is a fast and efficient encryption algorithm, with a large key space and high key sensitivity.

4 Security analysis

A practical image encryption method should resist the existing attacks such as brute-force attack, known-plaintext attack, chosen-plaintext attack, statistical attack, differential attacks, and so on. In this section, we analyze the properties of our algorithm to show its effectiveness in resisting these common attacks.

4.1 Key space analysis

The size of the key space determines the total number of different keys which can be used in the process of encryption. A good algorithm should have a sufficiently large key space to resist the brute-force attack. In the proposed method, there are 14 parameters, i.e., x 0, y 0, a 1, b 1, p, \(\bar{x}_{0}\), \(\bar{y}_{0}\), a 2, b 2, q, r, t, α, and β. Therefore, the key space is large enough to resist a brute-force attack.

4.2 Sensitivity analysis

It is observed from Figs. 3(c) and (d) that the proposed image encryption algorithm is sensitive to the keys. A small change 10−14 made to any part of the key results in a completely different decrypted image. The algorithm satisfies the sensitivity required by a secure encryption scheme [17]. Additionally, Fig. 3(f) shows the difference between two cipher-images using a slightly different initial condition. For other parameters, Figs. 3(g) and (h) are the wrong decrypted images with p=101 and β=20, respectively. The correctly decrypted image that all the parameters are correct can be found in Fig 3(i), which is identical to the plain-image.

To evaluate the influence of a single plain-image pixel on the cipher-image, the common NPCR and UACI [16, 17] measures governed by (10) and (11), respectively, are computed. Here, NPCR means the change rate of the number of pixels of the ciphered image when one pixel of the plain-image is modified. The unified average changing intensity (UACI) measures the average intensity of the differences between two ciphered images C 1(i,j) and C 2(i,j) whose corresponding plain-images differ in only one pixel.

(10)
(11)

where D(i,j)=0 if C 1(i,j)=C 2(i,j); otherwise, D(i,j)=1.

Table 2 lists the results of NPCR and UACI for different test images while Table 3 shows the NPCR and UACI values for one-bit difference at various positions in the Lena image. Only one round of encryption has been performed. The results justify that the proposed algorithm possesses a high sensitivity as over 99 % pixels in the cipher-image change their gray levels even with a tiny one-bit difference in any pixel of the plain-image. More encryption rounds are performed when the pixel values at positions (1, 1) and (50, 80) of the Lena test image are changed, respectively. The results listed in Table 4 show that the NPCR and UACI values are close to the ideal values of 0.996 and 0.334, respectively, for multiple encryption rounds.

Table 2 NPCR and UACI values for different test images
Full size table
Table 3 NPCR and UACI values corresponding to different locations of the changed pixel in a 256×256 Lena image
Full size table
Table 4 NPCR and UACI values at different rounds for Lena
Full size table

4.3 Histogram analysis

The histogram of an image is a plot of the distribution of its pixel values. An effective cryptosystem should lead to a uniform distribution in the histogram of the cipher-image. Figures 4(a) and (b) show the histogram of the original Rice image and that of the encrypted image, respectively. If a wrong key is used, the histogram of the decrypted image is also uniform, as plotted in Figs. 4(c) and (d). These justify that the proposed method results in a uniform histogram and can prevent statistical attacks on the cipher-image.

Fig. 4
figure 4

Histogram of: (a) the Rice plain-image (b) encrypted image (c) decrypted image with a tiny change in key y 0 (d) decrypted image with a small change in key \(\bar{y}_{0}\)

Full size image

4.4 Correlation analysis

A natural image usually has a high correlation between adjacent pixels. However, an ideal encryption algorithm should have the ability to generate cipher-images with zero correlation between adjacent pixels. Here, the correlation coefficients between two adjacent pixels in vertical, horizontal, and diagonal directions are calculated for the plain- and the cipher-images, respectively. The following formula (12) is employed in the calculation:

$$ r_{xy}=\frac{\mathit{cov}(x,y)}{\sqrt{D(x)D(y)}}$$
(12)

where \(\mathit{cov}(x,y)=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-E(x))(y_{i}-E(y))\), \(D(x)=\frac{1}{N}\sum_{i=1}^{N}(x_{i}-E(x))^{2}\), \(E(x)=\frac{1}{N}\sum_{i=1}^{N}x_{i}\).

We randomly select 2,500 pairs of adjacent pixels in each direction for calculating the correlation coefficients. Table 5 lists the results along different directions while Figs. 5(a) and (b) plot the correlation coefficients of two vertically adjacent pixels for the plain- and the cipher-images, respectively.

Fig. 5
figure 5

Lena image: (a) plain image (b) encrypted image

Full size image
Table 5 Correlation coefficients
Full size table

4.5 Resistance to known-plaintext and chosen-plaintext attacks

To resist the known-plaintext and chosen-plaintext attacks, the keystream generated in the diffusion stage must rely on the permuted plain-image [16]. It is observed from (6) and (7) that the pseudorandom sequences a, b depend on the values of x i , f i , y i , and e i . As a result, the generated keystream is different if the processed image does not match.

4.6 Speed analysis

Only the circular permutation and modulo function are employed in our algorithm, which does not require the solving of differential equations or other time-consuming calculations. Therefore, the proposed method can offer a fast and efficient way for digital image encryption. The time required for encryption images with different sizes are listed in Table 6.

Table 6 Encryption time
Full size table

Table 7 is a comparison of our algorithm with other methods with the same structure of permutation followed by diffusion. The proposed algorithm has the highest operating efficiency. The approach in [16] needs the longest running time as much time has been spent in the sorting process to find the index order of the chaotic map output.

Table 7 Comparison using a 256×256 image
Full size table

5 Conclusions and further work

An image encryption algorithm based on the chaotic generalized Arnold map has been investigated. The conventional confusion-diffusion architecture is adopted, in which the keystream used depends on the plain-image. Security analyses demonstrate that the proposed encryption algorithm possesses the advantages of large key space and high key and plain-image sensitivities. Hence, it is suitable for secure image communication.

The proposed method can be easily extended to adopt other chaotic systems, simply changing the generation of the chaotic sequences P1 and P2 in the confusion stage. For example, using four Logistic maps (13) with initial conditions x 0, y 0, \(\bar{x}_{0}\), \(\bar{y}_{0}\), we can get P1 and P2 by the same formula (2) and (3).

$$ x_{i+1}=1-\mu x_{i}^{2}$$
(13)

where 1.40015⋯<μ≤2, x i ∈(−1,1).

Our scheme can also adopt high-dimensional chaotic systems such as Chen’s system, spatial chaotic system, and 3D cat map. In the diffusion stage, we need to generate the pseudorandom sequence a and b in (6) and (7) which depend on the permutated image. Different permutated images result in different a and b in the diffusion function.