Chaos-Based Image Encryption Using DNA Manipulation and a Modified Arnold Transform

Abstract

Digital images, which we store and communicate everyday, may contain confidential information that must not be exposed to others. Numerous researches are interested in encryption, which protects the images from ending up in the hands of unauthorized third parties. This paper proposes an image encryption scheme using chaotic systems, DNA manipulation, and a modified Arnold transform. Both DNA manipulation and hyperchaotic Lorenz system are utilized in the substitution of the images’ pixel values. An additional role of hyperchaotic Lorenz system is that it generates the random numbers required within the DNA manipulation steps. DNA cycling is implemented based on simple DNA coding rules and DNA addition and subtraction rules with modulus operation. The modified Arnold transform alters the pixels’ positions, where it guarantees effective pixel permutation that never outputs the same input pixels arrangement again. The proposed design is simple and amenable for hardware realization. Several well established performance evaluation tests including statistical properties of the encrypted image, key space, and differential attack analysis were conducted for several images. The proposed scheme passed the tests and demonstrated good results compared to several recent chaos-based image encryption schemes.

1 Introduction

Communication methods have undergone significant changes in the recent few decades due to the quick development of computer and network technology. The need for secure communication of media and exchanged information has gradually developed [1]. Specifically, image encryption has been the topic of numerous researches to protect the user’s privacy [2]. The strong correlation and redundancy between neighbouring pixels of an image require devising new encryption schemes rather than the typical ones [3].

Chaotic systems are good candidates for image encryption systems because of their pseudorandomness, initial value sensitivity, parameter sensitivity, and unpredictability, among other qualities, which increase the security level [4,5,6]. Both Deoxyribonucleic acid (DNA) encoding and Arnold permutation have appeared in recent works as well. In [7], an image encryption algorithm based on bit-level Arnold transform and hyperchaotic maps was proposed. The algorithm divides the grayscale image into 8 binary images. Then, a chaotic sequence is used to shift the images. Afterwards, Arnold transform is applied. Finally, image diffusion is applied using the hyper chaotic map. The system requires image division, which increases the system’s complexity and may halt it from being optimized to applicable hardware design. In [6], Luo et al. used double chaotic systems, where two-dimensional Baker chaotic map is used to set the state variables and system parameters of the logistic chaotic map. In [8], Ismail et al. developed a generalised double humped logistic map, which is used in gray scale image encryption. In [9], a chaotic system and true random number generator were utilized for image encryption. The presence of both the chaotic system and true random number generator increases the system’s complexity making it less suitable for hardware implementation. In [1], a plaintext-related encryption scheme that utilises two chaotic systems and DNA manipulation was presented. The system depends on the values of some pixels for the encryption process, which threatens image restoration if they are changed.

This paper proposes an image encryption algorithm that uses hyperchaotic Lorenz system, an optimized DNA manipulation system and a new method for applying Arnold transform, which is more suitable for encryption applications. The rest of the paper is organized as follows: Sect. 2 provides a brief explanation of the utilized methods. Section 3 demonstrates the proposed encryption and decryption algorithms. Section 4 validates their good performance. Finally, Sect. 5 concludes the work.

2 Preliminaries

Generally, encryption systems require a source of randomness that can be regenerated in the decryption process. This section explains the main sources of randomness that are employed in the proposed scheme.

2.1 Hyperchaotic Lorenz System

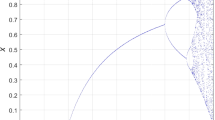
Hyperchaotic Lorenz system [10] provides the randomness needed for encryption. The system is solved using Euler’s method:

$$\begin{aligned} x_{i+1}&=x_{i}+h(a(y_{i}-x_{i})+w_{i}),\end{aligned}$$

(1a)

$$\begin{aligned} y_{i+1}&=y_{i}+h(cx_{i}-y_{i}-x_{i}z_{i}),\end{aligned}$$

(1b)

$$\begin{aligned} z_{i+1}&=z_{i}+h(x_{i}y_{i}-bz_{i}),\end{aligned}$$

(1c)

$$\begin{aligned} w_{i+1}&=w_{i}+h(y_{i}z_{i}+rw_{i}), \end{aligned}$$

(1d)

where $h = 0.01$, $a = 10$, $b = 8/3$, $c = 28$, and $r = -1$. Figure 1 shows the output results with initial conditions $x_0 = 0.23$, $y_0 = 0$, $z_0 = 0.7$, and $w_0 = 0.11$.

Fig. 1.

Output of hyperchaotic Lorenz system.

2.2 DNA Coding

DNA coding [11] is used to change the bit values according to some set of rules. This is done to enhance the security of the algorithm. DNA consists of 4 bases, which are Adenine (A), Thymine (T), Cytosine (C), and Guanine (G). The relation between these bases is that ‘A’ is complementary to ‘T’ and ‘G’ is complementary to ‘C’. Table 1 shows the used binary code for each DNA base.

Based on these relations, we can apply rules to manipulate the data as long as the relation between these bases does not change. Table 2 shows the list of all possible rules that are used in the encryption algorithm, where a random number is used to select the rule and then the two input bits are replaced with the corresponding DNA base. For example, if the chosen rule is 6 and the input is ‘T’, then the output will be ‘C’, which is equal to ‘11’.

Table 1. DNA binary codes

Table 2. DNA encoding and decoding rules

Table 3 shows the results of DNA addition and subtraction, which can be done using simple operations on the DNA bases if the binary representation of Table 1 is used. The DNA sequence has a cyclic behavior, where each base is repeated every 4 cycles (i.e., T, C, G, A, T, C, ...). This enables performing ‘DNA cycling’ by dividing the number of cycles by 4 and then referring to Table 4.

Table 3. DNA addition and subtraction rules

Table 4. DNA cycling

2.3 Arnold Transform

Arnold transform [12] is used to permute the pixels positions of the image. Arnold transform and the inverse operation are defined as follows:

$$\begin{aligned} \begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix}&= mod\left( \begin{bmatrix} \quad 1 &{} \quad 1\\ \quad 1 &{} \quad 2 \end{bmatrix} \begin{bmatrix} x\\ y \end{bmatrix} , M^2\right) ,\end{aligned}$$

(2a)

$$\begin{aligned} \begin{bmatrix} x\\ y \end{bmatrix}&= mod\left( \begin{bmatrix} \quad 2 &{} -1\\ -1 &{} \quad 1 \end{bmatrix} \begin{bmatrix} x^{'}\\ y^{'} \end{bmatrix} , M^2\right) . \end{aligned}$$

(2b)

where (x, y) represents the original pixel position and $\left( x^{'},y^{'}\right)$ represents the new pixel position after applying the transform on an $M \times M$ image.

Arnold transform is a periodic transform [12], which means that at a specific iteration or cycle, the permuted image becomes the same as the original image. The period of the transform depends on M as shown in Table 5 [12].

If the number of cycles of Arnold transform is random, the image will not be permuted if this random number happens to be 0 or P, where P is the Arnold transform period of image dimensions $M \times M$ shown in Table 5. To overcome this periodicity, we propose a modified Arnold transform, where the image will be permuted for any number of cycles chosen.

Table 5. Arnold transform (2) period with different M

3 Proposed Algorithm

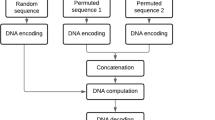
The proposed algorithm for encryption and decryption is shown in Fig. 2. The proposed modified Arnold transform is explained, after that the encryption and decryption process.

3.1 Modified Arnold Transform

To guarantee image permutation for any number of cycles, the number of cycles (Cyc) of the Arnold transform must not equal to 0 or P. Hence, we apply the following equation:

$$\begin{aligned} G =mod\left( Cyc , P-2\right) +1. \end{aligned}$$

(3)

This will make the effective number of cycles G be in the range of $1 \rightarrow (P-1)$, which avoids these two cases and eliminates the chances of periodicity.

Fig. 2.

(a) Encryption and (b) Decryption block diagrams.

3.2 Encryption Process

• Step 1: The 4 input sub keys ($K_1$, $K_2$, $K_3$, and $K_4$) are converted from hexadecimal to decimal representation to set the initial state of each variable of the hyperchaotic Lorenz system (1), $x_0$, $y_0$, $z_0$, and $w_0$. To make the initial conditions bounded by the chaotic system’s basin of attraction, they are computed as:

  $$\begin{aligned} x_0&=\left( \frac{K_1}{A/40}\right) -20,\end{aligned}$$

  (4a)
  $$\begin{aligned} y_0&=\left( \frac{K_2}{A/40}\right) -20,\end{aligned}$$

  (4b)
  $$\begin{aligned} z_0&=\left( \frac{K_3}{A/50}\right) ,\end{aligned}$$

  (4c)
  $$\begin{aligned} w_0&=\left( \frac{K_4}{A/200}\right) -100, \end{aligned}$$

  (4d)

  where $A = 2^{52}$. Then, the 4 chaotic sequences x, y, z and w are generated with length equals $M^2 +1000$.

• Step 2: The first 1000 iterations are removed from the four chaotic sequences to generate $X_h$, $Y_h$, $Z_h$ and $W_h$. Then, the vectors $U_1$, $U_2$, $U_3$, $U_4$, $U_5$, and $U_6$ are generated by the following equations:

  $$\begin{aligned} U_1&=mod(\left\lceil {X_h \times 10^{13}}\right\rceil , 8)+1,\end{aligned}$$

  (5a)
  $$\begin{aligned} U_2&=mod(\left\lceil {(U - \left\lceil {U} \right\rceil ) \times 10^{13}}\right\rceil , M^2),\end{aligned}$$

  (5b)
  $$\begin{aligned} U_3&=mod(\left\lceil {W_h \times 10^{13}}\right\rceil , 8)+1,\end{aligned}$$

  (5c)
  $$\begin{aligned} U_4&=mod(\left\lceil {(X_h + Y_h) \times 10^{13}}\right\rceil , 256)+1,\end{aligned}$$

  (5d)
  $$\begin{aligned} U_5&=mod(\left\lceil {Y_h \times 10^{13}}\right\rceil , 8)+1,\end{aligned}$$

  (5e)
  $$\begin{aligned} U_6&= mod(\left\lceil {(W_h+Z_h)\times 10^{13}} \right\rceil ,256), \end{aligned}$$

  (5f)

  where $\lceil {~ }\rceil$ is the ceiling operator, and $U=[X_h, Y_h, Z_h, W_h]$.

• Step 3: $U_1$ is used to select the DNA rule to encode the input image according to Table 2.

• Step 4: $U_2$ is used to perform DNA cycling on $S_1$. The result of $mod(U_2,4)$ chooses how many times the data is shifted according to Table 4.

• Step 5: $U_3$ is used to DNA encode $U_4$ to generate Q. Then, according to Table 3, the following equations are applied on $S_2$:

  $$\begin{aligned} q&= Q(1) - Q(M^2), \end{aligned}$$

  (6a)
  $$\begin{aligned} S_3(1)&= S_2(1)+Q(1)+q, \end{aligned}$$

  (6b)
  $$\begin{aligned} S_3(i)&= S_2(i-1) +S_2(i) + Q(i). \end{aligned}$$

  (6c)

• Step 6: $U_5$ is used to select the rule for DNA decoding for $S_3$ according to Table 2.

• Step 7: Every byte of $S_4$ is accumulated to calculate ‘$data_{sum}$’. The proposed modified Arnold transform (3) is applied on $S_4$ to generate $S_5$, where $cyc=data_{sum}$.

• Step 8: $S_5$ is then XORed with the $U_6$ to generate the encrypted image.

3.3 Decryption Process

• Steps 1 and 2: The same as the encryption process.

• Step 3: The input encrypted image is XORed with $U_6$.

• Step 4: The same as step 7 in the encryption process. The only difference is using Arnold inverse transform (2b), instead of Arnold transform. This step is possible even though we are taking the ‘$data_{sum}$’ before the Arnold inverse transform, which is not symmetric with the encryption process. This is because Arnold Transform does not change the pixels values, it only changes their positions.

• Step 5: $U_5$ is used to select the DNA coding rule for $S_4$.

• Step 6: $U_3$ is used to DNA encode $U_4$ to generate Q. Then, according to Table 3, the following equations are applied:

  $$\begin{aligned} q&= Q(1) - Q(M^2), \end{aligned}$$

  (7a)
  $$\begin{aligned} S_2(1)&= S_3(1)-Q(1)-q, \end{aligned}$$

  (7b)
  $$\begin{aligned} S_2(i)&= S_3(i)-Q(i)-S_3(i-1). \end{aligned}$$

  (7c)

• Step 7: $U_2$ is used to cyclic shift $S_2$, which is done by checking the result of $mod(U_2,4)$ to choose how many times the data is shifted.

• Step 8: $U_1$ is used to select the DNA decoding rule for $S_1$ to restore the original image.

4 Performance Evaluation

The proposed system is tested using the gray-scale ‘Lena’ $(256 \times 256)$, ‘Baboon’ $(512 \times 512)$, and ‘Pepper’ $(512 \times 512)$ images.

Fig. 3.

Histogram of the original image (left), and encrypted image (right) for Lena, Baboon, and Pepper in (a), (b), and (c), respectively.

4.1 Encryption Quality Metrics

Figure 3 shows the histogram of the original and encrypted images, which indicate flat and uniform distribution. Mean Square Error (MSE) [13] and Peak Signal-to-Noise Ratio (PSNR) [14] are used to test encryption quality and are given by:

$$\begin{aligned} MSE&=\frac{1}{M^2}\sum _{i=1}^{M}\sum _{j=1}^{M}\left[ O_{i,j}-E_{i,j}\right] ^2,\end{aligned}$$

(8a)

$$\begin{aligned} PSNR&=10 \log _{10} \frac{(2^n -1)^2}{MSE}, \end{aligned}$$

(8b)

where $O_{i,j}$ and $E_{i,j}$ are the original and encrypted image at position (i, j) respectively and n is the number of bits per pixel. MSE and PSNR $\in [0,\infty ]$, where high MSE and low PSNR values indicate huge difference between the original and encrypted images. Table 6 shows that the proposed system gives similar MSE and PSNR values compared to other researches.

4.2 Correlation Analysis

The correlation coefficient is given by:

$$\begin{aligned} \rho =&\dfrac{Cov(x,y)}{\sqrt{D(x)}\sqrt{D(y)}},\end{aligned}$$

(9a)

$$\begin{aligned} Cov(x,y)=&\dfrac{1}{M^2}\sum _{i=1}^{M^2} (x_i-\dfrac{1}{M^2}\sum _{i=j}^{M^2} x_j)(y_i-\dfrac{1}{M^2}\sum _{i=j}^{M^2} y_j), \end{aligned}$$

(9b)

$$\begin{aligned} D(x)=&\dfrac{1}{M^2}\sum _{i=1}^{M^2} (x_i-\dfrac{1}{M^2}\sum _{i=j}^{M^2} x_j)^2,\end{aligned}$$

(9c)

$$\begin{aligned} D(y)=&\dfrac{1}{M^2}\sum _{i=1}^{M^2} (y_i-\dfrac{1}{M^2}\sum _{i=j}^{M^2} y_j)^2, \end{aligned}$$

(9d)

where Cov(x, y) is the covariance between pixels x and y, and D is the standard deviation. The values of the correlation coefficients for the encrypted images must be close to 0, which means that even the neighbouring pixels are uncorrelated. The results in Table 6 show that the correlation coefficients are close to 0 and comparable to other works. Figure 4 further indicates that the original image pixel values are grouped in a region, which shows that they are correlated. On the contrary, the encrypted image pixel values are spread all over.

Fig. 4.

(a) Horizontal, (b) vertical, and (c) diagonal correlation of Baboon image (left) and encrypted Baboon image (right).

4.3 Information Entropy

Information entropy is the average amount of information conveyed by each pixel [14] and is given by:

$$\begin{aligned} Entropy = -\sum _{i=0}^{255}P(i)log_2 P(i), \end{aligned}$$

(10)

where P(i) is the probability of occurrence of i. For an 8 bit image, the ideal value is 8, which means that the information is distributed uniformly over all pixel values. The results in Table 6 shows that the entropy of the encrypted images successfully approach 8.

4.4 Key Space and Sensitivity Analysis

The proposed system has a total number of 4 sub keys, each represented by 52 bits, where $K_1$ = (FF123FF0567EF$)_{16}$, $K_2$ = (F655FF000FFFF$)_{16}$, $K_3$ = (FFAB0957FFFFF$)_{16}$ and $K_4$ = (46FF0108F214F$)_{16}$ are the values for the sub keys used. This results in a key space equals $2^{208} \approx 10^{63}$, which is large enough to resist brute force attacks [1, 15]. In addition, the key must have high sensitivity such that any slight change in the decryption key (single bit) prevents recovering the original image. Figure 5 shows the original image of ‘Baboon’ and the wrong decrypted image when changing the least significant bit of the first sub key.

Fig. 5.

Original Baboon image (left) and wrong decrypted image (right).

4.5 Robustness Against Differential Attacks

This test is done by changing the least significant bit of a random pixel in the original image and comparing the newly encrypted image to the original encrypted image using Number of Pixels Change Rate (NPCR) and Unified Average Changing Intensity (UACI) [16], which are given by:

$$\begin{aligned} NPCR&=\frac{1}{M^2}\sum _{i=1}^{M}\sum _{j=1}^{M}{DE(i,j) \times 100\%},\end{aligned}$$

(11a)

$$\begin{aligned} UACI&=\frac{1}{M^2} \sum _{i=1}^{M} \sum _{j=1}^{M} \dfrac{\mid E_1(i, j)-E_2(i, j)\mid }{255} \times 100\%,\end{aligned}$$

(11b)

$$\begin{aligned} DE(i,j)&= {\left\{ \begin{array}{ll} 0, &{} \text {if } E_1(i, j) = E_2(i, j),\\ 1, &{} \text {if } E_1(i, j) \ne E_2(i, j),\\ \end{array}\right. } \end{aligned}$$

(11c)

where the difference between corresponding pixels in the encrypted versions of the original image $E_1(i, j)$ and the modified image $E_2(i, j)$ is DE(i, j). The NPCR and UACI values are calculated as the average values of 50 iterations and given in Table 6. They are close to the ideal values 99.61% and 33.46%, respectively, [17] and comparable to recent works,

Table 6. Performance analysis

5 Conclusion

This paper presented an encryption algorithm, utilizes hyperchaotic system, DNA manipulation, and a modified Arnold transform. The modified Arnold transform enhances the encryption process by eliminating the cases at which pixel permutation is cancelled. The performance evaluation for the proposed system shows that it is reliable for image encryption compared to recent similar schemes. The design is simple and amenable for real life application hardware realization. For future work, it can be applied on colored images for each channel separately rather than grayscale images only.