1 Introduction

In the Three Gorges Reservoir area, which is located at the upper reaches of the Yangtze River in China, frequent landslides often result in significant casualties and property losses. So, the prediction of landslide-prone regions is essential for carrying out quicker and safer mitigation programs, as well as future planning of the area. It is well known that landslide hazard is a complex nonlinear dynamical system with the uncertainty (Chen and Zeng 2011; Msilimba 2010; Qin et al. 2001, 2002; Sorbino et al. 2010). The landslide displacement is basically determined by the potential energy and constraint condition of the slope, but it is also strongly influenced by rainfall and reservoir level fluctuation (Guzzetti et al. 2005; Kawabata and Bandibas 2009).

In recent years, a number of methods have been tried in the problem of displacement of landslide forecasting, such as autoregression (AR) (Xu et al. 2011), linear regression (Kaunda 2010), and artificial neural networks (ANNs) (e.g., Chen and Zeng 2011; Pradhan and Lee 2009, 2010; Melchiorre et al. 2008; Nefeslioglu et al. 2008). In particular, ANNs have become one of the frequent modeling approaches among these techniques, because of the characteristics of adaptability and they can approximate any continuous nonlinear function with arbitrary precision (Hornik 1991). However, most ANN-based landslide forecasting methods used gradient-based learning algorithms such as back-propagation neural network (BPNN), which are relatively slow in learning and may easily get into local minima points (Jaroudi and Makhoul 1990; Drucker and Cun 1992). Recently, a novel learning algorithm for single-hidden-layer feedforward neural networks (SLFNs) called extreme learning machine (ELM) has been proposed (Huang et al. 2006a, b; Zhu et al. 2005). ELM not only learns much faster with higher generalization performance than the traditional gradient-based learning algorithms but also avoids many difficulties faced by gradient-based learning methods such as stoping criteria, learning rate, learning epochs, and local minimum (Huang 2003; Huang and Babri 1998; Huang et al. 2006a, b; Tamura and Tateishi 1997). ELM has been successfully applied in many fields such as sales forecasting (Sun et al. 2008; Chen and Ou 2011), face recognition (Zong and Huang 2011), and reversible watermarking (Feng et al. 2012).

Inspired by the idea of “decomposition and ensemble” (Yu et al. 2008; Guo et al. 2012), the original time series can be decomposed into several sub-series. Each component can be predicted with the purpose of simplifying the predication tasks, and the final predicted value can be obtained by summing the predictive value of each sub-series. Considering the displacement deformation monitoring time series of landslide is unsystematic and nonlinear, the ensemble empirical mode decomposition (EEMD), which is introduced by Wu and Huang (2009), is used to decompose the accumulative displacement of landslide series. In this paper, a modified EEMD–ELM model is proposed for landslide displacement prediction. The first step is to decompose the displacement of landslide series into several sub-series with EEMD. The second step is to choose appropriate ELM model for each decomposed sub-series’s forecasting. At last, the final predicted value is obtained by summing the each component forecasting results. It should be pointed out that the change of landslide displacement is considered as one of the most difficult natural parameters to model and forecast due to the complex structures of factors which affect landslide displacement such as tectonic, rainfall, reservoir level fluctuation, difference in temperature of day and night, and even earthquake. Considering these influencing factors relate intricately and interact complexly, we only consider original landslide displacement time series in this paper because of landslide displacement time series contain the information of the interaction of these influencing factors which happened in the past.

2 Methodology formulation

2.1 EMD and EEMD

The empirical mode decomposition (EMD) is an adaptive and efficient time series decomposition technique applied to decompose nonlinear and non-stationary signals using the Hilbert–Huang transform (HHT) (Huang et al. 1998). The key innovation of EMD is the establishment of the concept of intrinsic mode function (IMF), each contains the local information embedded in the data series. Using EMD, any complex time series can be decomposed into several IMF components and a residue component which contains the main trend of the original series. According to Huang et al. (1998), IMFs must satisfy the following conditions:

  1. 1.

    In the whole data series, the number of extrema (sum of maxima and minima) and the number of zero crossings must be equal, or differ at most by one.

  2. 2.

    At any point, the mean value of the envelope defined by local maxima and local maxima must be zero.

With the above definition for IMF, any signal series s(t) (t = 1, 2,…, l), t is the time index and l is the total number of observations, can be decomposed as follows:

  • Step (1.1) Identify all the local extrema of original signal s(t). Use a cubic spline line that connects all local maxima (minima) to obtain the upper (lower) envelopes and calculate the point-by-point envelope mean m 1(t) of the upper and lower envelopes. Calculate the difference between s(t) and m 1(t), obtain the first component h 1(t):

    $$ h_1(t)=s(t)-m_1(t) $$
    (1)

    Step (1.2) To treat h 1(t) as the original signal series s(t) in the next iteration:

    $$ h_{11}(t)=h_1(t)-m_{11}(t) $$
    (2)

where m 11(t) is the mean of upper and low envelope values of h 1(t). This step will be repeated for k times, until h 1k (t) satisfy the definition of an IMF,

$$ h_{1k}(t)=h_{1(k-1)}(t)-m_{1k}(t) $$
(3)

Designate it as c 1(t) = h 1k (t). A suggested stoppage criterion (Huang et al. 1998), which is determined by using a Cauchy type of convergence test, is defined as follows:

$$ {\text{SD}}_k=\sum_{t=1}^\ell\frac{|h_{1(k-1)}(t)-h_{1k}(t)|^2}{h_{1(k-1)}^2(t)} $$
(4)

Here, SD k is less than a predetermined value.

Step (1.3) Once c 1(t) is determined, the residue r 1(t) can be obtained by separating c 1(t) from the rest of the data,

$$ r_1(t)=s(t)-c_1(t) $$
(5)

To replace s(t) with r 1(t), and repeating the steps (1.1) and (1.2), the second IMF and residue [c 2(t) and r 2(t)] can be obtained. If c 1(t) or r 1(t) is smaller than a predetermined value, or r 1(t) becomes a monotone function, the sifting process is stopped. Thus, a series of IMFs can be obtained. The original signal s(t) can be expressed as follows.

$$ s(t)=\sum_{i=1}^{\mu}c_i(t)+r_\mu(t) $$
(6)

where c i (t) (i = 1, …,  μ) are the μ number of IMFs, and r μ (t) is the residue after repeating the sifting procedure μ times.

However, there are also some shortcomings in EMD, and one of the most significant problem is the mode mixing, which means either some signals consisting of disparate scales exist in the same IMF or the signals with the same scale exist in different IMFs. In order to eliminate the mode mixing problem, a new noise-assisted analysis method, called EEMD was proposed. The EEMD algorithm can be described as follows:

  • Step (2.1) Add a white noise to the original signal series.

  • Step (2.2) Decompose the signal with added white noise into IMFs using EMD.

  • Step (2.3) Repeat steps (2.1) and (2.2) again and again, with different white noise each time.

  • Step (2.4) Obtain the means of corresponding IMFs of the decompositions as the final result.

  • Step (2.5) Obtain the mean of corresponding residue of the decomposition as the final result.

2.2 ELM

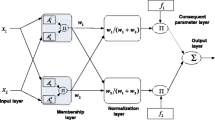
ELM is a single-hidden-layer feedforward neural network (SLFN) with randomly generated hidden nodes independent of the training data. Input weights and biases can be randomly chosen and the output weights can be analytically determined using the Moore–Penrose (MP) generalized inverse. Compared with traditional popular gradient-based learning algorithms for SLFNs, ELM not only learns much faster with higher generalization ability but also avoids many difficulties, such as the stopping criteria, learning rate, learning epochs, and local minima. The structure of ELM is demonstrated in Fig. 1. For N distinct samples (x i , t i ), where x i  = [x i1, x i2, …, x in]T ∈ R n and t i  = [t i1, t i2, …, t im]T ∈ R m, standard SLFNs with \(\tilde{N}\) hidden neurons and activation function g(x) are mathematically modeled as

$$ \sum_{i=1}^{\tilde N}\beta_ig({\bf w}_i\cdot{\bf x}_j+b_i)={\bf o}_j, \quad j=1,\ldots,N. $$
(7)

where w i  = [w i1, w i2, …, w in]T is the weight of the connection from the input neurons to the ith hidden neuron, β i  = [β i1, β i2, …, β im]T is the weight vector connecting the ith hidden neuron and the output neurons, o j  = [o j1, o j2, …, o jm]T is the jth output vector of the SLFN and b i is the threshold of the ith hidden neuron. w i ·x j denotes the inner product of w i and x j . The above N equations can be written compactly as:

$$ {\bf H}\beta={\bf O} $$
(8)

where

$$ {\mathbf{H}} = \left[ {\begin{array}{*{20}c} {g({\mathbf{w}}_{1} \cdot{\mathbf{x}}_{1} + b_{1} )} & \cdots & {g({\mathbf{w}}_{{\tilde{N}}} \cdot{\mathbf{x}}_{1} + b_{{\tilde{N}}} )} \\ \vdots & \cdots & \vdots \\ {g({\mathbf{w}}_{1} \cdot{\mathbf{x}}_{N} + b_{1} )} & \cdots & {g({\mathbf{w}}_{{\tilde{N}}} \cdot{\mathbf{x}}_{N} + b_{{\tilde{N}}} )} \\ \end{array} } \right]_{{N \times \tilde{N}}} $$
$$ \beta=\left[\begin{array}{cccc} \beta_{1}^{T} \\ \vdots\\ \beta_{\tilde N}^{T} \end{array}\right]_{{\tilde N}\times m} \text{and} \quad {\bf O}=\left[\begin{array}{cccc}{\bf o}_{1}^{T} \\ \vdots\\ {\bf o}_{N}^{T} \end{array}\right]_{N\times m} $$

where H is called the hidden-layer output matrix of the neural network. The ith column of H is the ith hidden neuron’s output vector with respect to inputs \({\bf x}_1, {\bf x}_2,\ldots,{\bf x}_N.\)

Fig. 1
figure 1

The structure of ELM

Full size image

ELM theories claim that the input weights w i and hidden biases b i can be randomly generated instead of tuned. To minimize the cost function \(\|{\bf O}-{\bf T}\|,\) where \({\bf T}=[{\bf t}_1,{\bf t}_2,\ldots,{\bf t}_N]^T\) is the target value matrix, the output weights is as simple as finding the least−square (LS) solution to the linear system H β = T, as follows:

$$ \hat{\beta}={\bf H}^{\dag}{\bf T} $$
(9)

where \({\bf H}^{\dag}\) is the Moore−Penrose (MP) generalized inverse of the matrix H. The minimum norm LS solution is unique and has the smallest norm among all the LS solutions. In addition, before the ELM training, the input and output data set should be firstly normalized as follows:

$$ X_{{\text{normalize}}}=\frac{(X_{ij}-{{\text{max}}}\{X_{ij}\})+(X_{ij} -{\text{min}}\{X_{ij}\})}{({\text{max}}\{X_{ij}\}-{\text{min}}\{X_{ij}\})}, $$
(10)
$$ i=1,2,\ldots,n;\quad j=1,2,\ldots,N $$

and the unnormalized method for the input and output data set is given as follows:

$$ O_{{\text{unnormalize}}}=\frac{O_{ij}({\text{max}}\{X_{ij}\} -{\text{min}}\{X_{ij}\})+{\text{max}}\{X_{ij}\}+{\text{min}}\{X_{ij}\}}{2} $$
(11)
$$ i=1,2,\ldots,n;\quad j=1,2,\ldots,N $$

2.3 Overall process of the modified EEMD-based ELM ensemble paradigm

An original displacement deformation monitoring time series of landslide can be decomposed into various frequency IMFs by EEMD. Inspired by Guo et al. (2012), the highest frequency component (IMF1) is always so small that has little contribution to model fitting, while it always gives a great disturbance for the forecasting precision of displacement of landslide. In order to improve the prediction precision, we remove IMF1 and the model is called M-EEND-ELM, where “M” represents “Modified.”

Suppose there are the displacement deformation monitoring time series of landslide \(s(t)(t=1,2,\ldots, \ell), \) in which one wants to make the η-step ahead prediction, that is, s(t + η). For example, η = 1 means forecasting one step head in advance and η = 5 means forecasting five steps head in advance. Based on the previous methods, the modified EEMD-based ELM ensemble paradigm is illustrated in Fig. 2.

Fig. 2
figure 2

The scheme of M–EEMD–ELM ensemble methodology

Full size image

The steps of constructing the landslide displacement prediction model are described as follows:

  1. 1.

    The displacement deformation monitoring time series of landslide \(s(t)(t=1,2,\ldots, \ell)\) is decomposed into μ IMFs, \(c_i(t) (i=1,\ldots, \mu), \) and one residual component r μ (t) by EEMD.

  2. 2.

    To forecast all extracted IMFs and one residual component but IMF1, by establishing appropriate ELM model.

  3. 3.

    The final predicted value can be obtained through the superposition of all IMFs and one residual component forecasting results but IMF1.

In order to illustrate the effectiveness of the proposed modified EEMD-based ELM ensemble methodology, a case study of Baishuihe landslide in the Three Gorges reservoir area is presented in the next section.

3 Experiments

3.1 Date collection

Baishuihe landslide is located on the south bank of Yantze River and its 56 km away from the Three Gorges Dam of China. The bedrock geology of the study area consists mainly of sandstone and mudstone, which is an easy slip stratum. The slope is of the category of bedding slopes. Figure 3 shows the scene of landslide collapse along roads on June 30, 2007 and Fig. 4 shows parts of landslide fissure in the warning zone. Fig. 5 shows the schematic diagram of monitoring arrangement in Baishuihe landslide. There are eleven GPS deformation monitoring points layout in the landslide surface. The monitoring data of landslide accumulative displacement at ZG118 monitoring point is selected as a case study. Figure 6 shows the monitoring data of landslide accumulative displacement at ZG118 monitoring point.

Fig. 3
figure 3

The scene of landslide collapse along roads on June 30, 2007

Full size image
Fig. 4
figure 4

Landslide fissure in the warning zone

Full size image
Fig. 5
figure 5

Schematic diagram of monitoring arrangement in Baishuihe landslide

Full size image
Fig. 6
figure 6

Monitoring curves of landslide accumulative displacement at ZG118 monitoring point

Full size image

The total number of data at ZG118 monitoring point is 101 observations from August 2003 to December 2011. The data between August 2003 and November 2009 are selected as training data in order to construct the forecasting model and the rest of 25 observations of data from December 2009 to December 2011 are selected as predicting data. Note that only one-step-ahead prediction is performed in the experiments. Actually, multi-step-ahead prediction can also be performed, but the prediction performance in such cases is unsatisfactory. And 1 month ahead prediction is enough to provide early warnings in the landslide prediction.

3.2 Evaluation of forecast performance

In order to measure the prediction performance, three loss functions are used as the criteria to evaluate the proposed models. The loss functions are the root mean square error (RMSE), mean absolute error (MAE), and mean absolute percentage error (MAPE) which are defined by:

$$ \hbox{RMSE}=\sqrt{\frac{1}{\rho}\sum_{t=1}^\rho e(t)^2} $$
(12)
$$ \hbox{MAE}=\frac{1}{\rho}\sum_{t=1}^\rho|e(t)| $$
(13)
$$ {\text{MAPE}} = \frac{1}{\rho }\sum\limits_{{t = 1}}^{\rho } {\left| {\frac{{e(t)}}{{s(t)}}} \right|} \times 100\,{\text{\% }} $$
(14)

where \(e(t)=s(t)-\hat{s}(t), s(t)\) is the actual value for the time period \(t, \hat{s}(t)\) is the predicted value for the same period, and ρ is the number of predictions.

In addition, one ensemble model, EEMD–ELM without modified, and four single ANN models, BPNN, RBF neural network (RBFNN), support vector regression (SVR), and ELM, are also used to predict landslide displacement for comparison purposes.

3.3 Experimental results

We use the mean monthly landslide accumulative displacement for prediction. The original time series is first decomposed into several IMFs and one residue using EEMD decomposition tool. The amplitude of add noise we used is 0.2, the number of ensemble is 100. The decomposition results with EEMD can be seen in Fig. 7.

Fig. 7
figure 7

EEMD decomposition of the monthly accumulative displacement

Full size image

Then, we choose appropriate ELM model to forecast all extracted IMFs. The input and output data should firstly normalized using Eq. (10). The activation function of all ELM model we used is the sigmoidal function g(x) = 1/(1 + e −x). With the output variable x(t), the other parameters, which can be determined by trial and error, used in ELMs are shown in Table 1, where the series of x(i) represents those six normalized series, respectively.

Table 1 Parameters used in the ELM
Full size table

Using the above settings, the forecasting results for IMFs and residue are shown in Fig. 8. As shown in Fig. 8, the predicted values and extracted values for each sub-series are very close for every calculation except IFM1. As mentioned previously, IMF1 mainly reflects the random component of the original sequence, which is the most disorder and unsystematic part of the landslide displacement sequence. ELM can approach any continuous nonlinear function with arbitrary precision and fit IMF1 well, but the prediction is unpredictable and even may reduce the accuracy of prediction.

Fig. 8
figure 8

Comparison of predicted and extracted values of each sub-series

Full size image

The final predicted value is obtained by adding the predictive values of IMFs (except IMF1) and one residual. The final predicted values are shown in Fig. 9.

Fig. 9
figure 9

The comparison among six forecast models

Full size image

As shown in Fig. 9, we can find that only two ensemble models successfully predict the obvious deformation from the 19th month to the 20th month, and there is an obvious predict time delay in the other single ANN models. In Table 2, the comparison of different methods for the landslide displacement prediction is given via RMSE, MAE, MAPE, maximum error, minimum error.

Table 2 Compare the performance for the above-mentioned six models
Full size table

Obviously, the results obtained from Table 2 indicate that the prediction performance of the two ensemble model, EEMD–ELM and M–EEMD–ELM, is better than those of the single ANN model. And the prediction precision of M–EEMD–ELM has an appropriate improvement to EEMD–ELM where the MSE, MAE, and MAPE reduce by 1.0961, 0.0387, and 0.1898 %, respectively; especially, we can see that M–EEMD–ELM model produces better results than the other five models in terms of getting the smallest maximum error and minimum error. And two ensemble models, EEMD–ELM and M–EEMD–ELM, have a big reducing in the maximum error. So, we can draw the conclusion that the proposed M–EEMD–ELM model is superior to the single ANN models and EEMD–ELM model. This illustrates that the idea of “decomposition and ensemble,” which is achieved using EEMD decomposition, can effectively improve the performance of landslide displacement prediction.

4 Conclusions

This study proposes a modified EEMD-based ELM ensemble paradigm to obtain accurate prediction results and improve landslide displacement prediction quality further. In terms of different criteria, RMSE, MAE, and MAPE, we can find that across different models for the test case of Baishuihe landslide, our proposed M–EEMD–ELM method performs the best. In comparison with the other classic single ANN models, only two ensemble models, EEMD–ELM and M–EEMD–ELM, successfully predict the obvious deformation without time delay, which is very important in landslide forecast warning. In conclusion, the M–EEMD–ELM prediction paradigm can effectively improve landslide displacement prediction and help make future planning of the area.