Synchronization of Coupled Memristor Neural Networks with Time Delay: Positive Effects of Stochastic Delayed Impulses

Abstract

This paper mainly investigates the positive effects of delay-dependent impulses on the synchronization of delayed memristor neural networks. Different from traditional impulsive control, the impulsive sequence in this paper is assumed to have the Markovian property, and is not always stabilizing. Based on a useful inequality, mean square synchronization criterion is derived under such a kind of impulsive effect. It can be seen that the stochastic impulses play an impulsive controller role, if they are stabilizing in an “average” sense. The validity of the theoretical results is illustrated by a numerical example.

1 Introduction

Nowdays, neural networks (NNs) has become a hot research topic, due to its wide applications [1,2,3,4]. In 1971, the concept of memristor was first proposed and some properties of memristor from theoretical level were discussed [5]. Memristor, as a new passive two-terminal circuit element, has been applied in designing integrated circuits and artificial NNs due to its good properties, such as low energy consumption, nanoscale, memory capability and good mimic of the human brain. Hence, the memristor neural networks (MNNs) have been designed to emulate human brains recently [6].

In recent years, synchronization, as a typical dynamical behavior of the NNs, has been studied extensively [7,8,9,10,11]. Compared with the traditional continuous NNs, the synchronization of MNNs is more difficult to investigate because of the switching characteristics of the connection weights [6, 12, 13]. In addition, the internal parameters of memristor, such as length, cross-sectional area and heterogeneity, may also affect the performance of memristor. In [13], the synchronization issue of MNNs with the uncertain parameter is addressed by using the theory of differential inclusion. In [14], by constructing Lyapunov-Krasovskii functionals, two effective synchronization criteria are provided for the coupled MNNs.

In many real networked systems, information transmission and exchange between neighboring nodes will suffer some uncertain factors, such as network attacks [15, 16] or communication delay [17,18,19]. Undoubtedly, the time-delay has become an important factor which should be considered for the synchronization problem of MNNs [12, 20]. In [12], it has been shown that the fixed-time synchronization for DMNNs can be achieved by designing the state-feedback controllers and adaptive controller, respectively. In [20], conservatism of synchronization criteria is reduced by using the average impulsive interval (AII) approach.

Impulsive effect, whether artificial or natural, is common in real networks [21]. In the past few years, more and more attention is paid to the synchronization of NNs with impulsive effects [22]. On the one hand, impulsive control is an effective and economical control technique in networked systems, since it is a discontinuous control and only applied to the nodes in some discrete time instants [2, 23, 24]. On the other hand, a real-world network may suffer from impulsive disturbance. Generally, according to the impulsive intensity, all impulses can be divided into two types: synchronizing impulses, or desynchronizing impulses [25, 26]. In [27,28,29], a uniform synchronization criterion for impulsive dynamic networks is proposed based on AII, where the impulsive strengths are assumed to be determined constants.

As is well known, when impulsive intensity is assumed to be determined, synchronization of a network can be destroyed by desynchronizing impulses, and a pre-designed impulsive controller can synchronize an asynchronous network [30,31,32]. However, impulsive disturbance is often stochastic, while an impulsive controller can also exhibit randomness because of some unstable factors. Hence, it seems more reasonable that the impulsive strengths are stochastic [33,34,35]. The above classification may no longer be applicable when impulsive strengths are not determined. An interesting question naturally arises: can a stochastic impulsive sequence act as an impulsive controller? If yes, what conditions should be satisfied?

Inspired by the discussions above, this paper will focus on the positive effects that stochastic impulses might have on synchronizing a DMNNs. The main contributions of this paper can be listed as follows:

• (1) A useful inequality is proposed in this paper which enriches the famous Halanay inequality. Compared with the previous result in [17], it is no longer required that all impulsive strengths are a fixed constant.

• (2) Different from [17, 27], the impulsive sequence in this paper is assumed to have the Markovian property. An easy-to-verify criterion is derived to guarantee the mean square synchronization of the concerned DMNNs.

• (3) Discussions on the synchronization criterion are made in this paper. It is revealed that the stochastic impulsive sequence can act as a controller and contribute to the synchronous behavior. Unlike the traditional impulsive controller [17], impulses in this paper only need to be stabilizing in an “average" sense, rather than always be stabilizing.

Notations: See Table 1.

Table 1 Table of notations

2 Preliminaries & Model Description

In this section, some assumptions, definitions, lemmas and the model description are given so as to get the main results.

Definition 1

[23]. Consider $\frac{{\text {d}}x}{{\text {d}}t}=\digamma (t,x)$, where $\digamma (t,x)$ is discontinuous in x. Define the set-valued map of $\digamma (t,x)$ as

$$\begin{aligned} \varPhi (t,x)={\bigcap _{\delta >0}}\,{\bigcap _{\mu ({\mathcal {N}})=0}}{\bar{co}}[\digamma (t,{\mathcal {B}}(x,\varkappa )\backslash {\mathcal {N}})], \end{aligned}$$

where ${\mathcal {B}}(x,\varkappa )=\{y:||y-x||\le \varkappa \}$, $\mu ({\mathcal {N}})$ is the Lebesgue measure of set ${\mathcal {N}}$. For this system, a Filippov solution with initial condition $\digamma (0)=\digamma _0$ is absolutely continuous on any subinterval $t\in [t_1, t_2]$ of [0, T], and the differential inclusion $\frac{{\text {d}}x}{{\text {d}}t}\in \varPhi (t, x), a.e. t\in [0, T].$

Definition 2

[27]. (Average Impulsive Interval(AII)) $T_a$ is said to be the AII of the impulsive sequence $\zeta =\{t_1,t_2,\cdots \}$, if there exist positive integer $\daleth _0$ and positive scalar $T_a$ such that

$$\begin{aligned} \frac{T-t}{T_a}-\daleth _0\le \daleth _\zeta (t,T)\le \frac{T-t}{T_a}+\daleth _0, \,\,\forall 0\le t\le T, \end{aligned}$$

where $\daleth _\zeta (t,T)$ stands for the number of impulses during the time interval (t, T).

Remark 1

The concept of AII reduces the conservatism for the synchronization of the NNs under impulsive effects since the positive number $T_a$ can be used to estimate the number of impulses during the time interval (t, T).

Definition 3

[17] (Average Impulsive Delay(AID)) ${\bar{\tau }} > 0$ is called the AID of a sequence of impulsive delays $\{\tau _k\}_{k \in {\mathbb {Z}}_+}$, if there is a constant $\tau ^{(0)} > 0$ satisfying

$$\begin{aligned} {\bar{\tau }} k - \tau ^{(0)} \le \sum _{j=1}^{k}\tau _k \le {\bar{\tau }} k + \tau ^{(0)},\,\,\,k \in {\mathbb {Z}}_+. \end{aligned}$$

This paper considers the DMNNs described by the following equations:

$$\begin{aligned} {\dot{x}}_i(t)&= -Dx_i(t) + A(x_i(t)) f(x_i(t)) + B(x_i(t)) f(x_i(t-\tau )) + {\bar{I}}(t) \nonumber \\&\quad + c\sum _{j=1}^{N}H_{ij}x_j (t),\,\,\,i = 1,2,\cdots ,N. \end{aligned}$$

(1)

where $x_i(t)=(x_{i1}(t),\cdots ,x_{in}(t))^T\in {\mathbb {R}}^n$ denotes the state variable of the ith neuron at time t, the matrix $D>0$. $A(x_i(t)) = (a_{lj}(x_{ij}(t)))_{n \times n}$ and $B(x_i(t)) = (b_{lj}(x_{ij}(t)))_{n \times n}$ indicate the connection weight matrix and the delayed connection weight matrix, respectively. $f(\cdot )$ represents the activation function. ${\bar{I}}(t)$ denotes the external input, and $\tau$ is a positive constant which represents the transmission delay. ${\mathcal {L}}_H = (H_{ij})_{N \times N}$ is the negative Laplacian matrix of the DMNNs. The initial condition of system (1) is given by $x_i (t)=\varphi _i(t)\in {{\mathbb {P}}}{{\mathbb {C}}}([-\tau , 0],{\mathbb {R}}^n)$.

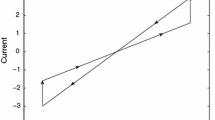
According to the typical current-voltage characteristics of the memristor (see Fig. 1), $a_{lj}(x_{ij}(t))$ and $b_{lj}(x_{ij}(t))$ in (1) are defined as

Fig. 1

Hysteresis curves of memristor at different frequencies

$$\begin{aligned} a_{lj}(x_{ij}(t))=\left\{ \begin{array}{ll} {\hat{a}}_{lj}, &{} {\vert {x_{ij}}(t)\vert } \le {T_{j}},\\ {\check{a}}_{lj}, &{} {\vert {x_{ij}}(t)\vert }>{T_{j}} \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} b_{lj}(x_{ij}(t))=\left\{ \begin{array}{lcl} {\hat{b}}_{lj}, &{} {{|x_{ij}}(t)|}\le {T_{j}},\\ {\check{b}}_{lj}, &{} {{|x_{ij}}(t)|}>{T_{j}}. \end{array} \right. \end{aligned}$$

Here, ${T_j>0}$ are memristive switching rules, ${{\hat{a}}_{lj}}$, ${{\check{a}}_{lj}}$, ${{\hat{b}}_{lj}}$, ${{\check{b}}_{lj}}$ are constants relating to memristance. For further discussion, based on [23] and Definition 1, the system (1) can be rewritten as:

$$\begin{aligned} {\dot{x}}_i(t)\in & {} -Dx_i(t)+{\bar{co}}[A(x_{i}(t))]f(x_i(t))+{\bar{co}}[B(x_i(t))]\nonumber \\&\times f(x_i(t-\tau )) + {\bar{I}}(t) + c \sum _{j=1}^{N}H_{ij}x_j(t), \end{aligned}$$

(2)

where ${\bar{co}}[A(x_i(t))]=[{\underline{A}}, {\bar{A}}]$, ${\bar{co}}[B(x_i(t))]=[{\underline{B}}, {\bar{B}}]$, ${\underline{A}} = (\acute{a}_{lj})_{n \times n}$, ${\bar{A}} = (\grave{a}_{lj})_{n \times n}$, ${\underline{B}} = (\acute{b}_{lj})_{n \times n}$, ${\bar{B}} = (\grave{b}_{lj})_{n \times n}$, $\acute{a}_{lj} \triangleq \min \{{\hat{a}}_{lj}, {\check{a}}_{lj}\}$, $\grave{a}_{lj} \triangleq \max \{{\hat{a}}_{lj}, {\check{a}}_{lj}\}$, $\acute{b}_{lj} \triangleq \min \{{\hat{b}}_{lj}, {\check{b}}_{lj}\}$, $\grave{b}_{lj} \triangleq \max \{{\hat{b}}_{lj}, {\check{b}}_{lj}\}$.

Let $a_{lj}^*=\frac{1}{2}(\grave{a}_{lj}+\acute{a}_{lj}), b_{lj}^*=\frac{1}{2}(\grave{b}_{lj}+\acute{b}_{lj})$, which express the intervals $[\acute{a}_{lj},\grave{a}_{lj}]$, $[\acute{b}_{lj}, \grave{b}_{lj}]$ in terms of the midpoints, $a_{lj}^{**}=\frac{1}{2}(\grave{a}_{lj}-\acute{a}_{lj})$ and $b_{lj}^{**}=\frac{1}{2}(\grave{b}_{lj}-\acute{b}_{lj})$ represent the half-lengths. By denoting $A^*\triangleq (a_{lj}^*)_{n \times n}$ and $B^*\triangleq (b_{lj}^*)_{n \times n}$, we can rewrite system (2) as follows:

$$\begin{aligned} {\dot{x}}_i(t)&= -D x_i(t) + (A^*+ R_A)f(x_i(t)) + (B^*+R_B)f(x_i(t-\tau ))\nonumber \\&\quad + {\bar{I}}(t) + c\sum _{j=1}^{N}H_{ij}x_j(t), \end{aligned}$$

(3)

where $R_A = E_A \Sigma _A F_A$, $R_B = E_B \Sigma _B F_B$, $\Sigma _{A,B} \in \Sigma$, and

$$\begin{aligned} \Sigma = {\text {diag}}[\varkappa _{11},\cdots ,\varkappa _{1n},\cdots ,\varkappa _{n1},\cdots ,\varkappa _{nn}] \in {\mathbb {R}}^{n^2 \times n^2}: | \varkappa _{ij} | \le 1 , \\ E_A = \big [\sqrt{a_{11}^{**}} e_1,\cdots ,\sqrt{a_{1n}^{**}} e_1,\cdots ,\sqrt{a_{n1}^{**}} e_n,\cdots ,\sqrt{a_{nn}^{**}} e_n\big ] \in {\mathbb {R}}^{n \times n^2} , \\ F_A = \big [\sqrt{a_{11}^{**}} e_1,\cdots ,\sqrt{a_{1n}^{**}} e_n,\cdots ,\sqrt{a_{n1}^{**}} e_1,\cdots ,\sqrt{a_{nn}^{**}} e_n\big ]^T \in {\mathbb {R}}^{n^2 \times n} , \\ E_B = \big [\sqrt{b_{11}^{**}} e_1,\cdots ,\sqrt{b_{1n}^{**}} e_1,\cdots ,\sqrt{b_{n1}^{**}} e_n,\cdots ,\sqrt{b_{nn}^{**}} e_n\big ] \in {\mathbb {R}}^{n \times n^2} , \\ F_B = \big [\sqrt{b_{11}^{**}} e_1,\cdots ,\sqrt{b_{1n}^{**}} e_n,\cdots ,\sqrt{b_{n1}^{**}} e_1,\cdots ,\sqrt{b_{nn}^{**}} e_n\big ]^T \in {\mathbb {R}}^{n^2 \times n} , \end{aligned}$$

where $e_i$ stands for the i-th column of the identity matrix $I_n$.

To deal with the uncertain terms $R_A$ and $R_B$, let $E = [E_A, E_B]$ and

$$\begin{aligned} \varDelta _i (t) = {\text {diag}}\{\Sigma _A, \Sigma _B\} \begin{bmatrix} F_A f(x_i(t))\\ F_Bf(x_i(t-\tau )) \end{bmatrix} \end{aligned}$$

(4)

Then, we can recast system (2) as

$$\begin{aligned} {\dot{x}}_i(t)&= -D x_i(t) + A^*f(x_i(t)) + B^*f(x_i(t-\tau )) \nonumber \\&\quad + {\bar{I}}(t) + c\sum _{j=1}^{N}H_{ij}x_j(t) + E \varDelta _i (t). \end{aligned}$$

(5)

In this paper, it is assumed that the following assumptions are satisfied.

Assumption 1

The function f is Lipschitz continuous. That is, for some constant $\varpi > 0$ and $\forall y_1,\,y_2 \in {\mathbb {R}}^n$, $\Vert f(y_1) - f(y_2) \Vert \le \varpi \Vert y_1 - y_2 \Vert$.

Assumption 2

${\mathcal {L}}_H$ is symmetric and irreducible.

This paper focuses on how a stochastic impulsive sequence can promote the synchronization of network (1). Due to limited transmission speed, imperfect pulse output devices and some other factors, time delay always inevitably occurs in real-world networks. For this reason, we consider the one delayed impulsive effect, which can be formulated as follows:

$$\begin{aligned} x_j (t_k^+) - x_i(t_k^+) \le \sigma _k [x_j (t_k^- - \tau _k) - x_i(t_k^- - \tau _k)] \text { if } H_{ij} > 0, \end{aligned}$$

(6)

where $\zeta = \{t_k\}_{k=1,2,\cdots }$ is a strictly increasing sequence which represents the impulsive instants subject to Definition 2, and ${\lim _{k \rightarrow +\infty }t_k=\infty }$. $\tau _k$ is a delay sequence as described in Definition 3. Moreover, it is assumed that $t_k - t_{k-1} \ge \tau > \tau _k \ge 0$, $\forall k \in {\mathbb {Z}}_+$. $\{\sigma _k\}$ is the sequence of impulsive strengths, and satisfies the following assumption.

Assumption 3

Let $r_k \triangleq r(t_k)$ be a discrete Markov chain which is independent with the initial conditions $\varphi _i(\cdot )$. $\varOmega = \{1,2,\cdots ,\beta \}$ is the set of states, from which $r(t_k)$ takes its values. ${\mathcal {P}} = (p_{ij})_{\beta \times \beta }$ and $\Pi _1 = (\pi _{11},\cdots ,\pi _{1\beta })$ are the transition matrix and initial distribution of $r(t_k)$, respectively. $r(t_k)$ determines the impulsive strength at $t_k$, that is, $\sigma _k = \sigma ^{(r_k)}$, where $\sigma ^{(i)} > 0$ are $\beta$ different constant representing different impulsive strengths, $i = 1,\cdots ,\beta$.

By combining (5) with (6), we can obtain the following DMNNs with delay-dependent impulsive effect:

$$\begin{aligned} \left\{ \begin{array}{lll} {\dot{x}}_i(t) = -D x_i(t) + A^*f(x_i(t)) + B^*f(x_i(t-\tau )) + {\bar{I}}(t)\\ \qquad + c\sum _{j=1}^{N}H_{ij}x_j(t) + E \varDelta _i (t),\,\,\,t \ne t_k,\,\,\, i = 1,\cdots ,N,\\ x_j (t_k^+) - x_i(t_k^+) \le \sigma _k [x_j (t_k^- - \tau _k) - x_i(t_k^- - \tau _k)] \text { if }H_{ij} > 0 ,\\ x_i(t) = \varphi _i(t),\,\,\, t \in [t_0-\tau , t_0]. \end{array} \right. \end{aligned}$$

(7)

Remark 2

Under Assumption 3, the impulsive network (7) can be regarded as a Markovian mode-jump system which switches among $\beta$ different “impulsive modes” $\sigma ^{(1)},\cdots ,\sigma ^{(\beta )}$. As mentioned in [37], systems with Markovian jump can be used to describe many real-world applications, such as economic systems, chemical systems, power systems and so on. Dynamic systems that experience random abrupt variations in their structures or parameters can be well described by Markovian jump systems. Hence, it is meaningful to study impulsive DMNNs with such Markovian property.

To proceed, we introduce ${\bar{x}}(t) \triangleq \frac{1}{N}\sum _{i=1}^{N}x_i(t)$ as the average state. Denote the synchronization error as $\varepsilon _i(t)=x_i(t)-{\bar{x}}(t)$ and define $\varepsilon (t) \triangleq (\varepsilon _1^T (t),$ $\cdots ,\varepsilon _N^T (t))^T$. The following definition and lemmas are needed in the rest of this paper.

Definition 4

System (7) is said to achieve global exponential synchronization (GES) in mean square, if

$$\begin{aligned} {\mathbf {E}}[\Vert \varepsilon (t) \Vert ] \le M \Vert {\varepsilon }_{t_0} \Vert _\tau e^{-\chi (t-t_0)},\,\,\,\forall t \ge t_0, \end{aligned}$$

where M and $\chi$ are two positive constants.

Lemma 1

Assume that there exist ${\underline{\mu }} > 0$ and ${\bar{\mu }} \ge 1$ such that ${\underline{\mu }} \le \mu _k \le {\bar{\mu }}$. Let $w(\cdot ) \in {\mathbb {R}}$ be a piecewise continuous function satisfying

$$\begin{aligned} \left\{ \begin{array}{lcl} D^+ w(t) \le -q_1 w(t) + q_2 w(t-\tau ),\,\,\,t \ne t_k,\\ w(t_k^+) \le \mu _k w(t_k^- - \tau _k), \end{array} \right. \end{aligned}$$

(8)

where $q_1 \in {\mathbb {R}}$, $q_2 \in {\mathbb {R}}_+$, $t_k-t_{k-1} \ge \tau \ge \tau _k \ge 0$. Then, it holds that

$$\begin{aligned} w(t,x(t)) \le \Vert w_{t_0} \Vert _\tau \prod _{j=1}^{k}\mu _j \exp {\Big [{\bar{\kappa }} (t+\tau -t_0 - \sum _{j=0}^{k}\tau _j)\Big ]}, \,\,\, \forall t \in [t_k, t_{k+1}), \end{aligned}$$

(9)

where constant ${\bar{\kappa }} > 0$ satisfies $-q_1 + \frac{{\bar{\mu }}}{{\underline{\mu }}}q_2 - {\bar{\kappa }} < 0$.

Proof

It directly follows from Theorem 3.9 in [17] that (9) is true on $[t_0-\tau , t_1)$. Assume (9) is true for all $k \le m-1$, then

$$\begin{aligned} w(t_m^+)&\le \mu _m w(t_m^- - \tau _m) \nonumber \\&\le \mu _m \Vert w_{t_0} \Vert _\tau \prod _{j=1}^{m-1}\mu _j \exp {\Big [{\bar{\kappa }} (t_m - \tau _m + \tau -t_0 - \sum _{j=0}^{m-1}\tau _j)\Big ]} \nonumber \\&= \Vert w_{t_0} \Vert _\tau \prod _{j=1}^{m}\mu _j \exp {\Big [{\bar{\kappa }} (t_m + \tau -t_0 - \sum _{j=0}^{m}\tau _j)\Big ]}. \end{aligned}$$

(10)

It can be showed by contradiction that (9) is true for $k=m$. Otherwise, there must exists a $\acute{t} \in [t_m, t_{m+1})$ such that (9) is true on $[t_0, \acute{t})$,

$$\begin{aligned} w(\acute{t}) = \Vert w_{t_0} \Vert _\tau \prod _{j=1}^{m}\mu _j \exp {\Big [{\bar{\kappa }} (t+\tau -t_0 - \sum _{j=0}^{m}\tau _j)\Big ]} \triangleq \xi _m(t) \end{aligned}$$

(11)

and

$$\begin{aligned} D^+ w(t)|_{t=\acute{t}} \ge \frac{{\text {d}}}{{\text {d}}t} \xi _m (t) |_{t=\acute{t}} = {\bar{\kappa }} \xi _m (\acute{t}). \end{aligned}$$

(12)

But according to (8), (9) and $t_m - t_{m-1} \ge \tau \ge \tau _k$, we have

$$\begin{aligned} D^+ w(t) |_{t=\acute{t}}&\le -q_1 w(\acute{t}) + q_2 w(\acute{t} - \tau ) \nonumber \\&= -q_1 \xi _m (\acute{t}) + q_2 w(\acute{t} - \tau ) \nonumber \\&\le -q_1 \xi _m (\acute{t}) + q_2 {\bar{\mu }} \xi _{m-1}(\acute{t} - \tau ) \nonumber \\&\le (-q_1 + \frac{{\bar{\mu }}}{{\underline{\mu }}}q_2) \xi _m (\acute{t}) \nonumber \\&< {\bar{\kappa }} \xi _m (\acute{t}) = D^+ \xi _m (t)|_{t = \acute{t}}, \end{aligned}$$

(13)

which contradicts with (12). The proof is completed. $\square$

Remark 3

In particular, if $\mu _k \equiv \mu _0 \in (0,1)$, then Lemma 1 reduces to Theorem 3.9 in [17] by letting ${\underline{\mu }} = \mu _0$ and ${\bar{\mu }} = 1$. Hence, Lemma 1 can be seen as a generalization of the previous results in [17].

Lemma 2

[36] Assume a matrix $G = (g_{ij})_{n \times n} \in {\mathbb {R}}^{n \times n}$ satisfying the following:

• (a) G is irreducible and symmetric;

• (b) $\forall i \ne j$, $g_{ij} \ge 0$;

• (c) $g_{ii} = -\sum _{j=1,j \ne i}^{n}g_{ij}$, $\forall i=1,\cdots ,n$.

Then,

• (1) All eigenvalues of G are non-positive;

• (2) G has an eigenvalue 0 with multiplicity 1. In addition, $(1,\cdots ,1)^T$ is an eigenvector of 0.

3 Main Result

For the sake of convenience, we denote $q_1 = c \iota - \lambda _{max}\{-D+\frac{1}{2}B^*B^{*T} + \frac{1}{2} EE^T\} - \varpi \Vert A^*\Vert - \frac{\varpi ^2}{2}\Vert F_A \Vert ^2$ and $q_2 = \frac{\varpi ^2}{2}(1+\Vert F_B \Vert ^2)$, where $c,\,\varpi ,\,A^*,\,B^*,\,F_A,\,E,\,F_B$ are given in Sect. 2, $\iota = -\lambda _2({\mathcal {L}}_H)$ represents opposite number of the second largest eigenvalue of ${\mathcal {L}}_H$.

Now we are ready to provide the main theoretical result.

Theorem 1

Suppose that Assumptions 1–3 hold for DMNNs (1). Let ${\bar{\kappa }} > 0$ satisfy $-q_1 + \frac{{\bar{\sigma }}^2}{{\underline{\sigma }}^2} q_2 - {\bar{\kappa }} < 0$. Then, system (1) under impulsive effect (6) achieves GES in mean square if

$$\begin{aligned} {\widetilde{\mu }} < 1 \end{aligned}$$

(14)

and

$$\begin{aligned} {\bar{\kappa }}({\bar{\tau }} - T_a) - \ln {{\widetilde{\mu }}} = \rho _{{\bar{\kappa }}} > 0, \end{aligned}$$

(15)

where ${\bar{\sigma }} = \max _{i \in \varOmega }\{1, \sigma ^{(i)}\}$, ${\underline{\sigma }} = \min _{i \in \varOmega } \{\sigma ^{(i)}\}$ and ${\widetilde{\mu }} = \sum _{l=1}^{\beta } [(\sigma ^{(l)})^2 \max _{i \in \varOmega } \{p_{il}\}]$.

Proof

Recall that $\varepsilon _i(t)=x_i(t)-\frac{1}{N}\sum _{i=1}^{N}x_i(t)$ and construct a Lyapunov candidate function $V(t) = \frac{1}{2} \sum _{i=1}^{N}\varepsilon _i^T (t) \varepsilon _i(t)$. By repeatedly using the fact that $\sum _{i=1}^{N}\varepsilon _i(t) = 0$, the derivation of V(t) on $[t_k, t_{k+1})$ can be estimated as

$$\begin{aligned} D^+ V(t)&= \sum _{i=1}^{N}\varepsilon _i^T(t)[{\dot{x}}_i(t) - \frac{1}{N}\sum _{l=1}^{N}{\dot{x}}_l (t)] \nonumber \\&= \sum _{i=1}^{N}\varepsilon _i^T(t)[-D x_i(t) + A^*f(x_i(t)) + B^*f(x_i(t-\tau )) + {\bar{I}}(t) \nonumber \\&\qquad + c\sum _{j=1}^{N}H_{ij}x_j(t) + E\varDelta _i (t)] \nonumber \\&= \sum _{i=1}^{N}\varepsilon _i^T(t)[-D (\varepsilon _i(t) + {\bar{x}}(t)) + A^*(f(x_i(t)) - f({\bar{x}}(t))) \nonumber \\&\qquad + B^*(f(x_i(t-\tau )) - f({\bar{x}}(t-\tau ))+ c\sum _{j=1}^{N}H_{ij}\varepsilon _j(t) + E\varDelta _i (t)] \nonumber \\&\le -\sum _{i=1}^{N}\varepsilon _i^T(t) D \varepsilon _i(t) + \varpi \sum _{i=1}^{N}\Vert A^*\Vert \Vert \varepsilon _i^T(t) \Vert \Vert \varepsilon _i(t) \Vert \nonumber \\&\qquad + \frac{1}{2}\sum _{i=1}^{N}[\varepsilon _i^T(t)B^*B^{*T} \varepsilon _i(t) + \varpi ^2 \varepsilon _i^T(t-\tau )\varepsilon _i(t-\tau )]\nonumber \\&\qquad + c\varepsilon ^T(t)({\mathcal {L}}_H \otimes I_n) \varepsilon (t) + \sum _{i=1}^{N}\varepsilon _i^T(t) E \varDelta _i(t), \,\,\, t \in [t_k, t_{k+1}). \end{aligned}$$

(16)

Recall (4) and $E = [E_A, E_B]$, we have

$$\begin{aligned} \varDelta _i^T(t)\varDelta _i(t)&\le \varpi ^2 \Vert F_A \Vert ^2 \varepsilon _i^T(t) \varepsilon _i(t) + \varpi ^2 \Vert F_B \Vert ^2 \varepsilon _i^T(t-\tau ) \varepsilon _i(t-\tau ), \end{aligned}$$

(17)

which further indicates that

$$\begin{aligned} D^+ V(t)\le & {} \sum _{i=1}^{N}\varepsilon _i^T(t) \big [-D + (\varpi \Vert A^*\Vert + \frac{\varpi ^2}{2} \Vert F_A \Vert )I_n + \frac{1}{2}B^*B^{*T} + \frac{1}{2} E E^T\big ] \varepsilon _i(t) \nonumber \\&+ \frac{\varpi ^2}{2}(1 + \Vert F_B \Vert ^2) \sum _{i=1}^{N}\varepsilon _i^T(t-\tau )\varepsilon _i(t-\tau ) + c \varepsilon ^T(t) ({\mathcal {L}}_H \otimes I_n) \varepsilon (t), \end{aligned}$$

(18)

where Assumption 1 is used. Considering Assumption 2, ${\mathcal {L}}_H$ can be decomposed as

$$\begin{aligned} U \Lambda _H U^T = {\mathcal {L}}_H, \end{aligned}$$

(19)

where $U = (u_1,u_2,\cdots ,u_N)$ is an orthogonal matrix, $\Lambda _H = {\text {diag}}\{\lambda _1({\mathcal {L}}_H),\lambda _2({\mathcal {L}}_H),$ $\cdots ,\lambda _N({\mathcal {L}}_H)\}$, and $0=\lambda _1({\mathcal {L}}_H)>\lambda _2({\mathcal {L}}_H)\ge \cdots \ge \lambda _N({\mathcal {L}}_H)$ are eigenvalues of ${\mathcal {L}}_H$. In addition, $u_1 = \frac{1}{\sqrt{N}}(1,\cdots ,1)^T$ according to Lemma 2. Let $y(t) = (U^T \otimes I_n) \varepsilon (t) = (y_1^T(t),\cdots ,y_N^T(t))^T$, we have $y_1(t) = (u_1^T \otimes I_n) \varepsilon (t) = \frac{1}{\sqrt{N}}\sum _{i=1}^{N}\varepsilon _i(t) = 0$. Hence,

$$\begin{aligned} c \varepsilon ^T(t) ({\mathcal {L}}_H \otimes I_n) \varepsilon (t)&= c y^T(t) (\Lambda _H \otimes I_n) y(t) \nonumber \\&= c \sum _{i=2}^{N}\lambda _i({\mathcal {L}}_H) y_i^T(t) y_i(t)\nonumber \\&\le c\lambda _2({\mathcal {L}}_H)y^T(t) y(t) \nonumber \\&= -c \iota \varepsilon ^T(t)\varepsilon (t). \end{aligned}$$

(20)

(18) and (20) yield that

$$\begin{aligned} D^+ V(t)&\le \bigg (\varpi \Vert A^*\Vert + \frac{\varpi ^2}{2} \Vert F_A \Vert ^2 + \lambda _{max}\{-D + \frac{1}{2}B^*B^{*T} + \frac{1}{2}EE^T \} - c \iota \bigg ) V(t) \nonumber \\&\qquad + \bigg (\frac{\varpi ^2}{2}(1+ \Vert F_B \Vert ^2) \bigg ) V(t-\tau ) \nonumber \\&= -q_1 V(t) + q_2 V(t-\tau ),\,\,\, t \in [t_k, t_{k+1}). \end{aligned}$$

(21)

On the other hand, according to Assumption 2, for any two nodes i and j, there is at least one path between i and j. More precisely, there exist some integers $m_1,\,m_2,\,\cdots ,\,m_s$, such that $H_{im_1}>0$, $H_{m_1 m_2}>0$, $\cdots$, $H_{m_s j}>0$. Hence, at an impulsive instant $t_k$, we can infer from (7) that

$$\begin{aligned} V(t_k^+)&= \sum _{i=1}^{N} \varepsilon _i^T (t_k^+) \varepsilon _i(t_k^+) \nonumber \\&= \sum _{i=1}^{N} \bigg ( \frac{1}{N^2} \sum _{j=1}^{N}[x_i(t_k^+)-x_j(t_k^+)]^T \sum _{j=1}^{N}[x_i(t_k^+)-x_j(t_k^+)] \bigg ) \nonumber \\&{= \sum _{i=1}^{N} \bigg ( \frac{1}{N^2} \sum _{j=1}^{N}\big [x_i(t_k^+)-x_{m_1}(t_k^+) + x_{m_1}(t_k^+)- \cdots + x_{m_s}(t_k^+)-x_{j}(t_k^+)\big ]^T} \nonumber \\&{\qquad \times \sum _{j=1}^{N}\big [x_i(t_k^+)-x_{m_1}(t_k^+) + x_{m_1}(t_k^+)- \cdots + x_{m_s}(t_k^+)-x_{j}(t_k^+)\big ] \bigg )} \nonumber \\&{\le \sum _{i=1}^{N} \bigg ( \frac{\sigma _k^2}{N^2} \sum _{j=1}^{N}\big [x_i(t_k^- - \tau _k)-x_{m_1}(t_k^- - \tau _k) + \cdots + x_{m_s}(t_k^- - \tau _k)-x_{j}(t_k^- - \tau _k)\big ]^T} \nonumber \\&{ \qquad \times \sum _{j=1}^{N}\big [x_i(t_k^- - \tau _k)-x_{m_1}(t_k^- - \tau _k) + \cdots + x_{m_s}(t_k^- - \tau _k)-x_{j}(t_k^- - \tau _k)\big ] \bigg )} \nonumber \\&{=} \sigma _k^2 \sum _{i=1}^{N} \bigg ( \frac{1}{N^2} \sum _{j=1}^{N}[x_i(t_k^- - \tau _k)-x_j(t_k^- - \tau _k)]^T \sum _{j=1}^{N}[x_i(t_k^- - \tau _k)-x_j(t_k^- - \tau _k)] \bigg ) \nonumber \\&= \sigma _k^2 V(t_k^- - \tau _k). \end{aligned}$$

(22)

According to (21) and (22), V(t) satisfies all conditions in Lemma 1 by letting $\sigma _k^2 = \mu _k$, ${\bar{\sigma }}^2 = {\bar{\mu }}$ and ${\underline{\sigma }}^2 = {\underline{\mu }}$. Hence, for ${\bar{\kappa }} > -q_1 + \frac{{\bar{\mu }}}{{\underline{\mu }}}q_2$, we have

$$\begin{aligned} V(t)&\le \Vert V_{t_0} \Vert _\tau \prod _{j=1}^{k}\mu _j \exp {\Big [{\bar{\kappa }} (t+\tau -t_0 - \sum _{j=0}^{k}\tau _j)\Big ]},\,\,\,\forall t \in [t_k, t_{k+1}). \end{aligned}$$

(23)

Taking expectation on both sides of (23), we have

$$\begin{aligned} {\mathbf {E}}[V(t)] \le {\mathbf {E}}\big [\prod _{j=1}^{k}\mu _j\big ] \Vert V_{t_0} \Vert _\tau \exp {\Big [{\bar{\kappa }} (t+\tau -t_0 - \sum _{j=0}^{k}\tau _j)\Big ]},\,\,\,\forall t \in [t_k, t_{k+1}). \end{aligned}$$

(24)

Define $\mu ^{(i)} = (\sigma ^{(i)})^2,\,i = 1,\cdots ,\beta$. Considering Assumption 3, we have

$$\begin{aligned} {\mathbf {E}}\big [\prod _{j=1}^{k}\mu _j\big ]&= {\mathbf {E}}\big [{\mathbf {E}} \big [\prod _{j=1}^{k}\mu ^{(r_j)} {|} r_1=i_1,\cdots ,r_k=i_k \big ]\big ] \nonumber \\&= \sum _{i_1=1}^{\beta } \cdots \sum _{i_k=1}^{\beta }\Big (\big [\prod _{j=1}^{k}\mu ^{(i_j)}\big ] \times P(r_1=i_1,\cdots ,r_k=i_k)\Big ) \nonumber \\&= \sum _{i_1=1}^{\beta } \cdots \sum _{i_k=1}^{\beta } \Big (\mu ^{(i_1)} \prod _{j=2}^{k}\mu ^{(i_j)} \times \pi _{1i_1} \prod _{l=2}^{k}p_{i_{l-1}i_l}\Big ) \nonumber \\&\le \sum _{i_1=1}^{\beta } \mu ^{(i_1)}\pi _{1i_1} \Big (\sum _{i_2=1}^{\beta } \cdots \sum _{i_k=1}^{\beta } \big (\prod _{j=2}^{k}\mu ^{(i_j)} \max _{i \in \varOmega } \{p_{ii_j}\}\big )\Big ) \nonumber \\&= \sum _{i_1=1}^{\beta } \mu ^{(i_1)}\pi _{1i_1} \prod _{j=2}^{k}\Big (\sum _{l=1}^{\beta }\mu ^{(l)} \max _{i \in \varOmega } \{p_{il}\}\Big ) \nonumber \\&= {\widetilde{\mu }}^{k-1} \sum _{i=1}^{\beta }\mu ^{(i)}\pi _{1i}. \end{aligned}$$

(25)

By (24), (25) and the fact that ${\widetilde{\mu }} < 1$, we have

$$\begin{aligned} {\mathbf {E}}[V(t)]&\le {\widetilde{\mu }}^{k-1} \sum _{i=1}^{\beta }\mu ^{(i)}\pi _{1i} \Vert V_{t_0} \Vert _\tau \exp {\Big [{\bar{\kappa }} (t+\tau -t_0 - \sum _{j=0}^{k}\tau _j)\Big ]} \nonumber \\&\le {\widetilde{\mu }}^{-\daleth _0 - 1 + \frac{t-t_0}{T_a}} \sum _{i=1}^{\beta }\mu ^{(i)}\pi _{1i} \Vert V_{t_0} \Vert _\tau \exp {\Big [{\bar{\kappa }} (t+\tau -t_0 - {\bar{\tau }}k + \tau ^{(0)})\Big ]} \nonumber \\&\le \big ({\widetilde{\mu }}^{-\daleth _0 - 1}\sum _{i=1}^{\beta }\mu ^{(i)}\pi _{1i}\Vert V_{t_0} \Vert _\tau \big ) \exp {\Big (\frac{\ln {{\widetilde{\mu }}}}{T_a}(t-t_0)}\Big ) \nonumber \\&\qquad \times \exp {\big ({\bar{\kappa }}(t - t_0 + \tau + \tau ^{(0)}) + {\bar{\kappa }}[{\bar{\tau }}\daleth _0 - \frac{{\bar{\tau }}}{T_a}(t-t_0)]\big )} \nonumber \\&= {\widetilde{\mu }}^{-\daleth _0 - 1}\sum _{i=1}^{\beta }\mu ^{(i)}\pi _{1i}\Vert V_{t_0} \Vert _\tau \, e^{{\bar{\kappa }}(\tau + \tau ^{(0)} + {\bar{\tau }}\daleth _0)} \nonumber \\&\qquad \times \exp {\Big [-\frac{1}{T_a}[{\bar{\kappa }}({\bar{\tau }} - T_a) - \ln {{\widetilde{\mu }}}](t-t_0)\Big ]} \nonumber \\&= M\Vert V_{t_0} \Vert _\tau e^{-\frac{\rho _{{\bar{\kappa }}}}{T_a}(t-t_0)},\,\,\,\forall t \in [t_k,t_{k+1}), \end{aligned}$$

(26)

where the second and third inequalities use the AII and AID assumptions, $\rho _{{\bar{\kappa }}}$ is defined in (15). This completes the proof. $\square$

Remark 4

In order to achieve synchronization, the impulsive strengths should be stabilizing in a sense of “average” as shown in (14). It is worth mentioning that (14) does not require $\mu ^{(i)} < 1$ for all $i \in \varOmega$, which is different from traditional impulsive controller [17].

Remark 5

According to (15), small ${\bar{\kappa }}$ and ${\widetilde{\mu }}$ are helpful for synchronous behavior of the network. This can be explained by the following physical meaning: smaller ${\bar{\kappa }}$ means a better dynamic property of the network without impulses, while smaller ${\widetilde{\mu }}$ indicates higher costs at an impulsive instant. Another interesting fact is that the impulsive delay ${\bar{\tau }}$ may promote synchronization in some way according to (15). In fact, (15) is equivalent to

$$\begin{aligned} {\bar{\tau }} > \frac{\ln {{\widetilde{\mu }}}}{{\bar{\kappa }}} + T_a. \end{aligned}$$

Obviously, a larger ${\bar{\tau }}$ is preferred in order to meet the requirement of (15).

Remark 6

It should be mentioned that, the criterion in Theorem 1 is just a sufficient condition, and has some conservatism. This is mainly caused by some imprecise inequalities in the proof.

An important special case of Theorem 1 is when all $\tau _k$ are the same, that is, $\tau _k \equiv \tau _1$. In this case, we have the following two corollaries by utilizing Theorem 1.

Corollary 1

In Theorem 1, let the impulsive delays $\tau _k \equiv \tau _1$. Then, system (1) under impulsive effect (6) is globally exponentially synchronized, if

$$\begin{aligned} {\widetilde{\mu }} < 1 \end{aligned}$$

(27)

and

$$\begin{aligned} {\bar{\kappa }}(\tau _1 - T_a) - \ln {{\widetilde{\mu }}} > 0, \end{aligned}$$

(28)

where the parameters ${\widetilde{\mu }}$, ${\bar{\kappa }}$ and $T_a$ are the same as in Theorem 1.

Proof

When $\tau _k \equiv \tau _1$, we have ${\bar{\tau }} = \tau _1$. The proof can be completed by directly using Theorem 1. $\square$

Corollary 2

Let the impulsive delays $\tau _k \equiv 0$ in Theorem 1. Then, system (1) under impulsive effect (6) is globally exponentially synchronized, if

$$\begin{aligned} {\widetilde{\mu }} < 1 \end{aligned}$$

(29)

and

$$\begin{aligned} - {\bar{\kappa }} T_a - \ln {{\widetilde{\mu }}} > 0, \end{aligned}$$

(30)

where the parameters ${\widetilde{\mu }}$, ${\bar{\kappa }}$ and $T_a$ are the same as in Theorem 1.

When the impulsive sequence has no randomness, we have the following corollary.

Corollary 3

Let the impulsive strengths $\sigma _k \equiv \sigma _1$ in Theorem 1. Then, system (1) under impulsive effect (6) is globally exponentially synchronized, if

$$\begin{aligned} \sigma _1 < 1 \end{aligned}$$

(31)

and

$$\begin{aligned} {\bar{\kappa }}({\bar{\tau }} - T_a) - 2\ln {\sigma _1} > 0, \end{aligned}$$

(32)

where the parameters ${\bar{\tau }}$, ${\bar{\kappa }}$ and $T_a$ are the same as in Theorem 1.

Proof

Noticing that ${\widetilde{\mu }} = \sigma _1^2$, the proof is trivial. $\square$

4 Numerical Example

This section gives a simple example to illustrate the validity of our theoretical results. Moreover, the case of ${\bar{\tau }} = 0$ is also simulated to reflect the promotion of impulsive delay.

Example 1

Consider DMNNs (1) with $N=50$ and $n=1$. $A(x_i (t))$ and $B(x_i (t))$ are chosen to be

$$\begin{aligned} A(x_{i}(t))=\left\{ \begin{array}{lcl} 0.15, &{} &{} {|x_i(t)| \le 1},\\ 0.25, &{} &{} {|x_i(t)| > 1}, \end{array} \right. \end{aligned}$$

and

$$\begin{aligned} B(x_{i}(t))=\left\{ \begin{array}{lcl} -0.95, &{} &{} {|x_i(t)| \le 1},\\ -1.05, &{} &{} {|x_i(t)| > 1}. \end{array} \right. \end{aligned}$$

Moreover, $D = 0.5$, $f(x_i) = 1.5x_i + 0.5\tanh {(x_i)}$, $\tau = 1$, ${\bar{I}}(t) = 0$, $c = 1$, ${\mathcal {L}}_H$ is randomly generated with $\lambda _2({\mathcal {L}}_H) = -0.6239$ and the initial conditions are randomly chosen from $[-5,5]$. Figure 2 shows the state trajectories of all nodes when the DMNNs is free from impulsive effects. It is shown that the system is not synchronized without impulses.

Fig. 2

State trajectories of all nodes without impulsive effect in Example 1

Now we exert the delay-dependent impulsive effect (6) on (1). Let $\sigma ^{(1)} = 0.6$, $\sigma ^{(2)} = 1.05$. The initial distribution and the transition matrix are $\Pi _1 = (0.8,0.2)$ and ${\mathcal {P}} = \begin{bmatrix} 0.7 &{} 0.3\\ 0.8 &{} 0.2 \end{bmatrix}$, respectively. Furthermore, we choose $T_a = 1.05$ and ${\bar{\tau }} = 0.98$. Figure 3a shows the randomly generated impulsive sequence, and Fig. 3b is the impulsive delays.

Fig. 3

Impulsive strengths and delays in Example 1

Using the parameters above, we easily calculate that $q_1 = -0.0761$, $q_2 = 2.2000$, ${\widetilde{\mu }} = 0.6187$, ${\bar{\sigma }} = 1.05$ and ${\underline{\sigma }} = 0.6$. Choosing ${\bar{\kappa }} = 6.8236$, which satisfies $-q_1 + \frac{{\bar{\sigma }}^2}{{\underline{\sigma }}^2} q_2 - {\bar{\kappa }} = -0.01 < 0$, we obtain ${\bar{\kappa }}({\bar{\tau }} - T_a) - \ln {{\widetilde{\mu }}} = 0.0024 > 0$. By applying Theorem 1, the DMNNs (1) under delayed impulsive effect (6) can achieve synchronization, which can be seen from Fig. 4.

Fig. 4

State trajectories of all nodes under delayed impulsive effects in Example 1

As mentioned at the end of Remark5, the impulsive delay ${\bar{\tau }}$ may promote synchronization in some way. To illustrate this, the impulsive delay is changed to be ${\bar{\tau }}=0$, and all other parameters are the same as above. Figure 5 shows the state trajectories under such impulsive effects without impulsive delay, and it can be seen that synchronization is not achieved before $t = 12$. To some extent, this can reflect the promotion of impulsive delay ${\bar{\tau }}$.

Fig. 5

State trajectories under impulsive effects with ${\bar{\tau }}=0$ in Example 1

Remark 7

In Example 1, $\sigma ^{(1)} = 0.6 < 1$ is a stabilizing impulsive intensity, and $\sigma ^{(2)} = 1.05 > 1$ is destabilizing [17, 27]. Hence, the impulsive sequence in Example 1 is neither synchronizing nor desynchronizing according to the classification in [27]. By calculating ${\widetilde{\mu }}$, this paper provides a method to judge whether a stochastic impulsive sequence promotes synchronization or not.

5 Conclusion

This paper investigated the positive effects that stochastic delayed impulses might have on the synchronization of DMNNs. Based on an extended Halanay inequality, sufficient condition was derived to guarantee the mean square synchronization. It was revealed that the impulsive effect should be stabilizing in an “average” sense, rather than always be stabilizing. The theoretical results were verified by a numerical example.

It is worth mentioning that our main results are sometimes conservative. For instance, the hypothesis $t_k - t_{k-1} \ge \tau _k$, $\forall k \in {\mathbb {Z}}_+$ is hard to be satisfied in many cases, especially when the interval between two consecutive impulses is short. An interesting future work is to reduce the conservatism by allowing $t_k - t_{k-1} < \tau _k$. Another interesting future topic is to study the case with stochastic impulsive interval.