Introduction

The formation of deposits, as the result of massive material and energy accumulation, is controlled by the dynamic mineral systems of different scales of the earth (Blewett et al., 2010; Lü et al., 2015; Hagemann, et al., 2016). The precipitation and enrichment of metals are closely associated with the evolution of ore-forming fluids/melts controlled by multiple geological factors (Guo et al., 2020). Different geological factors control the formation of mineralization with different actions at different scales (Barnes & Robertson, 2018; Carranza et al., 2019; Groves et al., 2020; Lawley et al., 2021; Liu et al., 2021). Exploring the multiscale non-stationary effects of different geological factors on mineralization is important to understand metallogeny of mineral deposits and improve the reliability of mineral prospectivity mapping (Zuo, 2020).

Generally, different processes at different scales should be modeled separately in terms of the level and essence of physical property. One model is hard to solve multiscale problems of different processes simultaneously (Rudd and Broughton, 2000; Wang, 2004). The research on this aspect is rarely published. The Bayesian non-separable multiscale spatially varying coefficient (SVC) model is an exception, which can deal with the scales of different relationships in the same model (Gelfand et al., 2003; Fotheringham et al., 2017), but its parameters estimating is usually very time consuming (Wolf et al., 2017). Geographically weighted regression (GWR) is an SVC model and has been used to explore the non-stationarity in relationships between variables (Zhao et al., 2014; Huang et al., 2020, 2021). But GWR cannot operate in different geological processes at different scales. The newly proposed multiscale geographically weighted regression (MGWR) is a multi-process model in which different processes at different scales can be carried out simultaneously (Fotheringham et al., 2017).

The Jinchuan Ni–Cu sulfide deposit is one of the largest magmatic sulfide deposits in the world (Li et al., 2004; Porter, 2016). The deposit was formed in magma conduit system, in which sulfide and olivine-bearing magma flowed continuously in the Jinchuan intrusion accompanied by sulfide accumulation (Chen et al., 2013; Lightfoot and Evans-Lamswood, 2015; Duan et al., 2016; Mao et al., 2018a, b). With the Jinchuan Ni–Cu sulfide deposit as a case study, this study devotes to explore the non-stationarity and multiple scales of the impact of different ore-controlling factors on Ni–Cu mineralization. We first extend the MGWR model to three-dimensional space; and then evaluate it with simulated datasets from aspects of model performance, bandwidth, non-stationarity and parameters estimation accuracy; next, we apply the GWR and MGWR models to analyze the multiscale and non-stationary impact of different ore-controlling factors on mineralization; finally, we interpret the variations of parameter estimates in combination with the geological conditions.

Study Area and Datasets

Study Area

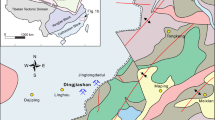
The Jinchuan Ni–Cu sulfide deposit is hosted by the Jinchuan mafic–ultramafic intrusion, which is located in the Longshoushan terrane, southwest margin of North China Craton, NW China (Fig. 1a, b). The regional NW–SE thrust faults F1 and F2 are, respectively, the northern and southern boundaries of the Longshoushan terrane, which are thought to be formed at Neoproterozoic (Tang and Li, 1995; Song et al., 2012). The Jinchuan intrusion is about 6500 m long and 20–500 m wide, and dips to the southwest with dip angles of 50°–80°. The ENE–WSW striking faults F8, F16-1, F23 crosscut the mafic–ultramafic intrusion and divided the Jinchuan intrusion into segments III, I, II, IV, respectively (Fig. 1c, d). The Jinchuan intrusion is exposed on the surface from F8 to NE–SW striking normal faults F17. The recent studies divided the Jinchuan intrusion into two portions, namely western and eastern intrusion, bounded by F16-1 (Song et al., 2009, 2012; Duan et al., 2016; Mao et al., 2018a, b, 2019). The western intrusion emplaced into the Paleoproterozoic gneiss and marble, while the eastern intrusion emplaced into the Paleoproterozoic marble and migmatites. The western intrusion is narrower, tubular-shaped and comprised of upper and lower lithology units (Chen et al., 2013). The upper lithology includes fine-grained dunite, lherzolite, and minor pyroxenite while the lower part mainly comprises coarse-grained dunite and lherzolites. Sulfide mineralization in western intrusion is also tubular-shaped and mainly occurs near the footwall of intrusion. Major Ni–Cu mineralization in the western intrusion shows the disseminated characteristics with relatively low grade.

Figure 1
figure 1

Geological sketch of the Jinchuan copper nickel sulfide deposit: (a) the location of the Jinchuan deposit in China, (b) a simplified geological map of the Longshoushan terrane based on Zhang et al. (2013), (c) geological map of the Jinchuan deposit based on Liang et al. (2022), (d) a projected long section of A-A’ and B-B’ based on Mao et al. (2019)

Full size image

The eastern intrusion shows V-shape cross section and occurs a wider feature from west to east (Mao et al., 2019). The lithology of intrusion includes medium- to coarse-grained lherzolite and dunite. The mineral grain size of dunite generally occurs in a variety of moderate to fine from center to outward. Sulfide mineralization in eastern intrusion occurs as a concentric shell with a net-textured sulfide (or massive sulfide) center, and comprises the two largest orebodies of the Jinchuan deposit, namely Nos. 1 and 2 orebodies (Fig. 1d). The net-textured and low-grade disseminated ores are the dominant mineralization of Nos. 1 and 2 orebodies. There are some massive ores at the bottom of the intrusion.

The magmatic conduit system for the formation of the Jinchuan Ni–Cu deposit is widely accepted (Tang and Li, 1995; Song et al., 2009, 2012). Previous studies have proposed that the Jinchuan Ni–Cu sulfide mineralization is the result of the accumulation and emplacement of sulfide after different amounts of prior removal before ascending shallow crust (Song et al., 2012; Chen et al., 2013; Mao et al., 2019). Based on the characteristics of platinum-group elements, chalcophile elements, petrology zonation and ore distribution, there are most likely several subclass magma conduits for the western and eastern intrusions (Zeng et al., 2016; Mao et al., 2019; Kang et al., 2022). The geological models of intrusions, magma conduits and faults in this study are displayed in Figure 2.

Figure 2
figure 2

The 3D models of intrusions, magma conduits and faults

Full size image

Data and Variables

The whole study area was divided into voxels with the size of 10 m × 10 m × 10 m. The attributes of each voxel included spatial coordinates, ore grades and features of related ore-controlling factors. The definitions and data characteristics for these attributes are presented in Table 1. Considering the different geochemical behaviors of Cu and Ni in the sulfide mineralization during ore-bearing magma flow, we selected the Cu and Ni grades as the dependent variables in this study. Their spatial distributions in 3D space are displayed in Figure 3. The ore-controlling factors (“dFault”, “dMC”, “dRatio” and “dTrend”) that can reflect the controls on mineralization by several geological bodies were extracted quantitatively according to the methods of Mao et al. (2018a, b, 2019). They were also selected as the independent variables. The detailed descriptions of the ore-controlling factors are as follows.

  1. 1.

    dFault. The shortest distance from the voxel to the relevant fault, represents the influence degree of the fault. A positive value indicates that the voxel is located on the hanging wall of the fault while a negative value indicates otherwise. Although the fault that originally provided space for ore pulp was transformed by later tectonic movement, it still has a certain indication of magma position.

  2. 2.

    dRatio. The ratio of distances to intrusion top and bottom from one voxel in thickness direction, represents the relative position in the intrusion. It may reflect the gravity differential characteristics of Cu and Ni mineralization.

  3. 3.

    dMC. The shortest distance to center of the magma conduit from a voxel, represents the influence of the magma conduit on metal enrichment.

  4. 4.

    dTrend. The shortest distance to the trend surface of intrusion bottom from the voxel, represents the original geometric features of country rocks or early fault. A positive value indicates that the intrusion bottom is convex relative to the trend while a negative value is otherwise. It may reflect the mineralization during magma flow affected by variable physical conditions caused by country-rock or early fault geometry.

Table 1 Data description
Full size table
Figure 3
figure 3

Spatial distributions of the grade of (a) Cu and (b) Ni. The whole deposit is divided into (c) western intrusion and (d) eastern intrusion by the fault F16-1

Full size image

For convenience of subsequent description, the datasets with dependent variables Cu and Ni were represented by datasetCu and datasetNi, respectively. The statistical description of the variables in the western intrusion and eastern intrusion is shown in Table 1 from which we find that the two intrusions have different distribution characteristics.

Data Preprocessing

Multicollinearity and Hypothesis Test

The multicollinearity test is the basis of regression analysis. This study employed the variance inflation factor (VIF) to justify whether multicollinearity exists among the independent variables. The VIF values in Table 2 are smaller than 7.5, which illustrates that the redundancy can be accepted (Marquardt, 1970). As the starting point for regression analysis, the OLS (ordinary least squares) was performed and the hypothesis testing results are obtained (Table 3). The Jarque–bera statistics illustrate that the predictions are biased, the Koenker statistics show that the modeled relationships are unstable. All these results illustrate that the OLS models cannot well express the relationships.

Table 2 Multicollinearity test result for the independent variables
Full size table
Table 3 Result of statistical significance tests
Full size table

Spatial Non-Stationarity Detection

GWR model is used to detect the spatial non-stationarity in spatial processes. In this study the global and local \(R^{2}\) values, global and local spatial autocorrelation of model residuals, and stationary index of parameters were employed to test whether the relationship between mineralization and its determinants is non-stationary.

The global \(R^{2}\) values of GWR and OLS models are shown in Table 4. The global \(R^{2}\) values of GWR on both datasets in two intrusions are all bigger than 0.96 while those of OLS are all smaller than 0.20, which reflect that GWR models express the relationships better than OLS models. The local \(R^{2}\) values of the two models are illustrated in Figure 4. Most of the local \(R^{2}\) values of GWR models are bigger than 0.75, which indicates that GWR models fit well in most areas. Both the global and local \(R^{2}\) values illustrate that the GWR models fit better than OLS models and the non-stationarity exists in the relationships.

Table 4 Comparison of global \({R}^{2}\) values and spatial autocorrelation of residuals
Full size table
Figure 4
figure 4

Local \(R^{2}\) distributions of GWR models for (a) Cu and (b) Ni

Full size image

The spatial autocorrelation of model residuals represented by Moran’s I was employed to measure the model ability to deal with non-stationarity between relationships of variables. The global Moran’s I values from both models are shown in Table 4 and the spatial distributions of local Moran’s I values are illustrated in Figure 5. The global Moran’s I values from GWR models are all smaller than those from OLS models (Table 4) and the local Moran’s I values from GWR models (Fig. 5(a-2) and (b-2)) are more evenly distributed than those from OLS models (Fig. 5(a-1) and (b-1)). All these results reflect that GWR models can better decrease the spatial autocorrelation in residuals.

Figure 5
figure 5

Local Moran’s I distributions of OLS and GWR models

Full size image

The non-stationarity degree of parameter estimates can be evaluated by the stationary index. Values bigger than 1 are considered non-stationary (Brunsdon et al., 2002; Huang et al., 2020). The values of all the parameter estimates were bigger than 1 (Table 5), which means that the relationships between ore grades and their controlling factors were non-stationary.

Table 5 Stationary index of parameter estimates from GWR models
Full size table

Method

The Basics of GWR in 3D Space

GWR is a local regression method that allows the parameters varying in space. Given \({\varvec{Y}} = \left\{ {y_{1} , y_{2} , ,y_{n} } \right\}\), \({\varvec{X}} = \left\{ {x_{11} , x_{12} , ,x_{nm} } \right\}\), the GWR model is stated:

$$y_{i} = { }{\varvec{X}}_{i} {\varvec{\beta}}_{i}^{T} + \varepsilon_{i}$$
(1)

where i is the point number, \(\varepsilon_{i}\) is the error, \({\varvec{\beta}}_{i}\) is the location-specific parameters that can be estimated:

$${\hat{\mathbf{\beta }}} = \left( {{\varvec{X}}^{T} {\varvec{WX}}} \right)^{ - 1} {\varvec{X}}^{T} {\varvec{Wy}}$$
(2)

where W is the weight matrix, usually determined by smooth kernel distance function and bandwidth (Fotheringham et al. 2002a, b). In this study, the number of nearest neighbors was adopted as the bandwidth and bi-square kernel was adopted as the weighting function, thus:

$$\begin{aligned} {\text{bi{-}square:}}w_{ij} & = \left[ {1 - \left( {d_{ij} /D_{i} } \right)^{2} } \right]^{2} \quad {\text{if}}\;d_{ij} < D_{i} \\ & = 0 \;{\text{otherwise}} \\ \end{aligned}$$
(3)

where \(d_{ij}\) represents the distance between points i and j,\(D_{i}\) is the distance determined by the bandwidth. The bi-square kernel ensures that observations outside of the bandwidth have no effect to the regression point, and observations within the bandwidth closer to the specific point have a larger weight.

The Basics of MGWR in 3D Space

The MGWR model was proposed by Fotheringham et al. (2017); it is a flexible model in which processes with different levels of spatial heterogeneity and different spatial scales can be simulated simultaneously. Different from the unique bandwidth in the GWR model which assumes that all the explanatory variables work on the response variable in the same scale, the MGWR model allows various bandwidths for different explanatory variables. The MGWR model is originally developed in python language in 2D space (Oshan et al., 2019). We extended it to 3D space and implemented it in MATLAB language by referencing the Econometrics Toolbox 7.0 (LeSage and Pace 2009). The formula is:

$$y_{i} = \mathop \sum \limits_{j = 0}^{m} \beta_{bj} \left( {e_{i} ,n_{i} ,h_{i} } \right)x_{ij} + \varepsilon \left( {e_{i} ,n_{i} ,h_{i} } \right)\quad i = 1 \cdots n$$
(4)

where bj is the bandwidth for the jth variable, \(\left( {e_{i} ,n_{i} ,h_{i} } \right)\) is the spatial coordinates. The calibration of MGWR follows the logic of generalized additive models (GAMs; Buja et al., 1989). Set \({\varvec{f}}_{j} = {\varvec{\beta}}_{bj} {\varvec{x}}_{j}\), which represents the jth additive term in MGWR, the GAM-style MGWR is expressed as (Fotheringham et al., 2017):

$${\varvec{y}} = \mathop \sum \limits_{j = 0}^{m} {\varvec{f}}_{j} + {\varvec{\varepsilon}}$$
(5)

The model can be calibrated with a back-fitting algorithm whose flow chart is displayed in Figure 6. First, initialize parameter estimates to zero, or to the results from a global or local model; and then regress each independent variable \({\varvec{x}}_{{\varvec{j}}}\) to \(\hat{\user2{\varepsilon }} + \hat{\user2{f}}_{j}\) using GWR model; finally, judge whether the convergence is reached, if so, output the parameters and end the calculation, else repeat the regression. The detailed process is described in Fotheringham et al. (2017) and the implementation code is available in the supplementary materials (Appendix). The convergence depends on the score of change (SOC), which represents the value of the differential between successive iterations whereby the process is deemed to have converged. The \({\text{SOC}}_{f}\) displayed below was adopted as the convergence function to justify whether the iterations end by comparing its value with a predetermined sufficiently small value.

$${\text{SOC}}_{f} = \sqrt {\frac{{\mathop \sum \nolimits_{j = 1}^{m} \frac{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\hat{f}_{ij}^{new} - \hat{f}_{ij}^{old} } \right)^{2} }}{n}}}{{\mathop \sum \nolimits_{i = 1}^{n} \left( {\mathop \sum \nolimits_{j = 1}^{m} \hat{f}_{ij}^{new} } \right)^{2} }}}$$
(6)
Figure 6
figure 6

Flow chart of MGWR (Fotheringham et al. 2017)

Full size image

Multiple GWR operations are required in a MGWR model. The calibration of MGWR model is a time-consuming process. It is seen that the MGWR model has a much higher computational complexity than GWR model.

Simulation Design

The original MGWR model was implemented in python language in 2D space (Fotheringham et al., 2017). This study extended it to 3D space based on the GWR model (Huang et al., 2020). To test the model effectiveness and accuracy, we designed three non-stationary processes with different scales represented by \({\varvec{\beta}}_{0}\), \({\varvec{\beta}}_{1}\) and \({\varvec{\beta}}_{2}\). Figure 7 shows their spatial distributions: \({\varvec{\beta}}_{0}\) values were all the same throughout the space, \({\varvec{\beta}}_{1}\) values increased from lower left corner to upper right corner and \({\varvec{\beta}}_{2}\) values formed multiple clusters. Obviously, from \({\varvec{\beta}}_{0}\), \({\varvec{\beta}}_{1}\) to \({\varvec{\beta}}_{2}\), the scale changed from big to small and the non-stationarity became higher and higher.

Figure 7
figure 7

The spatial distributions of \({\varvec{\beta}}_{0}\), \({\varvec{\beta}}_{1}\) and \({\varvec{\beta}}_{2}\) in 2D and 3D space

Full size image

The simulated datasets were constructed as:

$$y_{i} = \beta_{i0} + \beta_{i1} x_{i1} + \beta_{i2} x_{i2} + \varepsilon_{i} \quad i = 1,2, \ldots ,n$$
(7)

where {\(x_{11} ,x_{21} , \cdots ,x_{n1}\)} and {\(x_{12} ,x_{22} , \cdots ,x_{n2}\)} are randomly generated with a normal distribution N(0,1) and the error item {\(\varepsilon_{1} ,\varepsilon_{2} , \cdots ,\varepsilon_{n}\)} is randomly generated with a normal distribution N(0,2). The dataset size n in 2D space was \(40 \times 40\) and \(20 \times 20 \times 20\) in 3D space.

Model Evaluation

Using \({\text{SOC}}_{f} < 1E - 5\) as the termination criterion, the MGWR model was tested and evaluated with the above simulated datasets from four aspects: bandwidth, model performance, non-stationarity and estimation accuracy. The bandwidth for GWR model was unique while the bandwidths for MGWR model varied with independent variables. The performance of both GWR and MGWR models were measured by the adjusted R2 value. The non-stationarity of \(\hat{\user2{\beta }}\) was evaluated by the stationary index (Brunsdon et al. 2002) and the estimation accuracy of \(\hat{\user2{\beta }}\) was evaluated by the spatial distribution, bias and its root mean squares error (RMSE).

The bias of parameter estimate was the difference between the simulated and estimated values. It reflects the local estimation accuracy and can be denoted as (Yu et al., 2020):

$$\gamma_{ij} = \beta_{ij} - \hat{\beta }_{ij}$$
(8)

The \({\text{RMSE}}\) is formulated as:

$${\text{RMSE}}_{j} = \sqrt {\frac{1}{n}\mathop \sum \limits_{i = 0}^{n} \gamma_{ij}^{2} }$$
(9)

The smaller \({\text{RMSE}}_{j}\) is, the higher estimation accuracy of \(\hat{\user2{\beta }}_{j}\) is. It reflects the overall estimation accuracy of parameter \(\hat{\user2{\beta }}_{j}\).

Model Performance

The results of GWR and MGWR models on both simulated datasets are displayed in Table 6. The adjusted R2 values of the GWR models on dataset1 and dataset2 were 0.9845 and 0.9916, respectively, and the adjusted R2 values of the MGWR models on the two datasets were 0.9859 and 0.9923. Both models yielded high performance on the two datasets. This reflects that both GWR and MGWR models replicated the y accurately.

Table 6 The evaluation results from GWR and MGWR models
Full size table

Bandwidth Evaluation

From Table 6 we find that the unique bandwidth from the GWR model on 2D dataset was 38 while the bandwidths for \(\hat{\user2{\beta }}_{0}\), \(\hat{\user2{\beta }}_{1}\) and \(\hat{\user2{\beta }}_{2}\) from the MGWR model on the same dataset were separately 430, 160 and 20. The bandwidth from the GWR model on 3D dataset was 36 while the bandwidths from the MGWR model on the same dataset were separately 8000, 100 and 20. For both datasets, the bandwidths for \(\hat{\user2{\beta }}_{0}\) were the biggest while the bandwidths for \(\hat{\user2{\beta }}_{2}\) were the smallest. This agrees with the fact of the simulation design. That is, from \({\varvec{\beta}}_{0}\), \({\varvec{\beta}}_{1}\) to \({\varvec{\beta}}_{2}\), the scale changed from large to small.

Non-Stationarity Evaluation

Table 7 shows the stationary index values of \(\hat{\user2{\beta }}\) from both models. The stationary index values on 2D and 3D datasets from both models increased from \(\hat{\user2{\beta }}_{0}\), \(\hat{\user2{\beta }}_{1}\) and \(\hat{\user2{\beta }}_{2}\), indicating that the non-stationarity increased from \(\hat{\user2{\beta }}_{0}\), \(\hat{\user2{\beta }}_{1}\) to \(\hat{\user2{\beta }}_{2}\). This is in line with the simulation design. There was also the difference between the two models: the stationary index values of \(\hat{\user2{\beta }}_{0}\) from GWR were greater than 1 while those from MGWR were less than 1; that is to say, the simulated processes \(\hat{\user2{\beta }}_{0}\) from MGWR were stationary and those from GWR were non-stationary. Obviously, the MGWR results were more consistent with the simulation design. This may be because, in the GWR model, all the independent variables acted on the dependent variable with the same bandwidth, the simulated results of global processes were affected by other local processes, and at the same time the global parameters were estimated with a bandwidth smaller than its own, all of which led to the global process becoming more localized, while these were not the case in the MGWR model.

Table 7 The stationary index of \(\hat{\user2{\beta }}\)
Full size table

Estimation Accuracy Comparison and Evaluation

Figures 7 and 8 respectively show the spatial distributions of \({\varvec{\beta}}_{0} ,\user2{ \beta }_{1} \user2{ }{\text{and}}\user2{ \beta }_{2}\) from simulation design and \(\hat{\user2{\beta }}_{0}\), \(\hat{\user2{\beta }}_{1}\) and \(\hat{\user2{\beta }}_{2}\) calculated from GWR and MGWR models in 2D space. Figure 9 shows those in 3D space. From Figs. 7 and 8, we find that the \({\varvec{\beta}}_{0}\) values are all the same throughout the whole space and \(\hat{\user2{\beta }}_{0}\) values calculated from both models are also evenly distributed, \({\varvec{\beta}}_{1}\) and \(\hat{\user2{\beta }}_{1}\) both followed linear distributions with the coordinates, and the spatial distributions of \(\hat{\user2{\beta }}_{2}\) from both models follow the similar circular trends as that of \({\varvec{\beta}}_{2}\). The above result suggests that the distributions of the parameter estimates are similar to those of design in 2D space. The comparison of Figs. 7 and 9 shows the same similarity in 3D space. There was still a small difference between the two models: the spatial distributions of \(\hat{\user2{\beta }}_{0}\), \(\hat{\user2{\beta }}_{1}\) and \(\hat{\user2{\beta }}_{2}\) from MGWR were more like those of \({\varvec{\beta}}_{0} ,\user2{ \beta }_{1} \user2{ }{\text{and}}\user2{ \beta }_{2}\) than those from GWR.

Figure 8
figure 8

Comparison of \(\hat{\user2{\beta }}\) distributions from two models in 2D space

Full size image
Figure 9
figure 9

Comparison of \(\hat{\user2{\beta }}\) distributions from two models in 3D space

Full size image

Figure 10 shows the bias scatterplots of the two models. The slopes of trend lines in Figure 8(a-1), (a-2), (b-1) and (b-2) were less than one, which illustrates that mostly the biases of \(\hat{\user2{\beta }}_{0}\) and \(\hat{\user2{\beta }}_{1}\) from GWR models were bigger than those from MGWR. The slopes of trend lines in Figure 10(c-1) and (c-2) were close to one, which illustrates that the bias of \(\hat{\user2{\beta }}_{2}\) from the two models were almost the same. At the same time, from the comparison of RMSE for the GWR and MGWR (Table 6), we find that the RMSE values of parameter estimates from MGWR are all smaller than those from GWR. The RMSE values of \(\hat{\user2{\beta }}_{0}\) and \(\hat{\user2{\beta }}_{1}\) from MGWR are far less than those from GWR while little difference existed in those of \(\hat{\user2{\beta }}_{2}\) between the two models. From the comparisons of bias distributions and RMSE values between the two models, we find that the estimation accuracy of \(\hat{\user2{\beta }}_{0}\) and \(\hat{\user2{\beta }}_{1}\) from the MGWR models is far higher than that from GWR models while the estimation accuracy of \(\hat{\user2{\beta }}_{2}\) from the two models is not much different. This can be explained as the great difference of \(\hat{\user2{\beta }}_{0}\) and \(\hat{\user2{\beta }}_{1}\) scales and high similarity of \(\hat{\user2{\beta }}_{2}\) scales between the two models.

Figure 10
figure 10

The scatterplots of bias on 2D and 3D datasets

Full size image

All the results above confirm that MGWR models can achieve high performance, targeted scales, realistic non-stationarity, and better estimation accuracy for parameter estimates than GWR models. We can conclude that the MGWR model can better represent the relationships between variables in multiscale processes with different non-stationarity.

Results and Discussion

The GWR model treats all relationships between variables in a single process while the MGWR can deal with multiple processes simultaneously. In this study, we assumed that the impact of each ore-controlling factor on mineralization was a geological process, and the MGWR model was adopted to further analyze these processes.

Model Performance

Setting \({\text{SOC}}_{f} < 0.0001\) as the convergence criterion, the MGWR model was performed on the two datasets. Table 8 shows the performance comparison between the GWR and MGWR models from which we find that the adjusted R2 values of both models are all bigger than 0.95, which reflects that both models fit well the two datasets.

Table 8 Bandwidth and performance comparison of different models
Full size table

Non-Stationarity Analysis

Table 9 shows the stationary index for variables from MGWR models on the two intrusions. The stationary index values for all the variables on datasetNi were greater than those on datasetCu. This is because the same ore-controlling factors are adopted in the two datasets and the Ni mineralization is richer than Cu in the same intrusion (Table 1).

Table 9 Stationary index of parameter estimates for MGWR
Full size table

The stationary index values for variable “dMC” are all smaller than 1, indicating the stationary impact on mineralization throughout the space. This is consistent with the dominant role of magmatic channel for the formation of the deposit (Song et al., 2012; Su et al., 2014; Mao et al., 2019).

The stationary index values for variables “dFault” and “dTrend” are all greater than 1, indicating the spatial non-stationary impacts on the mineralization. This reflects that the controls of the faults and the intrusion bottom trend on mineralization vary with the spatial locations.

The stationary index values for variable “dRatio” are mostly smaller than 1, except the value on datasetNi in western intrusion. The stationary impact of “dRatio” on mineralization can be explained that it represents the gravity differentiation characteristics of the mineralization itself. As for the exception, the non-stationary impact on Ni mineralization in western intrusion, the first reason is that the Ni grade was higher than Cu grade, the other may be the Ni mineralization is distributed more concentrated in western intrusion (Fig. 11). In summary, the impact of relative position in thickness on Cu–Ni mineralization at Jinchuan is likely stationary.

Figure 11
figure 11

The spatial distributions of the grade of (a) Cu and (b) Ni in western intrusion

Full size image

Scale Analysis

The minimum bandwidth \(b_{\min }\), maximum bandwidth \(b_{\max }\) and bandwidth step \(b_{{{\text{step}}}}\) were set as 20, 10,000, 5, respectively. The two datasets got the optimal bandwidths for GWR models with 35 in western intrusion and 45 in eastern intrusion (Table 8), indicating much localized processes.

Unlike the GWR model with the same bandwidth for all the parameter estimates, the MGWR model optimizes bandwidth for each independent variable. Table 8 shows the bandwidths to different parameter estimates, which indicates that different factors control the mineralization in different scales.

From Table 8 we find that the similar bandwidth trends over the ore-controlling factors existed between the two intrusions and two datasets; that is, the bandwidth increased from \(b_{0}\), \(b_{dFault}\), \(b_{dRatio}\), to \(b_{dMC}\). This is coincident with the fact that the formation of mineralization in the two intrusions is substantially similar. The smallest bandwidth \(b_{0}\) was 20 in two intrusions, which illustrates the high localization of the error items. The bandwidths for variable “dFault” were separately 40 and 120 (Table 1); that is, the influence buffer size of the variable “dFault” on the mineralization was very limited in space. The bandwidths for “dRatio” were medium-sized, which illustrates that variables “dRatio” influence the mineralization moderately. The variable “dMC” got the largest bandwidths with 6029 and 9970, which reflect that the variable “dMC” influenced the mineralization in a very wide range.

The bandwidths for “dTrend” were also moderate-sized in most cases except on datasetNi in western intrusion (Table 8). The variable “dTrend” had much larger bandwidth on datasetNi in western intrusion, indicating that the influence of the western intrusion bottom shape on the Ni mineralization was different. This tallies with the fact that the two intrusions have different morphology characteristics and mineralization distributions (Mao et al., 2018a, b). For example, the bottom shape of the eastern intrusion was more complex and changeable than that of the western intrusion (Fig. 2) and the Cu grade was distributed as small clusters and the Ni grade shows layered distributions in the western intrusion while there was no such difference in the eastern intrusion (Figs. 11, 3). The relatively gentle intrusion bottom shape and larger mineralization cluster size were perhaps the causes of the influence of “dTrend” on the Ni mineralization in the western intrusion at a wider range.

The above influence scales for different ore-controlling factors are not only in line with the result of above non-stationarity analysis but also consistent with the metallogenic mechanism of the Jinchuan Ni–Cu sulfide deposit. As the representation of the magma conduit, the ore-controlling factor “dMC” influenced the mineralization at a very large scale. This is in line with the result that the control of “dMC” on mineralization is a stationary process (Table 9) and the “dMC” can be considered as an essential characteristic affecting the mineralization. The small influence scales of “dFault” reflect that the influence was local and the faults had no significant impact on mineralization. The “dRatio” influences the mineralization in a medium scale. This is because it is the combination of the relative position in the intrusion with local scale and the gravity differential characteristics of sulfide with global attribute. Combined with the above non-stationarity analysis, we thought that the impact of “dRatio” on mineralization was more inclined to be a stationary process. The “dTrend”, representing the morphological characteristics of the intrusion bottom, influenced the mineralization of different conditions at different scales, indicating that the morphological characteristics mainly controlled metal deposition locally.

Spatial Variability Analysis

As the results for the two datasets were similar, only the parameter estimates on datasetCu were further analyzed to seek the spatially varying relationships between the mineralization and its determinants. Table 10 shows the statistical comparison of parameter estimates from which we find that the ranges and standard deviation from GWR models were far greater than those from MGWR models. The change of parameter estimates from MGWR was relatively gentler than those from GWR. As the analysis space and the influencing geological bodies were continuous, the parameter estimates with gentle changes from MGWR model were more acceptable.

Table 10 Statistics for parameter estimates of GWR and MGWR models
Full size table

Owing to different spatial distributions of lithofacies and mineralization in the two intrusions, the values of parameter estimates for variables show statistical difference (Table 10) that the absolute values of each statistics of eastern intrusion are greater than those of western intrusion. Figure 12 displays the spatial distributions of parameter estimates, from which we find that totally the distributions from GWR models were highly localized and those from MGWR were smoother. The total trends of parameter estimates from both models for each variable were similar. Parameter estimates from GWR presented a small range of aggregation while those from MGWR rendered an overall trend. The estimated results of MGWR could present more clear relationships between ore-controlling factors and mineralization.

Figure 12
figure 12

Spatial distributions of parameter estimates from GWR and MGWR models

Full size image

Figures 12(a-1) and (b-1) show the parameter estimates distributions for the “dFault” variable from GWR and MGWR. The large values were preferably distributed near the faults and the magma conduit. The values in the other areas were evenly distributed. This demonstrates that the ore-controlling factor “dFault” contributed more to the mineralization along the faults in limited ranges, and near the magma conduit. This likely implies that the faults reflect the previous structural zones during the metallogenic period rather than a simple post fault. This is consistent with the characteristics of coeval mineralization and structural deformation. The result also reflects that the magma conduit contributed a lot on the mineralization.

The situations for parameter estimates distributions of the variables “dRatio” (Fig. 12(a-2) and (b-2)) and “dMC” (Fig. 12(a-3) and (b-3)) were similar: the values from GWR were localized while those from MGWR were relatively stable. The large values from GWR were distributed near the magma conduit and the largest values focused on the entrance of the magma conduit. This may be because their influences in GWR models are affected by other factors. The distributions from MGWR further reflect that the effects of the variables “dRatio” and “dMC” on the mineralization were stationary through the space.

Figure 12(a-4) and (b-4) exhibit the parameter estimates distributions for the “dTrend” variable from the two models. The values from the two models were highly localized and the large values occurred near the magma conduit, especially in the areas of downward enrichment. A possible reason is that when rising magma suddenly enters the open magma chamber, magma flows back and accumulates downward due to gravity (Barnes et al., 2017; Yao et al., 2020). This confirms the contribution of the magma conduit to mineralization.

In summary, the impacts of relative position in thickness and distance to magma conduit on mineralization were stationary global processes and those of distance to fault and intrusion bottom morphology were non-stationary local processes. The greatest impacts occurred near the magma conduit. This verifies the contribution of the magma conduit to the mineralization.

Conclusions

To quantitatively explore the multiscale non-stationary impact of ore-controlling factors, the MGWR model was extended to three-dimensional space and implemented with MATLAB language. Simulation tests in 2D and 3D space verified the accuracy and stability of the MGWR model. The GWR and MGWR models were applied to the Jinchuan Cu–Ni sulfide deposit and the multiple scales and non-stationarity of the influence were analyzed: both models achieved good performance. The parameter estimates from MGWR had smaller variance and more obvious overall trends than GWR. The non-stationarity analysis from MGWR illustrated non-stationary impacts of distance to fault, intrusion bottom morphology and stationary impact of distance to magma conduit and relative position in the thickness direction of intrusion. The scale analysis reflected the relative size of influence range of different ore-controlling factors on mineralization. The distance to magma conduit and relative position in thickness affected the mineralization globally while the distance to fault and intrusion bottom morphology influenced the mineralization locally. The parameter estimates distributions of local processes showed that the high-impact areas appeared near the magma conduit. Such a study may develop a new way for quantitatively exploring the non-stationarity and scales of the influence of different geological bodies on mineralization in complex tectonic and magmatic activities.