An Improved GWR Approach for Exploring the Anisotropic Influence of Ore-Controlling Factors on Mineralization in 3D Space

Abstract

Spatial non-stationarity is a common geological phenomenon, and the formation of orebodies is a typical non-stationary process. Therefore, a quantitative study of the non-stationary relationships between mineralization and its controlling factors in 3D space is of great significance for metallogenic prediction. Geographically weighted regression (GWR) is an effective method for exploring spatial non-stationarity by measuring the nearness between factors in the data. However, non-stationarity is affected not only by distances but also by factors related to direction. Traditional GWR cannot address the non-stationarity that arises from differences in direction. To address this issue, we propose an improved GWR method to characterize the directional characteristics of non-stationary relationships by introducing a direction weight to the GWR. The anisotropic influence of factors can be obtained by comparing the performance of models with different weights on direction terms. A case study of the Xiadian and Dayingezhuang gold deposits, Jiaodong Peninsula, Eastern China was carried out to verify the anisotropic nature of ore-controlling factors. First, multi-collinearity and OLS (ordinary least squares) diagnosis for the variables were performed and the necessity of the non-stationarity exploration was demonstrated. Second, GWR was applied to explore the spatial non-stationarity of the relationships among the variables by comparing the global R² value with that of OLS, evaluating the local R², values testing the t-statistic values, analyzing and comparing the spatial autocorrelation of residuals with that of OLS, and calculating the spatial stationary index of the parameter estimates of explanatory variables. Third, the improved GWR method was applied, and the directional characteristics of the non-stationary relationship were analyzed. Finally, the anisotropic influence of the controlling factors on mineralization was validated by comparing the performance of the improved GWR model with different bandwidths and different kernels, and the importance of the direction of the fault zone to mineralization was further verified.

Introduction

Spatial non-stationarity is a common geological phenomenon (Karpatne et al., 2017). In mineral exploration, capturing the non-stationary influences of geological entities, such as faults and rock units, on mineralization can help locate hidden ore bodies (Mao et al., 2016; Zuo, 2020; Zuo & Xiong, 2020). With the development of deep mineral prospecting and generation of vast amounts of geoscience data, revealing the spatial non-stationary relationship of the ore-controlling factors and mineralization is becoming an urgent problem.

Various solutions to the spatial heterogeneity problem have been proposed in metallogenic predictive models (Zhang et al., 2016, 2018). One contribution is to reduce spatial heterogeneity by removing spatial trends from predictions (Arpat, 2005; Caers & Zhang, 2002; Cheng, 1997, 1999; Zuo et al., 2016). Another is to introduce functions of coordinate variables to express their spatial autocorrelations (Agterberg, 1964, 1970; Casetti, 1972). One approach to the spatial non-stationary relationship is to introduce the geographically weighted regression (GWR) technique, which allows quantitative exploration and analysis of potential spatial heterogeneity in processes (Fotheringham et al., 2001, 2002). There are numerous examples of research and application of GWR in many fields, such as land use, resource and environment, society and economy (Andrew et al., 2015; Gilbert & Chakraborty, 2011; Nilsson, 2014; Tu & Xia, 2008). In metallogenic prediction, GWR was applied mainly in mineral prospectivity mapping (Wang et al., 2015; Zhang et al., 2018) and spatial non-stationarity exploration (Liu et al., 2013; Zhao et al., 2013, 2014). However, these applications are limited to 2D space. As the depth dimension of real geological space should not be ignored, Huang et al. (2020) expanded the GWR to 3D geological space.

GWR is based on Tobler's First Law (Fotheringham et al., 1996; Tobler, 1979), which argues that “everything is related to everything else, but near things are more related than distant things”. While GWR allows exploring spatial non-stationarity, defining an appropriate metric that measures nearness characteristics are challenging (Li et al., 2006a, 2006b). In 3D geological space, it is generally known that the association exists between deposits and geological entities including faults (cf. Carranza & Hale, 2002; Mao et al., 2016), and, further, this association is spatially anisotropic. While most of existing work (Huang et al., 2020; Tobler, 1979) uses the distance of the homogeneous space to measure nearness, the influence of directionality is not considered in GWR. Therefore, carefully considering the directionality of factors is essential for exploring the non-stationary relationships in GWR.

This study proposes an improved GWR method by defining a direction-weighted distance to express the nearness characteristics based on the GWR. For convenience of subsequent comparison with the improved GWR, the traditional GWR is called the standard GWR in this paper. A case study with the Xiadian (XD) and Dayingezhuang (DYGZ) orogenic gold deposits, Jiaodong Peninsula, Eastern China was carried out to analyze the anisotropy of the non-stationary relationships between variables by comparing the performance of the standard and improved GWR. In this comparison, ore grade was used as the dependent variable and potential geological determinants were used as explanatory variables in the regression.

Data

Study Area

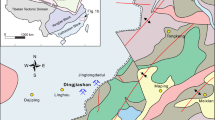
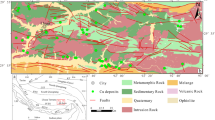
The Dayingezhuang and Xiadian gold deposits are located in the northwestern part of the Jiaodong Peninsula, in the southeastern North China Craton (Fig. 1a). Both deposits are hosted in the Zhaoping fault zone, which strikes SW–NE and dips 35°–60° SE (Mao et al., 2019). The Dayingezhuang gold deposit (Fig. 1b) is controlled by the middle segment of the fault zone with a NE strike of 10°–20° and SE dip of 30°–50°. The Xiadian gold deposit (Fig. 1b) is a typical altered rock type gold deposit, and it is mainly controlled by the south section of the Zhaoping fault zone with a NE strike of 45° and SE dip of 45°.

Figure 1

adapted from Mao et al., 2019)

Geological map showing faults and gold deposits in the study area (

Data and Variables

In this study, gold grade, as a quantitative measure of mineralization, was used as the dependent variable. Ore-controlling factors extracted from different geological conditions were used as the explanatory variables. A summary of all the variables is given in Table 1, and detailed descriptions and calculations can be found in Mao et al. (2019). The 3D spatial distribution of gold grade in the Xiadian and Dayingezhuang deposits is shown in Figure 2.

Table 1 Statistical description of variables

Figure 2

Spatial distributions of gold grade (view from south) in the (a) Xiadian deposit and (b) Dayingezhuang deposit

Method

Basics of GWR in 3D Space

GWR can be used to explore potential spatial non-stationarity in physical processes. It is a local regression model and it estimates local parameters through a data-borrowing scheme. It was originally proposed for 2D space, and Huang et al. (2020) extended it to 3D space. Given $n$ dependent variables ${\varvec{Y}}=\{{y}_{1}, {y}_{2}, \dots ,{y}_{n}\}$ and $m$ explanatory variables ${\varvec{X}}=\{{x}_{11}, {x}_{12}, \dots ,{x}_{nm}\}$, the GWR model can be formulated as:

$${y}_{i}={{\varvec{X}}}_{i}{{{\varvec{\beta}}}_{i}}^{T}+{\varepsilon }_{i}$$

(1)

where ${{\varvec{X}}}_{i}=\{{x}_{i1}, {x}_{i2}, \dots ,{x}_{im}\}$ represents the $m$ explanatory variables at regression point $i$, ${y}_{i}$ is the estimated value at regression point $i$, and ${{\varvec{\beta}}}_{i}=\{{\beta }_{i1}, {\beta }_{i2}, \dots ,{\beta }_{im}\}$ denotes the local parameter estimate at point $i$, and ${\varepsilon }_{i}$ is the error term at point $i$. The value of a parameter at a specific point $i$ can be estimated by weighting the surrounding observations with a kernel function that decays with distance, the formula of which is:

$${\widehat{{\varvec{\beta}}}}_{i}={({{\varvec{X}}}^{{\varvec{T}}}{{\varvec{W}}}_{i}{\varvec{X}})}^{-1}{{\varvec{X}}}^{{\varvec{T}}}{{\varvec{W}}}_{i}{\varvec{Y}}$$

(2)

where ${\widehat{{\varvec{\beta}}}}_{i}$ represents an unbiased estimate of ${{\varvec{\beta}}}_{i}$, and ${{\varvec{W}}}_{i}=\{{w}_{i1}, {w}_{i2}, \dots ,{w}_{im}\}$ is the weight that can be calculated based on a kernel function and bandwidth. The following two kernels were employed in this study:

$$ \begin{aligned} {\text{bisquare}}:w_{{ij}} & = \left[ {1 - \left( {d_{{ij}} /H} \right)^{2} } \right]^{2} {\text{if}}\;d_{{ij}} < H \\ & = 0\quad {\text{otherwise}} \\ \end{aligned} $$

(3)

$$\begin{aligned}{\rm{tricube}}: w_{ij}&=&{[1-{\left({{d}_{ij}}^{2}/{H}^{2}\right)}^{3}]}^{3/2}\,\rm{if}\,{d}_{ij}<H\\&=&0\quad \rm{otherwise}\end{aligned}$$

(4)

where ${d}_{ij}$ is distance from observation $j$ to regression point $i$, and $H$ is the parameter determined by bandwidth. In this study, the bandwidth was chosen to be the number of nearest neighbors and $H$ represents the distance from point $i$ to its farthest nearest neighbor within the bandwidth. The bandwidth can be either fixed or adaptive. A fixed bandwidth is a constant and cannot be changed during the model operation, while an adaptive bandwidth corresponds to the best model performance and can be obtained by model optimization.

Improved GWR in 3D Space

Based on the foregoing discussion, the non-stationarity of relationships in standard GWR is assumed to be caused only by distance, and the effect of directionality is ignored. That is to say, the influence of explanatory variables on a dependent variable is assumed to be the same in all directions. This paper extends the standard GWR in 3D space by defining a direction-weighted distance to analyze the anisotropy of the influence of explanatory variables. In this paper, the dominant influence direction (main direction) is introduced to represent the most influential direction, in which the model can achieve optimal performance. By comparing the performance of models with different assignments of the dominant influence direction, the anisotropy of the influence can be obtained.

As shown in Fig. 3a, ${p}_{a}$ is the regression point that coincides with the coordinate origin $o$; $\stackrel{\rightharpoonup}{{{\varvec{p}}}_{a}{\varvec{q}}}$ (or $\stackrel{\rightharpoonup}{{\varvec{o}}{\varvec{q}}}$) denotes the dominant influence direction (main direction) of the ore-controlling factors on mineralization passing through point ${p}_{a}({x}_{a},{y}_{a},{z}_{a})$; ${p}_{b}({x}_{b},{y}_{b},{z}_{b})$ is one of the points close to the regression point ${p}_{a}$ within the bandwidth; ${d}_{ab}$ is the Euclidean distance between points ${p}_{a}$ and ${p}_{b}$; the coordinates of vectors $\stackrel{\rightharpoonup}{{{\varvec{p}}}_{a}{{\varvec{p}}}_{b}}$ is $({x}_{b}-{x}_{a},{y}_{b}-{y}_{a},{z}_{b}-{z}_{a})$, abbreviated as (${x}_{ab},{y}_{ab},{z}_{ab}$); and ${\alpha }_{ab}$ represents the directional distance between the vectors $\stackrel{\rightharpoonup}{{{\varvec{p}}}_{a}{\varvec{q}}}$ and $\stackrel{\rightharpoonup}{{{\varvec{p}}}_{a}{{\varvec{p}}}_{b}}$.

Figure 3

Vectors in 3D space for (a) angles between vectors (b) vector (plunging line) in spherical coordinate

The measurement of nearness is a function of the two kinds of distance (i.e., Euclidean distance ${d}_{ab}$, and directional distance ${\alpha }_{ab}$) and can be expressed as:

$${s}_{ab}=F({d}_{ab},{\alpha }_{ab})$$

(5)

where ${s}_{ab}$ represents the spatial proximity of observation $b$ to point $a$. This equation reflects the property that the closer ${d}_{ab}$ is, the smaller ${\alpha }_{ab}$ is, and the greater the influence of the observation $b$ on point $a$. The nearest neighbors from the regression point within the same bandwidth selected according to the two spatial proximity metrics ${d}_{ab}$ and ${s}_{ab}$ are different.

Figure 4 shows the diagram of bandwidth shapes and nearest neighbors determined by the two metrics. Here, the regression point ${p}_{a}$ is the coordinate origin $o$. Figure 4a shows the bandwidth shape determined by ${s}_{ab}$, in which $oq$ is assumed to be the dominant influence direction, while Fig. 4b shows the bandwidth shape determined by ${d}_{ab}$. Data points within the bandwidth can be selected as the nearest neighbors. In Fig. 4a, the surrounding points are determined by ${s}_{ab}$ (Eq. 5), in which the points in the directions close to the dominant influence direction have higher priority than the points in other directions with the same Euclidean distance. This causes more points close to the dominant influence direction to be selected as the nearest neighbors (Fig. 4a). In contrast, if the surrounding points are determined by Euclidean distance ${d}_{ab}$, then the points in all directions have the same priority and have the same chance to be selected as the nearest neighbors (Fig. 4b).

Figure 4

Diagrams of bandwidth shapes and nearest neighbors for (a) improved GWR and (b) standard GWR. Red points represent ore-bearing units, which are commonly distributed unevenly in 3D space. The ellipsoid in (a) with the dominant influence direction (arrow $oq)$ indicates the most influential direction of ore-controlling factors on mineralization, while the sphere in (b) with the same influence in all directions cannot reflect the direction difference

The weighting function of observation $b$ for regression point $a$ is expressed as:

$${w}_{ab}=F\left({p}_{ab}\right)={f}_{1}\left({d}_{ab}\right){f}_{2}\left({\alpha }_{ab}\right)$$

(6)

where ${f}_{1}\left({d}_{ab}\right)$ and ${f}_{2}\left({\alpha }_{ab}\right)$ can be separately obtained according to Eq. 3 or 4. In the calculation of ${f}_{2}\left({\alpha }_{ab}\right)$, ${d}_{ab}$ is replaced by ${\alpha }_{ab}$, and the bandwidth is set to $\uppi$. The bandwidth of the regression point $a$ in both improved and standard GWR are shown in Fig. 4, in which $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{oq}}$ is taken to be the dominant influence direction. The directional distance ${\alpha }_{ab}$ is determined by the coordinates of vectors $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} q}}$ and $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} p_{b} }}$; it can be calculated as:

$$ \alpha _{{ab}} = \arccos \frac{{\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} q}} \cdot \overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} p_{b} }} }}{{\left| {\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} q}} } \right|\left| {\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} p_{b} }} } \right|}} $$

(7)

In 3D space, a point $A$ in a spherical coordinate system can be expressed as $A(r,\theta ,\varphi )$, where $r$ is distance from point $A$ to the origin, $\theta$ is angle between the vector and the positive direction of $z$ axis, and $\varphi$ is angle between the projection of the vector on the horizontal plane and the due north direction. The Cartesian coordinates ($x,y,z$) of point $A$ can be retrieved as:

$$x=rsin\theta\,sin \varphi \quad y=rsin\theta\,cos\varphi \quad z=rcos\theta$$

(8)

In general, a plunging line can be described with plunge direction and plunge in 3D space. The plunge direction is the angle between the horizontal projection of the plunging line in the vertical plane with the due north direction, and the plunge is the angle between the plunging line and the horizontal in the vertical plane. As shown in Fig. 3b, the vector $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{oq}}$ is taken to be the dominant influence direction whose plunge and plunge direction are ${\theta }_{g}$ and ${\varphi }_{g}$, respectively. It can be expressed as $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{oq}}$ in the spherical coordinate system, where ${r}_{q}$ is set to 1 because only its direction needs to be considered. The relation is:

$${r}_{q}=1, {\theta }_{q}={\theta }_{g}+90^\circ , {\varphi }_{q}={\varphi }_{g}$$

(9)

Similarly, the vector $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} p_{b} }}$ (Fig. 3a) can be expressed as $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} p_{b} }} \left({r}_{ab},{\theta }_{ab},{\varphi }_{ab}\right)$ in spherical coordinates where the radius ${r}_{ab}$, angles ${\theta }_{ab}$ and ${\varphi }_{ab}$ can be calculated from the Cartesian coordinates of points ${p}_{a}$ and ${p}_{b}$. Therefore, the angle ${\alpha }_{ab}$ between vectors $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{oq}}$ and $\overset{\hbox{$\smash{\scriptscriptstyle\rightharpoonup}$}}{{p_{a} p_{b} }}$ is only related to ${r}_{ab}$, ${\theta }_{q}$ and ${\varphi }_{q},$ and it can be calculated from the plunge and plunge direction as:

$${\alpha }_{ab}=\mathit{arccos}\left|\frac{{x}_{ab}\mathit{sin}\left({\theta }_{g}+90^\circ \right)\mathit{sin}{\varphi }_{g}+{y}_{ab}\mathrm{sin}\left({\theta }_{g}+90^\circ \right)\mathit{cos}{\varphi }_{g}+{z}_{ab}\mathit{cos}\left({\theta }_{g}+90^\circ \right)}{{r}_{ab}}\right|$$

$$=\mathit{arccos}\left|\frac{{x}_{ab}\mathit{cos}{\theta }_{g}\mathit{sin}{\varphi }_{g}+{y}_{ab}\mathrm{cos}{\theta }_{g}\mathit{cos}{\varphi }_{g}-{z}_{ab}\mathit{sin}{\theta }_{g}}{{r}_{ab}}\right|$$

(10)

where ${\theta }_{g}$ and ${\varphi }_{g}$ can be optimized by comparing the model performance with different segmentations of plunges and plunge directions. In this study, the experimental plunge was set from 0° to 90° and the experimental plunge direction was set from 0° to 360°.

The workflow is shown in Fig. 5. Given $n$ points with properties in 3D space, the process is described as follows: (1) divide the plunge range into ${p}_{1}$ equal parts and the plunge direction range into ${p}_{2}$ equal parts; (2) with the combination of each segmentation of ${p}_{1}$ and ${p}_{2}$ as the dominant influence direction, compute the direction weight and perform the improved GWR calculation; and (3) for each segmentation of ${p}_{1}$ and ${p}_{2}$, compare the ${R}^{2}$ values and find the influence distribution in all directions.

Figure. 5

Flowchart for the improved GWR method

Results

Multi-Collinearity Diagnosis

It is necessary to perform a multi-collinearity diagnosis for the explanatory variables before multiple regression analysis. We used the variance inflation factor (VIF) to test the degree of multi-collinearity. The VIF measures how much the variance of an estimated regression coefficient is increased because of collinearity. The collinearity is very strong if the VIF is > 10 (Chennamaneni e al, 2016; Marquardt, 1970). All the VIF values are < 10 (Table 2), which show that redundancy among the explanatory variables was acceptable for both deposits.

Table 2 Values of VIF for the explanatory variables (see Table 1)

OLS (Ordinary Least Squares) Diagnosis

The OLS method is the correct starting point for all spatial regression analyses. OLS diagnosis was used to evaluate the relationships among variables (or processes) by establishing a global model for them. The significance levels can be obtained by performing various statistical tests on the parameter estimates for the OLS model, such as the joint F-statistic, joint Wald statistic, Koenker (BP) Statistic, and Jarque–Bera Statistic. Table 3 shows the OLS model diagnostic results for the Xiadian and Dayingezhuang data. The adjusted R² values were both < 0.1, which indicate that the OLS models cannot adequately express the relationship among the variables. The values of Koenker (BP) statistic indicate that the models have statistically significant heteroscedasticity or inequalities. The values of the Jarque–Bera statistic show that the predictions were biased and the residuals were not normally distributed. All these diagnostic results show that the OLS models need to be expanded to solve the non-stationary relationship among the variables.

Table 3 OLS diagnostics

Spatial Non-stationarity Detection

This paper employs the GWR local model to explore the non-stationary relationship between gold grade and the ore-controlling factors by comparing it with the OLS global model. We tested and verified four aspects of the spatial non-stationarity: model performance, local t-statistics, spatial autocorrelation of residuals, and stationary index for explanatory variables.

R² values were adopted to evaluate the model performance. Table 4 shows the global performance comparison of GWR and OLS models. All global R² values of the GWR models were > 0.8, while those of the OLS models were < 0.1. These reflect that the GWR models, which consider local differences of variables, had better performance than the OLS models. Because the GWR achieved better performance when using the bisquare kernel compared to the tricube kernel (Table 4), the former was adopted in the following analysis. The local R² values of the GWR models are displayed in Fig. 6. We found that the local R² values were all > 0.77, which show that the GWR model fits well in the whole region. All the global and local R² values of the GWR models indicate that non-stationarity exists in the relationships among the variables.

Table 4 Performance comparison between standard GWR and OLS

Figure 6

Local R² of GWR models for the (a) Xiadian deposit and (b) Dayingezhuang deposit

The t-statistic values of the local estimates were calculated to measure the varying relationships between gold grade and the ore-controlling factors. Because the sample size was 50 (Table 4), values of the t-statistic greater than 2.009 or less than − 2.009 were considered significant at the 95% confidence level. The red and blue points in Fig. 7 shows that the absolute values of the t-statistic of all the parameter estimates were greater than 2.09. The distribution of the t-statistic exhibited obvious spatial variability. This indicates that the ore-controlling factors were important to the mineralization at these points and less important at other sites.

Figure 7

t-statistic of parameter estimates for variables (a) dF, (b) fA, (c) fP, (d) fV, (e) gF, (f) waF and (g) wbF. See Table for explanations of variables

We used Moran’s I statistics of model residuals to measure how much the model reduced the spatial non-stationarity. In Table 5, the global Moran’s I values were all < 0.1, which indicate weak positive spatial autocorrelation. The values of the OLS models are about 3 × more than those of the GWR models, which show that the GWR model can, to some degree, reduce the spatial autocorrelation compared to the OLS model.

Table 5 Spatial autocorrelation of residuals

Global autocorrelation is designed for homogeneous space and it is not applicable to heterogeneous space. We used local autocorrelation to express the spatial heterogeneity of the mineralization distribution. Figure 8a, b shows the local Moran’s I distributions for the OLS model, and Fig. 8c, d for the GWR model. We found that the spatial distributions in Fig. 8c, d are more even than those in Fig. 8a, b, which indicate that the GWR models reduced the spatial autocorrelations in residuals more efficiently than the OLS models did.

Figure 8

Local Moran’s I for (a) OLS and (c) GWR in the Xiadian deposit and for (b) OLS and (d) GWR in the Dayingezhuang deposit

The spatial stationary index was introduced to measure the significance of geographical variability (Brunsdon et al., 1996, 2002; Huang et al., 2020); values of > 1 mean non-stationary. Table 6 shows the spatial stationary index values of the parameter estimates, indicating that the relationships between gold grade and the seven ore-controlling factors were not uniform across space and, therefore, the relationships were non-stationary.

Table 6 Stationarity index of explanatory variables (see Table 1)

Anisotropic Analysis of Non-stationary Relationships

The preceding analysis of the standard GWR results proved that the relationships between gold grade and the ore-controlling factors were non-stationary, and so we used the improved GWR model to analyze further their directional difference. In this study, the anisotropy was obtained by observing the changes of R² values of the GWR models with different values of plunge direction and plunge.

Figures 9 and 10 show the performance change of the improved GWR models under adaptive bandwidth and fixed bandwidth, respectively. The series of concentric circles represents the plunge angles from 0° to 90°, which increased from the inside out. The plunge directions were expressed as beams ranging from 0° to 360°, which began from due north and increased clockwise. The black bold line represents the strike of the Zhaoping fault zone and the black bold line with arrow shows the dip direction of the fault. The influence patterns generated by the improved GWR models with adaptive and fixed bandwidths were strongly similar (Figs. 9 and 10), which indicate that the performance was unrelated to bandwidth.

Figure 9

Anisotropic pattern of improved GWR with adaptive bandwidth in the (a) Xiadian deposit and (b) Dayingezhuang deposit

Figure 10

Anisotropic pattern of improved GWR with fixed bandwidth in the (a) Xiadian deposit and (b) Dayingezhuang deposit

Figures 9a and 10a show the influence patterns for the Xiadian gold deposit, from which we found that the NE and NW plunge trends had the best performance, especially those with bearings of 285°–65° with angles of 25°–65°, respectively, which were the dominant influence directions. The NE dominant influence direction followed the NE 45° strike of the south part of the Zhaoping fault zone or is rotated by a small angle, indicating that the fault had a great effect on the mineralization along its strike. The NW dominant influence direction was opposite to the SE dip direction of the fault and had better performance than along the fault dip direction. The blue area located at plunge bearings of 105°–225° and plunge angles of 30°–50° had the weakest influence direction, which roughly followed the dip directions and dips of the fault zone controlling the deposit. The great difference between the two sides perpendicular to the strike of the Zhaoping fault was consistent with not only the direction of migration of ore-forming hydrothermal fluid but also with the change tendency of the shortest distance to the fault. These suggest that the controlling factor dF (Table 1), namely the shortest distance to the fault, contributed greatly to the gold grade.

Figures 9b and 10b illustrate the influence patterns of the Dayingezhuang gold deposit, in which the dominant directions corresponded to the N and the S plunge directions. The N dominant direction roughly followed the NNE 20° strike of the middle section of the Zhaoping fault zone or differed by a small angle, indicating that the fault had a great effect on the gold grade along its strike. The S dominant direction was along the SSW 20° fault strike with slight W deviation, which can be considered to be the combination of the SSW strike of the Zhaoping fault and the 100° strike of the Dayingezhuang fault. These suggest that the dominant influence direction of the Dayingezhuang gold deposit was the result of the combined activity of the two faults, indicating further that the Dayingezhuang fault either participated actively in the deposition of gold as a pre-existing fault or it offset the orebodies as a post-ore fault. The lowest-influence areas, which are shown in blue, were mainly located at the dip directions of 45°–125° and dips of 0°–35°, which followed the ESE dip direction of the Zhaoping fault zone with dips of 0°–35°. The direction perpendicular to the strike with plunges of 0°–45° was a relatively low-influence area but the up-dip direction of the fault had greater influence than the down-dip direction, and the influence followed the change tendency of the shortest distance to the fault. This indicates that the controlling factor dF (Table 1), namely the shortest distance to the fault, had a great effect on the gold grade.

Therefore, the ore-controlling factors of the Xiadian and Dayingezhuang gold deposits had an anisotropic influence on mineralization. The dominant influence directions of both deposits were roughly along the strike of the Zhaoping fault, indicating that the Zhaoping fault zone had great control on mineralization of both deposits. On the one hand, the common result that the up-dip direction of the fault had higher influence than the down-dip direction makes it clear that the ore-controlling factor dF (Table 1), which represents the shortest distance to the Zhaoping fault, contributed strongly to mineralization of both deposits. On the other hand, a difference was discovered between the two deposits. That is, the Xiadian gold deposit was controlled only by the Zhaoping fault, but the Dayingezhuang gold deposit was the result of the activity of both the Zhaoping and Dayingezhuang faults, which demonstrates the positive effect of the Dayingezhuang fault on the metallogenesis of the Dayingezhuang gold deposit.

Discussion

From the above analysis, we found that the standard GWR can be used to detect non-stationarity of relationships among variables caused by distance, while the improved GWR can be used further to analyze the anisotropic pattern of non-stationary relationships.

Comparison of Model Performance of the Improved and Standard GWR

It can be seen that most of the R² values of the improved GWR calculated with an adaptive bandwidth in Fig. 9 are less than those of the standard GWR, while most of the R² values of the improved GWR with a fixed bandwidth in Fig. 10 are greater than those of the standard GWR. This happened because the calibration process of bandwidth is a tradeoff between bias and standard error. The model performance should be compared at the same bandwidth.

Using the Xiadian and Dayingezhuang gold deposits as examples, we analyzed how the R² values changed with the same fixed bandwidth to evaluate the performance of the improved GWR model (Fig. 11). Each curve in Fig. 11 represents the dependence of model on different plunge directions with a certain plunge, which is an element in the set {5 15 25 35 45 55 65 75}. Different curves represent different plunge angles. The red lines in Fig. 11 represents the R² values of the standard GWR. Figure 11a, c shows the results for the improved GWR for the Xiadian gold deposit, and Fig. 11b, d for the Dayingezhuang gold deposit. To test further the accuracy and robustness of the algorithm, the model performance with different kernel functions was compared. Figure 11a, b demonstrates the improved GWR results with the bisquare kernel, and Fig. 11c, d with the tricube kernel. The R² values with the bisquare kernel (Fig. 11a, b) were greater than those with the tricube kernel (Fig. 11c, d) in the same directions, which illustrate that the improved GWR model with the bisquare kernel performed better than the model with the tricube kernel. The similar trends in Fig. 11a, b, c, d indicates that the directional performance of the improved GWR model was not affected strongly by the choice of kernel function. All the R² values of the improved GWR models with their optimal direction angles were greater than those of the standard GWR models. This demonstrates that the improved GWR model with the optimal direction weight performed better than the standard GWR model.

Figure 11

Performance changes with plunge and plunge direction in the Xiadian deposit using the (a) bisquare kernel and the (c) tricube kernel, and in the Dayingezhuang deposit using the (b) bisquare kernel and (d) tricube kernel

Analysis of Anisotropic Patterns

The anisotropic patterns from the improved GWR model using the tricube kernel with fixed bandwidth are illustrated in Fig. 12 for both deposits. Comparing the anisotropic patterns for the deposits in Figures. 9 and 10, the dependence of performance on direction was almost the same, and optimal values were located in the same directions. It can be concluded that similar anisotropic patterns of the relationships between gold grade and the ore-controlling factors can be obtained with the improved GWR model, using either fixed or adaptive bandwidth with the bisquare or tricube kernel. Apparently, the improved GWR model can help discover the common cause of the anisotropic relationships between the ore-controlling factors and gold grade. At the same time, from the consistency of the optimal directions with the strike of the Zhaoping fault zone in both the Xiadian and Dayingezhuang gold deposits, we further demonstrated the influence of the fault zone on gold grade and the role of the ore-controlling factor dF on mineralization. All these results provide powerful support for the applicability of these parameters in predictive modeling and they can be used to improve the accuracy of predictions. Moreover, the results provide evidence that the Dayingezhuang fault played an active role in mineralization in the Dayingezhuang gold deposit.

Figure 12

Anisotropic pattern of improved GWR using the tricube kernel with fixed bandwidth in the (a) Xiadian deposit and (b) Dayingezhuang deposit

Exploration of Fluid Migration

Based on Fig. 11, we also found that the performance changed with plunge direction from steep to gentle. The transition of plunge from steep to gentle was about 55° in the Xiadian gold deposit and 45° in the Dayingezhuang gold deposit. These angles are basically consistent with the dip angle of the Zhaoping fault zone. This result suggests that the influence of the controlling factors on mineralization was relatively stable for all azimuths when the plunge was greater than the fault dip angle, while the influence depended more strongly on the azimuth when the plunge was less than the fault dip angle. This indicates that, to some extent, fluid flow below the fracture surface was isotropic and was dominated by infiltration, whereas fluid flow above the fracture surface was affected by the dip angle of the fault and by other factors.

Conclusions

In this study, we described an improved GWR method to analyze the anisotropy of non-stationary relationships between ore-controlling factors and ore grade by optimizing and comparing the R² values of models with different direction weights. The results from the case studies for the Xiadian and Dayingezhuang gold deposits revealed that the improved GWR method can be used to discover anisotropy hidden in spatial correlations, and the important influence of the Zhaoping fault zone on mineralization was confirmed for these two deposits. Comparison with the standard GWR showed that the improved GWR with proper weighting function in the dominant influence direction performed better than the standard GWR. With different settings of bandwidths, the results exhibit the same anisotropic pattern using the same data, which further validates the stability of the improved GWR for exploring anisotropy of relationships between mineralization and its determinants. These findings can provide useful insight for research on metallogenic mechanisms and exploration targeting. The existence of non-stationarity and anisotropy of relationships between mineralization and its determinants is expected to open up a new method of 3D quantitative prediction modeling. The improved GWR can also be applied in the prevention and mitigation of geological disasters in 3D space, 3D oil and gas exploration and productivity, and other areas.