Introduction

Over the past few years, measurement and control of total dissolved gas (TDG) concentration in water upstream and downstream of spillways at hydropower dams have received great importance. TDG concentration expressed as a percentage (%) or pressure measured in millimeters of mercury (Witt et al. 2017a) is a mixture of several gases such as oxygen, nitrogen, argon and carbon dioxide (Schneider 2012). TDG concentration > 110% of saturation has a negative effect on aquatic life and is a serious environmental problem (Colt 1986). TDG elevation causes “gas bubble trauma” (GBT) that can lead to fish mortality (Weitkamp and Katz 1980). According to Colt and Westers (1982), one of the major disadvantages caused by elevated TDG is the limitation of the utility of highly efficient submerged aerators. Consequently, the negative impacts of elevated TDG could be greatly minimized. According to research findings conducted by Politano et al. (2007) and later confirmed by Schneider (2012), spillway deflectors contribute significantly to the reduction in TDG supersaturation at the tailrace of the dams (Witt et al. 2017b). Over the years, the effects of several environmental factors such as water temperature and atmospheric pressure, spill from dam and discharge on TDG formation and development at hydropower dams were studied and highlighted. Spillway and powerhouse discharges fluctuations could have a strong impact on TDG in downstream of a dam (Tanner et al. 2013; Politano et al. 2017). Recently, Li et al. (2019) conducted an investigation to demonstrate and to explore the effect of TDG supersaturation on the hatchability of Chinese sucker. The authors demonstrated that the hatching rate decreased with increasing TDG levels.

Various studies have made use of many modeling approaches such as mass transfer theories (Roesner and Norton 1971), numerical hydrodynamic and mass exchange processes (Weber et al. 2004) and polydisperse two-phase flow and unsteady 3D two-phase flow approaches (Politano et al. 2007, 2009, 2012; Fu et al. 2010; Ma et al. 2016). Using data collected at hourly time step from hydropower dams at mid-Columbia River, USA, Witt et al. (2017a) proposed at the first time a model for predicting mean TDG travel time from the tailrace of one dam to the forebay of the next downstream dam. The proposed model was formulated using cross-correlation of hourly TDG data and based on the idea of relating mean TDG to mean discharge. Witt et al. (2017b) proposed a simple model for predicting TDG uptake that is the difference between the TDG concentration in the forebay and the TDG in the tailwater of the dams. His proposed model is a simple reduced-order TDG uptake equation. Recently, Ma et al. (2018) investigated the effect of the cascade hydropower stations on water TDG supersaturation and demonstrated that concentration of TDG can be significantly increased and become oversaturated in the forebay and transported via the tailwater with the development of cascade hydropower stations. The cumulative effect of cascade hydropower stations is also investigated by Feng et al. (2018). Using data from several power stations located at the Dadu River, the largest tributary of the Min River, China, they demonstrated that the cascade contributes to an important increase in TDG level due to the elevated discharge and water depth. Yuan et al. (2018) investigated the effect of the vegetation on the dissipation of supersaturated TDG and demonstrated that as the density of vegetation increased, the dissipation rate of the supersaturated TDG became higher. Deng et al. (2017) demonstrated that the addition of baffle bocks to the spillway chute would likely reduce the TDG produced by spill flow into the tailrace. Stewart et al. (2015a, b) proposed a simplified model for predicting TDG level using four input variables: powerhouse flow, spillway flow, tailwater depth and the calculated entrainment of powerhouse flow into spillway flow, and they obtained high accuracy with a coefficient of determination better than 92%. Shen et al. (2019) proposed at the first time a three-dimensional supersaturated TDG model, based on the Reynolds-averaged Navier–Stokes (RANS) equations at the confluence zone during discharge period of dam. The proposed model combines experimental and numerical study. The authors demonstrated that the utilization of a low-TDG saturation region at the confluences helps significantly improve the river ecosystem and reduce the amount of GBT.

Studies on characterization of TDG using directly measured hydraulic, climatic and water quality variables, such as water temperature and barometric pressure, are scarce. However, models based on a combination of direct measurement of such variables could provide a more complete description of TDG process and can help accurately predict TDG. Data-driven techniques have played a key role in many areas of hydrological and environmental sciences, especially with the recent proliferation of high-quality data available worldwide. Previously, data-driven methods have been used for modeling pan evaporation at different timescales (Wang et al. 2016a, 2017a, b, c), prediction of diffuse photosynthetically active radiation (Wang et al. 2017d), prediction of solar radiation (Wang et al. 2016b), estimation of daily aerosol optical depth and aerosol radiative effect (Qin et al. 2018), high-density photosynthetically active radiation (Qin et al. 2019). On the other hand, several researchers worldwide have demonstrated that data-driven methods have significantly contributed to the advancement of research, and a number of computational models have been proposed, including forecasting monthly rainfall with uncertainty (Yaseen et al. 2019), streamflow simulation (Al-Sudani et al. 2019), precipitation pattern modeling using cross-station perception (Sulaiman et al. 2018) and forecasting air temperature using geographic information as model predictors (Sanikhani et al. 2018). In this study, we present a novel method to predict TDG concentration using a combination of water quality and climatic variables, in addition to the measured spill from dams and discharge. To the best of the author’s knowledge, only one study has reported the application of the data-driven techniques for modeling TDG concentration. Heddam (2017) applied the generalized regression neural network (GRNN) for predicting TDG uptake using six input variables, namely total dissolved gas measured in the forebay of the dam (TDG_F), water temperature, barometric pressure, spill from dam, sensor depth and total flow. The author demonstrated that inclusion of TDG_F significantly improves the performances of the model, and the GRNN is more accurate than the standard multiple linear regression. This paper aims to develop new data-driven models for predicting TDG concentration using kriging interpolation method (KIM) and response surface method (RSM). These two models were compared with the standard feedforward neural networks (FFNN).

Material and Methodology

Case Studies

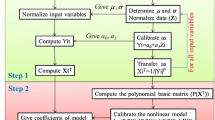
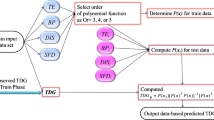
The historical water temperature (TE), barometric pressure (BP), spill from dam (SFD) and discharge (DIS) measured on a daily scale were selected as predictor’s variables to predict TDG measured as percent of saturation (%). The data were collected at four different dams’ reservoir sites located in Columbia River, USA. The data were obtained from the USGS Web site: https://waterdata.usgs.gov. Latitude, longitude and stations codes are reported in Table 1. Figure 1 shows the location of the four dams’ sites. The John Day Dam is a concrete gravity dam spanning the Columbia River in the northwestern United States. John Day Dam is part of the Columbia River Basin system of dams, its length is 2327 m, altitude above sea level is 81 m and the total height was about 56 m. The spillway has a structure with 20 gates; its length is 374 m (https://www.nwp.usace.army.mil/John-Day/). The Dalles Dam is a concrete gravity dam spanning the Columbia River, two miles east of the city of The Dalles, Oregon, USA, its length is 2693 m, altitude above sea level is 24 m and the total height was about 61 m. The spillway has a structure with 23 gates; its length is 441 m, (https://www.nwp.usace.army.mil/The-Dalles/). For the first three stations (TDDO, TDA and JHAW), we selected a period of record from 1998 to 2017, and for the fourth station (JDY), the period of record running from 2004 to 2017 (Table 2). However, it is worth noting that the selected stations have incomplete dataset from year to year and nearly half of data are missing. Periods of records with total, incomplete and final pattern are summarized in Table 2. Detailed statistics for the variables selected (TE, BP, SFD and DIS) as inputs for modeling TDG are provided in Table 3, where Xmean, Xmax, Xmin, Sx and Cv denote the mean, the maximum, the minimum, the standard deviation and the coefficient of variation, respectively. There is an inverse proportion between TE (BP) and TDG. Among the input variables, SFD has the highest variation (see CV) while the BP has the lowest variation in all stations. According to the correlation values in Table 3, the SFD is the most effective variable on TDG, closely followed by the DIS variable, whereas the BP has the lowest correlation which means that it is the least effective variable on TDG. The dataset was randomly divided into two sub-datasets: (1) training set (70%) and (2) validation set (30%). In order to show the relative importance of the four input variables, we compared several scenarios, each and every one of them has several combinations of the four input variables. Scenarios’ description is reported in Table 4.

Table 1 Description of the selected stations
Full size table
Fig. 1
figure 1

Map showing the location of the four dams’ sites and total dissolved gas monitoring stations, lower Columbia River, Oregon and Washington, USA (Tanner et al. 2009, 2011, 2012, 2013)

Full size image
Table 2 Period of records for the USGS stations selected in the present study
Full size table
Table 3 Statistical parameters of the used datasets for all stations
Full size table
Table 4 Input combinations of different models
Full size table

Modeling Approaches

Feedforward Neural Network (FFNN)

Artificial neural network (ANN) has been mainly adopted for developing and providing nonlinear relation between a set of input and output variables, using a learning process for optimization of the model parameters. The purpose of an ANN is to provide accurate predictions for an output response, i.e., TDG, based on the input dataset such as TE, BP, DIS and SFD. FFNN is one of the most used ANN models and can be used to estimate the TDG by the following mathematical relation:

$$\hat{y}(X) = f_{2} \left[\mathop B\nolimits_{0} + \sum\limits_{j = 1}^{M} {\mathop w\nolimits_{jk} } f_{1} \left(B_{j} + \sum\limits_{i = 1}^{n} {\mathop w\nolimits_{ij} } x_{i}\right)\right]$$
(1)

where B0 is the bias of the output neuron, wij denotes the weights of jth neuron in the hidden layer with respect to ith input variable, wjk represents the weights of output neuron corresponding to jth neuron in the hidden layer and f is an activation function adopted for each of the hidden and output neurons. The sigmoid function is commonly used for the neurons in the hidden layer (Minns and Hall 1996):

$$f\left( X \right) = \frac{1}{1 + \exp ( - X)}$$
(2)

The structure of the FFNN is plotted in Figure 2. It can be seen that the model has n input variable (i.e., n = 4) and M hidden neurons which is 10, determined using trial and error, for this study. A best learning approach for the weights of the FFNN is obtained when the designed network produces predictions with the minimum errors between the desired and predicted values of TDG in the training data. The most common learning approach is the backpropagation which is used to calibrate the FFNN model using iterative approach. The Levenberg–Marquardt (LM) backpropagation algorithm used in the present study for the FFNN showed the best performance with efficient predictions (Esfe et al. 2015). The input and output datasets were normalized between − 1 and 1 for better scale of the variables to just with sigmoid functions.

Fig. 2
figure 2

Schematic view of feedforward neural network (FFNN)

Full size image

Response Surface Method (RSM)

The RSM provides a nonlinear prediction based on simple predictor basis second-order polynomial functions as follows (Keshtegar and Kisi 2017):

$$\hat{y}(X) = b + \sum\limits_{i = 1}^{n} {w_{i} } x_{i} + \sum\limits_{i = 1}^{n} {\sum\limits_{j = i}^{n} {w_{ij} } } x_{i}^{{}} x_{j}^{{}}$$
(3)

where ŷ(X) is the predicted TDG, \(n\) is the number of input variables including TE, BP, DIS or SFD and b, wi and wij are unknown coefficients. Least square estimator is generally implemented to compute these unknown coefficients. Detailed information about this method can be obtained from the previous studies (Keshtegar and Kisi 2017; Keshtegar and Heddam 2018).

Kriging Interpolation Method (KIM)

The kriging model is a well-known interpolation framework for estimating geostatistics problems (Lucy 1977). It was recently implemented for optimum design (Li et al. 2017), structural reliability analysis (Jian et al. 2017) and the predictions of solar radiation (Keshtegar et al. 2018). The kriging model is given as follows:

$$\hat{y}(X) = \varGamma (\beta ,X) + U(X) = G(X)^{T} \beta + U(X)$$
(4)

where β is the vector of unknown coefficients, Γ(β, X) is the deterministic term and U(X) represents the random part of the models which is generally considered based on Gaussian process. Γ(β, X) involves the data of the basic functions of G(X) and their relative coefficients β. G(X) can be given as a scalar or polynomial basis functions that the second-order function was selected in the current study. The stochastic term of kriging model, i.e., U(X), should follow the stationary Gaussian process. The covariance between U(Xi) and U(Xj) is computed as:

$$\text{cov} (U(X_{i} ),U(X_{j} )) = \sigma^{2} R(X_{i} ,X_{j} ,\theta )$$
(5)

where σ2 denotes the variance, R(Xi, Xj, θ) represents the correlation function for U(X), and θ is unknown correlation parameters θ > 0. It can be realized from the kriging model in Eq. 4 that the predicted data ŷ(X) is obtained using the mean function of Γ(β, X) and covariance function cov(.,.). The correlation matrix \(R\), which is n × n matrix, can be improved by the flexibility of modeling approach to obtain the accurate predictions using nonlinear relation by the following form:

$$R = \left[ {\begin{array}{*{20}c} 1 & {} & {r(\mathop X\nolimits_{1} ,\mathop X\nolimits_{2} )} & \ldots \\ {r(\mathop X\nolimits_{2} ,\mathop X\nolimits_{1} )} & {} & 1 & {} \\ {} & \vdots & {} & \ddots \\ {r(\mathop X\nolimits_{n} ,\mathop X\nolimits_{1} )} & {} & {r(\mathop X\nolimits_{n} ,\mathop X\nolimits_{1} )} & \cdots \\ \end{array} \begin{array}{*{20}c} {r(\mathop X\nolimits_{1} ,\mathop X\nolimits_{n} )} \\ {r(\mathop X\nolimits_{2} ,\mathop X\nolimits_{n} )} \\ \vdots \\ 1 \\ \end{array} } \right]$$
(6)

where r(Xi, Xj) is the covariance basis function between a prior sample of Xi and Xj, and it can be computed as:

$$r\left( {\mathop X\nolimits_{i} ,\mathop X\nolimits_{j} } \right) = \mathop e\nolimits^{{\theta \mathop r\nolimits_{ij}^{2} }}$$
(7)

where rij is distance as ǁXi − Xjǁ. The unknown correlation parameter θ can strongly affect the accuracy of model predictions. Different values for θ may be conducted to get different accuracies for the prediction of TDG. Consequently, the maximum likelihood estimator can be applied to optimize the parameter vector θ as follows (Jian et al. 2017):

$$\theta = \arg {\text{Max}}\left( { - \log (\det R)n\log (\hat{\sigma }^{2} )} \right)$$
(8)

where n is the number of points for training and \(\hat{\sigma }^{2}\) is estimated variance of the model, which can be computed as:

$$\hat{\sigma }^{2} = \frac{{(Y - G(X)^{T} \beta )^{T} \mathop R\nolimits^{ - 1} (Y - G(X)^{T} \beta )}}{n}$$
(9)

Based on computing the unknown correlation parameter, the predictive model of kriging can be easily obtained as:

$$\hat{y}(X) = G(X)^{T} \beta + r(X)^{T} \gamma$$
(10)

where

$$\beta = (G^{T} R^{ - 1} G)^{ - 1} G^{T} R^{ - 1} Y$$
(11)
$$\gamma = R^{ - 1} (Y - G^{T} \beta )$$
(12)
$$G = [G(X_{1} ),\,G(X_{2} ), \ldots ,G(X_{n} )]^{T}$$
(13)
$$r(X) = [R(X_{1} ,X;\theta ),\,R(X_{2} ,X;\theta ), \ldots ,R(X_{n} ,X;\theta )]^{T}$$
(14)

The kriging-based meta-modeling approach is structured based on the polynomial basis function as well as RSM for G(X), while the random part using Gaussian process in terms of correlation function R is added into the predicted models. Consequently, the flexible predictive tool using kriging may provide a highly nonlinear relation in complex engineering problems. ANN has several linear functions in hidden neurons while the RSM has polynomial terms with second-order functions. The ANN can provide an accurate prediction for nonlinear problems with low cross-correlation between input data, but the predictions of problems having input data with high cross-correlation may be improved by applying RSM with high cross-terms or kriging. Consequently, the nonlinear forms achieved using an ANN model using an activated function in the hidden layer can enhance the ability of the ANN for predicting highly nonlinear problems having input data with low cross-correlation.

Performances Indices

To evaluate and compare the accuracy of the developed models, we used four performance indices. The indices are the coefficient of correlation (R), the Nash–Sutcliffe efficiency (NSE), the root-mean-squared error (RMSE) and the mean absolute error (MAE):

$$R = \left[ {\frac{{\frac{1}{\text{N}}\sum\nolimits_{{}}^{{}} {\left( { \, O_{i} - \, O_{m} } \right)\left( { \, P_{i} - \, P_{m} } \right)} }}{{\sqrt {\frac{1}{\text{N}}\sum\nolimits_{i = 1}^{n} {\left( { \, O_{i} - \, O_{m} } \right)^{2} } } \sqrt {\frac{1}{\text{N}}\sum\nolimits_{i = 1}^{n} {\left( { \, P_{i} - \, P_{m} } \right)^{2} } } }}} \right]^{{}}$$
(15)
$${\text{NSE}} = 1 - \frac{{\sum\nolimits_{i = 1}^{N} {\left[ { \, O_{i} - \, P_{i} } \right]^{2} } }}{{\sum\nolimits_{i = 1}^{N} {\left[ { \, O_{i} - \, O_{m} } \right]^{2} } }}$$
(16)
$${\text{RMSE}} = \sqrt {\frac{1}{\rm N}\sum\limits_{i = 1}^{\rm N} {\mathop {\left( {\mathop O\nolimits_{i} - \mathop P\nolimits_{i} } \right)}\nolimits^{2} } }$$
(17)
$${\text{MAE}} = \frac{1}{N}\sum\limits_{i = 1}^{N} {\left| {\mathop O\nolimits_{i} - \mathop P\nolimits_{i} } \right|}$$
(18)

where N is the number of data points, Oi is the measured value, Pi is the corresponding model prediction and Om and Pm are the average values of Oi and Pi. More details can be found in (Ghorbani et al. 2018a, b; Yaseen et al. 2018; Tao et al. 2018).

Models Development

In the present study, the FFNN, RSM and KIM models were developed using MATLAB software. All models were first calibrated during the training phase and later validated using the validation dataset. The parameters of the models were optimized during the training phase using a trial and error approach to identify suitable structures of the models. Various hidden node numbers were tried for FFNN models, and the optimal values were found to vary from 5 to 13 for the best models.

Results and Discussion

The estimated TDG for the selected period of record was compared to the measured data collected at four USGS stations. A total of seven models with different input combinations were developed and evaluated with the KIM, RSM and FFNN methods, to determine the most effective approach. According to the obtained results, the measured TDG values are in a good agreement with the estimated values using the applied models. We evaluated the quality of our results using RMSE, MAE, R and NSE, showing that the overall fit between the measured and calculated data is good (Tables 5, 6, 7, and 8). During the validation phase, RMSE and MAE in all stations are below 3%. The average RMSE and MAE of all validations sets are 2.212% and 1.741%, respectively, and the best results with lower RMSE and MAE are 1.462% and 1.122%, respectively. The best performing TDG station is the USGS 14105700 showing the average RMSE and MAE of 1.741% and 1.362%, respectively. However, the worst performing station is the USGS 454314120413701 station whose average RMSE and MAE are 2.687% and 2.094%, respectively. In overall, by analyzing the results obtained at all the four stations, we conclude that there is no dominant model that works as the best at all stations, but on the contrary, RSM is the worst method at three stations when compared to the KIM and FFNN. KIM models showed better fitting results compared to FFNN and RSM as shown in Table 5 for the USGS 14105700 station; however, FFNN estimates TDG more accurately than the other two methods in validation phase in terms of R, NSE, RMSE and MAE at the USGS 453712121071200 station, and it estimates TDG equally with the KIM models at the USGS 454249120423500 and USGS 454314120413701 stations. In the following, the performances of the models are assessed through the comparison with in situ measurement and modeled data at each station separately.

Table 5 Performances of different models in modeling TDG at USGS 14105700 station
Full size table
Table 6 Performances of different models in modeling TDG at USGS 453712121071200 station
Full size table
Table 7 Performances of different models in modeling TDG at USGS 454314120413701 station
Full size table
Table 8 Performances of different models in modeling TDG at USGS 454249120423500 station
Full size table

For the USGS 14105700 station (Table 5), for which a more robust and high accuracy was obtained, preliminary analysis revealed that the best accuracy was obtained using the KIM models followed by the FFNN models and the RSM was ranked in the third place (Table 5). During the validation phase, the KIM1 has the highest R and NSE (R = 0.973, NSE = 0.941) and the lowest RMSE and MAE (RMSE = 1.462%, MAE = 1.122%). With regard to the FFNN models, FFNN1 has the highest R and NSE (R = 0.966, NSE = 0.933) and the lowest RMSE and MAE (RMSE = 1.562%, MAE = 1.198%). Finally, RSM1 has the highest R and NSE (R = 0.952, NSE = 0.906) and the lowest RMSE and MAE (RMSE = 1.848%, MAE = 1.426%). In Table 5, the R and NSE values and the corresponding RMSE and MAE between the measured and estimated TDG values using the modeling approaches are analyzed. The average RMSE and MAE of the KIM models are quite low and equal to 1.617% and 1.265%, respectively. FFNN models provided the second lowest average RMSE and MAE with values equal to 1.682% and 1.321%, respectively. Finally, RSM models possess the largest average RMSE and MAE with values equal to 1.924% and 1.498%, respectively. With respect to the R and NSE values, the average R and NSE using KIM models are quite high and equal to 0.969 and 0.928, respectively. FFNN models provided the second highest average R and NSE with values equal to 0.961 and 0.922, respectively. Finally, RSM models possess the lowest average R and NSE with values equal to 0.948 and 0.898, respectively. Using only three input variables, the best accuracy varies from one model to another. KIM4 with SFD, TE and BP input variables is the best model (R = 0.966, NSE = 0.933), slightly higher than FFNN2 with SFD, DIS TE input variables (R = 0.961, NSE = 0.922), while the RSM4 possess the lowest accuracy and ranked in the third place (R = 0.950, NSE = 0.903). KIM1 decreased the RMSE and MAE of the KIM4 by 10.47% and 12.55%, respectively. FFNN1 decreased the RMSE and MAE of the FFNN2 by 7.13% and 8.97%, respectively. Finally, RSM1 decreased the RMSE and MAE of the RSM4 by 1.38% and 2.57%, respectively. Hence, it is clear from the analysis reported above that KIM models are the best, not only by providing the best accuracy, but also they present the best improvement when more input variables are included as inputs to the models. Finally, we analyze the performances of the models using only two input variables. From the results reported in Table 5, it is clear that using only two input variables, the best accuracy was obtained using KIM5 (R = 0.968, NSE = 0.936) with SFD and DIF inputs, FFNN7 (R = 0.966, NSE = 0.932) and RSM7 (R = 0.946, NSE = 0.895), having only SFD and TE as input variables; however, KIM5 is the best compared to FFNN7 and RSM7. Figure 3 shows the scatterplot of measured vs. calculated values of TDG, the frequency distribution histogram of the predicting errors and the boxplots for the USGS 14105700 station. As evident from the scatterplots, the fit line equation of the KIM1 model is closer to the exact line (y = x line) compared to other two models. It is obviously observed from the relative error histograms that the error variation of the KIM1 model is less than that of the FFNN1 and RSM1 models. The TDG prediction errors of the KIM1 are generally accumulated between − 3 and + 3 while those of the FFNN1 and RSM1 are in the range [− 5, + 5].

Fig. 3
figure 3

A scatterplot (left), boxplot (center) and frequency distribution histogram of the predicting errors (right) for USGS 14105700 station during the validation phase

Full size image

Results at the USGS 453712121071200 station are reported in Table 6. It can be seen from Table 6 that the FFNN method guaranteed high-accuracy prediction results using the combination of four input variables (with R = 0.909 and NSE = 0.827), performed better than the KIM and RSM methods. Taking into account the R and NSE values, RSM models performed the worst compared to the KIM and FFNN models. Further analysis of Table 6 for the individual prediction results indicated that the RMSE and MAE indices of the FFNN models are the lowest, equal to 2.161% and 1.710%, in average. The RMSE and MAE errors of KIM models were the greatest in average (RMSE = 2.572%, MAE = 2.025%). The average values of the RMSE and MAE of the RSM models are relatively high compared to the FFNN models, reaching 2.290% and 1.802%, respectively. According to Table 6, the best accuracy with high R and NSE was obtained using the four variables as inputs (SFD, DIS, TE and BP) and the KIM1, RSM1 and FFNN1 performed the best compared to the other six models. FFNN1 decreased the RMSE and MAE of the KIM1 by 33.28% and 36.77%, respectively, and decreased the RMSE and MAE of the RSM1 by 9.15% and 9.40%, respectively. The accuracy of the models was analyzed according to different input combinations as reported in Table 6. We mainly evaluated the accuracy based on RMSE, MAE, R and NSE. It is clear from Table 6 that using only three input variables, the best accuracy was obtained using KIM4, RSM4 and FFNN3, taking into account the RMSE and MAE values. All the RMSE and MAE values range from 2.092% to 2.524%, and 1.664% to 2.067%, respectively. However, the values of R and NSE for all models show marginal differences. FFNN3 increased the R of the KIM3 by 0.2%, and there is no improvement in the NSE value, and FFNN3 increased the R and NSE of the KIM3 by 2.4% and 1.3%, respectively. Using only two input variables, the FFNN5 had the highest estimation accuracy and its R and NSE values are 0.883 and 0.780, and RMSE and MAE values are 2.212% and 1.763%, respectively. The KIM5 model also maintained higher estimation accuracy with the R and NSE values of 0.884 and 0.745 and the RMSE and MAE values of 2.447% and 1.902%, respectively. It can be also concluded from Table 6 that using the three models, the estimation accuracy showed a certain increase with the increase in the input variables from two to four. Figure 4 shows the scatterplot of measured vs. calculated values of TDG, the frequency distribution histogram of the predicting errors and the boxplots for the USGS 453712121071200 station. As clearly seen from the scatterplots, FFNN1 model has the scattered TDG estimates and its error fit line is closer to the ideal line compared to the RSM1 and KIM1. As clearly observed from the scatterplots, boxplots and error histograms, KIM1 considerably overestimates TDG for this station and FFNN1 has the least standard deviation or variance in error distribution.

Fig. 4
figure 4

A scatterplot (left), boxplot (center) and frequency distribution histogram of the predicting errors (right) for USGS 453712121071200 station during the validation phase

Full size image

Accuracies of the proposed models at the USGS 454314120413701 station are summarized in Table 7. It shows that the KIM1, RSM1 and FFNN1 are the best models and provide relatively similar accuracy with marginal difference, regarding the four statistical indices, and the best accuracy was obtained when the four input variables were used together. The FFNN1 had the best accuracy with the R and NSE of 0.869 and 0.753, respectively. The RSM1 has the second best accuracy. The KIM1 provided the lowest accuracy and explained TDG less than the FFNN1 and RSM1. The FFNN1 model reduces daily RMSE from 2.610% to 2.471% (compared to the KIM1), and from 2.544% to 2.471% (compared to the RSM1), indicating that the FFNN1 predicted the TDG better than the RSM1 and KIM1 models. When using only three input variables, KIM3, RSM3 and FFNN3 are the best models and perform slightly worse than the KIM1, RSM1 and FFNN1, with marginal decrease in performances. For example, it was observed that the RMSE and MAE of the KIM3 were increased to 2.629% and 2.063%, respectively, which are negligible when compared to the values obtained using KIM1 (RMSE = 2.610%, MAE = 2.038%), while the RSM3 approach gave RMSE and MAE of 2.568% and 2.008%, respectively. Finally, the FFNN3 approach provided RMSE and MAE of 2.529% and 1.987%, respectively. This shows that inclusion of water TE as input variable slightly improves the accuracy of the models. Analysis of the models having only two input variables reveals that, in general, TDG concentration predicted using only two input variables agrees well with measured data and three models (KIM5, RSM5 and FFNN5) provided relatively high accuracy; although there is a clear discrepancy in TDG estimation accuracy between the models with three and four inputs and those using only two input variables. Nevertheless, the most striking result is that the three models (KIM5, RSM5 and FFNN5) provided the same accuracy with very marginal differences. The R and NSE ranged from 0.688 to 0.701 and from 0.838 to 0.839, respectively. Figure 5 shows the scatterplot of measured vs. calculated values of TDG, the frequency distribution histogram of the predicting errors and the boxplots for the USGS 454314120413701 station. From the scatterplots, it is clear that the FFNN1 and KIM1 estimates are similar to each other and they are less scattered than the RSM1. Boxplots also provided that the both FFNN1 and KIM1 have similar estimates and distributions.

Fig. 5
figure 5

A scatterplot (left), boxplot (center) and frequency distribution histogram of the predicting errors (right) for USGS 454249120423500 station during the validation phase

Full size image

Accuracies of the models at the USGS 454249120423500 station are summarized in Table 8. In summary, the KIM models provided relatively similar accuracy compared to FFNN models and they both have better accuracies compared to RSM models. The statistical results of the KIM models during the validation phase showed that TDG was estimated with an average RMSE and MAE equal to 1.918% and 1.500%, respectively. R and NSE, however, were from 0.950 to 0.962 and from 0.902 to 0.923, respectively, considerably higher than the RSM models. Further comparisons of the accuracy obtained with the three models demonstrated that the best accuracy was obtained using the models having the four input variables (KIM1, FFNN1 and RSM1). During the validation phase, KIM1 and FFNN1 provided the same accuracy, and they are significantly better than the RSM1 model. KIM1 decreased the RMSE and MAE of the RSM1 by 21.67% and 25.97%, respectively. The KIM3 model using SFD, DIS, BP as input was also able to successfully predict TDG, with a good accuracy during the validation phase with R of 0.960 and NSE of 0.918 (Table 8). The FFNN4 performed worse well compared to the KIM3 with R of 0.960 and NSE of 0.916. The KIM3 slightly decreased the RMSE and MAE of the FFNN4 by 1.18% and 2.98, respectively. The RSM3 was worse than the KIM3 and FFNN4 with R of 0.929 and NSE of 0.869. However, there are much larger differences in the RMSE and MAE between the RSM3 and the KIM3. The KIM3 decreased the RMSE and MAE of the RSM3 by 21.15% and 26.17%, respectively. Results obtained by the models having only two input variables demonstrated that the KIM7 and FFNN5 performed well and the KIM7 was slightly worse than the FFNN5, and the RSM5 was less accurate compared to the KIM7 and FFNN5. Figure 6 shows the scatterplot of measured vs. calculated values of TDG, the frequency distribution histogram of the predicting errors and the boxplots for the USGS 454249120423500 station. Taylor diagram showing the performance of different FFNN1, KIM1 and RSM1 models in terms of correlation coefficient and standard deviation between measured and calculated TDG (%) during the validation phase for the four stations is shown in Figure 7. It is obvious from the scatterplots that the fit line equation of the KIM1 is closer to the ideal line (450 line) compared to FFNN1 and RSM1. From Figure 6, it is observed that the KIM1 model has the closest standard deviation to the observed TDG in three stations. In this station, however, the RSM1 is better than the other two models. In two stations (USGS 454249120423500 and USGS 454314120413701), the FFNN1 and KIM1 indicators overlap.

Fig. 6
figure 6

A scatterplot (left), boxplot (center) and frequency distribution histogram of the predicting errors (right) for USGS 454314120413701 station during the validation phase

Full size image
Fig. 7
figure 7

Taylor diagram showing the performance of different FFNN1, KIM1 and RSM1 models in terms of correlation coefficient and standard deviation between measured and calculated TDG (%) during the validation phase for the four stations

Full size image

Finally, for practical application, our proposed models have their own weaknesses and advantages and they must be properly applied. Firstly, the models are only appropriate when input variables are available simultaneously at the same station. Secondly, the models can provide rapid and robust estimation of TDG if correctly calibrated. Thirdly and finally, we believe that there is a need for alternative modeling approaches that can be more readily implementable for modeling nonlinear problems with high-cross-correlation input data.

Conclusion

We presented and compared the ability of new modeling tools (KIM, RSM and FFNN) to predict total dissolved gas (TDG) concentration using water temperature, barometric pressure, spill from dam and discharge data as input variables. The proposed models were trained (calibrated) over a dataset collected at four USGS stations located in Columbia River, USA. The validation of the proposed models over the four sites and using data measured on daily scale revealed a remarkable estimation accuracy of the KIM models as compared to RSM models and relatively similar accuracy compared to the FFNN. For example, direct comparison between the models demonstrated that at USGS 14105700 station, KIM1 model was more accurate (R = 0.973 and RMSE = 1.462) than RSM1 (R = 0.952 and RMSE = 1.848) and FFNN1 (R = 0.962 and RMSE = 1.643). The accuracy of the proposed models is limited by the available dataset. Important effort should therefore be undertaken to improve the accuracy of the models. To draw more reliable conclusions about the proposed models, it is mandatory to extend the present investigations by using more data from more sites.