Introduction

Over the last few decades, with the great importance attributed to the management and control of dam’s reservoirs, the linkage between total dissolved gas (TDG) supersaturation and some environmental problems has been widely recognized (Parker et al. 1984; Boyd et al. 1994; Tanner et al. 2012). In particular, and without limitation to the foregoing, the “gas bubble trauma GBT” in fish also designated by “gas bubble disease GBD” is the most important and serious problem associated with the elevation of TDG (Beeman et al. 2003; Skov et al. 2013; Wang et al., 2018a), and the interest to demonstrate that TDG supersaturation may be having an adverse effect on the aquatic life of fish is not new and dates back to the beginning of the last century (Gorham, 1898; Marsh and Gorham 1904; Alikhuni et al., 1951; Parker et al. 1984; Boyd et al. 1994; Colt 1986). In general, TDG supersaturation is quantified in percent (%) and calculated as the difference between TDG pressure and atmospheric pressure, for which TDG pressure is calculated for any temperature, as the sum of the partial pressures of all TDG plus the vapor pressure of water, and generally limited to 110% (Skov et al. 2013; Politano et al. 2016). Nitrogen and oxygen form the essential dissolved gas and hence play an important role in the determination of the final TDG concentration. However, the limited level of gas concentration varies depending on the nature of gas dissolved in water, and generally, nitrogen and dissolved oxygen have been considered unsafe above 110% and 300%, respectively (Parker et al. 1984). TDG supersaturation is produced in a major part by the “spill” at “hydroelectric projects” (Weitkamp et al. 2003). Water is generally spilled whether through drum gates or also through a series of outlet work conduits (Bragg and Johnston 2016). According to Beeman and Maule (2006), the rate of TDG supersaturation increases if the pressure of TDG falls below the hydrostatic pressure in dam tailraces.

The objectives related to the monitoring and control of TDG supersaturation in water ranged, on the one hand, from providing the relevant physicochemical phenomena which are causing TDG supersaturation and, on the other hand, understanding the anthropogenic and natural causes (CCME 1999). Consequently, an effective understanding of the TDG supersaturation represents a high priority, especially for the regions with high network of dam reservoirs (e.g., Columbia River, USA), and in this case, the database for all measured variables plays a crucial role and can help in the development of models for estimating TDG. Previous studies have shown that TDG can be analyzed using numerical models (NM), using laboratory and field experiment. However, NM possesses an important disadvantage that generalization is inappropriate for the majority of empirical equation derived. Therefore, the results cannot be generalized statistically to the outside of used data during the calibration phase (Wang et al., 2018b). Review of literature clearly demonstrated that various empirical and physical models were proposed for predicting TDG supersaturation (Roesner and Norton 1971; Hibbs and Gulliver 1997; Shaw 1998; Geldert et al. 1998; Orlins and Gulliver 2000; Hadjerioua et al. 2012; Feng et al. 2013; Picket et al. 2004; Tawfik and Diez 2014; Wang et al., 2018a; Yuan et al. 2018).

Roesner and Norton (1971) were the first authors in the literature that have attributed particular importance to develop a predictive model for TDG downstream of spillway. The proposed model was applied at Columbia and Snake rivers, USA. As a result of the model, it is reported that an effective depth to reduce the rate of TDG supersaturation is directly related to a specific discharge. Tawfik and Diez (2014) proposed a model for predicting TDG supersaturation up to the onset of bubble nucleation at the electrodes (heterogeneous nucleation). In order to demonstrate the effect of solid media in water, Yuan et al. (2018) conducted an investigation and proposed a model linking the density of vegetation with the TDG dissipation process. The model was able to significantly increase the performances of predictive models of TDG “transport” and “dissipation” in downstream high dam spilling. From the obtained results, the authors demonstrated that the dissipation rate of TDG supersaturation increased with the increase in vegetation density. A first-order kinetics reaction model is proposed by Picket et al. (2004). Feng et al. (2013) used the CE-QUAL-W2 developed by the US Army Corps of Engineers, for developing a two-dimensional laterally averaged hydrodynamic model for TDG transportation and dissipation in the deep Dachaoshan reservoir. The authors demonstrated that the percent saturation increases with the water depth at the layers near the water surface. A model based on volume of fluid method was proposed by Wang et al. (2018b) and applied for predicting TDG downstream of spillways. TDG was quantified using a mathematical formula taking into account the masse transfers between bubbles and water.

Orlins and Gulliver (2000) used a combined model having two components: physical and numerical for total dissolved gas concentration. The physical model takes into account the hydraulic information related to the modification of spillway, while the numerical model estimates the concentration of TDG using mass transport relation between air and water. Shaw (1998) implemented a new equation for TDG production from spill using the Columbia River salmon passage model (CRiSP.1). The proposed equation links the discharge to the TDG % exiting the tailrace of a dam. Hibbs and Gulliver (1997) proposed a numerical model for determining an effective bubble depth (EPD) in spillway taking into account three variables: spillways, flow parameters, and the tailwater depth. The determined EPD is incorporated into the models used for predicting TDG in downstream of spillways. In another study, Geldert et al. (1998) used data collected from three spillways on the Columbia and Snake rivers for developing a physical predictive model for TDG caused by the stilling basin in downstream of the dam. The proposed model takes into account several ideas, namely transfer across the air water interface, and the hypothesis that TDG% is mainly related to the stilling basin depth and the downstream river depth. Hadjerioua et al. (2012) proposed a generalized model for predicting TDG level. The proposed model included a large number of parameters including structural, operational, and environmental parameters, among them are the following: (i) the depth of the stilling basin, (ii) total head, (iii) volume spill, (iv) powerhouse flow, (v) TDG pressure, (vi) water temperature, (vii) barometric pressure, (viii) geometry of the spillway, (ix) spillway flow deflectors, (x) training walls, and (xi) and baffle blocks. Several other models can be found in the literature (Politano et al. 2007, 2009, 2012, 2017; Stewart et al. 2015; Witt et al.2017a, b).

Paradoxically, despite the importance attached to the study and modeling TDG supersaturation and to the application of DD models in many areas of scientific researches, none of the above reported investigations have applied or used data-driven (DD) models for predicting TDG. Recently, Heddam (2017) proposed for the first time the generalized regression neural network (GRNN) for predicting TDG at Columbia River dams. In the present study, we applied four DD models for predicting TDG (%), namely high-order response surface method (H-RSM), least squares support vector machine (LSSVM), M5 model tree (M5Tree), and multivariate adaptive regression splines (MARS) using data collected at four dam reservoirs at Columbia rivers, USA.

Methods

Study area and data used

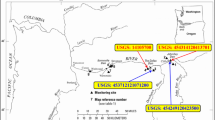
The data used for developing the models were obtained from the United States Geological Survey (USGS) database (https://waterdata.usgs.gov). The study includes four stations, namely USGS453439122223900 at Columbia River, right bank, at Washougal, Clark County, WA (latitude, 45° 34′ 39″; longitude, 122° 22′ 39″); USGS453630122021400 at Columbia River, left bank, near Dodson, Multnomah County, OR (latitude, 45° 36′ 30″; longitude, 122° 02′ 14″); USGS4538451215620000 at Columbia River at Bonneville Dam Forebay, Skamania County, WA (latitude, 45° 38′ 45″; longitude, 121° 56′ 20″); and USGS453845121564001 at Columbia River at Cascade Island, Skamania County, WA (latitude, 45° 38′ 45″; longitude, 121° 56′ 40″). The statistical parameters of the selected data used in our investigation are summarized in Table 1. Four variables measured at daily time step were selected as input variables for developing the models. These variables were respectively the following: (i) daily water temperature (TE), (ii) daily barometric pressure (BP), (iii) daily spill from dam (SFD), and (iv) daily discharge (DIS). In addition, the total dissolved gas measured in % of saturation is used as the output of the models. Note from Table 1 that the SFD and DIS have high correlations with the TDG in all stations. Data used in the present investigation are based on large period of measure and cover a period from 1 January 1998 to 31 December 2017 for three stations: USGS 453439122223900, USGS 453630122021400, and USGS 453845121562000, respectively, while for the fourth station (USGS 453845121564001), the data cover a period from 1 January 2004 to 31 December 2017. However, during the period of record, the stations have some incomplete data from year to year. The data set was randomly divided into two sub-data sets in this study: (i) training subset (70%) for model calibration and (ii) validation subset (30%) for model testing. The validation subset, sometimes called test subset, was used to assess the performances of the proposed models (Moghaddasi and Noorian-Bidgoli 2018; Li et al. 2019).

Table 1 Statistical parameters of the used data sets for all stations
Full size table

High-order response surface method

The response surface method (RSM) is an efficient and simple approximating experiment-based the quadratic polynomial set function corresponding to several data bases (Keshtegar and Kisi 2017). Generally, the second-order polynomial function is utilized for predicting TDG in the RSM by the following function (Keshtegar and Heddam 2018).

$$ T\hat{D}G={a}_0+\sum \limits_{i=1}^n{a}_i{x}_i+\sum \limits_{i=1}^n\sum \limits_{j=1}^n{a}_{ij}{x}_i{x}_j $$
(1)

where, \( T\hat{D}G \) is the approximated TDG using the input data sets x including TE, BP, SFD, and DIS. n is the number of input variables, and a0, ai, and aij are the unknown coefficients. The total number of coefficients is NC = (n + 1)(n + 2)/2. Least squared estimator is applied to approximate the unknown coefficients of the response surface function in Eq. (1). Thus, the predicted data basis RSM is given as follows (Keshtegar and Seghier 2018):

$$ {TDG}_p=P\left({x}_i\right){\left[P{(x)}^TP(x)\right]}^{-1}\left[P{(x)}^T\right]\boldsymbol{TDG} $$
(2)

where, TDGP is the predicted TDG using ith input variables (xi ϵ [TEi, BPi, SFDi, and DISi]). Here, x and TDG are respectively the input data set and the observed TDG in the training phase. P(.) is the polynomial basis function. Second-order functions for 4-input data with 15 coefficients can be expressed as:

$$ P(x)=\left[1,{x}_1,{x}_2,{x}_3,{x}_4,{x}_1^2,{x}_1,{x}_2,{x}_1,{x}_3,{x}_1,{x}_4,{x}_2^2,{x}_2,{x}_3,{x}_2,{x}_4{x}_3^2,{x}_3,{x}_4,{x}_4^2\right] $$
(3)

As seen from Eq. (3), the P(xi) is computed based on the input data of (xi ϵ [TEi, BPi, SFDi, and DISi]) at ith data; thus, we have a matrix with N × NC dimensions for P(x) where N is the number of the training data and NC is the number of the unknown coefficients and the polynomial basis functions P(x) is developed based on the linear cross-correlations of the input variables (i.e., xi xj i ≠ j). Consequently, highly nonlinear cross-correlation between variables xi and xj is not considered in the RSM. The recent studies showed that the original RSM may provide inaccurate results compared with the modified versions of the response surface method which transfers the input database by power or exponential forms (Keshtegar and Heddam 2018; Keshtegar and Kisi; 2017; Keshtegar and Seghier 2018). Consequently, the highly nonlinear cross-correlations of the input data may improve the accuracy of the RSM as well as the modified RSM. In this current study, the high-nonlinear basis polynomial functions are investigated for the prediction of TDG using nonlinear forms of the basic RSM.

As seen from Eq. (1), the RSM is a simple and efficient modeling approach for predicting TDG, but this explicit mathematical form basis polynomial function with cross-linear terms may provide inaccurate results for complex processes. Therefore, the second-order polynomial basis set functions are needed to improve RSM in solving complex real engineering problems. The flexibility of RSM in Eq. (1) may be enhanced for predictions of TDG using the high-order polynomial basis function with second, third or fourth cross terms, which is presented by the following polynomial set functions:

(4)

in which TĎG is the predicted TDG with high-order polynomial function (PF) with n input data set. a0, ai, aij, bij, dij, and kij are the unknown coefficients with a total number of coefficients:

$$ NC=\left(n+1\right)\left(n+2\right)/2+\left( Or-2\right){n}^2 $$
(5)

where (Or) is the order of PF and 3 to 5 orders were used in this study. The least square estimator is generally applied to solve Eq. (4) using training data. Consequently, the predicted data using high-order PF is computed based on Eq. (2) where P(.) and P(xi) are determined by using the high-order polynomial basis function. For example, the high-order polynomial basis functions for three input data of x1, x2, x3, and PF with 3-order is given as below:

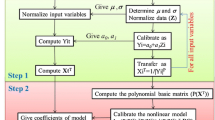
$$ P(x)=\left[1,{x}_1,{x}_2,{x}_3,{x}_1^2,{x}_1,{x}_2,{x}_1,{x}_3,{x}_2^2,{x}_2,{x}_3,{x}_3^2,{x}_1^3,{x}_1,{x}_2^2,{x}_1,{x}_3^2,{x}_2,{x}_1^2,{x}_2^3,{x}_2,{x}_3^2,{x}_3,{x}_1^2{x}_3,{x}_2^2,{x}_3^3\right] $$
(6)

As seen from Eqs. (3) and (4), the high-order PF is structured by the high cross-correlation nonlinear of the input data in the H-RSM modeling approach. More accurate results may be obtained using the high-order PF compared with the second-order PF for complex processes. The steps of the predicted TDG using H-RSM are presented as below:

  1. Step 1:

    Give the training databases including input data set as (xi ϵ [TE, BP, SFD, and DIS]) and output TDG.

  2. Step 2:

    Set the order of PF and compute P(x) in terms of high-order polynomial basis function.

  3. Step 3:

    Give the input data in test phase (xi ϵ [TEi, BPi, SFDi, and DISi]) and determine the high-order PF P (xi).

  4. Step 4:

    Predict the TDG (TDGp) using the training datasets of x, TDG, and test input data of xi as:

$$ {TDG}_p=P\left({x}_i\right){\left[P{(x)}^TP(x)\right]}^{-1}\left[P{(x)}^T\boldsymbol{TDG}\right] $$
(7)

The framework of H-RSM for prediction of the TDG is presented in Fig. 1. As seen from Fig. 1, the H-RSM is a simple modeling approach as well as the RSM. For applying the above steps to predict TDG, a program code was developed by MATLAB software.

Fig. 1
figure 1

The schematic view of the H-RSM for predictions of TDG

Full size image

Least squares support vector machine

Least squares support vector machine (LSSVM) proposed by Suykens and Vandewalle (1999) is a supervised machine learning model introduced as an improved version of the original SVM. The LSSVM possesses the general form of any regression model that works on linking a set of inputs variables (xi) to one target output variable (y) by using the linear least squares (LLS) criteria rather than the convex quadratic programming (CQP) used for the SVM as follow (Suykens and Vandewalle 1999):

$$ y=f(x)={w}^t\phi (x)+b\left(w,x\in {\mathrm{R}}^{\mathrm{d}}\right) $$
(8)

for which w and b are the weights and biases, x is the matrix of input variables, and y is the target variable. Using the LSSVM, the objective function (OF) is calculated using the principle of structural risk minimization (SRM) (Zhu et al. 2018) as follow:

$$ {\operatorname{Min}}_{w,\gamma}\mathrm{J}\left(w,\gamma \right)=\frac{1}{2}{w}^Tw+\frac{1}{2}\gamma \sum \limits_{k=1}^n{e}_k^2 $$
(9)

Consequently, Eq. (8) is written as follow:

$$ y=w.\varphi (x)+b+{e}_k $$
(10)

where γ denotes regularization parameter and ek denotes the random error between observed and calculated value, and φ (x) is the kernel function Mercer conditions as follow (Zhu et al. 2018; Yang 2018):

$$ k\left({x}_i,{x}_j\right)=\varphi {\left({x}_i\right)}^T\varphi \left({x}_j\right) $$
(11)

Finally, the regression equation of the LSSVM model is obtained by a group of single linear equations as follow (Xiong et al. 2018; Wang et al. 2018):

$$ f(x)=\sum \limits_{i=1}^n{\alpha}_ik\left({x}_i,{x}_j\right)+b $$
(12)

In the present study, LSSVM model is developed using the LS-SVMlab software (http: //www.esat.kuleuven.be/sista/lssvmlab/.).

Multivariate adaptive regression splines

One of the most and well-known adaptive, nonlinear and nonparametric regression models is certainly the multivariate adaptive regression spline (MARS) model introduced by Friedman (1991). The MARS is mainly used for mapping a set of predictors to a dependent variable using high-dimensional arguments (Nalcaci et al. 2018), with respect to the principal of “divide” and “conquers” method (Zhang et al. 2018). The MARS approach divides the input space into several subspaces and then for each subspace, a basic function (BF) is developed. Each BF takes into account the information provided by one or several predictors, and the BFs are fixed between two limits: “primary” and “end” points called “knote” (Arabameri et al. 2018). The BF relates the regressors to the dependent variable in the form of Max (0, X−c) or Max (0, c−X) (Friedman 1991), for which c is the threshold and X is the input variable. MARS model can be expressed as follow:

$$ Y=f\left({x}_i\right)={\psi}_0+j=\sum \limits_{j=1}^P\sum \limits_{b=1}^B\left[{\psi}_{jb}\left(+\right)\mathit{\operatorname{Max}}\left(0,{x}_i-{\mathrm{K}}_{bj}\right)+{\psi}_{jb}\left(-\right)\mathit{\operatorname{Max}}\left(0,{\mathrm{K}}_{bj}-{x}_j\right)\right] $$
(13)

where x is one of the predictors, Y is the dependent variable; P and B are the number of the predictors and the number of the generated BF, respectively, ψ0 is constant or intercept, ψjb is the coefficient of the jth BF, and the Κ values are called knots (Arabameri et al. 2018). In the present study, MARS model is developed using the Matlab toolbox ARESLab (Jekabsons, 2016b).

M5Tree model

Inspired from the original regression trees (RT), the M5Tree model (M5Tree) was developed by Quinlan (1992) as a new machine learning technique. The M5Tree model builds recursively a RT model (Pulkknen et al. 2018), by dividing the space of the training data into several subsets, and a multivariate linear regression is formulated for each one, which relates the input variables to the dependent variable. The partitioning is achieved by recursive splits that minimize intra-subset variation (Ajmera and Goyal 2012). The M5Tree model contains three steps: splitting, creating, and extracting the knowledge from the tree (Fatehnia et al. 2016). During the first stage, a linear regression model is developed based on the division of the space of the data, and at the end of this step, the required information is provided that form the tree and the nodes are constructed. Generally, M5Tree model employs splitting criterion using the standard deviation reduction (SDR), calculated as follow (Pal and Deswal 2009; Fatehnia et al. 2016; Sattari et al. 2018):

$$ SDR= sd(T)-\sum \frac{\left|{T}_i\right|}{T} sd\left({T}_i\right) $$
(14)

where T is the set of data points that reach the node, Ti denotes the subset of cases that have the ith outcome of the potential test, and sd represents the standard deviation of the observed values. In the present study, the M5Tree is implemented using the Matlab toolbox M5PrimeLab (Jekabsons, 2016a).

Performance assessment of the models

To evaluate and compare the accuracy of the developed models, we used five performance indices. These five indices are the following: the coefficient of correlation (R), the Nash-Sutcliffe efficiency (NSE), the Willmott index of agreement (d), the root mean squared error (RMSE), and the mean absolute error (MAE).

$$ R=\left[\frac{\frac{1}{\mathrm{N}}\sum \left({\mathrm{O}}_i-{\mathrm{O}}_m\right)\left({\mathrm{P}}_i-{\mathrm{P}}_m\right)}{\sqrt{\frac{1}{\mathrm{N}}}\sum \limits_{i=1}^n{\left({\mathrm{O}}_i-{\mathrm{O}}_m\right)}^2\sqrt{\frac{1}{\mathrm{N}}}\sum \limits_{i-1}^n{\left({\mathrm{P}}_i-{\mathrm{P}}_m\right)}^2}\right] $$
(15)
$$ NSE=1-\frac{\sum \limits_{i=1}^N{\left[{\mathrm{O}}_i-{P}_i\right]}^2}{\sum \limits_{i=1}^N{\left[{\mathrm{O}}_i-{\mathrm{O}}_m\right]}^2} $$
(16)
$$ d=1-\frac{\sum \limits_{i=1}^N{\left({\mathrm{P}}_i-{\mathrm{O}}_i\right)}^2}{\sum \limits_{i=1}^N{\left(\left|{\mathrm{P}}_i-{\mathrm{O}}_m\right|\left|+\right|\left|{\mathrm{O}}_i-{\mathrm{O}}_m\right|\right)}^2} $$
(17)
$$ RMSE=\sqrt{\frac{1}{N}\sum \limits_{i=1}^N{\left({\mathrm{O}}_i-{P}_i\right)}^2} $$
(18)
$$ MAE=\frac{1}{N}\sum \limits_{i=1}^N\left|{\mathrm{O}}_i-{\mathrm{P}}_i\right| $$
(19)

where N is the data number, Oi is the measured TDG value, and Pi is the predicted TDG. Om and Pm indicate the average of Oi and Pi.

Results and discussion

In this study, TDG measured at four dam reservoirs at Columbia River, USA, was predicted using four data-driven models as reported above. The developed models were LSSVM, MARS, M5Tree, and high-order RSM (H-RSM) with three different orders, from 3 to 5. The models were developed using four input variables, namely TE, BP, SFD, and DIS, served as predictors. The models were developed and evaluated using five statistical indices: R, NSE, d, RMSE, and MAE. Several combinations of the input variables were utilized and four scenarios were evaluated: (i) SFD, DIS, BP, and TE; (ii) SFD, DIS, and TE; (iii) SFD, DIS, and BP; (iv) SFD, BP, and TE. Consequently, LSSVM1, MARS1, M5TRee1, 3H-RSM1, 4H-RSM1, and 5H-RSM1 correspond to the first combination; LSSVM2, MARS2, M5Tree2, 3H-RSM2, 4H-RSM2, and 5H-RSM2 correspond to the second and so on, until the fourth combination. The performances of the simulated models compared with measured TDG are shown in Tables 2, 3, 4, and 5, illustrating the calculated statistical indices.

Table 2 Performances of different models in modeling TDG at USGS 453439122223900 station
Full size table
Table 3 Performances of different models in modeling TDG at USGS 453630122021400 station
Full size table
Table 4 Performances of different models in modeling TDG at USGS 453845121562000 station
Full size table
Table 5 Performances of different models in modeling TDG at USGS 453845121564001 station
Full size table

According to the obtained results, the following conclusions can be derived. First, comparison of models indicated that model 5H-RSM1 that includes the four input variables (SFD, DIS, BP, and TE) yields the best performance among the considered models with respect to R, NSE, d, RMSE, and MAE criteria, at four stations. Using 5H-RSM1, a good agreement is observed in all stations with R, NSE, and d ranging from 0.911 to 0.965, 0.829 to 0.931, and 0.952 to 0.982, respectively. The highest accuracy using the 5H-RSM1 was obtained at USGS453630122021400, while the lowest accuracy has been achieved at USGS 453845121562000. Similarly, the RMSE ranges from 1.456 to 2.263% with an average of 1.835%. In addition, the MAE ranges from 1.022 to 1.751% with an average of 1.392%. Second, it is clear from the results reported in Tables 2, 3, 4, and 5 that the M5Tree approach produced a model with low accuracy at the four stations, with high RMSE and MAE, and low R, NSE, and d. Finally, although the 5H-RSM1 provided the high accuracy, it is evident that the 5H-RSM1 slightly improved the accuracy of the other three models which use only three input variables, and the improvement is marginal especially between 5H-RSM1 and 5H-RSM2, for which the MAE observed from validation data between the two models in the four stations tended to be of a similar magnitude. Similarly, RMSE values were fairly consistent across stations between the two models.

Results obtained at USGS453439122223900 station are reported in Table 2. Hereafter, we compared the performance (e.g., RMSE, MAE, R, NSEN, and d) of the H-RSM methods against the other three methods: LSSVM, MARS, and M5TRee. An accuracy assessment was conducted to evaluate the results. Table 2 showed that the best accuracy was obtained using the 5H-RSM1 slightly better than 4H-RSM1, 3H-RSM1, LSSVM1, and MARS1, and considerably higher than the M5TRee1. 5H-RSM1 yielded a result with an RMSE of 1.943%, an MAE of 1.496%, an R of 0.923, an NSE of 0.851, and an d = 0.959. For numerical comparison, using the 5H-RSM1, the RMSE of the M5TRee1 was decreased by 14.48%, the MAE is reduced by 14.56%, the R was lifted by 2.6%, the NSE was promoted by 5.5%, and finally the d is increased by 1.2%. For further analysis, when looking at the models with only three inputs, it is obvious that the best performance was obtained using combination number 4 with SFD, BP, and TE as input variables, with the exception of the M5Tree models so that the best accuracy with three input variables was found for the M5TRee3 with SFD, DIS, and BP as input variables. However, it is worth noting that the most significant improvement between four-input and three-input models was achieved using MARS and LSSVM. Four-input LSSVM1 decreased the RMSE and MAE of the three-input LSSVM4 model by 3.36% and 3.45%, respectively. In addition, MARS1 decreased the RMSE and MAE of the MARS4 by 1.748% and 1.013%, respectively. For the other approaches, the difference between the models with four and three input variables is completely negligible. Finally, according to Table 2, the four M5Tree models provided relatively similar accuracy with very marginal difference. Calculated TDG (%) using the best models are plotted against corresponding measurements values in Fig. 2.

Fig. 2
figure 2

Scatterplot of calculated versus measured TDG (%) for the optimum developed models during the validation phase: USGS 453439122223900

Full size image

For USGS453630122021400 station, the R, NSE, d, RMSE, and MAE statistics are provided in Table 3, for all models, with all input combinations. Among the all proposed methods, model 5H-RSM1 contains the smaller RMSE and MAE, with values equal to 1.677 and 1.300, respectively. Compared with the worst method, the 5H-RSM1 decreased the RMSE and MAE of the M5Tree1 by 16.066% and 10.53%, respectively. According to Table 3, the results obtained demonstrated that combination of three input variables compared with the best model with four input variables slightly decreases the performance. Specifically, 5H-RSM4 with SFD, BP, and TE was slightly less than the 5H-RSM1 with negligible difference in the RMSE and MAE values. Based on the validation results in Table 3, the 5H-RSM, 4H-RSM, and 3H-RSM are promising for TDG modeling while the LSSVM and MARS are comparable to the H-RSM with relatively similar accuracy when using only three input variables. The statistical indices showed that there was no considerable difference between LSSVM and MARS predictions, but they were both considerably different from the M5Tree1 for TDG (%) modeling. LSSVM1 decreased the RMSE and MAE of the M5Tree1 by 12.41% and 6.81%, respectively. In addition, the MARS1 decreased the RMSE and MAE of the M5Tree1 by 11.81% and 4.47%, respectively. The 4H-RSM1 and 3H-RSM1 achieved a comparable result with similar R and d values (R = 0.965, d = 0.982) and slightly different values of NSE: 0.929 for 3H-RSM1 and 0.931 for 4H-RSM1. Figure 3 shows the linear regressions (scatterplot) between the calculated and the measured TDG (%) values using the validation dataset. As clearly observed from the scatter graphs, the 5H-RSM1 has less scattered estimates (R2 = 0.9315) and its fit line is closer to the exact line (slope and bias of the fit line equation is closer to 1 and 0, respectively) compared with other models.

Fig. 3
figure 3

Scatterplot of calculated versus measured TDG (%) for the optimum developed models during the validation phase: USGS 453630122021400

Full size image

Table 4 reports the results of the proposed models for TDG prediction at USGS 453845121562000 station. The overall accuracy of the best models compared with the measured TDG was discussed hereafter. It can be seen from Table 4 that the 5H-RSM1 model has both the highest R, NSE, and d values (R = 0.911, NSE = 0.829, d = 0.952) and the lowest error measures (RMSE = 2.263 and MAE = 1.751). The 5H-RSM1 model is more accurate compared with the other models, is considerably higher than the M5TRee1, and it slightly improved the accuracy of 4H-RSM1, 3H-RSM1, LSSVM1, and MARS1. The 5H-RSM1 model reduced the MAE and RMSE measurements of the M5TRee1 with a percentage reduction of 34.54% and 16.70%, respectively. In addition, the values of R, NSE, and d of the M5TRee1 were promoted by 9.7%, 22.9%, and 5.4%, respectively, while for the 3H-RSM1 and 4H-RSM1, the values of RMSE, MAE, R, NSE, and d did not show considerable differences. MARS1 model predictions are slightly more accurate than those from LSSVM1 in terms of the all five statistical indices. Utilizing the MARS1 model resulted in a reduction of RMSE and MAE of about 2% and 3%, respectively, compared with the LSSVM1. Table 4 indicates that, on the average, the results from the two input combinations (combinations 2 and 3) differ by only a few. Table 4 highlights a better performance of the MARS3 having input variables SFD, DIS, and BP, with respect to all statistical indices. For instance, MARS3 has RMSE, MAE, R, NSE, and d of 2.398, 1.865, 0.899, 0.808, and 0.944, respectively, slightly superior to the values provided by the LSSVM3, 5H-RSM3, 4H-RSM3, and 3H-RSM3 and significantly better than the M5TRee3. Contrary to the two previous stations, the lowest accuracy was obtained by the models using combination 4, with SFD, BP, and TE. Overall, except the models using all the four input variables, for which the best accuracy was obtained, the models with three input variables provided relatively similar accuracy with low differences. Figure 4 shows the scatterplot of measured and predicted TDG, for the six best models. Here also the less scattered estimates of the 5H-RSM1 model can be clearly seen especially for the peak TDG values compared with other models. This confirms the lower RMSE values (see Table 4) of this model than the alternative models.

Fig. 4
figure 4

Scatterplot of calculated versus measured TDG (%) for the optimum developed models during the validation phase: USGS 453845121562000

Full size image

Table 5 summarizes the results of applied models in terms of statistical indices at USGS453845121564001. Clearly, the results suggest that the 5H-RSM1 model consistently outperforms the other models and produces high accuracies in terms of R, NSE, d, RMSE, and MAE; however, the results also show that the 5H-RSM1 and 4H-RSM1 give similar accuracy regarding all the statistical indices. In addition, the difference among the 3H-RSM1, LSSVM1, and MARS1 models are marginal. MARS1 had the second best accuracy, and LSSVM1 performed less than the MARS1 and better than the M5TRee1. Similarly, poor accuracy was obtained using M5TRee1 compared with that obtained using all developed models. The M5TRee1 model yielded the substantially lowest R, NSE, and d and the highest RMSE and MAE. Using three input variables, the best accuracy was obtained using 5H-RSM2 with SFD, DIS, and TE as input variables. However, the RMSE and MAE differences between the proposed models are small when the SFD, DIS, and BP are included as predictor variables suggesting that the relationships between TDG and those predictor variables can be captured equally by all models, and none of them was capable to provide an accuracy improvement. Comparison of first and second input combinations reveals that including BP variable in inputs considerably increases the models’ accuracies in estimating TDG even though there is a very low correlation between BP and TDG as seen from Table 1. This is also valid for the other three stations. This indicates that there might be nonlinear relationship between the BP and TDG variables. Figure 5 shows the scatterplot of measured and calculated TDG using the best models. The figure clearly shows the superiority of the 5H-RSM1.

Fig. 5
figure 5

Scatterplot of calculated versus measured TDG (%) for the optimum developed models during the validation phase: USGS 453845121564001

Full size image

Conclusions

The investigation presented in this paper has demonstrated the potential of data-driven models to accurately predict an important variable at dam’s reservoirs: total dissolved gas (TDG) concentration. The estimation of TDG was made possible through the exploitation of large data base freely available and contains several easily measured variables. Providing such kind of models can be of great interest, compared with the physical and numerical models which require a large number of variables to be calibrated. Four models were developed and compared, three well known and widely reported in the literature as a powerful tool for solving several environmental problems (LSSVM, MARS, and M5Tree) and one new model (RSM) presented for the first time as a powerful tool. While the demonstration of the usefulness and robustness of the proposed approaches is based on data collected at four USGS stations, the generalization of the methods is relatively straightforward, in the light of all data-driven models. Several conclusions can be drawn at the closing of this investigation. Firstly, among the proposed four models, M5Tree models had the lowest accuracy at the four stations, and this leads us to conclude that M5Tree was unable to provide high and precise accuracy for modeling TDG concentration. Secondly, LSSVM and MARS models provided relatively similar accuracy with slightly and marginal difference. Finally, high-order response surface method (5H-RSM) using all the four input variables successfully built the relationship between TDG concentration and the selected predictors. The high-order RSM provides the high correlation terms based on the polynomial functions while the coefficient vector is increased by increasing the polynomial term basis high-order consideration. According to these reasons, applying the high-order correlation of basis input data may improve the accuracy prediction of nonlinear problems compared with original RSM. However, the H-RSM needs more data point for training a nonlinear model due to the increasing number of coefficients, which could provide a useful method with high flexibility for both accuracy and efficiency. However, it can be applied for modeling the problems with smaller input variables with larger training database. Furthermore, it was demonstrated that the performance of the 5H-RSM was only slightly decreased when the model included fewer input variables.