DOA estimation with double L-shaped array based on Hadamard product and joint diagonalization in the presence of sensor gain-phase errors

Abstract

A method with double L-shaped array for direction-of-arrival (DOA) estimation in the presence of sensor gain-phase errors is presented. The reason for choosing double L-shaped array is that the shared elements between sub-arrays are the most and rotation invariant property can be applied for this array. The proposed method is introduced as follows. (1) If the number of signal is one, first the gain errors are estimated and removed with the diagonal of the covariance matrix of the array output. Then the array is rotated by an unknown angle and DOA can be estimated with the relationship between signal subspace and steering vector of signal. (2) If signals are more than one, the method for eliminating gain errors is the same with the previous case, and then the phase errors are removed by the Hadamard product of the (cross) covariance matrix and its conjugate. After the errors are eliminated, the DOAs can be estimated by rotation invariant property and orthogonal joint diagonalization for the Hadamard product. This method requires neither calibrated sources nor multidimensional parameter search, and its performance is independent of the phase errors. Simulation results demonstrate the effectiveness of the proposed method.

1 Introduction

As an important branch of array signal processing, direction of arrival (DOA) estimation has attracted much attention since it is an important task that arises in many applications including radar, sonar, wireless communications, speech processing and navigation (Krim and Viberg 1996; Godara 1997). In the past decades, there have been many DOA estimation methods proposed such as MUSIC (Schmidt 1986), ESPRIT (Roy and Kailath 1989), Capon’s beamformer (1969), maximum likelihood (ML) method (Stoica and Sharman 1990) and so on. However, these methods are based on the assumption that the array steering vector is exactly known, which means that their performance is critically dependent on the knowledge of the array manifold. In practice, the array steering vector can not be obtained precisely owning to the presence of some uncertainties such as the mutual coupling, gain-phase errors and positions uncertainties (Ferréol et al. 2010). Therefore, it is necessary to calibrate array characteristics prior to carrying out DOA estimation.

The focus of this paper is on the problem of DOA estimation with unknown gain-phase errors. In recent years, this problem has been studied in numerous papers. Some robust methods proposed in Blunt et al. (2011), Stoica et al. (2005) and Li et al. (2003) are based on the knowledge of the statistics of the array model errors which is not easily available in practice, and the estimator’s capability is affected by errors.

Other methods proposed deal with the problem of array calibration by taking errors as array parameters. The methods in Cheng (2000) and Ng et al. (2009) exploit calibrated signals with known directions to estimate the sensor gain-phase errors, and they have excellent performance when the DOAs of calibrated signals are precisely known. However, it is difficult to implement them as the existence of the calibrated sources is rarely guaranteed in practice. In Weiss and Friedlander (1990), and Friedlander and Weiss (1993), the methods proposed by Weiss and Friedlander named as W–F method are based on alternative iteration algorithm, which can simultaneously estimate the DOAs of signals and the gain-phase error of each sensor on line. However they may suffer from suboptimal convergence because the DOAs and gain-phase errors are not independently identifiable and they are based on the assumption that the array perturbations are small, meaning that they may fail when the errors are large. The instrumental sensors method (ISM) was presented in Wang et al. (2003, 2004). The DOAs of signals and gain-phase errors can be obtained simultaneously without ambiguity by instrumental sensors which are with no gain-phase errors. The number of instrumental sensors, however, must be larger than that of signals, which is a great obstacle especially when the number of signals is large. The methods proposed in Paulraj and Kailath (1985) and Li et al. (2006) estimate the sensor gain-phase errors with the Toeplitz structure of the covariance matrix without calibrated signals or alternative iteration process; however, their performance is influenced by gain-phase errors. Liu et al. (2011) proposed a method based on Eigen-decomposition of a covariance matrix which is constructed by the dot product of the array output and its conjugate. This method has the advantage that DOA estimates are independent of phase errors, but it has four drawbacks: (a) the need for 2-D MUSIC search; (b) it can’t distinguish signals which are spatially close to each other; (c) too many demands for statistical characteristics of signals and noise; (d) the sources should be more than one.

Inspired by Liu et al. (2011) and aiming at the four problems mentioned above, we propose this novel method. The method can be decomposed into three steps. The first is to estimate and remove the gain errors using the diagonal of the covariance matrix of the array output. In the second step, the process can be discussed on two cases: (a) if the number of source is one, we rotate the array and estimate DOA with the relationship between signal subspace and steering vector of signal; (b) if the sources are more than one, the phase errors are eliminated by the Hadamard product of the (cross) covariance matrix and its conjugate whose gain errors have been removed in step one. And in this step, each element of the new matrix subtracts sum of squares of the power, which is estimated by the relationship between determinant and rank of matrix, to improve estimator’s resolution especially when signals are spatially close to each other. The last step is to estimate the DOAs with formulas from rotation invariant property and joint diagonalization algorithm for the whole array. From the second step it is seen that the proposed method also has the advantage that DOA estimates are independent of phase errors. In addition, it overcomes drawbacks (a)–(d) in Liu et al. (2011). First this method takes use of the covariance matrix and its conjugate to construct Hadamard product matrix, which means that statistics of real and imaginary parts of the signals or noise in Liu et al. (2011) are not required. Second, this method provides solution if the number of signal is one, which can’t be solved with the method in Liu et al. (2011). Third, this method exploits rotation invariant property between sub-arrays to replace 2-D MUSIC algorithm, so the computational complexity can be reduced obviously. Last the proposed method subtracts the 1 component which leads to a ridge near the diagonal line of the two-dimensional spectrum which makes the peaks of the spectrum deviate from their real locations or merge the peaks, so it means that the proposed method does not require the condition of two signals spatially far from each other and can improve estimate accuracy when the signals are close to each other. Simulation results demonstrate the effectiveness of the proposed method.

The paper is organized as follows. Section 2 describes the formulation of the problem. The proposed method is given in Sect. 3. In Sect. 4 some discussions are presented. Section 5 gives simulation results. Section 6 concludes this paper.

Throughout the paper, the mathematical notations are denoted as follows.

${\mathbf{I}}$ :

identity matrix;

${\mathbf{1}}$ :

one matrix(vector);

${\mathbf{0}}$ :

zero matrix(vector);

$^{\circ}$ :

Hadamard product;

$( \cdot )^{ * }$ :

conjugation;

$( \cdot )^{T}$ :

transpose;

$( \cdot )^{H}$ :

Hermitian transpose;

$( \cdot )^{ - 1}$ :

inversion;

$( \cdot )^{ + }$ :

pseudo inversion;

$\text{rank}( \cdot )$ :

rank;

$\angle ( \cdot )$ :

the phase of complex;

$\det ( \cdot )$ :

determinant;

$( \cdot )^{\left( p \right)}$ :

pth element of a vector;

$( \cdot )^{{\left( {p,q} \right)}}$ :

element of a matrix which is at the pth row and the qth column;

$( \cdot )^{{\left( {:,q} \right)}}$ :

qth column of a matrix;

$( \cdot )^{{\left( {p,:} \right)}}$ :

pth row of a matrix;

$\left[ \cdot \right]_{p \times q}$ :

a matrix(vector) with $p \times q$;

$\text{E}[ \cdot ]$ :

mathematical expectation;

$\text{diag}({\mathbf{u}})$ :

a diagonal matrix whose diagonals are the elements of vector ${\mathbf{u}}$;

$\text{diag}({\mathbf{M}})$ :

a vector constructed by diagonals of matrix ${\mathbf{M}}$.

2 Problem formulation

Before presenting the data model and the proposed method, we introduce some assumptions about the properties of the signals and noise, and the proposed method is based on these assumptions.

Assumption 1

The signals are zero-mean, stationary and unrelated.

Assumption 2

The signals are independent of the noise, and the noise is zero-mean, stationary and spatially white.

Assumption 3

All the signals come from different directions.

With these assumptions, the data model is presented as follows.

Consider K narrowband far-field signals $s_{k} (t)$ ($k = 1,2, \ldots ,K$) with wavelength $\lambda$ impinging on a double L-shaped array with 2M (M  = 2N − 3) Omni-directional sensors, and the array is shown as Fig. 1. The array can be divided into three sub-arrays X, Y and Z, and each sub-array is an L-shaped array whose elements are located along x and y axes (direction). The numbers of sensors of all sub-arrays along x and y axes (direction) are equal to N-1, and the inter-sensor intervals of sub-array along x axis (direction) and y axis (direction) are denoted by $d_{x}$ and $d_{y}$ respectively. For simplicity we assume that the signal sources and the array sensors are coplanar, and the DOA of the kth signal is denoted by $\theta_{k} \in \left( {{{ - \uppi } \mathord{\left/ {\vphantom {{ - \uppi } {2,{\uppi \mathord{\left/ {\vphantom {\uppi 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {2,{\uppi \mathord{\left/ {\vphantom {\uppi 2}} \right. \kern-0pt} 2}}}} \right)$. With the origin element as reference, the outputs of sub-array X, Y and Z can be written as

$$ {\mathbf{X}}(t) = \sum\limits_{k = 1}^{K} {\varvec{\upalpha}} (\theta_{k} )s_{k} (t) + {\mathbf{n}}_{X} (t) = {\mathbf{A}}({\varvec{\uptheta}}){\mathbf{S}}(t) + {\mathbf{n}}_{X} (t) $$

(1)

$$ \begin{aligned} {\mathbf{Y}}(t) & = \sum\limits_{k = 1}^{K} {e^{{ - j\frac{{2\uppi d_{y} \cos \theta_{k} }}{\lambda }}} {\varvec{\upalpha}}} (\theta_{k} )s_{k} (t) + {\mathbf{n}}_{Y} (t) \\ & = {\mathbf{A}}({\varvec{\uptheta}}){\varvec{\Phi}}({\varvec{\uptheta}}){\mathbf{S}}(t) + {\mathbf{n}}_{Y} (t) \\ \end{aligned} $$

(2)

$$ \begin{aligned} {\mathbf{Z}}(t) & = \sum\limits_{k = 1}^{K} {e^{{ - j\frac{{2\uppi d_{x} \sin \theta_{k} }}{\lambda }}} {\varvec{\upalpha}}} (\theta_{k} )s_{k} (t) + {\mathbf{n}}_{Z} (t) \\ & = {\mathbf{A}}({\varvec{\uptheta}}){\varvec{\Omega}}({\varvec{\uptheta}}){\mathbf{S}}(t) + {\mathbf{n}}_{Z} (t) \\ \end{aligned} $$

(3)

where ${\mathbf{n}}_{i} (t)$ ($i = X,Y,Z$) denotes the vector of additive noise, and ${\varvec{\upalpha}}(\theta_{k} )$ represents the ideal steering vector for the kth signal, described by

$$ \begin{aligned} {\varvec{\upalpha}}(\theta_{k} ) = & \bigg[e^{{ - j\frac{{2\uppi (N - 2 )d_{x} \sin \theta_{k} }}{\lambda }}} ,e^{{ - j\frac{{2\uppi (N - 3 )d_{x} \sin \theta_{k} }}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{x} \sin \theta_{k} }}{\lambda }}} ,1, \\ & e^{{ - j\frac{{2\uppi d_{y} \cos \theta_{k} }}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi (N - 3 )d_{y} \cos \theta_{k} }}{\lambda }}} ,e^{{ - j\frac{{2\uppi (N - 2 )d_{y} \cos \theta_{k} }}{\lambda }}} \bigg]^{T} \\ \end{aligned} $$

(4)

where ${\mathbf{A}}({\varvec{\uptheta}})$ is the ideal steering matrix, constructed by ${\varvec{\upalpha}}(\theta_{k} )$ as

$$ {\mathbf{A}}({\varvec{\uptheta}}) = \left[ {{\varvec{\upalpha}}(\theta_{1} ),{\varvec{\upalpha}}(\theta_{2} ), \ldots ,{\varvec{\upalpha}}(\theta_{k} ), \ldots ,{\varvec{\upalpha}}(\theta_{K} )} \right] $$

(5)

and the kth element of ${\mathbf{S}}(t)$ is $s_{k} (t)$;

Fig. 1

Double L-shaped array configuration

where ${\varvec{\Phi}}({\varvec{\uptheta}})$ and ${\varvec{\Omega}}({\varvec{\uptheta}})$ denote rotation invariant factors along y and x axes respectively, which can be described as

$$ {\varvec{\Phi}}({\varvec{\uptheta}}) = \text{diag}\left( {\left[ {e^{{ - j\frac{{2\uppi d_{y} \cos \theta_{1} }}{\lambda }}} ,e^{{ - j\frac{{2\uppi d_{y} \cos \theta_{2} }}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{y} \cos \theta_{K} }}{\lambda }}} } \right]^{T} } \right) $$

(6)

$$ {\varvec{\Omega}}({\varvec{\uptheta}}) = \text{diag}\left( {\left[ {e^{{ - j\frac{{2\uppi d_{x} \sin \theta_{1} }}{\lambda }}} ,e^{{ - j\frac{{2\uppi d_{x} \sin \theta_{2} }}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{x} \sin \theta_{K} }}{\lambda }}} } \right]^{T} } \right) $$

(7)

Remark 1

The reasons for choosing this array configuration are: (a) the array consists of three sub-arrays with the same configuration as the proposed method takes use of rotation invariant method; (b) the shared elements between sub-arrays are the most, meaning that this configuration employs the least sensors (cross array can also meet this requirement; however, DOA should satisfy the conditions in the proposed method for cross array:

$$ \begin{aligned} & \cos \alpha_{i} - \cos \alpha_{l} \ne \cos \alpha_{m} - \cos \alpha_{n} \quad \left( {i \ne l \ne m \ne n} \right) \\ & \sin \alpha_{i} - \sin \alpha_{l} \ne \sin \alpha_{m} - \sin \alpha_{n} \quad \left( {i \ne l \ne m \ne n} \right) \\ & \cos \alpha_{l} \ne \cos \alpha_{n} \quad \left( {l \ne n} \right) \\ \end{aligned} $$

which are difficult to satisfy in practice).

When $d_{x}$ and $d_{y}$ are less than half of wavelength $\lambda$, the steering vector is different from each other due to Assumption 3. It means that type I ambiguity (Schmidt 1986) can’t occur so long as the requirements for $d_{x}$ and $d_{y}$ are satisfied, which can be seen clearly.

Assumption 4

If each steering vector is different from others in a steering matrix, and the rank of steering matrix is equal to the number of steering vectors under the condition that sensors are not less than sources, this steering matrix can be defined as unambiguity steering matrix. In this paper, ${\mathbf{A}}({\varvec{\uptheta}})$ is assumed to be the unambiguity steering matrix.

Remark 2

The case that steering matrix should be an unambiguity steering matrix is necessary for all the subspace-based methods. In the case of a uniform linear array, if signals come from different directions the steering matrix must be an unambiguity steering matrix; however in the case of an array of other shape, it is not easy to give the requirements for DOAs to make steering matrix unambiguous (Sylvie et al. 1995). It is still an open question which is not the focus of this paper.

The data models (1)–(3) are without gain-phase errors. Taking the gain-phase errors into account, the models should be modified as

$$ {\mathbf{X}}(t) = {\mathbf{G}}_{X} {\varvec{\Psi}}_{X} {\mathbf{A}}({\varvec{\uptheta}}){\mathbf{S}}(t) + {\mathbf{n}}_{X} (t) $$

(8)

$$ {\mathbf{Y}}(t)\; = {\mathbf{G}}_{Y} {\varvec{\Psi}}_{Y} {\mathbf{A}}({\varvec{\uptheta}}){\varvec{\Phi}}({\varvec{\uptheta}}){\mathbf{S}}(t) + {\mathbf{n}}_{Y} (t) $$

(9)

$$ {\mathbf{Z}}(t)\; = {\mathbf{G}}_{Z} {\varvec{\Psi}}_{Z} {\mathbf{A}}({\varvec{\uptheta}}){\varvec{\Omega}}({\varvec{\uptheta}}){\mathbf{S}}(t) + {\mathbf{n}}_{Z} (t) $$

(10)

where diagonal matrices ${\mathbf{G}}_{i}$ and ${\varvec{\Psi}}_{i}$ ($i = X,Y,Z$) denote gain error matrix and phase error matrix respectively, and without loss of generality we assume that the reference element is without gain or phase errors.

Thus, the problem addressed here is to simultaneously estimate the DOA and array gain-phase errors using the array outputs ${\mathbf{X}}(t)$, ${\mathbf{Y}}(t)\;$ and ${\mathbf{Z}}(t)\;$. Based on the modified models, the proposed method is introduced as follows.

3 The proposed method

3.1 Estimate and remove gain errors

In the following, for simplicity the time variable is omitted. Based on the data models and the assumptions on the properties of the signals and noise, the covariance matrix of each sub-array output can be written as

$$ {\mathbf{R}}_{i} = {\mathbf{G}}_{i} {\varvec{\Psi}}_{i} {\mathbf{A}}({\varvec{\uptheta}}){\mathbf{R}}_{S} {\mathbf{A}}^{H} ({\varvec{\uptheta}}){\varvec{\Psi}}_{i}^{H} {\mathbf{G}}_{i}^{H} + \sigma_{n}^{2} {\mathbf{I}}\quad \left( {i = X,Y,Z} \right) $$

(11)

where ${\mathbf{R}}_{S} = \text{E}\left[ {{\mathbf{SS}}^{H} } \right] = \text{diag}\left( {\left[ {\sigma_{1}^{2} ,\sigma_{2}^{2} , \cdots ,\sigma_{K}^{2} } \right]^{T} } \right)$ is covariance matrix of power of the signal, and $\sigma_{n}^{2}$ denotes the power of noise.

Decompose ${\mathbf{R}}_{i}$ and we have

$$ {\mathbf{R}}_{i} = \sum\limits_{m = 1}^{M} {{\varvec{\upgamma}}_{i}^{(m)} } {\mathbf{U}}_{i}^{(:,m)} \left( {{\mathbf{U}}_{i}^{(:,m)} } \right)^{H} $$

(12)

where ${\varvec{\upgamma}}_{i}$ for ${\mathbf{R}}_{i}$ represents Eigen-value vector in which Eigen-values are arranged in descending order, and ${\mathbf{U}}_{i}$ denotes Eigen-matrix whose column vectors are Eigen-vectors corresponding to the elements in ${\varvec{\upgamma}}_{i}$.

With the relationship between the diagonal elements of ${\mathbf{R}}_{i}$ and ${\mathbf{G}}_{i}$, it is easy to estimate the gain errors as

$$ {\hat{\mathbf{G}}}_{i}^{(m,m)} = \sqrt {\frac{{{\mathbf{R}}_{i}^{(m,m)} - \hat{\sigma }_{n}^{2} }}{{{\mathbf{R}}_{X}^{(N - 1,N - 1)} - \hat{\sigma }_{n}^{2} }}} $$

(13)

where $\hat{\sigma }_{n}^{2}$ as the estimation of $\sigma_{n}^{2}$ can be given by

$$ \hat{\sigma }_{n}^{2} = \frac{1}{M - K}\sum\limits_{m = K + 1}^{M} {{\varvec{\upgamma}}_{i}^{(m)} } $$

(14)

The gain error estimated by (13) is independent of phase errors and it is proved in Liu et al. (2011).

3.2 Estimate DOA

3.2.1 When K = 1

With the estimation of gain error matrix ${\hat{\mathbf{G}}}_{i}$, the covariance matrix can be compensated as

$$ {\bar{\mathbf{R}}}_{i} (\theta ) = {\hat{\mathbf{G}}}_{i}^{ - 1} \left( {{\mathbf{R}}_{i} (\theta ) - \hat{\sigma }_{n}^{2} {\mathbf{I}}} \right)\left( {{\hat{\mathbf{G}}}_{i}^{ - 1} } \right)^{H} = \sigma^{2} {\varvec{\Psi}}_{i} {\varvec{\upalpha}}(\theta ){\varvec{\upalpha}}^{H} (\theta ){\varvec{\Psi}}_{i}^{H} $$

(15)

Decomposing ${\bar{\mathbf{R}}}_{i} (\theta )$, we can obtain

$$ {\bar{\mathbf{R}}}_{i} (\theta ) = \bar{\gamma }_{i} (\theta ){\bar{\mathbf{u}}}_{i} (\theta ){\bar{\mathbf{u}}}_{i}^{H} (\theta ) $$

(16)

Owning to the relationship between the signal subspace and the steering vector, it can be seen that

$$ \xi_{i} (\theta ){\varvec{\Psi}}_{i} {\varvec{\upalpha}}(\theta ) = {\bar{\mathbf{u}}}_{i} (\theta ) $$

(17)

where $\xi_{i} (\theta ) = {\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta )$.

Then rotating the whole array around origin by an unknown angle $\Delta \theta$, we have the new covariance matrix ${\bar{\mathbf{R}}}_{i} (\theta + \Delta \theta )$. Similar to (15)–(17), an expression for $\theta + \Delta \theta$ is given as

$$ \xi_{i} (\theta + \Delta \theta ){\varvec{\Psi}}_{i} {\varvec{\upalpha}}(\theta + \Delta \theta ) = {\bar{\mathbf{u}}}_{i} (\theta + \Delta \theta ) $$

(18)

With (17) and (18), it is easy to note that

$$ \begin{aligned} \left( {{\varvec{\Psi}}_{i} {\varvec{\upalpha}}(\theta )} \right) \circ \left( {{\varvec{\Psi}}_{i} {\varvec{\upalpha}}(\theta + \Delta \theta )} \right)^{*} & = {\varvec{\upalpha}}(\theta ) \circ {\varvec{\upalpha}}^{ * } (\theta + \Delta \theta ) \hfill \\ & = \left( {\frac{{{\bar{\mathbf{u}}}_{i} (\theta )}}{{\xi_{i} (\theta )}}} \right) \circ \left( {\frac{{{\bar{\mathbf{u}}}_{i} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)^{*} \end{aligned} $$

(19)

Expanding (19), we have

$$ e^{{ - j\frac{{2\uppi (N - m - 1 )d_{x} (\sin \theta - \sin (\theta + \Delta \theta ))}}{\lambda }}} = {{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(m)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(m)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(m)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)^{{}} }}} \right. \kern-0pt} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(m)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)^{{}} }} $$

(20)

$$ e^{{ - j\frac{{2\uppi md_{y} (\cos \theta - \cos (\theta + \Delta \theta ))}}{\lambda }}} = {{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N + m - 1)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N + m - 1)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N + m - 1)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)}}} \right. \kern-0pt} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N + m - 1)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)}} $$

(21)

$$ \left( {m = 1,2, \ldots ,N - 2} \right) $$

Property

Define a new steering vector ${\varvec{\upgamma}}(\theta_{i} ,\theta_{j} )$ as ${\varvec{\upgamma}}(\theta_{i} ,\theta_{j} ) = {\varvec{\upalpha}}(\theta_{i} ) \circ {\varvec{\upalpha}}^{ * } (\theta_{j} )$ ($\theta_{i} \ne \theta_{j}$). If $d_{x}$ and $d_{y}$ are less than $\lambda /4$ and $\lambda /2$ respectively, type I ambiguity can’t occur. In other words, there exist no DOA pairs $(\theta_{k} ,\theta_{l} ) \ne (\theta_{i} ,\theta_{j} )$ ($\theta_{i} \ne \theta_{j}$, $\theta_{k} \ne \theta_{l}$) which can make ${\varvec{\upgamma}}(\theta_{i} ,\theta_{j} ) = {\varvec{\upgamma}}(\theta_{k} ,\theta_{l} )$.

The proof of property is given in “Appendix A”.

According to the property, we assume that $d_{x}$ is less than $\lambda /4$ and $d_{y}$ is less than $\lambda /2$, and DOA can be estimated from:

$$ \sin (\theta + \Delta \theta ) - \sin \theta = \frac{{\lambda \cdot \angle \left\{ {{{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)}}} \right. \kern-0pt} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)}}} \right\}}}{{2\uppi d_{x} }} $$

(22)

$$ \cos (\theta + \Delta \theta ) - \cos \theta = \frac{{\lambda \cdot \angle \left\{ {{{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)}}} \right. \kern-0pt} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)}}} \right\}}}{{2\uppi d_{y} }} $$

(23)

The analytical solution of $\theta$ and $\Delta \theta$ can be obtained from the proof of property in “Appendix A”, which is omitted here.

The DOA estimation $\hat{\theta }$ is independent of phase errors, which is proved in “Appendix B”.

3.2.2 When K > 1

In order to take advantage of rotation invariant property, the cross covariance matrices between sub-arrays X and Y, X and Z are required and denoted by ${\mathbf{R}}_{YX}$ and ${\mathbf{R}}_{ZX}$:

$$ {\mathbf{R}}_{YX} = \text{E}\left[ {{\mathbf{YX}}^{H} } \right]^{{}} = {\mathbf{G}}_{Y} {\varvec{\Psi}}_{Y} {\mathbf{A}}({\varvec{\uptheta}}){\varvec{\Phi}}({\varvec{\uptheta}}){\mathbf{R}}_{S} {\mathbf{A}}^{H} ({\varvec{\uptheta}}){\varvec{\Psi}}_{X}^{H} {\mathbf{G}}_{X}^{H} + \sigma_{n}^{2} {\varvec{\Sigma}} $$

(24)

$$ {\mathbf{R}}_{ZX} = \text{E}\left[ {{\mathbf{ZX}}^{H} } \right]^{{}} = {\mathbf{G}}_{Z} {\varvec{\Psi}}_{Z} {\mathbf{A}}({\varvec{\uptheta}}){\varvec{\Omega}}({\varvec{\uptheta}}){\mathbf{R}}_{S} {\mathbf{A}}^{H} ({\varvec{\uptheta}}){\varvec{\Psi}}_{X}^{H} {\mathbf{G}}_{X}^{H} + \sigma_{n}^{2} {\varvec{\Gamma}} $$

(25)

where

$$ \begin{aligned} {\varvec{\Sigma}} & = \left[ {\begin{array}{*{20}c} {{\mathbf{0}}_{(N - 2) \times (N - 2)} } & {{\mathbf{0}}_{(N - 2) \times (N - 1)} } \\ {{\mathbf{0}}_{(N - 1) \times (N - 2)} } & {{\mathbf{J}}_{(N - 1) \times (N - 1)} } \\ \end{array} } \right]\quad {\varvec{\Gamma}} = \left[ {\begin{array}{*{20}c} {{\mathbf{L}}_{(N - 1) \times (N - 1)} } & {{\mathbf{0}}_{(N - 1) \times (N - 2)} } \\ {{\mathbf{0}}_{(N - 2) \times (N - 1)} } & {{\mathbf{0}}_{(N - 2) \times (N - 2)} } \\ \end{array} } \right] \\ {\mathbf{J}} & = \left[ {\begin{array}{*{20}c} 0 & 1 & 0 & \cdots & 0 \\ 0 & 0 & 1 & \ddots & \vdots \\ 0 & 0 & \ddots & \ddots & 0 \\ \vdots & \ddots & \ddots & \ddots & 1 \\ 0 & \cdots & \cdots & 0 & 0 \\ \end{array} } \right]\quad {\mathbf{L}} = \left[ {\begin{array}{*{20}c} 0 & 0 & 0 & \cdots & 0 \\ 1 & 0 & 0 & \ddots & \vdots \\ 0 & 1 & \ddots & \ddots & 0 \\ \vdots & \ddots & \ddots & \ddots & 0 \\ 0 & \cdots & \cdots & 1 & 0 \\ \end{array} } \right] \\ \end{aligned} $$

As the gain error and noise have been estimated in step A, the cross covariance matrices can be compensated as

$$ \begin{aligned} {\bar{\mathbf{R}}}_{YX} ({\varvec{\uptheta}}) &= {\hat{\mathbf{G}}}_{Y}^{ - 1} \left( {{\mathbf{R}}_{YX} ({\varvec{\uptheta}}) - \hat{\sigma }_{n}^{2} {\varvec{\Sigma}}} \right)\left( {{\hat{\mathbf{G}}}_{X}^{ - 1} } \right)^{H} \hfill \\ &= {\varvec{\Psi}}_{Y} {\mathbf{A}}({\varvec{\uptheta}}){\varvec{\Phi}}({\varvec{\uptheta}}){\mathbf{R}}_{S} {\mathbf{A}}^{H} ({\varvec{\uptheta}}){\varvec{\Psi}}_{X}^{H} \hfill \\ \end{aligned} $$

(26)

$$ \begin{aligned} {\bar{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}}) &= {\hat{\mathbf{G}}}_{Z}^{ - 1} \left( {{\mathbf{R}}_{ZX} ({\varvec{\uptheta}}) - \hat{\sigma }_{n}^{2} {\varvec{\Gamma}}} \right)\left( {{\hat{\mathbf{G}}}_{X}^{ - 1} } \right)^{H} \hfill \\ & = {\varvec{\Psi}}_{Z} {\mathbf{A}}({\varvec{\uptheta}}){\varvec{\Omega}}({\varvec{\uptheta}}){\mathbf{R}}_{S} {\mathbf{A}}^{H} ({\varvec{\uptheta}}){\varvec{\Psi}}_{X}^{H} \hfill \\ \end{aligned} $$

(27)

Similarly, the covariance matrix of sub-array X with gain errors and noise eliminated can be written as

$$ {\bar{\mathbf{R}}}_{X} ({\varvec{\uptheta}}) = {\hat{\mathbf{G}}}_{X}^{ - 1} \left( {{\mathbf{R}}_{X} ({\varvec{\uptheta}}) - \hat{\sigma }_{n}^{2} {\mathbf{I}}} \right)\left( {{\hat{\mathbf{G}}}_{X}^{ - 1} } \right)^{H} = {\varvec{\Psi}}_{X} {\mathbf{A}}({\varvec{\uptheta}}){\mathbf{R}}_{S} {\mathbf{A}}^{H} ({\varvec{\uptheta}}){\varvec{\Psi}}_{X}^{H} $$

(28)

As the gain errors have been removed, the following task is to eliminate the phase errors. It is noted that the phase errors are unit complex and they exist only in the phase of ${\bar{\mathbf{R}}}_{YX}$ (${\bar{\mathbf{R}}}_{ZX}$,${\bar{\mathbf{R}}}_{X}$), so Hadamard product of the (cross) covariance matrix and its conjugate is considered to remove the phase errors.

Define Hadamard product matrix ${\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}})$ as

$$ {\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}}) = {\bar{\mathbf{R}}}_{YX} ({\varvec{\uptheta}}) \circ {\bar{\mathbf{R}}}_{YX}^{ * } ({\varvec{\uptheta}}) $$

(29)

Based on (26), we have

$$ {\bar{\mathbf{R}}}_{YX}^{(p,q)} ({\varvec{\uptheta}}) = \frac{{{\varvec{\Psi}}_{Y}^{(p,p)} }}{{{\varvec{\Psi}}_{X}^{(q,q)} }}\sum\limits_{k = 1}^{K} {e^{{ - j\frac{{2\uppi d_{y} \cos \theta_{k} }}{\lambda }}} {\varvec{\upalpha}}^{(p)} } (\theta_{k} )\left( {{\varvec{\upalpha}}^{(q)} (\theta_{k} )} \right)^{ * } \sigma_{k}^{2} $$

(30)

Then the element of ${\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}})$ can be written as

$$ \begin{aligned} {\tilde{\mathbf{R}}}_{YX}^{(p,q)} ({\varvec{\uptheta}}) & = {\bar{\mathbf{R}}}_{YX}^{(p,q)} ({\varvec{\uptheta}}) \cdot \left( {{\bar{\mathbf{R}}}_{YX}^{(p,q)} ({\varvec{\uptheta}})} \right)^{ * } \\ & = \left( {\sum\limits_{k = 1}^{K} {e^{{ - j\frac{{2\uppi d_{y} \cos \theta_{k} }}{\lambda }}} {\varvec{\upalpha}}^{(p)} } (\theta_{k} )\left( {{\varvec{\upalpha}}^{(q)} (\theta_{k} )} \right)^{ * } \sigma_{k}^{2} } \right)\left( {\sum\limits_{k = 1}^{K} {e^{{ - j\frac{{2\uppi d_{y} \cos \theta_{k} }}{\lambda }}} {\varvec{\upalpha}}^{(p)} } (\theta_{k} )\left( {{\varvec{\upalpha}}^{(q)} (\theta_{k} )} \right)^{ * } \sigma_{k}^{2} } \right)^{ * } \\ & = \sum\limits_{k2 = 1}^{K} {\sum\limits_{k1 = 1}^{K} {{\varvec{\upalpha}}^{(p)} (\theta_{k1} )\left( {{\varvec{\upalpha}}^{(p)} (\theta_{k2} )} \right)^{ * } } } \left( {{\varvec{\upalpha}}^{(q)} (\theta_{k1} )\left( {{\varvec{\upalpha}}^{(q)} (\theta_{k2} )} \right)^{ * } } \right)^{ * } e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{k1} - \cos \theta_{k2} )}}{\lambda }}} \sigma_{k1}^{2} \sigma_{k2}^{2} \\ & = \sum\limits_{k2 = 1}^{K} {\sum\limits_{k1 = 1}^{K} {{\varvec{\upgamma}}^{(p)} (\theta_{k1} ,\theta_{k2} )} } \left( {{\varvec{\upgamma}}^{(q)} (\theta_{k1} ,\theta_{k2} )} \right)^{ * } e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{k1} - \cos \theta_{k2} )}}{\lambda }}} \sigma_{k1}^{2} \sigma_{k2}^{2} \\ \end{aligned} $$

(31)

So ${\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}})$ can be represented as

$$ \begin{aligned} {\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}}) & = \sum\limits_{k2 = 1}^{K} {\sum\limits_{k1 = 1}^{K} {{\varvec{\upgamma}}(\theta_{k1} ,\theta_{k2} ){\varvec{\upgamma}}^{H} (\theta_{k1} ,\theta_{k2} )} } e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{k1} - \cos \theta_{k2} )}}{\lambda }}} \sigma_{k1}^{2} \sigma_{k2}^{2} \\ & = \sum\limits_{k2 = 1}^{K} {\sum\limits_{\begin{subarray}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} k1 = 1 \\ k1 \ne k2 \end{subarray} }^{K} {{\varvec{\upgamma}}(\theta_{k1} ,\theta_{k2} ){\varvec{\upgamma}}^{H} (\theta_{k1} ,\theta_{k2} )} } e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{k1} - \cos \theta_{k2} )}}{\lambda }}} \sigma_{k1}^{2} \sigma_{k2}^{2} + \sum\limits_{k = 1}^{K} {\sigma_{k}^{4} } {\mathbf{1}}_{M \times 1} {\mathbf{1}}^{T}_{M \times 1} \\ & = {\varvec{\Xi}^{\prime}}({\varvec{\uptheta}}){\tilde{\boldsymbol{\Phi}}}({\varvec{\uptheta}}){\tilde{\mathbf{R}}}_{S} {\boldsymbol{\Xi}^{\prime}}^{H} ({\varvec{\uptheta}}) \\ \end{aligned} $$

(32)

where

$$ \begin{aligned} & {\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}}) = \left[ {{\varvec{\upgamma}}(\theta_{1} ,\theta_{2} ),{\varvec{\upgamma}}(\theta_{1} ,\theta_{3} ), \ldots ,{\varvec{\upgamma}}(\theta_{k1} ,\theta_{k2} ), \ldots ,{\varvec{\upgamma}}(\theta_{K} ,\theta_{K - 1} ),{\mathbf{1}}_{M \times 1} } \right] \\ & {\tilde{\mathbf{R}}}_{S} = \text{diag}\left( {\left[ {\sigma_{1}^{2} \sigma_{2}^{2} ,\sigma_{1}^{2} \sigma_{3}^{2} , \ldots ,\sigma_{k1}^{2} \sigma_{k2}^{2} , \ldots ,\sigma_{K}^{2} \sigma_{K - 1}^{2} ,\sum\limits_{k = 1}^{K} {\sigma_{k}^{4} } } \right]^{T} } \right) \\ & {\tilde{\varvec{\Phi}}}({\varvec{\uptheta}}) = \text{diag}\left( {\left[ {e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{1} - \cos \theta_{2} )}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{k1} - \cos \theta_{k2} )}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{K} - \cos \theta_{K - 1} )}}{\lambda }}} ,1} \right]^{T} } \right). \\ \end{aligned} $$

In the same way, Hadamard product matrix ${\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}})$ and ${\tilde{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}})$ can be expressed as

$$ {\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}}) = {\bar{\mathbf{R}}}_{X} ({\varvec{\uptheta}}) \circ {\bar{\mathbf{R}}}_{X}^{ * } ({\varvec{\uptheta}}) = {\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}}){\tilde{\mathbf{R}}}_{S} {\boldsymbol{\Xi}^{\prime}}^{H} ({\varvec{\uptheta}}) $$

(33)

$$ {\tilde{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}}) = {\bar{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}}) \circ {\bar{\mathbf{R}}}_{ZX}^{ * } ({\varvec{\uptheta}}) = {\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}}){\tilde{\boldsymbol{\Omega}}}({\varvec{\uptheta}}){\tilde{\mathbf{R}}}_{S} {\boldsymbol{\Xi}^{\prime}}^{H} ({\varvec{\uptheta}}) $$

(34)

where

$$ {\tilde{\boldsymbol{\Omega}}}({\varvec{\uptheta}}) = \text{diag}\left( {\left[ {e^{{ - j\frac{{2\uppi d_{x} (\sin \theta_{1} - \sin \theta_{2} )}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{x} (\sin \theta_{k1} - \sin \theta_{k2} )}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{x} (\sin \theta_{K} - \sin \theta_{K - 1} )}}{\lambda }}} ,1} \right]^{T} } \right). $$

Assumption 5

The new steering matrix ${\varvec{\Xi}}({\varvec{\uptheta}})$ constructed by ${\varvec{\upgamma}}(\theta_{i} ,\theta_{j} )$ is assumed to be the unambiguity steering matrix, which should be also satisfied in Liu et al. (2011); however the author doesn’t mention it. ${\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}})$ can be seen as a particular ${\varvec{\Xi}}({\varvec{\uptheta}})$, so based on this assumption it is also an unambiguity steering matrix.

Remark 3

The number of sensors of sub-array should be larger than $K(K - 1) + 1$ at least; in order to estimate DOAs unambiguously, $d_{x}$ is less than $\lambda /4$ and $d_{y}$ is less than $\lambda /2$ (sufficient conditions for estimating DOAs unambiguously), which should be noticed in this paper.

On condition that $d_{x}$ is less than $\lambda /4$ and $d_{y}$ is less than $\lambda /2$ (each steering vector is different from others in ${\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}})$), and $K(K - 1) + 1 \le M$ (${\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}})$ is a thin matrix), based on Assumption 5 the rank of ${\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}})$ must be equal to the number of columns of ${\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}})$, which indicates that subspace method can be used to estimate DOAs. Unfortunately, the vector ${\mathbf{1}}_{M \times 1}$ may dominate in the column space of ${\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}})$ (${\tilde{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}})$,${\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}})$) as its weight is much larger than others. In other words, it can be regarded as a strong interference signal from a common DOA. Especially when $\theta_{k1}$ is spatially close to $\theta_{k2}$, ${\varvec{\upgamma}}(\theta_{k1} ,\theta_{k2} ) \approx {\mathbf{1}}$ and it is difficult to distinguish $\theta_{k1}$ and $\theta_{k2}$ (Liu et al. 2011). So it is necessary to eliminate the effect of ${\mathbf{1}}_{M \times 1}$, and then the problem can be transformed to estimate $\sum\nolimits_{k = 1}^{K} {\sigma_{k}^{4} }$.

Based on the property of ${\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}})$, we extract the middle $K(K - 1) + 1$ rows from ${\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}})$ to construct the new steering matrix ${\tilde{\boldsymbol{\Xi}^{\prime}}}({\varvec{\uptheta}})$ (it can be seen as ${\boldsymbol{\Xi}^{\prime}}({\varvec{\uptheta}})$ with corresponding sensors as many as sources), and it is noted that square matrix ${\tilde{\boldsymbol{\Xi}^{\prime}}}({\varvec{\uptheta}})$ is full rank. So the rank of corresponding Hadamard product matrix ${\tilde{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}}) = {\tilde{\boldsymbol{\Xi}^{\prime}}}({\varvec{\uptheta}}){\tilde{\boldsymbol{\Phi}}}({\varvec{\uptheta}}){\tilde{\mathbf{R}}}_{S} {\tilde{\boldsymbol{\Xi}^{\prime}}}^{H} ({\varvec{\uptheta}})$ is full (we extract the middle $K(K - 1) + 1$ rows and the middle $K(K - 1) + 1$ columns from ${\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}})$ to construct ${\tilde{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}})$), as ${\tilde{\boldsymbol{\Xi}^{\prime}}}({\varvec{\uptheta}})$,${\tilde{\mathbf{R}}}_{S}$ and ${\tilde{\boldsymbol{\Phi}}}({\varvec{\uptheta}})$ are all non-singular.

Now define

$$ {\hat{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}}) = {\tilde{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}}) - \kappa {\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} {\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} $$

(35)

From (35) we note that, in general, if and only if $\kappa = \sum\nolimits_{k = 1}^{K} {\sigma_{k}^{4} }$,

$$ \text{rank}\left( {{\hat{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}})} \right) = K(K - 1) < \text{rank}\left( {{\tilde{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}})} \right) = K(K - 1) + 1 $$

(36)

which means that

$$ \det \left( {{\hat{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}})} \right) = 0 $$

(37)

Combining (35) with (37), we have

$$ \begin{aligned} & \det \left( {{\tilde{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}}) - \kappa {\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} {\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } \right) \\ & \quad = \det ({\tilde{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}})) \cdot \det \left( {{\mathbf{I}} - \kappa {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} {\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } \right) \\ & \quad = 0 \\ \end{aligned} $$

(38)

As ${\tilde{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}})$ is non-singular, the determinant of ${\tilde{\tilde{\mathbf{R}}}}_{YX} ({\varvec{\uptheta}})$ can not be zero. Therefore, it is obvious that

$$ \begin{aligned} & \det \left( {{\mathbf{I}} - \kappa {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} {\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } \right) \\ & \quad = \det \left( {\left[ {\begin{array}{*{20}c} {{\mathbf{I}} - \kappa {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} {\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } & {\kappa {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } \\ {{\mathbf{0}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } & 1 \\ \end{array} } \right]} \right) \\ & \quad = \det \left( {\left[ {\begin{array}{*{20}c} {\mathbf{I}} & {\kappa {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } \\ {{\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } & 1 \\ \end{array} } \right]} \right) \\ & \quad = \det \left( {\left[ {\begin{array}{*{20}c} {\mathbf{I}} & {\kappa {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } \\ {{\mathbf{0}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } & {1 - \kappa {\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} } \\ \end{array} } \right]} \right) \\ & \quad = 1 - \kappa {\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} \\ & \quad = 0 \\ \end{aligned} $$

(39)

So (39) has the analytical solution $\kappa$ as

$$ \kappa = \frac{1}{{{\mathbf{1}}^{T}_{{\left[ {K(K - 1) + 1} \right] \times 1}} {\tilde{\tilde{\mathbf{R}}}}_{YX}^{ - 1} ({\varvec{\uptheta}}){\mathbf{1}}_{{\left[ {K(K - 1) + 1} \right] \times 1}} }} $$

(40)

Cao and Ye (2013) has also presented a method to estimate $\sum\nolimits_{k = 1}^{K} {\sigma_{k}^{4} }$. However, the method in Cao and Ye (2013) is based on Eigen-decomposition, and it has no closed form solution. The comparisons are given in Sect. 4.

With 1 component being subtracted, the Hadamard product matrices can be modified as

$$ {\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}}) = \sum\limits_{k2 = 1}^{K} {\sum\limits_{\begin{subarray}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} k1 = 1 \\ k1 \ne k2 \end{subarray} }^{K} {{\varvec{\upgamma}}(\theta_{k1} ,\theta_{k2} ){\varvec{\upgamma}}^{H} (\theta_{k1} ,\theta_{k2} )} } \sigma_{k1}^{2} \sigma_{k2}^{2} = {\varvec{\Xi}}({\varvec{\uptheta}}){\tilde{\mathbf{R}^{\prime}}}_{S} {\varvec{\Xi}}^{H} ({\varvec{\uptheta}}) $$

(41)

$$ \begin{aligned} {\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}}) & = \sum\limits_{k2 = 1}^{K} {\sum\limits_{\begin{subarray}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} k1 = 1 \\ k1 \ne k2 \end{subarray} }^{K} {{\varvec{\upgamma}}(\theta_{k1} ,\theta_{k2} ){\varvec{\upgamma}}^{H} (\theta_{k1} ,\theta_{k2} )} } e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{k1} - \cos \theta_{k2} )}}{\lambda }}} \sigma_{k1}^{2} \sigma_{k2}^{2} \\ & = {\varvec{\Xi}}({\varvec{\uptheta}}){\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}}){\tilde{\mathbf{R}^{\prime}}}_{S} {\varvec{\Xi}}^{H} ({\varvec{\uptheta}}) \\ \end{aligned} $$

(42)

$$ \begin{aligned} {\tilde{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}}) & = \sum\limits_{k2 = 1}^{K} {\sum\limits_{\begin{subarray}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} k1 = 1 \\ k1 \ne k2 \end{subarray} }^{K} {{\varvec{\upgamma}}(\theta_{k1} ,\theta_{k2} ){\varvec{\upgamma}}^{H} (\theta_{k1} ,\theta_{k2} )} } e^{{ - j\frac{{2\uppi d_{x} (\sin \theta_{k1} - \sin \theta_{k2} )}}{\lambda }}} \sigma_{k1}^{2} \sigma_{k2}^{2} \\ & = {\varvec{\Xi}}({\varvec{\uptheta}}){\tilde{\boldsymbol{\Omega }^{\prime}}}({\varvec{\uptheta}}){\tilde{\mathbf{R}^{\prime}}}_{S} {\varvec{\Xi}}^{H} ({\varvec{\uptheta}}) \\ \end{aligned} $$

(43)

where

$$ \begin{aligned} & {\varvec{\Xi}}({\varvec{\uptheta}}) = \left[ {{\varvec{\upgamma}}(\theta_{1} ,\theta_{2} ),{\varvec{\upgamma}}(\theta_{1} ,\theta_{3} ), \ldots ,{\varvec{\upgamma}}(\theta_{k1} ,\theta_{k2} ), \ldots ,{\varvec{\upgamma}}(\theta_{K} ,\theta_{{K{ - }1}} )} \right] \\ & {\tilde{\mathbf{R}^{\prime}}}_{S} = \text{diag}\left( {\left[ {\sigma_{1}^{2} \sigma_{2}^{2} ,\sigma_{1}^{2} \sigma_{3}^{2} , \ldots ,\sigma_{k1}^{2} \sigma_{k2}^{2} , \ldots ,\sigma_{K}^{2} \sigma_{K - 1}^{2} } \right]^{T} } \right) \\ & {\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}}) = \text{diag}\left( {\left[ {e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{1} - \cos \theta_{2} )}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{k1} - \cos \theta_{k2} )}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{y} (\cos \theta_{K} - \cos \theta_{K - 1} )}}{\lambda }}} } \right]^{T} } \right) \\ & {\tilde{\boldsymbol{\Omega }^{\prime}}}({\varvec{\uptheta}}) = \text{diag}\left( {\left[ {e^{{ - j\frac{{2\uppi d_{x} (\sin \theta_{1} - \sin \theta_{2} )}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{x} (\sin \theta_{k1} - \sin \theta_{k2} )}}{\lambda }}} , \ldots ,e^{{ - j\frac{{2\uppi d_{x} (\sin \theta_{K} - \sin \theta_{K - 1} )}}{\lambda }}} } \right]^{T} } \right) \\ \end{aligned} $$

In order to obtain ${\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}})$ and ${\tilde{\boldsymbol{\Omega }^{\prime}}}({\varvec{\uptheta}})$, the orthogonal joint diagonalization based on second-order statistics for (41)–(43) is introduced.

First whiten (41)–(43) by a whitening matrix ${\mathbf{W}}$ as

$$ {\tilde{\mathbf{R}^{\prime}}}_{X} ({\varvec{\uptheta}}) = {\mathbf{W}\boldsymbol{\Xi }}({\varvec{\uptheta}}){\tilde{\mathbf{R}^{\prime}}}_{S} {\varvec{\Xi}}^{H} ({\varvec{\uptheta}}){\mathbf{W}}^{H} = {\mathbf{UU}}^{H} = {\mathbf{I}} $$

(44)

$$ {\tilde{\mathbf{R}^{\prime}}}_{YX} ({\varvec{\uptheta}}) = {\mathbf{W}\boldsymbol{\Xi }}({\varvec{\uptheta}}){\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}}){\tilde{\mathbf{R}^{\prime}}}_{S} {\varvec{\Xi}}^{H} ({\varvec{\uptheta}}){\mathbf{W}}^{H} = {\mathbf{U}}\tilde{{\boldsymbol{\varPhi}} }^{\prime}({\varvec{\uptheta}}){\mathbf{U}}^{H} $$

(45)

$$ {\tilde{\mathbf{R}^{\prime}}}_{ZX} ({\varvec{\uptheta}}) = {\mathbf{W}\boldsymbol{\Xi }}({\varvec{\uptheta}}){\tilde{\boldsymbol{\Omega}}^{\prime}}({\varvec{\uptheta}}){\tilde{\mathbf{R}^{\prime}}}_{S} {\varvec{\Xi}}^{H} ({\varvec{\uptheta}}){\mathbf{W}}^{H} = {\mathbf{U}}\tilde{{\boldsymbol{\Omega }}}^{\prime}({\varvec{\uptheta}}){\mathbf{U}}^{H} $$

(46)

where whitening matrix ${\mathbf{W}}$ is defined as

$$ {\mathbf{W}} = \left[ {\left( {{\varvec{\upvarepsilon}}^{(1)} } \right)^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {\mathbf{V}}^{(:,1)} ,\left( {{\varvec{\upvarepsilon}}^{(2)} } \right)^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {\mathbf{V}}^{(:,2)} , \ldots ,\left( {{\varvec{\upvarepsilon}}^{(K(K - 1))} } \right)^{{ - {1 \mathord{\left/ {\vphantom {1 2}} \right. \kern-0pt} 2}}} {\mathbf{V}}^{(:,K(K - 1))} } \right]^{H} $$

where ${\varvec{\upvarepsilon}}$ represents Eigen-value vector of ${\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}})$ in which Eigen-values are arranged in descending order, and ${\mathbf{V}}$ denotes Eigen-matrix whose column vectors are Eigen-vectors of ${\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}})$ corresponding to the elements in ${\varvec{\upvarepsilon}}$.

So the problem of estimating ${\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}})$ and ${\tilde{\boldsymbol{\Omega}}^{\prime}}({\varvec{\uptheta}})$ can be transformed to jointly diagonalize ${\tilde{\mathbf{R}^{\prime}}}_{YX} ({\varvec{\uptheta}})$ and ${\tilde{\mathbf{R}^{\prime}}}_{ZX} ({\varvec{\uptheta}})$. Let ${\tilde{\mathbf{R}^{\prime}}}({\varvec{\uptheta}}) = \left\{ {{\tilde{\mathbf{R}^{\prime}}}_{YX} ({\varvec{\uptheta}}),{\tilde{\mathbf{R}^{\prime}}}_{ZX} ({\varvec{\uptheta}})} \right\}$ be a set of two matrices. The “joint diagonality” (JD) criterion is defined for any $\left[ {K(K - 1)} \right] \times \left[ {K(K - 1)} \right]$ matrix ${\mathbf{Q}}$, as the following non-negative function of ${\mathbf{Q}}$:

$$ C({\mathbf{Q}})\mathop = \limits^{\text{def}} \sum\limits_{i = Y,Z} {\left\| {\text{diag}\left( {{\mathbf{Q}}\tilde{{\mathbf{R}}}^{\prime}_{iX} ({\varvec{\uptheta}}){\mathbf{Q}}^{H} } \right)} \right\|_{2}^{2} } $$

(47)

A unitary matrix is said to be a joint diagonalizer of the set ${\tilde{\mathbf{R}^{\prime}}}({\varvec{\uptheta}})$ if it maximizes the JD criterion (47) over the set, which can be expressed as

$$ \begin{aligned} \mathop {\hbox{max} }\limits_{{\mathbf{Q}}} \;C({\mathbf{Q}}) & = \sum\limits_{i = Y,Z} {\left\| {\text{diag}\left( {{\mathbf{Q}}\tilde{{\mathbf{R}}}^{\prime}_{iX} ({\varvec{\uptheta}}){\mathbf{Q}}^{H} } \right)} \right\|_{2}^{2} } \\ \text{s.t.}\;\;{\mathbf{QQ}}^{H} & = {\mathbf{Q}}^{H} {\mathbf{Q}} = {\mathbf{I}} \\ \end{aligned} $$

(48)

The estimate of ${\mathbf{Q}}$ in (48) approximate to ${\mathbf{U}}^{H}$ can be deduced by the simultaneous diagonalization method such as Jacobi technique, which can be seen in “Appendix C”.

To determine DOA pair $(\theta_{k1} ,\theta_{k2} )$, based on (45) and (46), as ${\mathbf{Q}}^{H}$ can be regarded as the eigenvector of both ${\tilde{\mathbf{R}^{\prime}}}_{YX} ({\varvec{\uptheta}})$ and ${\tilde{\mathbf{R}^{\prime}}}_{ZX} ({\varvec{\uptheta}})$, the one-to-one correspondence preserved in the positional correspondence on the diagonals between ${\tilde{\boldsymbol{\Phi}}^{\prime(i,i)}} ({\varvec{\uptheta}})$’s and ${\tilde{\boldsymbol{\Omega}}^{\prime(i,i)}} ({\varvec{\uptheta}})$’s can be obtained. And then the analytical solution of $\theta_{k1}$ and $\theta_{k2}$ can be estimated from the diagonals of ${\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}})$ and ${\tilde{\boldsymbol{\Omega}}^{\prime}}({\varvec{\uptheta}})$ referring to “Appendix A”.

Remark 4

As all three Hadamard product matrices ${\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}})$, ${\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}})$ and ${\tilde{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}})$ are independent of the phase errors, the DOAs estimated with the three matrices are independent of the phase errors.

Remark 5

${\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}})$ and ${\tilde{\boldsymbol{\Omega}}^{\prime}}({\varvec{\uptheta}})$ can be estimated by joint diagonalization method, and the elements of them in the positional correspondence on the diagonals can be paired through this process, which means that pair matching techniques for $(e^{{ - j\frac{{2{\uppi }d_{y} (\cos \theta_{k1} - \cos \theta_{k2} )}}{\lambda }}} ,e^{{ - j\frac{{2{\uppi }d_{x} (\sin \theta_{k1} - \sin \theta_{k2} )}}{\lambda }}} )$ is not required.

3.3 Estimate phase errors

The phase errors can be calculated with the estimated DOAs as in the method used in Weiss and Friedlander (1990):

$$ \hat{\boldsymbol{\Psi}}_{Whole} = \frac{{{\mathbf{T}}^{ - 1} (\hat{\boldsymbol{\theta}}) \cdot {\mathbf{w}}}}{{{\mathbf{w}}^{T} {\mathbf{T}}^{ - 1} (\hat{\boldsymbol{\theta}}){\mathbf{w}}}} $$

(49)

where

$$ \begin{aligned} & {\mathbf{T}}(\hat{\boldsymbol{\theta}}) = \sum\limits_{k = 1}^{K} {{\mathbf{F}}^{H} (\hat{\theta }_{k} )} {\mathbf{U}}_{Whole - N} {\mathbf{U}}_{Whole - N}^{H} {\mathbf{F}}(\hat{\theta }_{k} ) \\ & {\mathbf{F}}(\hat{\theta }_{k} ) = \text{diag}({\varvec{\upalpha}}_{Whole} (\hat{\theta }_{k} )) \\ & {\mathbf{w}} = \left[ {1,0,0, \ldots ,0} \right]^{T} \\ \end{aligned} $$

where ${\varvec{\upalpha}}_{Whole}$ and ${\mathbf{U}}_{Whole - N}$ denote the ideal steering vector of the whole array and the noise subspace of covariance matrix of the whole array respectively.

Consequently, the proposed method is summarized as follows.

• Step 1 Gain errors are estimated by (13) and compensated;

• Step 2 If the number of signal is only one, the DOA can be estimated with (22) and (23); if the number of signals is larger than one, the DOAs can be obtained from ${\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}})$ and ${\tilde{\boldsymbol{\Omega}}^{\prime}}({\varvec{\uptheta}})$ in (45) and (46) estimated with joint diagonalization method;

• Step 3 Based on the DOA estimates from step 2, phase errors are estimated by (49).

The DOA estimation is presented above in the presence of gain-phase errors. The gain and phase errors can also be calculated in step A and C respectively. Based on the analysis, it is clear that the proposed method is independent of phase errors and it requires neither calibrated sources nor parameter search. However, its drawback is also obvious that sensors of sub-array should be more than sources and this method is difficult to be implemented in estimating 2-D DOAs.

4 Discussions

4.1 Compared with the method proposed in Cao and Ye (2013)

Now the comparison between the proposed method and the one in Cao and Ye (2013) is presented in this section. It can be found that these methods have some similarities. Both of them consist of three steps and the steps for gain errors estimation and phase errors estimation are the same. And these methods perform independently of phase errors.

Of course, there are some differences between the proposed one and the method in Cao and Ye (2013), which can be seen as the improvements of the one in Cao and Ye (2013).

First, the proposed method exploits the relationship between the signal subspace and the steering vector, and Hadamard product of signal subspace and its conjugate to solve the problem of DOA estimation when the number of signal is only one, which is difficult to deal with by the method in Cao and Ye (2013).

Second, the proposed method proposes a method to estimate the coefficient of 1 component with the relationship between rank and determinant, which can obtain analytical solution of $\kappa$. However, the solution of $\kappa$ in Cao and Ye (2013) has no closed form. The detail is demonstrated in section B.

Third, in proposed method, rotation invariant property between sub-arrays of double L-shaped array and orthogonal joint diagonalization are utilized to estimate ${\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}})$ and ${\tilde{\boldsymbol{\Omega}}^{\prime}}({\varvec{\uptheta}})$, which include the information on DOA. While the method in Cao and Ye (2013) adopts 2-D MUSIC to search DOA pair which indicates the heavy load of complexity, and the discussion on complexity is presented as follows.

If the number of signal is only one, in the proposed method the complexity mainly comes from the Eigen-decomposition of ${\mathbf{R}}_{i} (\theta )$ in (12) and ${\bar{\mathbf{R}}}_{i} (\theta )$ (${\bar{\mathbf{R}}}_{i} (\theta + \Delta \theta )$) in (15), and the total complexity is $3M^{3}$. If the number of signal is larger than one, the complexity mainly comes from the Eigen-decomposition of ${\mathbf{R}}_{i}$ and orthogonal joint diagonalization of ${\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}})$, ${\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}})$ and ${\tilde{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}})$ in (41)–(43). The complexity of Eigen-decomposition of ${\mathbf{R}}_{i}$ is $M^{3}$, and complexity of orthogonal joint diagonalization of ${\tilde{\mathbf{R}}}_{X} ({\varvec{\uptheta}})$, ${\tilde{\mathbf{R}}}_{YX} ({\varvec{\uptheta}})$ and ${\tilde{\mathbf{R}}}_{ZX} ({\varvec{\uptheta}})$ is similar to three times diagonalization of a single $K(K - 1)$-dimensional square matrix, which means that complexity of diagonalization is $3[K(K - 1)]^{3}$. So the total complexity is $3M^{3} + 3[K(K - 1)]^{3}$ when K > 1.

Meanwhile, the complexity of the method in Cao and Ye (2013) is from the Eigen-decomposition of the covariance matrix, the estimate of $\kappa$ and peak search of the spatial spectrum. Obviously, the Eigen-decomposition is $(2M)^{3}$. The load of estimate of $\kappa$ is $Q(2M)^{3}$ which is discussed in the following section B ($Q$ denotes the times of Eigen-decomposition of ${\mathbf{R}}_{4}$), and the complexity of 2-D MUSIC peak search of the spatial spectrum is $(2M)[4M - 2K(K - 1) + 1]\nu$ ($\nu = ({\uppi \mathord{\left/ {\vphantom {\uppi {\Delta \alpha }}} \right. \kern-0pt} {\Delta \alpha }})^{2}$ denotes the search number, where $\Delta \alpha$ denotes the search step; if $\Delta \alpha = 0.1^\circ$, the search number is more than $3 \times 10^{6}$). So the total complexity is $(2M)[4M - 2K(K - 1) + 1]\nu + Q(2M)^{3} + (2M)^{3}$. From the comparison it is clear that the complexity of proposed method is much lower than the method in Cao and Ye (2013), which can be seen as an improvement relative to method in Cao and Ye (2013).

4.2 Discussion on eliminating 1 component

Cao and Ye (2013) also presents a method to estimate the coefficient of 1 component, which is based on the relationship between large Eigen-values corresponding to signal subspace and rank of matrix. It can be described as a non-convex optimization problem on $\kappa$:

$$ \hat{\kappa } = \mathop {\hbox{min} }\limits_{\kappa } \;\frac{{{\varvec{\upchi}}^{(K(K - 1) + 1)} }}{{\sum\nolimits_{i = 1}^{K(K - 1)} {{\varvec{\upchi}}^{(i)} } }}\quad \kappa \in \left[ {{{\left( {\sum\limits_{k = 1}^{K} {\sigma_{k}^{2} } } \right)^{2} } \mathord{\left/ {\vphantom {{\left( {\sum\limits_{k = 1}^{K} {\sigma_{k}^{2} } } \right)^{2} } {K,\left( {\sum\limits_{k = 1}^{K} {\sigma_{k}^{2} } } \right)^{2} }}} \right. \kern-0pt} {K,\left( {\sum\limits_{k = 1}^{K} {\sigma_{k}^{2} } } \right)^{2} }}} \right] $$

(50)

$$ {\mathbf{R}}_{4} (\kappa ) = {\mathbf{R}}_{2} - \kappa {\mathbf{1}} \cdot {\mathbf{1}}^{T} $$

(51)

where ${\mathbf{R}}_{2}$ represents Hadamard product of the covariance matrix of the whole array output removing gain errors and noise and its conjugate, ${\varvec{\upchi}}$ denotes Eigen-value vector of ${\mathbf{R}}_{4}$, and the Eigen-values in ${\varvec{\upchi}}$ are arranged in descending order.

As the objective function in (50) is not convex, the common convex optimization methods are not available. The method in Cao and Ye (2013) is searching the minimum of (50) with a limited sample of $\kappa$, whose performance depends on the search step of $\kappa$. Furthermore, the estimation of (50) at each iteration requires Eigen-value vector ${\varvec{\upchi}}$, which means the Eigen-decomposition of a 2M-dimensional square matrix. And in order to guarantee the accuracy, the search step can’t be too large, which may bring on a huge search number, indicating Eigen-decomposing a 2M-dimensional square matrix lots of times.

Unlike Cao and Ye (2013), the estimate of $\kappa$ is owing to the relationship between determinant and rank of matrix in proposed method. From (35) to (40) it can be seen that analytical solution of $\kappa$ can be obtained and the complexity mainly comes from the inversion of ${\tilde{\tilde{\mathbf{R}}}}_{YX}$, which is only $[K(K - 1) + 1]^{3}$. So compared with Cao and Ye (2013), the proposed method has an advantage of estimating the coefficient of 1 component obviously.

5 Simulation results

In this section, simulation results are presented to illustrate the validity of the proposed method. The range of the DOAs of signals is confined in $\left( {{{ - \;\uppi } \mathord{\left/ {\vphantom {{ - \;\uppi } {2,\,{\uppi \mathord{\left/ {\vphantom {\uppi 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {2,\,{\uppi \mathord{\left/ {\vphantom {\uppi 2}} \right. \kern-0pt} 2}}}} \right)$. Consider a double L-shaped array consisting of 18 elements (M = 9) with $d_{x} = \lambda /4$ and $d_{y} = \lambda /2$. The gain-phase uncertainties are described by (Liu et al. 2011)

$$ {\mathbf{G}}_{i}^{(m,m)} = 1 + \sqrt {12} \delta {\kern 1pt} {\varvec{\upxi}}_{i}^{(m,m)} \quad \angle {\varvec{\Psi}}_{i}^{(m,m)} = \sqrt {12} \mu {\kern 1pt} {\boldsymbol{\varsigma }}_{i}^{(m,m)} $$

where ${\kern 1pt} {\varvec{\upxi}}_{i}^{(m,m)}$ and ${\boldsymbol{\varsigma }}_{i}^{(m,m)}$ are independent and identically distributed random variables distributed uniformly over $\left( { - 0.5,0.5} \right)$, $\delta$ and $\mu$ are the standard deviations of ${\mathbf{G}}_{i}^{(m,m)}$ and $\angle {\varvec{\Psi}}_{i}^{(m,m)}$, respectively.

The simulations include two cases as follows:

• Case 1 K = 1 Here we compare the performance of the proposed method with W–F method and the method proposed in Ng et al. (2009) named by B–J method, which are the representative on-line and off-line methods respectively.

• Case 2 K > 1 The compared methods chosen are W–F method, B–J method, the method in Liu et al. (2011) named by Liu’s method and the method in Cao and Ye (2013) named by Cao’s method. The reason for choosing the first two methods as reference is the same with Case 1, and comparing the proposed method with the last two methods is to illustrate the improvements of the proposed method. In Liu et al. (2011) the authors also proposed a strategy of combining Liu’s method with the W–F method, which is not considered here. The reason is that this combined strategy requires both alternative iteration and 2-D MUISC search, which means its computation load is heavier than Liu’s method.

In the simulations below, $\delta = 0.1$ and for all Monte Carlo experiments, the number of trials is 200.

5.1 Case 1 K = 1

In this case there are four experiments on the effects of array rotating angle $\Delta \theta$, phase errors, signal-to-noise ratio (SNR) and sample number presented as follows.

5.1.1 Effect of $\Delta \theta$

In this experiment the SNR is 10 dB, number of samples is 500 and $\mu$ is 25°. The single source comes from 40°. Figure 2 shows the root mean square error (RMSE) of DOA estimate versus $\Delta \theta$. From Fig. 2 it is shown that the performance gets better as $\Delta \theta$ increases in the proposed method. The reason is that the proposed method can be seen as a calibrated method using two disjoint sources (unknown DOAs) with separated angle $\Delta \theta$, and as $\Delta \theta$ increases the correlation of signal subspace ${\bar{\mathbf{U}}}_{i} (\theta )$ and ${\bar{\mathbf{U}}}_{i} (\theta + \Delta \theta )$ decreases, which indicates that the accuracy and resolution of DOA estimates increase.

Fig. 2

RMSE of DOA estimates versus array rotating angle

5.1.2 Effect of phase errors

Consider a signal impinging on the array from direction 40°, and the array rotating angle $\Delta \theta = 5^\circ$. The calibrated source for B–J method is at 25°. The SNR is 10 dB and number of samples is 500. Based on Monte Carlo experiments, the RMSE curves of DOA versus the standard deviation of the phase errors $\mu$ are shown in Fig. 3.

Fig. 3

RMSE of DOA estimates versus μ

From Fig. 3 it is clear that the accuracy of B–J method is the best in the three methods as it is an off-line method which can estimate the gain-phase errors exactly with a calibrated source. Meanwhile W–F method performs better than the proposed method in the case of small phase errors, and as phase errors increase the accuracy of the proposed method becomes higher than W–F method because W–F method fails when phase errors are large. The reason is that the W–F method converges to suboptimal solutions in large phase errors, which leads to the degradation of its performance. And it is noted that both the proposed method and B–J method perform independently of phase errors, while the performance of W–F method is affected by phase errors seriously.

5.1.3 Effect of SNR

This experiment is to confirm the performance of the three methods versus SNR. Consider a signal impinging on the array from direction 40°, and the array rotating angle $\Delta \theta = 5^\circ$. The calibrated source for B–J method is at 25°. The number of samples is 500 and $\mu$ is 25°.

Figure 4 shows the RMSE of the DOA estimates versus SNR. From Fig. 4 it is shown that both the proposed method and B–J method perform better as the SNR increases. And regardless of SNR, the performance of B–J method is better than the proposed method, which is the advantage of off-line method. However, in such large phase errors, the W–F method stays at a low level as it fails no matter how high the SNR is.

Fig. 4

RMSE of DOA estimates versus SNR

5.1.4 Effect of sample number

To demonstrate the effect of sample number, we provide an experiment for DOA estimates versus sample number. Consider a signal impinging on the array from direction 40°, and the array rotating angle $\Delta \theta = 5^\circ$. The calibrated source for B–J method is at 25°. The SNR is 10 dB and $\mu$ is 25°. The RMSE of the DOA estimates is shown in Fig. 5.

Fig. 5

RMSE of DOA estimates versus sample number

From this figure we can see that in large phase errors, the W–F method fails regardless of the number of samples, meanwhile the other two methods behave better as the sample number increases as covariance matrix is closer to its true value as the number of samples increases, which can result in the signal subspace of covariance matrix approximate to the true value. And similar to Fig. 4, the proposed method performs worse than B–J method for the same reason with the previous simulation.

5.2 Case 1 K > 1

In this case there is a comparison on estimating $\kappa$ and four experiments on the effects of DOA separation, phase errors, SNR and sample number presented as follows.

5.2.1 Comparison on estimating $\kappa$

In this experiment there are three signals impinging on the array with the power 1.8, 5.7 and 10.4 W from direction 10°, 32° and − 48°, and the true value of $\kappa$ is 143.89 $W^{2}$. The power of noise is 1 W, number of samples is 500 and $\mu$ is 25°.

Carry out Cao’s method and the proposed method, and we can obtain Tables 1 and 2 as follows.

Table 1 Estimation error and complexity of Cao’s method for $\kappa$

Table 2 Estimation error and complexity of proposed method for $\kappa$

Form Table 1 it is shown that in Cao’s method as the search step decreases the estimation accuracy of $\kappa$ becomes better because estimation resolution is dependent on search step, and meanwhile the search number increases which indicates the number of Eigen-decomposition grows up.

From Table 2 it can be seen that the estimate accuracy of $\kappa$ can reach 0.07% in the proposed method, and running time is 1.2 ms. To achieve the approximate accuracy in Cao’s method the search step should be 0.01 W, and the number of Eigen-decomposition is larger than $2 \times 10^{4}$ whose running time is 22.4 s. From the comparison it can be seen that the proposed method is superior to Cao’s method; especially when the number of sources are large, meaning the high dimension array being used, the complexity can be reduced visibly compared with Cao’s method.

5.2.2 Effect of DOA separation

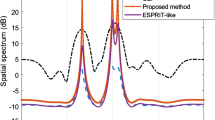
To verify the effect of the DOA separation, an experiment for the case is presented when DOA separation of the signals are different. Assume that there are two signals impinging on the array with the power 5.7 and 10.4 W, whose DOAs are denoted by $\theta_{1}$ and $\theta_{2}$ respectively. $\theta_{1}$ is fixed at 10° and $\theta_{2}$ varies from 11° to 40°. So the DOA separation varies from 1° to 30°. In order to guarantee the running time of Cao’s method, the search step is 1 W. The calibrated source for B–J method is at 25°. Other simulation parameters are the same as those in the previous experiment. The RMSE curves of DOA versus DOA separation are shown in Fig. 6. The Cramer–Rao bound (CRB) for on-line method is also displayed.

Fig. 6

RMSE of DOA estimates versus DOA separation

From Fig. 6 it is shown that when DOA separation is small, all calibrated methods fail. As the DOA separation gets larger, the performance of all methods becomes better except W–F method because of the large $\mu$. From this figure we can also note that all on-line methods cannot reach the CRB. In all of these methods (including CRB), the B–J method behaves best as expected because this off-line method employs more effective information from calibrated sources. Except the B–J method the proposed method has the best performance regardless of DOA separation. The proposed method outperforms Cao’s method mainly resulting from higher accuracy of $\kappa$ estimated in proposed method, and as Liu’s method doesn’t eliminate effect of 1 component its performance must be worst among the three methods especially when the DOA separation is not large.

5.2.3 Effect of phase errors

In this experiment the simulation of DOA estimation versus the standard deviation of the phase errors $\mu$ is given. Assume that there are three signals impinging on the array with the power 1.8, 5.7 and 10.4 W from direction 10°, 32° and − 48°. The power of noise is 1 W, number of samples is 500. The search step for Cao’s method and the DOA of calibrated source for B–J method are the same with the previous experiment respectively.

Figure 7 shows the curves of DOA estimation versus $\mu$. From Fig. 7 we can see the W–F method is affected by phase errors obviously: when $\mu < 15^\circ$ it can work however when $\mu > 15^\circ$ it fails. On the contrary, the rest four methods can perform independently of phase errors. And the B–J method remains the best performance with the drawback of requirement for calibrated source. Among the rest three methods whose performance is independent of phase errors, the proposed one has the highest accuracy as expected. Cao’s method behaves better than Liu’s as the effect of 1 component is eliminated. The CRB is also independent of the sensor phase which is consistent with the Property 1 in Sect. 4 of Xie et al. (2017a).

Fig. 7

RMSE of DOA estimates versus μ

5.2.4 Effect of SNR

Consider three signals with the same power from 10°, 32° and − 48°. The number of samples is 500 and $\mu$ is 25°. SNR verifies from 0 to 30 dB. Figure 8 shows the RMSE of the DOA estimates versus SNR.

Fig. 8

RMSE of DOA estimates versus SNR

From Fig. 8 it is shown that all methods perform better as the SNR increases. In low SNR interval, the performance of W–F method gets better visibly meanwhile when SNR exceeds 10 dB, the variety of its performance is not obvious as the performance is subject to phase errors. Among the other four methods, the B–J method still has the highest accuracy; and the performance of the proposed method comes second. Cao’s method performs still better than Liu’s. As the SNR increases the performance of the four methods gets closer.

5.2.5 Effect of sample number

This is the last experiment in this section. Consider three signals with the same power from 10°, 32° and − 48°. The SNR is 10 dB and $\mu$ is 25°. The sample number verifies from 100 to 1000. Figure 9 shows the RMSE of the DOA estimates versus sample number.

Fig. 9

RMSE of DOA estimates versus sample number

From Fig. 9 it can be found that all methods perform better as the sample number increases, and among these methods the performance of W–F method meliorates least obviously. The B–J method behaves better than the rest three methods regardless of sample number. The proposed method can work when sample number reaches 300, meanwhile Cao’s method and Liu’s method achieve the same accuracy the threshold of sample number should be more than 500 and 700, respectively.

6 Conclusion

In this paper, we present a novel method to deal with the DOA estimation problem in the presence of gain and phase errors. Considering taking use of rotation invariant property and employing the least sensors, we choose the double L-shaped array as received array. The proposed method based on double L-shaped array requires neither calibrated sources nor multidimensional parameter search, and its performance is independent of the phase errors. And Compared with Liu’s method, it inherits the advantage of Liu’s method and can overcome the four drawbacks of Liu’s method mentioned above. Its drawback is also obvious that sensors of sub-array should be more than sources and this method is difficult to be implemented in estimating 2-D DOAs. How to deal with the 2-D DOA estimation problem in the presence of gain and phase errors independently of the phase errors is still an open question, which may take use of more information on signals or require more complicated array configuration. And this method is also difficult to deal with multipath signals (Xie et al. 2017b). So there is much room for improvement for this method according to these drawbacks.

Appendices

Appendix A: Proof of the Property

Assume that there can exist different DOA pairs $(\theta_{k} ,\theta_{l} ) \ne (\theta_{i} ,\theta_{j} )$($\theta_{i} \ne \theta_{j}$, $\theta_{k} \ne \theta_{l}$), which can make ${\varvec{\upgamma}}(\theta_{i} ,\theta_{j} ) = {\varvec{\upgamma}}(\theta_{k} ,\theta_{l} )$. So each element in ${\varvec{\upgamma}}(\theta_{i} ,\theta_{j} )$ is the same with the corresponding one in ${\varvec{\upgamma}}(\theta_{k} ,\theta_{l} )$. Based on this assumption, we have

$$ {\varvec{\upgamma}}^{(N - 2)} (\theta_{i} ,\theta_{j} ) = {\varvec{\upgamma}}^{(N - 2)} (\theta_{k} ,\theta_{l} ) $$

(52)

$$ {\varvec{\upgamma}}^{(N)} (\theta_{i} ,\theta_{j} ) = {\varvec{\upgamma}}^{(N)} (\theta_{k} ,\theta_{l} ) $$

(53)

Expanding (52) and (53), we obtain

$$ e^{{ - j\frac{{2{\uppi }d_{x} (\sin \theta_{i} - \sin \theta_{j} )}}{\lambda }}} = e^{{ - j\frac{{2{\uppi }d_{x} (\sin \theta_{k} - \sin \theta_{l} )}}{\lambda }}} $$

(54)

$$ e^{{ - j\frac{{2{\uppi }d_{y} (\cos \theta_{i} - \cos \theta_{j} )}}{\lambda }}} = e^{{ - j\frac{{2{\uppi }d_{y} (\cos \theta_{k} - \cos \theta_{l} )}}{\lambda }}} $$

(55)

It follows from (54) and (55) that

$$ \frac{{d_{x} (\sin \theta_{i} - \sin \theta_{j} )}}{\lambda } = \frac{{d_{x} (\sin \theta_{k} - \sin \theta_{l} )}}{\lambda } + n $$

(56)

$$ \frac{{d_{y} (\cos \theta_{i} - \cos \theta_{j} )}}{\lambda } = \frac{{d_{y} (\cos \theta_{k} - \cos \theta_{l} )}}{\lambda } + m $$

(57)

$$ \left( {m,n = 0, \pm 1, \pm 2, \ldots } \right) $$

As $\theta_{i}$, $\theta_{j}$, $\theta_{k}$ and $\theta_{l}$ are all in the interval $\left( {{{ - \uppi } \mathord{\left/ {\vphantom {{ - \uppi } {2,{\uppi \mathord{\left/ {\vphantom {\uppi 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {2,{\uppi \mathord{\left/ {\vphantom {\uppi 2}} \right. \kern-0pt} 2}}}} \right)$, and under the condition that $d_{x}$ is less than one quarter of wavelength $\lambda$ and $d_{y}$ is less than the half, it can be seen that

$$ \frac{{d_{x} (\sin \theta_{i} - \sin \theta_{j} )}}{\lambda } - \frac{{d_{x} (\sin \theta_{k} - \sin \theta_{l} )}}{\lambda } = n \in ( - 1,1) $$

(58)

$$ \frac{{d_{y} (\cos \theta_{i} - \cos \theta_{j} )}}{\lambda } - \frac{{d_{y} (\cos \theta_{k} - \cos \theta_{l} )}}{\lambda } = m \in ( - 1,1) $$

(59)

From (58) and (59) we obtain

$$ n = m = 0 $$

(60)

Based on (56), (57) and (60) can be modified as

$$ \sin \theta_{i} - \sin \theta_{j} = \sin \theta_{k} - \sin \theta_{l} = p $$

(61)

$$ \cos \theta_{i} - \cos \theta_{j} = \cos \theta_{k} - \cos \theta_{l} = q $$

(62)

As sinusoidal function in the interval $\left( {{{ - \;\uppi } \mathord{\left/ {\vphantom {{ - \;\uppi } {2,{\uppi \mathord{\left/ {\vphantom {\uppi 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {2,{\uppi \mathord{\left/ {\vphantom {\uppi 2}} \right. \kern-0pt} 2}}}} \right)$ is monotonically increasing, $\sin \theta_{i} - \sin \theta_{j}$ can’t be zero. Meanwhile $\cos \theta_{i} - \cos \theta_{j}$ may be zero due to non-monotonicity of cosine function in the same interval. So there are two cases on (62).

Case 1

$$ \cos \theta_{i} - \cos \theta_{j} = \cos \theta_{k} - \cos \theta_{l} = q = 0 $$

(63)

Combining (61) with (63), we have

$$ \theta_{i} = \theta_{k} = - \theta_{j} = - \theta_{l} = \arcsin \frac{p}{2} $$

(64)

which contradicts the assumption $(\theta_{k} ,\theta_{l} ) \ne (\theta_{i} ,\theta_{j} )$.

Case 2

$$ \cos \theta_{i} - \cos \theta_{j} = \cos \theta_{k} - \cos \theta_{l} = q \ne 0 $$

(65)

From (61) and (62) we have

$$ \tan \frac{{\theta_{i} - \theta_{j} }}{2} = \tan \frac{{\theta_{k} - \theta_{l} }}{2} = - \frac{q}{p} $$

(66)

So

$$ \cos^{2} \frac{{\theta_{i} + \theta_{j} }}{2} = \cos^{2} \frac{{\theta_{k} + \theta_{l} }}{2} = \frac{{q^{2} }}{{p^{2} + q^{2} }} $$

(67)

As $\theta_{i}$, $\theta_{j}$, $\theta_{k}$ and $\theta_{l}$ are all in the interval $\left( {{{ - {\uppi }} \mathord{\left/ {\vphantom {{ - {\uppi }} {2,\,{{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {2,\,{{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-0pt} 2}}}} \right)$, $\frac{{\theta_{i} + \theta_{j} }}{2} \in \left( {{{ - {\uppi }} \mathord{\left/ {\vphantom {{ - {\uppi }} {2,\,{{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {2,\,{{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-0pt} 2}}}} \right)$ and $\frac{{\theta_{k} + \theta_{l} }}{2} \in \left( {{{ - {\uppi }} \mathord{\left/ {\vphantom {{ - {\uppi }} {2,{{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-0pt} 2}}}} \right. \kern-0pt} {2,{{\uppi } \mathord{\left/ {\vphantom {{\uppi } 2}} \right. \kern-0pt} 2}}}} \right)$. It follows (67) that

$$ \cos \frac{{\theta_{i} + \theta_{j} }}{2} = \cos \frac{{\theta_{k} + \theta_{l} }}{2} = \frac{\left| q \right|}{{\sqrt {p^{2} + q^{2} } }} $$

(68)

Submitting (61)–(68), we can obtain

$$ \sin \frac{{\theta_{i} - \theta_{j} }}{2} = \sin \frac{{\theta_{k} - \theta_{l} }}{2} = \frac{{p\sqrt {p^{2} + q^{2} } }}{2\left| q \right|} $$

(69)

Combining (68) with (69), we have

$$ \theta_{i} = \theta_{k} = \arccos \frac{\left| q \right|}{{p^{2} + q^{2} }} + \arcsin \frac{{p\sqrt {p^{2} + q^{2} } }}{2\left| q \right|} $$

(70)

$$ \theta_{j} = \theta_{l} = \arccos \frac{\left| q \right|}{{p^{2} + q^{2} }} - \arcsin \frac{{p\sqrt {p^{2} + q^{2} } }}{2\left| q \right|} $$

(71)

which also contradicts the assumption $(\theta_{k} ,\theta_{l} ) \ne (\theta_{i} ,\theta_{j} )$.

From cases 1 to 2, it can be seen that the assumption that $(\theta_{k} ,\theta_{l} ) \ne (\theta_{i} ,\theta_{j} )$($\theta_{i} \ne \theta_{j}$, $\theta_{k} \ne \theta_{l}$) can’t hold. So there exist no DOA pairs $(\theta_{k} ,\theta_{l} ) \ne (\theta_{i} ,\theta_{j} )$ ($\theta_{i} \ne \theta_{j}$, $\theta_{k} \ne \theta_{l}$) which can make ${\varvec{\upgamma}}(\theta_{i} ,\theta_{j} ) = {\varvec{\upgamma}}(\theta_{k} ,\theta_{l} )$.

In consequence, the proof of the property is completed, and it can also be regarded as a special case of Theorem 2 in Xie et al. (2017), which gives the proof by geometrical explanation of vectors on $\theta_{p} ,\theta_{q}$.

Appendix B: Proof of the phase errors independence of DOA estimation when K = 1

Combining (15) with (16), we have

$$ {\bar{\mathbf{R}}}_{i} (\theta ) = \sigma^{2} {\varvec{\Psi}}_{i} {\varvec{\upalpha}}(\theta ){\varvec{\upalpha}}^{H} (\theta ){\varvec{\Psi}}_{i}^{H} = \bar{\gamma }_{i} (\theta ){\bar{\mathbf{u}}}_{i} (\theta ){\bar{\mathbf{u}}}_{i}^{H} (\theta ) $$

(72)

Now define a new covariance matrix ${\bar{\mathbf{R}^{\prime}}}_{i} (\theta )$ as (73)

$$ {\bar{\mathbf{R}^{\prime}}}_{i} (\theta ) = {\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{R}}}_{i} (\theta ){\varvec{\Psi}}_{i} $$

(73)

So (73) can be written as

$$ {\bar{\mathbf{R}^{\prime}}}_{i} (\theta ) = {\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{R}}}_{i} (\theta ){\varvec{\Psi}}_{i} = \sigma^{2} {\varvec{\upalpha}}(\theta ){\varvec{\upalpha}}^{H} (\theta ) = \bar{\gamma }_{i} (\theta ){\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta )({\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta ))^{H} $$

(74)

Because of the properties of ${\varvec{\Psi}}_{i}$ that ${\varvec{\Psi}}_{i}$ is a diagonal matrix and the absolute values of diagonal elements are equal to unity, it is noted that

$$ {\bar{\mathbf{u}}}_{i}^{H} (\theta ){\bar{\mathbf{u}}}_{i} (\theta ) = {\bar{\mathbf{u}}}_{i}^{H} (\theta ){\varvec{\Psi}}_{i} {\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta ) = 1 $$

(75)

Owing to (75), we right multiply (74) by ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta )$ and obtain that

$$ {\bar{\mathbf{R}^{\prime}}}_{i} (\theta ){\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta ) = \bar{\gamma }_{i} (\theta ){\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta ) $$

(76)

which indicates that ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta )$ is the eigenvector of ${\bar{\mathbf{R}^{\prime}}}_{i} (\theta )$ corresponding to the only non-zero Eigen-value.

As ${\bar{\mathbf{R}^{\prime}}}_{i} (\theta ) = \sigma^{2} {\varvec{\upalpha}}(\theta ){\varvec{\upalpha}}^{H} (\theta )$ is independent of the phase errors, its eigenvector ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta )$ must be independent of the phase errors.

Similarly, ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta + \Delta \theta )$ must be independent of the phase errors.

So (22) can be rewritten with ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta )$

$$ \begin{aligned} \sin (\theta + \Delta \theta ) - \sin \theta = \frac{{\lambda \cdot \angle \left\{ {{{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )}}{{\xi_{i} (\theta )}}} \right)} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)}}} \right. \kern-0pt} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )}}{{\xi_{i} (\theta + \Delta \theta )}}} \right)}}} \right\}}}{{2{\uppi }d_{x} }} \hfill \\ = \frac{{\lambda \cdot \angle \left\{ {{{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )}}{{{\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta )}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )}}{{{\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta )}}} \right)} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )}}{{{\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta + \Delta \theta )}}} \right)}}} \right. \kern-0pt} {\left( {\frac{{{\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )}}{{{\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta + \Delta \theta )}}} \right)}}} \right\}}}{{2{\uppi }d_{x} }} \hfill \\ = \frac{{\lambda \cdot \angle \left\{ {{{\left( {\frac{{{\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )}}{{{\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta )}}} \right)} \mathord{\left/ {\vphantom {{\left( {\frac{{{\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )}}{{{\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta )}}} \right)} {\left( {\frac{{{\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )}}{{{\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta + \Delta \theta )}}} \right)}}} \right. \kern-0pt} {\left( {\frac{{{\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )}}{{{\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta + \Delta \theta )}}} \right)}}} \right\}}}{{2{\uppi }d_{x} }} \hfill \\ \end{aligned} $$

(77)

As ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta )$ and ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i} (\theta + \Delta \theta )$ are both independent of the phase errors, their elements ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta )$, ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 1)} (\theta + \Delta \theta )$, ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta )$ and ${\varvec{\Psi}}_{i}^{H} {\bar{\mathbf{u}}}_{i}^{(N - 2)} (\theta + \Delta \theta )$ in (77) are all independent of the phase errors.

The independence of (23) can be proved in the same way.

Consequently, (22) and (23) are both independent of the phase errors, so DOA estimated from them must be independent of phase errors.

Appendix C: Realization of joint diagonalization

Similar to use Jacobi technique to achieve Eigen-decomposition, we can also extend it to the joint diagonalization of a set of normal matrices. Just like the realization of Eigen-decomposition of single matrix, joint diagonalization can be carried out by successive Givens rotations, and each rotation leads to maximize criterion (47).

Considering a rotation indexed by ($\varepsilon ,\eta$), the Givens rotation matrix ${\mathbf{g}}(\varepsilon ,\eta ,\vartheta )$ can be expressed as

$$ \begin{aligned} {\mathbf{g}}(\varepsilon ,\eta ,\vartheta ) =&\left[ {\begin{array}{*{20}c} 1 &\cdots &0 &\cdots &0 &\cdots &0 \\ \vdots &\ddots &\vdots &{} &\vdots &{} &\vdots \\ 0 &\cdots &{c^{ * } } &\cdots &{s^{ * } } &\cdots &0 \\ \vdots &{} &\vdots &\ddots &\vdots &{} &\vdots \\ 0 &\cdots &{ - s} &\cdots &c &\cdots &0 \\ \vdots &{} &\vdots &{} &\vdots &\ddots &\vdots \\ 0 &\cdots &0 &\cdots &0 &\cdots &1 \\ \end{array} } \right]\quad \begin{array}{*{20}c} {} \\ {} \\ \varepsilon \\ {} \\ \eta \\ {} \\ {} \\ \end{array} \hfill \\ &\qquad \,\,\begin{array}{llllll} &&&{\;\;\,\varepsilon } &{} &{\qquad\,\eta } \\ \end{array} \hfill \\ \end{aligned} $$

(78)

where $\varepsilon = 1,2, \cdots K(K - 1) - 1$, $\eta = \varepsilon + 1,\varepsilon + 2, \cdots ,K(K - 1)$.

As ${\tilde{\mathbf{R}^{\prime}}}_{YX} ({\varvec{\uptheta}})$ and ${\tilde{\mathbf{R}^{\prime}}}_{ZX} ({\varvec{\uptheta}})$ are real symmetric matrices, the Eigen-matrix must be real-valued. So real-valued $c$ and $s$ can be represented by one parameter $\vartheta$ as

$$ c = \cos \vartheta \quad s = \sin \vartheta $$

(79)

With the property of Givens rotation matrix, the problem of (48) can be transformed to the following formula at each rotation:

$$ \mathop {\hbox{max} }\limits_{{\mathbf{g}}} \;\sum\limits_{i = Y,Z} {\left\| {\text{diag}\left( {{\tilde{\boldsymbol{\Gamma }}}_{iX} ({\varvec{\uptheta}}) = {\mathbf{g}}(\varepsilon ,\eta ,\vartheta ){\tilde{\mathbf{R}^{\prime}}}_{iX} ({\varvec{\uptheta}}){\mathbf{g}}^{H} (\varepsilon ,\eta ,\vartheta )} \right)} \right\|_{2}^{2} } $$

(80)

Expanding (80), we can obtain

$$ \mathop {\hbox{max} }\limits_{\vartheta } \;\sum\limits_{i = Y,Z} {[({\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}))^{2} + ({\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}}))^{2} ]} $$

(81)

Noticing that

$$ \begin{aligned} & 2[({\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}))^{2} + ({\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}}))^{2} ] \\ & \quad = \left({\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) + {\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}}))^{2} + ({\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) - {\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}})\right)^{2} \\ \end{aligned} $$

(82)

and that the trace ${\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) + {\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}})$ is invariant in a unitary transformation, at each Givens step optimization of criterion (81) is equivalent to

$$ \mathop {{\text{max} }}\limits_{\vartheta } \,\sum\limits_{i = Y,Z} {\left({\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) - {\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}})\right)^{2} } $$

(83)

It is checked that

$$ \begin{aligned} & {\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) - {\tilde{\boldsymbol{\Gamma }}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}}) \\ & \quad = ({\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) - {\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}}))(c^{2} - s^{2} ) - ({\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\varepsilon ,\eta )} ({\varvec{\uptheta}}) + {\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\eta ,\varepsilon )} ({\varvec{\uptheta}}))2cs \\ & \quad = ({\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) - {\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}}))\cos 2\vartheta - ({\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\varepsilon ,\eta )} ({\varvec{\uptheta}}) + {\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\eta ,\varepsilon )} ({\varvec{\uptheta}}))\sin 2\vartheta \\ & \quad = \left[ {\begin{array}{*{20}c} { - ({\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\varepsilon ,\eta )} ({\varvec{\uptheta}}) + {\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\eta ,\varepsilon )} ({\varvec{\uptheta}}))} & {({\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) - {\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}}))} \\ \end{array} } \right]\,\left[ {\begin{array}{*{20}c} {\sin 2\vartheta } \\ {\cos 2\vartheta } \\ \end{array} } \right] \\ & \quad = {\varvec{\upalpha}}_{iX}^{T} (\varepsilon ,\eta ){\varvec{\upbeta}}(\vartheta ) \\ \end{aligned} $$

(84)

where

$$ \begin{aligned} {\varvec{\upalpha}}_{iX} (\varepsilon ,\eta ) & = \left[ {\begin{array}{*{20}c} { - ({\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\varepsilon ,\eta )} ({\varvec{\uptheta}}) + {\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\eta ,\varepsilon )} ({\varvec{\uptheta}}))} & {({\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\varepsilon ,\varepsilon )} ({\varvec{\uptheta}}) - {\tilde{\mathbf{R}^{\prime}}}_{iX}^{(\eta ,\eta )} ({\varvec{\uptheta}}))} \\ \end{array} } \right]^{T} \\ {\varvec{\upbeta}}(\vartheta ) & = \left[ {\begin{array}{*{20}c} {\sin 2\vartheta } \\ {\cos 2\vartheta } \\ \end{array} } \right] \\ \end{aligned} $$

So (83) can be rewritten as

$$ \begin{aligned} & \mathop {\hbox{max} }\limits_{\vartheta } \;\sum\limits_{i = Y,Z} {{\varvec{\upbeta}}^{T} (\vartheta ){\varvec{\upalpha}}_{iX} (\varepsilon ,\eta ){\varvec{\upalpha}}_{iX}^{T} (\varepsilon ,\eta ){\varvec{\upbeta}}(\vartheta )} \\ & \quad = \mathop {\hbox{max} }\limits_{\vartheta } {\varvec{\upbeta}}^{T} (\vartheta ){\mathbf{G}}(\varepsilon ,\eta ){\mathbf{G}}^{T} (\varepsilon ,\eta ){\varvec{\upbeta}}(\vartheta ) \\ & \quad = \mathop {\hbox{max} }\limits_{\vartheta } \frac{{{\varvec{\upbeta}}^{T} (\vartheta ){\mathbf{G}}(\varepsilon ,\eta ){\mathbf{G}}^{T} (\varepsilon ,\eta ){\varvec{\upbeta}}(\vartheta )}}{{{\varvec{\upbeta}}^{T} (\vartheta ){\varvec{\upbeta}}(\vartheta )}} \\ \end{aligned} $$

(85)

where ${\mathbf{G}}(\varepsilon ,\eta ){\mathbf{G}}^{T} (\varepsilon ,\eta ) = \sum\nolimits_{i = Y,Z} {{\varvec{\upalpha}}_{iX} (\varepsilon ,\eta ){\varvec{\upalpha}}_{iX}^{T} (\varepsilon ,\eta )}$.

Maximizing a quadratic form under the unit norm constraint of its argument is classically obtained by taking ${\varvec{\upbeta}}(\vartheta )$ to be the eigenvector of ${\mathbf{G}}(\varepsilon ,\eta ){\mathbf{G}}^{T} (\varepsilon ,\eta )$ associated with the largest Eigen-value. Once ${\varvec{\upbeta}}(\vartheta )$ is obtained, the Givens rotation matrix ${\mathbf{g}}(\varepsilon ,\eta ,\vartheta )$ can be obtained.

Joint diagonalization of a set of normal matrices can be achieved by successive Givens rotations, in other words it can be carried out by product of successive Givens rotation matrices. The product of successive Givens rotation matrices can be considered as a joint diagonalizer and as the iteration has been finished, ${\tilde{\boldsymbol{\Gamma }}}_{YX} ({\varvec{\uptheta}})$ (${\tilde{\boldsymbol{\Gamma }}}_{ZX} ({\varvec{\uptheta}})$) can be seen as ${\tilde{\boldsymbol{\Phi}}^{\prime}}({\varvec{\uptheta}})$ (${\tilde{\boldsymbol{\Omega}}^{\prime}}({\varvec{\uptheta}})$) respectively.