1 Introduction

Direction of arrival (DOA) estimation of signals is a hotspot in the field of array signal processing. In this application, an array is composed of a plurality of sensors placed in different positions, and array signal processing is used to process the spatial signal and extract the target and its characteristics while simultaneously suppressing interference and noise. Compared with traditional orientation using a single sensor, the sensor array allows for flexible beam control, higher signal gain, stronger anti-interference properties, and ultra-high spatial resolution. These advantages have caused array signal processing technology to undergo rapid development in recent decades.

A basic application of array signal processing is DOA estimation, which is one of most important tasks in radar, sonar, and other fields. The basic goal of DOA estimation is to obtain the location of a plurality of interest targets within a spatial region simultaneously. The information required is essentially the angular direction of each signal as it arrives at the reference array element.

The resolution of DOA estimation is determined by the array length, which is called the Rayleigh limit. Methods that provide a resolution exceeding the Rayleigh limit are called super-resolution methods. For sensor arrays, numerous subspace algorithms with super-resolution capability that minimize the computational complexity have been proposed to estimate the DOA of targets, such as the Multiple Signal Classification (MUSIC) algorithm, the Estimation of Signal Parameters via Rotational Invariance Techniques ESPRIT algorithm, and subsequent improvements to these algorithms [1]. These algorithms estimate the target’s direction by decomposing the covariance matrix eigenvalues of the received data. This strategy requires a large number of snapshots from the sensor array, and is greatly influenced by the number of array elements and the signal to noise ratio (SNR). Additionally, the angular resolution is poor in the presence of multiple coherent sources [2].

To solve these problems, we propose an algorithm that uses an extended array and singular value decomposition (SVD). After establishing virtual elements, the algorithm estimates received data at these extended elements via bi-linear prediction, then constructs an over-complete dictionary through an extended array manifold [3]. Essentially, we translate the DOA estimation problem into identifying sparse signals that correspond to the data received by the array from the over-complete dictionary, and then obtain the target location information from the DOA signal. To overcome the problem of high computational complexity in the multi-snap case, SVD is used to preprocess the data and obtain the main component of the signals, and then the \(l_1 \) norm method is used to find the optimal solution [4].

2 Related work

The history of array signal processing can be traced back to adaptive antenna technology developed in the 1940s, which used phase-locked loops to track targets. An important step in array signal processing was the side lobe canceller using an adaptive notch proposed by Howells in 1965 [5]. In 1976, Applebaum developed the feedback control algorithm to maximize the signal to interference plus noise ratio (SINR) [6]. Another significant development was the least mean square (LMS) adaptive algorithm proposed by Widrow in 1967 [7]. Several other landmark works include the following: Capon proposed constant gain points in the minimum variance beam former in 1969 [8], Schmidt developed the MUSIC algorithm in 1979 [9], Roy proposed the ESPRIT algorithm to estimate signal parameters in 1986 [10], and Gabriel was the first to propose the term “Smart Array” in adaptive beam forming [11]. In 1978, adaptive antennas were used in military communication systems [12], and antenna arrays started being used in civil cellular communication in the 1990s [13].

Subspace methods open a new era in super-resolution direction finding (DF). These methods use the orthogonality between signal subspace and noise subspace (obtained using SVD and eigenvalue decomposition (EVD)) to obtain spatial pseudo spectra. There are a number of improved algorithms that are based on MUSIC, such as Root-MUSIC [14], MD-MUSIC [15], and the propagator algorithm [16]. Subspace methods are established on the basis of signals that are irrelevant or have weak correlation. To overcome the signal correlation caused by multipath propagation, we need to de-correlate the lower-rank matrix with spatial smoothing methods [17–19], which reduces the effective array aperture. Maximum likelihood (ML) is a more intuitive idea that is used to estimate DOA and other target parameters. It contains two paths: deterministic ML (DML) [20] and stochastic ML (SML) [21, 22]. However, the practicality of these approaches is affected by the high complexity of the required multidimensional search. Viberg proved that a series of algorithms including DML, MD-MUSIC, and ESPRIT could be summarized as subspace fitting problems with a different weight matrix [23]. They solved the weighted subspace fitting (WSF) problem under the minimum mean square error criterion [24]. WSF and ML are both fitting class techniques in DOA estimation, and the results are obtained by using a multidimensional search. Xu et al. [25, 26] proposed cluster based method for processing big data.

In the 1990s, Gorodnitsky discussed the sparse representation issue in biomedical image analysis in a series of articles [27–29], and proposed a classic sparse reconstruction based on weighted iteration. This is known as the FOCal Underdetermined System Solver (FOCUSS). However, the original FOCUSS is only suitable for single snap cases, which makes the detection probability very small in low SNR environments. Researchers developed the M-FOCUSS algorithm for multi-measurement vectors, but the computational complexity increased significantly as the number of snapshots was increased [30]. Malioutov discussed sparse representation of array output data and DOA estimation based on sparse reconstruction, and proposed the \(l_1 -{\textit{SVD}}\) algorithm [31]. The original starting point of \(l_1 -{\textit{SVD}}\) is to estimate the target using a single snapshot, which is equivalent to sparse reconstruction of a single-measurement vector. This estimates the DOA by solving the corresponding basis pursuit (BP) problem. The most outstanding contribution of \(l_1 -{\textit{SVD}}\) is a reduction in the size of the data matrix by using SVD under the multi-snap condition. As a result, the computational complexity no longer increases with the number of snapshots. They also proposed constructing and solving the BP problem based on statistical noise characteristics that are almost independent on any hyper-parameters. The \(l_1 -{\textit{SVD}}\) algorithm has now become a classical method in sparse reconstruction DOA estimation, and is widely used with coherent signals. The resolution is far higher than other traditional methods, and the achievable estimation accuracy is high.

The basic idea of beam forming is to sum different elements’ output signals weighted and gather the signal-gain in one direction. With the direction pointing beam, DOA can be estimated by searching maximum output of desired signals in all directions. Conventional beam forming methods adjust received signal’s amplitude and phase of different element by weighting factor to realizing different element’s superimposing in same direction [32]. But DOA estimation by conventional beam forming has low resolution and needs a large number of array elements. When the number of elements is small, the estimation results are inaccurate. Therefore, conventional beam forming methods are rarely used in practice.

Subspace decomposition super-resolution DOA estimation methods could break the Rayleigh limit [33]. These methods estimate parameters by dividing receiving data into orthogonal signal subspace and noise subspace. Subspace decomposition methods mainly include MUSIC algorithms and ESPRIT algorithms. MUSIC algorithms need power spectral peak search and have high requirement for computation and storage. ESPRIT algorithms decompose sensor array into two sub-arrays with same structure. These algorithms estimate signal DOA using the rotational invariance of data covariance matrix’s signal subspace. ESPRIT algorithms have a large amount of computation and strict requirement for array formation.

Weighted subspace fitting methods can be divided into two categories: signal subspace fitting and noise subspace fitting. The main advantages of these methods are high precision and applicable for both coherent signals and non-coherent signals. The disadvantage of these methods is high complexity.

In comparison with these traditional methods, spatial spectrum estimation methods based on sparse theory have higher spatial resolution and obvious advantages in dealing with coherent signals. These methods can achieve better DOA estimation performance in low SNR and small snapshots.

3 Model

In DOA estimation, the target azimuth is sparse over the entire possible angle space. We can therefore divide the sparse space into a spatial grid. DOA in sparse spaces uses the natural sparsity of the target orientation in angle space and establishes an over-complete dictionary according to the array structure and signal form. The received data from the array is decomposed using the over-complete dictionary to obtain the best atoms. The data then has a one-to-one correspondence with its spatial position, thus realizing DOA estimation of the targets.

3.1 Sparse signal representation

In traditional Fourier transforms and time-frequency transforms, a signal is completely decomposed into orthogonal bases. The original signal can be recovered by inverse transformation. Signal decomposition describes the signal from another perspective. One key aspect in the development of signal processing technology is to try and represent a signal in the most concise form possible. Samos and Aymes put forward the concept of sparse signal decomposition for the first time [34]. In this concept, the bases used to represent the signal no longer guarantee orthogonality, but are selected according to the characteristics of the signal. The base here is renamed to atom because it is redundant, and does not have the properties of a base. The set consisting of these atoms is called an over-complete dictionary. To summarize, sparse decomposition decomposes a signal into a function that is represented by atoms from an over-complete dictionary, and the result of the decomposition is also sparse.

In accordance with the nature of an over-complete dictionary, the signal representation of atoms is not unique. This corresponds to an underdetermined system, and we cannot obtain a unique solution for the over-complete dictionary when solving the underdetermined system. Sparsity priori of x is needed. For a given signal, a higher level of sparsity leads to a lower correlation between atoms after decomposition. This concept can be used as a performance measure of the algorithm. There are several definitions of sparsity:

  1. (a)

    Defined by the \(\ell _0 \) norm Sparsity is used to describe the number of non-zero elements in the transformation coefficients. Fewer non-zero elements in the transform coefficients means that the signal is more sparse. In mathematics, sparsity is usually quantified by the \(\ell _0 \) norm:

    $$\begin{aligned} \left\| a \right\| _0 =\sum _{n=1}^N {1_{\left\{ {na_n \ne 0} \right\} } } , \end{aligned}$$
    (1)

    where a is the transform coefficients of signal x. This formula represents the number of non-zero components in a.

  2. (b)

    Defined by the \(\ell _p \) norm The transform coefficients cannot all be zero when the signal contains noise, and the \(\ell _0 \) norm cannot effectively express the sparsity of a signal. In this case, the sparsity can be defined by the \(\ell p\) norm:

    $$\begin{aligned} \left\| a \right\| _p =\Bigg (\sum _{n=1}^N {\left| {a_n } \right| ^{p}\Bigg )^{1/p}} ,p\le 1 \end{aligned}$$
    (2)
  3. (c)

    Defined by the sparse factor The sparse factor is set by the transform coefficient’s threshold, \(a_T \). Sparsity is defined by the ratio between the number of coefficients with an absolute value greater than threshold and the total number of transform coefficients, shown as follows:

    $$\begin{aligned} S_f =\frac{1}{N}\sum _{n=1}^N {1_{\{n\left| {a_n } \right| >a_T \}} } . \end{aligned}$$
    (3)

To start the analysis, the signal is decomposed into a linear combination of a series of basic functions. For the set \(\Phi =\{\varphi _n (t),n=1,2,\ldots ,N\}\), all of the elements are unit vectors. In Hilbert space \(H=R^{M}\), and the signal is decomposed into linear combinations of several basic functions \(\varphi _n (t)\):

$$\begin{aligned} X\left( t \right) =\sum _{n=1}^N {a_n {\varvec{\varphi }} _n (t)=\Phi a}, \end{aligned}$$
(4)

where \(a=[a_1 ,a_2 ,\ldots ,a_N ]^{T}\) is the transform coefficient vector. Orthogonal decomposition means decomposing the signal into linear combinations of a series of basic functions where the combination is unique. Common orthogonal decompositions include the Fourier transform, the short-time Fourier transform, and the wavelet transform. Orthogonal decomposition can decompose a signal with a limited set of vectors or basis functions. However, the decomposition is inflexible because the basic functions are fixed. In sparse decomposition, the structure of the over-complete dictionary is based on the characteristics of the signal. This gives a more compact representation that is closer to the real signal.

Sparse decomposition selects atoms from a redundant over-complete dictionary, and the resulting decomposition is not unique. Sparse decomposition contains two steps: first, appropriate atoms based on the objective function are selected, and then the best K atom combinations are chosen. In compressive sensing theory, the signal must meet the requirement of sparsity. That is, the signal can be a sparse representation in a particular transformation.

For example, the signal \({\varvec{x}}\in R^{N}\) can be represented by the orthonormal basis set \(\Psi \) as:

$$\begin{aligned} a=\Psi ^{T}x, \end{aligned}$$
(5)

where a is the coefficient vector of the orthonormal basis \(\Psi \). If its \(\ell _p \) norm satisfies the condition:

$$\begin{aligned} \left\| a \right\| _p \le K, \end{aligned}$$
(6)

in which \(0<p<2\) and \(K>0\), then we say x is sparse in the transform domain \(\Psi \).

There are no restrictions regarding the dictionary structure in the sparse representation. The dictionary is selected flexibly according to the characteristics of the signals, and mainly includes discrete cosine transform bases, fast Fourier transform bases, discrete wavelet transform bases, Curvelet transform bases, and Gabo transform bases.

For the given over-complete dictionary \(\Psi =\{\Psi _i ,i=1,2,\ldots n\}\), the elements satisfy the condition \(\Psi _i \in R^{d}\). The items can be normalized as \(\left\| {\Psi _i } \right\| 2=1\) and \(n>d\). For any signal \(x\in R^{d}\), we can adaptively select a group of atoms in \(\Psi \) to decompose the signal as:

$$\begin{aligned} x=\sum _{ieI} {a_i \Psi _i } , \end{aligned}$$
(7)

where \(I\subseteq \{1,2,\ldots ,n\}\) is the subscript set of \(\Psi _i \), and \(A=\{a_{i\in I} \}\) is the coefficient set. The dimension of the subscript set is always far less than the dimension of the over-complete dictionary, and signals can be expressed by using a small number of atoms. The above problem can be represented in matrix form as:

$$\begin{aligned} x=\Psi a, \end{aligned}$$
(8)

where \(x\in R^{d}\), \(\Psi \in R^{d\times n}\), \(a\in R^{d}\), and x is a sparse vector.

The key issue of sparse decomposition is obtaining a sparse vector a, which can be expressed as:

$$\begin{aligned} \arg \min \left\| a \right\| _0 \,\,\,\,\,\,\,s.t.\,\,\,\,\,x={\varvec{\psi }} a \end{aligned}$$
(9)

where \(\left\| a \right\| _0 \) is a measure of the sparsity of vector a.

Suppose the length of a signal \(x\in R^{d}\) is d. We can select m atoms from the over-complete dictionary \(\Psi \) to get a sparse approximation of x as:

$$\begin{aligned} \hat{{x}}=\sum _{i=1}^m {a_{{\varvec{\gamma }} _i } {\varvec{\psi }} _{{\varvec{\gamma }}_i } +{\varvec{\eta }} } , \end{aligned}$$
(10)

where \(\gamma _i \in \{1,2,\ldots ,n\}\), and \(\eta \) is the approximation error.

We can define the approximation error energy as \(\varepsilon =\left\| {\varvec{x}}-\hat{{{\varvec{x}}}} \right\| ^{2}\). When \(\varepsilon \) is smaller than a certain value, we select the most sparse linear combination (where m is minimized) as the sparse decomposition of x, that is:

$$\begin{aligned} \arg \min \left\| a \right\| _0 \,\,\,\,\,\,\,s.t.\,\,\,\,\left\| {x-{\varvec{\psi }} a} \right\| _2^2 \le {\varvec{\varepsilon }}. \end{aligned}$$
(11)

3.2 Airspace sparse model

Traditional DOA estimation theories always search for targets over the entire angle space. However, there are generally only a small number of angular orientations in which a target will be present. The target azimuth can be assumed as sparse over the entire angle space, and Fig. 1 shows the airspace sparsity diagram.

Fig. 1
figure 1

Diagram of airspace sparsity

Full size image

In Fig. 1, the gray box is an array element, the circles are possible spatial orientations of the targets, and the black circles are the positions of the real targets. The entire angle space can be divided into \(\{\theta _1 ,\theta _2 ,...,\theta _N \}\) for one-dimensional DOA estimation. The corresponding azimuths of the real targets are \(\{\varphi _1 ,\varphi _2 ,...,\varphi _k \}\), where \(\{\varphi _1 ,\varphi _2 ,...,\varphi _k \}\subset \{\theta _1 ,\theta _2 ,...,\theta _N \}\) and \(k\ll N\). The constructed sparse signal space \(s=[{\begin{array}{llll} {s_1 }&{} {s_2 }&{} {...}&{} {s_N } \\ \end{array} }]\) includes k real targets to represent the sparsity of the sources, and \(s_k \) only has a nonzero value when the target exists [35]. The DOA estimation signal model is:

$$\begin{aligned} y=As+n, \end{aligned}$$
(12)

where y is the received data from the array, A is the manifold matrix of an \(M\times N\) dimensional array, and n is received noise from the array. DOA estimation in a sparse space is the same as reconstructing the sparse vector s using the received data y and the corresponding array manifold A. The first k largest components represent the corresponding target, and we can then obtain the azimuth of the targets [36]:

$$\begin{aligned} {\mathop {{s}}\limits ^{\frown }} = \text {arg} \text {min} \parallel s\parallel _1 ,s.t.\parallel y-As\parallel _2 \le {\varvec{\sigma }} . \end{aligned}$$
(13)

The array manifold A under sparse conditions can be seen as an over-complete dictionary. The atom density depends on the division size of the spatial angle. Suppose the estimated space \([-{\varvec{\pi }} /2,{\varvec{\pi }} /2]\) is divided according to the interval of \(1^{\circ }\) as:

$$\begin{aligned} A=\left[ {{\begin{array}{l} {\begin{array}{l} 1 \\ e^{-j{\varvec{\pi }} \sin {\varvec{\theta }} _1 } \\ \vdots \\ e^{-j\left( {M-1} \right) {\varvec{\pi }} \sin {\varvec{\theta }}_1 } \\ \end{array}} {\begin{array}{l} 1 \\ e^{-j{\varvec{\pi }} \sin {\varvec{\theta }}_2 } \\ \vdots \\ e^{-j\left( {M-1} \right) {\varvec{\pi }} \sin {\varvec{\theta }} _2 } \\ \end{array}} \\ \end{array} }{\begin{array}{l} {\begin{array}{l} \cdots \\ \cdots \\ \cdots \\ \end{array}} {\begin{array}{l} 1 \\ e^{-j{\varvec{\pi }} \sin {\varvec{\theta }} _{2N+1} } \\ \vdots \\ e^{-j\left( {M-1} \right) {\varvec{\pi }} \sin {\varvec{\theta }} _{2N+1} } \\ \end{array}} \\ \end{array} }} \right] , \end{aligned}$$
(14)

where \(\theta _n =-\pi /2+\pi \cdot (n-1)/2N\). Other methods can also be used, such as the equal sine space partition method [37].

To simplify the problem, the commonly used one-dimensional uniform linear array (ULA) can be used as the target array reception model. The assumptions are as follows:

  1. (a)

    Reception characteristics of array elements are independent of the element size, and are only related to their spatial positions. The output gain of each element is the same, and coupling between elements is ignored. The noise received by each element is Gaussian white noise, and is irrelevant to the signal.

  2. (b)

    The target is in the far field, the spatial signal is approximately a straight line in the medium, and the medium is homogeneous.

  3. (c)

    The radiation signal from the excited target is narrowband such that the direction vector is independent of the signal frequency.

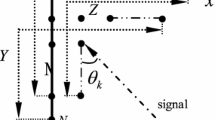
The model for the receiving array is shown in Fig. 2.

Fig. 2
figure 2

One-dimensional ULA receiving array model

Full size image

For narrowband signals, different delays between the signals can be represented by phase differences. Under the condition of a single source, the received signal can be simply expressed as:

$$\begin{aligned} X(t)=a({\varvec{\theta }} )s(t)+n(t). \end{aligned}$$
(15)

The weighted output received signal is:

$$\begin{aligned} y(t)=W^{H}X(t)=X^{T}(t)W^{{*}}, \end{aligned}$$
(16)

where \(W=[w_1 ,w_2 ,\ldots ,w_M ]^{T}\) is the weight vector. Therefore:

$$\begin{aligned} y(t)=W^{H}[a({\varvec{\theta }} )s(t)+n(t)]. \end{aligned}$$
(17)

4 The proposed algorithm

In sparse space DOA estimation, increasing the number of array elements can improve estimation accuracy. However, in real detection environments, increasing the number of elements increases both the cost and the difficulty of the physical layout. We propose a DOA estimation algorithm based on an extended array using virtual elements. The algorithm first estimates the received data of the virtual elements via bi-linear prediction, and then obtains the DOA by using SVD. Thus, this algorithm can improve the positioning performance of the sparse space method while maintaining a reasonable number of array elements.

4.1 Extended array

Suppose an array consists of N real elements with a uniform element spacing of d, and the real elements from left to right are represented by \(j=1,2,\ldots ,N\). The elements are then outwardly extended by bi-linear prediction to constitute an extended array [38]. This is shown in Fig. 3, where the black points are real elements and the white points are virtual elements.

Fig. 3
figure 3

Diagram of the extended array

Full size image

The forward extended elements are numbered as \(N+1,N+2,\ldots ,L\), and the backward extended elements are numbered as \(0,\ldots ,-M+2,-M+1\). For the real element j, the output signal at time t is:

$$\begin{aligned} x_j (t)=s_j (t-{\varvec{\tau }} _j )+n_j (t), \end{aligned}$$
(18)

where s(t) is the target signal, and \(\tau _j \) is the signal arrival time interval between element j and a reference element. \(\tau _j =(j-1)d\sin \theta /c\), where \(\theta \) is the radiation angle and c is the signal propagation speed within the medium. The real element data is first used to estimate the forward and backward prediction coefficients. For the real elements 1 and N at time t, we can write:

$$\begin{aligned} -\left[ {x_{N-1}^T \hbox { }x_{N-2}^T \hbox { }\cdots \hbox { }x_1^T } \right] \left[ {\begin{array}{l} a_1^f \\ a_2^f \\ \vdots \\ a_{N-1}^f \\ \end{array}} \right] =x_N^T \end{aligned}$$
(19)

and

$$\begin{aligned} -\left[ {x_2^T \hbox { }x_3^T \hbox { }\cdots \hbox { }x_N^T } \right] \left[ {\begin{array}{l} a_1^b \\ a_2^b \\ \vdots \\ a_{N-1}^b \\ \end{array}} \right] =x_1^T , \end{aligned}$$
(20)

where \(a_k^f \) and \(a_k^b \) \((k=1,2,\cdots ,N-1)\) are the forward and backward prediction coefficients, respectively. The two prediction coefficients can be calculated by solving the linear prediction Wiener-Hopf equation. The predicted output value of the extended elements 0 and \(N+1\) can then be written as:

$$\begin{aligned} x_0^T =-\sum _{k=1}^{N-1} {a_k^b x_k^T } \end{aligned}$$
(21)

and

$$\begin{aligned} x_{N+1}^T =-\sum _{k=1}^{N-1} {a_k^f x_{N-k+1}^T } . \end{aligned}$$
(22)

Similarly, we can predict the output value of the other virtual elements to get extended array output data. Expanding the real array allows the array aperture to be virtually extended, which yields an improvement in DOA estimation performance and enables multi-target estimation with fewer elements. The extended array manifold is configured as an over-complete dictionary A through formula (14), and the extended array data y is used to reconstruct the sparse vector and obtain the signal DOA.

4.2 SVD DOA estimation based on an extended array

The problem of DOA estimation based on a sparse space is converted to solving an \(l_0 \) norm optimization problem of the sparse signal s. In fact, this is a NP-hard problem which can be solved by MP or other algorithms. The problem can also be transformed such that the goal is to obtain the optimal \(l_1 \) norm.

When solving with the \(l_1 \) norm method, the objective function is:

$$\begin{aligned} \min \left\| s \right\| _1 \hbox { }s.t.\hbox { }\left\| {y-As} \right\| _2^2 \le \sigma , \end{aligned}$$
(23)

where \(\sigma \) is the noise level. The formula can be written as an equation unfettered by noise as follows:

$$\begin{aligned} \min \left\| {y-As} \right\| _2^2 +\lambda \left\| s \right\| _1 , \end{aligned}$$
(24)

where \(\lambda \) is the sparsity parameter. Its value is determined by the intensity of the noise.

Suppose the detection array consists of M elements and it receives K (K<M) far-field propagation signals. The K signals are expressed as \(u_k (t),k=1,2,\ldots ,K\), and the received signals from the M elements are expressed as \(y_m (t),m=1,2,\ldots ,M\). Assuming the noise received by the elements \(n_m (t),n=1,2,\ldots ,M\) is Gaussian, the data received by array is:

$$\begin{aligned} Y(t)=A(\theta )u(t)+n(t), \end{aligned}$$
(25)

where \(Y(t)=[y_1 (t)y_2 (t)\cdots y_M (t)]\), \(u(t)=[u_1 (t)u_2 (t)\cdots u_K (t)]\), and \(n(t)=[n_1 (t)n_2 (t)\cdots n_M (t)]\).

The traditional spatial spectrum method estimates the DOA \(\theta =[\theta _1 \hbox { }\theta _2 \cdots \theta _k ]\) and the number of targets by using the received data. DOA estimation based on sparse space represents \(A(\theta )\) in accordance with formula (14). \(A(\theta )\) can be seen as an over-complete dictionary which contains all of the angle information.

In the single snap case, \(A(\theta )\) is the over-complete dictionary and the model is:

$$\begin{aligned} y=As+n. \end{aligned}$$
(26)

The problem of target DOA estimation is converted into the problem of identifying the sparse signal s corresponding to the received array data y from the over-complete dictionary \(A(\theta )\). The objective function is:

$$\begin{aligned} \min \left\| {y-As} \right\| _2^2 +\lambda \left\| s \right\| _1 \end{aligned}$$
(27)

In the multi-snap case, the objective function can be extended and expressed as:

$$\begin{aligned} \min \left\| {Y-AS} \right\| _f^2 +\lambda \left\| {s^{\xi _2 }} \right\| _1 , \end{aligned}$$
(28)

where \(\left\| {Y-AS} \right\| _f^2 =\left\| {vec(Y-AS)} \right\| _2^2 \), \(s^{\varepsilon _2 }\) is the function of S, and \(s_i^{^{\xi _2 }} =\left\| {[s_1 (t_1 )s_i (t_2 )\cdots s_i (t_T )]} \right\| 2\). Since the subscript \(i\in \{1,2,\ldots N_\theta \}\sin ^{-1}\theta \), the signal can be written as \(s_i^{^{\xi _2 }} =[{\begin{array}{llllll} {s_1^{\xi _2 } }&{} {s_2^{\xi _2 } }&{} \ldots &{} {s_{N\theta }^{\xi _2 } } \\ \end{array} }]\).

Under the same conditions, multi-snap data can provide a more accurate DOA estimation. However, the increase in the amount of data leads to an increased number of calculations, which makes real-time processing difficult. To overcome this issue, SVD is used to preprocess the data and obtain the main component of the signal. The DOA is then estimated using the \(l_1 \) norm method.

Suppose there are K known waves. By using SVD on received array data from T snapshots, we obtain:

$$\begin{aligned} Y=ULV^{H}=[U_{SV} \hbox { }U_{NV} ]LV^{H}. \end{aligned}$$
(29)

From SVD knowledge, we know that \(U_{SV} \) contains the main target information and is composed of K left singular vectors with large singular values, and that \(U_{NV} \) is the noise subspace matrix and is composed of M-K left singular vectors with small singular values. \(U_{SV} \) contains almost all of the energy. By letting \(Y_{SV} =U_{SV} \), we can obtain multi-snap data after dimension reduction from:

$$\begin{aligned} Y_{SV} =AS_{SV} +N_{SV} . \end{aligned}$$
(30)

By using SVD on the array data, the number of unknown quantities decreases from T snapshots to the number of target sources K, and \(K\ll T\) in a real environment. The amount of data is significantly reduced by SVD, therefore the computational speed of the \(l_1 \) norm method is greatly improved. The objective function is:

$$\begin{aligned} \min \left\| {Y_{SV} -AS_{SV} } \right\| _f^2 +\lambda \left\| {s^{\xi _2 }} \right\| _1 . \end{aligned}$$
(31)

Thus, we obtain the target azimuth estimation.

5 Simulation and analysis

The performance of the algorithm was tested through simulations. The simulation conditions are based on a ULA, and the number of real array elements is 6. The proposed algorithm expands the 6 real elements to an extended array of 10 elements via bi-linear prediction, with two virtual elements added on each side of the linear array.

5.1 Single source estimation performance

First, the estimation performance of different algorithms is tested for a single target with different SNRs.

Suppose there is a narrowband signal incident on the ULA at an angle of 10\(^{\circ }\). The element spacing is half of the center wavelength, the wave velocity is 200 m/s and 64 snapshots were used in this test. MUSIC algorithm, L1-SVD algorithm and the proposed Extended Array SVD algorithm are used to estimate the target direction for SNRs of 10 dB and −10 dB. The results of this test are shown in Fig. 4.

Fig. 4
figure 4

DOA estimation results for a single target

Full size image

As can be seen from Fig. 4a, when SNR = 10 dB, all algorithms can estimate the DOA of the single target. It should be noted that the estimation result from MUSIC algorithm has some deviations, while L1-SVD algorithm and Extended Array SVD algorithm can estimate the DOA accurately. When SNR=−10 dB as shown in Fig. 4b, MUSIC algorithm and L1-SVD algorithm lost the target, but Extended Array SVD algorithm still can estimate the DOA of the target accurately. These results show that Extended Array SVD algorithm offers better DOA estimation performance than MUSIC algorithm and L1-SVD algorithm for a single target.

Furthermore, the DOA estimation performance between MUSIC algorithm, L1-SVD algorithm and Extended Array SVD algorithm was compared for different SNRs. Figure 5 shows the root mean square error (RMSE) curve of the estimation obtained from the three algorithms for different SNRs in Gaussian white noise. The SNR ranges for −20 to 30 dB. This test was run for 64 snapshots, and the results are obtained by performing 2000 Monte Carlo simulations.

Fig. 5
figure 5

RMSE curve for different SNRs

Full size image

Figure 5 shows that Extended Array SVD algorithm has better estimation performance than MUSIC algorithm and L1-SVD algorithm under different SNRs. The performance gap is minimal between three algorithms when SNR is in −5 to 5 dB. In this range, the prediction accuracy of virtual elements is low while MUSIC algorithm and L1-SVD algorithm still have some estimation accuracy. When SNR > 5 dB, estimation accuracy of MUSIC algorithm and L1-SVD algorithm no longer increase with SNR and reach the algorithm limit, while estimation accuracy of Extended Array SVD algorithm still improves significantly with SNR increases. This shows the excellent estimation performance of Extended Array SVD algorithm at high SNR. When SNR < −5 dB, estimation error of MUSIC algorithm and L1-SVD algorithm increases significantly and cannot get correct DOA, while Extended Array SVD algorithm still can estimate the target.

5.2 Multiple approximate sources resolution performance

Next, the estimation performance of the different algorithms in the presence of multiple non-coherent signal sources that are separated by both large and small angles is tested and compared.

The first study tests the resolution performance of different algorithms on two targets that are spaced far apart. The wave velocity is 200m/s and the SNR = 15 dB. Suppose there are two non-coherent signals at a frequency of 20Hz incident on the ULA at angles of 30\(^{\circ }\) and 40\(^{\circ }\), respectively. Three different algorithms were used to estimate the DOA of the two targets, and the results are shown in Fig. 6.

Fig. 6
figure 6

DOA estimation for angles of 30\({^{\circ }}\) and 40\({^{\circ }}\)

Full size image

As can be seen from the Fig. 6, all algorithms can estimate the direction of the targets when the angle between the two targets is large, wherein L1-SVD algorithm and Extended Array SVD algorithm have higher estimation accuracy.

Next, the resolution performance of different algorithms for two targets that are in close proximity is studied. Using the same velocity and SNR as the previous case, two non-coherent signals are incident on the ULA at angles of 30\(^{\circ }\) and 33\(^{\circ }\). Three algorithms were used to estimate the DOA of the two targets, and the results are shown in Fig. 7.

Fig. 7
figure 7

DOA estimation at angles of 30\({^{\circ }}\) and 33\({^{\circ }}\)

Full size image
Fig. 8
figure 8

DOA estimation for coherent targets

Full size image

Figure 7 shows that when the two DOAs are close, MUSIC algorithm and L1-SVD algorithm are unable to distinguish them; however Extended Array SVD algorithm is still able to distinguish the two targets with moderate accuracy.

5.3 Coherent sources estimation performance

Lastly, the estimation performance of different algorithms in the presence of multiple coherent sources is tested and compared.

For sensor array where signal transmitting with multiplexing, multi-interface reflection or velocity difference in different medium, such as underwater sensor array, signal may be coherent or mix received. For example, when signal reflected at the interface, sensor array receives original wave and reflected wave at the same time but they have different DOAs. Due to radiating from the same source, the two signals will be coherent if the phase delay is small.

Suppose there are two coherent signals at a frequency of 20Hz incident on the ULA at angles of 20\({^{\circ }}\) and 50\({^{\circ }}\), respectively. The SNR=15dB, and 64 snapshots were used in this test. Three algorithms were used to estimate the DOA of the two targets, and the results are shown in Fig. 8.

As can be seen from the Fig. 8, MUSIC algorithm cannot estimate two coherent sources effectively. L1-SVD algorithm can distinguish the sources but with an obvious bias. That is because the coherent nature of the signals leads to a deficit in the rank of the signal covariance matrix. In contrast, Extended Array SVD algorithm can estimate the direction of the coherent signals accurately. Thus, when compared with traditional algorithms, Extended Array SVD algorithm exhibits better estimation performance and can be used for estimating the DOA of multiple coherent sources.

6 Conclusion

In this paper, we proposed a SVD DOA estimation algorithm based on an extended array. The characteristics of space sparsity were first analyzed, and the target sparse space model was established. The algorithm constructs the extended array by using virtual elements, and the DOA is estimated based on the sparsity of the target space. Simulations show that the algorithm can provide accurate estimates for both the single-target and multi-target cases, and also provides high estimation accuracy for coherent sources. Thus, the proposed algorithm can accurately obtain the location of single target and multi targets while also significantly improving the sparse space positioning capability for arrays with a limited number of elements. This method can be applied to target detection systems like underwater acoustic sensor array.