Convergent method for designing high-accuracy bi-equiripple variable-delay filters using new delay-error expression

Abstract

This paper proposes a fast non-iterative approach to the design of an odd-order bi-equiripple variable-delay (VD) digital filter whose mathematical model is a multi-variable (MV) transfer function. The objective of the bi-equiripple design is to minimize the maximum frequency-response deviation of this MV transfer function while mitigating the large overshoots of the VD response at the same time. Since the group-delay function is nonlinear with respect to the MV transfer-function coefficients, it is first linearized through using an approximate approach. This linearization enables the bi-equiripple VD filter to be designed with linear constraints, and the bi-equiripple design is then formulated as a convex minimization problem. The convex minimization does not require any iterations and thus it is fast and yields a convergent optimal solution. Solving the convex minimization problem produces a bi-equiripple VD filter with minimized worst-case frequency-response error and mitigated VD-deviation overshoots (jumps). An illustrating example is presented to demonstrate the above simultaneous deviation suppressions.

1 Introduction

Variable non-integer group-delay digital filters are recognized as an important class of signal processing systems. Since such a delay system has continuously variable-delay (VD) characteristics, arbitrary delay value can be obtained on-line in the process of signal processing applications (Farrow 1988; Liu and Wei 1992). The VD filters have lots of applications, including sampling-rate alteration (arbitrary noninteger-ratio up-sampling or down-sampling), signal interpolation, and delay estimation. Different from the traditional filter having unchangeable frequency response, the VD filter has a multi-parameterized transfer function, i.e., its mathematical model is a multi-variable (MV) transfer function. The extra parameter in the MV transfer function tunes the delay characteristics and thus introduces the delay tunability. The VD filter design problem is basically an approximation problem involving two-dimensional (2-D) indices (delay element and delay parameter), and the approximation problem itself is to approximate the desired VD characteristics in the least-squares sense or minimax sense. Most of the developed design methods yield a VD filter approximating the desired frequency-response (FreRes) by minimizing either the integral squared error or the maximum FreRes error (Deng 2001, 2004; Deng and Lian 2006; Deng 2007; Soontornwong and Chivapreecha 2015; Tseng and Lee 2012; Liu and You 2007; Pei et al. 2012; Deng 2011; Deng and Qin 2013; Deng 2012b), but this may produce a VD filter whose group-delay deviations are too large. Hence, some efforts have been devoted to the suppressions of the VD-error overshoots (jumps) such that the overshoots can be mitigated (Deng 2012a; Deng and Qin 2014; Deng and Soontornwong 2016; Deng et al. 2012). For simplicity, we refer to such a design the bi-equiripple design. In Deng (2012a) and Deng and Qin (2014), iterative procedures are taken to solve the bi-equiripple design problem. The difficulty lies in the nonlinearity of the VD function because the group-delay characteristic is nonlinear with respect to the transfer-function coefficients. The nonlinear VD function makes the bi-equiripple design extremely nonlinear, which cannot be solved by using a convex minimization technique. In Deng (2012a), the nonlinear group-delay expression is first simplified as a bi-linear one, and then iterative procedures are taken to find the two coefficient vectors by iteratively minimizing a mixed error function. In Deng and Qin (2014), a weighting function is further adopted in the iterative process to further enhance the delay-error suppression. As mentioned in Deng and Qin (2014), one can only uses a heuristic method to find an appropriate weighting function and no way to guarantee the optimality of the weighting function. Furthermore, the iterative design process takes a long time to converge and the final solution is definitely a locally optimal solution.

This paper aims to overcome the above difficulty through approximately linearizing the group-delay error function as a perfectly linear one (not bi-linear function). By employing this newly proposed linearization technique, we can obtain a completely linearized group-delay error formula. This linearized group-delay error enables us to formulate the bi-equiripple design as a convex minimization problem. More specifically, a bi-equiripple VD filter can be designed by converting the bi-equiripple design problem to a convex minimization problem. The cost function to be minimized is a weighted summation of the upper bounds on the delay errors and FreRes errors. That is, this cost function is a mixed one, where a weighting factor is utilized to link the two error bounds. The VD-filter designer can change the factor to adjust the trade-off between the two error bounds. The convex minimization includes two sets of design constraints. One set includes linear-inequality constraints, and the other includes quadratic-cone (Qcone) constraints. The linear-inequality constraints are imposed on the upper bound of group-delay errors, and the Qcone constraints are imposed on the upper bound of absolute FreRes errors. Solving the convex minimization problem produces the optimal bi-equiripple solution. To summarize, this non-iterative bi-equiripple design strategy has the following distinct features and important advantages.

• 1. Since the constraints imposed on the VD errors are linear inequalities, they become linear programming (LP) constraints in the bi-equiripple design. Thus, the bi-equiripple design are non-iterative. This non-iterative design is much simpler and faster than the iterative ones in Deng (2012a) and Deng and Qin (2014);

• 2. A weighting function is no longer needed in the bi-equiripple design because the newly derived VD-error formula is much more accurate than the existing one in Deng (2012a) and Deng and Qin (2014). In Deng and Qin (2014), the weighting function is selected by trial and error;

• 3. The proposed bi-equiripple design algorithm is weighting-free and non-iterative, which is always convergent and can get more accurate design with much less computations than the iterative ones in Deng (2012a) and Deng and Qin (2014).

2 Two kinds of error expressions

Since this paper uses both the complex-valued FreRes error function and group-delay error function to formulate the bi-equiripple design, the next subsection first briefly reviews the complex-valued FreRes error function derived in Deng (2007, 2012a) and Deng and Qin (2014). This is for the easy-understanding reason. After reviewing the complex-valued FreRes error function, we proceed to the key point of this section, i.e., we derive a completely linearized group-delay error function. The core of this paper is to formulate a new non-iterative bi-equiripple design approach by employing the two error expressions.

2.1 VFR error

For the sake of easy understanding, this subsection needs to first briefly review the previously derived FreRes in Deng (2007) and the complex-valued FreRes error function in Deng (2007, 2012a) and Deng and Qin (2014). This is because they will be used later in deriving the linearized VD error and formulating the new non-iterative design.

The desired FreRes characteristic of the odd-order design is

$$\begin{aligned} \hat{D}(\omega ,\hat{\tau }) = e^{-j \omega \hat{\tau } }, \quad \hat{\tau } \in [0,1] \end{aligned}$$

(1)

where $\hat{ \tau }$ is the ideal group-dealy. Obviously, this is a 2-D function that involves both $\omega$ and $\hat{\tau }$. In regard to the frequency $\omega$, it is defined in the full frequency band $\omega \in [0, \pi ]$, but we only approximate $\hat{D}(\omega ,\hat{\tau })$ in the interested band $\omega \in [0, \omega _c]$, $0< \omega _c < \pi$ during the design, and no approximation in the uninterested frequency band $\omega \in (\omega _c,\pi ]$ is done. This is based on the assumption that important frequency components of the signals are located only in the frequency band of interest.

By using $\tau$ to substitute $\hat{\tau }$ as

$$\begin{aligned} \hat{ \tau } = 0.5 + \tau \end{aligned}$$

we arrive at

$$\begin{aligned} \hat{ D}(\omega ,\hat{ \tau } ) = e^{-j 0.5 \omega } D(\omega ,\tau ) \end{aligned}$$

(2)

with

$$\begin{aligned} \begin{aligned}&D(\omega ,\tau ) = e^{-j \omega \tau } \\&\tau \in [-0.5,0.5]. \end{aligned} \end{aligned}$$

(3)

Then, it is necessary to approximate $\hat{ D}(\omega ,\hat{ \tau } )$ in (2) by utilizing the transfer function

$$\begin{aligned} \hat{ H}(z,\tau ) = \sum _{k=-N}^{N_1} h_k(\tau ) z^{-k} \end{aligned}$$

(4)

with $N_1=N+1$, and

$$\begin{aligned} h_k(\tau )= \sum _{i=0}^I c(k,i) \tau ^i \end{aligned}$$

(5)

where I is the order of the polynomials $h_k(\tau )$. The primary objective is to determine the optimal coefficients c(k, i) . Once c(k, i) are found, we can change the coefficients $h_k(\tau )$ by changing the value of $\tau$. This generates a new FreRes of $\hat{ H}(z,\tau )$.

By incorporating (5) into (4), we obtain the 2-variable transfer function

$$\begin{aligned} \begin{aligned} \hat{ H}(z,\tau )&= \sum _{k=-N}^{N_1} \sum _{i=0}^I c(k,i) z^{-k} \tau ^i \\&= \sum _{i=0}^{I_\mathrm{e}} \hat{ E}_i(z) \tau ^{2i} + \sum _{i=1}^{I_\mathrm{o}} \hat{ O}_i(z) \tau ^{2i-1} \end{aligned} \end{aligned}$$

(6)

with

$$\begin{aligned} I_\mathrm{e} = \left\lfloor \frac{I}{2} \right\rfloor , \quad I_\mathrm{o} = \left\lceil \frac{I}{2} \right\rceil \end{aligned}$$

(7)

where $\lfloor \; \rfloor$, $\lceil \; \rceil$ are the floor function and the ceiling function, respectively. Also, the filters

$$\begin{aligned} \begin{aligned}&\hat{ E}_i(z) = \sum _{k=-N}^{N_1} c(k,2i) z^{-k}, \quad i=0,1, \ldots , I_\mathrm{e} \\&\hat{ O}_i(z) = \sum _{k=-N}^{N_1} c(k,2i-1) z^{-k}, \quad i=1,2, \ldots , I_\mathrm{o} \end{aligned} \end{aligned}$$

(8)

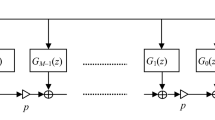
have fixed coefficients and thus unchangeable frequency charactersitics (Farrow 1988). In filtering applications, we only need to change the value of $\tau$ and get a new filter characteristic.

By adopting the symmetries

$$\begin{aligned} \begin{array}{ll} c(k,2i) = c(1-k,2i), &{}\quad i=0, 1, \ldots , I_{\mathrm{e}} \\ c(k,2i-1) = -c(1-k,2i-1), &{}\quad i=1, 2, \ldots , I_{\mathrm{o}} \end{array} \end{aligned}$$

(9)

given in Deng (2007), we can change (6) to the form

$$\begin{aligned} \hat{ H}(z,\tau ) = z^{- 0.5 } H(z,\tau ) \end{aligned}$$

(10)

with

$$\begin{aligned} \begin{aligned}&H(z,\tau ) = \sum _{i=0}^{I_\mathrm{e}} E_i(z) \tau ^{2i} + \sum _{i=1}^{ I_\mathrm{o}} O_i(z) \tau ^{2i-1} \\&E_i(z) = \sum _{k=1}^{N_1} c(k,2i) \left[ z^{(k- 0.5 )} + z^{-(k- 0.5 )} \right] \\&O_i(z) = - \sum _{k=1}^{N_1} c(k,2i-1) \left[ z^{(k- 0.5 )} - z^{-(k- 0.5 )} \right] . \end{aligned} \end{aligned}$$

(11)

Since $\hat{ H}(z,\tau )$ in (10) approximates $\hat{ D}(\omega ,\hat{ \tau } )$ in (2), this implies that $H(z,\tau )$ needs to approximate $D(\omega ,\tau )$ in (3). As shown in Deng (2007), the sub-filters $E_i(z)$ and $O_i(z)$ can be designed to have different orders so as to further reduce the filter cost. By using such an unequal-order formulation, we write the frequency responses

$$\begin{aligned} \begin{aligned} E_i(\omega )&= \sum _{k=1}^{ N_{\mathrm{e}}(i)+1} a_i(k) \cos (k- 0.5 ) \omega = {\varvec{c}}_i^T(\omega ) {\varvec{a}}_i \\ O_i(\omega )&= (-j) \cdot \sum _{k=1}^{N_{\mathrm{o}}(i)+1} b_i(k) \sin (k- 0.5 ) \omega = (-j) \cdot {\varvec{s}}_i^T(\omega ) {\varvec{b}}_i \end{aligned} \end{aligned}$$

(12)

where

$$\begin{aligned}&\begin{array}{ll} a_i(k) = 2 c(k,2i), &{}\quad k=1,2,\ldots , N_{\mathrm{e}}(i)+1 \\ b_i(k) = 2 c(k,2i-1), &{}\quad k=1,2,\ldots , N_{\mathrm{o}}(i)+1 \end{array}\nonumber \\&\begin{aligned}&{\varvec{c}}_i^T(\omega )= \begin{bmatrix} \cos (\frac{\omega }{2})&\quad \cos (\frac{3 \omega }{2})&\quad \ldots&\quad \cos (N_{\mathrm{e}}(i)+ 0.5 ) \omega \end{bmatrix} \\&{\varvec{s}}_i^T(\omega ) = \begin{bmatrix} \sin (\frac{\omega }{2})&\quad \sin (\frac{3 \omega }{2})&\quad \ldots&\quad \sin (N_{\mathrm{o}}(i)+ 0.5 ) \omega \end{bmatrix}. \end{aligned} \end{aligned}$$

(13)

By using the vectors

$$\begin{aligned} {\varvec{a}}_i= & {} \begin{bmatrix} a_i(1) \\ a_i(2) \\ \vdots \\ a_i (N_{\mathrm{e}}(i)+1) \end{bmatrix}, \quad i=0, 1, \ldots , I_\mathrm{e}\\ {\varvec{b}}_i= & {} \begin{bmatrix} b_i(1) \\ b_i(2) \\ \vdots \\ b_i( N_{\mathrm{o}}(i)+1) \end{bmatrix}, \quad i=1, 2, \ldots , I_\mathrm{o} \end{aligned}$$

we obtain the vector-form FreRes

$$\begin{aligned} \begin{aligned} H(\omega ,\tau )&= \sum _{i=0}^{I_\mathrm{e}} \left[ {\varvec{c}}_i^T(\omega ) {\varvec{a}}_i \right] \tau ^{2i} - j \sum _{i=1}^{I_\mathrm{o}} \left[ {\varvec{s}}_i^T(\omega ) {\varvec{b}}_i \right] \tau ^{2i-1} \\&= \sum _{i=0}^{I_\mathrm{e}} {\varvec{u}}_i^T {\varvec{a}}_i -j \sum _{i=1}^{I_\mathrm{o}} {\varvec{v}}_i^T {\varvec{b}}_i \\&= {\varvec{u}}^T {\varvec{a}} - j {\varvec{v}}^T {\varvec{b}} \\&= \mathfrak {R}(\omega ,\tau ) -j \mathfrak {I}(\omega ,\tau ) \end{aligned} \end{aligned}$$

(14)

with

$$\begin{aligned} \mathfrak {R}(\omega ,\tau )= & {} {\varvec{u}}^T {\varvec{a}} \nonumber \\ \mathfrak {I}(\omega ,\tau )= & {} {\varvec{v}}^T {\varvec{b}}\nonumber \\ {\varvec{u}}^T= & {} \begin{bmatrix} {\varvec{u}}_0^T&\quad {\varvec{u}}_1^T&\quad \ldots&\quad {\varvec{u}}_{I_\mathrm{e}}^T \end{bmatrix}, \quad {\varvec{u}}_i^T(\omega ) = {\varvec{c}}_i^T(\omega ) \tau ^{2i} \nonumber \\ {\varvec{v}}^T= & {} \begin{bmatrix} {\varvec{v}}_1^T&\quad {\varvec{v}}_1^T&\quad \ldots&\quad {\varvec{v}}_{I_\mathrm{o}}^T \end{bmatrix}, \quad {\varvec{v}}_i^T(\omega ) = {\varvec{s}}_i^T(\omega ) \tau ^{2i-1}\nonumber \\ {\varvec{a}}= & {} \begin{bmatrix} {\varvec{a}}_0 \\ {\varvec{a}}_1 \\ \vdots \\ {\varvec{a}}_{I_\mathrm{e}} \end{bmatrix}, \quad {\varvec{b}} = \begin{bmatrix} {\varvec{b}}_1 \\ {\varvec{b}}_2 \\ \vdots \\ {\varvec{b}}_{ I_\mathrm{o}} \end{bmatrix}. \end{aligned}$$

(15)

Thus, the complex-valued FreRes error can be computed as

$$\begin{aligned} \begin{aligned} e_H(\omega ,\tau )&= H(\omega ,\tau )- D(\omega ,\tau ) \\&= \mathfrak {R}(\omega ,\tau ) -j \mathfrak {I}(\omega ,\tau )- e^{-j \omega \tau } \\&= e_c(\omega ,\tau ) - j e_s(\omega ,\tau ) \end{aligned} \end{aligned}$$

(16)

with

$$\begin{aligned} \begin{aligned} e_c(\omega ,\tau )&= \mathfrak {R}(\omega ,\tau ) - \cos (\omega \tau ) \\ e_s(\omega ,\tau )&= \mathfrak {I}(\omega ,\tau ) - \sin (\omega \tau ). \end{aligned} \end{aligned}$$

(17)

The next section will use (16) to formulate the new bi-equiripple design.

2.2 New delay-error expression: linearized group-delay error

We have shown that the group-delay error is a nonlinear function of the VD-filter coefficients (Deng 2012a; Deng and Qin 2014). This makes the bi-equiripple design problem difficult to solve. To tackle this design problem, the bi-equiripple methods proposed in Deng (2012a) and Deng and Qin (2014) have to incorporate iterative procedures. Unfortunately, such iterations not only require heavy computation burden, but also may diverge. Furthermore, there is not a systematic way to find the optimal weighting function, and this can only be done through trial and error (Deng and Qin 2014). The final design accuracy is certainly affected by the selected weighting function as well as the stopping (termination) criterion.

The main purpose of this paper is to present a non-iterative design approach that needs no iterations and gets better design results. This non-iterative approach requires much less computational burden and does not involve any divergence issue as the existing iterative approach (Deng and Qin 2014). The core of this non-iterative design approach lies in the following newly developed technique for linearizing the group-delay error function. The technique can approximately linearize the group-delay error function as a linear one.

Let $\varTheta _d(\omega ,\tau )$ and $\varTheta (\omega ,\tau )$ be the desired phase and actual phase, respectively. The desired FreRes in (3) implies that the desired phase is

$$\begin{aligned} \varTheta _d(\omega ,\tau )= -\omega \tau . \end{aligned}$$

Thus, the phase error is

$$\begin{aligned} \begin{aligned} e_\varTheta (\omega ,\tau )&= \varTheta (\omega ,\tau ) - \varTheta _d(\omega ,\tau ). \end{aligned} \end{aligned}$$

(18)

If $\varTheta (\omega ,\tau )$ approximates $\varTheta _d(\omega ,\tau )$ well, i.e., if $e_\varTheta (\omega ,\tau )$ is small enough, then

$$\begin{aligned} \begin{aligned} e_\varTheta (\omega ,\tau )&\approx \sin e_\varTheta (\omega ,\tau ) \\&= \hat{e}_\varTheta (\omega ,\tau ) \\&= \sin (\varTheta (\omega ,\tau )- \varTheta _d(\omega ,\tau )) \\&= \sin \varTheta (\omega ,\tau ) \cos \varTheta _d(\omega ,\tau ) - \sin \varTheta _d(\omega ,\tau ) \cos \varTheta (\omega ,\tau ) \\&= \frac{-\mathfrak {I}(\omega ,\tau )}{A(\omega ,\tau )} \cos \varTheta _d(\omega ,\tau ) - \sin \varTheta _d(\omega ,\tau ) \frac{\mathfrak {R}(\omega ,\tau )}{A(\omega ,\tau )} \end{aligned} \end{aligned}$$

(19)

where $A(\omega ,\tau )$ is the amplitude response of $H(\omega ,\tau )$ in (14), i.e.,

$$\begin{aligned} \begin{aligned} A(\omega ,\tau )&= | H(\omega ,\tau ) | \\&= | \mathfrak {R}(\omega ,\tau ) -j \mathfrak {I}(\omega ,\tau ) | \\&= \sqrt{ \mathfrak {R}^2(\omega ,\tau ) + \mathfrak {I}^2(\omega ,\tau ) }. \end{aligned} \end{aligned}$$

(20)

Since the desired amplitude in (3) is

$$\begin{aligned} A_d(\omega ,\tau ) = | D(\omega ,\tau ) |= | e^{-j \omega \tau } | = 1 \end{aligned}$$

if $H(\omega ,\tau )$ approximates $D(\omega ,\tau )$ well, then we have

$$\begin{aligned} A(\omega ,\tau ) \approx A_d(\omega ,\tau )= 1. \end{aligned}$$

This leads to the approximation

$$\begin{aligned} \begin{aligned} \hat{e}_\varTheta (\omega ,\tau )&\approx - \mathfrak {I}(\omega ,\tau ) \cos \varTheta _d(\omega ,\tau ) - \sin \varTheta _d(\omega ,\tau ) \mathfrak {R}(\omega ,\tau ). \end{aligned} \end{aligned}$$

(21)

Utilizing (21) gets the group-delay error (or variable-delay error: VD error)

$$\begin{aligned} \begin{aligned} e_g(\omega ,\tau )&= - \frac{\partial e_\varTheta (\omega ,\tau )}{\partial \omega } \\&\approx \hat{e}_g(\omega ,\tau ) \\&= -\frac{\partial \hat{e}_\varTheta (\omega ,\tau )}{\partial \omega } \\&= \frac{\partial \mathfrak {I}(\omega ,\tau )}{\partial \omega } \cos \varTheta _d(\omega ,\tau ) - \sin \varTheta _d(\omega ,\tau ) \mathfrak {I}(\omega ,\tau ) \cdot (-\tau ) \\&\quad + \frac{\partial \mathfrak {R}(\omega ,\tau )}{\partial \omega } \sin \varTheta _d(\omega ,\tau ) + \cos \varTheta _d(\omega ,\tau ) \mathfrak {R}(\omega ,\tau ) \cdot (-\tau ) \\&= \left[ \hat{\mathfrak {R}}(\omega ,\tau ) \sin \varTheta _d(\omega ,\tau ) - \mathfrak {R}(\omega ,\tau ) \cdot \tau \cos \varTheta _d(\omega ,\tau ) \right] \\&\quad + \left[ \hat{\mathfrak {I}}(\omega ,\tau ) \cos \varTheta _d(\omega ,\tau ) + \mathfrak {I}(\omega ,\tau ) \cdot \tau \sin \varTheta _d(\omega ,\tau ) \right] \end{aligned} \end{aligned}$$

(22)

where $\hat{\mathfrak {R}}(\omega ,\tau )$ and $\hat{\mathfrak {I}}(\omega ,\tau )$ are the partial derivatives of $\mathfrak {R}(\omega ,\tau )$ and $\mathfrak {I}(\omega ,\tau )$ with respect to $\omega$, respectively, i.e.,

$$\begin{aligned} \begin{aligned} \hat{\mathfrak {R}}(\omega ,\tau )&= \frac{\partial \mathfrak {R}(\omega ,\tau )}{\partial \omega } = \hat{\varvec{u}}^T {\varvec{a}} \\ \hat{\mathfrak {I}}(\omega ,\tau )&= \frac{\partial \mathfrak {I}(\omega ,\tau )}{\partial \omega } = \hat{\varvec{v}}^T {\varvec{b}} \\ \end{aligned} \end{aligned}$$

(23)

with

$$\begin{aligned} \hat{\varvec{u}}^T= & {} \frac{\partial {\varvec{u}}^T}{\partial \omega } = \begin{bmatrix} \hat{\varvec{u}}_0^T&\quad \hat{\varvec{u}}_1^T&\quad \ldots&\quad \hat{\varvec{u}}_{I_\mathrm{e}}^T \end{bmatrix} \\ \hat{\varvec{u}}_i^T= & {} \hat{\varvec{c}}_i^T(\omega ) \tau ^{2i},\quad i=0, 1, \ldots , I_\mathrm{e} \\ \hat{\varvec{v}}^T= & {} \frac{\partial {\varvec{v}}^T}{\partial \omega } = \begin{bmatrix} \hat{\varvec{v}}_1^T&\quad \hat{\varvec{v}}_2^T&\quad \ldots&\quad \hat{\varvec{v}}_{I_\mathrm{o}}^T \end{bmatrix} \\ \hat{\varvec{v}}_i^T= & {} \hat{\varvec{s}}_i^T(\omega ) \tau ^{2i-1},\quad i=1, 2, \ldots , I_\mathrm{o} \end{aligned}$$

and

$$\begin{aligned} \begin{aligned} \hat{\varvec{c}}_i^T(\omega )&= \frac{ \partial {\varvec{c}}_i^T(\omega ) }{ \partial \omega } \\&= - \begin{bmatrix} 0.5 \sin ( 0.5 \omega )&\quad 1.5 \sin ( 1.5 \omega )&\quad \ldots&\quad ( N_{\mathrm{e}}(i) + 0.5 ) \sin ( N_{\mathrm{e}}(i) + 0.5 ) \omega \end{bmatrix} \\ \hat{\varvec{s}}_i^T(\omega )&= \frac{ \partial {\varvec{s}}_i^T(\omega )}{ \partial \omega } \\&= \begin{bmatrix} 0.5 \cos ( 0.5 \omega )&\quad 1.5 \cos ( 1.5 \omega )&\quad \ldots&\quad ( N_{\mathrm{o}}(i) + 0.5 ) \cos ( N_{\mathrm{o}}(i) + 0.5 ) \omega \end{bmatrix}. \end{aligned} \end{aligned}$$

Consequently, the group-delay error $e_g(\omega ,\tau )$ can be approximated as

$$\begin{aligned} \begin{aligned} \hat{e}_g(\omega ,\tau )&= \left[ \hat{\varvec{u}}^T \sin \varTheta _d(\omega ,\tau )- {\varvec{u}}^T \cdot \tau \cos \varTheta _d(\omega ,\tau ) \right] {\varvec{a}} \\&\quad + \left[ \hat{\varvec{v}}^T \cos \varTheta _d(\omega ,\tau )+ {\varvec{v}}^T \cdot \tau \sin \varTheta _d(\omega ,\tau ) \right] {\varvec{b}} \\&= {\varvec{\mu }}^T {\varvec{a}}+ {\varvec{\nu }}^T {\varvec{b}} \end{aligned} \end{aligned}$$

(24)

with

$$\begin{aligned} \begin{aligned} {\varvec{\mu }}^T&= \hat{\varvec{u}}^T \sin \varTheta _d(\omega ,\tau )- {\varvec{u}}^T \cdot \tau \cos \varTheta _d(\omega ,\tau ) \\ {\varvec{\nu }}^T&= \hat{\varvec{v}}^T \cos \varTheta _d(\omega ,\tau )+ {\varvec{v}}^T \cdot \tau \sin \varTheta _d(\omega ,\tau ). \end{aligned} \end{aligned}$$

(25)

Clearly, the resulting $\hat{e}_g(\omega ,\tau )$ is a completely linear function of the unknown vectors ${\varvec{a}}$ and ${\varvec{b}}$.

3 Non-iterative bi-equiripple approach

To reduce the delay-error overshoots while retaining the FreRes errors at a specified low level, we state the bi-equiripple design as

$$\begin{aligned} \begin{aligned}&\text {minimize} \quad \epsilon = \gamma \epsilon _H + (1- \gamma ) \epsilon _g \\&\text {subject to (s.t.)} \quad \left\{ \begin{array}{l} \text {constraint-1:} \quad |e_H(\omega ,\tau )| \le \epsilon _H \\ \text {constraint-2:} \quad |\hat{e}_g(\omega ,\tau )| \le \epsilon _g \\ \end{array} \right. \end{aligned} \end{aligned}$$

(26)

where the cost function $\epsilon$ combines the two error bounds $\epsilon _H$ and $\epsilon _g$, and $\gamma$ is a weighting factor, $0 \le \gamma \le 1$. A large $\gamma$ implies that the minimization of the FreRes-errors is emphasized, and a small $\gamma$ implies that the minimization of the group-delay errors is emphasized. Therefore, there is a trade-off between $\epsilon _H$ and $\epsilon _g$. Clearly, this design problem is a constrained minimization problem subject to two error bounds.

Next, let us analyze the two constraints in detail. The constraint-1

$$\begin{aligned} |e_H(\omega ,\tau )| = \sqrt{e_c^2(\omega ,\tau )+ e_s^2(\omega ,\tau )} | \le \epsilon _H \end{aligned}$$

in (26) is imposed on the FreRes errors to constrain the FreRes errors below the upper bound $\epsilon _H$. More specifically, this constraint is a Qcone constraint, which can be written as

$$\begin{aligned} \begin{bmatrix} \epsilon _H \\ e_c(\omega ,\tau ) \\ e_s(\omega ,\tau ) \end{bmatrix} = \begin{bmatrix} \epsilon _H \\ {\varvec{u}}^T {\varvec{a}} - \cos (\omega \tau ) \\ {\varvec{v}}^T {\varvec{b}} - \sin (\omega \tau ) \end{bmatrix} \in {\mathcal {K}}_q \end{aligned}$$

(27)

where ${\mathcal {K}}_q$ stands for Qcone. On the other hand, the constraint-2

$$\begin{aligned} | \hat{e}_g(\omega ,\tau )| \le \epsilon _g \end{aligned}$$

in (26) is imposed on the group-delay errors, which means

$$\begin{aligned} -\epsilon _g \le \hat{e}_g(\omega ,\tau ) \le \epsilon _g \end{aligned}$$

and can be further split into two inequalities

$$\begin{aligned} \begin{aligned} \epsilon _g + \hat{e}_g(\omega ,\tau ) \ge 0 \\ \epsilon _g - \hat{e}_g(\omega ,\tau ) \ge 0 \end{aligned} \end{aligned}$$

(28)

where $\hat{e}_g(\omega ,\tau )$ is given in (24). Since $\hat{e}_g(\omega ,\tau )$ is a linear function of the unknown vectors, the constraints in (28) are simply the LP-constraints. This is the core point of the proposed non-iterative design approach.

By combining the above two constraints (Qcone constraint and LP constraints) together, we can rewrite the original form in (26) as

$$\begin{aligned} \begin{aligned}&\text {minimize} \quad \epsilon = \gamma \epsilon _H + (1- \gamma ) \epsilon _g \\&\text {s.t.} \quad \\&\begin{bmatrix} \epsilon _H \\ e_c(\omega ,\tau ) \\ e_s(\omega ,\tau ) \end{bmatrix} = \begin{bmatrix} \epsilon _H \\ {\varvec{u}}^T {\varvec{a}} - \cos (\omega \tau ) \\ {\varvec{v}}^T {\varvec{b}} - \sin (\omega \tau ) \end{bmatrix} \in {\mathcal {K}}_q \\&\begin{array}{l} \epsilon _g + \hat{e}_g(\omega ,\tau ) \ge 0 \\ \epsilon _g - \hat{e}_g(\omega ,\tau ) \ge 0. \end{array} \end{aligned} \end{aligned}$$

(29)

By letting

$$\begin{aligned} \begin{array}{ll} {\varvec{\beta }}^T = - \begin{bmatrix} \gamma &{} (1- \gamma ) &{} 0 &{} \ldots &{} 0 \end{bmatrix}, &{} \quad {\varvec{y}} = \begin{bmatrix} \epsilon _H \\ \epsilon _g \\ {\varvec{a}} \\ {\varvec{b}} \end{bmatrix} \\ {\varvec{c}}_1 = \begin{bmatrix} 0 \\ - \cos (\omega \tau ) \\ - \sin (\omega \tau ) \end{bmatrix}, &{} {\varvec{A}}_1^T = - \begin{bmatrix} 1 &{}\quad 0 &{}\quad {\varvec{0}} &{}\quad {\varvec{0}} \\ 0 &{}\quad 0 &{}\quad {\varvec{u}}^T &{}\quad {\varvec{0}} \\ 0 &{}\quad 0 &{}\quad {\varvec{0}} &{}\quad {\varvec{v}}^T \\ \end{bmatrix} \\ {\varvec{c}}_2 = \begin{bmatrix} 0 \\ 0 \end{bmatrix}, &{} {\varvec{A}}_2^T = - \begin{bmatrix} 0 &{}\quad 1 &{}\quad {\varvec{\mu }}^T &{}\quad {\varvec{\nu }}^T \\ 0 &{}\quad 1 &{}\quad -{\varvec{\mu }}^T &{}\quad -{\varvec{\nu }}^T \\ \end{bmatrix} \end{array} \end{aligned}$$

the minimization expression in (29) can be converted to the maximization problem

$$\begin{aligned} \begin{aligned}&\text {maximize} \quad -\epsilon = {\varvec{\beta }}^T {\varvec{y}} \\&\text {s.t.} \\&{\varvec{c}}_1 - {\varvec{A}}_1^T {\varvec{y}} \in {\mathcal {K}}_q \\&{\varvec{c}}_2 - {\varvec{A}}_2^T {\varvec{y}} \ge \mathbf{0}. \end{aligned} \end{aligned}$$

(30)

This is the dual problem of the primal minimization problem in (26), which is solved subject to two kinds of constraints (Qcone and LP constraints).

Fig. 1

FreRes errors $|e_H(\omega ,\tau )|$ (Qcone method)

Fig. 2

FreRes errors $|e_H(\omega ,\tau )|$ for $\tau =0.2,0.4,0.5$ (Qcone method)

To solve this problem, $L_1$ sampled points in $\omega \in [0,\omega _c]$ and $L_2$ sampled points in $\tau \in [0,0.5]$ are used. That is, the maximization problem in (30) is solved at $L_1 L_2$ grid points. In addition, as mentioned in (12), this paper uses unequal orders

$$\begin{aligned} \begin{aligned} {\varvec{N}}_\mathrm{e}&= \begin{bmatrix} N_{\mathrm{e}}(0)&N_{\mathrm{e}}(1)&\ldots&N_{\mathrm{e}}(I_{\mathrm{e}}) \end{bmatrix} \\ {\varvec{N}}_\mathrm{o}&= \begin{bmatrix} N_{\mathrm{o}}(1)&N_{\mathrm{o}}(2)&\ldots&N_{\mathrm{o}}(I_{\mathrm{o}}) \end{bmatrix} \end{aligned} \end{aligned}$$

(31)

Fig. 3

Group-delay errors $|e_g(\omega ,\tau )|$ (Qcone method)

Fig. 4

Group-delay errors $|e_g(\omega ,\tau )|$ for $\tau =0.2,0.4,0.5$ (Qcone method)

and those orders can be determined by using an order-optimization technique similar to that in Deng (2011). This optimization algorithm is originally proposed for finding the optimal orders for the even-order case, but we can readily extend it to this odd-order case. In Deng and Qin (2014), the above orders are found by using this optimization technique. The first step is to determine the optimal orders by minimizing the FreRes errors only such that the maximum FreRes error is smaller than a given upper bound $\hat{\epsilon }_H$, for example, $\hat{\epsilon }_H= -103$ decibel (dB). Then, the second step is to apply the proposed non-iterative bi-equiripple method to design a bi-equiripple VD filter with group-delay-error overshoots suppressed. For comparison, the next section will use the same orders optimized in Deng and Qin (2014).

Table 1 Peak errors and CPU-time (min)

Fig. 5

Relation between $\gamma$ and $\epsilon _H$ (non-iterative bi-equiripple)

Before ending this section, we need to further comment on the trade-off between the FreRes errors and the VD errors. Generally speaking, a large value of the weighting factor $\gamma$ in (26) leads to small peak value ($\epsilon _H$) of the absolute FreRes errors, but this conversely leads to large group-delay overshoots. Therefore, the proposed bi-equiripple design compromises the two peak values $\epsilon _H$ and $\epsilon _g$. Once an upper bound $\tilde{\epsilon }_H$ dB of the final FreRes errors is given, for example, $\tilde{ \epsilon }_H= -100$ dB, we can always find a $\gamma$ to meet the design requirement. The next section will use a bi-equripple design example to demonstrate the trade-off between $\epsilon _H$ and $\epsilon _g$. We will also show the relation between $\gamma$ and $\epsilon _H$ and the relation between $\gamma$ and $\epsilon _g$.

Fig. 6

Relation between $\gamma$ and $\epsilon _g$ (non-iterative bi-equiripple)

4 Odd-order bi-equiripple example

Let us approximate $D(\omega ,\tau )$ in (3) for $\omega _c= 0.9 \pi$. That is, the interested frequency band is $\omega \in [0,0.9 \pi ]$. For the comparison with Deng and Qin (2014), other design parameters are also set the same. More specifically, the polynomial order is $I=7$, i.e., $(I_\mathrm{e},I_\mathrm{o})=(3,4)$, the grid-point numbers are $(L_1,L_2)=(201,31)$, and the optimized orders are

$$\begin{aligned} \begin{aligned}&\begin{bmatrix} N_{\mathrm{e}}(0)&\quad N_{\mathrm{e}}(1)&\quad N_{\mathrm{e}}(2)&\quad N_{\mathrm{e}}(3) \end{bmatrix} = \begin{bmatrix} 34&\quad 33&\quad 25&\quad 13 \end{bmatrix} \\&\begin{bmatrix} N_{\mathrm{o}}(1)&\quad N_{\mathrm{o}}(2)&\quad N_{\mathrm{o}}(3)&\quad N_{\mathrm{o}}(4) \end{bmatrix} = \begin{bmatrix} 18&\quad 17&\quad 11&\quad 3 \end{bmatrix}. \end{aligned} \end{aligned}$$

(32)

As mentioned previously, those orders are optimized subject to the upper bound $\hat{\epsilon }_H= -103$ dB (Deng and Qin 2014). Thus, the designed VD-filter $\hat{ H}(z,\tau )$ employs 162 coefficients. Because these orders are determined by minimizing the largest value of the absolute FreRes errors, the design may cause too large group-delay errors around the boundaries of $\omega \in [0,\omega _c], \tau \in [-0.5,0.5]$. Hence, it is necessary to proceed to the non-iterative bi-equiripple design to weaken the overshoots of the group-delay errors. The objective of the non-iterative bi-equiripple design is to further weaken the overshoots of the group-delay errors subject to the condition that the peak value ($\epsilon _H$) of the absolute FreRes-errors does not exceed the predetermined upper bound $\tilde{\epsilon }_H= -100$ dB.

The design accuracy is evaluated by using the maximum absolute FreRes-error $\epsilon _H$ and the maximum group-delay error $\epsilon _g$ defined by

$$\begin{aligned} \begin{aligned}&\epsilon _H = \max \left\{ 20 \log _{10}| e_H(\omega ,\tau )| \right\} \\&\epsilon _g = \max \left\{ |e_g(\omega ,\tau )| \right\} \end{aligned} \end{aligned}$$

and the two errors are computed by using the samples of $\omega \in [0,\omega _c], \tau \in [-0.5,0.5]$. The sampling intervals for $\omega$ and $\tau$ are $\omega _c/(L_1-1)$ and $0.5/(L_2-1)$, respectively. Therefore, $201 \times 61$ grid points are used in the error computations.

For comparing the proposed non-iterative bi-equiripple design with other existing designs, we first begin by performing the Qcone design proposed in Deng (2012b) that only minimizes the peak value of the absolute FreRes-errors $|e_H(\omega ,\tau )|$. The resulting FreRes errors $|e_H(\omega ,\tau )|$ are illustrated in Fig. 1. For the three individual values of $\tau =0.2, 0.4, 0.5$, the corresponding errors $|e_H(\omega ,\tau )|$ are separately plotted in Fig. 2. Although this Qcone design yields flat FreRes errors, the group-delay errors $|e_g(\omega ,\tau )|$ have overshoots as shown in Fig. 3. Figure 4 plots the details for the three individual values $\tau =0.2, 0.4, 0.5$. Obviously, the errors $|e_g(\omega ,\tau )|$ near the boundaries become very large (overshoots). The non-iterative bi-equiripple design aims to cut such overshoots. Table 1 lists the peak values ($\epsilon _H$ and $\epsilon _g$) of $|e_H(\omega ,\tau )|$ and $|e_g(\omega ,\tau )|$, where the Qcone design yields $\epsilon _H=-103.2997$ dB and $\epsilon _g=0.000551$.

Fig. 7

Trade-off between $\epsilon _H$ and $\epsilon _g$ (non-iterative bi-equiripple)

Fig. 8

FreRes errors $|e_H(\omega ,\tau )|$ (non-iterative bi-equiripple, $\gamma =0.94$)

Before performing the newly proposed non-iterative bi-equiripple design, we first investigate the relation between the weighting factor $\gamma$ and $\epsilon _H$ as well as the relation between $\gamma$ and $\epsilon _g$. Figure 5 depicts $\epsilon _H$ versus $\gamma$, and Fig. 6 plots $\epsilon _g$ versus $\gamma$. The two figures show that as $\gamma$ increases, $\epsilon _H$ gradually decreases whereas $\epsilon _g$ gradually increases. As $\gamma$ approaches one, $\epsilon _g$ becomes significantly large. Therefore, we can select an appropriately large value of $\gamma$ to mitigate $\epsilon _g$ without significantly increasing $\epsilon _H$. Figure 7 illustrates the trade-off between $\epsilon _H$ and $\epsilon _g$ when $\gamma$ varies in the range [0.8, 1) .

Fig. 9

Absolute FreRes errors for $\tau =0.2,0.4,0.5$ (non-iterative bi-equiripple, $\gamma =0.94$)

Fig. 10

Actual group-delay (non-iterative bi-equiripple, $\gamma =0.94$)

Fig. 11

Group-delay errors $|e_g(\omega ,\tau )|$ (non-iterative bi-equiripple, $\gamma =0.94$)

Here, we design a bi-equiripple VD filter by using the new non-iterative approach such that it satisfies the requirement $\tilde{ \epsilon }_H= -100$ dB. The same illustrative example has also been taken in Deng and Qin (2014). To satisfy this requirement, we take $\gamma =0.94$ and design a bi-equiripple VD filter using a PC with 3.20GHz-CPU. The resulting errors $\epsilon _H$, $\epsilon _g$ and CPU-time are given in Table 1. For the sake of comparison, Table 1 also provides the design results by employing the existing design approaches in Deng (2012a) and Deng and Qin (2014) that intend to weaken the overshoots of the group-delay errors. Evidently, the final $\epsilon _H$ from the proposed non-iterative bi-equiripple is just below the upper-bound requirement $\tilde{ \epsilon }_H= -100$ dB. Also, the maximum group-delay error $\epsilon _g$ is the smallest. As for the computation time, the non-iterative approach also costs much shorter CPU-time than the iterative designs (Deng 2012a; Deng and Qin 2014). For reference, Table 1 also shows the computer simulation results of using the Qcone method in Deng (2012b) to satisfy the requirement $\tilde{ \epsilon }_H= -100$ dB. It follows that less coefficients (154 coefficients) are required to satisfy the requirement, but the overshoot (0.000719) of the group-delay errors is fairly large.

Figure 8 plots the absolute FreRes errors $|e_H(\omega ,\tau )|$ from the non-iterative bi-equiripple design with $\lambda =0.94$, and Fig. 9 depicts $|e_H(\omega ,\tau )|$ for the three individual values $\tau =0.2, 0.4, 0.5$. Clearly, the errors $|e_H(\omega ,\tau )|$ are nearly equiripple. Figure 10 plots the group-delay response, and Fig. 11 shows the errors $|e_g(\omega ,\tau )|$, where the peak value is 0.000192. The group-delay errors $|e_g(\omega ,\tau )|$ for $\tau =0.2, 0.4, 0.5$ are individually illustrated in Fig. 12. We can see that the overshoots of $|e_g(\omega ,\tau )|$ have been mitigated through using the non-iterative design technique as compared to Fig. 2. Therefore, our design results have verified that the proposed non-iterative bi-equiripple approach can obtain a bi-equiripple VD filter with greatly weakened delay-error overshoots. Moreover, the non-iterative bi-equiripple design costs much shorter CPU-time than the existing iterative approaches (Deng 2012a; Deng and Qin 2014). Another key point that is worthy to notice again is that this non-iterative bi-equiripple approach does not involve any divergence issue because the design problem is converted into a convex minimization problem, while the weighting function selected in the existing iterative approach Deng and Qin (2014) affects the VD-filter accuracy and may lead to a non-convergent solution. Therefore, the proposed non-iterative bi-equiripple design is simpler, faster, and more accurate than the iterative ones.

In Deng and Soontornwong (2016), an allpass bi-equiripple design has been proposed, and its computer simulation results are given in Table 1 ($\tau \in [-0.5,0.5]$). It follows from Table 1 that the new non-iterative method can achieve better results than the allpass counterpart.

Fig. 12

Group-delay errors $|e_g(\omega ,\tau )|$ for $\tau =0.2,0.4,0.5$ (non-iterative bi-equiripple, $\gamma =0.94$)

5 Conclusion

This paper has introduced a new algorithm for linearizing the group-delay error of a VD filter and this linearized delay-error function has been successfully employed in converting the bi-equiripple VD-filter design to a convex minimization problem. The cost function of the convex minimization problem is a linear combination of both the peak value of absolute FreRes-errors and the peak value of absolute group-delay errors. Solving the convex minimization problem yields a bi-equiripple VD filter with greatly mitigated delay-error overshoots while the upper-bound requirement on the FreRes errors can be perfectly satisfied. Since the non-iterative approach does not need any iterations, it is computationally efficient and can always arrive at a convergent solution. From the viewpoint of computation time, the proposed non-iterative bi-equiripple design also requires much shorter CPU-time than the iterative approaches (Deng 2012a; Deng and Qin 2014). Thanks to the newly derived group-delay error function, the bi-equiripple VD-filter can be designed fast and accurately. A bi-equiripple example has verified the accuracy improvement and the computational reduction. It is possible to extend this odd-order non-iterative scheme to the design of even-order VD filters with weakened overshoots of the group-delay errors.