A New Time-Domain Approach for the Design of Variable FIR Filters Using the Spectral Parameter Approximation Technique

Abstract

In the spectral parameter approximation (SPA) technique, the frequency response of a variable filter is approximated by the frequency response of the Farrow structure which is used to implement the SPA-based filter. In this paper, we propose a new approach in the time domain for the design of variable cutoff frequency finite impulse response filter using the SPA technique. We first design the practical filters which satisfy the given transition bandwidth, passband ripple, and stopband attenuation specifications and then approximate the coefficients of these filters by the impulse response of the Farrow structure. Approximation problem is solved using the least-squares technique. Various design examples are presented to illustrate the feasibility and the effectiveness of the proposed time-domain approach when the desired specifications are stringent. Interesting observations regarding the desired cutoff frequency range, the order, and the number of the sub-filters in the Farrow structure are also presented.

1 Introduction

Digital filters that can change their frequency response characteristics based on the application requirement are called as the variable digital filters. Such variable finite impulse response (FIR) filters are required in many signal processing applications such as radar, sonar, and control systems, adaptive systems, vibration analysis, audio and biomedical signal processing, and wireless communications. In a special case of the variable FIR filters, the cutoff frequency of the filter needs to be varied, and the passband ripple, the stopband attenuation, and the transition bandwidth should be below predefined specified values.

For the variable coefficient filter, cutoff frequency is controlled by changing all the coefficients of the filter. However, when the cutoff frequency needs to be changed frequently, this approach becomes unsuitable for higher order filters due to the tedious updating routine (large number of memory access operations) and huge memory requirement (to store all the filter coefficients corresponding to all the desired responses). In practice, it is desirable to control the cutoff frequency using fewer number of parameters to keep the updating routine simple. A number of such reconfigurable filter design techniques have been developed to control the cutoff frequency by modifying the impulse response of the fixed-coefficient prototype filter. Details and reviews of such reconfigurable filter design techniques can be found in [3, 14] and the references therein.

In the spectral parameter approximation (SPA) technique [2, 4–12], the variable filter is implemented using Farrow structure. The SPA-based filter has smaller group delay, fixed transition bandwidth, requires very small number of variable multipliers (to be used for the variable weights), and its cutoff frequency can be controlled through only one variable parameter. The frequency response of the SPA-based filter is modeled as a polynomial function of the cutoff frequency parameter ($\alpha$). The frequency responses of the fixed sub-filters in the Farrow structure are equivalent to the coefficients of the polynomial, and the frequency response (i.e., the cutoff frequency) of the SPA-based filter is controlled by the variable $\alpha$. The use of other polynomial functions such as Chebyshev polynomial [10], shifted Chebyshev polynomial [8], Bernstein polynomial [8], or shifted Legendre polynomial [8] has also been investigated in the literature. The cutoff frequency (or equivalently the passband frequency, as the transition bandwidth is fixed) of the SPA-based filter varies in the desired tuning range as $\alpha$ varies from 0 to 1.

The Farrow structure implementation of the SPA-based filter consists of $L+1$ sub-filters, each of order N, as shown in Fig. 1. For the FIR filter design case, the frequency response of the SPA-based filter, $H(\omega ,\alpha )$ is given by,

$$\begin{aligned} H(\omega , \alpha )=\sum _{k=1}^{L+1} {\sum _{n=0}^N {\alpha ^{k-1}} {hs}_k (n)e^{-j\omega n}} \end{aligned}$$

(1)

where ${hs}_{k}(n)$ is the impulse response of the kth sub-filter.

Fig. 1

Farrow structure implementation of SPA-based filter

The objective here is to find the optimal coefficients ${hs}_{k}(n)$ such that the frequency response of the SPA-based filter will approximate the frequency response of the ideal filter for each cutoff frequency (in the desired tuning range), i.e., for each value of $\alpha$ (in 0–1). The ideal filter is defined as the filter with magnitude equal to 1 in its passband and 0 in its stopband. The approximation problem can be solved using the least-squares (LS) [4, 7, 8, 12] or minimax techniques [6, 9–11], by incorporating the desired peak to peak passband ripple ($\delta _{\mathrm{p}}$) and stopband attenuation ($\delta _{\mathrm{s}}$) constraints in the problem formulation. Some other approaches such as vector array decomposition [5], semi-infinite quadratic optimization [2], etc. have also been proposed to design the SPA-based filter. The optimal solutions can be obtained from the closed-form formulae [6–8, 12], or by solving the system of linear equations obtained by the discretization method [2, 4, 5, 9–11].

Traditionally, the approximation problem for the SPA-based filter is formulated in the frequency domain as explained above. In this paper, we propose a new approach for the design of SPA-based filter in the time domain. We model the approximation problem such that the optimal coefficients for the sub-filters are found so as to approximate the impulse responses of the practical filters, i.e., the impulse responses of the filters which satisfy the desired specifications on $\delta _{\mathrm{p}}$, $\delta _{\mathrm{s}}$, and transition bandwidth. In Sect. 2, we present the proposed time-domain approach in detail. Various design examples are presented in Sect. 3, along with the comparisons and some observations. The concluding remarks are presented in the Sect. 4.

2 Proposed Time-Domain Approach for the Design of SPA-Based Filter

Let the cutoff frequency tuning range of the SPA-based filter be $f_{\mathrm{cl}}$ to $f_{\mathrm{cm}}$, i.e., the cutoff frequency varies linearly as $f_{\mathrm{cl}} \le f_{\mathrm{c}} \le f_{\mathrm{cm}}$ for $0 \le \alpha \le 1$. Let the corresponding passband and stopband ranges be $f_{\mathrm{pl}}$ to $f_{\mathrm{pm}}$ and $f_{\mathrm{sl}}$ to $f_{\mathrm{sm}}$, respectively. In this case, we will formulate the SPA-based filter design problem so as to approximate the impulse response of the practical filter by the impulse response of the SPA-based filter for the desired tuning range. We use the discretization approach to formulate the approximation problem as follows.

First, design M practical filters, each of order N, with cutoff frequencies $f_{\mathrm{cl}},f_{\mathrm{cl}}+\Delta f, f_{\mathrm{cl}} + 2\Delta f,\ldots , f_{\mathrm{cm}}$, and the transition bandwidth tbw, where $\Delta f = (f_{\mathrm{cm}}-f_{\mathrm{cl}})/(M - 1)$. These filters are designed using the standard filter design algorithm such as the Remez exchange algorithm or the Parks–McClellan algorithm [13].

Let the matrix of the impulse responses of the practical filters be denoted as

$$\begin{aligned} G_{\mathrm{p}}=\left[ \begin{array}{ccccccc} {h_{0,1} }&{} {h_{1,1} }&{} {h_{2,1} }&{} .&{} .&{} .&{} {h_{N,1} } \\ {h_{0,2} }&{} {h_{1,2} }&{} {h_{2,2} }&{} .&{} .&{} .&{} {h_{N,2} } \\ .&{} .&{} .&{} &{} .&{} &{} . \\ .&{} .&{} .&{} &{} .&{} &{} . \\ .&{} .&{} .&{} &{} .&{} &{} . \\ {h_{0,M} }&{} {h_{1,M} }&{} {h_{2,M} }&{} .&{} .&{} .&{} {h_{N,M} } \\ \end{array}\right] \end{aligned}$$

(2)

where $h_{i,j}$ denotes the ith sample of the impulse response of the jth filter, i.e., ith coefficient of the jth filter.

Discretize the cutoff frequency parameter, $\alpha$, in M equidistant points in the range 0–1. The matrix of the impulse responses of the SPA-based filter is given by,

$$\begin{aligned} G = WG_{\mathrm{s}} \end{aligned}$$

(3)

where

$$\begin{aligned} W=\left[ \begin{array}{ccccccc} 1&{} {\alpha _1 }&{} {\alpha _1 ^{2}}&{} .&{} .&{} .&{} {\alpha _1 ^{L}} \\ 1&{} {\alpha _2 }&{} {\alpha _2 ^{2}}&{} .&{} .&{} .&{} {\alpha _2 ^{L}} \\ .&{} .&{} .&{} &{} .&{} &{} . \\ .&{} .&{} .&{} &{} .&{} &{} . \\ .&{} .&{} .&{} &{} .&{} &{} . \\ 1&{} {\alpha _M }&{} {\alpha _M ^{2}}&{} .&{} .&{} .&{} {\alpha _M ^{L}} \\ \end{array}\right] \end{aligned}$$

(4)

where $\alpha _{j}^{i}$ denotes the ith power of $\alpha _{j}$, with $\alpha _{1} = 0$, and

$$\begin{aligned} G_{\mathrm{s}}=\left[ \begin{array}{ccccccc} {{hs}_{0,1} }&{} {{hs}_{1,1} }&{} {{hs}_{2,1} }&{} .&{} .&{} .&{} {{hs}_{N,1} } \\ {{hs}_{0,2} }&{} {{hs}_{1,2} }&{} {{hs}_{2,2} }&{} .&{} .&{} .&{} {{hs}_{N,2} } \\ .&{} .&{} .&{} &{} .&{} &{} . \\ .&{} .&{} .&{} &{} .&{} &{} . \\ .&{} .&{} .&{} &{} .&{} &{} . \\ {{ hs}_{0,L+1} }&{} {{ hs}_{1,L+1} }&{} {{ hs}_{2,L+1}}&{} .&{} .&{} .&{} {{ hs}_{N,L+1} } \\ \end{array}\right] \end{aligned}$$

(5)

is the matrix of the coefficients of the sub-filters of the Farrow structure and ${hs}_{i,j}$ denotes the ith coefficient of the jth sub-filter.

Thus the approximation problem can be stated as: Find the optimal coefficients ${hs}_{i,j}$ such that the impulse responses in $G_{\mathrm{p}}$ are approximated by the impulse responses in G. The system of linear equations, $G_{\mathrm{p}} = { WG}_{\mathrm{s}}$, can be solved using the LS technique to find the optimal coefficients ${hs}_{i,j}$.

As, for $\alpha = 0$ the impulse response of the SPA-based filter is equal to the impulse response of the first sub-filter, in the proposed method, the first sub-filter in the Farrow structure is designed to have cutoff frequency $f_{\mathrm{cl}}$ and transition bandwidth tbw, i.e.,

$$\begin{aligned} \left\{ \begin{array}{lllll} {{hs}_{0,1} }&{} .&{} .&{} .&{} {{hs}_{N,1} } \\ \end{array}\right\} =\left\{ \begin{array}{lllll} {h_{0,1} }&{} .&{} .&{} .&{} {h_{N,1} } \\ \end{array}\right\} \end{aligned}$$

(6)

Therefore, in the proposed method, the design problem further reduces to finding the optimal coefficients for only the remaining L sub-filters. Therefore, it is sufficient to model the differences between the $M-1$ practical filters and the first practical filter (i.e., the filter with cutoff frequency $f_{\mathrm{cl}})$ using the remaining L sub-filters of the Farrow structure. Therefore, the matrices $G_{\mathrm{p}}$, W, and $G_{\mathrm{s}}$ are modified as follows.

• 1. Matrix $G_{\mathrm{p}}$:

  $$\begin{aligned} G_{\mathrm{p1}}(i, :) = G_{\mathrm{p}}(1, :) - G_{\mathrm{p}}(i, :)\hbox { for }i > 1 \end{aligned}$$

  (7)

i.e., all the elements in each of the rows (for rows other than the first row) are subtracted from the corresponding elements in the first row.

$$\begin{aligned} G_{\mathrm{p2}}(i, :) = G_{\mathrm{p1}}(i+1, :)\quad \hbox { for }i = 1\hbox { to }M-1 \end{aligned}$$

(8)

i.e., the first row in the matrix $G_{\mathrm{p1}}$ is removed, as it is quite redundant for the new approximation problem. The matrix $G_{\mathrm{p2}}$ is an $(M-1) \times (N+1)$ matrix.

• 2. Matrix W:

  $$\begin{aligned} W_{1}(i, :)= & {} W(i+1, :)\hbox { for }i = 1\hbox { to }M-1 \end{aligned}$$

  (9)
  $$\begin{aligned} W_{2}(:, k)= & {} W_{1}(:, k+1)\hbox { for }k = 1\hbox { to }L \end{aligned}$$

  (10)

i.e., the first row and the first column in the matrix W are removed, and $W_{2}$ is an $(M-1)\times L$ matrix.

• 3. Matrix $G_{\mathrm{s}}$:

  $$\begin{aligned} G_{\mathrm{s1}}(i, :) = G_{\mathrm{s}}(i+1, :)\hbox { for }i = 1\hbox { to }L \end{aligned}$$

  (11)

i.e., the first row in the matrix $G_{\mathrm{s}}$ is removed, and $G_{\mathrm{s1}}$ is an $L\times (N+1)$ matrix.

The optimal coefficients ${hs}_{i,j}$ (for the remaining L sub-filters) are then obtained by solving the system of linear equations, given by $G_{\mathrm{p2}}=W_{2}G_{\mathrm{s1}}$. Further, in the case of linear-phase filters, only half the matrices can be used due to the coefficient symmetry.

The magnitude response of the SPA-based filter designed following above procedure is checked for the M values used for the filter design, as well as for arbitrary values of $\alpha$, to ensure that the desired specifications on $\delta _{\mathrm{p}}$ and $\delta _{\mathrm{s}}$ are satisfied. If these specifications are not satisfied, the above mentioned design procedure can be repeated by varying N and/or L such that the magnitude response of the SPA-based filter satisfies the desired specifications on $\delta _{\mathrm{p}}$ and $\delta _{\mathrm{s}}$.

The matrix $W_{2}$ may be rank deficient, which sometimes (but not always) might affect the LS solution. (However, this is equally applicable to the proposed as well as existing methods utilizing LS technique [4, 7, 8, 12]). For instance, the matrix $W_{2}$ in design example 3 (in Sect. 3) is rank deficient (dimensions: $79\times 22$, rank: 20); however, the obtained results are not affected by its rank deficiency.

3 Design Examples

We present three design examples with total six cases (different tuning ranges and different transition bandwidths) for the SPA-based filter design. One of the design cases is a benchmark example considered throughout the literature [6–12]. In addition, five more design cases are considered in this paper. For every case, the SPA-based filters are designed using the proposed time-domain approach utilizing LS technique and the conventional frequency-domain approach (as outlined in Sect. 1) utilizing the LS [4] and minimax [9] techniques. For every SPA-based filter, the weights are the powers of $\alpha$ (i.e., no special polynomial is used) and all the sub-filters of its Farrow structure are of equal order N. All the filter designs are based on the discretization method. (Closed-form method also results in the same or approximately same complexity, and hence, is not considered separately.) For every case, following points are considered for the design and testing of the SPA-based filters.

• 1. Total M equidistant values of $f_{\mathrm{c}}$ in the range $f_{\mathrm{cl}}$ to $f_{\mathrm{cm}}$ are used for practical filter or ideal filter, i.e., M practical filters are considered for the proposed time-domain approach-based filter design, and M ideal filters are used for the conventional frequency-domain approach-based filter designs.

• 2. The set of corresponding M values of $\alpha$ (equidistant between 0 and 1) is referred to as grid of $\alpha _{\mathrm{des}}$. Therefore, every SPA-based filter designed in each case is based on the same grid of $\alpha _{\mathrm{des}}$.

• 3. For specifying the frequency response of the ideal filter to be used in the frequency-domain approach-based designs, the frequency axis is discretized in 180 points.

• 4. Once an SPA-based filter is designed, its frequency response is evaluated for multiple sets of values of $\alpha$ (equidistant between 0 and 1), referred to as grid of $\alpha _{\mathrm{test}1}$, grid of $\alpha _{\mathrm{test}2}$, grid of $\alpha _{\mathrm{test}3}$, etc.

• 5. Frequency response of the SPA-based filter is evaluated on the 180 frequency axis points considered for the design as well as on a dense grid of 8192 frequency axis points to ensure that the filter response satisfies the desired specifications.

• 6. Each filter is evaluated on grid of $\alpha _{\mathrm{test}1} = \hbox {grid}$ of $\alpha _{\mathrm{des}}$. Additionally, each filter is evaluated on the dense grids of $\alpha _{\mathrm{test}2} = 10\times \alpha _{\mathrm{des}}$ and $\alpha _{\mathrm{test}3} = 20\times \alpha _{\mathrm{des}}$, to ensure that the filter response satisfies the desired specifications for values of $\alpha$ other than that used for the filter design.

• 7. Therefore, all the filters that are designed for same grid of $\alpha _{\mathrm{des}}$ are tested on the same grids of $\alpha _{\mathrm{test}1}$, $\alpha _{\mathrm{test}2}$, $\alpha _{\mathrm{test}3}$, etc. in every case.

• 8. If the designed filter evaluated on various grids of $\alpha _{\mathrm{test}}$ does not satisfy the desired constraints on $\delta _{\mathrm{p}}$ and $\delta _{\mathrm{s}}$, it is redesigned by varying the value of N and/or L.

• 9. A set of pairs of N and L is obtained by trying all possible pairs such that the designed filter satisfies the desired constraints on $\delta _{\mathrm{p}}$ and $\delta _{\mathrm{s}}$. An optimal pair from this set is the one for which the number of multipliers required to realize the filter is minimum. Note that for the symmetric coefficient sub-filters and even-valued N, the total number of multipliers required to realize an SPA-based filter for a particular pair of N and L is given by $\{(N/2 + 1) \times (L+1) + L\}$.

Based on these design examples, some interesting observations and comparisons (in terms of the total number of multipliers required to realize the SPA-based filter) are also presented.

3.1 Design Example 1 (Cases 1, 2, and 3)

Let the desired cutoff frequency range be $f_{\mathrm{cl}} = 0.3$ to $f_{\mathrm{cm}} = 0.5$. (All the frequency values mentioned in this paper are normalized with respect to $\pi$.) For this cutoff frequency range, we consider three cases (Case 1 through Case 3) for SPA-based filter design corresponding to three transition bandwidth specifications of 0.2, 0.1, and 0.05. Case 1 is same as that considered in the literature, i.e., cutoff frequency range = 0.2 and tbw = 0.2 [6–12]. For every case, let $\delta _{\mathrm{p}} = 0.1\hbox { dB}$ and $\delta _{\mathrm{s}} = -45\hbox { dB}$.

For Case 1 and Case 2, $M = 21$ is used, i.e., grid of $\alpha _{\mathrm{des}} = 21$ equally spaced values of $\alpha$ between 0 and 1. Once a filter is designed, its frequency responses are evaluated for grids of $\alpha _{\mathrm{test}1} = \alpha _{\mathrm{des}} = 21, \alpha _{\mathrm{test}2} = 210$, and $\alpha _{\mathrm{test}3} = 420$ equally spaced values of $\alpha$ between 0 and 1. Additionally, its frequency responses are evaluated separately for $\alpha _{\mathrm{test}4} = 30$ equally spaced values of $\alpha$ between 0 and 1, and $\alpha _{\mathrm{test}5} = 60$ equally spaced values of $\alpha$ between 0 and 1. As the desired transition bandwidth specification is stringent for Case 3, $M = 100$ is used, i.e., grid of $\alpha _{\mathrm{des}} = 100$ equally spaced values of $\alpha$ between 0 and 1. Once a filter is designed, its frequency responses are evaluated for grids of $\alpha _{\mathrm{test}1} = \alpha _{\mathrm{des}} = 100$, $\alpha _{\mathrm{test}2} = 1000$, and $\alpha _{\mathrm{test}3} = 2000$ equally spaced values of $\alpha$ between 0 and 1. Additionally, its frequency responses are evaluated separately for grid of $\alpha _{\mathrm{test}4} = 52$ equally spaced values of $\alpha$ between 0 and 1, grid of $\alpha _{\mathrm{test}5} = 200$ equally spaced values of $\alpha$ between 0 and 1, and grid of $\alpha _{\mathrm{test}6} = 300$ equally spaced values of $\alpha$ between 0 and 1.

The values of N and L so obtained, that result in the minimum number of total multipliers required, for the filter designs for these three cases are summarized in Table 1. The ($\pm x)$ values indicate the percentage increase or decrease in the number of multipliers required for the particular SPA-based filter when compared to the SPA-based filter designed using the proposed time-domain approach.

Table 1 Design example 1 (Case 1, Case 2, and Case 3)

3.2 Design Example 2 (Cases 4 and 5)

Let the desired passband frequency range be $f_{\mathrm{pl}} = 0.05$ to $f_{\mathrm{pm}} = 0.5$. For this passband frequency range, two cases are considered as tbw = 0.2 and 0.1. For each case, let $\delta _{\mathrm{p}} = 0.1\hbox { dB}$ and $\delta _{\mathrm{s}} = -45\hbox { dB}$.

As the tuning range is wider, $M = 46$ is used for Case 4, i.e., grid of $\alpha _{\mathrm{des}} = 46$ equally spaced values of $\alpha$ between 0 and 1. Once a filter is designed, its frequency responses are evaluated for grids of $\alpha _{\mathrm{test}1} = \alpha _{\mathrm{des}} = 46$, $\alpha _{\mathrm{test}2} = 460$, and $\alpha _{\mathrm{test}3}= 920$ equally spaced values of $\alpha$ between 0 and 1. Additionally, its frequency responses are evaluated separately for grid of $\alpha _{\mathrm{test}4} = 21$ equally spaced values of $\alpha$ between 0 and 1, grid of $\alpha _{\mathrm{test}5} = 60$ equally spaced values of $\alpha$ between 0 and 1, and grid of $\alpha _{\mathrm{test}6} = 92$ equally spaced values of $\alpha$ between 0 and 1. As the desired transition bandwidth specification is stringent for Case 5, $M = 100$ is used, i.e., grid of $\alpha _{\mathrm{des}} = 100$ equally spaced values of $\alpha$ between 0 and 1. The filter responses are evaluated for grids of $\alpha _{\mathrm{test}1} = \alpha _{\mathrm{des}} = 100$, $\alpha _{\mathrm{test}2} = 1000$, and $\alpha _{\mathrm{test}3} = 2000$ equally spaced values of $\alpha$ between 0 and 1. Additionally, the filter responses are evaluated separately for grid of $\alpha _{\mathrm{test}4} = 52$ equally spaced values of $\alpha$ between 0 and 1, grid of $\alpha _{\mathrm{test}5} = 200$ equally spaced values of $\alpha$ between 0 and 1, and grid of $\alpha _{\mathrm{test}6} = 300$ equally spaced values of $\alpha$ between 0 and 1.

Table 2 Design example 2 (Case 4 and Case 5)

The values of N and L so obtained, that result in the minimum number of total multipliers required, for the filter designs for these three cases are summarized in Table 2. As the tuning range for this design example is wider compared to the tuning range considered in most of the literature (which is same as the tuning range in the design example 1), in this case we consider the SPA-based filter design using the piecewise polynomial approach also (as suggested in [12] for LS technique). For a fair comparison, we consider the piecewise approach for the frequency-domain design with minimax technique also. In the piecewise polynomial approach, wider tuning range is divided into two smaller tuning ranges, and two separate SPA-based filters are designed and two Farrow structures are implemented for these two ranges. Therefore, two values of N and two values of L (corresponding to the two SPA-based filter designs for the two equal smaller ranges) are mentioned in Table 2 for the filter designs based on the piecewise polynomial approach (with 46 and 100 ideal filters being used for each range for Cases 4 and 5, respectively). The ($\pm x$) values indicate the percentage increase or decrease in the number of multipliers required for the particular filter when compared to the SPA-based filter designed using the proposed time-domain approach.

3.3 Design Example 3 (Case 6)

The spectral parameter approximation and modified coefficient decimation-based variable digital filter (SPA-MCDM-VDF) in [3], utilizes an SPA-based filter as a prototype filter. This prototype SPA-based filter needs to be designed for the cutoff frequency range of 0.25–0.5. Therefore, for the third design example, we consider $f_{\mathrm{cl}} = 0.25$ to $f_{\mathrm{cm}} = 0.5$, tbw = 0.05, $\delta _{\mathrm{p}} = 0.1\hbox { dB}$, and $\delta _{\mathrm{s}} = -45\hbox { dB}$.

For this case, $M = 80$ is used, i.e., grid of $\alpha _{\mathrm{des}} = 80$ equally spaced values of $\alpha$ between 0 and 1. Once a filter is designed its frequency response is evaluated for grids of $\alpha _{\mathrm{test}1} = \alpha _{\mathrm{des}} = 80$, $\alpha _{\mathrm{test}2} = 800$, and $\alpha _{\mathrm{test}3} = 1600$ equally spaced values of $\alpha$ between 0 and 1. Additionally, the filter responses are evaluated separately for grid of $\alpha _{\mathrm{test}4} = 52$ equally spaced values of $\alpha$ between 0 and 1, grid of $\alpha _{\mathrm{test}5} = 100$ equally spaced values of $\alpha$ between 0 and 1, grid of $\alpha _{\mathrm{test}6} = 200$ equally spaced values of $\alpha$ between 0 and 1, and grid of $\alpha _{\mathrm{test}7} = 300$ equally spaced values of $\alpha$ between 0 and 1.

Table 3 Design example 3 (Case 6)

The values of N and L so obtained, that result in the minimum number of total multipliers required, for the filter designs for these three cases are summarized in Table 3. The ($\pm x$) values indicate the percentage increase or decrease in the number of multipliers required for the particular filter when compared to the SPA-based filter designed using the proposed time-domain approach.

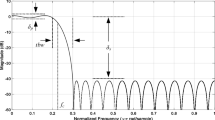
The magnitude responses of the SPA-based filter (evaluated for grid of $\alpha _{\mathrm{test7}} = 300$ values of $\alpha$) designed (for $M = 80$, i.e., grid of $\alpha _{\mathrm{des}} = 80$ equally spaced values of $\alpha$ between 0 and 1) using the proposed time-domain approach are shown in Fig. 2. The zoomed and cropped versions of the responses are also shown in the insets of the figure to show the passband ripples and the details of the transition bands. As can be clearly seen, the desired specifications are satisfied by the filter for 300 values of $\alpha$, even though it is designed with $M = 80$.

Fig. 2

Magnitude responses of the SPA-based filter in design example 3 designed using the proposed time-domain approach with $M = 80$ and evaluated for 300 values of $\alpha$

3.4 Observations

In this section, we present some interesting observations about the degree of polynomial, i.e., L, based on the results summarized in Tables 1, 2, and 3. The relation between N and L becomes clear from Cases 1 through 3, and Cases 4 and 5. As the value of N approximately doubles, the value of L also approximately doubles, i.e., it suggests that L is directly proportional to N, and therefore, inversely proportional to the transition bandwidth. (The filter order is inversely proportional to the transition bandwidth [1].)

The relation between the tuning range and value of L becomes clear from Cases 1 and 4, Cases 2 and 5, and Cases 3 and 6, which suggest that the value of L is directly proportional to the tuning range. As the tuning range approximately doubles (Case 1 and Case 4, and Case 2 and Case 5), the value of L also approximately doubles.

The cumulative effect of these relations is clear from Cases 1 and 5. As a result of halving the transition bandwidth and approximately doubling the tuning range, in Case 5 the value of L is approximately four times of that in Case 1.

3.5 Comparisons

For the comparison purpose, we consider the total number of multipliers required for the SPA-based filter as the measure of complexity. For small tuning range and wider or moderately wide transition bandwidths (Cases 1, 2 and 4), the frequency-domain approaches (with the LS or minimax techniques) have slightly less complexity compared to the proposed time-domain approach (on an average 11 % less number of multipliers). However, when narrower transition bandwidth is desired (Cases 3 and 6) or wider tuning range is desired along with moderately wide transition bandwidth (Case 5), the frequency-domain approaches require, on an average, 45 % more number of multipliers compared to the proposed time-domain approach. As can be seen from Table 2, in some cases, the frequency-domain approach with piecewise polynomial requires up to 20 % more number of multipliers compared to the proposed time-domain approach.

When absolute control over the cutoff frequency is desired on the entire Nyquist band, the SPA-MCDM-VDF is advantageous [3]. This SPA-MCDM-VDF utilizes an SPA-based filter as a prototype filter variable on the cutoff frequency range of 0.25–0.5, and therefore, the design of SPA-based filter for the cutoff frequency range of 0.25–0.5, along with narrow transition bandwidth, i.e., Case 6, is of particular interest. As evident from Table 3, the frequency-domain approach requires 57 % more number of multipliers compared to the proposed time-domain approach. Therefore, the SPA-MCDM-VDF with the prototype filter designed using the time-domain approach has similar savings in the number of adders and multiplexers (and therefore in total area) when compared to the SPA-MCDM-VDF with the prototype filter designed using the frequency-domain approach, which highlights the advantage of the proposed approach.

In the proposed method, as the first sub-filter is same as the first practical filter, we already have a good estimate on the value N. Similarly, in case of existing methods using frequency-domain approach, the value of N can be estimated based on the desired specifications using the formula from [1]. Therefore, equipped with this knowledge, we need to test only a few pairs (typically around 6–8) of N and L to find the pair which satisfies the desired specifications. Then a few more pairs of N and L “in the neighborhood”, i.e., pairs with values close to values of this initial pair which satisfies the desired specifications are considered to find out the optimal pair. Even though the offline design time, i.e., the time required to find the optimal filter coefficients for the sub-filters in the Farrow structure is not critical, it can be mentioned that the offline design time (for one pair of N and L) for the proposed time-domain approach and the frequency-domain approach utilizing the LS technique is much shorter (difference of two orders of magnitude) compared to the frequency-domain approach utilizing the minimax technique. (However, this difference is the direct result of the difference in the computational complexities of the LS and minimax techniques.) As mentioned above, as multiple pairs need to be considered to find the optimal pair to design a filter satisfying the desired constraints, the proposed method and frequency-domain approach utilizing LS technique are significantly faster when compared to the frequency-domain approach utilizing minimax technique.

The square of the difference between value of each of the sample of the impulse response of the practical filter and the value of the respective sample of the impulse response of the designed SPA-based filter is calculated to get total $N+1$ squared errors. The average of these squared errors is the average squared error per coefficient for one value of $\alpha$ (denoted as $E_{\alpha }$). This average squared error $E_{\alpha }$ is calculated for each value of $\alpha$ in grid of $\alpha _{\mathrm{test1}}$. The average of these $E_{\alpha }$, termed as E1, is the average squared error per coefficient per $\alpha$. It is observed that the average squared error per coefficient per value of $\alpha$ calculated for the SPA-based filter designed using the proposed time-domain approach is negligible (maximum value is $1.36\times 10^{-7}$ for Case 4) and is smaller by at least one order of magnitude when compared to that of the frequency-domain approach (both LS and minimax). However, it should be kept in mind that the error performance (either in time or in frequency domain) cannot be considered as a metric for comparison, as each of these methods tries to minimize different type of error (LS technique on impulse responses—proposed time-domain approach, whereas LS and minimax techniques on frequency responses—conventional frequency-domain approach).

4 Conclusion

This paper presented a new time-domain approach for the design of spectral parameter approximation based filter. In the proposed approach, the optimal coefficients for the sub-filters in the Farrow structure are found so as to approximate the impulse responses of the practical filters by the impulse response of the Farrow structure. Approximation problem is solved using the least-squares technique. Filter responses are evaluated for the values of spectral parameter used for filter design as well as for arbitrary values. Various design examples illustrate the effectiveness of the proposed time-domain approach compared to the conventional frequency-domain approach when the desired specifications are stringent. Interesting observations about the tuning range, the order and the number of sub-filters are also presented.