The data filtering based generalized stochastic gradient parameter estimation algorithms for multivariate output-error autoregressive systems using the auxiliary model

Abstract

Parameter estimation has wide applications in one-dimensional and multidimensional signal processing and filtering. This paper focuses on the parameter estimation problem of multivariate output-error autoregressive systems. Based on the data filtering technique and the auxiliary model identification idea, we derive a filtering based auxiliary model generalized stochastic gradient algorithm. The key is to choose an appropriate filter to filter the input-output data and to study a novel method to get the system model parameters and noise model parameters respectively. By employing the multi-innovation identification theory, a filtering based auxiliary model multi-innovation generalized stochastic gradient algorithm is proposed. Compared with the auxiliary model generalized stochastic gradient algorithm, the proposed algorithms can generate more accurate parameter estimates. Finally, an illustrative example is provided to verify the effectiveness of the proposed algorithms.

1 Introduction

With the development of control theory and the demand of engineering practices, the multivariable systems widely exist in all kinds of control processes (Cheng and Ugrinovskii 2016) and signal processing (Li and Zhang 2015). Compared with single variable systems, multivariable systems have more complex structures (Saikrishna et al. 2017) and uncertain disturbances (Xing et al. 2016; Jafari et al. 2014). As a consequence, the identification problems for multivariable systems have attracted a lot of attention (Mercère and Bako 2011; Mu and Chen 2013; Cham et al. 2017). Katayama and Ase (2016) considered the linear approximation and identification of multi-input multi-output (MIMO) Wiener–Hammerstein systems and applied the separable least squares algorithm to estimate the parameters. In order to improve the estimation accuracy, Wang and Ding (2016) proposed an auxiliary model based recursive least squares parameter estimation algorithm for MIMO systems by filtering input-output data. Cheng et al. (2017) proposed the subspace identification methods for two-dimensional causal, recursive, and separable-in-denominator systems, which are applicable to both open-loop and closed-loop data. Recently, a gradient based parameter estimation method has been proposed for multivariate pseudo-linear systems using the multi-innovation and the data filtering (Ma and Ding 2017). In this paper, we use the multidimensional input and output signals to study the parameter identification problems for the multivariate system.

The data filtering technique is used to eliminate noises and outliers to reduce the noise-to-signal ratio in signal processing (Dhabal and Venkateswaran 2017; Ding et al. 2017; Tseng and Lee 2017; Zhao et al. 2017b), and has been employed to deal with the parameter estimation problem of systems which contains colored noises (Afshari et al. 2017). Differing from eliminating noises, the data filtering method in system identification only changes the structure of the system and does not change the relationship between the inputs and outputs (Pan et al. 2016; Ding et al. 2017a). Pan et al. (2017) used the filtering technique and the multi-innovation identification theory to identify the multivariable system with moving average noise, and proposed the filtering based multi-innovation extended stochastic gradient algorithm for improving the parameter estimation accuracy.

Many identification methods has been studied for linear systems and nonlinear systems (Li et al. 2017a, b, c), such as the least squares (Wan et al. 2016), the Newton iteration (Xu 2016, 2015; Xu et al. 2015) and the stochastic methods (Xu and Ding 2017b). Compared with the recursive least square algorithm (Wang et al. 2016; Zhang and Mao 2107), the stochastic gradient algorithm requires less computational cost and has been applied in parameter estimation (Liang et al. 2014; Levanony and Berman 2004). However, the stochastic gradient algorithm has a slow convergence rate and can not reach a satisfactory estimation accuracy (Li et al. 2014). To solve this problem, we use the multi-innovation identification theory to improve the performance of the stochastic gradient algorithm (Xu and Ding 2017c; Xu et al. 2017). Ding et al. (2017) presented a filtering based multi-innovation gradient algorithm for linear state space systems with time-delay by adopting the data filtering technique.

This paper studies the parameter estimation methods for multivariate output-error systems whose disturbance is an autoregressive noise (Aslam 2016) using the data filtering and the auxiliary model (Ding et al. 2017b; Jin et al. 2015). The main idea is to use a filter to filter the input-output data, then the system can be transformed into two identification models: a multivariate output-error model with white noise and an autoregressive noise model. The difficulty is that the two models have unmeasurable variables. We employ the auxiliary model identification idea to establish the auxiliary models and replace the unknown variables with the outputs of the auxiliary models. The main contributions of this paper are in the following aspects.

• A filtering based auxiliary model generalized stochastic gradient algorithm is derived for multivariate output-error autoregressive systems by using the data filter technique and the auxiliary model. Compared with the auxiliary model based generalized stochastic gradient algorithm, the proposed algorithm can generate more accurate estimates.

• A filtering based auxiliary model multi-innovation generalized stochastic gradient algorithm is proposed in order to improve the performance of the filtering based auxiliary model generalized stochastic gradient algorithm and it can get more accurate parameter estimates than the auxiliary model multi-innovation generalized stochastic gradient algorithm for the same innovation length.

The rest of this paper is organized as follows. In Sect. 2, we give some definitions and the identification model for multivariate output-error autoregressive systems. Section 3 gives the auxiliary model based stochastic gradient algorithm and the auxiliary model based multi-innovation stochastic gradient algorithm for comparisons. Section 4 derives the filtering identification model and presents the filtering based auxiliary model generalized stochastic gradient algorithm and the filtering based auxiliary model multi-innovation generalized stochastic gradient algorithm. An illustrative example is shown to verify the effectiveness of the proposed algorithms in Sect. 5. Finally, we offer some concluding remarks in Sect. 6.

2 The system description

Some notation is introduced. “$A=:X$” or “$X:=A$” stands for “A is defined as X”; the superscript T stands for the vector/matrix transpose; the symbol $\varvec{I}_n$ denotes an identity matrix of appropriate size ($n\times n$); $\hat{\varvec{{\vartheta }}}(t)$ denotes the estimate of $\varvec{{\vartheta }}$ at time t; $\mathbf{1}_n$ stands for an n-dimensional column vector whose elements are 1; the norm of a matrix (or a column vector) $\varvec{X}$ is defined by $\Vert \varvec{X}\Vert ^2:=\mathrm{tr}[\varvec{X}\varvec{X}^{\tiny \text{ T }}]$.

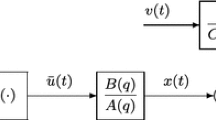
Consider the following multivariate output-error autoregressive (M-OEAR) system in Fig. 1,

$$\begin{aligned} \varvec{y}(t)=\frac{\varvec{\varPhi }_{\mathrm{s}}(t)}{A(z)}\varvec{{\theta }}+\frac{1}{C(z)}\varvec{v}(t), \end{aligned}$$

(1)

where $\varvec{y}(t):=[y_1(t), y_2(t),\ldots , y_m(t)]^{\tiny \text{ T }}\in {\mathbb R}^{m}$ is the output vector of the system, $\varvec{\varPhi }_{\mathrm{s}}(t)\in {\mathbb R}^{m\times n}$ is the information matrix consisting of the input signals $\varvec{u}(t)=[u_1(t), u_2(t), \ldots , u_r(t)]\in {\mathbb R}^{r}$ and output signals $\varvec{y}(t)$, $\varvec{{\theta }}\in {\mathbb R}^{n}$ is the parameter vector to be identified and $\varvec{v}(t):=[v_1(t), v_2(t), \ldots , v_m(t)]^{\tiny \text{ T }}\in {\mathbb R}^{m}$ is a white noise vector with zero mean, A(z) and C(z) are the polynomials in the unit backward shift operator $z^{-1}$ [$z^{-1}y(t)=y(t-1)$], and defined as

$$\begin{aligned} A(z):= & {} 1+a_1z^{-1}+a_2z^{-2}+\cdots +{a_{n_a}}z^{-n_a},\ a_i\in {\mathbb R},\\ C(z):= & {} 1+c_1z^{-1}+c_2z^{-2}+\cdots +c_{n_c}z^{-n_c},\ c_i\in {\mathbb R}. \end{aligned}$$

Assume that the orders m, n, $n_a$ and $n_c$ are known and $\varvec{y}(t)=\mathbf{0}$, $\varvec{\varPhi }_{\mathrm{s}}(t)=\mathbf{0}$ and $\varvec{v}(t)=\mathbf{0}$ for $t\leqslant 0$.

Fig. 1

A multivariate output-error autoregressive system

Define the parameter vectors:

$$\begin{aligned} \varvec{a}:= & {} [a_1, a_2, \ldots , a_{n_a}]^{\tiny \text{ T }}\in {\mathbb R}^{n_a},\\ \varvec{c}:= & {} [c_1, c_2, \ldots , c_{n_c}]^{\tiny \text{ T }}\in {\mathbb R}^{n_c},\\ \varvec{{\vartheta }}:= & {} [\varvec{{\theta }}^{\tiny \text{ T }}, \varvec{a}^{\tiny \text{ T }}, \varvec{c}^{\tiny \text{ T }}]^{\tiny \text{ T }}\in {\mathbb R}^{n+n_a+n_c} \end{aligned}$$

and the information matrices:

$$\begin{aligned} \varvec{{\phi }}_a(t):= & {} [-\varvec{x}(t-1),-\varvec{x}(t-2), \ldots , -\varvec{x}(t-n_a)]\in {\mathbb R}^{m\times n_a},\\ \varvec{{\phi }}_c(t):= & {} [-\varvec{w}(t-1),-\varvec{w}(t-2), \ldots , -\varvec{w}(t-n_c)]\in {\mathbb R}^{m\times n_c},\\ \varvec{\varPhi }(t):= & {} [\varvec{\varPhi }_{\mathrm{s}}(t), \varvec{{\phi }}_a(t), \varvec{{\phi }}_c(t)]\in {\mathbb R}^{m\times (n+n_a+n_c)}. \end{aligned}$$

Define the intermediate variables:

$$\begin{aligned} \varvec{x}(t):= & {} \frac{\varvec{\varPhi }_{\mathrm{s}}(t)}{A(z)}\varvec{{\theta }}\nonumber \\= & {} [1-A(z)]\varvec{x}(t)+\varvec{\varPhi }_{\mathrm{s}}(t)\varvec{{\theta }}\nonumber \\= & {} -\sum ^{n_a}_{j=1}a_j\varvec{x}(t-j)+\varvec{\varPhi }_{\mathrm{s}}(t)\varvec{{\theta }}\nonumber \\= & {} \varvec{\varPhi }_{\mathrm{s}}(t)\varvec{{\theta }}+\varvec{{\phi }}_a(t)\varvec{a}, \end{aligned}$$

(2)

$$\begin{aligned} \varvec{w}(t):= & {} \frac{1}{C(z)}\varvec{v}(t)\nonumber \\= & {} [1-C(z)]\varvec{w}(t)+\varvec{v}(t)\nonumber \\= & {} -\sum ^{n_c}_{j=1}c_j\varvec{w}(t-j)+\varvec{v}(t)\nonumber \\= & {} \varvec{{\phi }}_c(t)\varvec{c}+\varvec{v}(t). \end{aligned}$$

(3)

Equation (3) is the noise identification model.

Substituting (2) and (3) into (1) gives

$$\begin{aligned} \varvec{y}(t)= & {} \varvec{x}(t)+\varvec{w}(t)\nonumber \\= & {} \varvec{\varPhi }_{\mathrm{s}}(t)\varvec{{\theta }}+\varvec{{\phi }}_a(t)\varvec{a}+\varvec{w}(t) \end{aligned}$$

(4)

$$\begin{aligned}= & {} \varvec{\varPhi }_{\mathrm{s}}(t)\varvec{{\theta }}+\varvec{{\phi }}_a(t)\varvec{a}+\varvec{{\phi }}_c(t)\varvec{c}+\varvec{v}(t)\nonumber \\= & {} \varvec{\varPhi }(t)\varvec{{\vartheta }}+\varvec{v}(t). \end{aligned}$$

(5)

Equation (5) is the identification model for the M-OEAR system and the parameter vector $\varvec{{\vartheta }}$ contains all the parameters to be estimated. The object of this paper is to derive a new algorithm for the M-OEAR system by using the data filtering technique and the multi-innovation theory, which can generate more accurate estimates.

This paper studies the parameter estimation problem for the multivariate system by using the multidimensional input and output signals. The information matrix $\varvec{\varPhi }_{\mathrm{s}}(t)$ is composed of the m-dimensional output signals and the r-dimensional input signals. Therefore, the problem under consideration belongs to the multidimensional signal processing and estimation.

3 The auxiliary model based generalized stochastic gradient identification algorithm

In this section, we give the generalized stochastic gradient (AM-GSG) identification algorithm based on the auxiliary model identification idea. In order to improve the convergence rate and parameter estimation accuracy, an auxiliary model based multi-innovation stochastic gradient (AM-MI-GSG) algorithm is derived.

3.1 The AM-GSG algorithm

The stochastic gradient algorithm has been used to identify the multivariable system, and its convergence has been analyzed under weak conditions (Ding et al. 2008). On the basis of the work in Ding et al. (2008), we derive the AM-GSG algorithm for M-OEAR systems.

According to the identification model (5), we can define a gradient criterion function

$$\begin{aligned} J_1(\varvec{{\vartheta }}):=\frac{1}{2}\Vert \varvec{y}(t)-\varvec{\varPhi }(t)\varvec{{\vartheta }}\Vert ^2, \end{aligned}$$

Using the negative gradient search and minimizing the criterion function $J_1(\varvec{{\vartheta }})$ give

$$\begin{aligned} \hat{\varvec{{\vartheta }}}(t)= & {} \hat{\varvec{{\vartheta }}}(t-1)-\frac{1}{r(t)}\mathrm{grad}[J_1(\hat{\varvec{{\vartheta }}}(t-1))]\nonumber \\= & {} \hat{\varvec{{\vartheta }}}(t-1)+\frac{\varvec{\varPhi }^{\tiny \text{ T }}(t)}{r(t)}[\varvec{y}(t)-\varvec{\varPhi }(t)\hat{\varvec{{\vartheta }}}(t-1)], \end{aligned}$$

(6)

$$\begin{aligned} r(t)= & {} r(t-1)+\Vert \varvec{\varPhi }(t)\Vert ^2,\quad r(0)=1. \end{aligned}$$

(7)

Here, some problems arise. The information matrix $\varvec{\varPhi }(t)$ contains the unknown terms $\{\varvec{x}(t-i)$, $i=1, 2, \ldots , n_a\}$ and $\{\varvec{w}(t-i)$, $i=1, 2, \ldots , n_c\}$, thus the estimate $\hat{\varvec{{\vartheta }}}(t)$ in (6–7) is impossible to compute. An effective method to solve this problem is to employ the auxiliary model identification idea. Establish the appropriate auxiliary models, use their outputs $\varvec{x}_{\mathrm{a}}(t-i)$ and $\hat{\varvec{w}}(t-i)$ to replace the unknown variables $\varvec{x}(t-i)$ and $\varvec{w}(t-i)$. The estimates $\hat{\varvec{{\phi }}}_a(t)$ and $\hat{\varvec{{\phi }}}_c(t)$ of $\varvec{{\phi }}_a(t)$ and $\varvec{{\phi }}_c(t)$ can be formed by $\varvec{x}_{\mathrm{a}}(t-i)$ and $\hat{\varvec{w}}(t-i)$. Then we can get the estimate $\hat{\varvec{\varPhi }}(t)$ by using $\varvec{\varPhi }_{\mathrm{s}}(t)$, $\hat{\varvec{{\phi }}}_a(t)$ and $\hat{\varvec{{\phi }}}_c(t)$. Define

$$\begin{aligned} \hat{\varvec{{\phi }}}_a(t):= & {} [-\varvec{x}_{\mathrm{a}}(t-1),-\varvec{x}_{\mathrm{a}}(t-2), \ldots , -\varvec{x}_{\mathrm{a}}(t-n_a)]\in {\mathbb R}^{m\times n_a},\\ \hat{\varvec{{\phi }}}_c(t):= & {} [-\hat{\varvec{w}}(t-1),-\hat{\varvec{w}}(t-2), \ldots , -\hat{\varvec{w}}(t-n_c)]\in {\mathbb R}^{m\times n_c},\\ \hat{\varvec{\varPhi }}(t):= & {} [\varvec{\varPhi }_{\mathrm{s}}(t), \hat{\varvec{{\phi }}}_a(t), \hat{\varvec{{\phi }}}_c(t)]\in {\mathbb R}^{m\times (n+n_a+n_c)}. \end{aligned}$$

According to (2), replacing the $\varvec{{\phi }}_a(t)$, $\varvec{{\theta }}$ and $\varvec{a}$ with their estimates $\hat{\varvec{{\phi }}}_a(t)$, $\hat{\varvec{{\theta }}}(t)$ and $\hat{\varvec{a}}(t)$, the output $\varvec{x}_{\mathrm{a}}(t)$ of the auxiliary model can be computed by

$$\begin{aligned} \varvec{x}_{\mathrm{a}}(t):=\varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t)+\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t). \end{aligned}$$

Similarly, from (4), $\hat{\varvec{w}}(t)$ can be computed through

$$\begin{aligned} \hat{\varvec{w}}(t):= & {} \varvec{y}(t)-\varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t)-\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t)\\= & {} \varvec{y}(t)-\varvec{x}_{\mathrm{a}}(t). \end{aligned}$$

For convenience, define the innovation vector

$$\begin{aligned} \varvec{e}(t):=\varvec{y}(t)-\hat{\varvec{\varPhi }}(t)\hat{\varvec{{\vartheta }}}(t-1)\in {\mathbb R}^{m}. \end{aligned}$$

Replacing $\varvec{\varPhi }(t)$ in (6–7) with its estimate $\hat{\varvec{\varPhi }}(t)$, we can obtain the auxiliary model based generalized stochastic gradient (AM-GSG) algorithm:

$$\begin{aligned} \hat{\varvec{{\vartheta }}}(t)= & {} \hat{\varvec{{\vartheta }}}(t-1)+\frac{\hat{\varvec{\varPhi }}^{\tiny \text{ T }}(t)}{r(t)}\varvec{e}(t), \end{aligned}$$

(8)

$$\begin{aligned} \varvec{e}(t)= & {} \varvec{y}(t)-\hat{\varvec{\varPhi }}(t)\hat{\varvec{{\vartheta }}}(t-1), \end{aligned}$$

(9)

$$\begin{aligned} r(t)= & {} r(t-1)+\Vert \hat{\varvec{\varPhi }}(t)\Vert ^2, \end{aligned}$$

(10)

$$\begin{aligned} \hat{\varvec{\varPhi }}(t)= & {} [\varvec{\varPhi }_{\mathrm{s}}(t),\hat{\varvec{{\phi }}}_a(t),\hat{\varvec{{\phi }}}_c(t)], \end{aligned}$$

(11)

$$\begin{aligned} \hat{\varvec{{\phi }}}_a(t)= & {} [-\varvec{x}_{\mathrm{a}}(t-1),-\varvec{x}_{\mathrm{a}}(t-2), \ldots , -\varvec{x}_{\mathrm{a}}(t-n_a)], \end{aligned}$$

(12)

$$\begin{aligned} \hat{\varvec{{\phi }}}_c(t)= & {} [-\hat{\varvec{w}}(t-1),-\hat{\varvec{w}}(t-2), \ldots , -\hat{\varvec{w}}(t-n_c)], \end{aligned}$$

(13)

$$\begin{aligned} \varvec{x}_{\mathrm{a}}(t)= & {} \varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t)+\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t), \end{aligned}$$

(14)

$$\begin{aligned} \hat{\varvec{w}}(t)= & {} \varvec{y}(t)-\varvec{x}_{\mathrm{a}}(t), \end{aligned}$$

(15)

$$\begin{aligned} \hat{\varvec{{\vartheta }}}(t)= & {} [\hat{\varvec{{\theta }}}^{\tiny \text{ T }}(t), \hat{\varvec{a}}^{\tiny \text{ T }}(t), \hat{\varvec{c}}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}. \end{aligned}$$

(16)

The procedure for computing the parameter estimation vector $\hat{\varvec{{\vartheta }}}(t)$ in the AM-GSG algorithm (8–16) is as follows.

• 1. Set the initial values: let $t=1$, $\hat{\varvec{{\vartheta }}}(0)=\mathbf{1}_{n+n_a+n_c}/p_0$, $r(0)=1$, $\varvec{x}_{\mathrm{a}}(t-i)=\mathbf{1}_m/p_0$, $\hat{\varvec{w}}(t-i)=\mathbf{1}_m/p_0$, $i=1$, 2, $\ldots$, $\max [n_a,n_c]$, $p_0=10^6$ and set a small positive number $\varepsilon$.

• 2. Collect the observation data $\varvec{y}(t)$ and $\varvec{\varPhi }_{\mathrm{s}}(t)$, and construct the information matrices $\hat{\varvec{{\phi }}}_a(t)$, $\hat{\varvec{{\phi }}}_c(t)$ and $\hat{\varvec{\varPhi }}(t)$ using (12–13) and (11).

• 3. Compute the innovation vector $\varvec{e}(t)$ and the step-size r(t) according to (9) and (10).

• 4. Update the parameter estimation vector $\hat{\varvec{{\vartheta }}}(t)$ using (8).

• 5. Compute $\varvec{x}_{\mathrm{a}}(t)$ and $\hat{\varvec{w}}(t)$ using (14–15).

• 6. Compare $\hat{\varvec{{\vartheta }}}(t)$ with $\hat{\varvec{{\vartheta }}}(t-1)$: if $\Vert \hat{\varvec{{\vartheta }}}(t)-\hat{\varvec{{\vartheta }}}(t-1)\Vert <\varepsilon$, terminate recursive calculation procedure and obtain $\hat{\varvec{{\vartheta }}}(t)$; otherwise, increase t by 1 and go to Step 2.

Remark 1

: In order to improve the transient performance and parameter estimation accuracy of the AM-GSG algorithm, we can introduce a forgetting factor (FF) $\lambda$ in (10):

$$\begin{aligned} r(t)=\lambda r(t-1)+\Vert \hat{\varvec{\varPhi }}(t)\Vert ^2,\quad 0 \leqslant \lambda < 1,\ r(0)=1. \end{aligned}$$

(17)

Equations (8–9), (11–16) and (17) form the auxiliary model based forgetting factor gradient stochastic gradient (AM-FF-GSG) algorithm for the M-OEAR system. When $\lambda$=1, the AM-FF-GSG algorithm reduces to the AM-GSG algorithm (8–16).

Remark 2

In order to improve the stable state performance, a convergence index $\varepsilon$ can be introduced in (8),

$$\begin{aligned} \hat{\varvec{{\vartheta }}}(t)=\hat{\varvec{{\vartheta }}}(t-1)+\frac{\hat{\varvec{\varPhi }}^{\tiny \text{ T }}(t)}{r^{\varepsilon }(t)}\varvec{e}(t),\ \frac{1}{2} < \varepsilon \leqslant 1. \end{aligned}$$

(18)

Then Eqs. (9–16) and (18) form the Modified AM-GSG (M-AM-GSG) algorithm. When $\varepsilon =1$, the M-AM-GSG algorithm reduces to the AM-GSG algorithm in (8–16).

3.2 The AM-MI-GSG algorithm

In order to improve the convergence rate and parameter estimation accuracy of the AM-GSG algorithm, we expand the dimension of the innovation vector $\varvec{e}(t)$ by employing the multi-innovation identification theory and derive the auxiliary model based multi-innovation generalized stochastic gradient algorithm for the M-OEAR system.

Let p represents the innovation length, consider p data from $j=t-p+1$ to $j=t$ and define a new multi-innovation vector:

$$\begin{aligned} \varvec{E}(p,t):=\left[ \begin{array}{c} \varvec{e}(t) \\ \varvec{e}(t-1) \\ \vdots \\ \varvec{e}(t-p+1) \end{array}\right] =\left[ \begin{array}{c} \varvec{y}(t)-\hat{\varvec{\varPhi }}(t)\hat{\varvec{{\vartheta }}}(t-1) \\ \varvec{y}(t-1)-\hat{\varvec{\varPhi }}(t-1)\hat{\varvec{{\vartheta }}}(t-2) \\ \vdots \\ \varvec{y}(t-p+1)-\hat{\varvec{\varPhi }}(t-p+1)\hat{\varvec{{\vartheta }}}(t-p) \end{array}\right] \in {\mathbb R}^{mp}. \end{aligned}$$

It is usually considered that the estimate $\hat{\varvec{{\vartheta }}}(t-1)$ is more closer to the true value than $\hat{\varvec{{\vartheta }}}(t-i)$ and $\varvec{E}(p,t)$ is modified as

$$\begin{aligned} \varvec{E}(p,t):= & {} \left[ \begin{array}{c} \varvec{y}(t)-\hat{\varvec{\varPhi }}(t)\hat{\varvec{{\vartheta }}}(t-1) \\ \varvec{y}(t-1)-\hat{\varvec{\varPhi }}(t-1)\hat{\varvec{{\vartheta }}}(t-1) \\ \vdots \\ \varvec{y}(t-p+1)-\hat{\varvec{\varPhi }}(t-p+1)\hat{\varvec{{\vartheta }}}(t-1) \end{array}\right] . \end{aligned}$$

Define the stacked output vector $\varvec{Y}(p,t)$ and the stacked information matrix $\hat{{{\varvec{\varGamma }}}}(p,t)$ as

$$\begin{aligned} \varvec{Y}(p,t):= & {} \left[ \begin{array}{c} \varvec{y}(t) \\ \varvec{y}(t-1) \\ \vdots \\ \varvec{y}(t-p+1) \end{array}\right] \in {\mathbb R}^{mp},\\ \hat{{{\varvec{\varGamma }}}}(p,t):= & {} \left[ \begin{array}{c} \hat{\varvec{\varPhi }}(t) \\ \hat{\varvec{\varPhi }}(t-1) \\ \vdots \\ \hat{\varvec{\varPhi }}(t-p+1) \end{array}\right] \in {\mathbb R}^{(mp)\times (n+n_a+n_c)}. \end{aligned}$$

Then the innovation vector $\varvec{E}(p,t)$ can be equivalently expressed as

$$\begin{aligned} \varvec{E}(p,t)=\varvec{Y}(p,t)-\hat{{{\varvec{\varGamma }}}}(p,t)\hat{\varvec{{\vartheta }}}(t-1)\in {\mathbb R}^{mp}. \end{aligned}$$

Thus, we have

$$\begin{aligned} \hat{\varvec{{\vartheta }}}(t)= & {} \hat{\varvec{{\vartheta }}}(t-1)+\frac{\hat{{{\varvec{\varGamma }}}}^{\tiny \text{ T }}(p,t)}{r(t)}\varvec{E}(p,t), \end{aligned}$$

(19)

$$\begin{aligned} \varvec{E}(p,t)= & {} \varvec{Y}(p,t)-\hat{{{\varvec{\varGamma }}}}(p,t)\hat{\varvec{{\vartheta }}}(t-1), \end{aligned}$$

(20)

$$\begin{aligned} r(t)= & {} r(t-1)+\Vert \hat{\varvec{\varPhi }}(t)\Vert ^2, \end{aligned}$$

(21)

$$\begin{aligned} \varvec{Y}(p,t)= & {} [\varvec{y}^{\tiny \text{ T }}(t), \varvec{y}^{\tiny \text{ T }}(t-1), \ldots , \varvec{y}^{\tiny \text{ T }}(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$

(22)

$$\begin{aligned} \hat{{{\varvec{\varGamma }}}}(p,t)= & {} [\hat{\varvec{\varPhi }}^{\tiny \text{ T }}(t), \hat{\varvec{\varPhi }}^{\tiny \text{ T }}(t-1), \ldots , \hat{\varvec{\varPhi }}^{\tiny \text{ T }}(t-p+1)]^{\tiny \text{ T }}. \end{aligned}$$

(23)

Equations (19–23) and (11–16) consist the AM-MI-GSG algorithm. When the innovation length $p=1$, the AM-MI-GSG algorithm reduces to the AM-GSG algorithm in (8–16). That is to say, the AM-GSG is a special case of the AM-MI-GSG algorithm. Similarly, a forgetting factor $\lambda$ can be introduced in (21),

$$\begin{aligned} r(t)=\lambda r(t-1)+\Vert \hat{\varvec{\varPhi }}(t)\Vert ^2,\ r(0)=1, \ 0< \lambda \leqslant 1. \end{aligned}$$

(24)

Equations (19–20), (24), (22–23) and (11–16) form the auxiliary model based forgetting factor multi-innovation stochastic generalized gradient (AM-FF-MI-GSG) algorithm for the M-OEAR system.

To initialize the AM-MI-GSG algorithm, we should set the innovation length p and some initial values, e.g., $\hat{\varvec{{\vartheta }}}(0)=\mathbf{1}_{n+n_a+n_c}/p_0$, $\varvec{x}_{\mathrm{a}}(t-i)=\mathbf{1}_m/p_0$, $\hat{\varvec{w}}(t-i)=\mathbf{1}_m/p_0$, $i=1$, 2, $\ldots$, $\max [n_a,n_c]$ and $p_0=10^6$. The flowchart of computing $\hat{\varvec{{\vartheta }}}(t)$ in the AM-MI-GSG algorithm is shown in Fig. 2.

Fig. 2

The flowchart of computing the AM-MI-GSG parameter estimates $\hat{\varvec{{\vartheta }}}(t)$

4 The filtering based AM-GSG identification algorithm

In this section, a linear filter L(z) is introduced to deal with the colored noises. We derive two identification models by filtering the input and output data including a system model and a noise model, and identify each subsystems respectively. A filtering base AM-GSG (F-AM-GSG) and a filtering base AM-MI-GSG (F-AM-MI-GSG) identification algorithms are proposed in order to improve the convergence rate and parameter estimation accuracy.

4.1 The F-AM-GSG algorithm

For the M-OEAR model in (1), choose the polynomial C(z) as the filter, that is to say, $L(z)=C(z)$. Multiplying the both sides of (1) by C(z) gives

$$\begin{aligned} C(z)\varvec{y}(t)=C(z)\frac{\varvec{\varPhi }_{\mathrm{s}}(t)}{A(z)}\varvec{{\theta }}+\varvec{v}(t). \end{aligned}$$

(25)

Define the filtered output vector $\varvec{y}_{\mathrm{f}}(t)$ and the filtered information matrix $\varvec{\varPhi }_{\mathrm{f}}(t)$ as

$$\begin{aligned} \varvec{y}_{\mathrm{f}}(t):= & {} L(z)\varvec{y}(t)\nonumber \\= & {} {C(z)}\varvec{y}(t)\in {\mathbb R}^m, \end{aligned}$$

(26)

$$\begin{aligned} \varvec{{\phi }}_{\mathrm{f}}(t):= & {} L(z)\varvec{\varPhi }_{\mathrm{s}}(t)\nonumber \\= & {} {C(z)}\varvec{\varPhi }_{\mathrm{s}}(t)\in {\mathbb R}^{m\times n}, \end{aligned}$$

(27)

which can be expressed as the following recursive forms:

$$\begin{aligned} \varvec{y}_{\mathrm{f}}(t)= & {} C(z)\varvec{y}(t)\nonumber \\= & {} \varvec{y}(t)+[\varvec{y}(t-1), \varvec{y}(t-2),\ldots , \varvec{y}(t-n_c)]\varvec{c}, \end{aligned}$$

(28)

$$\begin{aligned} \varvec{{\phi }}_{\mathrm{f}}(t)= & {} C(z)\varvec{\varPhi }_{\mathrm{s}}(t)\nonumber \\= & {} \varvec{\varPhi }_{\mathrm{s}}(t)+[\varvec{\varPhi }_{\mathrm{s}}(t-1), \varvec{\varPhi }_{\mathrm{s}}(t-2),\ldots , \varvec{\varPhi }_{\mathrm{s}}(t-n_c)]\varvec{c}. \end{aligned}$$

(29)

From (25), we have

$$\begin{aligned} \varvec{y}_{\mathrm{f}}=\frac{\varvec{{\phi }}_{\mathrm{f}}(t)}{A(z)}\varvec{{\theta }}+\varvec{v}(t). \end{aligned}$$

(30)

Define an inner variable

$$\begin{aligned} \varvec{x}_{\mathrm{f}}(t):= & {} \frac{\varvec{{\phi }}_{\mathrm{f}}(t)}{A(z)}\varvec{{\theta }}\nonumber \\= & {} [1-A(z)]\varvec{x}_{\mathrm{f}}(t)+\varvec{{\phi }}_{\mathrm{f}}(t)\varvec{{\theta }}\nonumber \\= & {} -\sum ^{n_a}_{j=1}a_j\varvec{x}_{\mathrm{f}}(t-j)+\varvec{{\phi }}_{\mathrm{f}}(t)\varvec{{\theta }}\nonumber \\= & {} \varvec{\varPhi }_{\mathrm{f}}(t)\varvec{{\theta }}_{\mathrm{f}}\in {\mathbb R}^{m}, \end{aligned}$$

(31)

where

$$\begin{aligned} \varvec{\varPhi }_{\mathrm{f}}(t):= & {} [\varvec{{\phi }}_{\mathrm{f}}(t), -\varvec{x}_{\mathrm{f}}(t-1), -\varvec{x}_{\mathrm{f}}(t-2), \ldots , -\varvec{x}_{\mathrm{f}}(t-n_a)]\in {\mathbb R}^{m\times (n+n_a)},\\ \varvec{{\theta }}_{\mathrm{f}}:= & {} \left[ \begin{array}{c} \varvec{{\theta }} \\ \varvec{a} \end{array} \right] \in {\mathbb R}^{n+n_a}. \end{aligned}$$

Then Eq. (30) can be rewritten as

$$\begin{aligned} \varvec{y}_{\mathrm{f}}(t)=\varvec{\varPhi }_{\mathrm{f}}(t)\varvec{{\theta }}_{\mathrm{f}}+\varvec{v}(t). \end{aligned}$$

(32)

For the filter identification model in (32) and the noise identification model in (3), defining and minimizing the two gradient criterion functions

$$\begin{aligned} J_2(\varvec{{\theta }}_{\mathrm{f}}):= & {} \frac{1}{2}\Vert \varvec{y}_{\mathrm{f}}(t)-\varvec{\varPhi }_{\mathrm{f}}(t)\varvec{{\theta }}_{\mathrm{f}}\Vert ^2,\\ J_3(\varvec{c}):= & {} \frac{1}{2}\Vert \varvec{w}(t)-\varvec{{\phi }}_c(t)\varvec{c}\Vert ^2, \end{aligned}$$

result in the following gradient recursive relations:

$$\begin{aligned} \hat{\varvec{{\theta }}}_{\mathrm{f}}(t)= & {} \hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1)+\frac{\varvec{\varPhi }_{\mathrm{f}}^{\tiny \text{ T }}(t)}{r_1(t)}[\varvec{y}_{\mathrm{f}}(t)-\varvec{\varPhi }_{\mathrm{f}}(t)\hat{\varvec{{\theta }}_{\mathrm{f}}}(t-1)], \end{aligned}$$

(33)

$$\begin{aligned} r_1(t)= & {} r_1(t-1)+\Vert \varvec{\varPhi }_{\mathrm{f}}(t)\Vert ^2,\quad r_1(0)=1. \end{aligned}$$

(34)

$$\begin{aligned} \hat{\varvec{c}}(t)= & {} \hat{\varvec{c}}(t-1)+\frac{\varvec{{\phi }}^{\tiny \text{ T }}_c(t)}{r_2(t)}[\varvec{w}(t)-\varvec{{\phi }}_c(t)\hat{\varvec{c}}(t-1)]\nonumber \\= & {} \hat{\varvec{c}}(t-1)+\frac{\varvec{{\phi }}^{\tiny \text{ T }}_c(t)}{r_2(t)}[\varvec{y}(t)-\varvec{\varPhi }_{\mathrm{s}}(t)\varvec{{\theta }}-\varvec{{\phi }}_a(t)\varvec{a}-\varvec{{\phi }}_c(t)\hat{\varvec{c}}(t-1)], \end{aligned}$$

(35)

$$\begin{aligned} r_2(t)= & {} r_2(t-1)+\Vert \varvec{{\phi }}_c(t)\Vert ^2,\quad r_2(0)=1. \end{aligned}$$

(36)

As we can see, Eqs. (33–36) cannot generate the estimates of $\hat{\varvec{{\theta }}}_{\mathrm{f}}(t)$ and $\hat{\varvec{c}}(t)$, because the filter C(z) is unknown, then the filtered matrix $\varvec{\varPhi }_{\mathrm{f}}$ is unknown, in addition, $\varvec{x}(t-i)$ and $\varvec{w}(t-i)$ are unmeasurable, the information matrices $\varvec{{\phi }}_a(t)$ and $\varvec{{\phi }}_c(t)$ contain those unknown terms. In order to solve those difficulties, we employ the auxiliary model method to replace the unknown variables with the output of the auxiliary model.

Use the outputs of the auxiliary models $\varvec{x}_{\mathrm{a}}(t-i)$ and $\hat{\varvec{w}}(t-i)$ to construct the estimates

$$\begin{aligned} \hat{\varvec{{\phi }}}_a(t)= & {} [-\varvec{x}_{\mathrm{a}}(t-1), -\varvec{x}_{\mathrm{a}}(t-2), \ldots , -\varvec{x}_{\mathrm{a}}(t-n_a)]\in {\mathbb R}^{m\times n_a}, \\ \hat{\varvec{{\phi }}}_c(t)= & {} [-\hat{\varvec{w}}(t-1), -\hat{\varvec{w}}(t-2), \ldots , -\hat{\varvec{w}}(t-n_c)]\in {\mathbb R}^{m\times n_c}. \end{aligned}$$

Similarly, we use the estimate $\varvec{x}_{\mathrm{f}\mathrm{a}}(t-i)$ of $\varvec{x}_{\mathrm{f}}(t-i)$ and the estimate $\hat{\varvec{{\phi }}}_{\mathrm{f}}(t)$ of $\varvec{\varPhi }_{\mathrm{f}}(t)$ to define

$$\begin{aligned} \hat{\varvec{\varPhi }}_{\mathrm{f}}(t):=[\hat{\varvec{{\phi }}}_{\mathrm{f}}(t), -\varvec{x}_{\mathrm{f}\mathrm{a}}(t-1), -\varvec{x}_{\mathrm{f}\mathrm{a}}(t-2), \ldots , -\varvec{x}_{\mathrm{f}\mathrm{a}} (t-n_a)]\in {\mathbb R}^{m\times (n+n_a)}. \end{aligned}$$

From (2), (4) and (31), we can compute the outputs $\varvec{x}_{\mathrm{a}}(t)$, $\hat{\varvec{w}}(t)$ and $\varvec{x}_{\mathrm{f}\mathrm{a}}(t)$ of the auxiliary models by

$$\begin{aligned} \varvec{x}_{\mathrm{a}}(t)= & {} \varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t)+\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t),\\ \hat{\varvec{w}}(t)= & {} \varvec{y}(t)-\varvec{x}_{\mathrm{a}}(t),\\ \varvec{x}_{\mathrm{f}\mathrm{a}}(t)= & {} \hat{\varvec{\varPhi }}_{\mathrm{f}}(t)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t). \end{aligned}$$

Use the parameter estimates of the noise model

$$\begin{aligned} \hat{\varvec{c}}(t):=[\hat{c}_1(t), \hat{c}_2(t),\ldots , \hat{c}_{n_c}(t)]^{\tiny \text{ T }}\in {\mathbb R}^{n_c}, \end{aligned}$$

to construct the estimate of C(z):

$$\begin{aligned} \hat{C}(t,z):=1+\hat{c}_1(t)z^{-1}+\hat{c}_2(t)z^{-2}+\cdots +\hat{c}_{n_c}(t)z^{-{n_c}}. \end{aligned}$$

Replacing the C(z) in (26) and (27) with $\hat{C}(t,z)$, the estimates of the filtered output vector $\varvec{y}_{\mathrm{f}}(t)$ and the filtered information matrix $\varvec{{\phi }}_{\mathrm{f}}(t)$ can be computed by

$$\begin{aligned} \hat{\varvec{y}}_{\mathrm{f}}(t)= & {} \hat{C}(t,z)\varvec{y}(t)\\= & {} \varvec{y}(t)+[\varvec{y}(t-1), \varvec{y}(t-2),\ldots , \varvec{y}(t-n_c)]\hat{\varvec{c}}(t),\\ \hat{\varvec{{\phi }}}_{\mathrm{f}}(t)= & {} \hat{C}(t,z)\varvec{\varPhi }_{\mathrm{s}}(t)\\= & {} \varvec{\varPhi }_{\mathrm{s}}(t)+[\varvec{\varPhi }_{\mathrm{s}}(t-1), \varvec{\varPhi }_{\mathrm{s}}(t-2),\ldots , \varvec{\varPhi }_{\mathrm{s}}(t-n_c)]\hat{\varvec{c}}(t). \end{aligned}$$

Replace the unknown information matrix $\varvec{\varPhi }_{\mathrm{f}}(t)$ in (33–34) with its estimate $\hat{\varvec{\varPhi }}_{\mathrm{f}}(t)$, $\varvec{{\phi }}_c(t)$ in (35–36) with $\hat{\varvec{{\phi }}}_c(t)$, $\varvec{{\phi }}_a(t)$ in (36) with $\hat{\varvec{{\phi }}}_a(t)$, and the filtered output $\varvec{y}_{\mathrm{f}}(t)$ in (33) with $\hat{\varvec{y}}_{\mathrm{f}}(t)$, the parameter vector $\varvec{{\theta }}$ and $\varvec{a}$ in (36) with $\hat{\varvec{{\theta }}}(t-1)$ and $\hat{\varvec{a}}(t-1)$ respectively. Furthermore, define the innovation vectors:

$$\begin{aligned} \varvec{e}_1(t):= & {} \hat{\varvec{y}}_{\mathrm{f}}(t)-\hat{\varvec{\varPhi }}_{\mathrm{f}}(t)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1)\in {\mathbb R}^{m},\\ \varvec{e}_2(t):= & {} \varvec{y}(t)-\varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t-1)-\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t-1)-\hat{\varvec{{\phi }}}_c(t)\hat{\varvec{c}}(t-1)\in {\mathbb R}^{m}. \end{aligned}$$

Then, we can derive a filtering based auxiliary model generalized stochastic gradient (F-AM-GSG) algorithm to estimate the parameter vectors $\hat{\varvec{{\theta }}}_{\mathrm{f}}(t)$ and $\hat{\varvec{c}}(t)$ for the M-OEAR system:

$$\begin{aligned} \hat{\varvec{{\theta }}}_{\mathrm{f}}(t)= & {} \hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1)+\frac{\hat{\varvec{\varPhi }}_{\mathrm{f}}^{\tiny \text{ T }}(t)}{r_1(t)}\varvec{e}_1(t), \end{aligned}$$

(37)

$$\begin{aligned} \varvec{e}_1(t)= & {} \hat{\varvec{y}}_{\mathrm{f}}(t)-\hat{\varvec{\varPhi }}_{\mathrm{f}}(t)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1), \end{aligned}$$

(38)

$$\begin{aligned} r_1(t)= & {} r_1(t-1)+\Vert \hat{\varvec{\varPhi }}_{\mathrm{f}}(t)\Vert ^2, \end{aligned}$$

(39)

$$\begin{aligned} \hat{\varvec{c}}(t)= & {} \hat{\varvec{c}}(t-1)+\frac{\hat{\varvec{{\phi }}}^{\tiny \text{ T }}_c(t)}{r_2(t)}\varvec{e}_2(t), \end{aligned}$$

(40)

$$\begin{aligned} \varvec{e}_2(t)= & {} \varvec{y}(t)-\varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t-1)-\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t-1)-\hat{\varvec{{\phi }}}_c(t)\hat{\varvec{c}}(t-1), \end{aligned}$$

(41)

$$\begin{aligned} r_2(t)= & {} r_2(t-1)+\Vert \hat{\varvec{{\phi }}}_c(t)\Vert ^2, \end{aligned}$$

(42)

$$\begin{aligned} \hat{\varvec{\varPhi }}_{\mathrm{f}}(t)= & {} [\hat{\varvec{{\phi }}}_{\mathrm{f}}(t), -\varvec{x}_{\mathrm{f}\mathrm{a}}(t-1), -\varvec{x}_{\mathrm{f}\mathrm{a}}(t-2), \ldots , -\varvec{x}_{\mathrm{f}\mathrm{a}}(t-n_a)], \end{aligned}$$

(43)

$$\begin{aligned} \hat{\varvec{y}}_{\mathrm{f}}(t)= & {} \varvec{y}(t)+[\varvec{y}(t-1), \varvec{y}(t-2),\ldots , \varvec{y}(t-n_c)]\hat{\varvec{c}}(t), \end{aligned}$$

(44)

$$\begin{aligned} \hat{\varvec{{\phi }}}_{\mathrm{f}}(t)= & {} \varvec{\varPhi }_{\mathrm{s}}(t)+[\varvec{\varPhi }_{\mathrm{s}}(t-1), \varvec{\varPhi }_{\mathrm{s}}(t-2),\ldots , \varvec{\varPhi }_{\mathrm{s}}(t-n_c)]\hat{\varvec{c}}(t), \end{aligned}$$

(45)

$$\begin{aligned} \hat{\varvec{{\phi }}}_a(t)= & {} [-\varvec{x}_{\mathrm{a}}(t-1), -\varvec{x}_{\mathrm{a}}(t-2),\ldots , -\varvec{x}_{\mathrm{a}}(t-n_a)], \end{aligned}$$

(46)

$$\begin{aligned} \hat{\varvec{{\phi }}}_c(t)= & {} [-\hat{\varvec{w}}(t-1), -\hat{\varvec{w}}(t-2),\ldots , -\hat{\varvec{w}}(t-n_c)], \end{aligned}$$

(47)

$$\begin{aligned} \varvec{x}_{\mathrm{f}\mathrm{a}}(t)= & {} \hat{\varvec{\varPhi }}_{\mathrm{f}}(t)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t), \end{aligned}$$

(48)

$$\begin{aligned} \varvec{x}_{\mathrm{a}}(t)= & {} \varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t)+\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t), \end{aligned}$$

(49)

$$\begin{aligned} \hat{\varvec{w}}(t)= & {} \varvec{y}(t)-\varvec{x}_{\mathrm{a}}(t), \end{aligned}$$

(50)

$$\begin{aligned} \hat{\varvec{{\theta }}}_{\mathrm{f}}(t)= & {} [\hat{\varvec{{\theta }}}^{\tiny \text{ T }}(t), \hat{\varvec{a}}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}. \end{aligned}$$

(51)

The steps involved in the F-AM-GSG algorithm are listed as follows.

• 1. Set the initial values: let $t=1$, $\hat{\varvec{{\theta }}}_{\mathrm{f}}(0)=\mathbf{1}_{n+n_a}/p_0$, $\hat{\varvec{c}}(0)=\mathbf{1}_{n_c}/p_0$, $r_1(0)=1$, $r_2(0)=1$, $\varvec{x}_{\mathrm{f}\mathrm{a}}(t-i)=\mathbf{1}_m/p_0$, $\varvec{x}_{\mathrm{a}}(t-i)=\mathbf{1}_m/p_0$, $\hat{\varvec{w}}(t-i)=\mathbf{1}_m/p_0$, $i=1$, 2, $\ldots$, $\max [n_a,n_c]$, $p_0=10^6$, and set a small positive number $\varepsilon$.

• 2. Collect the observation data $\varvec{y}(t)$ and $\varvec{\varPhi }_{\mathrm{s}}(t)$, construct the information matrices $\hat{\varvec{{\phi }}}_a(t)$ and $\hat{\varvec{{\phi }}}_c(t)$ by (46) and (47).

• 3. Compute $\varvec{e}_2(t)$ by (41), $r_2(t)$ by (42).

• 4. Update the parameter estimate $\hat{\varvec{c}}(t)$ by (40).

• 5. Compute the filtered output vector $\hat{\varvec{y}}_{\mathrm{f}}(t)$ by (44) and the filtered information matrix $\hat{\varvec{{\phi }}}_{\mathrm{f}}(t)$ by (45), and form $\hat{\varvec{\varPhi }}_{\mathrm{f}}(t)$ by (43).

• 6. Compute $\varvec{e}_1(t)$ by (38) and $r_1(t)$ by (39).

• 7. Update the parameter estimate $\hat{\varvec{{\theta }}}_{\mathrm{f}}(t)$ by (37).

• 8. Compute $\varvec{x}_{\mathrm{f}\mathrm{a}}(t)$ by (48). Read $\hat{\varvec{{\theta }}}(t)$ and $\hat{\varvec{a}}(t)$ from $\hat{\varvec{{\theta }}}_{\mathrm{f}}(t)$ and compute $\varvec{x}_{\mathrm{a}}(t)$ and $\hat{\varvec{w}}(t)$ by (49–50).

• 9. Compare $\hat{\varvec{{\theta }}}_{\mathrm{f}}(t)$ with $\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1)$ and compare $\hat{\varvec{c}}(t)$ with $\hat{\varvec{c}}(t-1)$: if $\Vert \hat{\varvec{{\theta }}}_{\mathrm{f}}(t)-\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1)\Vert <\varepsilon$ and $\Vert \hat{\varvec{c}}(t)-\hat{\varvec{c}}(t-1)\Vert <\varepsilon$, terminate recursive calculation procedure and obtain $\hat{\varvec{{\vartheta }}}(t)$; otherwise, increase t by 1 and go to Step 2.

4.2 The F-AM-MI-GSG algorithm

The F-AM-GSG algorithm can identify the parameter vectors $\hat{\varvec{{\theta }}}_{\mathrm{f}}(t)$ and $\hat{\varvec{c}}(t)$, but has slow convergence speed. To improve the convergence rate and parameter estimation accuracy of the F-AM-GSG algorithm, according to the multi-innovation identification theory, we expand the innovation vectors $\varvec{e}_1(t)=\hat{\varvec{y}}_{\mathrm{f}}(t)-\hat{\varvec{\varPhi }}_{\mathrm{f}}(t)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1)\in {\mathbb R}^{m}$ in (38) and $\varvec{e}_2(t)=\varvec{y}(t)-\varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t-1)-\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t-1)-\hat{\varvec{{\phi }}}_c(t)\hat{\varvec{c}}(t-1)\in {\mathbb R}^{m}$ in (41) into large innovation vectors (p represents the innovation length):

$$\begin{aligned} \varvec{E}_1(p,t):= & {} \left[ \begin{array}{c} \hat{\varvec{y}}_{\mathrm{f}}(t)-\hat{\varvec{\varPhi }}_{\mathrm{f}}(t)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1) \\ \hat{\varvec{y}}_{\mathrm{f}}(t-1)-\hat{\varvec{\varPhi }}_{\mathrm{f}}(t-1)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1) \\ \vdots \\ \hat{\varvec{y}}_{\mathrm{f}}(t-p+1)-\hat{\varvec{\varPhi }}_{\mathrm{f}}(t-p+1)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1) \end{array}\right] \in {\mathbb R}^{mp},\\ \varvec{E}_1(p,t)\\:= & {} \left[ \begin{array}{c} \varvec{y}(t)-\varvec{\varPhi }_{\mathrm{s}}(t)\hat{\varvec{{\theta }}}(t-1)-\hat{\varvec{{\phi }}}_a(t)\hat{\varvec{a}}(t-1)-\hat{\varvec{{\phi }}}_c(t)\hat{\varvec{c}}(t-1) \\ \varvec{y}(t-1)-\varvec{\varPhi }_{\mathrm{s}}(t-1)\hat{\varvec{{\theta }}}(t-1)-\hat{\varvec{{\phi }}}_a(t-1)\hat{\varvec{a}}(t-1)-\hat{\varvec{{\phi }}}_c(t-1)\hat{\varvec{c}}(t-1) \\ \vdots \\ \varvec{y}(t-p+1)-\varvec{\varPhi }_{\mathrm{s}}(t-p+1)\hat{\varvec{{\theta }}}(t-1)-\hat{\varvec{{\phi }}}_a(t-p+1)\hat{\varvec{a}}(t-1)-\hat{\varvec{{\phi }}}_c(t-p+1)\hat{\varvec{c}}(t-1) \end{array}\right] \in {\mathbb R}^{mp}. \end{aligned}$$

Define the stacked filtered output vector $\hat{\varvec{Y}}_{\mathrm{f}}(p,t)$, the stacked filtered information matrix $\hat{{{\varvec{\varGamma }}}}_{\mathrm{f}}(p,t)$, the stacked output vector $\varvec{Y}(p,t)$, the stacked information matrices ${{\varvec{\varGamma }}}_{\mathrm{s}}(p,t)$, $\hat{\varvec{\varOmega }}_a(p,t)$ and $\hat{\varvec{\varOmega }}_c(p,t)$ as

$$\begin{aligned} \hat{\varvec{Y}}_{\mathrm{f}}(p,t):= & {} [\hat{\varvec{y}}^{\tiny \text{ T }}_{\mathrm{f}}(t), \hat{\varvec{y}}^{\tiny \text{ T }}_{\mathrm{f}}(t-1), \ldots , \hat{\varvec{y}}^{\tiny \text{ T }}_{\mathrm{f}}(t-p+1)]^{\tiny \text{ T }}\in {\mathbb R}^{mp},\\ \hat{{{\varvec{\varGamma }}}}_{\mathrm{f}}(p,t):= & {} [\hat{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t), \hat{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t-1), \ldots , \hat{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t-p+1)]^{\tiny \text{ T }}\in {\mathbb R}^{(mp)\times (n+n_a)},\\ \varvec{Y}(p,t):= & {} [\varvec{y}^{\tiny \text{ T }}(t), \varvec{y}^{\tiny \text{ T }}(t-1), \ldots , \varvec{y}^{\tiny \text{ T }}(t-p+1)]^{\tiny \text{ T }}\in {\mathbb R}^{mp},\\ {{\varvec{\varGamma }}}_{\mathrm{s}}(p,t):= & {} [\varvec{\varPhi }^{\tiny \text{ T }}_{\mathrm{s}}(t), \varvec{\varPhi }^{\tiny \text{ T }}_{\mathrm{s}}(t-1), \ldots , \varvec{\varPhi }^{\tiny \text{ T }}_{\mathrm{s}}(t-p+1)]^{\tiny \text{ T }}\in {\mathbb R}^{(mp)\times n},\\ \hat{\varvec{\varOmega }}_a(p,t):= & {} [\hat{\varvec{{\phi }}}^{\tiny \text{ T }}_a(t), \hat{\varvec{{\phi }}}^{\tiny \text{ T }}_a(t-1), \ldots , \hat{\varvec{{\phi }}}^{\tiny \text{ T }}_a(t-p+1)]^{\tiny \text{ T }}\in {\mathbb R}^{(mp)\times n_a},\\ \hat{\varvec{\varOmega }}_c(p,t):= & {} [\hat{\varvec{{\phi }}}^{\tiny \text{ T }}_c(t), \hat{\varvec{{\phi }}}^{\tiny \text{ T }}_c(t-1), \ldots , \hat{\varvec{{\phi }}}^{\tiny \text{ T }}_c(t-p+1)]^{\tiny \text{ T }}\in {\mathbb R}^{(mp)\times n_c}. \end{aligned}$$

Then $\varvec{E}_1(p,t)$ and $\varvec{E}_2(p,t)$ can be equivalently expressed as

$$\begin{aligned} \varvec{E}_1(p,t):= & {} \hat{\varvec{Y}}_{\mathrm{f}}(p,t)-\hat{{{\varvec{\varGamma }}}}_{\mathrm{f}}(p,t)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1)\in {\mathbb R}^{mp},\\ \varvec{E}_2(p,t):= & {} \varvec{Y}(p,t)-{{\varvec{\varGamma }}}_{\mathrm{s}}(p,t)\hat{\varvec{{\theta }}}(t-1)-\hat{\varvec{\varOmega }}_a(p,t)\hat{\varvec{a}}(t-1)-\hat{\varvec{\varOmega }}_c(p,t)\hat{\varvec{c}}(t-1)\in {\mathbb R}^{mp}. \end{aligned}$$

According to the F-AM-GSG algorithm in (37–51), we can obtain the following equations:

$$\begin{aligned} \hat{\varvec{{\theta }}}_{\mathrm{f}}(t)= & {} \hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1)+\frac{\hat{{{\varvec{\varGamma }}}}_{\mathrm{f}}^{\tiny \text{ T }}(p,t)}{r_1(t)}\varvec{E}_1(p,t), \end{aligned}$$

(52)

$$\begin{aligned} \varvec{E}_1(p,t)= & {} \hat{\varvec{Y}}_{\mathrm{f}}(p,t)-\hat{{{\varvec{\varGamma }}}}_{\mathrm{f}}(p,t)\hat{\varvec{{\theta }}}_{\mathrm{f}}(t-1), \end{aligned}$$

(53)

$$\begin{aligned} r_1(t)= & {} r_1(t-1)+\Vert \hat{\varvec{\varPhi }}_{\mathrm{f}}(t)\Vert ^2, \end{aligned}$$

(54)

$$\begin{aligned} \hat{\varvec{c}}(t)= & {} \hat{\varvec{c}}(t-1)+\frac{\hat{\varvec{\varOmega }}^{\tiny \text{ T }}_c(p,t)}{r_2(t)}\varvec{E}_2(p,t), \end{aligned}$$

(55)

$$\begin{aligned} \varvec{E}_2(p,t)= & {} \varvec{Y}(p,t)-{{\varvec{\varGamma }}}_{\mathrm{s}}(p,t)\hat{\varvec{{\theta }}}(t-1)-\hat{\varvec{\varOmega }}_a(p,t)\hat{\varvec{a}}(t-1)-\hat{\varvec{\varOmega }}_c(p,t)\hat{\varvec{c}}(t-1), \end{aligned}$$

(56)

$$\begin{aligned} r_2(t)= & {} r_2(t-1)+\Vert \hat{\varvec{{\phi }}}_c(t)\Vert ^2, \end{aligned}$$

(57)

$$\begin{aligned} \hat{\varvec{Y}}_{\mathrm{f}}(p,t)= & {} [\hat{\varvec{y}}^{\tiny \text{ T }}_{\mathrm{f}}(t), \hat{\varvec{y}}^{\tiny \text{ T }}_{\mathrm{f}}(t-1), \ldots , \hat{\varvec{y}}^{\tiny \text{ T }}_{\mathrm{f}}(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$

(58)

$$\begin{aligned} \hat{{{\varvec{\varGamma }}}}_{\mathrm{f}}(p,t)= & {} [\hat{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t), \hat{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t-1), \ldots , \hat{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$

(59)

$$\begin{aligned} \varvec{Y}(p,t)= & {} [\varvec{y}^{\tiny \text{ T }}(t), \varvec{y}^{\tiny \text{ T }}(t-1), \ldots , \varvec{y}^{\tiny \text{ T }}(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$

(60)

$$\begin{aligned} {{\varvec{\varGamma }}}_{\mathrm{s}}(p,t)= & {} [{{\varvec{\varGamma }}}^{\tiny \text{ T }}_{\mathrm{s}}(t), {{\varvec{\varGamma }}}^{\tiny \text{ T }}_{\mathrm{s}}(t-1), \ldots , {{\varvec{\varGamma }}}^{\tiny \text{ T }}_{\mathrm{s}}(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$

(61)

$$\begin{aligned} \hat{\varvec{\varOmega }}_a(p,t)= & {} [\hat{\varvec{{\phi }}}^{\tiny \text{ T }}_a(t), \hat{\varvec{{\phi }}}^{\tiny \text{ T }}_a(t-1), \ldots , \hat{\varvec{{\phi }}}^{\tiny \text{ T }}_a(t-p+1)]^{\tiny \text{ T }}, \end{aligned}$$

(62)

$$\begin{aligned} \hat{\varvec{\varOmega }}_c(p,t)= & {} [\hat{\varvec{{\phi }}}^{\tiny \text{ T }}_c(t), \hat{\varvec{{\phi }}}^{\tiny \text{ T }}_c(t-1), \ldots , \hat{\varvec{{\phi }}}^{\tiny \text{ T }}_c(t-p+1)]^{\tiny \text{ T }}. \end{aligned}$$

(63)

The equations above and (43–51) form the data filtering based auxiliary model multi-innovation generalized stochastic gradient (F-AM-MI-GSG) algorithm. When $p=1$, the F-AM-MI-GSG algorithm reduce to the F-AM-GSG algorithm in (37–51). The proposed method in this paper can be extended to study the parameter estimation of transfer functions (Xu 2014; Xu and Ding 2017a), time-varying systems (Ding et al. 2016) and signal models (Xu 2017; Wang et al. 2018), and applied to other fields (Feng et al. 2016; Li et al. 2017d; Ji and Ding 2017; Cao and Zhu 2017; Chu et al. 2017; Zhao et al. 2017a).

Table 1 The AM-MI-GSG parameter estimates and errors ($\sigma ^2=0.50^2$)

Table 2 The F-AM-MI-GSG parameter estimates and errors ($\sigma ^2=0.50^2$)

5 Example

Consider the following multivariate output-error autoregressive system:

$$\begin{aligned} \varvec{y}(t)= & {} \frac{\varvec{\varPhi }_{\mathrm{s}}(t)}{A(z)}\varvec{{\theta }}+\frac{1}{C(z)}\varvec{v}(t),\\ \varvec{\varPhi }_{\mathrm{s}}(t)= & {} \left[ \begin{array}{cccc} -y_1(t-1), &{} y_1(t-2)\sin (y_2(t-2)), &{} y_2(t-1), &{} y_2(t-2)u_1(t-2),\\ -y_1(t-1), &{} y_1(t-2)\sin (t/\pi ), &{} y_2(t-1), &{} y_1(t-2)u_2(t-2),\end{array}\right. \\&\ \ \left. \begin{array}{ccc} u_1(t-1), &{} u_1(t-2)u_2(t-2), &{} u_2(t-1)\cos (t)\\ u_1^2(t-1), &{} \sin (u_2(t-2)), &{} u_1(t-1)+u_2(t-2)\end{array}\right] \in {\mathbb R}^{2\times 7},\\ A(z)= & {} 1+a_1z^{-1}+a_2z^{-2}\\= & {} 1+0.12z^{-1}+0.3z^{-2},\\ C(z)= & {} 1+c_1z^{-1}+c_2z^{-2}\\= & {} 1-0.11z^{-1}+0.8z^{-2},\\ \varvec{{\theta }}= & {} [0.70, 0.41, 0.47, -0.52, 0.10, -0.30, 0.40]^{\tiny \text{ T }},\\ \varvec{a}= & {} [a_1,a_2]=[0.12,0.3]^{\tiny \text{ T }},\\ \varvec{c}= & {} [c_1,c_2]=[-0.11,0.8]^{\tiny \text{ T }},\\ \varvec{{\vartheta }}= & {} [\varvec{{\theta }}^{\tiny \text{ T }},\varvec{a}^{\tiny \text{ T }},\varvec{c}^{\tiny \text{ T }}]^{\tiny \text{ T }},\\ \varvec{{\theta }}_{\mathrm{f}}= & {} [\varvec{{\theta }}^{\tiny \text{ T }},\varvec{a}^{\tiny \text{ T }}]^{\tiny \text{ T }}. \end{aligned}$$

In simulation, the inputs $\{u_1(t)\}$ and $\{u_2(t)\}$ are taken as two independent persistent excitation signal sequences with zero mean and unit variances, $\{v_1(t)\}$ and $\{v_2(t)\}$ are taken as two white noise sequences with zero mean and variances $\sigma ^2_1$ for $v_1(t)$ and $\sigma ^2_2$ for $v_2(t)$. Taking $\sigma ^2_1=\sigma ^2_2=\sigma ^2=0.50^2$ and based on the above model, we generate the system’s output signals $\varvec{y}(t)=[y_1(t),y_2(t)]^{\tiny \text{ T }}$. By using $u_1(t)$, $u_2(t)$, $y_1(t)$ and $y_2(t)$ and applying the AM-MI-GSG algorithm and the F-AM-MISG algorithm to estimate the parameters of this system, the parameter estimates and errors are shown in Tables 1 and 2 with $p=1$, 2, 4, 6 and 12. The estimation errors $\delta :=\Vert \hat{\varvec{{\vartheta }}}(t)-\varvec{{\vartheta }}\Vert /\Vert \varvec{{\vartheta }}\Vert$ versus t are shown in Figs. 3 and 4.

Fig. 3

The AM-MI-GSG parameter estimation errors $\delta$ versus t

Fig. 4

The F-AM-MI-GSG parameter estimation errors $\delta$ versus t

From Tables 1 and 2 and Figs. 3 and 4, we can draw the following conclusions.

• 1. The parameter estimation errors of the AM-MI-GSG and the F-AM-MI-GSG algorithms become smaller with the data length t increasing – see the estimation errors of the last columns in Tables 1 and 2.

• 2. A larger innovation length p leads to smaller parameter estimation errors both for the AM-MI-GSG algorithm and the F-AM-MI-GSG algorithm–see from Figs. 3 and 4. The estimation errors can almost converge to zero if the innovation length p is large enough and the data length goes to infinity.

• 3. Under the same innovation length p, the F-AM-MI-GSG algorithm can give more accurate parameter estimates than the AM-MI-GSG algorithm.

6 Conclusions

In this paper, we employ the data filtering technique to propose an F-AM-GSG algorithm for M-OEAR systems and derive an F-AM-MI-GSG algorithm by adopting the multi-innovation identification theory, taking account into an autoregressive noise. This work can be extended to the case with an autoregressive moving average noise. Compared with the AM-MI-GSG algorithm, the F-AM-MI-GSG algorithm has smaller estimation errors under the same innovation length. The proposed filtering based identification method can be applied to study the parameter estimation of other multivariate systems with different structures and disturbance noise, e.g., nonlinear multidimensional multivariate systems with colored noise. These are worth further studying in multidimensional multivariate systems in the future.