1 Introduction

Parameter estimation and system identification can be used to many areas [2, 16, 18, 53] such as signal modeling [41, 42]. Modeling is always the first step when one tries to design a control system [54], and the model quality directly affects the performance of the entire control system [9, 46]. System identification, which mainly includes the parameter identification [6, 43, 44] and the state estimation and filtering [12, 17, 57], is the methodology of system modeling and has been used in linear systems and nonlinear systems [5, 19, 40]. Recently, Greblicki, and Pawlak presented a nearest neighbor algorithm for Hammerstein systems and established the optimal convergence rate which is independent of the shape of the input density [14]. Li et al. gave the input–output representation of a bilinear system through eliminating the state variables and derived an iterative algorithm by using the maximum likelihood principle [21]. Other methods can be found in [3, 10, 11, 22, 24, 34, 37, 55]. It is well known that multivariable systems, i.e., multi-input multi-output (MIMO) systems, are frequently encountered in practical engineering. However, multivariable systems have large dimensions, complex strictures and coupled relations between inputs and outputs [39]. Therefore, the identification for multivariable systems is important and has attracted a lot of attention [33, 56]. For MIMO systems with unknown inner variables, an auxiliary model-based algorithm was studied by means of the iterative search principle [4]. Multivariable systems have many categories and multivariate systems are a class of multivariable systems, which can describe not only linear systems but also nonlinear systems.

The least squares is a conventional method and plays an important role in system identification [1, 45]. The basic idea is to define and minimize a quadratic function and to get the minimum solution [35]. However, the recursive least squares (RLS) algorithm has a heavy computational burden due to the calculation of the inversion of the covariance matrix. In this paper, we employ the data filtering technique to improve the performance of the RLS algorithm [8]. By filtering the input–output data, the original system is divided into two subsystems with fewer variables. Then the dimensions of the involved covariance matrices in each subsystem become smaller than the original system [20]. Moreover, the filtering technique can reduce the parameter estimation errors [38]. For example, a decomposition-based iterative algorithm was developed for multivariate pseudo-linear autoregressive moving average systems using the data filtering, and this algorithm had less computational burden and higher estimation accuracy compared with the least squares-based iterative algorithm [7]. In the previous work [31], we combined the data filtering technique and the multi-innovation theory to improve the performance of the stochastic gradient algorithm.

This paper studies the parameter estimation methods for multivariate output-error systems with autoregressive noise (i.e., colored noise). In order to reduce the influence of the colored noise on the parameter estimation accuracy, we modify the RLS algorithm by employing the data filtering technique and the auxiliary model. In addition, the data filtering technique can improve the computational efficiency. The main idea is to use a filter to filter the input–output data; then the system can be transformed into two models: a multivariate output-error model with white noise and an autoregressive noise model. To cope with the unknown variables in the identification models, we establish the auxiliary models and replace the unknown variables in the algorithm with the outputs of the auxiliary models. The main contributions of this paper are in the following aspects.

  • A filtering-based auxiliary model recursive generalized least squares (F-AM-RGLS) algorithm is derived for multivariate output-error autoregressive systems by using the data filtering and the auxiliary model.

  • The F-AM-RGLS algorithm has smaller parameter estimation errors than the auxiliary model-based recursive generalized least squares (AM-RGLS) algorithm under the same noise levels.

  • The F-AM-RGLS algorithm has higher computational efficiency than the AM-RGLS algorithm.

The rest of this paper is organized as follows. In Sect. 2, we give some definitions and the identification model for multivariate output-error autoregressive systems. Section 3 employs the data filtering technique to derive two identification models and presents the F-AM-RGLS algorithm. Section 4 proposes the AM-RGLS algorithm for comparison. An illustrative example is shown to verify the effectiveness of the proposed algorithms in Sect. 5. Finally, we offer some concluding remarks in Sect. 6.

2 The System Description

Some symbols are introduced. \(``A=:X''\) or \(``X:=A''\) stands for “A is defined as \(X''\); the superscript T stands for the vector/matrix transpose; the symbol \({\varvec{I}}_n\) denotes an identity matrix of size \(n\times n\); \(\mathbf{1}_n\) stands for an n-dimensional column vector whose elements are 1; \(\mathbf{1}_{m\times n}\) represents a matrix of size \(m\times n\) whose elements are 1; the symbol \(\otimes \) represents the Kronecker product, for example, \({\varvec{A}}:=a_{ij}\in {\mathbb R}^{m\times n}\), \({\varvec{B}}:=b_{ij}\in {\mathbb R}^{p\times q}\), \({\varvec{A}}\otimes {\varvec{B}}= [a_{ij}{\varvec{B}}]\in {\mathbb R}^{(mp)\times (nq)}\), in general, \({\varvec{A}}\otimes {\varvec{B}}\ne {\varvec{B}}\otimes {\varvec{A}}\); \(\mathrm{col}[{\varvec{X}}]\) is defined as a vector consisting of all columns of matrix \({\varvec{X}}\) arranged in order, for example, \({\varvec{X}}:=[{\varvec{x}}_1,{\varvec{x}}_2,\ldots ,{\varvec{x}}_n]\in {\mathbb R}^{m\times n}\), \({\varvec{x}}_i\in {\mathbb R}^{m}\)\((i=1,2,\ldots ,n)\), \(\mathrm{col}[{\varvec{X}}]:=[{\varvec{x}}^{\tiny \text{ T }}_1,{\varvec{x}}^{\tiny \text{ T }}_2,\ldots ,{\varvec{x}}^{\tiny \text{ T }}_n]\in {\mathbb R}^{mn}\); \(\hat{{\varvec{{\vartheta }}}}(t)\) denotes the estimate of \({\varvec{{\vartheta }}}\) at time t; the norm of a matrix (or a column vector) \({\varvec{X}}\) is defined by \(\Vert {\varvec{X}}\Vert ^2:=\mathrm{tr}[{\varvec{X}}{\varvec{X}}^{\tiny \text{ T }}]\).

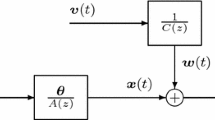
Consider the following multivariate output-error system,

$$\begin{aligned} {\varvec{y}}(t)=\frac{{\varvec{\varPhi }}_{\mathrm{s}}(t)}{A(z)}{\varvec{{\theta }}}+{\varvec{w}}(t), \end{aligned}$$
(1)

where \({\varvec{y}}(t):=[y_1(t), y_2(t),\ldots , y_m(t)]^{\tiny \text{ T }}\in {\mathbb R}^{m}\) is the output vector of the system, \({\varvec{\varPhi }}_{\mathrm{s}}(t)\in {\mathbb R}^{m\times n}\) is the information matrix which can be linear or nonlinear function of the past input–output data \({\varvec{u}}(t-i)\) and \({\varvec{y}}(t-i)\), \({\varvec{{\theta }}}\in {\mathbb R}^{n}\) is the parameter vector to be identified and A(z) is a polynomial in the unit backward shift operator \(z^{-1}\) [\(z^{-1}y(t)=y(t-1)\)], and

$$\begin{aligned} A(z):=1+a_1z^{-1}+a_2z^{-2}+\cdots +a_{n_a}z^{-n_a},\ a_i\in {\mathbb R}, \end{aligned}$$

\({\varvec{w}}(t):=[w_1(t), w_2(t), \ldots , w_m(t)]^{\tiny \text{ T }}\in {\mathbb R}^{m}\) is a disturbance vector. In general, \({\varvec{w}}(t)\) includes several special cases, (a) \({\varvec{w}}(t)\) is a stochastic white noise process with zero mean; (b) \({\varvec{w}}(t)\) is an autoregressive (AR) process; (c) \({\varvec{w}}(t)\) is a moving average (MA) process; (d) \({\varvec{w}}(t)\) is an ARMA process. In this paper, \({\varvec{w}}(t)\) is taken as an AR process of the white noise vector \({\varvec{v}}(t):=[v_1(t),v_2(t),\ldots ,v_m(t)]^{\tiny \text{ T }}\in {\mathbb R}^{m}\), and there are still two cases for the description of the AR noise term,

Case 1: \({\varvec{w}}(t):=\frac{1}{C(z)}{\varvec{v}}(t)\), where C(z) is a scalar polynomial and expressed as

$$\begin{aligned} C(z):=1+c_1z^{-1}+c_2z^{-2}+\cdots +c_{n_c}z^{-n_c},\ c_i\in {\mathbb R}. \end{aligned}$$

Case 2: \({\varvec{w}}(t):={\varvec{C}}^{-1}(z){\varvec{v}}(t)\), where \({\varvec{C}}(z)\) is a matrix polynomial and expressed as

$$\begin{aligned} {\varvec{C}}(z):={\varvec{I}}_m+{\varvec{C}}_1z^{-1}+{\varvec{C}}_2z^{-2}+\cdots +{\varvec{C}}_{n_c}z^{-n_c},\ {\varvec{C}}_i\in {\mathbb R}^{m\times m}. \end{aligned}$$

Case 2 is chosen to derive the identification models and identification algorithms in this paper. Assume that the orders m, n, \(n_a\), and \(n_c\) are known and \({\varvec{y}}(t)=\mathbf{0}\), \({\varvec{\varPhi }}_{\mathrm{s}}(t)=\mathbf{0}\) and \({\varvec{v}}(t)=\mathbf{0}\) for \(t\leqslant 0\).

Define the parameter vectors \({\varvec{a}}\) and \({\varvec{{\theta }}}_{\mathrm{s}}\) and parameter matrix \({\varvec{{\theta }}}_c\) as

$$\begin{aligned} {\varvec{a}}:= & {} [a_1, a_2, \ldots , a_{n_a}]^{\tiny \text{ T }}\in {\mathbb R}^{n_a},\\ {\varvec{{\theta }}}_{\mathrm{s}}:= & {} [{\varvec{{\theta }}}^{\tiny \text{ T }},{\varvec{a}}^{\tiny \text{ T }}]^{\tiny \text{ T }}\in {\mathbb R}^{n+n_a},\\ {\varvec{{\theta }}}_c:= & {} [{\varvec{C}}_1, {\varvec{C}}_2, \ldots , {\varvec{C}}_{n_c}]^{\tiny \text{ T }}\in {\mathbb R}^{(mn_c)\times m}, \end{aligned}$$

and the information matrices \({{{\phi }}}_a(t)\) and \({\varvec{\varPhi }}(t)\), and parameter vector \({{{\phi }}}_c(t)\) as

$$\begin{aligned} {{{\phi }}}_a(t):= & {} [-{\varvec{x}}(t-1),-{\varvec{x}}(t-2), \ldots , -{\varvec{x}}(t-n_a)]\in {\mathbb R}^{m\times n_a},\\ {\varvec{\varPhi }}(t):= & {} [{\varvec{\varPhi }}_{\mathrm{s}}(t), {{{\phi }}}_a(t)]\in {\mathbb R}^{m\times (n+n_a)},\\ {{{\phi }}}_c(t):= & {} [-{\varvec{w}}^{\tiny \text{ T }}(t-1),-{\varvec{w}}^{\tiny \text{ T }}(t-2), \ldots , -{\varvec{w}}^{\tiny \text{ T }}(t-n_c)]^{\tiny \text{ T }}\in {\mathbb R}^{(mn_c)}. \end{aligned}$$

Then \({\varvec{w}}(t)\) in Case 2 can be expressed as

$$\begin{aligned} {\varvec{w}}(t)= & {} {\varvec{C}}^{-1}(z){\varvec{v}}(t) \nonumber \\= & {} [{\varvec{I}}_m-{\varvec{C}}(z)]{\varvec{w}}(t)+{\varvec{v}}(t) \end{aligned}$$
(2)
$$\begin{aligned}= & {} -\,{\varvec{C}}_1{\varvec{w}}(t-1)-{\varvec{C}}_2{\varvec{w}}(t-2)-\cdots -{\varvec{C}}_{n_c}{\varvec{w}}(t-n_c)+{\varvec{v}}(t)\nonumber \\= & {} {\varvec{{\theta }}}^{\tiny \text{ T }}_c{{{\phi }}}_c(t)+{\varvec{v}}(t). \end{aligned}$$
(3)

Define an intermediate variable:

$$\begin{aligned} {\varvec{x}}(t):= & {} \frac{{\varvec{\varPhi }}_{\mathrm{s}}(t)}{A(z)}{\varvec{{\theta }}}\nonumber \\= & {} [1-A(z)]{\varvec{x}}(t)+{\varvec{\varPhi }}_{\mathrm{s}}(t){\varvec{{\theta }}}\nonumber \\= & {} -\,\sum ^{n_a}_{j=1}a_j{\varvec{x}}(t-j)+{\varvec{\varPhi }}_{\mathrm{s}}(t){\varvec{{\theta }}}\nonumber \\= & {} {\varvec{\varPhi }}_{\mathrm{s}}(t){\varvec{{\theta }}}+{{{\phi }}}_a(t){\varvec{a}}\nonumber \\= & {} {\varvec{\varPhi }}(t){\varvec{{\theta }}}_{\mathrm{s}}. \end{aligned}$$
(4)

Substituting (2)–(4) into (1), we can obtain

$$\begin{aligned} {\varvec{y}}(t)= & {} {\varvec{x}}(t)+{\varvec{w}}(t) \end{aligned}$$
(5)
$$\begin{aligned}= & {} {\varvec{\varPhi }}(t){\varvec{{\theta }}}_{\mathrm{s}}+{\varvec{C}}^{-1}(z){\varvec{v}}(t) \end{aligned}$$
(6)
$$\begin{aligned}= & {} {\varvec{\varPhi }}(t){\varvec{{\theta }}}_{\mathrm{s}}+{\varvec{{\theta }}}^{\tiny \text{ T }}_c{{{\phi }}}_c(t)+{\varvec{v}}(t). \end{aligned}$$
(7)

Equation (7) is the hierarchical identification model for the multivariate output-error autoregressive (M-OEAR) system in (1). Observing (7), we can see that there is not only a system parameter vector \({\varvec{{\theta }}}_{\mathrm{s}}\) to be identified, but also a noise model parameter matrix \({\varvec{{\theta }}}_c\) to be identified. The objective of this paper is to derive a new recursive algorithm for the M-OEAR system by using the auxiliary model and the data filtering.

3 The Filtering-Based Auxiliary Model Recursive Generalized Least Squares Algorithm

From (5), we can see that the output \({\varvec{y}}(t)\) contains the colored noise \({\varvec{w}}(t)\), which leads to large parameter estimation errors. In this section, we use a filter \({\varvec{L}}(z)={\varvec{C}}(z)\) to filter the input and output data and derive an F-AM-RGLS algorithm for the M-OEAR system to improve the parameter estimation accuracy.

For the M-OEAR system in (1), multiplying the both sides of (1) by \({\varvec{C}}(z)\) gives

$$\begin{aligned} {\varvec{C}}(z){\varvec{y}}(t)= & {} {\varvec{C}}(z)\frac{{\varvec{\varPhi }}_{\mathrm{s}}(t)}{A(z)}{\varvec{{\theta }}}+{\varvec{C}}(z){\varvec{w}}(t) \nonumber \\= & {} {\varvec{C}}(z)\frac{{\varvec{\varPhi }}_{\mathrm{s}}(t)}{A(z)}{\varvec{{\theta }}}+{\varvec{v}}(t). \end{aligned}$$
(8)

Define the filtered output vector \({\varvec{y}}_{\mathrm{f}}(t)\) and the filtered information matrix \({\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t)\) as

$$\begin{aligned} {\varvec{y}}_{\mathrm{f}}(t):= & {} {\varvec{C}}(z){\varvec{y}}(t)\in {\mathbb R}^{m},\\ {\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t):= & {} {\varvec{C}}(z){\varvec{\varPhi }}_{\mathrm{s}}(t) \in {\mathbb R}^{m\times n}, \end{aligned}$$

which can be expressed as the following recursive forms:

$$\begin{aligned} {\varvec{y}}_{\mathrm{f}}(t)= & {} {\varvec{C}}(z){\varvec{y}}(t)\nonumber \\= & {} {\varvec{y}}(t)+{\varvec{C}}_1{\varvec{y}}(t-1)+{\varvec{C}}_2{\varvec{y}}(t-2)+\cdots +{\varvec{C}}_{n_c}{\varvec{y}}(t-n_c) \nonumber \\= & {} {\varvec{y}}(t)+{\varvec{{\theta }}}^{\tiny \text{ T }}_c{{{\phi }}}_y(t), \end{aligned}$$
(9)
$$\begin{aligned} {\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t)= & {} {\varvec{C}}(z){\varvec{\varPhi }}_{\mathrm{s}}(t) \nonumber \\= & {} {\varvec{\varPhi }}_{\mathrm{s}}(t)+{\varvec{C}}_1{\varvec{\varPhi }}_{\mathrm{s}}(t-1)+{\varvec{C}}_2{\varvec{\varPhi }}_{\mathrm{s}}(t-2)+\cdots +{\varvec{C}}_{n_c}{\varvec{\varPhi }}_{\mathrm{s}}(t-n_c) \nonumber \\= & {} {\varvec{\varPhi }}_{\mathrm{s}}(t)+{\varvec{{\theta }}}^{\tiny \text{ T }}_c{\varvec{\varPsi }}_{\mathrm{s}}(t), \end{aligned}$$
(10)

where

$$\begin{aligned} {{{\phi }}}_y(t):= & {} \left[ \begin{array}{c} {\varvec{y}}(t-1) \\ {\varvec{y}}(t-2) \\ \vdots \\ {\varvec{y}}(t-n_c) \end{array}\right] \in {\mathbb R}^{(mn_c)},\\ {\varvec{\varPsi }}_{\mathrm{s}}(t):= & {} \left[ \begin{array}{c} {\varvec{\varPhi }}_{\mathrm{s}}(t-1) \\ {\varvec{\varPhi }}_{\mathrm{s}}(t-2) \\ \vdots \\ {\varvec{\varPhi }}_{\mathrm{s}}(t-n_c) \end{array}\right] \in {\mathbb R}^{(mn_c)\times n}. \end{aligned}$$

Then Eq. (8) can be rewritten as

$$\begin{aligned} {\varvec{y}}_{\mathrm{f}}(t)=\frac{{\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t)}{A(z)}{\varvec{{\theta }}}+{\varvec{v}}(t). \end{aligned}$$
(11)

Define an inner variable:

$$\begin{aligned} {\varvec{x}}_{\mathrm{f}}(t):= & {} \frac{{\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t)}{A(z)}{\varvec{{\theta }}}\nonumber \\= & {} [1-A(z)]{\varvec{x}}_{\mathrm{f}}(t)+{\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t){\varvec{{\theta }}}\nonumber \\= & {} -\,\sum ^{n_a}_{j=1}a_j{\varvec{x}}_{\mathrm{f}}(t-j)+{\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t){\varvec{{\theta }}}\nonumber \\= & {} {\varvec{\varPhi }}_{\mathrm{f}}(t){\varvec{{\theta }}}_{\mathrm{s}}\in {\mathbb R}^{m}, \end{aligned}$$
(12)

where

$$\begin{aligned} {\varvec{\varPhi }}_{\mathrm{f}}(t):=[{\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t),-{\varvec{x}}_{\mathrm{f}}(t-1),-{\varvec{x}}_{\mathrm{f}}(t-2),\ldots ,-{\varvec{x}}_{\mathrm{f}}(t-n_a)]\in {\mathbb R}^{m\times (n+n_a)}. \end{aligned}$$

Substituting (12) into (11) gives

$$\begin{aligned} {\varvec{y}}_{\mathrm{f}}(t)={\varvec{\varPhi }}_{\mathrm{f}}(t){\varvec{{\theta }}}_{\mathrm{s}}+{\varvec{v}}(t). \end{aligned}$$
(13)

For the filtered identification model (13) and the noise identification model (3), define two quadratic functions:

$$\begin{aligned} J_1({\varvec{{\theta }}}_{\mathrm{s}}):= & {} \sum ^{t}_{j=1}\Vert {\varvec{y}}_{\mathrm{f}}(j)-{\varvec{\varPhi }}_{\mathrm{f}}(j){\varvec{{\theta }}}_{\mathrm{s}}\Vert ^2,\\ J_2({\varvec{{\theta }}}_c):= & {} \sum ^{t}_{j=1}\Vert {\varvec{w}}(j)-{\varvec{{\theta }}}^{\tiny \text{ T }}_c{{{\phi }}}_c(j)\Vert ^2. \end{aligned}$$

Based on the least squares principle [32], minimizing \(J_1({\varvec{{\theta }}}_{\mathrm{s}})\) and \(J_2({\varvec{{\theta }}}_c)\) gives

$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)= & {} \hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1)+{\varvec{L}}_1(t)[{\varvec{y}}_{\mathrm{f}}(t)-{\varvec{\varPhi }}_{\mathrm{f}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1)], \end{aligned}$$
(14)
$$\begin{aligned} {\varvec{L}}_1(t)= & {} {\varvec{P}}_1(t){\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t) \nonumber \\= & {} {\varvec{P}}_1(t-1){\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t)[{\varvec{I}}_{m}+{\varvec{\varPhi }}_{\mathrm{f}}(t){\varvec{P}}_1(t-1){\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{f}}(t)]^{-1}, \end{aligned}$$
(15)
$$\begin{aligned} {\varvec{P}}_1(t)= & {} [{\varvec{I}}_{n+n_a}-{\varvec{L}}_1(t){\varvec{\varPhi }}_{\mathrm{f}}(t)]{\varvec{P}}_1(t-1), \end{aligned}$$
(16)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_c(t)= & {} \hat{{\varvec{{\theta }}}}_c(t-1)+{\varvec{L}}_2(t)[{\varvec{w}}(t)-\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}_c(t-1){{{\phi }}}_c(t)]^{\tiny \text{ T }}, \end{aligned}$$
(17)
$$\begin{aligned} {\varvec{L}}_2(t)= & {} {\varvec{P}}_2(t-1){{{\phi }}}_c(t)[1+{{{\phi }}}^{\tiny \text{ T }}_c(t){\varvec{P}}_2(t-1){{{\phi }}}_c(t)]^{-1}, \end{aligned}$$
(18)
$$\begin{aligned} {\varvec{P}}_2(t)= & {} [{\varvec{I}}_{mn_c}-{\varvec{L}}_2(t){{{\phi }}}^{\tiny \text{ T }}_c(t)]{\varvec{P}}_2(t-1). \end{aligned}$$
(19)

As we can see, Eqs. (14)–(19) cannot generate the estimates \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\) and \(\hat{{\varvec{{\theta }}}}_c(t)\), because the filter \({\varvec{C}}(z)\) is unknown, then the filtered output vector \({\varvec{y}}_{\mathrm{f}}(t)\) and the filtered matrix \({\varvec{\varPhi }}_{\mathrm{f}}(t)\) are unknown. In addition, the information matrix \({{{\phi }}}_a(t)\) and the information vector \({{{\phi }}}_c(t)\) contain the unknown terms \({\varvec{x}}(t-i)\) and \({\varvec{w}}(t-i)\). Here, we establish the appropriate auxiliary models and use their outputs \({\varvec{x}}_{\mathrm{a}}(t-i)\), \(\hat{{\varvec{w}}}(t-i)\), and \({\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-i)\) to replace the unknown variables \({\varvec{x}}(t-i)\), \({\varvec{w}}(t-i)\), and \({\varvec{x}}_{\mathrm{f}}(t-i)\). Then the estimates \(\hat{{{{\phi }}}}_a(t)\) and \(\hat{{{{\phi }}}}_c(t)\) of \({{{\phi }}}_a(t)\) and \({{{\phi }}}_c(t)\) can be formed by \({\varvec{x}}_{\mathrm{a}}(t-i)\) and \(\hat{{\varvec{w}}}(t-i)\) as

$$\begin{aligned} \hat{{{{\phi }}}}_a(t):= & {} [-{\varvec{x}}_{\mathrm{a}}(t-1),-{\varvec{x}}_{\mathrm{a}}(t-2), \ldots , -{\varvec{x}}_{\mathrm{a}}(t-n_a)]\in {\mathbb R}^{m\times n_a},\\ \hat{{{{\phi }}}}_c(t):= & {} [-\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-1),-\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-2), \ldots , -\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-n_c)]^{\tiny \text{ T }}\in {\mathbb R}^{(mn_c)}. \end{aligned}$$

Similarly, we use \({\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-i)\) and the estimate \(\hat{{\varvec{\varPhi }}}_{\mathrm{f}\mathrm{s}}(t)\) of \({\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t)\) to define

$$\begin{aligned} \hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t):=[\hat{{\varvec{\varPhi }}}_{\mathrm{f}\mathrm{s}}(t),-{\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-1),-{\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-2),\ldots ,-{\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-n_a)]\in {\mathbb R}^{m\times (n+n_a)}. \end{aligned}$$

Then we can get the estimate of \({\varvec{\varPhi }}(t)\):

$$\begin{aligned} \hat{{\varvec{\varPhi }}}(t):=[{\varvec{\varPhi }}_{\mathrm{s}}(t),\hat{{{{\phi }}}}_a(t)]\in {\mathbb R}^{m\times (n+n_a)}. \end{aligned}$$

According to (4)–(6), replacing \({\varvec{\varPhi }}(t)\) and \({\varvec{{\theta }}}_{\mathrm{s}}\) with their estimates \(\hat{{\varvec{\varPhi }}}(t)\) and \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\) in (4), the outputs \({\varvec{x}}_{\mathrm{a}}(t)\) and \(\hat{{\varvec{w}}}(t)\) of the auxiliary models can be computed by

$$\begin{aligned} {\varvec{x}}_{\mathrm{a}}(t)= & {} \hat{{\varvec{\varPhi }}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t),\\ \hat{{\varvec{w}}}(t)= & {} {\varvec{y}}(t)-\hat{{\varvec{\varPhi }}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\\= & {} {\varvec{y}}(t)-{\varvec{x}}_{\mathrm{a}}(t). \end{aligned}$$

From (12), we can obtain \({\varvec{x}}_{\mathrm{f}\mathrm{a}}(t)\) through

$$\begin{aligned} {\varvec{x}}_{\mathrm{f}\mathrm{a}}(t)=\hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t). \end{aligned}$$

Use the parameter estimates \(\hat{{\varvec{{\theta }}}}_c(t):=[\hat{{\varvec{C}}}_1(t),\hat{{\varvec{C}}}_2(t),\ldots ,\hat{{\varvec{C}}}_{n_c}(t)]^{\tiny \text{ T }}\in {\mathbb R}^{(mn_c)\times m}\) of the noise model to construct the estimate of \({\varvec{C}}(z)\) as

$$\begin{aligned} \hat{{\varvec{C}}}(t,z)={\varvec{I}}_{m}+\hat{{\varvec{C}}}_1(t)z^{-1}+\hat{{\varvec{C}}}_2(t)z^{-2}+\cdots +\hat{{\varvec{C}}}_{n_c}(t)z^{-n_c}. \end{aligned}$$

Replacing \({\varvec{C}}(z)\) in (9), (10) with \(\hat{{\varvec{C}}}(t,z)\), the estimates of the filtered output vector \({\varvec{y}}_{\mathrm{f}}(t)\) and the filtered information matrix \({\varvec{\varPhi }}_{\mathrm{f}\mathrm{s}}(t)\) can be obtained by

$$\begin{aligned} \hat{{\varvec{y}}}_{\mathrm{f}}(t)= & {} \hat{{\varvec{C}}}(t,z){\varvec{y}}(t)\\= & {} {\varvec{y}}(t)+\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}_c(t){{{\phi }}}_y(t),\\ \hat{{\varvec{\varPhi }}}_{\mathrm{f}\mathrm{s}}(t)= & {} \hat{{\varvec{C}}}(t,z){\varvec{\varPhi }}_{\mathrm{s}}(t)\\= & {} {\varvec{\varPhi }}_{\mathrm{s}}(t)+\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}_c(t){\varvec{\varPsi }}_{\mathrm{s}}(t). \end{aligned}$$

Replace the unknown information matrix \({\varvec{\varPhi }}(t)\), the information vector \({{{\phi }}}_c(t)\), the filtered output vector \({\varvec{y}}_{\mathrm{f}}(t)\), and the filtered information matrix \({\varvec{\varPhi }}_{\mathrm{f}}(t)\) with their estimates \(\hat{{\varvec{\varPhi }}}(t)\), \(\hat{{{{\phi }}}}_c(t)\), \(\hat{{\varvec{y}}}_{\mathrm{f}}(t)\), and \(\hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t)\) in (14)–(19), respectively. For convenience, define two innovation vectors:

$$\begin{aligned} {\varvec{e}}_1(t):= & {} \hat{{\varvec{y}}}_{\mathrm{f}}(t)-\hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1)\in {\mathbb R}^{m},\\ {\varvec{e}}_2(t):= & {} \hat{{\varvec{w}}}(t)-\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}_c(t-1)\hat{{{{\phi }}}}_c(t)\\= & {} {\varvec{y}}(t)-\hat{{\varvec{\varPhi }}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1)-\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}_c(t-1)\hat{{{{\phi }}}}_c(t)\in {\mathbb R}^{m}. \end{aligned}$$

Then, we can obtain the filtering-based auxiliary model recursive generalized least squares (F-AM-RGLS) algorithm:

$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)= & {} \hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1)+{\varvec{L}}_1(t){\varvec{e}}_1(t), \end{aligned}$$
(20)
$$\begin{aligned} {\varvec{e}}_1(t)= & {} \hat{{\varvec{y}}}_{\mathrm{f}}(t)-\hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1), \end{aligned}$$
(21)
$$\begin{aligned} {\varvec{L}}_1(t)= & {} {\varvec{P}}_1(t-1)\hat{{\varvec{\varPhi }}}^{\tiny \text{ T }}_{\mathrm{f}}(t)[{\varvec{I}}_{m}+\hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t){\varvec{P}}_1(t-1)\hat{{\varvec{\varPhi }}}^{\tiny \text{ T }}_{\mathrm{f}}(t)]^{-1}, \end{aligned}$$
(22)
$$\begin{aligned} {\varvec{P}}_1(t)= & {} [{\varvec{I}}_{n+n_a}-{\varvec{L}}_1(t)\hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t)]{\varvec{P}}_1(t-1), \end{aligned}$$
(23)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_c(t)= & {} \hat{{\varvec{{\theta }}}}_c(t-1)+{\varvec{L}}_2(t){\varvec{e}}^{\tiny \text{ T }}_2(t), \end{aligned}$$
(24)
$$\begin{aligned} {\varvec{e}}_2(t)= & {} {\varvec{y}}(t)-\hat{{\varvec{\varPhi }}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1)-\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}_c(t-1)\hat{{{{\phi }}}}_c(t), \end{aligned}$$
(25)
$$\begin{aligned} {\varvec{L}}_2(t)= & {} {\varvec{P}}_2(t-1)\hat{{{{\phi }}}}_c(t)[1+\hat{{{{\phi }}}}^{\tiny \text{ T }}_c(t){\varvec{P}}_2(t-1)\hat{{{{\phi }}}}_c(t)]^{-1}, \end{aligned}$$
(26)
$$\begin{aligned} {\varvec{P}}_2(t)= & {} [{\varvec{I}}_{mn_c}-{\varvec{L}}_2(t)\hat{{{{\phi }}}}^{\tiny \text{ T }}_c(t)]{\varvec{P}}_2(t-1), \end{aligned}$$
(27)
$$\begin{aligned} \hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t)= & {} [\hat{{\varvec{\varPhi }}}_{\mathrm{f}\mathrm{s}}(t), -{\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-1), -{\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-2), \ldots , -{\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-n_a)], \end{aligned}$$
(28)
$$\begin{aligned} \hat{{\varvec{y}}}_{\mathrm{f}}(t)= & {} {\varvec{y}}(t)+\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}_c(t){{{\phi }}}_y(t), \end{aligned}$$
(29)
$$\begin{aligned} \hat{{\varvec{\varPhi }}}_{\mathrm{f}\mathrm{s}}(t)= & {} {\varvec{\varPhi }}_{\mathrm{s}}(t)+\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}_c(t){\varvec{\varPsi }}_{\mathrm{s}}(t), \end{aligned}$$
(30)
$$\begin{aligned} {{{\phi }}}_y(t)= & {} [{\varvec{y}}^{\tiny \text{ T }}(t-1),{\varvec{y}}^{\tiny \text{ T }}(t-2),\ldots ,{\varvec{y}}^{\tiny \text{ T }}(t-n_c)]^{\tiny \text{ T }}, \end{aligned}$$
(31)
$$\begin{aligned} {\varvec{\varPsi }}_{\mathrm{s}}(t)= & {} [{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{s}}(t-1),{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{s}}(t-2),\ldots ,{\varvec{\varPhi }}^{\tiny \text{ T }}_{\mathrm{s}}(t-n_c)]^{\tiny \text{ T }}, \end{aligned}$$
(32)
$$\begin{aligned} \hat{{\varvec{\varPhi }}}(t)= & {} [{\varvec{\varPhi }}_{\mathrm{s}}(t),\hat{{{{\phi }}}}_a(t)], \end{aligned}$$
(33)
$$\begin{aligned} \hat{{{{\phi }}}}_a(t)= & {} [-{\varvec{x}}_{\mathrm{a}}(t-1), -{\varvec{x}}_{\mathrm{a}}(t-2),\ldots , -{\varvec{x}}_{\mathrm{a}}(t-n_a)], \end{aligned}$$
(34)
$$\begin{aligned} \hat{{{{\phi }}}}_c(t)= & {} [-\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-1), -\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-2),\ldots , -\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-n_c)]^{\tiny \text{ T }}, \end{aligned}$$
(35)
$$\begin{aligned} {\varvec{x}}_{\mathrm{f}\mathrm{a}}(t)= & {} \hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t), \end{aligned}$$
(36)
$$\begin{aligned} {\varvec{x}}_{\mathrm{a}}(t)= & {} \hat{{\varvec{\varPhi }}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t), \end{aligned}$$
(37)
$$\begin{aligned} \hat{{\varvec{w}}}(t)= & {} {\varvec{y}}(t)-{\varvec{x}}_{\mathrm{a}}(t), \end{aligned}$$
(38)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)= & {} [\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}(t),\hat{{\varvec{a}}}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}, \end{aligned}$$
(39)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_c(t)= & {} [\hat{{\varvec{C}}}_1(t), \hat{{\varvec{C}}}_2(t), \ldots , \hat{{\varvec{C}}}_{n_c}(t)]^{\tiny \text{ T }}. \end{aligned}$$
(40)

The steps involved in the F-AM-RGLS algorithm in (20)–(40) are listed as follows.

  1. 1.

    Set the initial values: let \(t=1\), \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(0)=\mathbf{1}_{n+n_a}/p_0\), \(\hat{{\varvec{{\theta }}}}_c(0)=\mathbf{1}_{(mn_c)\times m}\), \({\varvec{P}}_1(0)=p_0{\varvec{I}}_{n+n_a}\), \({\varvec{P}}_2(0)=p_0{\varvec{I}}_{mn_c}\), \({\varvec{x}}_{\mathrm{f}\mathrm{a}}(t-i)=\mathbf{1}_m/p_0\), \({\varvec{x}}_{\mathrm{a}}(t-i)=\mathbf{1}_m/p_0\), \(\hat{{\varvec{w}}}(t-i)=\mathbf{1}_m/p_0\), \(i=1\), 2, \(\ldots \), \(\max [n_a,n_c]\), \(p_0=10^6\) and set a small positive number \(\varepsilon \).

  2. 2.

    Collect the observation data \({\varvec{y}}(t)\) and \({\varvec{\varPhi }}_{\mathrm{s}}(t)\), and construct the information vectors and matrices \({{{\phi }}}_y(t)\), \({\varvec{\varPsi }}_{\mathrm{s}}(t)\), \(\hat{{{{\phi }}}}_a(t)\), \(\hat{{{{\phi }}}}_c(t)\) and \(\hat{{\varvec{\varPhi }}}(t)\) using (31), (32), (34), (35), and (33).

  3. 3.

    Compute \({\varvec{L}}_2(t)\), \({\varvec{P}}_2\), and \({\varvec{e}}_2(t)\) using (26), (27), and (25).

  4. 4.

    Update the parameter estimation matrix \(\hat{{\varvec{{\theta }}}}_c(t)\) using (24).

  5. 5.

    Compute the filtered output vector \(\hat{{\varvec{y}}}_{\mathrm{f}}(t)\) by (29) and the filtered information matrix \(\hat{{\varvec{\varPhi }}}_{\mathrm{f}\mathrm{s}}(t)\) by (30), and form \(\hat{{\varvec{\varPhi }}}_{\mathrm{f}}(t)\) by (28).

  6. 6.

    Compute \({\varvec{L}}_1(t)\), \({\varvec{P}}_1(t)\), and \({\varvec{e}}_1(t)\) by (22), (23), and (21).

  7. 7.

    Update the parameter estimate \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\) by (20).

  8. 8.

    Compute the outputs \({\varvec{x}}_{\mathrm{f}\mathrm{a}}(t)\), \({\varvec{x}}_{\mathrm{a}}(t)\), and \(\hat{{\varvec{w}}}(t)\) by (36)–(38).

  9. 9.

    Compare \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\) with \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1)\) and compare \(\hat{{\varvec{{\theta }}}}_c(t)\) with \(\hat{{\varvec{{\theta }}}}_c(t-1)\): if \(\Vert \hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)-\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t-1)\Vert <\varepsilon \) and \(\Vert \hat{{\varvec{{\theta }}}}_c(t)-\hat{{\varvec{{\theta }}}}_c(t-1)\Vert <\varepsilon \), terminate recursive calculation procedure and obtain \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\) and \(\hat{{\varvec{{\theta }}}}_c(t)\); otherwise, increase t by 1 and go to Step 2.

The flowchart of computing \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\) and \(\hat{{\varvec{{\theta }}}}_c(t)\) in the F-AM-RGLS algorithm is shown in Fig. 1.

Fig. 1
figure 1

The flowchart of computing the F-AM-RGLS parameter estimates \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\) and \(\hat{{\varvec{{\theta }}}}_c(t)\)

Full size image

Remark 1

To obtain the F-AM-RGLS algorithm in (20)–(40), we use the matrix polynomial \(\hat{{\varvec{C}}}(t,z)\) to filter the input–output data and derive a filtered model with the white noise and a noise model. As for the calculation procedure, the F-AM-RGLS algorithm identifies the noise parameter matrix \(\hat{{\varvec{{\theta }}}}_c(t)\) first and constructs the filtered output vector \(\hat{{\varvec{y}}}_{\mathrm{f}}(t)\) and the filtered information matrix \(\hat{{\varvec{\varPhi }}}_{\mathrm{f}\mathrm{s}}(t)\) before calculating the system parameter vector \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\).

4 The Auxiliary Model-Based Recursive Generalized Least Squares Algorithm

As a comparison, this section gives the AM-RGLS algorithm to show the advantages of the F-AM-RLS algorithm in (20)–(40). For the identification model in (7), combine the information matrix \({\varvec{\varPhi }}(t)\) and the information vector \({{{\phi }}}_c(t)\) into a new information matrix \({\varvec{\varPsi }}(t)\), and the parameter vector \({\varvec{{\theta }}}_{\mathrm{s}}\) and the parameter matrix \({\varvec{{\theta }}}_c\) into a parameter vector \({\varvec{{\vartheta }}}\):

$$\begin{aligned} {\varvec{\varPsi }}(t):= & {} [{\varvec{\varPhi }}(t), {\varvec{I}}_m \otimes {{{\phi }}}^{\tiny \text{ T }}_c(t)]\in {\mathbb R}^{m\times n_1},\quad n_1:=n+n_a+m^2n_c,\\ {\varvec{{\vartheta }}}:= & {} \left[ \begin{array}{c} {\varvec{{\theta }}}_{\mathrm{s}} \\ \mathrm{col}[{\varvec{{\theta }}}_c] \end{array} \right] \in {\mathbb R}^{n_1}. \end{aligned}$$

Then, we have the following identification model

$$\begin{aligned} {\varvec{y}}(t)={\varvec{\varPsi }}(t){\varvec{{\vartheta }}}+{\varvec{v}}(t). \end{aligned}$$
(41)

The parameter vector \({\varvec{{\vartheta }}}\) contains all parameters to be estimated. Referring to the derivation of the F-AM-RGLS algorithm in (20)–(40), we can obtain the following AM-RGLS algorithm:

$$\begin{aligned} \hat{{\varvec{{\vartheta }}}}(t)= & {} \hat{{\varvec{{\vartheta }}}}(t-1)+{\varvec{L}}(t)[{\varvec{y}}(t)-\hat{{\varvec{\varPsi }}}(t)\hat{{\varvec{{\vartheta }}}}(t-1)], \end{aligned}$$
(42)
$$\begin{aligned} {\varvec{L}}(t)= & {} {\varvec{P}}(t-1)\hat{{\varvec{\varPsi }}}^{\tiny \text{ T }}(t)[{\varvec{I}}_m+\hat{{\varvec{\varPsi }}}(t){\varvec{P}}(t-1)\hat{{\varvec{\varPsi }}}^{\tiny \text{ T }}(t)]^{-1}, \end{aligned}$$
(43)
$$\begin{aligned} {\varvec{P}}(t)= & {} [{\varvec{I}}_{n_1}-{\varvec{L}}(t)\hat{{\varvec{\varPsi }}}(t)]{\varvec{P}}(t-1), \end{aligned}$$
(44)
$$\begin{aligned} \hat{{\varvec{\varPsi }}}(t)= & {} [\hat{{\varvec{\varPhi }}}(t),{\varvec{I}}_m \otimes \hat{{{{\phi }}}}^{\tiny \text{ T }}_c(t)], \end{aligned}$$
(45)
$$\begin{aligned} \hat{{\varvec{\varPhi }}}(t)= & {} [{\varvec{\varPhi }}_{\mathrm{s}}(t),\hat{{{{\phi }}}}_a(t)], \end{aligned}$$
(46)
$$\begin{aligned} \hat{{{{\phi }}}}_a(t)= & {} [-{\varvec{x}}_{\mathrm{a}}(t-1),-{\varvec{x}}_{\mathrm{a}}(t-2), \ldots , -{\varvec{x}}_{\mathrm{a}}(t-n_a)], \end{aligned}$$
(47)
$$\begin{aligned} \hat{{{{\phi }}}}_c(t)= & {} [-\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-1),-\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-2), \ldots , -\hat{{\varvec{w}}}^{\tiny \text{ T }}(t-n_c)]^{\tiny \text{ T }}, \end{aligned}$$
(48)
$$\begin{aligned} {\varvec{x}}_{\mathrm{a}}(t)= & {} \hat{{\varvec{\varPhi }}}(t)\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t), \end{aligned}$$
(49)
$$\begin{aligned} \hat{{\varvec{w}}}(t)= & {} {\varvec{y}}(t)-{\varvec{x}}_{\mathrm{a}}(t), \end{aligned}$$
(50)
$$\begin{aligned} \hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)= & {} [\hat{{\varvec{{\theta }}}}^{\tiny \text{ T }}(t), \hat{{\varvec{a}}}^{\tiny \text{ T }}(t)]^{\tiny \text{ T }}, \end{aligned}$$
(51)
$$\begin{aligned} \hat{{\varvec{{\vartheta }}}}(t)= & {} \left[ \begin{array}{c} \hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t) \\ \mathrm{col}[\hat{{\varvec{{\theta }}}}_c(t)] \end{array} \right] . \end{aligned}$$
(52)

The procedure for computing the parameter estimation vector \(\hat{{\varvec{{\vartheta }}}}(t)\) in the AM-RGLS algorithm in (42)–(52) is listed as follows.

  1. 1.

    Set the initial values: let \(t=1\), \(\hat{{\varvec{{\vartheta }}}}(0)=\mathbf{1}_{n_1}/p_0\), \({\varvec{P}}(0)=p_0{\varvec{I}}_{n_1}\), \({\varvec{x}}_{\mathrm{a}}(t-i)=\mathbf{1}_m/p_0\), \(\hat{{\varvec{w}}}(t-i)=\mathbf{1}_m/p_0\), \(i=1\), 2, \(\ldots \), \(\max [n_a,n_c]\), \(p_0=10^6\) and set a small positive number \(\varepsilon \).

  2. 2.

    Collect the observation data \({\varvec{y}}(t)\) and \({\varvec{\varPhi }}_{\mathrm{s}}(t)\), and construct the information matrix \(\hat{{{{\phi }}}}_a(t)\) and the information vector \(\hat{{{{\phi }}}}_c(t)\) using (47), (48), and form \(\hat{{\varvec{\varPhi }}}(t)\) and \(\hat{{\varvec{\varPsi }}}(t)\) using (46) and (45).

  3. 3.

    Compute the gain matrix \({\varvec{L}}(t)\) using (43) and compute the covariance matrix \({\varvec{P}}(t)\) using (44).

  4. 4.

    Update the parameter estimation vector \(\hat{{\varvec{{\vartheta }}}}(t)\) using (42).

  5. 5.

    Read \(\hat{{\varvec{{\theta }}}}_{\mathrm{s}}(t)\) from \(\hat{{\varvec{{\vartheta }}}}(t)\), and compute \({\varvec{x}}_{\mathrm{a}}(t)\) and \(\hat{{\varvec{w}}}(t)\) using (49), (50).

  6. 6.

    Compare \(\hat{{\varvec{{\vartheta }}}}(t)\) with \(\hat{{\varvec{{\vartheta }}}}(t-1)\): if \(\Vert \hat{{\varvec{{\vartheta }}}}(t)-\hat{{\varvec{{\vartheta }}}}(t-1)\Vert <\varepsilon \), terminate recursive calculation procedure and obtain \(\hat{{\varvec{{\vartheta }}}}(t)\); otherwise, increase t by 1 and go to Step 2.

In the F-AM-RGLS algorithm in (20)–(40), the dimensions of the covariance matrices \({\varvec{P}}_1(t)\) and \({\varvec{P}}_2(t)\) are \((n+n_a) \times (n+n_a)\) and \((mn_c) \times (mn_c)\). In the AM-RGLS algorithm in (42)–(52), the dimension of the covariance matrix \({\varvec{P}}(t)\) in Eq. (44) is \(n_1 \times n_1\)\((n_1=n+n_1+m^2n_c)\). Here, we give the computational efficiencies of the two algorithms at each recursive step in Tables 1, 2, where flops represent the floating point operations. In order to compare the computational burden of the two algorithms, we do

$$\begin{aligned}&N_1-N_2=2m^{3}+2n^{3}_1-m^2-n^2_1+4m^2n_1\\&\quad +\,6mn^2_1+mn_1-(2m^{3}+2(mn_c)^{3}+5(mn_c)^2+2(n+n_a)^{3}\\&\quad -\,(n+n_a)^2+12mnn_a+m^2(6n_c+4n_a+4n+2nn_c-1)\\&\quad +\,m(6n^2+6n_a^2+5n+5n_a+n_c-1)), \end{aligned}$$

where \(n_1=n+n_a+m^2n_c\), then

$$\begin{aligned}&N_1-N_2=3n^2n_a+3n_a^2n+5m^{4}n^2_cn+6m^{4}n_c^2n_a\\&\quad +\,m+2m^{3}n_c^{3}(m^{3}-1)+m^{4}n_c^2(n-1)+mn_c(m^2-1)\\&\quad +\,4m^{4}n_c+m^2n_c^2(6m^{3}-5)\\&\quad +\,m^2n_cn(12m-4)+m^2n_cn_a(12m-2)+6m^2n_c(2n_an-1)\\&\quad +\,mn(6mnn_c-1)+mn_a(6mn_an_c-4). \end{aligned}$$

In general, when the orders \(m, n, n_a, n_c \geqslant 1\), it is obvious that the computational burden of the F-AM-RGLS algorithm in (20)–(40) is less than the AM-RGLS algorithm in (42)–(52), that is to say, \(N_1 \gg N_2\).

Table 1 The computational efficiency of the AM-RGLS algorithm
Full size table
Table 2 The computational efficiency of the F-AM-RGLS algorithm
Full size table
Table 3 The AM-RGLS estimates and errors (\(\sigma ^2=0.50^2\))
Full size table
Table 4 The F-AM-RGLS estimates and errors (\(\sigma ^2=0.50^2\))
Full size table
Table 5 The AM-RGLS estimates and errors (\(\sigma ^2=0.80^2\))
Full size table
Table 6 The F-AM-RGLS estimates and errors (\(\sigma ^2=0.80^2\))
Full size table

Remark 2

The system considered in this paper is disturbed by an autoregressive noise. In order to reduce the influence of the colored noise on the system, the F-AM-RGLS algorithm in (20)–(40) filters the input and output data by using the filter \({\varvec{C}}(z)\) and divides the original identification model (7) into a filtered identification model (13) and a noise identification model (3). Compared with the AM-RGLS algorithm in (42)–(52), the F-AM-RGLS algorithm gives more accurate estimates. Furthermore, the F-AM-RGLS algorithm also improves the computational efficiency.

Fig. 2
figure 2

The AM-RGLS and F-AM-RGLS estimation errors versus t with \(\sigma ^2=0.50^2\)

Full size image
Fig. 3
figure 3

The AM-RGLS estimates \(\hat{\theta }_1(t)\), \(\hat{\theta }_5(t)\), \(\hat{\theta }_6(t)\), \(\hat{a}_2(t)\), \(\hat{c}_4(t)\) versus t (\(\sigma ^2=0.50^2\))

Full size image

5 Example

Consider the following multivariate output-error autoregressive system:

$$\begin{aligned}&{\varvec{y}}(t)=\frac{{\varvec{\varPhi }}_{\mathrm{s}}(t)}{A(z)}{\varvec{{\theta }}}+{\varvec{C}}^{-1}(z){\varvec{v}}(t),\\&{\varvec{\varPhi }}_{\mathrm{s}}(t)= \left[ \begin{array}{llll} -\,y_1(t-1) &{}\quad y_1(t-2)\sin (y_2(t-2)) &{} y_2(t-1) &{}\quad y_2(t-2)u_1(t-2)\\ -\,y_1(t-1) &{}\quad y_1(t-2)\sin (t/\pi ) &{} y_2(t-1) &{}\quad y_1(t-2)u_2(t-2)\end{array}\right. \\&\left. \begin{array}{lll} u_1(t-1) &{}\quad u_1(t-2)u_2(t-2) &{}\quad u_2(t-1)\cos (t)\\ u_1^2(t-1) &{}\quad \sin (u_2(t-2)) &{}\quad u_1(t-1)+u_2(t-2)\end{array}\right] \in {\mathbb R}^{2\times 7},\\&A(z)=1+a_1z^{-1}+a_2z^{-2}\\&=1+0.37z^{-1}+0.37z^{-2},\\&{\varvec{C}}(z)={\varvec{I}}_{2}+{\varvec{C}}_1z^{-1}\\&={\varvec{I}}_{2}+\left[ \begin{array}{cc}0.65 &{} 0.63 \\ 0.75 &{} -0.59\end{array}\right] z^{-1},\\&{\varvec{{\theta }}}=[0.90, 0.45, 0.48, -\,0.49, 0.10, -\,0.29, 0.42]^{\tiny \text{ T }},\\&{\varvec{a}}=[a_1,a_2]^{\tiny \text{ T }}=[0.37,0.37]^{\tiny \text{ T }},\\&{\varvec{{\theta }}}^{\tiny \text{ T }}_n={\varvec{C}}_1=\left[ \begin{array}{cc}c_1 &{} c_2 \\ c_3 &{} c_4\end{array}\right] =\left[ \begin{array}{cc}0.65 &{} 0.63 \\ 0.75 &{} -\,0.59\end{array}\right] ,\\&{\varvec{{\theta }}}_{\mathrm{s}}=[{\varvec{{\theta }}}^{\tiny \text{ T }},{\varvec{a}}^{\tiny \text{ T }}]^{\tiny \text{ T }},\\&{\varvec{{\vartheta }}}=\left[ \begin{array}{c} {{\varvec{{\theta }}}_{\mathrm{s}}}\\ {\mathrm{col}[{\varvec{{\theta }}}_{\mathrm{n}}]}. \end{array}\right] \end{aligned}$$

In simulation, the inputs {\(u_1(t)\)} and {\(u_2(t)\)} are taken as two independent persistent excitation signal sequences with zero mean and unit variances, {\(v_1(t)\)} and {\(v_2(t)\)} are taken as two white noise sequences with zero mean and variances \(\sigma ^2_1\) for \(v_1(t)\) and \(\sigma ^2_2\) for \(v_2(t)\). Taking \(\sigma ^2_1=\sigma ^2_2=\sigma ^2=0.50^2\) and \(\sigma ^2_1=\sigma ^2_2=\sigma ^2=0.80^2\), respectively, we use them to generate the output vector \({\varvec{y}}(t)=[y_1(t),y_2(t)]^{\tiny \text{ T }}\). Applying the F-AM-RGLS algorithm in (20)–(40) and the AM-RGLS algorithm in (42)–(52) to estimate the parameters of this system, the parameter estimates and errors are shown in Tables 3, 4, 5, and 6. The parameter estimation errors \(\delta :=\Vert \hat{{\varvec{{\vartheta }}}}(t)-{\varvec{{\vartheta }}}\Vert /\Vert {\varvec{{\vartheta }}}\Vert \) versus t are shown in Figs. 2 and 5.

Fig. 4
figure 4

The F-AM-RGLS estimates \(\hat{\theta }_1(t)\), \(\hat{\theta }_5(t)\), \(\hat{\theta }_6(t)\), \(\hat{a}_2(t)\), \(\hat{c}_4(t)\) versus t (\(\sigma ^2=0.50^2\))

Full size image
Fig. 5
figure 5

The AM-RGLS and F-AM-RGLS estimation errors versus t with \(\sigma ^2=0.80^2\)

Full size image
Fig. 6
figure 6

The AM-RGLS estimates \(\hat{\theta }_1(t)\), \(\hat{\theta }_5(t)\), \(\hat{\theta }_6(t)\), \(\hat{a}_2(t)\), \(\hat{c}_4(t)\) versus t (\(\sigma ^2=0.80^2\))

Full size image
Fig. 7
figure 7

The F-AM-RGLS estimates \(\hat{\theta }_1(t)\), \(\hat{\theta }_5(t)\), \(\hat{\theta }_6(t)\), \(\hat{a}_2(t)\), \(\hat{c}_4(t)\) versus t (\(\sigma ^2=0.80^2\))

Full size image

From Tables 3, 4, 5, and 6 and Figs. 2, 3, 4, 5, 6, and 7, we can draw the following conclusions.

  1. 1.

    The parameter estimation errors of the AM-RGLS algorithm and the F-AM-RGLS algorithm become smaller with the data length t increasing—see the estimation errors of the last columns in Tables 3, 4, 5, and 6.

  2. 2.

    Under the same noise level, the F-AM-RGLS algorithm can give more accurate parameter estimates than the AM-RGLS algorithm—see Tables 3, 4, 5, and 6 and Figs. 2 and 5.

  3. 3.

    A lower noise level results in smaller parameter estimation errors—see Tables 3, 4, 5, and 6 and Figs. 2 and 5.

6 Conclusions

In this paper, we employ the data filtering technique to propose an F-AM-RGLS algorithm for M-OEAR systems by adopting the auxiliary model identification idea. Compared with the AM-RGLS algorithm, the F-AM-RGLS algorithm can improve the parameter estimation accuracy and reduce the computational burden. The proposed approaches in the paper can combine other mathematical tools [25,26,27,28,29,30] and statistical strategies [13, 48,49,50,51,52] to study the performances of some parameter estimation algorithms and can be applied to other multivariable systems with different structures and disturbance noises and other literature [15, 23, 36, 47, 58, 59].