1 Introduction

Optimal design of two-dimensional (2-D) nonlinear-phase finite impulse response (FIR) filters has attracted much attention of many researchers because they are more desirable than linear-phase FIR filters in many applications, e.g., the low group-delay FIR filters (Lu 2002; Lu and Hinamoto 2006) and fractional delay FIR filters (Deng and Lu 2000; Laakso et al. 1996; Shyu et al. 2009) in image and video processing, prototype FIR filters in 2-D filter banks (Dam et al. 2005; de Haan et al. 2003; Yan and Ikehara 1999) and allpass FIR filters in phase compensation (Zhu et al. 1999). In addition, optimal designs of 2-D infinite impulse response (IIR) filters are often transformed into convex subproblems in the same or similar formulations as 2-D nonlinear-phase FIR filter designs (Chottera and Jullien 1982; Dumitrescu 2005; Lu et al. 1998).

In constrained least-square (CLS) and minimax designs of 2-D nonlinear-phase FIR filters (Lu 2002; Lu and Hinamoto 2006), constraints are usually imposed merely on the filter’s frequency response error. The resultant maximum magnitude error and phase error are about the same value. In order to obtain smaller magnitude error than phase error, Lai (2009) imposes constraints simultaneously on the frequency response error and phase error. The phase-error constrained minimax design in Lai et al. (2009) constrains the frequency response using elliptic-error and phase-error constraints, resulting in smaller magnitude error than those obtained by using frequency-response-error and phase-error constraints.

The impulse response coefficients of 2-D FIR filters are naturally arranged in matrices. Most existing algorithms for optimal designs of 2-D FIR filters, say, those in Algazi et al. (1986), Dumitrescu (2006), Gislason et al. (1993), Lai (2009), Lai et al. (2009), Lang et al. (1996), Lu (2002), Lu and Hinamoto (2006, 2011), Rusu and Dumitrescu (2012), rearrange the coefficient matrices into vectors and then solve the design problems using algorithms for one-dimensional (1-D) FIR filters. This leads to high computational complexities of the design algorithms and much design time for large size filters.

There are also several works (Ahmad and Wang 1989; Aravena and Gu 1996; Gu and Aravena 1994; Hong et al. 2013; Zhao and Lai 2011, 2013; Zhu et al. 1997, 1999) that formulate the design problems in terms of the coefficient matrices and develop algorithms to directly solve for the coefficient matrices rather than vectorizing them first, leading to lower computational complexities than corresponding algorithms vectorizing the coefficient matrices. The algorithms in Ahmad and Wang (1989), Aravena and Gu (1996), Gu and Aravena (1994), Zhao and Lai (2011, 2013), Zhu et al. (1997, 1999) only consider (weighted) least-squares designs of 2-D FIR filters without any other constraints. The algorithm in Hong et al. (2013) considers the constrained least-squares (CLS) design of 2-D FIR filters but is only applicable to the design of exact linear-phase filters.

This paper considers the elliptic-error and phase-error constrained least-squares (EPCLS) design of 2-D FIR filters. The problem can be solved by the Goldfarb–Idnani (GI) based algorithm in Lai (2009) after minor modifications. However, the algorithm in Lai (2009) is a vectorized one and thus has high computational complexity. To reduce the complexity, a matrix-based algorithm is developed in this paper to directly solve the EPCLS problem for the co-efficient matrix. Through design examples, the presented method is shown to be much more efficient than competing methods.

The rest of this paper is organized as follows. In Sect. 2, the EPCLS design of 2-D nonlinear-phase FIR filters is formulated as a semi-infinite convex quadratic programming (QP) problem in terms of the coefficient matrix. In Sect. 3, a matrix-based version of the GI-based algorithm in Lai (2009) is developed for the semi-infinite convex QP problem resulting from the EPCLS design. Design examples and comparisons with existing algorithms are given in Sect. 4. Conclusions of this paper are drawn in Sect. 5.

2 Matrix-based formulation for EPCLS design problem

The frequency response of a 2-D FIR filter with real impulse response coefficients \(\{h(n_{1},n_{2}):n_{1}=0,1,\ldots ,N_{1}-1; n_{2}= 0,1,\ldots ,N_{2}-1\}\) can be expressed as

$$\begin{aligned} G(\omega _{1} ,\omega _{2} )=\sum _{n_{1} =0}^{N_{1} -1} {\sum _{n_{2} =0}^{N_{2} -1} {h(n_{1} ,\,n_{2} )e^{-i(n_{1} \omega _{1} +n_{2} \omega _{2} )}} } , \end{aligned}$$
(1)

where \(\omega _{1}\) and \(\omega _{2}\) are the horizontal and vertical frequencies, and \( i\) is the imaginary unit.

By introducing a function vector of \(\omega \),

$$\begin{aligned} \varphi (\omega ,N)=[1,\,e^{-i\omega },\,\ldots ,\,e^{-i(N-1)\omega }]^{H}, \end{aligned}$$
(2)

where the symbol “\(H\)” in the superscript denotes the conjugate transpose operation, the frequency response can be rewritten in a matrix form as

$$\begin{aligned} G(\omega _{1} ,\omega _{2} ,\mathbf{A})=\varphi ^{H}(\omega _{1} ,N_{1} )\mathbf{A}\varphi (-\omega _{2} ,N_{2} ), \end{aligned}$$
(3)

where A is an \(N_{1}\times N_{2}\) real matrix whose elements are the impulse response coefficients, i.e., \(\mathbf{A}=[h(n_{1},n_{2})], n_{1}=0,1,\ldots , N_{1}-1; n_{2}=0,1,\ldots ,N_{2}-1.\)

Denote by \(D(\omega _{1},\omega _{2})=\bar{{D}}(\omega _{1} ,\omega _{2} )e^{i\beta (\omega _{1} ,\omega _{2} )}\) the desired complex frequency response, where \(\bar{{D}}(\omega _{1} ,\omega _{2} )\) and \(\beta (\omega _{1},\omega _{2})\) are respectively the magnitude and phase of \(D(\omega _{1},\omega _{2})\). The approximation of \(D(\omega _{1},\omega _{2})\) by \(G(\omega _{1},\omega _{2})\) is defined on the frequency plane \(\Omega =\{(\omega _{1},\omega _{2}){\vert }-\pi \le \omega _{1}\le ,\pi ,{\vert }-\pi \le \omega _{2}\le \pi \}\). In practical designs, we discretize the continuous frequency plane \(\Omega \) by a sufficiently dense rectangular frequency grid given by \(\Pi =\{(\omega _{1j},\omega _{2k}){\vert }\omega _{1j}=2\pi (j-1)/(M_{1}-1)-\pi , \omega _{2k}=2\pi (k-1) /(M_{2}-1)-\pi \hbox {with} (j,k)\in F\}\), where \(F=\{(j,k){\vert }j=1,2,\ldots ,M_{1}; k=1,2,\ldots ,M_{2}\}\). Then the frequency response approximation error is defined as

$$\begin{aligned} E(\omega _{1} ,\omega _{2} ,\mathbf{A})\equiv G(\omega _{1} ,\omega _{2} ,\mathbf{A})-D(\omega _{1} ,\omega _{2} ),\quad \forall (\omega _{1} ,\omega _{2} )\in \Pi , \end{aligned}$$
(4)

and the magnitude approximation error and phase approximation error are represented by \(E_{m}(\omega _{1},\omega _{2},\mathbf{A})={\vert }G(\omega _{1},\omega _{2},\mathbf{A}){\vert }- \bar{{D}}(\omega _{1} ,\omega _{2} )\) and \(E_{p}(\omega _{1},\omega _{2},\mathbf{A})=\phi (\omega _{1},\omega _{2},\mathbf{A})-\beta (\omega _{1},\omega _{2})\), where \(\phi (\omega _{1},\omega _{2},\mathbf{A})\) is the phase of \(G(\omega _{1},\omega _{2},\mathbf{A})\).

We further define a transformed error by

$$\begin{aligned} \bar{{E}}(\omega _{1} ,\,\omega _{2} ,\mathbf{A})=e^{-i\beta (\omega _{1} ,\,\omega _{2} )}E(\omega _{1} ,\,\omega _{2} ,\mathbf{A}), \end{aligned}$$
(5)

and an elliptic error as

$$\begin{aligned} \bar{{E}}_\sigma (\omega _{1} ,\omega _{2} ,\mathbf{A})=\mathrm{Re}\left[ {\bar{{E}}(\omega _{1} ,\omega _{2} ,\mathbf{A})} \right] +i\sigma ^{-1} \mathrm{Im}\left[ {\bar{{E}}(\omega _{1} ,\omega _{2} ,\mathbf{A})} \right] , \end{aligned}$$
(6)

where \(\sigma \ge 1\) is a prescribed model parameter. When \(\sigma > 1\), the boundary of the constraint

$$\begin{aligned} \left| {\bar{{E}}_{\sigma } (\omega _{1} ,\,\omega _{2} ,\mathbf{A})} \right| \le \rho (\omega _{1} ,\,\omega _{2} ),\quad \forall (\omega _{1} ,\omega _{2} ) \end{aligned}$$
(7)

for any \(\rho (\omega _{1},\omega _{2})>0\) is an ellipse, and thus the name elliptic error for \(\bar{{E}}_\sigma (\omega _{1} ,\omega _{2} ,\mathbf{A})\). When \(\sigma =1, \bar{{E}}_{\sigma } (\omega _{1} ,\omega _{2} ,\mathbf{A})\) reduces to the circular error \(\bar{{E}}(\omega _{1} ,\omega _{2} ,\mathbf{A})\) and the elliptic error constraint (7) reduces to the following circular error constraint:

$$\begin{aligned} {\vert }\bar{{E}}(\omega _{1} ,\,\omega _{2} ,\mathbf{A})\le \rho (\omega _{1} ,\omega _{2} ). \end{aligned}$$
(8)

In this paper, we consider the EPCLS design of the 2-D nonlinear-phase FIR filters. That is, we minimize the energy of the frequency response error and impose constraints simultaneously on the elliptic error and the phase error as follows:

$$\begin{aligned} \mathop {\min }\limits _{\mathbf{A}} f(\mathbf{A})=\sum {\sum {\left| {E(\omega _{1} ,\,\omega _{2} ,\mathbf{A})} \right| ^{2}} } ,\quad \forall (\omega _{1} ,\omega _{2} )\in \Pi ,\end{aligned}$$
(9a)
$$\begin{aligned} \hbox {s}.\hbox {t}.:|\bar{{E}}_{\sigma } (\omega _{1} ,\,\omega _{2} ,\mathbf{A})|\le \rho (\omega _{1} ,\omega _{2} ),\quad \forall (\omega _{1} ,\omega _{2} )\in {\mathop \Pi } _{1} ,\end{aligned}$$
(9b)
$$\begin{aligned} {\vert }\bar{{E}}(\omega _{1} ,\,\omega _{2} ,\mathbf{A}){\vert } \le \rho (\omega _{1} ,\omega _{2} ),\quad \forall (\omega _{1} ,\omega _{2} )\in {\mathop \Pi } _{2} ,\end{aligned}$$
(9c)
$$\begin{aligned} |E_p (\omega _{1} ,\omega _{2} ,\mathbf{A})|\le \gamma (\omega _{1} ,\omega _{2} ),\quad \forall (\omega _{1} ,\omega _{2} )\in {\mathop \Pi } _{1} , \end{aligned}$$
(9d)

where \(\Pi _{1}\) and \(\Pi _{2}\) are two subsets of the passband and stopband frequencies on \(\Pi \), “s.t.” stands for “subject to”, and \(0<\gamma (\omega _1, \omega 2) < \pi /2\). The above EPCLS problem (9) reduces to the CPCLS problem considered in Lai (2009) when \(\sigma =1\).

It is obvious that, \(\{\mathbf{A}\big |{\vert }\bar{{E}}(\omega _{1} ,\,\omega _{2} ,\mathbf{A}){\vert }\le \rho (\omega _{1},\omega _{2})\}\subset \{\mathbf{A}\big |{\vert }\bar{{E}}_\sigma (\omega _{1} ,\,\omega _{2} ,\mathbf{A}){\vert }\le \rho (\omega _{1},\omega _{2})\}\) for any \((\omega _{1},\omega _{2})\in \Pi _{1}\). This implies that the feasible domain of the CPCLS problem in Lai (2009) is a subset of the feasible domain of EPCLS problem (9). Thus, solving the EPCLS problem (9) will result in better filters than solving the CPCLS problem in Lai (2009).

By introducing the following notation:

$$\begin{aligned} \mathbf{p}_{j}&= \varphi (\omega _{1j},N_{1}) (j=1,2,\cdots ,M_{1}),\mathbf{P}=[\mathbf{p}_{1},\mathbf{p}_{2},\ldots ,\mathbf{p}_{M1}],\end{aligned}$$
(10a)
$$\begin{aligned} \mathbf{q}_{k}&= \varphi (-\omega _{2k},N_{2}) (k=1,2,\cdots ,M_{2}),\mathbf{Q}=[\mathbf{q}_{1},\mathbf{q}_{2},\ldots ,\mathbf{q}_{M2}],\end{aligned}$$
(10b)
$$\begin{aligned} d_{jk}&= D(\omega _{1j},\omega _{2k}) (j,k)\in F, \mathbf{D}=(d_{j\times k})_{M1\times M2}, \end{aligned}$$
(10c)

the frequency response \(G(\omega _{1} ,\,\omega _{2} ,\mathbf{A})\) and cost function \(f(\mathbf{A})\) can be rewritten as

$$\begin{aligned} G(\omega _{1j} ,\omega _{2k} ,\mathbf{A})&\equiv g_{jk} (\mathbf{A})=\mathbf{p}_j^H \mathbf{Aq}_{k} ,\,\,\quad \forall (j,k)\in F,\end{aligned}$$
(11a)
$$\begin{aligned} f(\mathbf{A})&= \hbox {tr}\left\{ \!{\left( {\mathbf{P}^{H}\mathbf{AQ-D}} \right) ^{H}\left( {\mathbf{P}^{H}\mathbf{AQ-D}} \right) }\!\right\} \!, \end{aligned}$$
(11b)

where \(\hbox {tr}\{\bullet \}\) denotes the trace operation. It can be proved that \(f(\mathbf{A})\) is convex when \(M_{1}\ge N_{1}\) and \(M_{2}\ge N_{2}\) (Zhu et al. 1999).

We further introduce \(\rho _{jk}=\rho (\omega _{1j}, \omega _{2k}), \gamma _{jk}=\gamma (\omega _{1j}, \omega _{2k}), \bar{{d}}_{jk} =\bar{{D}}(\omega _{1j}, \omega _{2k}), \beta _{jk}=\beta (\omega _{1j},\omega _{2k}),\, F_{1}=\{(j,k){\vert }(\omega _{1j}, \omega _{2k})\in \Pi _{1}\},\, F_{2}=\{(j,k){\vert }(\omega _{1j}, \omega _{2k})\in \Pi _{2}\}\). Then, the elliptic-error constraints (9b), the circular-error constraints (9c) and the phase-error constraints (9d) can be transformed respectively into

$$\begin{aligned}&\left( {\cos (\alpha )\cos (\beta _{jk} )-\sigma ^{-1}\sin (\alpha )\sin (\beta _{jk} )} \right) g_{jk}^R (\mathbf{A})\nonumber \\&\quad +\left( {\cos (\alpha )\sin (\beta _{jk} )+\sigma ^{-1}\sin (\alpha )\cos (\beta _{jk} )} \right) g_{jk}^I (\mathbf{A})\le \rho _{jk}+\cos (\alpha )\bar{{d}}_{jk} ,\nonumber \\&\quad \quad \forall \alpha \in [0,2\pi ), (j,k)\in F_{1} ,\end{aligned}$$
(12a)
$$\begin{aligned}&\left( {\cos (\alpha )\cos (\beta _{jk} )-\sin (\alpha )\sin (\beta _{jk} )} \right) g_{jk}^R (\mathbf{A})\nonumber \\&\quad +\left( {\cos (\alpha )\sin (\beta _{jk} )+\sin (\alpha )\cos (\beta _{jk} )} \right) g_{jk}^{I} (\mathbf{A})\le \rho _{jk}, \quad \forall \alpha \in [0,{2}\pi ), (j,k)\in F_{2} ,\nonumber \\ \end{aligned}$$
(12b)
$$\begin{aligned}&\left( {\cos (\alpha )\cos (\beta _{jk} )-\sin (\alpha )\sin (\beta _{jk} )} \right) g_{jk}^{R} (\mathbf{A})+\left( {\cos (\alpha )\sin (\beta _{jk} )+\sin (\alpha )\cos (\beta _{jk} )} \right) \nonumber \\&\quad g_{jk}^{I} (\mathbf{A})\le 0, \quad \forall \alpha \in \{\pm (\pi /{2} +\gamma _{jk} )\}, (j,k)\in F_{1}. \end{aligned}$$
(12c)

where \(g_{jk}^{R} (\mathbf{A})\) and \(g_{jk}^{I} (\mathbf{A})\) are the real and imaginary parts of \(g_{jk} (\mathbf{A})\) respectively, and \(\alpha \) is an angle parameter. While the constraints in (12a) (12b) are linear but of infinite number because of the continuity of parameter \(\alpha \), the constraints in (12c) are linear and of finite number.

We now introduce a quadruplet \((\alpha ,j,k,l)\) to index the constraints in (12), where \(l\in \{1,2,3\}, (j,k)\in F_{1}\) and \(\alpha \in [0,2\pi )\) when \(l=1, (j,k)\in F_{2}\) and \(\alpha \in [0,2 \pi )\) when \(l=2\), and \((j,k)\in F_{1}\) and \(\alpha \in \{\pm (\pi /2+\gamma _{jk})\}\) when \(l=3\). Let

$$\begin{aligned} \Theta \equiv [0,{2}\pi ),\Xi _{jk} \equiv \{\pm (\pi /{2}+\gamma _{jk} )\}, \end{aligned}$$
(13)
$$\begin{aligned} I_{1}&= \{(\alpha ,j,k,l)|\alpha \in \Theta , (j,k)\in F_{1} ,l={1}\},\end{aligned}$$
(14a)
$$\begin{aligned} I_{2}&= \{(\alpha ,j,k,l)|\alpha \in \Theta , (j,k)\in F_{2} ,l={2}\},\end{aligned}$$
(14b)
$$\begin{aligned} I_{3}&= \{(\alpha ,j,k,l)|\alpha \in \Xi _{jk} , (j,k)\in F_{1} ,l={3}\}. \end{aligned}$$
(14c)

Then, the matrix-based EPCLS design problem (9) can be rewritten as

$$\begin{aligned}&\mathop {\min }\limits _{\mathbf{A}} f(\mathbf{A})=\hbox {tr}\left\{ \!{\left( {\mathbf{P}^{H}\mathbf{AQ-D}} \right) ^{H}\left( {\mathbf{P}^{H}\mathbf{AQ-D}} \right) }\!\right\} \!,\end{aligned}$$
(15a)
$$\begin{aligned}&\quad \hbox {s.t. } \Gamma _{jkl} (\alpha )g_{jk}^{R} (\mathbf{A})+\bar{{\Gamma }}_{jkl} (\alpha )g_{jk}^{I} (\mathbf{A})\le \theta _{jkl} (\alpha ),\quad \forall (\alpha ,j,k,l)\in I_{1} \hbox {U}I_{2} \hbox {U}I_{3}, \end{aligned}$$
(15b)

where

$$\begin{aligned} \Gamma _{jkl} (\alpha )&= \left\{ {{\begin{array}{lll} {\cos (\alpha )\cos (\beta _{jk} )-\sigma ^{-1}\sin (\alpha )\sin (\beta _{jk} ),}&{} {(\alpha ,j,k,l)\in I_{1} ,}\\ {\cos (\alpha )\cos (\beta _{jk} )-\sin (\alpha )\sin (\beta _{jk} ),}&{} {(\alpha ,j,k,l)\in I_{2} \cup I_{3} ,} \\ \end{array} }} \right. \end{aligned}$$
(15c)
$$\begin{aligned} \bar{{\Gamma }}_{jkl} (\alpha )&= \left\{ {{\begin{array}{lll} {\cos (\alpha )\sin (\beta _{jk} )+\sigma ^{-1}\sin (\alpha )\cos (\beta _{jk} ),}&{} {(\alpha ,j,k,l)\in I_{1} ,} \\ {\cos (\alpha )\sin (\beta _{jk} )+\sin (\alpha )\cos (\beta _{jk} ),}&{} {(\alpha ,j,k,l)\in I_{2} \cup I_{3} ,} \\ \end{array} }} \right. \end{aligned}$$
(15d)
$$\begin{aligned} \theta _{jkl} (\alpha )&= \left\{ {{\begin{array}{lll} {\rho _{jk} +\cos (\alpha )\bar{{d}}_{jk} ,}&{} {(\alpha ,j,k,l)\in I_{1} ,} \\ {\rho _{jk} ,}&{} {(\alpha ,j,k,l)\in I_{2} ,} \\ {0,}&{} {(\alpha ,j,k,l)\in I_{3}.} \\ \end{array} }} \right. \end{aligned}$$
(15e)

Problem (15) is a linearly constrained semi-infinite convex QP problem because the index set \(I_{1}\) and \(I_{2}\) are two infinite sets.

3 Matrix-based algorithm for linearly constrained semi-infinite convex QP problem

3.1 The matrix-based EPCLS-GI algorithm

In Sect. 2, the EPCLS design of 2-D FIR filters has been expressed as a matrix-based linearly constrained semi-infinite convex QP problem. In this section, an improved GI algorithm referred to as the matrix-based EPCLS-GI algorithm will be developed to solve the problem.

Like the original GI algorithm (Goldfarb and Idnani 1983), the matrix-based EPCLS-GI algorithm belongs to an active method that maintains an active set of constraints which are satisfied as equalities. We assume in the \(\ell \)th iteration, the active set is \(J(\ell )=\{(\alpha _{m}, j_{m}, k_{m}, l_{m}), m=1,2,\ldots ,t\}\). The solution matrix of problem (15a) subject only to the equality constraints indexed by the active set \(J(\ell )\) is \(\mathbf{A}(\ell )\), and the corresponding Lagrangian multiplier vector is \(\varvec{\lambda }(\ell )\).

To proceed, we first identify the most violated constraint among the infinite set of constraints in (12), or, (15) at the current solution matrix A \((\ell )\). By introducing the following notation:

$$\begin{aligned} \bar{{g}}_{jk} (\mathbf{A}(\ell ))=\left\{ {{\begin{array}{l} {\hbox {Re}[e^{-i\beta _{jk} }g_{jk} (\mathbf{A}(\ell ))]+i\sigma ^{-1} \hbox {Im}[e^{^{-i\beta _{jk} }}g_{jk} (\mathbf{A}(\ell ))], \quad \hbox {for } (j,k)\in F_{1} ,} \\ {\hbox {Re}[e^{-i\beta _{jk} }g_{jk} (\mathbf{A}(\ell ))]+ \hbox {Im}[e^{^{-i\beta _{jk} }}g_{jk} (\mathbf{A}(\ell ))], \quad \hbox {for } (j,k)\in F_{2} ,} \\ \end{array} }} \right. \end{aligned}$$
(16a)

the most violated constraint among the infinite set of constraints (15) with \((\alpha ,j,k,l)\in I_{1}\bigcup I_{2}\), if any, is chosen as the one indexed by \((\alpha _{u},j_{u},k_{u},l_{u})\) where

$$\begin{aligned} (j_u ,\,k_{u} )&= \arg \mathop {\max }\limits _{{(j,k)\in F_{1} \cup F_2 }} \left\{ {\left| {\bar{{g}}_{jk} (\mathbf{A}(\ell ))-\bar{{d}}_{jk} } \right| -\rho _{jk} } \right\} ,\end{aligned}$$
(16b)
$$\begin{aligned} \alpha _{u}&= \tan ^{-1}\left( {\frac{\hbox {Im}\left( {\left| {\bar{{g}}_{j_u k_u } (\mathbf{A}(\ell ))-\bar{{d}}_{j_u k_u } } \right| } \right) }{\hbox {Re}\left( {\left| {\bar{{g}}_{j_u k_u } (\mathbf{A}(\ell ))-\bar{{d}}_{j_u k_u } } \right| } \right) }} \right) ,\end{aligned}$$
(16c)
$$\begin{aligned} {l}_{u}&= \left\{ {{\begin{array}{lll} {1,}&{} \hbox {for}\, (j_u ,k_u )\in F_{1} , \\ {2,}&{} \hbox {for}\,(j_u ,k_u )\in F_{2}. \\ \end{array} }} \right. \end{aligned}$$
(16d)

In the complex plane of \(\bar{{G}}(\omega _{1j},\omega _{2k})\equiv \bar{{g}}_{jk} (\mathbf{A}(\ell ))\), the most violated constraint is the one whose boundary is a tangent of the circle \({\vert }\bar{{G}}(\omega _{1j},\omega _{2k})-\bar{{d}}_{jk} {\vert }=\rho _{jk}\), the tangency point of which is the perpendicular projection of \(\bar{{G}}(\omega _{1j},\omega _{2k})\) on the circle along the radial direction with angle \(\alpha _{u}\) (see, e.g., Lai 2009).

Among the finite set of constraints (15) with \((\alpha ,j,k,l)\in I_{3}\), the most violated constraint, if any, is identified by the index quadruplet \((\alpha _{v},j_{v},k_{v},l_{v})\) with

$$\begin{aligned} (\alpha _{v} ,j_{v} ,k_{v} )&= \hbox {arg} \mathop {\max }\limits _{{\alpha \in \Xi (j,k)\in F_{1}}}\{\Gamma _{jk3}(\alpha )g_{jk}^{R}(\mathbf{A}(\ell )) +\bar{\Gamma }_{jk3}(\alpha )g_{jk}^{I}(\mathbf{A}(\ell ))\},\end{aligned}$$
(17a)
$$\begin{aligned} l_{v}&= 3. \end{aligned}$$
(17b)

Then, with Eqs. (16) and (17), the most violated constraint at the current iterative point \(\mathbf{A}(\ell )\) among all constraints in (12) can be determined by Step 2 of the matrix-based EPCLS-GI algorithm given later in this section.

Suppose now we are going to add the most violated constraint to the active set \(J(\ell )\) as the \((t+1)\)th active constraint to obtain the new active set \(J^{+}\). Denote by A \(^{+}\) the new solution matrix to problem (15a) subject to the equality constraints indexed by \(J^{+}\) and by \(\varvec{\lambda }^{+}\) the corresponding new multiplier vector. If we let

$$\begin{aligned} \varvec{\lambda } ^{+}&= \left[ {{\begin{array}{l} {{\varvec{\lambda }}(\ell )} \\ 0 \\ \end{array} }} \right] +w\left[ {{\begin{array}{l} {-\mathbf{r}} \\ 1 \\ \end{array} }} \right] ,\end{aligned}$$
(18)
$$\begin{aligned} \mathbf{A}^{+}&= \mathbf{A}(\ell )+ w\mathbf{Z}, \end{aligned}$$
(19)

where the \([-\mathbf{r}^{H},1]^{H}\) is the step direction vector in the dual space, i.e., the direction from the old multiplier vector \([\varvec{\lambda }(\ell )^{H}, 0]^{H}\) to the new multiplier vector \(\varvec{\lambda }^{+}\), Z is the step direction matrix in the primal space, i.e., the direction from the old solution matrix \(\mathbf{A}(\ell )\) to the new solution matrix \(\mathbf{A}^{+}\), and \(w>0\) is a hypothetical common step length in the dual and primal spaces. We have the following theorem regarding the primal and dual step directions. The proof of the theorem is given in the “Appendix”.

Theorem 1

The vector r and matrix Z in the dual and primal step directions can be given by

$$\begin{aligned} \mathbf{r}&= \mathbf{S}^{-\mathbf{1}}\xi ,\end{aligned}$$
(20)
$$\begin{aligned} \mathbf{Z}&= \sum _{m=1}^{t} {r_{m} \mathbf{R}_{m} } -\mathbf{R}_{t+1} , \end{aligned}$$
(21)

where \(r_{m}\) represents the \(m\)th component of r, and

$$\begin{aligned} \mathbf{S}&= (S_{mn} )_{t\times t} ,\mathrm{where}\, S_{mn} =\Gamma _{j_{m} k_{m} l_{m} } (\alpha _{m} )g_{j_{m} k_{m} }^{ R} \left( {\mathbf{R}_{n} } \right) \nonumber \\&\quad +\bar{{\Gamma }}_{j_{m} k_{m} l_{m} } (\alpha _{m} )g_{j_{m} k_{m} }^I \left( {\mathbf{R}_{n} } \right) , m,n=1,\,2,\,\ldots ,\,t,\end{aligned}$$
(22a)
$$\begin{aligned} \xi&= (\xi _{1} ,\,\xi _2 ,\,\ldots ,\,\xi _{t} )^{H},\mathrm{where}\, \xi _{m} =\Gamma _{j_{m} k_{m} l_{m} } (\alpha _{m} )g_{j_{m} k_{m} }^{R} \left( {\mathbf{R}_{t+1} } \right) \nonumber \\&\quad +\bar{{\Gamma }}_{j_{m} k_{m} l_{m} } (\alpha _{m} )g_{j_{m} k_{m} }^{I} \left( {\mathbf{R}_{t+1} } \right) , m=1,\,\ldots ,\,t,\end{aligned}$$
(22b)
$$\begin{aligned} \mathbf{R}_{n}&= \left( {\mathbf{PP}^{H}} \right) ^{-1}\left[ {\Gamma _{j_{n} k_{n} l_{n} } (\alpha _{n} )\mathrm{Re}\left( {\mathbf{p}_{j_{n} } \mathbf{q}_{k_{n} }^{H} } \right) } \right. \left. {-\bar{{\Gamma }}_{j_{n} k_{n} l_{n} } (\alpha _{n} )\mathrm{Im}\left( {\mathbf{p}_{j_{n} } \mathbf{q}_{k_{n} }^{H} } \right) } \right] \left( {\mathbf{QQ}^{H}} \right) ^{-1},\nonumber \\&\quad n=1,\,\ldots ,\,t+1. \end{aligned}$$
(22c)

After the primal and dual step directions are determined, we may compute the maximum dual step length \(w_{1}\) and the minimum primal step length \(w_{2}\). Then we can update the active set \(J(\ell )\), solution matrix \(\mathbf{A}(\ell )\) and multiplier vector \(\varvec{\lambda }(\ell )\) using the primal and dual step directions and the primal and dual step lengths. The procedure details for determination of the step lengths and that for calculation of the active set, new solution matrix and new multiplier vector are described in Steps 4 and 5 of the following matrix-based EPCLS-GI algorithm for problem (15).

Step 1. Prepare the data matrices P, Q and D by (10), compute the solution to the unconstrained LS problem (15a) by

$$\begin{aligned} \mathbf{A}_{0} =\left( {\mathbf{PP}^{H}} \right) ^{-1}\mathbf{PDQ}^{H}\left( {\mathbf{QQ}^{H}} \right) , \end{aligned}$$
(23)

and initialize the algorithm by \(\mathbf{S}=[], \mathbf{A}(0)=\mathbf{A}_{0},\varvec{\lambda }(0)=[], t=0\), and \(\ell =0\).

Step 2. Identify the most violated constraint.

  1. (a)

    Compute \((\alpha _{u},j_{u},k_{u},l_{u})\) and \((\alpha _{v},j_{v},k_{v},l_{v})\) by (16), (17), and then let

    $$\begin{aligned} E_{c}^{mv}&= \left| {\bar{{g}}_{j_u k_u } (\mathbf{A}(\ell ))-\bar{{d}}_{j_u k_u } } \right| -\rho _{j_u k_u } ,\end{aligned}$$
    (24a)
    $$\begin{aligned} E_{p}^{mv}&= \Gamma _{j_v k_v 3} (\alpha _v )g_{j_v k_v }^R (\mathbf{A}(\ell ))+\bar{{\Gamma }}_{j_v k_v 3} (\alpha _v )g_{j_v k_v }^{I} (\mathbf{A}(\ell )). \end{aligned}$$
    (24b)
  2. (b)

    If \(E_{c}^{mv} \le \varepsilon _{1} \rho _{j_u k_u } \) and \(E_{p}^{mv} \le \varepsilon _{2} \) (where \(\varepsilon _{1}>0\) is a tolerance of the relative complex error, \(\varepsilon _{2}>0\) is a small positive number) which means no constraints are violated, then terminate the algorithm and \(\mathbf{A}(\ell )\) is the solution to problem (15).

  3. (c)

    If \(E_{p}^{mv} \ge E_{c}^{mv} \), choose the constraint indexed by \((\alpha _{v},j_{v},k_{v},l_{v})\) as the most violated one. Let \((\alpha _{t+1},j_{t+1},k_{t+1},l_{t+1})= (\alpha _{v},j_{v},k_{v},l_{v})\), and compute R \(_{t+1}\) and \(\xi _{m}\hbox {s}(m=1,2,\ldots ,t)\) by (22c) and (22b).

  4. (d)

    If \(E_{p}^{mv} <\,E_{c}^{mv} \), choose the constraint indexed by \((\alpha _{u},j_{u},k_{u},l_{u})\) as the most violated one. Let \((\alpha _{t+1},j_{t+1},k_{t+1},l_{t+1})= (\alpha _{u},j_{u},k_{u},l_{u})\), and compute R \(_{t+1}\) and \(\xi _{m}\hbox {s} (m=1,2,\ldots ,t)\) by (22c) and (22b).

Step 3. Determine the step directions. Let r=[] if \(t=0\); Or compute r by (20) otherwise. Compute Z by (21).

Step 4. Compute the step lengths.

  1. (a)

    Compute the maximum dual step length \(w_{1}\) within which the dual feasibility would not be violated. If \(\mathbf{r}\le 0\) or \(t\)=0, let \(w_{1}=\infty \); Otherwise, let

    $$\begin{aligned} \bar{{m}}=\arg \mathop {\min }\limits _{{\{m=1,\ldots ,t|r_m >0\}}}\left\{ {\frac{\lambda _m (\ell )}{r_m }} \right\} \, \hbox {and}\, w_{1} =\frac{\lambda _{\bar{{m}}} (\ell )}{r_{\bar{{m}}} }, \end{aligned}$$
    (25)

    where \(\bar{{m}}\) is actually the subscript of the multiplier that would change sign earliest when the multiplier vector changes along the dual step direction.

  2. (b)

    Compute the minimum primal step length \(w_{2}\) with which the most violated constraint would become feasible. If \(\Vert \mathbf{Z}\Vert =0\), let \(w_{2}=\infty \); Otherwise, let

    $$\begin{aligned} w_{2} =\frac{\Gamma _{j_{t+1} k_{t+1} l_{t+1} } (\alpha _{t+1} )g_{j_{t+1} k_{t+1} }^{R} \left( \mathbf{A}(\ell ) \right) +\bar{{\Gamma }}_{j_{t+1} k_{t+1} l_{t+1} } (\alpha _{t+1} )g_{j_{t+1} k_{t+1} }^{I} \left( \mathbf{A}(\ell ) \right) -\theta _{j_{t+1} k_{t+1} l_{t+1} } (\alpha _{t+1} )}{\Gamma _{j_{t+1} k_{t+1} l_{t+1} } (\alpha _{t+1} )g_{j_{t+1} k_{t+1} }^{R} \left( \mathbf{Z} \right) +\bar{{\Gamma }}_{j_{t+1} k_{t+1} l_{t+1} } (\alpha _{t+1} )g_{j_{t+1} k_{t+1} }^I \left( \mathbf{Z} \right) }. \end{aligned}$$
    (26)
  3. (c)

    Let \(w=\hbox {min}(w_{1},w_{2})\).

Step 5. Update the active set, and compute the new solution matrix and new multiplier vector.

  1. (a)

    If \(w=\infty \), problem (15) is infeasible, terminate the algorithm.

  2. (b)

    If \(w=w_{1}\), delete the \(\bar{{m}}\)th element of \(\varvec{\xi }\), and the \(\bar{m}\) th column and \(\bar{{m}}\)th row of S; Update \(\mathbf{R}_{m}\)s by \(\mathbf{R}_{m} \leftarrow \mathbf{R}_{m+1}\) for \(m=\bar{{m}},\bar{{m}}+1,\ldots ,t\); Update the multiplier vector by firstly computing \(\varvec{\lambda }(\ell +1)=\varvec{\lambda }^{+}\) with (18) and then deleting its \(\bar{{m}}\)th element; If \(w_{2}<\infty \), update the solution matrix by \(\mathbf{A}(\ell +1)=\mathbf{A}^{+}\) with (19); Update the active constraints by \((\alpha _{m},j_{m},k_{m},l_{m})\leftarrow (\alpha _{m+1},j_{m+1},k_{m+1},l_{m+1})\) for \(m=\bar{{m}},\bar{{m}}+1,\ldots ,t\); Let \(t \leftarrow t-1, \ell \leftarrow \ell +1\), and go back to Step 3.

  3. (c)

    If \(w=w_{2}\), update the multiplier vector and solution matrix by \(\varvec{\lambda }(\ell +1)=\varvec{\lambda }^{+}\) and \(\mathbf{A}(\ell +1)=\mathbf{A}^{+}\) using (18) and (19); Let \(t \leftarrow t+1, \ell \leftarrow \ell +1\); Compute S by (22a) and go back to Step 2.

Remark 1

Since we use the perpendicular projection method to identify the most violated constraint and the GI primal–dual method to update the active set, solution matrix and multiplier vector, theoretically, without taking into account the numerical precision, the matrix-based EPCLS-GI algorithm has the same convergence properties, say, the same iteration number, as the vectorized CPCLS-GI algorithm in Lai (2009).

Remark 2

When the coefficient vector of a newly added (most violated) constraint obtained in Step 2 is linearly dependent on those of the constraints in the active set, it can be proved that \(\mathbf{R}_{t+1} =\sum _{m=1}^{t} {r_m \mathbf{R}_m } \), and thus Z = 0 from (21). In that case, the \(\bar{m}\) th constraint will be deleted from the active set until the direction matrix Z becomes nonzero. This ensures the non-singularity of matrix S.

Remark 3

Since the matrix S in each iterate is actually obtained either by adding to or by deleting from S in the previous iterate one column and one row, we can use the methods presented in Lemmas 1 and 2 of Hong et al. (2013) to update the inverse matrix \(\mathbf{S}^{-1}\).

3.2 Complexity analysis and comparison

The computational complexity of the matrix-based EPCLS-GI algorithm is dominated by Steps 2, 3, 4 and 5. We assume the frequency grid lengths are \(M_{1}=L_{1}N_{1}\) and \(M_{2}=L_{2}N_{2}\), where \(L_{1}\) and \(L_{2}\) are the grid density constants. Then in each iterate, the multiplication number in Step 2 is \(2M_{1}N_{1}N_{2}+4M_{1}M_{2}N_{2}+12M_{1}M_{2}+N_{1 }^{2}N_{2}+N_{1}N_{2}^{2}+2 {tN}_{1}N_{2}+8N_{1}N_{2}+4N_{2}t_{ }+2t+4N_{2}+3=[(2L_{1}+1)N_{1}+(4L_{1}L_{2}+1)N_{2}+2t+12L_{1}L_{2}+8]N_{1}N_{2}+4N_{2}t_{ }+2t+4N_{2}+3\), that in Step 3 is \(t^{2}\)+tN \(_{1}N_{2}\), that in Step 4 is \(4N_{1}N_{2}+8N_{2}+t\), and that in Step 5 is \(3N_{1}N_{2}+2t^{2}+3t+4N_{2}+3\) for adding a constraint and \(N_{1}N_{2}+t^{2}\) for deleting a constraint, respectively.

The number \(t\) of the Lagrangian multipliers varies with iteration. We assume problem (15), or equivalently, the EPCLS problem (9), is feasible. Then, the value of \(t\) changes from zero to some \(t_{max}\le N_{1}N_{2}\), where \(t_{max}\) depends on the tightness of the problem constraints. When \(t\) is very small, say, \(t \le \) max{\(N_{1},N_{2}\}\), the complexity of the matrix-based EPCLS-GI algorithm for one iterate is \(O\)(max{\(N_{1},N_{2}\}N_{1}N_{2})\). When \(t\approx N_{1}N_{2}\), the complexity for one iterate is \(O(N_{1}^{2}N_{2}^{2})\). Therefore, the complexity of the matrix-based EPCLS-GI algorithm for one iterate is between\( O\)(max{\(N_{1},N_{2}\}N_{1}N_{2})\) and \(O(N_{1}^{2}N_{2}^{2})\).

For comparison, the complexity of the vectorized CPCLS-GI algorithm (Lai 2009) for the EPCLS design problem in one iterate is between \(O(N_{1 }^{2}N_{2}^{2})\) when \(t \le \) max{\(N_{1}, N_{2}\)} and \(O(N_{1 }^{3}N_{2}^{3})\) when \(t\approx N_{1}N_{2}\). Since the matrix-based EPCLS-GI and vectorized CPCLS-GI algorithms consume the same number of iterations (Remark 1), the complexity of the matrix-based EPCLS-GI algorithm is smaller than the vectorized CPCLS-GI algorithm.

4 Design examples and comparisons

Two design examples are provided in this section. While Example 1 is mainly for the efficiency comparison between the matrix-based EPCLS-GI algorithm and the vectorized CPCLS-GI algorithm in Lai (2009) and the SDP method in Lu (2002), Example 2 is provided to show the better performance of the filter obtained by the EPCLS design than that by the CPCLS design. All algorithms are implemented in MATLAB 7.11.0.584 (R2010b). All designs are conducted on a personal computer with an Intel(R) Core(TM) i7-4510U CPU @ 2.00 GHz and an 8.0 GB memory. We pointed out here that minor changes have been made to the original SDP method in Lu (2002) with merely circular complex-error constraints since the design problem in this paper has not only elliptic-error constraints but also phase-error constraints. Minor changes has also been made to the CPCLS-GI algorithm to meet the elliptic-error constrains. Moreover, the SDP method is implemented in this paper using the SDPT3 (Tütüncü et al. 2003) in CVX (Grant and Boyd 2013). Without loss of generality, we assume the 2-D FIR filters are of square size, i.e., \(N_{1}=N_{2}=N\). The size of the frequency grid is taken as \(M_{1}=M_{2}= 8N\). The phase of the desired complex frequency response is defined by

$$\begin{aligned} \beta (\omega _{1} ,\omega _{2} )=-i(\tau _{1} \omega _{1} +\tau _{2} \omega _{2} ), \end{aligned}$$
(27)

where \(\tau _{1}\) and \(\tau _{2}\)are the desired group delays along the \(\omega _{1}\) and \(\omega _{2}\) directions.

Both of the matrix-based EPCLS-GI and vectorized CPCLS-GI algorithms use the same stopping conditions, i.e., they return feasible solutions when \(E_{c}^{mv} \le \varepsilon _{1} \rho _{i_u k_u } \) and \(E_{p}^{mv} \le \varepsilon _{2} \) with the same tolerance parameters \(\varepsilon _{1}=10^{-5}\) and \(\varepsilon _{2}=10^{-12}\).

Example 1

The first example considers the EPCLS design of circular lowpass filters with a passband \(\Omega _{p}=\{(\omega _{1}, \omega _{2})| \sqrt{\omega _{1}^{2} +\omega _{2}^{2} }\le \omega _{p}\)} and a stopband \(\Omega _{s}=\{(\omega _{1},\omega _{2}){\vert }\sqrt{\omega _{1}^{2} +\omega _{2}^{2} } \ge \omega _{s}, {\vert }\omega _{1}{\vert }\le \pi , {\vert }\omega _{2}{\vert }\le \pi \}\), where \(\omega _{p}=0.4 \pi \) and \(\omega _{s}=0.6\pi \). The desired group delays are \(\tau _{1}\) and \(\tau _{2 }\) and the desired magnitude response is described by

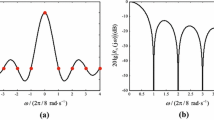
$$\begin{aligned} \bar{{D}}(\omega _{1} ,\omega _{2} )=\left\{ \begin{array}{llll} {1,}&{} {\omega \in \Omega _{p} ,} \\ \frac{\omega _\mathrm{s} -\sqrt{\omega _{1}^{2} +\omega _{2}^{2} }}{\omega _{\mathrm{s}} -\omega _{p}},&{} \omega \in \Omega \setminus (\Omega _{p} \cup \Omega _{s} ), \\ {0,}&{} \omega \in \Omega _{s}. \\ \end{array} \right. \end{aligned}$$
(28)

Such filters of size \(N \times N\) with \(N\) ranging from 9 to 31 have been designed using the matrix-based EPCLS-GI algorithm, the vectorized CPCLS-GI algorithm and the SDP method. Table 1 gives a comparison of the three methods in terms of the mean squared complex error (MSCE) of the filter and the CPU time and iteration number of the algorithm under the specified maximum magnitude error (MME) (i.e., \(\rho \)), maximum phase error MPE (i.e., \(\gamma \)), group delays \(\tau _{1}\) and \(\tau _{2}\), and the model parameter \(\tau \). It is seen from Table 1 that, under the same \(N,\rho ,\gamma , \tau _{1}, \tau _{2}\) and \(\sigma \), the matrix-based EPCLS-GI, vectorized CPCLS-GI and SDP methods obtain almost the same MSCE, but the matrix-based EPCLS-GI algorithm consumes much less CPU time than other two methods. For the designs with the same specifications, the matrix-based EPCLS-GI takes the same number of iterations as the vectorized CPCLS-GI. Figure 1 draws the magnitude response and passband phase error of the \(31\times 31\) circular filter with \(\rho =0.01, \gamma =0.002, \tau _{1}=\tau _{2}=13.5\) and \(\sigma =3\).

Fig. 1
figure 1

a Magnitude response and b passband phase error of the \(31\times 31\) circular filter obtained by the matrix-based EPCLS-GI with \(\rho =0.01,\gamma =0.002,\tau _{1}=\tau _{2}=13.5\) and \(\sigma =3\)

Full size image
Table 1 Efficiency comparison of the matrix-based EPCLS-GI with the vectorized CPCLS-GI and SDP using SDPT3 in CVX in Example 1
Full size table

Filters with the same size \(N=21\) and group delays \(\tau _{1}=8\) and \(\tau _{2}=9\) but different \(\rho \hbox {s}\) and \(\gamma \hbox {s}\) have also been designed using the matrix-based EPCLS-GI and vectorized CPCLS-GI algorithms under \(\sigma =5\). Table 2 gives a comparison of the design results. It is seen that the matrix-based EPCLS-GI is much more efficient than the vectorized CPCLS-GI in all designs.

Example 2

The second example considers the design of fan filters with a passband \(\Omega _{p}=\{(\omega _{1},\omega _{2}){\vert }0\le \omega _{1 }\le \omega _{2} \tan \chi , 0\le \omega _{2}\le \pi \}\) and a stopband \(\Omega _{s}=\{(\omega _{1},\omega _{2}){\vert }\phi \le \omega _{1}\le \pi , 0\le \omega _{2}\le (\omega _{1}-\phi )\tan \chi \}\), where \(\chi =\pi /6\), and \(\phi =0.1\pi \) is a positive number used to control the width of transition band. The desired group delays are \(\tau _{1}\) and \(\tau _{2 }\)and the desired magnitude response is taken as

$$\begin{aligned} \bar{{D}}(\omega _{1} ,\omega _{2} )=\left\{ {{\begin{array}{llll} {1,}&{} {\omega \in \Omega _{p} ,} \\ {\frac{\phi -(\left| {\omega _{1} } \right| -\left| {\omega _{2} } \right| \tan \chi )}{\phi },}&{} {\omega \in \Omega \backslash (\Omega _{p} \cup \Omega _{s} ),} \\ {0,}&{} {\omega \in \Omega _{s}.} \\ \end{array} }} \right. \end{aligned}$$
(29)
Table 2 Efficiency comparison of the matrix-based EPCLS-GI and the vectorized CPCLS-GI algorithms for filters with \(N=21, \tau _{1}=8\) and \(\tau _{2}=9\) in Example 1
Full size table

Several such fan filters of size \(25\times 25\) with the same \(\gamma , \rho , \tau _{1}\) and \(\tau _{2 }\) have been designed using the EPCLS and CPCLS criterions. Table 3 gives the results for the CPCLS design and EPCLS designs with various \(\sigma \hbox {s}\), where the CPCLS design is actually the EPCLS design under \(\sigma = 1\). Results show that the MSCEs of the resultant EPCLS filters, decreasing with \(\sigma \), are all smaller than that of the CPCLS filter. That is to say, the EPCLS designs obtain better filters than the CPCLS design. It is interesting that the iteration number and CPU time of the matrix-based EPCLS algorithm also decrease with \(\sigma \). This is because the domain of the elliptic-error and phase-error constraints becomes larger and thus the constraints become easier to meet when \(\sigma \)gets larger. Figure 2 draws the magnitude response and passband phase error of the \(25\times 25\) fan filter with \(\rho =0.051,\gamma =0.03, \tau _{1}=\tau _{2}=11\) and \(\sigma =5\)

Fig. 2
figure 2

a Magnitude response and b passband phase error of the \(25\times 25\) fan filter obtained by the matrix-based EPCLS-GI with \(\rho =0.051, \gamma =0.03, \tau _{1}=\tau _{2}=11\) and \(\sigma =5\)

Full size image

.

Table 3 Comparison of the filter’s MSCE obtained by the CPCLS design and EPCLS designs with various \(\sigma \hbox {s}\) in Example 2
Full size table

We also design several such fan filters of size \(25\times 25\) with minimal MME using a combination of the sequential CLS (SCLS) method (see, e.g., Hong et al. 2013)) and the matrix-based EPCLS-GI algorithm with various \(\sigma \hbox {s}\). Table 4 shows the design results. Under the same MPE, the minimal MME decreases with \(\sigma \), with a sacrifice of possible increase in MSCE. This implies that an EPCLS design may obtain filters with smaller MME than a CPCLS design.

Table 4 Comparison of the filter’s minimal MME that can be obtained by the CPCLS design and EPCLS designs with various \(\sigma \hbox {s}\) in Example 2
Full size table

5 Conclusions

A matrix-based GI algorithm has been developed for the elliptic-error and phase-error constrained least-squares design of 2-D FIR filters with arbitrarily specified frequency responses. The developed matrix-based EPCLS-GI algorithm is a matrix-based extension of the vectorized CPCLS-GI algorithm in Lai (2009) but has a lower computational complexity than it. Design examples and comparisons demonstrate that the matrix-based EPCLS algorithm consumes much less CPU time than the vectorized CPCLS-GI algorithm and the SDP method, and the EPCLS design may obtain better filters in terms of smaller MSCE and/or MME than the CPCLS design.

6 Appendix

Proof of Theorem 1

Using the Lagrangian method, we can obtain the following equations for the multiplier vector \(\varvec{\lambda }(\ell )\) and the solution matrix \(\mathbf{A}(\ell )\) of problem (15a) subject to the equality constraints indexed by the active set \(J(\ell )\),

$$\begin{aligned} \mathbf{S}\lambda (\ell )=\mathbf{b},\, \mathbf{A}(\ell )=\mathbf{A}_{0} -\sum _{m=1}^{t} {\lambda _{m} (\ell )R_{m} } , \end{aligned}$$
(30)

where \(\lambda _{m}(\ell )\) is the \(m\)th multiplier in \(\varvec{\lambda }(\ell )\), S and \(\mathbf{R}_n \) are defined in (22a) and (22c), and \(\mathbf{b}=[b_{m} ]_{t\times 1} \) with

$$\begin{aligned} b_{m}&= \Gamma _{j_m k_m l_m } (\alpha _{m} )g_{j_m k_m }^{R} (\mathbf{A}_{0} )+\bar{{\Gamma }}_{j_m k_m l_m } (\alpha _{m} )g_{j_m k_m }^{I} (\mathbf{A}_{0} )\nonumber \\&\quad -\theta _{j_m k_m l_m } (\alpha _{m} ), m=1,\,2,\,\ldots ,\,t. \end{aligned}$$
(31)

If the \((t+1)\)th equality constraint is added into the active set, the matrix S and vector b become respectively into

$$\begin{aligned} \mathbf{S}^{+}=\left[ {{\begin{array}{lll} \mathbf{S}&{} \varvec{\xi } \\ \varvec{\xi ^{H}}&{} {\xi _{t+1} } \\ \end{array} }} \right] , \mathbf{b}^{+}=[\mathbf{b}^{H},\,b_{t+1} ]^{H}, \end{aligned}$$
(32)

where \(\xi \) is defined in (22b), \(b_{t+1} \) and \(\xi _{t+1} \) are defined by (31) and (22b) for \(m=t+1\). Then, by (30) and from (18), (19) and (32), we have

$$\begin{aligned} \mathbf{S}^{+}\varvec{\lambda } ^{+}&= \left[ \begin{array}{lll} \mathbf{S}&{} \varvec{\xi } \\ {\varvec{\xi } ^{H}}&{} {\xi _{t+1} } \end{array}\right] \left[ \begin{array}{l} \varvec{\lambda }(\ell )-w\mathbf{r} \\ w \\ \end{array} \right] =\mathbf{b}^{+} =\left[ \begin{array}{l} \mathbf{b} \\ b_{t+1} \end{array}\right] ,\nonumber \\ \mathbf{A}^{+}&= \mathbf{A}_{0} -\sum _{m=1}^{t+1} {\lambda _{m}^+ \mathbf{R}_{m} } =A_0 -\sum _{m=1}^{t} {\lambda _{m} (\ell )\mathbf{R}_{m}} +w\mathbf{Z}, \end{aligned}$$
(33)

where \(\lambda ^{+}_{m}\) is the \(m\)th element of \(\varvec{\lambda }^{+}\). Equations (20) and (21) immediately follow from (18), (19) and (33).\(\square \)