Closed-Form FIR Filter Design with Accurately Controllable Cut-Off Frequency

Abstract

To enhance the efficiency of designing finite impulse response (FIR) filters with a controllable cut-off frequency that possess excellent transfer characteristics, this paper proposes a closed-form filter design based on transfer characteristic compensation. First, a novel filter design based on a convolution window is presented, and the relationship between the spectrum of this window and the filter performance is elaborated. We then derive a three-stage filter design scheme that describes the design of an irregular filter, design of a compensation filter and filter summation. This scheme can be simplified into a closed-form design characterized by two analytic formulas by merging the intermediate steps. The configuration of a vital Kaiser window parameter is also derived. Numerical results show that the proposed closed-form design accurately controls the cut-off frequencies and exhibits a transfer performance comparable to the Remez design and the closed-form weighted least square (WLS) design. Moreover, our method is more efficiency than the closed-form WLS method for the design of high-order FIR filters.

1 Introduction

Currently, there is a widespread demand for configurable finite impulse response (FIR) filters in areas such as software-defined radio [9, 10] and multirate signal processing [19, 22]. However, the rapid and accurate control of the cut-off frequency remains an intractable problem in FIR filter design. It is known that classical filter designs such as the window function method and frequency sampling method [14, 16] inevitably suffer from smearing around the location of the cut-off frequency. As for modern optimum filter designs (such as the Remez method [13, 18], neural network algorithms [1, 2], immune algorithms [4, 8], swarm algorithms [12, 21], cat swarm optimization [5, 20] and genetic algorithms [11, 17, 25]), the imposition of constraints on some discrete grid frequencies enables accurate control on these frequency grids (including the critical frequency points). However, these designs are inefficient, as global optimization requires multiple parameter updates to attain convergence.

The efficiency of FIR filter design would undoubtedly be enhanced if we could develop an analytic approach that involved no parameter update iterations and in which all tap coefficients could be calculated in closed form. However, in general, a closed-form design does not ensure excellent filter performance. For example, in the classical frequency sampling method [16], although all the tap coefficients $h(0)\sim h(N-1)$ can be directly calculated by implementing inverse discrete Fourier transform (IDFT) on a specified N-length frequency sampling vector $\varvec{H}$ (i.e., IDFT plays the role of a closed-form design), the transfer curve suffers from large ripples in both the pass-band and the stop-band.

In recent years, variable digital filters, whose pass-band bandwidth and cut-off frequency can be flexibly tuned, have received increasing attention in communications [19], control systems [3] and radar [15]. The main variable filter design is the variable-bandwidth closed-form design proposed in [6], whose filter structure consists of fixed FIR sub-filters and a tunable linear combination. By adjusting a parameter $\phi$, the pass-band bandwidth and cut-off frequency can be easily altered. Based on this filter structure, a number of variant designs have been proposed, such as the polynomial-based variable-bandwidth FIR filter design [7, 23]. However, because fixed FIR sub-filters are acquired from a matrix inversion, variable-bandwidth design is computationally complex. Moreover, large errors due to numerical instability are likely to occur when designing high-order FIR filters. Therefore, an accurate, high-efficiency closed-form linear-phase FIR design method is urgently needed.

This paper proposes a novel filter design, in which the tap coefficients g(n) can be easily acquired by implementing an analytic operation on the aforementioned tap coefficients h(n) designed by the frequency sampling methods. In this design, a $(2N-1)$-length convolution window $w_c(n), -N+1\le n \le N-1$ plays an important role in achieving high efficiency and excellent performance (e.g., small ripples in the pass-band and large attenuation in the stop-band). In addition, we propose two symmetric frequency sampling modes and an adjustable cut-off-frequency scheme named ‘amplitude–frequency characteristic compensation.’ By integrating this adjustable scheme with the two frequency sampling modes and the convolution window-based design, we derive a three-stage design scheme capable of precisely controlling the 0-dB cut-off frequency. Furthermore, this three-stage scheme (which includes the design of an irregular filter, design of a compensation filter and filter summation) can be further simplified into a closed-form design characterized by two analytic formulas. Compared with existing closed-form weighted least square design [24], the proposed method enables the computationally simple design of high-order FIR filters.

2 Convolution Window-Based FIR Filter Design

In this section, we describe a convolution window-based filter design. This design inherits the concept of transfer characteristic interpolation from the classical frequency sampling method.

2.1 Derivation Process

For the frequency sampling method, given an N-length frequency sampling vector $\varvec{H}=[H(0),H(1),\ldots ,H(N-1)]$ satisfying

$$\begin{aligned} H(k)= H(N-k),{\quad }k=1,\ldots ,N-1, \end{aligned}$$

(1)

it is known that implementing IDFT on $\varvec{H}$ yields the real-valued filter coefficient h(n) as

$$\begin{aligned} h(n)=\frac{1}{N}\sum \limits _{k = 0}^{N - 1}{H(k){\hbox {e}^{jnk2\pi /N}}},\quad n = 0,\ldots ,N - 1. \end{aligned}$$

(2)

Note that, for the frequency vector $\varvec{H}$, if the direct current (DC) item H(0) is excluded, then the remaining elements exhibit central symmetry (i.e., $H(1)=H(N-1), H(2)=H(N-2),\ldots$). Hence, in this paper, the vector $\varvec{H}$ is referred to a DC-excluded symmetric frequency vector.

Our design attempts to integrate the merits of the traditional frequency sampling method and the traditional windowing method. However, unlike windowing method, our design does not directly employ the commonly used N-length window f(n) (such as the Hanning window or the triangular window). Instead, f(n) is convolved with the reversed version of an N-length rectangular window $r_N(n)$ to generate a novel window $w_c(n)$, i.e.,

$$\begin{aligned} w_c(n)=f(n)*r_N(-n), \end{aligned}$$

(3)

Since both f(n) and $r_N(n)$ have a finite length N, we have that

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} f(n), \;r_N(n) \ne 0,&{}\quad n \in [0,N - 1]\\ f(n) = r_N(n) = 0,&{}\quad n \in [ - \infty , - 1] \cup [N, + \infty ]. \end{aligned} \end{array} \right. \end{aligned}$$

(4)

Hence, combining (3) with (4), we have

$$\begin{aligned} \left\{ \begin{array}{l} \begin{aligned} w_c(n)\ne 0,&{}\quad n \in [-N+1,N - 1]\\ w_c(n) = 0,&{}\quad n \in [ - \infty , - N] \cup [N, + \infty ]. \end{aligned} \end{array} \right. \end{aligned}$$

(5)

Thus, the nonzero elements of $w_c(n)$ fall in the range $n\in [-N+1,N-1]$.

Accordingly, if we extend the definition domain of h(n) in (2) from $n \in [0,N - 1]$ to $n \in [-N+1,N - 1]$ and multiply this double-sided h(n) with the aforementioned convolution window $w_c(n)$, we can derive the a novel $(2N-1)$-length FIR filter g(n) as

$$\begin{aligned} g(n)=w_c(n)h(n),\quad n\in [-N+1,N-1]. \end{aligned}$$

(6)

2.2 Properties of the Convolution Window

Applying Fourier transform to (3) yields

$$\begin{aligned} W_c(j\omega )=F(j\omega )\cdot R_N^*(j\omega ). \end{aligned}$$

(7)

If f(n) is symmetric, i.e., $f(n)= f(N-1-n), n=0,\ldots ,N-1$, the conjugate product operation in (7) gives a real-valued $W_c(j\omega )$. As is known, the normalized rectangular window’s Fourier spectrum $R_N(j\omega )$ possesses the following sampling property:

$$\begin{aligned} {R_N}\left( { {{j k2 \pi } N}} \right) = \left\{ \begin{aligned} 1,~&{\quad }k = 0\\ 0, ~&{\quad }k = \pm 1,\pm 2, \cdots \end{aligned} \right. . \end{aligned}$$

(8)

If f(n) is normalized by its DC value $C=\Sigma _{n=0}^{N-1}{f(n)}$ in advance, then it is easy to prove that $W_c(j\omega )$ also possesses the following sampling property:

$$\begin{aligned} {W_c}\left( { {{j k2 \pi } N}} \right) = \left\{ \begin{aligned} 1,~&{\quad }k = 0\\ 0, ~&{\quad }k = \pm 1,\pm 2, \cdots \end{aligned} \right. , \end{aligned}$$

(9)

Take $N=8$ as an example and specify f(n) as the triangular window. The magnitude curves and logarithmic magnitude curves of $R_N(j\omega )$ and $W_c(j\omega )$ are illustrated in Figs. 1 and 2.

Fig. 1

a Magnitude curve, b curve of magnitude in logarithm of the rectangular window ($N=8$)

Fig. 2

a Magnitude curve, b curve of magnitude in logarithm of the $(2N-1)$-length convolution window ($N=8$)

Comparing Fig. 1 with Fig. 2, one can see that the spectrum characteristic of $W_c(j\omega )$ is much better than that of $R_N(j\omega )$. Specifically, compared with $R_N(j\omega )$ in Fig. 1a, the sidelobe ripples of $W_c(j\omega )$ in Fig. 2a are much smaller and their coverage is much narrower. Moreover, the first and second sidelobe attenuation values shown in Fig. 2b are $-$27.97 and $-$47.75 dB, much lower than those of $R_N(j\omega )$ ($-$13 and $-$17 dB, shown in Fig. 1b). In addition, both $R_N(j\omega )$ and $W_c(j\omega )$ are Dirac functions at $\omega _k=k2\pi /N,k=0,\pm 1,\pm 2,\ldots$, shown by Figs. 1a and 2a (red solid points).

The above spectrum characteristics of $W_c(j\omega )$ ensure that the proposed filter has an excellent transfer characteristic, as demonstrated later.

2.3 Analysis of the Transfer Performance of the Proposed Filter

Applying Fourier transform to (6), we can obtain the proposed filters transfer function $G(j\omega )$ as

$$\begin{aligned} G(j\omega )=\sum \limits _{n= -N+1}^{N - 1}{w_c(n)h(n)\hbox {e}^{-jn\omega }}. \end{aligned}$$

(10)

Further, substituting the normalized $w_c(n)$ and h(n) in (2) into (10) and exchanging the summation order of the variables n and k yields

$$\begin{aligned} G(j\omega )=\sum \limits _{k=0}^{N-1}{ H(k)W_c[j(\omega -k2\pi /N)] }. \end{aligned}$$

(11)

Equation (11) shows that $G(j\omega )$ can be generated by implementing an interpolation process on the specified frequency points H(k) with the Fourier spectrum $W_c(j\omega )$.

As has been pointed out [16], the transfer characteristic $H(j\omega )$ of h(n) can also be generated by implementing an interpolation operation on H(k) as

$$\begin{aligned} H(j\omega )=\sum \limits _{k = 0}^{N - 1}{H(k) R_N[j(\omega -k2\pi /N)]}. \end{aligned}$$

(12)

Comparing (11) with (12), one can find that the interpolation function of $G(j\omega )$ is $W_c(j\omega )$ (the Fourier spectrum of the convolution window), whereas the interpolation function of $H(j\omega )$ is $R_N(j\omega )$ (the Fourier spectrum of the rectangular window). Since $W_c(j\omega )$ has better spectrum characteristics than $R_N(j\omega )$, we may assume that $G(j\omega )$ is superior to $H(j\omega )$.

Furthermore, substituting $\omega =k' \Delta \omega , \Delta \omega =2\pi /N$ and (9) into (11) yields $G\left( { jk'2\pi /N} \right) = H(k'),\quad k' = 0,\ldots ,N - 1.$, i.e., $G(j\omega )$ passes exactly through the specified frequency points H(k). Without loss of generality, suppose that $\varvec{H}$ possesses the following DC-excluded symmetric structure

$$\begin{aligned} \varvec{H} = [1 \ \underbrace{1,\ldots ,1}_{m} \underbrace{0,\ldots ,0}_{N - 2m -1} \underbrace{1,\ldots ,1}_{m }]. \end{aligned}$$

(13)

Then, substituting (13) into (11) yields

$$\begin{aligned} G(j2k\pi /N)={\left\{ \begin{array}{ll} 1,~~&{}k\in [0,m]\cup [N-m,N-1]\\ 0,~~&{}k\in [m+1,N-m-1] \end{array}\right. } \end{aligned}$$

(14)

By combining (14) with the fact that $W_c(j\omega )$ has large sidelobe attenuation, the proposed filter design has the ability to accurately control the cut-off frequency (the 0-dB cut-off frequency is exactly located at $m \Delta \omega$).

For example, consider $N=8,~m=2$ (thus $\varvec{H}=[1~1~ 1~ 0 ~0~ 0~1 ~1]$ ) and suppose that f(n) is the triangular window. Substituting these parameters into (11), (12) yields $H(j\omega )$ and $G(j\omega )$, as plotted in Fig. 3.

Fig. 3

Magnitude curves of $|H(j\omega )|$ and $|G(j\omega )|$ ($N=8,m=2$)

One can observe that, compared with $|H(j\omega )|$, the ripples in $|G(j\omega )|$ are significantly suppressed. Specifically, as the enlarged picture in Fig. 3 illustrates, the conventional frequency sampling design has a maximum uprush near the 0-dB cut-off frequency $\omega _p$ (i.e., the Gibbs effect) of 14 %, whereas the uprush of the Gibbs effect in the proposed design is only about 4 %. This is because the sidelobe attenuation of the interpolation function $W_c(j\omega )$ is much greater than that of $R_N(j\omega )$, as shown by Fig. 2.

Moreover, similar to $|H(j\omega )|$, $|G(j\omega )|$ passes through $\varvec{H}=[1~1~ 1~ 0 ~0~ 0~1 ~1]$ at $\omega =k2\pi /N,k=0,\ldots ,N-1$. As a result, the 0-dB cut-off frequency is accurately located at $\omega =m\Delta \omega =2\Delta \omega$ and the transition band is almost clamped in the interval $[m\Delta \omega , (m+1)\Delta \omega ]=[2\Delta \omega ,3\Delta \omega ]$.

However, limited by the resolution $\Delta \omega =2\pi /N$, the number of candidate 0-dB cut-off frequencies is finite. To accurately locate the 0-dB cut-off frequency $\omega _p$ at an arbitrary position, the next section describes an adjustable scheme named ‘amplitude–frequency characteristic compensation.’

3 Design of Amplitude–Frequency Compensation Filter

This section mainly illustrates a three-stage filter design scheme based on amplitude–frequency characteristic compensation, which involves a kind of direct symmetric frequency sampling mode.

3.1 Direct Symmetric Frequency Sampling Mode

Different with the aforementioned DC-excluded symmetric mode in (13), the low-pass filter (LPF) in direct symmetric mode requires that the N-length frequency vector $\varvec{H}$ is of the following structure

$$\begin{aligned} \varvec{H} = [\underbrace{1,\cdots ,1}_{m}~\underbrace{0,\cdots ,0}_{N-2m}~\underbrace{1,\cdots ,1}_{m}]. \end{aligned}$$

(15)

In other words, $\varvec{H}$ in (15) satisfies

$$\begin{aligned} H(k) = H(N-1-k), {\quad }k=0,1,\ldots ,N-1.\end{aligned}$$

(16)

Let $N=8,~m=2$. In terms of (13) and (15), Fig. 4 illustrates the frequency points of the DC-excluded symmetric case (sampled at $\omega =k\Delta \omega ,k=0,\ldots ,N-1$, as shown by blue stars) and the direct symmetric case (sampled at $\omega =(k+0.5)\Delta \omega ,k=0,\ldots ,N-1$, as shown by red circles).

Fig. 4

DC-excluded symmetric sampling mode and direct symmetry sampling mode ($N=8$)

Unlike with the DC-excluded symmetric frequency vector $\varvec{H}$ in (13), the IDFT of the direct symmetric vector $\varvec{H}$ is complex-valued. To obtain real-valued coefficients, it is necessary to define a $(2N-1)$-length frequency-shift vector $\varvec{v}=[v(-N+1), \ldots , v(0),\ldots , v(N-1)]$ as

$$\begin{aligned} v(n)=\hbox {e}^{j0.5\Delta \omega n} =\hbox {e}^{j\pi n/N}, -N+1\le n \le N-1. \end{aligned}$$

(17)

Then, multiplying the double-sided h(n), the normalized convolution window $w_c(n)$ with v(n) yields an even-symmetric frequency sampling-based filter $g_e(n)$

$$\begin{aligned} g_e(n)=w_c(n)h(n)v(n)=g(n)\hbox {e}^{j0.5\Delta \omega n}, \quad -N+1\le n \le N-1 \end{aligned}$$

(18)

Figure 5 plots the transfer curve $G_e(j\omega )$ of the filter $g_e(n)$ ($N=8,~m=2$).

Fig. 5

Transfer curve derived from direct symmetric sampling mode ($N=8,\,m=2$)

One can find that $G_e(j\omega )$ passes exactly through H(k) sampled at $\omega =(k+0.5)\Delta \omega ,k=0,\ldots ,N-1$. The reason is as follows. As mentioned previously, because the transfer curve $G(j\omega )$ of the filter g(n) passes through the frequency points sampled at $\omega =k\Delta \omega ,k=0,\ldots ,N-1$, the frequency-shift property of the Fourier transform means that the transfer curve $G_e(j\omega )$ of the modulated filter $g_e(n)=g(n)\hbox {e}^{j0.5\Delta \omega n}$ should pass through the frequency points sampled at $\omega =(k+0.5)\Delta \omega ,k=0,\ldots ,N-1$. In other words, $G_e(j\omega )$ passes through the direct symmetric frequency sampling points.

As Fig. 5 clearly illustrates, for the direct symmetric frequency sampling mode, the 0-dB cut-off frequency $\omega _p$ is accurately located at $\omega =(m-0.5)\Delta \omega$. Moreover, the 6-dB cut-off frequency $\omega _{6\mathrm{dB}}$ (i.e., $G_e(\omega _{6\mathrm{dB}})=0.5$) is accurately located at $\omega =m\Delta \omega$ (shown by the squares). Recall that for the DC-excluded symmetric frequency sampling mode, $\omega _p$ is accurately located at $\omega =m \Delta \omega$, i.e., the even multiples of $0.5 \Delta \omega$. Therefore, by deciding between the DC-excluded symmetric sampling mode and the direct symmetric sampling mode, the 0-dB cut-off frequency $\omega _p$ can be located at the integer multiples of $0.5 \Delta \omega$. In other words, the introduction of the direct symmetric sampling mode doubles the number of realizable $\omega _p$.

However, the number of candidate 0-dB cut-off frequencies is still finite. To locate the 0-dB cut-off frequency $\omega _p$ at an arbitrary position, we develop a design scheme named ‘amplitude–frequency compensation.’

3.2 Three Stages of Amplitude–Frequency Compensation

Our proposed amplitude–frequency compensation-based filter design scheme consists of three stages: the design of an irregular filter, design of a compensation filter and filter summation.

3.2.1 Design of an Irregular Filter

Designing an irregular filter involves locating the 0-dB cut-off frequency $\omega _p$ at an arbitrary position. Nevertheless, irregular transfer characteristic in low-frequency regions may also arise.

To derive the irregular filter, the direct symmetric frequency vector $\varvec{H}$ is divided into two sub-vectors $\varvec{H_1}$, $\varvec{H_2}$ as

$$\begin{aligned} \begin{aligned} \varvec{H_1}&= [\underbrace{1,\cdots ,1}_{m}~\underbrace{0,\cdots ,0}_{N-m}]\\ \varvec{H_2}&= [\underbrace{0,\cdots ,0}_{N-m}~\underbrace{1,\cdots ,1}_{m}] \end{aligned} \end{aligned}$$

(19)

Implementing the definition-extended IDFT on $\varvec{H_1}$, $\varvec{H_2}$, we have

$$\begin{aligned} \left\{ \begin{aligned} h_1(n)&=\frac{1}{N}\sum _{k=0}^{m-1}{\hbox {e}^{jk\frac{2\pi n}{N}}} \\ h_2(n)&=\frac{1}{N}\sum _{k=N-m}^{N-1}{\hbox {e}^{jk\frac{2\pi n}{N}}} \end{aligned}\right. ,\quad -N+1\le n\le N-1 \end{aligned}$$

(20)

Accordingly, $g_e(n)$ in (18) can also be split into two sub-filters $\tilde{g}_1(n)$, $\tilde{g}_2(n)$ as

$$\begin{aligned} \left\{ \begin{aligned} \tilde{g_1} (n)&=w_c(n)h_1(n)\hbox {e}^{j0.5\Delta \omega n} \\ \tilde{g_2} (n)&=w_c(n)h_2(n)\hbox {e}^{j0.5\Delta \omega n} \end{aligned}\right. ,\quad -N+1\le n\le N-1 \end{aligned}$$

(21)

Noted that $\tilde{g_1} (n)$ and $\tilde{g_2} (n)$ are conjugate and thus their transfer responses $\tilde{G_1} (j\omega )$ and $\tilde{G_2} (j\omega )$ are symmetric about $\omega =\pi$. Their magnitude–frequency curves are shown in Fig. 6a.

Fig. 6

Magnitude–frequency curves of two sub-filters ($N=16,~m=3$)

Figure 6a shows that, in the region near $\omega =0$, $\tilde{G_1} (j\omega )$ has a gap and $\tilde{G_2} (j\omega )$ has a complementary uprush. The summation causes the transfer curve $G_e(j\omega )=\tilde{G}_1 (j\omega )+\tilde{G} _2(j\omega )$ to have a flat shape near $\omega =0$, as illustrated in Fig. 6b.

To flexibly adjust the 0-dB cut-off frequency $\omega _p$, it is necessary to move $\tilde{G_1} (j\omega )$ and $\tilde{G_2} (j\omega )$ in opposite directions. Therefore, $\tilde{g_1} (n)$ and $\tilde{g_2} (n)$ should be multiplied by opposite frequency-shift terms $v_1(n)$, $v_2(n)$ as

$$\begin{aligned} \left\{ \begin{aligned} v_1(n)&=\hbox {e}^{j\lambda \Delta \omega n } \\ v_2(n)&=\hbox {e}^{-j\lambda \Delta \omega n} \end{aligned}\right. , \quad -N+1\le n\le N-1, \end{aligned}$$

(22)

where $\lambda$ is the fractional frequency shift ($-0.5 <\lambda \le 0.5$). Accordingly, the two shifted sub-filters $g_1 (n)$ and $g_2 (n)$ are

$$\begin{aligned} \left\{ \begin{aligned} {g_1} (n)&=\tilde{g}_1 (n)v_1(n) \\ {g_2} (n)&=\tilde{g}_2 (n)v_2(n) \end{aligned}\right. , \quad -N+1\le n\le N-1 \end{aligned}$$

(23)

Summing $g_1(n)$ and $g_2(n)$ yields

$$\begin{aligned} g_0(n)=g_1(n)+g_2(n) \end{aligned}$$

(24)

Let $N=16$, $m=3$ and $\lambda =0.35$. Figure 7a, b illustrates the magnitude–frequency curves of the shifted transfer functions $G_1 (j\omega )$, $G_2 (j\omega )$ and their synthesized result $G_0(j\omega )=G_1 (j\omega )+G_2 (j\omega )$, respectively.

Fig. 7

Magnitude–frequency curves of two shifted sub-filters ($N=16,~m=3,~\lambda =0.35$)

As shown by Fig. 7b, after a further shift, the 0-dB cut-off frequency $\omega _p$ falls exactly at an expected position $\omega =(m-0.5+\lambda )\Delta \omega =2.85 \Delta \omega$. This property can be attributed to the direct symmetric sampling vector $\varvec{H}$, from which two symmetric sub-vectors $\varvec{H}_1$ and $\varvec{H}_2$ can be derived using (19). Thus, two symmetric transfer functions $G_1 (j\omega )$, $G_2 (j\omega )$ can be generated through opposite frequency-shift operations. Clearly, the DC-excluded symmetric sampling mode does not possess this property.

It should also be noted that, in the region near $\omega =0$ in Fig. 7a, the gap of $G_1 (j\omega )$ and the uprush of $G_2 (j\omega )$ are not complementary. Consequently, as Fig. 7b shows, the shape of $|G_1 (j\omega )+G_2 (j\omega )|$ is no longer flat and a conspicuous gap appears in the region $\omega \in [0, \Delta \omega ]$. As a result of this gap, the filter $g_0(n)$ does not possess the expected low-pass characteristic, and its transfer curve also becomes irregular. Thus, the filter $g_0(n)$ is named an ‘irregular filter.’

3.2.2 Design of a Compensation Filter

To regularize the filter $g_0(n)$, we must design a filter that compensates for the gap in the low-frequency region $\omega \in [0, \Delta \omega ]$. Furthermore, from Fig. 4, it is apparent that two frequency points ($H(j0)=1$ and $H(j\Delta \omega )=1$) of the DC-excluded symmetric sampling mode fall in this region, whereas only one frequency point ( $H(j0.5\Delta \omega )=1$) exists in the direct symmetric sampling mode. Hence, we adopt the DC-excluded symmetric frequency sampling mode, in which the frequency vector $\varvec{H_c}$ should satisfy

$$\begin{aligned} {H_c}(k) = {H_c}(N - k), {\quad } k\in [1, N-1] \end{aligned}$$

(25)

In the DC-excluded symmetric sampling mode, the transfer curve passes through the specified samples of $\varvec{H_c}$. Thus, it is necessary to sample $G_0(j\omega )$ at $\omega =0$ and $\omega =2\pi /N$ to obtain two sampling values a, b as

$$\begin{aligned} \left\{ \begin{aligned} a&=G_0(j0)=\sum _{n=-N+1}^{N-1}g_0(n)\\ b&= G_0(j2\pi /N)=g_0+2\sum _{n=1}^{N-1}{g(n)\cos (n2\pi /N)}. \end{aligned}\right. \end{aligned}$$

(26)

These two sampling points are shown in Fig. 7b. To realize the low-pass property in the irregular region $\omega \in [0, \Delta \omega ]$ of $G_0(j\omega )$, we expect that the sum of the transfer characteristics of the irregular filter and the compensation filter will be equal to 1. Hence, in combination with (25) and (26), $\varvec{H_c}$ should be set as

$$\begin{aligned} \varvec{H_c}=[1-a~1-b~\underbrace{0, \cdots , 0}_{N-3}~1-b]. \end{aligned}$$

(27)

Suppose a normalized convolution window $w_\alpha (n)$ is employed to design the compensation filter $g_c(n)$. Then, in terms of (2) and (6), we have that

$$\begin{aligned} g_c(n)=\frac{w_\alpha (n)}{N}\sum _{k=0}^{N-1}{H_c(k){\hbox {e}^{j\frac{2\pi }{N}nk}}}, \quad -N+1\le n\le N-1 \end{aligned}$$

(28)

where $w_\alpha (n)$ is generated by convolving a normalized N-length Kaiser window $\omega _K(n; \alpha )$ with the N-length rectangular window $r_N(n)$, i.e.,

$$\begin{aligned} {w_\alpha }(n) = {w_K}(n; \alpha ) * {r_N}( - n) \end{aligned}$$

(29)

Note that the compensation performance depends on the configuration of the Kaiser parameter $\alpha$, which will be elaborated later.

3.2.3 Filter Summation

In this stage, summing the irregular filter $g_0(n)$ and the compensation filter $g_c(n)$ yields the final $(2N-2)$-order filter g(n) as

$$\begin{aligned} g(n) = {g_0}(n) + {g_c}(n),\quad -N+1\le n\le N-1. \end{aligned}$$

(30)

4 Closed-Form Filter Design

This section describes how the three-stage filter design proposed in Sect. 3.2 can be simplified into a closed-form design. In addition, the configuration of some relevant parameters is also be addressed.

4.1 Derivation of Closed-Form Formulas

Substituting (20) $\sim$ (23) into (24), one can derive the irregular filter $g_0(n)$ as

$$\begin{aligned} \begin{aligned} {g_0}(n)&=\frac{{{w_c}(n)}}{{N}}{\hbox {e}^{j\frac{\pi }{N}n}} \cdot \left( {{\hbox {e}^{j\frac{{2\pi }}{N}\lambda n}} \cdot \sum \limits _{k = 0}^{m - 1} {{\hbox {e}^{j\frac{{2\pi }}{N}kn}}} } \right. + \left. {\;\;{\hbox {e}^{ - j\frac{{2\pi }}{N}\lambda n}} \cdot \sum \limits _{k = N - m}^{N - 1} {{\hbox {e}^{j\frac{{2\pi }}{N}kn}}} } \right) . \end{aligned} \end{aligned}$$

(31)

Define

$$\begin{aligned} {\check{g}}(n)= {\hbox {e}^{j\frac{{2\pi }}{N}\lambda n}} \cdot \sum \limits _{k = 0}^{m - 1} {{\hbox {e}^{j\frac{{2\pi }}{N}kn}} + {\hbox {e}^{ - j\frac{{2\pi }}{N}\lambda n}} \cdot \sum \limits _{k = N - m}^{N - 1} {{\hbox {e}^{j\frac{{2\pi }}{N}kn}}} } \end{aligned}$$

(32)

On the basis of the geometric series summation and Euler equation, $\check{g}(n)$ can be further written as

$$\begin{aligned} \check{g}(n) ={\hbox {e}^{ - j\pi n/N}}\frac{{2\sin \left( {\pi mn/N} \right) \cos \left[ {\pi \left( {m + 2\lambda } \right) n/N} \right] }}{{\sin \left( {\pi n/N} \right) }}. \end{aligned}$$

(33)

Combining (31)–(33), the irregular filter $g_0(n)$ can be analytically denoted as

$$\begin{aligned} {g_0}(n)= \frac{{2{w_c}(n)\sin \left( {\pi mn/N} \right) \cos \left[ {\pi \left( {m + 2\lambda } \right) n/N} \right] }}{{N\sin \left( {\pi n/N} \right) }} \end{aligned}$$

(34)

Note that (34) does not apply when $n=0$, as the denominator becomes 0. In this case, directly substituting $n=0$ into (31) yields ${g_0}(0) = 2m/N$. Therefore, the complete formula for the irregular filter $g_0(n)$ is

$$\begin{aligned} g_0(n)={\left\{ \begin{array}{ll} \frac{2\omega _c(n)\sin (\pi mn/N)\cos [\pi (m+2\lambda )n/N]}{N\sin (\pi n/N)}, &{}\quad n\in [-N+1, -1]\cup [1, N-1]\\ 2m/N, &{}\quad n=0. \end{array}\right. } \end{aligned}$$

(35)

To simplify the compensation filter $g_c(n)$, we substitute $H_c(k)$ in (27) into (28) to obtain

$$\begin{aligned} {g_c}(n)= w_\alpha (n) \cdot [1 - a+2(1 - b)\cos (2\pi n/N)]/N, \quad -N+1\le n\le N-1. \end{aligned}$$

(36)

Finally, summing $g_0(n)$ and $g_c(n)$ generates the final $(2N-2)$-order filter g(n).

4.2 Kaiser Parameter Configuration

The Kaiser parameter $\alpha$ is closely related to the final transfer characteristic. If $\alpha$ is improperly configured, the gap in the irregular filter resulting from the shift parameter $\lambda$ would not be well compensated. Hence, a reasonable $\alpha$ function with respect to $\lambda$ should be developed.

Equations (7) and (11) imply that the Kaiser parameter $\alpha$ is closely tied to the irregular filter’s convolution window $w_c(n)$. For convenience, $w_c(n)$ is given by the convolution of a triangular window with a rectangular window. To investigate the characteristics of this real-valued $W_c(j\omega )$, the curves of $W_c(j\omega )$ for $N=8, 16$ and 20 are plotted in Fig. 8.

Fig. 8

Convolution window spectrums of irregular filters

From Fig. 8, one can observe the common phenomenon that, for each value of N, $\omega =\pm 1.25\Delta \omega$ are located at inflection points. In other words, when $|\omega |>1.25\Delta \omega$, the decay of the sidelobe of $W_c(j\omega )$ accelerates acutely. Since the mainlobe covers a width of $\Delta \omega$, it can be inferred that $\lambda =\pm 0.25$ are the inflection points of the shift factor $\lambda$. Thus, to achieve a good amplitude–frequency compensation, we further discuss how to configure the Kaiser parameter $\alpha$ for $|\lambda |\le 0.25$ and $|\lambda |>0.25$.

Fig. 9

The curves of magnitude in logarithm of Kaiser windows with different $\alpha$ values

For the case $|\lambda |\le 0.25$, the Kaiser parameter $\alpha$ should be extremely small. There are two reasons. First, as Fig. 9 shows, the smaller the value of $\alpha$, the narrower the mainlobe of $20\texttt {log}_{10}{|W_K(\omega ;\alpha )|}$ in the compensation filter’s Kaiser window $w_K(n; \alpha )$, which accords with the irregular filter’s narrow gap caused by the small $|\lambda |$. Second, as Fig. 8 shows, $W_c(j\omega )$ in the region $\Delta \omega \le |\omega | \le 1.25\Delta \omega$ is much steeper than in the region $|\omega | >1.25\Delta \omega$, which means that the compensation transfer curve should also be very steep and highly oscillatory. Based on these considerations, $\alpha$ is set to zero when $|\lambda |\le 0.25$, since the Kaiser window with $\alpha =0$ is actually the rectangular window, which has the highest oscillation among the commonly used windows.

For the case $|\lambda |>0.25$, i.e., the gap of the irregular filter is wider, the Kaiser parameter $\alpha$ should be enlarged accordingly. This is in accordance with the tendency shown in Fig. 9 (plotted by calling the MATLAB function ‘kaiser’): The mainlobe width of $20\texttt {log}_{10}{|W_K(\omega ;\alpha )|}$ increases with $\alpha$. Hence, the widening gap resulting from the increase in $|\lambda |$ can be suitably filled.

To determine the relationship between the parameter $\alpha$ and the shift factor $\lambda$, we tested various combined parameter pairs ($\alpha ,\lambda )$ to identify good compensation (i.e., parameter values for which the gap was filled smoothly). In these tests, different values of N and m were also considered. The piecewise linear function

$$\begin{aligned} \alpha ={\left\{ \begin{array}{ll} 0,&{}\quad |\lambda |\le 0.25\\ 18|\lambda |-4.5,&{}\quad 0.25<|\lambda |\le 0.5, \end{array}\right. } \end{aligned}$$

(37)

proves to be an acceptable empirical configuration formula that meets the aforementioned expectations (i.e., $\alpha$ should be extremely small for $|\lambda |\le 0.25$ and become larger as the distance from $|\lambda |- 0.25$ to an inflection point increases).

4.3 Parameter Settings and Filter Design Flow

Given the expected 0-dB cut-off frequency $\omega _p$ and the number of frequency samples N ($\Delta \omega = 2\pi /N$ and the 6-dB cut-off frequency $\omega _{6\mathrm{dB}}$=$\omega _p+0.5\Delta \omega$), the filter parameters of m, $\lambda$ should be specified as follows.

As mentioned above, for $\omega _p=(m-0.5+\lambda )\Delta \omega$ and $-0.5<\lambda \le 0.5$, the integer m should be set as

$$\begin{aligned} m = \left\lceil {{\omega _p}/\Delta \omega } \right\rceil , \end{aligned}$$

(38)

where $\lceil \cdot \rceil$ denotes rounding operation to the next higher integer. Accordingly, the fractional number $\lambda$ should be set as

$$\begin{aligned} \lambda = {\omega _p}/\Delta \omega - m + 0.5. \end{aligned}$$

(39)

Equations (38) and (39) provide the initial values of m, $\lambda$ for the filter design. We can then summarize our simplified filter design flow as follows:

• step 1: Given the expected 0-dB cut-off frequency $\omega _p$ and the parameter N, use (38) and (39) to determine the integer parameter m and the fractional parameter $\lambda$. Construct a normalized $(2N-1)$-length window $w_c(n)$ by convolving the N-length triangular window and the N-length rectangular window. Substitute $w_c(n), N$, m and $\lambda$ into (35) to design the irregular filter $g_0(n)$.

• step 2: Use (37) to configure the Kaiser parameter $\alpha$ and use (29) to construct the Kaiser convolution window $w_\alpha (n)$. Substitute $a=|G_0(j0)|$, $b=|G_0(j2\pi /N)|$, N and $w_\alpha (n)$ into (36) to design the compensation filter $g_c(n)$.

• step 3: Sum $g_0(n)$ and $g_c(n)$ to obtain the final filter g(n).

Clearly, the above three-step design is expressed in closed form, which greatly simplifies the design scheme of the amplitude–frequency compensation addressed in Sect. 3.2.

4.4 Computation Complexity of the Proposed Closed-Form Design

Since multiplication operations consume far more hardware resources than additions, a quantitative analysis of the multiplication calculations performed by the proposed closed-form design was conducted.

In Step 1, the calculation of the $(2N-1)$-length window $w_c(n)$ requires a convolution operation between two N-length windows. It is known that time-domain convolution corresponds to frequency-domain multiplication. Assuming that $\tilde{N}=2^{\lceil \log _2 N \rceil }$ (thus satisfies $\tilde{N}=N$ when $n=\log _2N\in Z^+$ ), we can use two $2\tilde{N}$-point fast Fourier transforms (FFTs) and one $2\tilde{N}$-point inverse FFT to compute this time-domain convolution. Thus, the calculation of this convolution window requires three $2\tilde{N}$-point FFTs and one $2\tilde{N}$-point complex multiplication. Each $2\tilde{N}$-point FFT requires $2 \tilde{N}/2 \log _2 (2\tilde{N})$ complex multiplications, each of which can be decomposed into four real-valued multiplications. Therefore, the number of real-valued multiplication operations required to calculate $w_c(n)$ is $3\times 4\times 2 \tilde{N}/2 \log _2 (2\tilde{N})+4\times 2\tilde{N}$=$12\tilde{N}\log _2 \tilde{N}+20\tilde{N}$. Additionally, as shown by (35), calculating each entry of $g_0(n), n\in [1, N-1]$ consumes four multiplication operations. Since $g_0(n)=g_0(-n)$, the $(2N-1)$ tap coefficients of $g_0(n)$ require $1+2\times 4\times (N-1)=8N-7\approx 8N$ multiplications. Thus the total number of multiplications involved in Step 1 is $12\tilde{N}\log _2 \tilde{N}+20\tilde{N}+8N$.

In Step 2, the complexity of calculating the Kaiser parameter $\alpha$ is almost negligible. Similar to the calculation of $w_c(n)$ in Step 1, the calculation of $w_\alpha (n)$ consumes $12\tilde{N}\log _2 \tilde{N}+20\tilde{N}$ multiplications. As shown by (28), the $(2N-1)$ tap coefficients of $g_c(n)$ consume $1+2\times (N-1)\approx 2N$ multiplications. Thus the total number of multiplications involved in Step 2 is $12\tilde{N}\log _2 \tilde{N}+20\tilde{N}+2N$.

In Step 3, there are no multiplication operations.

Overall, therefore, the total number of multiplications required to design a $(2N-2)$-order FIR filter is $12\tilde{N}\log _2 \tilde{N}+20\tilde{N}+10N$.

Compared with the closed-form algorithm in [6, 7], in which the design of a $(2N-2)$-order FIR filter is derived from the inversion operation of an $(L+1)N\times (L+1)N, L\in Z^+$ matrix, the computational complexity of the proposed closed-form design is greatly reduced.

5 Numerical Results

In this section, we verify the accuracy of the proposed filter design method in terms of controlling the 0-dB cut-off frequency. Furthermore, the proposed filter design is compared with the Remez design and the closed-form WLS design [24].

5.1 Comparison with the Remez Design

We consider an example in which $N=32$, the expected 0-dB cut-off frequency $\omega _p=4.75\Delta \omega =0.2969 \pi$ ($m=5$, $\lambda =0.25$), and the transition bandwidth $1\Delta \omega =0.0625\pi$. The proposed three-step closed-form procedure summarized in Sect. 4.3 and the Remez method were used to design two 62-order FIR filters with the above performance indexes. In terms of (37), the parameter $\alpha$ was set to 0. Figure 10a, b illustrates the magnitude–frequency curves and attenuation–frequency curves of these two designs.

Fig. 10

Amplitude–frequency curves and attenuation curves

From Fig. 10a, b, the following conclusions can be drawn:

• 1) The 0-dB cut-off frequency of the proposed design is located exactly at the expected $\omega _p=4.75\Delta \omega$, whereas the 0-dB cut-off frequency of the Remez design exhibits a slight deviation from $\omega _p$. Nevertheless, it should be emphasized that the Remez design is not intended to have a pass band edge that pass through the 0-dB point. If linear programming were used to enforce such a condition, it would certainly pass through the exact point.

• 2) In a narrow region near the transition band, the ripples of the Remez design (about 1.1 %) are smaller than that of the proposed design (about 4.2 %). This uprush can be viewed as the Gibbs effect, an intrinsic drawback of the existing spectrum interpolation-based designs (e.g., the conventional frequency sampling method and the proposed design). Although the proposed design’s Gibbs effect is smaller than that of the conventional frequency sampling method (as shown by Fig. 3), it is inferior to that of the Remez design. The Gibbs effect may be alleviated by modifying the transition points of the frequency vector $\varvec{H}$. Optimizing the transition points remains an open problem.

• 3) The transition bands of both designs almost overlap, exactly covering the expected width $\Delta \omega$.

In general, the transfer performance of the proposed design approximates that of the Remez design. However, the computational complexity of the proposed design is much lower than that of the Remez design, as the proposed method operates in closed form. In contrast, to achieve an equiripple approximation, the Remez design must execute a large number of iterations to update the alternation frequencies. Hence, the high efficiency of the proposed method makes it suitable for the design of high-order FIR filters.

5.2 Comparison with the Closed-Form WLS Design

The proposed design was also compared with the closed-form WLS design [24]. Given the filter length L (assumed to be odd), 0-dB pass-band cut-off frequency $\omega _p$, stop-band cut-off frequency $\omega _s$ and an error weighting factor $\alpha$, a three-step closed-form procedure for WLS filter design can be derived as follows.

• Step 1 Construct an $N\times N$ matrix $\varvec{P}$ whose entries $P(n,m), 0\le n,m \le N-1$, are calculated as ($N=(L-1)/2$):

  $$\begin{aligned} P(n,m)= & {} \dfrac{{(1 - \alpha )}}{\pi }\Big [{\omega _p} - \dfrac{{\sin m{\omega _p}}}{m} - \dfrac{{\sin n{\omega _p}}}{n} + \dfrac{{\sin (m + n){\omega _p}}}{{2(m + n)}} \nonumber \\&+\,\dfrac{{\sin (n - m){\omega _p}}}{{2(n - m)}}\Big ] - \dfrac{\alpha }{\pi }\Big [\dfrac{{\sin (n - m){\omega _s}}}{{2(n - m)}} + \dfrac{{\sin (n + m){\omega _s}}}{{2(n + m)}}\Big ],\nonumber \\&\quad \,n \ne m,\;m \ne 0,\;n \ne 0 \end{aligned}$$

  (40a)
  $$\begin{aligned} P(n,m)= & {} \frac{{ - \alpha }}{{\pi m}}\sin (m{\omega _s}),{\quad }n = 0,\;m \ne 0 \end{aligned}$$

  (40b)
  $$\begin{aligned} P(n,m)= & {} \frac{{ - \alpha }}{{\pi n}}\sin (n{\omega _s}),{\quad }n \ne 0,\;m = 0 \end{aligned}$$

  (40c)
  $$\begin{aligned} P(n,m)= & {} \frac{\alpha }{\pi }(\pi - {\omega _s}),{\quad }n = 0,\;m = 0 \end{aligned}$$

  (40d)
  $$\begin{aligned} P(n,m)= & {} \frac{{1 - \alpha }}{{\pi }}\left[ {\frac{{3{\omega _p}}}{2} - \frac{{8\sin (n{\omega _p}){{- }}\sin (2n{\omega _p})}}{{4n}}} \right] \nonumber \\&+\,\frac{\alpha }{\pi }\left[ {\frac{{\pi - {\omega _s}}}{2} - \frac{{\sin (2n{\omega _s})}}{{4n}}} \right] ,n = m,\;n \ne 0 \end{aligned}$$

  (40e)

• Step 2 Implement eigenvalue decomposition on $\varvec{P}$ and determine the eigenvector $\varvec{b}=[b(0), b(1),\ldots , b(N-1)]^T$ corresponding to the smallest eigenvalue.

• Step 3 Calculate the L filter coefficients $h(-N+1)\sim h(N-1)$ as

  $$\begin{aligned} h(n) = \left\{ \begin{array}{l} b(0),\quad \quad \quad n = 0\\ b(n)/2,\quad \quad n = 1,\ldots ,N - 1\\ b( - n)/2,\quad n = - N + 1,\ldots , - 1 \end{array} \right. \end{aligned}$$

  (41)

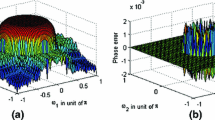
Consider the case of $N=32$ (i.e., the filter length $L=2N-1=63$). We aim to design two 62-order FIR filters with 0-dB cut-off frequencies of $\omega _{p_1}=4.1\Delta \omega$ (i.e., $m=5$, $\lambda =-0.4$) and $\omega _{p_2}=4.6\Delta \omega$ (i.e., $m=5$, $\lambda =0.1$) and the stop-band cut-off frequencies of $\omega _{s_1}=5.1\Delta \omega$ and $\omega _{s_2}=5.6\Delta \omega$. The magnitude curves and the logarithmic magnitude curves of the proposed design and the closed-form WLS design (the error weighting factor $\alpha =0.5$ ) are presented in Fig. 11.

From Fig. 11, the following conclusions can be drawn:

• 1) For the closed-form WLS design, Fig. 11a, b, indicates that the 0-dB cut-off frequencies deviate slightly from the expected points $\omega _{p1}=4.1\Delta \omega$ and $\omega _{p2}=4.6\Delta \omega$. In contrast, the proposed design can accurately locate these two frequencies at their expected positions.

• 2) From the logarithmic magnitude curves illustrated in Fig. 11c, d, one can easily observe that the transition bandwidths of the proposed design are narrower than those of the WLS design.

• 3) As the enlarged pictures in Fig. 11a, b indicate, the pass-band ripples of the proposed design and the closed-form WLS design exhibit no evident differences.

• 4) In the band-edge regions of both cases, the uprushes of the closed-form WLS design (about 1.2 %) are smaller than those of the proposed design (about 4.1 %).

In addition, Table 1 lists the runtimes of these two closed-form filter designs for different filter orders (equipped with Intel(R) Core(TM) i5-4300U CPU @ 1.9 GHz 2.50 GHz, 4 GB RAM, in the software platform of MATLAB 2013).

Fig. 11

Amplitude–frequency curves and attenuation curves of the proposed and closed-form WLS design ($N=32$)

From Table 1, as the filter order increases from 62 to 510, we can see that the runtime of the closed-form WLS design increases from 0.091450 to 1.228074 s, whereas the runtime of the proposed closed-form design remains at 0.1 s. This is because, as analyzed in Sect. 4.4, the major computation of the proposed design is the convolution operation. This can be realized by FFTs, which greatly reduces the number multiplication operations. In contrast, as the filter order increases, the $N\times N$ matrix $\varvec{P}$ becomes larger, requiring more memory and thus entailing additional computational complexity. Therefore, in the case of large filter orders, our method overwhelmingly outperforms the closed-form WLS method in terms of the design efficiency.

Table 1 Execution time of the proposed design and the closed-form WLS design

6 Conclusions

This paper has presented a three-step closed-form FIR filter design that not only accurately locates the 0-dB cut-off frequency at the expected position, but also possesses high efficiency and reliability. This enhanced performance makes the proposed method, especially suitable for the design of high-order FIR filters. In recent years, variable and tunable digital filters (which require the fast configuration of filter parameters) have been widely applied in fields such as soft-defined radio, cognitive radio and channel equalization in wireless communication systems. This tendency is expected to make our proposed configurable closed-form FIR filter broadly applicable. Future work will focus on applying our filter design in these fields.