1 Introduction

The multibody system is one of the most important subsystems in mechanical engineering, which has an irreplaceable contribution to modern industrial civilization, especially in the production of machines, automobiles, robots, aerospace industry, and so on. The dynamic computation of traditional rigid multibody systems has been well investigated. In recent decades, to consider the large deformation of components in multibody systems, there have been more and more studies focusing on the flexible and rigid–flexible multibody systems.

The large rotation and deformation usually happen in flexible components of multibody systems, but traditional finite element methods are based on the assumption of small deformation and rotation, so these methods may produce improper dynamic results [20]. Shabana [18] proposed the Absolute Nodal Coordinate Formulation (ANCF) to model the elements of flexible components, which leads to the constant mass matrix and no centrifugal and Coriolis forces in the system equations [19, 21]. The ANCF has been considered as a benchmark approach in the research of flexible multibody dynamics in recent decades. García-Vallejo et al. [8] combined ANCF with the Natural Coordinate Formulation (NCF) to build the dynamic model of the rigid–flexible multibody systems, and then the ANCF–NCF method was used by Tian [26] to compute the dynamic response of a large scale rigid–flexible multibody system. Shabana [22] used the ANCF reference nodes (ANCF-RNs) and ANCF elements to describe the rigid and flexible bodies, respectively, so the complicated rigid–flexible multibody systems could be modeled by using the integral framework of the ANCF-based method. More applications about the ANCF-based method on the flexible and rigid–flexible multibody systems can be found in [8, 9, 25, 27, 41].

The aforementioned methods only consider the deterministic conditions. However, there are many uncertain factors in practical applications of multibody systems, and they have an influence on the dynamic performance. For instance, the geometric size of a component in the mechanism has a tolerance to facilitate manufacturing process; the inhomogeneous distribution of the material may lead to the variation of material properties, e.g., Young’s modulus and Poisson’s ratio. To improve the accuracy of the dynamic analysis of rigid–flexible multibody systems, the influence of these unavoidable uncertain factors has to be investigated. The uncertain parameters can be classified into probabilistic and non-probabilistic uncertainty. The probabilistic uncertainty is described by random variables or random fields, while the non-probabilistic uncertain analysis methods include the interval method, convex model method, and so on [2, 14, 42].

The Young’s modulus and Poisson’s ratio of the flexible components in rigid–flexible multibody systems may change continuously depending on the space location, so they are characterized by the random field. The random field theory has been used in structural analysis [3, 4, 11], but there are few applications in the multibody systems. Since the random field is defined as a continuous uncountable indexed set of random variables, it should be discretized by a set of countably many random variables. The series expansion methods are widely used to discretize random fields, including the Karhunen–Loeve (K–L) expansion [11], orthogonal series expansion (OSE) [40], and expansion optimal linear estimation (EOLE) method [15]. The EOLE method has a good balance between the accuracy and application range [23], so it has been used in the discretization of material properties of flexible components in multibody systems [33, 36].

After the random field is discretized to countably many random variables, two types of probabilistic methods can be used to solve the propagation of probabilistic uncertainty, i.e., the statistical and non-statistical methods. The statistical methods [12] collect a lot of samples of system output according to their probability distribution of random variables and then estimate the mean, variance, and even the probability density function of the output directly. The Monte Carlo method [6] is the most important statistical method, but its accuracy depends on the sampling size, in accordance with the weak law of large numbers. Therefore, it is extremely expensive for the dynamic computation of rigid–flexible multibody systems. To save the sampling cost, the Latin Hypercube sampling (LHS) can be used to improve the convergence ratio of a statistical method [36]. To improve the efficiency even further, the non-statistical methods can be used, e.g., the perturbation method, Neumann expansion method, and Polynomial Chaos (PC) expansion method [38]. The PC expansion method approximates the response of a system by a truncated orthogonal series and then uses the characteristics of orthogonal polynomials to estimate the first and second moment of the random response. The PC expansion methods have been used in various engineering problems, such as in fluid mechanics [39], vehicle dynamics [16], and structure analysis [17]. Wu et al. [36] compared the PC expansion method and the LHS method in solving rigid–flexible multibody systems with random parameters, which demonstrated that the PC expansion method had a higher accuracy for the smooth problems while the LHS method showed a better performance in non-smooth problems.

The probability information for some uncertain parameters is hard to be acquired, so they can be expressed by interval variables, which only need the bounds’ information to describe the uncertain parameters. The interval methods have been used in the structural analysis, in which the nonlinearity of system response with respect to uncertain variables is not high. For the multibody systems, the dynamic response of systems has an obviously nonlinear characteristic, so they tend to be more difficult to solve than structural problems. The geometric size of components or external loads in multibody systems can be well described by interval variables due to their design tolerance, so the interval method is suitable for the dynamic analysis of multibody systems including geometry and load uncertainty. Wu et al. proposed a Chebyshev interval method to solve the rigid multibody dynamic systems containing interval parameters [30]. One priority of the Chebyshev interval method is that it is a non-intrusive method, which means that it can be used in many complicated engineering models and even in black-box models. As a result, Wang et al. [28] could combine the Chebyshev interval method with the ANCF-based method to solve the rigid–flexible multibody systems containing interval variables.

In practical cases, the rigid–flexible multibody systems contain both the random and interval uncertainty simultaneously, so it is necessary to investigate the hybrid uncertain computational method which can solve both types of uncertainty in one integral framework. Most of the hybrid uncertain analysis methods are proposed to solve the reliability-based design optimization (RBDO) in structural problems, e.g., the random interval moment method [7], random interval perturbation method [37], nested Monte Carlo and scanning method [5], and unified interval stochastic sampling (UISS) method [32]. A more detailed review about the hybrid uncertain analysis methods in RBDO can be found in [13]. These hybrid uncertain analysis methods are computationally expensive, so they are not fit for solving the rigid–flexible multibody systems. Wang et al. [29] combined the perturbation-based method and Chebyshev collocation method to solve the flexible multibody systems with hybrid uncertain parameters. However, the perturbation-based method requires the variation of uncertain parameters to be small, so it may bring the deviation when the uncertain range increases. Wu et al. [31] proposed a non-intrusive PCCI method, which integrated the PC expansion method and Chebyshev interval method in one integral framework to solve the hybrid uncertain problems, and it has been used in the problems of structural optimization [35] and topology optimization [34]. The PCCI method can handle the large uncertain extent problems, as well as nonlinear problems, so it is suitable for solving the rigid–flexible multibody systems.

This paper will propose an improved PCCI method to solve the rigid–flexible multibody systems with hybrid uncertainty, where the geometric size and external loads of rigid components are expressed by interval variables while the Young’s modulus and Poisson’s ratio of flexible components are considered to be a random field. The ANCF-based method is employed to build the dynamic model of rigid–flexible multibody systems. The random field will be discretized to countably many random variables by using EOLE method, and then the improved PCCI method can be used to solve the dynamic problems with random and interval variables. The main difference between the improved PCCI method and PCCI method is that the sampling points of the former can be located on the bounds of interval variables, which produces a higher accuracy in estimating the bounds of a response. The numerical example involving a slider and crank shows the high accuracy and efficiency of the improved PCCI method.

2 Description of hybrid uncertain problems

2.1 Evaluation index for hybrid uncertain problems

If a model \(f\) only contains some random input, its output (response) is expressed as \(f(\boldsymbol{\xi })\), where \(\boldsymbol{\xi } \in \mathbf{R}^{n}\) is an \(n\)-dimensional random input variable. Since the probabilistic information of the random variable \(\boldsymbol{\xi }\) is known, including its mean, variance, probability density function, the probabilistic information of the output can also be obtained. The most widely used evaluation index for the response is the mean and standard deviation (or variance), denoted by \(\mu _{f}\) and \(\sigma _{f}\), respectively. In engineering, to intuitively show the uncertain extent of response, the error bar is also usually employed. The minimum and maximum values of the error bar are expressed as

$$ eb_{l} = \mu _{f} - \sigma _{f},\qquad eb_{u} = \mu _{f} + \sigma _{f} $$
(1)

where \(eb _{l}\) is the minimum value of error bar, and \(e b _{u}\) is the maximum value of error bar.

If model \(f\) only contains interval input, its output is expressed as \(f([\boldsymbol{\eta }])\), where \([\boldsymbol{\eta } ] \in \mathbf{IR}^{m}\) is an \(m\)-dimensional interval variable. The output of the model is also an interval which is expressed by its lower and upper bounds, i.e.,

$$ [ f ] = \Bigl[ \min_{\boldsymbol{\eta }} f ( \boldsymbol{\eta } ),\max _{\boldsymbol{\eta }} f ( \boldsymbol{\eta } ) \Bigr]. $$
(2)

Considering that model \(f \)contains both random and interval variables, its output is expressed as \(f(\boldsymbol{\xi },[\boldsymbol{\eta }])\). In this case, the mean and standard deviation of the response will not be a deterministic value but a function with respect to the interval variables, i.e., \(\mu _{f} ([\boldsymbol{\eta }])\) and \(\sigma _{f} ([\boldsymbol{\eta }])\). As a result, the mean will be transformed to the interval mean, defined as

$$ [ \mu _{f} ] = \Bigl[ \min_{\boldsymbol{\eta }} \mu _{f} ( \boldsymbol{\eta } ),\max_{\boldsymbol{\eta }} \mu _{f} ( \boldsymbol{\eta } ) \Bigr]. $$
(3)

The minimum and maximum values of the error bar are also transformed to the interval numbers, i.e.,

$$ \begin{aligned} {}[ eb_{l} ] &= \Bigl[ \min _{\boldsymbol{\eta }} \bigl( \mu _{f} ( \boldsymbol{\eta } ) - \sigma _{f} ( \boldsymbol{\eta } ) \bigr),\max_{\boldsymbol{\eta }} \bigl( \mu _{f} ( \boldsymbol{\eta } ) - \sigma _{f} ( \boldsymbol{\eta } ) \bigr) \Bigr], \\ {}[ eb_{u} ] &= \Bigl[ \min_{\boldsymbol{\eta }} \mu _{f} \bigl( ( \boldsymbol{\eta } ) + \sigma _{f} ( \boldsymbol{\eta } ) \bigr),\max_{\boldsymbol{\eta }} \bigl( \mu _{f} ( \boldsymbol{\eta } ) + \sigma _{f} ( \boldsymbol{ \eta } ) \bigr) \Bigr] .\end{aligned} $$
(4)

It should be noted that the lower bound of [\(eb _{l}\)] is always smaller than the lower bound of [\(eb _{u}\)], while the upper bound of [\(eb _{u}\)] is always larger than the upper bound of [\(eb _{l}\)]. Therefore, we can introduce an interval error bar to express the hybrid uncertain extent, defined as

$$ {}[ eb ] = \Bigl[ \min_{\boldsymbol{\eta }} \bigl( \mu _{f} ( \boldsymbol{\eta } ) - \sigma _{f} ( \boldsymbol{\eta } ) \bigr),\max _{\boldsymbol{\eta }} \bigl( \mu _{f} ( \boldsymbol{\eta } ) + \sigma _{f} ( \boldsymbol{\eta } ) \bigr) \Bigr]. $$
(5)

2.2 Reference method for solving hybrid uncertain problems

When only the random variables are considered, the Monte Carlo method is usually used as the reference method to solve the probabilistic uncertain problems. Use the random sampling method to produce a large number of sampling points of the random variables, and then compute the output of model \(f\) by fixing the random variables at these sampling points. Unbiased estimates of the mean and variance of the response can be obtained by

$$ \mu _{f} = \frac{1}{N}\sum_{i = 1}^{N} f \bigl( \boldsymbol{\xi }^{(i)} \bigr), \qquad\sigma _{f}^{2} = \frac{1}{N - 1}\sum_{i = 1}^{N} \bigl( f \bigl( \boldsymbol{\xi }^{(i)} \bigr) - \mu _{f} \bigr)^{2}, $$
(6)

where \(N\) is the number of sampling points, and \(\boldsymbol{\xi } ^{(i)}\) are the sampling points of random variables. Based on the law of large numbers, the convergence rate of the Monte Carlo method is proportional to \(1 / \sqrt{N}\), so it requires a large number of sampling points to get an acceptable accuracy. The computational cost for each sampling point is quite high in the dynamic analysis of rigid–flexible multibody systems, so we cannot use too many sampling points to get the reference solution. To improve the efficiency of the Monte Carlo method, an approach is to use a more efficient sampling method to select the sampling points. The LHS method shows quite good performance in statistics, so it will be employed to produce the sampling points. After the sampling points are produced, we can repeat the same procedure of the Monte Carlo method, and then the mean and variance of the response can be obtained, termed as LHS-based statistical method. Wu and coauthors [36] show that the convergence rate of LHS-based statistical method is much higher than that of the Monte Carlo method.

When only interval variables are considered, the bounds of the response shown in Eq. (2) may be computed by using optimization algorithms. However, most of optimization algorithms are easily trapped in the local optimum points. To seek the global minimum and maximum points, the scanning method is considered to be a reference method, in which the interval variables are sampled by using a dense uniform grid. When the grid is dense enough, the global minimum and maximum points can be captured in the neighborhood of the grid. If the number of sampling points for each dimensional interval variable is \(p\), the total number of sampling points for the \(m\)-dimensional interval variables will be \(M = p ^{m}\). Considering Eq. (2), the bounds of response can be computed by the following equation:

$$ [ f ] = \Bigl[ \min_{j}f \bigl( \boldsymbol{\eta }^{ ( j )} \bigr),\max_{j}f \bigl( \boldsymbol{\eta }^{ ( j )} \bigr) \Bigr],\quad j = 1,\ldots,M, $$
(7)

where \(\boldsymbol{\eta }^{(j)}\) denote the sampling points of interval variables.

When both the interval and random variables are contained in the model, we need to use Eqs. (3) and (5) to compute the evaluation indexes, i.e., interval mean and interval error bar. Combining the \(N\) sampling points of the random variables and \(M\) sampling points of interval variables, the set of sampling points will be the tensor product of the two sets of sampling points, i.e., (\(\boldsymbol{\xi }^{(i)}, \boldsymbol{\eta }^{(j)}\)) where \(i=1, \ldots , N\), and \(j=1, \ldots , p ^{m}\), so the total number of sampling points will be \(N \times p ^{m}\). Substituting Eqs. (6) and (7) into Eqs. (3) and (5), the interval mean and interval error bar can be computed by the following equations:

$$\begin{gathered}{} [ \mu _{f} ] = \Biggl[ \min_{j} \frac{1}{N}\sum_{i = 1} ^{N} f \bigl( \boldsymbol{\xi }^{(i)},\boldsymbol{\eta }^{(j)} \bigr), \max_{j}\frac{1}{N}\sum _{i = 1}^{N} f \bigl( \boldsymbol{\xi }^{(i)}, \boldsymbol{\eta }^{(j)} \bigr) \Biggr], \end{gathered}$$
(8)
$$\begin{gathered}{} [ eb ] = \Biggl[ \min_{j}\frac{1}{N}\sum _{i = 1}^{N} f \bigl( \boldsymbol{\xi }^{(i)},\boldsymbol{\eta }^{(j)} \bigr) - \sigma _{f}^{(j)},\max_{j}\frac{1}{N} \sum_{i = 1}^{N} f \bigl( \boldsymbol{\xi }^{(i)},\boldsymbol{\eta }^{(j)} \bigr) + \sigma _{f}^{(j)} \Biggr], \end{gathered}$$
(9)

where

$$ \sigma _{f}^{(j)} = \sqrt{\frac{1}{N - 1}\sum _{i = 1}^{N} \Biggl( f \bigl( \boldsymbol{\xi }^{(i)},\boldsymbol{\eta }^{(j)} \bigr) - \frac{1}{N} \sum_{i = 1}^{N} f \bigl( \boldsymbol{\xi }^{(i)}, \boldsymbol{\eta }^{(j)} \bigr) \Biggr)^{2}},\quad j = 1,\ldots,M. $$
(10)

Since the sampling points are produced by the LHS and scanning methods, the reference method is termed as LHS–Scanning method. It should be noted that the LHS–Scanning method is still expensive in terms of the computational cost, e.g., in the case of \(N=100\), \(q=10\), and \(m=2\), the total number of sampling points will be \(100\times 10^{2} = 10000\), which takes a long time for the dynamic computation of rigid–flexible multibody systems.

3 Improved hybrid uncertain analysis method

3.1 PCCI method for hybrid uncertain analysis

The PCCI method is an orthogonal series expansion method, which integrates the PC expansion method and Chebyshev interval method into one framework to solve the hybrid uncertain problems. When both the Gaussian random variables and interval variables are contained in a continuous function \(f(\boldsymbol{\xi },[\boldsymbol{\eta }])\), where the random and interval variables are defined as \(\boldsymbol{\xi } \sim N(0,1)^{n}\), \([\boldsymbol{\eta }] = [-1,1]^{m}\), this function can be expanded by using the Hermite series of order \(k\) and Chebyshev series of order \(q\) sequentially, termed as PCCI method [31]

$$ f \bigl( \boldsymbol{\xi }, [ \boldsymbol{\eta } ] \bigr) \approx \sum _{j = 1}^{N} \Biggl( \sum _{i = 1}^{M} \beta _{i,j}\Phi _{i} \bigl( [ \boldsymbol{\eta } ] \bigr) \Biggr)\Psi _{j} ( \boldsymbol{\xi } ). $$
(11)

Here \(N = (k+1)^{n}\) and \(M = (q+1)^{m}\) are the numbers of terms of Hermite and Chebyshev series, respectively, \(\Phi _{i}\) denotes the \(i\)th term of Chebyshev series, \(\Psi _{j}\) denotes the \(j\)th term of Hermite series, and \(\boldsymbol{\beta }\) is the coefficient matrix, which can be computed by using the least squares method twice, shown as follows:

$$ \boldsymbol{\beta } = \bigl( \boldsymbol{\Phi } ( \tilde{\boldsymbol{\eta }} )^{\mathrm{T}}\boldsymbol{\Phi } ( \tilde{\boldsymbol{\eta }} ) \bigr)^{ - 1} \boldsymbol{\Phi } ( \tilde{\boldsymbol{\eta }} )^{ \mathrm{T}}\tilde{\mathbf{F}} ( \tilde{\boldsymbol{\xi }}, \tilde{\boldsymbol{ \eta }} )^{\mathrm{T}}\boldsymbol{\Psi } ( \tilde{\boldsymbol{\xi }} ) \bigl( \boldsymbol{\Psi } ( \tilde{\boldsymbol{\xi }} )\boldsymbol{\Psi } ( \tilde{\boldsymbol{\xi }} )^{\mathrm{T}} \bigr)^{ - 1} $$
(12)

where the size of the coefficient matrix \(\boldsymbol{\beta }\) is \(M \times N\), \(\tilde{\boldsymbol{\xi }} \) and \(\tilde{\boldsymbol{\eta }} \) denote the sampling points of random and interval variables. The sampling points of random variables are the tensor product of the roots of univariate Hermite polynomials of order \(k+1\) in the \(n\)-dimensional space, that is,

$$ \tilde{\boldsymbol{\xi }} = \boldsymbol{\xi }_{1} \otimes \cdots \otimes \boldsymbol{\xi }_{n},\quad \boldsymbol{\xi }_{i} = \bigl[ \xi ^{(1)}, \ldots \xi ^{(k + 1)} \bigr]^{\mathrm{T}},\ i = 1,2,\ldots,n, $$
(13)

where \(\xi^{(j)}\), \(j=1,\ldots , k+1\) are the roots of univariate Hermite polynomials of order \(k+1\), and they can be computed by numerical methods in advance. Similarly, the sampling points of interval variables are the tensor product of the zeros of univariate Chebyshev polynomials of order \(q+1\) in the \(m\)-dimensional space, i.e.,

$$ \tilde{\boldsymbol{\eta }} = \boldsymbol{\eta }_{1} \otimes \cdots \otimes \boldsymbol{\eta }_{m}, \quad\boldsymbol{\eta }_{i} = \cos \biggl( \biggl[ \frac{\pi }{2 ( q + 1 )},\frac{3\pi }{2 ( q + 1 )}, \ldots ,\frac{ ( 2q + 1 )\pi }{2 ( q + 1 )} \biggr]^{\mathrm{T}} \biggr), $$
(14)

where \(\boldsymbol{\eta } _{i}\) are the zeros of univariate Chebyshev polynomial of order \(q+1\). Therefore, the total number of sampling points will be \(N \times M\). Also \(\boldsymbol{\Psi } ( \tilde{\boldsymbol{\xi }} )\) and \(\boldsymbol{\Phi } ( \tilde{\boldsymbol{\eta }} )\) are the transform matrices of random and interval variables [31].

After the coefficient matrix \(\boldsymbol{\beta }\) is obtained, considering the orthogonality of Hermite polynomials [38], the mean and variance of \(f(\boldsymbol{\xi },[ \boldsymbol{\eta }])\) can be expressed as

$$ \mu _{f} \approx \sum_{i = 1}^{M} \beta _{i,1}\Phi _{i} ( \boldsymbol{\eta } ),\qquad \sigma _{f}^{2} \approx \sum_{j = 2}^{N} \Biggl( \sum_{i = 1}^{M} \beta _{i,j}\Phi _{i} ( \boldsymbol{\eta } ) \Biggr)^{2}\gamma _{j}. $$
(15)

Substituting Eq. (15) into Eqs. (3) and (5), using the scanning method to compute the interval mean and interval error bar, we obtain

$$\begin{gathered}{} [ \mu _{f} ] \approx \Biggl[ \min_{l}\sum _{i = 1}^{M} \beta _{i,1}\Phi _{i} \bigl( \boldsymbol{\eta }^{(l)} \bigr),\max _{l} \sum_{i = 1}^{M} \beta _{i,1}\Phi _{i} \bigl( \boldsymbol{\eta }^{(l)} \bigr) \Biggr], \end{gathered}$$
(16)
$$\begin{gathered}{} [ eb ] \approx \Biggl[ \min_{l}\sum _{i = 1}^{M} \beta _{i,1}\Phi _{i} \bigl( \boldsymbol{\eta }^{(l)} \bigr) - \sigma _{f} \bigl( \boldsymbol{\eta }^{(l)} \bigr),\max _{l}\sum_{i = 1}^{M} \beta _{i,1}\Phi _{i} \bigl( \boldsymbol{\eta }^{(l)} \bigr) + \sigma _{f} \bigl( \boldsymbol{\eta }^{(l)} \bigr) \Biggr], \end{gathered}$$
(17)

where

$$ \sigma _{f} \bigl( \boldsymbol{\eta }^{(l)} \bigr) = \sqrt{\sum_{j = 2}^{N} \Biggl( \sum _{i = 1}^{M} \beta _{i,j}\Phi _{i} \bigl( \boldsymbol{\eta }^{(l)} \bigr) \Biggr)^{2}\gamma _{j}}. $$
(18)

Here \(\boldsymbol{\eta }^{(l)}\) denotes the sampling points used in the scanning method. It is worth noting that the main computational cost of the PCCI method is to obtain the value matrix \(\tilde{\mathbf{F}}\), because each call of function \(f\) is time-costly. The total number of calls of the original function is determined by the size of matrix \(\tilde{\mathbf{F}}\), expressed by \(N \times M = (k+1)^{n} \times (q+1)^{m}\), which depends on the order of polynomial expansion and the dimension of random and interval variables.

3.2 Improved PCCI method

The Chebyshev interval method actually first constructs a surrogate model of the original function on a given design space, then uses the scanning method to compute the bounds based on the surrogate model. Each dimensional interval variable has been transformed into the standard design space, i.e., \([-1, 1]\). The sampling points of the Chebyshev interval method are the zeros of Chebyshev polynomials, which are located in the interior of the interval variables range rather than on the bounds of the interval variables. From Eq. (14), it can be found that for the Chebyshev polynomial of order \(q+1\), the most outside sampling points are \(\cos (\frac{(2q + 1)\pi }{2q + 2})\) and \(\cos (\frac{\pi }{2q + 2})\). With the order of Chebyshev polynomials increasing, the two sampling points approach the bounds −1 and 1 gradually, but they can never achieve the two bounds. When all the sampling points are located in the inner domain of the design space, the surrogate model becomes an extrapolation model in computing the output at the local design space of bounds. The accuracy of the extrapolation model is usually lower than that of the interpolation model, so the Chebyshev interval method produces lower accuracy in computing the response at the bounds of input. The key of the interval method is to compute the bounds of output, and the bounds of output happen at the bounds of input in many cases, especially for the multibody dynamic systems. Therefore, improving the accuracy of the Chebyshev interval method at the bounds of input is necessary.

To change the extrapolation model to an interpolation model, the most outside sampling points should be mapped to the bounds of the interval variable. Using a linear transformation, all the sampling points are scaled by a factor which relocates the most outside sampling points to the bounds of an interval variable, i.e.,

$$ \begin{aligned}[b] &\tilde{\boldsymbol{\eta }}{} ' = \boldsymbol{\eta}'_{1} \otimes \cdots \otimes \boldsymbol{\eta }'_{m}, \\ &\quad \boldsymbol{\eta }'_{i} = \cos \biggl( \biggl[ \frac{\pi }{2 ( q + 1 )},\frac{3\pi }{2 ( q + 1 )}, \cdots ,\frac{ ( 2q + 1 )\pi }{2 ( q + 1 )} \biggr]^{\mathrm{T}} \biggr) \Big/ \cos \biggl( \frac{\pi }{2 ( q + 1 )} \biggr) \end{aligned} $$
(19)

where \(\tilde{\boldsymbol{\eta } }{}'\) denotes the new sampling points. Except for the sampling points which are scaled, the rest of the computation process is the same as for the Chebyshev interval method, so this method is termed as an improved Chebyshev interval method.

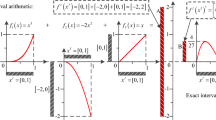
To show the difference between the Chebyshev interval method and improved Chebyshev interval method, we consider a mathematical example. Using the 2nd order Chebyshev interval method and improved Chebyshev interval method to compute the bounds of function \(y=\cos( \pi [ \eta ])\) with \([\eta ]=[-1, 1]\), the plots of the 2nd order Chebyshev series are shown in Fig. 1(a). The error of the Chebyshev series is shown in Fig. 1(b). It can be found that the maximum error of the improved Chebyshev interval method is even larger than that of the Chebyshev interval method, but its error at the bounds of the interval variable is zero.

Fig. 1
figure 1

(a) Plots of Chebyshev series; (b) error of Chebyshev series

Full size image

In this example, the lower bound of output happens at the bounds of interval variable, so using the improved Chebyshev interval method, we can get the exact bounds of output, while the Chebyshev interval method produces large deviation for computing the lower bound of output. Based on the obtained Chebyshev series, the interval results of the output can be computed by the scanning method, resulting in

$$ [ y ] = [ - 1,1 ],\qquad [ \tilde{y} ] = [ - 1.5503,1 ],\qquad \bigl[ \tilde{y}' \bigr] = [ - 1,1 ] $$
(20)

where [\(y\)] is the exact interval, [\(\tilde{y}\)] is the interval obtained by Chebyshev interval method, and [\(\tilde{y}'\)] denotes the interval obtained by the improved Chebyshev interval method. It can be found that the improved Chebyshev method provides the same result as the exact interval, while the Chebyshev method produces a large deviation for the lower bound.

Substituting Eq. (19) into Eq. (12), the coefficient matrix \(\boldsymbol{\beta }\) can be obtained by

$$ \boldsymbol{\beta } = \bigl( \boldsymbol{\Phi } \bigl( \tilde{\boldsymbol{\eta }} ' \bigr)^{\mathrm{T}}\boldsymbol{\Phi } \bigl( \tilde{ \boldsymbol{\eta } }' \bigr) \bigr)^{ - 1} \boldsymbol{ \Phi } \bigl( \tilde{\boldsymbol{\eta } }' \bigr)^{ \mathrm{T}} \tilde{\mathbf{F}} \bigl( \tilde{\boldsymbol{\xi }}, \tilde{\boldsymbol{\eta } }' \bigr)^{\mathrm{T}}\boldsymbol{\Psi } ( \tilde{\boldsymbol{ \xi }} ) \bigl( \boldsymbol{\Psi } ( \tilde{\boldsymbol{\xi }} )\boldsymbol{\Psi } ( \tilde{\boldsymbol{\xi }} )^{\mathrm{T}} \bigr)^{ - 1}. $$
(21)

Substituting the obtained coefficients into Eqs. (16)–(18), the interval mean and interval error bar can be computed. Since the sampling points of the interval variables are from the improved Chebyshev interval method, this method will be termed as improved PCCI method.

To show the difference of the sampling points between the PCCI method and improved PCCI method, the sampling points for the case of \(n=1\), \(m=1\), \(k=3\), \(q=3\) are shown in Fig. 2. It can be found that the sampling points for the random variable are the same for the two methods, but for the interval variable the sampling points of the improved PCCI method have been scaled to the bounds −1 and 1, while that of the PCCI method are located inside of \([-1, 1]\).

Fig. 2
figure 2

Sampling points of PCCI and improved PCCI methods

Full size image

4 ANCF-based method for solving multibody systems

4.1 Dynamic modeling for rigid–flexible multibody systems

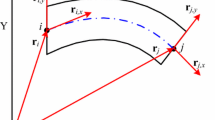
The modeling of ANCF elements can be found in [8, 10, 21], while the two-dimensional ANCF beam elements will be briefly reviewed in this section. The planar shear deformable beam element is shown in Fig. 3, in which the \(X\)–\(Y\) expresses the global coordinate system. In the global coordinate system, the displacement field of the element is defined as

$$ \mathbf{r} = \left [ \textstyle\begin{array} {c@{\quad }c} r_{1} & r_{2} \end{array}\displaystyle \right ]^{\mathrm{T}} = \mathbf{Se}, \quad \mathbf{e} = \left[ \textstyle\begin{array} {c@{\quad }c} \mathbf{e}_{i}^{\mathrm{T}} & \mathbf{e}_{j}^{\mathrm{T}} \end{array}\displaystyle \right]^{\mathrm{T}} = \left[ \textstyle\begin{array} {c@{\quad }c@{\quad }c@{\quad }c@{\quad }c@{\quad }c} \mathbf{r}_{i}^{\mathrm{T}} & \mathbf{r}_{i,x}^{\mathrm{T}} & \mathbf{r}_{i,y}^{\mathrm{T}} & \mathbf{r}_{j}^{\mathrm{T}} & \mathbf{r}_{j,x}^{\mathrm{T}} & \mathbf{r}_{j,y}^{\mathrm{T}} \end{array}\displaystyle \right]^{\mathrm{T}}, $$
(22)

where \(\mathbf{r}\) denotes the nodal coordinates in the global coordinate system, \(\mathbf{S}\) is the shape function of the element, \(\mathbf{e}\) denotes the absolute nodal coordinate vector of node \(i\) and \(j\), \(\mathbf{r} _{q}\) (\(q = i, j\)) marks the position coordinates in the global coordinate system, \(\mathbf{r}\)q,x and \(\mathbf{r}_{q,y}\) are the derivatives of \(\mathbf{r} _{q}\) with respect to local coordinates \(x\) and \(y\).

Fig. 3
figure 3

Two-dimensional ANCF beam element

Full size image

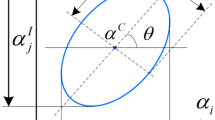
The rigid bodies are expressed by using the ANCF-RNs [22], shown in Fig. 4, where \(X^{i}\)–\(Y^{i}\) is the local coordinate system. The absolute coordinate vector of node \(i\) in ANCF-RNs is defined as

$$ \mathbf{e}_{i} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \mathbf{r}_{i}^{\mathrm{T}} & \mathbf{r}_{i,x}^{\mathrm{T}} & \mathbf{r}_{i,y}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}}, $$
(23)

where \(\mathbf{r} _{i}\) denotes the position coordinates of node \(i\) in the global coordinate system, \(\mathbf{r}\)i,x and \(\mathbf{r}\)i,y are two vectors parallel to the local coordinate axes \(X^{k}\) and \(Y^{k}\), respectively. The following three constraint equations are added to describe a planar rigid body by ANCF-RNs:

$$ \Vert \mathbf{r}_{i,x} \Vert = 1,\qquad \Vert \mathbf{r} _{i,y} \Vert = 1, \qquad\mathbf{r}_{i,x} \cdot \mathbf{r}_{i,y} = 0. $$
(24)
Fig. 4
figure 4

Two-dimensional ANCF-RNs

Full size image

From Fig. 4, it can be found that any point \(j\) on the rigid body can be expressed by

$$ \mathbf{r}_{j} = \mathbf{r}_{i} + \mathbf{e}_{ir} = \mathbf{r}_{i} + \left [ \textstyle\begin{array}{c@{\quad }c} \mathbf{r}_{i,x} & \mathbf{r}_{i,y} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c@{\quad }c} x & y \end{array}\displaystyle \right ]^{\mathrm{T}} = \left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \mathbf{I}_{2} & x\mathbf{I}_{2} & y\mathbf{I}_{2} \end{array}\displaystyle \right ]\left [ \textstyle\begin{array}{c@{\quad }c@{\quad }c} \mathbf{r}_{i}^{\mathrm{T}} & \mathbf{r}_{i,x}^{\mathrm{T}} & \mathbf{r}_{i,y}^{\mathrm{T}} \end{array}\displaystyle \right ]^{\mathrm{T}} = \mathbf{S}_{r}\mathbf{e}_{i}, $$
(25)

where \(\mathbf{e} _{i r}\) is the local position coordinate vector of point \(j\), \(x\) and \(y\) are the local coordinates, \(\mathbf{I} _{2}\) is the \(2 \times 2\) unit matrix, and \(\mathbf{S} _{r}\) denotes the shape function of the rigid body.

4.2 Dynamic equations of rigid–flexible multibody systems

Transforming the nodal coordinates \(\mathbf{e}\) into the generalized coordinates \(\mathbf{q}\), the equations of motion for a constrained rigid–flexible multibody system can be expressed by the following differential algebraic equations (DAEs) [5]:

$$ \left \{ \textstyle\begin{array}{l} \mathbf{M}\ddot{\mathbf{q}} + \boldsymbol{\Phi }_{\mathbf{q}}^{ \mathrm{T}}\boldsymbol{\lambda } + \mathbf{F} ( \mathbf{q} ) = \boldsymbol{Q} ( \mathbf{q} ) , \\ \boldsymbol{\Phi } ( \mathbf{q},t ) = \boldsymbol{0} \end{array}\displaystyle \right . $$
(26)

where \(\mathbf{M}\) is the system mass matrix, \(\boldsymbol{\Phi }( \mathbf{q}, t)\) is the vector that contains the system constraint equations corresponding to the ideal joints, \(t\) represents the time, \(\boldsymbol{\Phi } _{\mathbf{q}}\) is the derivative matrix of constraint equations with respect to the generalized coordinates \(\mathbf{q}\), \(\boldsymbol{\lambda }\) contains the Lagrangian multipliers associated with the constraints, \(\mathbf{Q}(\mathbf{q})\) is the system external generalized forces, and \(\mathbf{F}\)(\(\mathbf{q}\)) is the system elastic force vector which depends on the generalized coordinates and the material Young’s modulus and Poisson’s ratio. A more detailed expression of the mass matrix and elastic force can be found in [36].

Several numerical methods can be used to solve the DAEs shown in Eq. (26), which can be found in the literature [24]. The generalized-\(\boldsymbol{\alpha }\) method [1] will be used in this paper, since it has a good trade-off between the numerical accuracy at low-frequency and numerical damping at high-frequency. In the algorithm, Eq. (26) is first discretized to the following algebraic equations at each time step, and then the Newton iteration is employed to solve the following algebraic equations:

$$ \mathbf{G}\left ( \mathbf{q}_{i + 1},\boldsymbol{\lambda } _{i + 1} \right ) = \left [ \textstyle\begin{array}{c} \mathbf{M}\ddot{\mathbf{q}}_{i + 1} + \boldsymbol{\Phi }_{\mathbf{q}} ^{\mathrm{T}}\boldsymbol{\lambda }_{i + 1} + \mathbf{F} ( \mathbf{q}_{i + 1} ) - \mathbf{Q} ( \mathbf{q}_{i + 1} ) \\ \boldsymbol{\Phi }( \mathbf{q}_{i + 1},t_{i + 1} ) \end{array}\displaystyle \right ] = \boldsymbol{0}. $$
(27)

A more detailed iteration procedure of the generalized-\(\boldsymbol{\alpha }\) algorithm can be found in [1].

5 Hybrid uncertain analysis for rigid–flexible multibody systems

5.1 Uncertain factors in rigid–flexible multibody systems

The geometric size and external load are the main uncertainty sources of the rigid bodies. The tolerance of a component will make the geometric size of a rigid body uncertain, so the geometric size of each component manufactured by the same process is still different. The external load may change with environment conditions or some unknown factors. However, they are subject to change in a range (tolerance), so the interval variables are used to describe the uncertainty of rigid components. Symbol [\(\boldsymbol{\eta }\)] denotes the uncertain geometric size and external load existing in the rigid components, system matrix, as well as system generalized external force, and some constraints depend on these interval variables, so they will be expressed as

$$ \mathbf{M} = \mathbf{M} \bigl( [ \boldsymbol{\eta } ] \bigr),\qquad \mathbf{Q} ( \mathbf{q} ) = \mathbf{Q} \bigl( \mathbf{q}, [ \boldsymbol{\eta } ] \bigr),\qquad \boldsymbol{\Phi } ( \mathbf{q},t ) = \boldsymbol{\Phi } \bigl( \mathbf{q}, [ \boldsymbol{\eta } ],t \bigr). $$
(28)

For the flexible components, besides their geometric size, the material properties are also the main uncertain factors, such as the Young’s modulus and Poisson’s ratio. The material properties of a flexible body may change in the space domain, so they need to be described by a random field. The uncertain geometric size of flexible components can be handled in the same way as for rigid components, so the uncertain material properties will be mainly considered in the flexible components. The Young’s modulus and Poisson’s ratio are expressed by the random fields, expressed by \(G(\mathbf{x}, \theta )\) and \(\kappa (\mathbf{x}, \theta )\), respectively. Based on the definition, the continuous random field is defined as an uncountable indexed set of random variables, which are not convenient to implement in the numerical computation, so the field needs to be discretized to countably many random variables. Using the EOLE method [15] to discretize the random field, the continuous random fields can be approximately expressed by

$$ G(\mathbf{x},\theta ) \approx \mu _{G} + \sigma _{G} \sum_{i = 1} ^{n} \frac{\xi _{i} ( \theta )}{\sqrt{\chi _{i}}} \tilde{\boldsymbol{\rho }}_{\mathbf{xX}}^{\mathrm{T}}\phi _{i}, \qquad \kappa (\mathbf{x},\theta ) \approx \mu _{\kappa } + \sigma _{ \kappa } \sum_{i = 1}^{n} \frac{\xi _{i} ( \theta )}{\sqrt{ \chi _{i}}} \tilde{\boldsymbol{\rho }}_{\mathbf{xX}}^{\mathrm{T}} \phi _{i}, $$
(29)

where \(\mu _{G}\) and \(\mu _{\kappa }\) are the mean of random fields for Young’s modulus and Poisson’s ratio, \(\sigma _{G}\) and \(\sigma _{\kappa }\) denote the standard deviation of random fields for Young’s modulus and Poisson’s ratio, \(\{ \xi _{i}( \theta )\}\) (\(i=1, \ldots , n\)) denotes a set of independent standard Gaussian random variables (i.e., \(\xi _{i}( \theta ) \sim N(0,1)\)), \(\chi _{i}\) are the \(n\) largest eigenvalues of the covariance matrix \(\mathbf{C}_{\mathbf{XX}}\) at the given nodes, with entries \(\mathbf{C}_{\mathbf{XX}} ( k,l ) = C ( \mathbf{x}_{k},\mathbf{x}_{l} )\), \(\phi _{i}\) are the corresponding eigenvectors, and \(\boldsymbol{\rho }_{\mathbf{xX}}\) is the correlation function vector at given nodes \(\mathbf{x} _{1}, \ldots , \mathbf{x} _{p}\) (\(p>n\)), i.e., \(\tilde{\boldsymbol{\rho }} _{\mathbf{xX}} = [ \tilde{\rho } ( \mathbf{x}, \mathbf{x}_{1} ),\ldots,\tilde{\rho } ( \mathbf{x}, \mathbf{x}_{p} ) ]^{\mathrm{T}}\). The typical square exponential correlation function is given as the following equation, and more correlation functions can be found in [23]:

$$ \tilde{\rho } \bigl( \mathbf{x},\mathbf{x}' \bigr) = \exp \bigl( - \bigl\Vert \mathbf{x} - \mathbf{x}' \bigr\Vert ^{2} / a^{2} \bigr), $$
(30)

where \(a\) is the correlation length, which has a large influence on the discretization of the random field.

The variance of the error for Eq. (29) is given as

$$ \mathrm{Var} = \sigma ^{2} - \sum_{i = 1}^{n} \frac{1}{\chi _{i}} \bigl( \tilde{\boldsymbol{\rho }}_{\mathbf{xX}}^{\mathrm{T}} \phi _{i} \bigr) ^{2}. $$
(31)

The value of \(n\) can be determined by make the relative variance error lower than a small constant, e.g., 5% used in this study. Using Eq. (29), the random fields of Young’s modulus and Poisson’s ratio can be approximated by a series governed by the independent standard Gaussian random variables \(\boldsymbol{\xi }=\{ \xi _{i}\}\), \(i=1, \ldots , n\).

The elastic force depends on the Young’s modulus and Poisson’s ratio, so the elastic force will be expressed by a function of the random variables \(\boldsymbol{\xi }\), i.e.,

$$ \mathbf{F} ( \mathbf{q} ) = \mathbf{F} ( \mathbf{q},\boldsymbol{\xi } ). $$
(32)

5.2 Numerical implementation process

Substituting Eqs. (28) and Eq. (32) into Eq. (26), the dynamic equations of the rigid–flexible multibody systems with interval and random parameters will be finally expressed by

$$ \left \{ \textstyle\begin{array}{l} \mathbf{M}\bigl( [ \boldsymbol{\eta } ] \bigr) \ddot{\mathbf{q}} + \boldsymbol{\Phi }_{\mathbf{q}}^{ \mathrm{T}}\boldsymbol{\lambda } + \mathbf{F} ( \mathbf{q},\boldsymbol{\xi } ) = \mathbf{Q}\bigl( \mathbf{q}, [ \boldsymbol{\eta } ] \bigr) , \\ \boldsymbol{\Phi } \bigl( \mathbf{q}, [ \boldsymbol{\eta } ],t \bigr) = \boldsymbol{0} . \end{array}\displaystyle \right . $$
(33)

Similar to Eq. (27), Eq. (33) can be discretized to algebraic equations at each time step as follows:

$$ \mathbf{G} \bigl( \mathbf{q}_{i + 1},\boldsymbol{\lambda } _{i + 1},\boldsymbol{\xi }, [ \boldsymbol{\eta } ] \bigr) = \left[ \textstyle\begin{array} {c} \mathbf{M} \bigl( [ \boldsymbol{\eta } ] \bigr) \ddot{\mathbf{q}}_{i + 1} + \boldsymbol{\Phi }_{\mathbf{q}} ^{\mathrm{T}}\boldsymbol{\lambda }_{i + 1} + \mathbf{F} ( \mathbf{q}_{i + 1},\boldsymbol{\xi } ) - \mathbf{Q} \bigl( \mathbf{q}_{i + 1}, [ \boldsymbol{\eta } ] \bigr) \\ \boldsymbol{\Phi } \bigl( \mathbf{q}_{i + 1}, [ \boldsymbol{\eta } ],t_{i + 1} \bigr) \end{array}\displaystyle \right] = \boldsymbol{0}. $$
(34)

The aim for solving the above equation is to compute \(\mathbf{q}_{i+1}\) and \(\boldsymbol{\lambda }_{i+1}\) solution, we have the following expression:

$$ \mathbf{f} = \left \{ \left . \left [ \textstyle\begin{array}{c} \mathbf{q}_{i + 1} \\ \boldsymbol{\lambda }_{i + 1} \end{array}\displaystyle \right ] \right |\mathbf{G}\bigl( \mathbf{q}_{i + 1}, \boldsymbol{\lambda }_{i + 1},\boldsymbol{\xi },[ \boldsymbol{\eta } ] \bigr) = \boldsymbol{0} \right \}. $$
(35)

As a result, the solution can be thought as a function with respect the random variables \(\boldsymbol{\xi }\) and interval variables [\(\boldsymbol{\eta }\)], denoted by \(\mathbf{f}(\boldsymbol{\xi }, [ \boldsymbol{\eta }])\). It should be noted that the analytical expression of this function is not known, so the function value can only be obtained by using numerical methods, i.e., solving Eq. (34) by fixing the random variables and interval variables at given values, which is actually the sampling process for solving the uncertain problems. Therefore, by combining the improved PCCI method proposed in Sect. 3, the rigid–flexible multibody systems with hybrid uncertain problems can be solved.

The flowchart to implement the numerical process is given in Fig. 5. The proposed numerical method effectively integrates the multibody dynamic modeling method (ANCF-based method), random field discretization method (EOLE method), and hybrid uncertain analysis method (improved PCCI method) to solve the rigid–flexible multibody systems with hybrid uncertainty. The numerical implementation process mainly contains 5 steps, which are: (1) identifying the uncertain parameters, including the interval parameters for rigid components and random field for flexible components, as well as the discretization of random field; (2) producing the sampling points of random variables and interval variables by using improved PCCI method; (3) building the dynamic equations of rigid–flexible multibody systems using ANCF-based method; (4) solving the dynamic equations at given sampling points to obtain the sampling information of output; (5) computing the coefficients matrix by using improved PCCI method and then computing the final results of interval mean and interval error bar.

Fig. 5
figure 5

Flowchart of the numerical implementation process

Full size image

5.3 Numerical example for a slider–crank mechanism

A planar slider–crank mechanism is shown in Fig. 6, where only the link is considered to be a flexible body, and it is made of aluminum. The rotation velocity of the crank is \(\omega =4 \pi \) rad/s, and the deformation of the spring is zero when the rotational angle of the crank is zero.

Fig. 6
figure 6

Schematic of planar rigid–flexible slider–crank mechanism

Full size image

The parameter values under deterministic conditions are shown in Table 1. Two interval parameters are considered in the mechanism, which are the length of the crank and the spring stiffness of external load. Assuming the uncertainty extent is 3%, the interval parameters will be \(L = 0.2+0.006[ \eta _{1}]\) m, \(K = 1000+30[ \eta _{2}]\) N/m, where \([ \eta _{1}] = [-1, 1]\) and \([ \eta _{2}] = [-1, 1]\). Both the Young’s modulus and Poisson’s ratio of the link are considered to be random fields, the standard deviation is 1% of its mean, so the mean and standard deviation are set as \(\mu _{G} = 69\) GPa, \(\mu _{\kappa } = 0.34\), \(\sigma _{G} = 0.69\) GPa, and \(\sigma _{\kappa } = 0.0034\). The length of correlation length for the random field is \(a = 2\) m.

Table 1 The parameters of the slider–crank mechanism
Full size table

We use the EOLE method to discretize the random fields, truncated by 1 term, which means the random field is discretized to one Gaussian random variable. The error of variance after the discretization is shown in Fig. 7, which indicates that the maximum error is about 0.025 satisfying the requirement of this study. Therefore, either the Young’s modulus or Poisson’s ratio can be expressed by one Gaussian random variable \(\xi \sim N(0, 1)\). As a result, there are two random variables and two interval variables in this system, i.e., \([\boldsymbol{\eta }] = [-1, 1]^{2}\), \(\boldsymbol{\xi } \sim N(0, 1)^{2}\).

Fig. 7
figure 7

The discretization error of random field

Full size image

To compute the dynamic response of the slider is 1% crank mechanism, the link is discretized by three ANCF elements, so each element length is 0.15 m. The ANCF-based method shown in Sect. 4.1 is used to build the dynamic equations, which are solved by the generalized-\(\boldsymbol{\alpha }\) method shown in Sect. 4.2. Setting the initial position as \(\theta = 0\), under deterministic conditions, the reaction forces at joint A are given in Fig. 8, in which \(F_{{X}}\) and \(F _{{Y}}\) denote the reaction force in the \(X\) and \(Y\) direction, respectively.

Fig. 8
figure 8

(a) Reaction force in the \(X\) direction; (b) reaction force in the \(Y\) direction

Full size image

Using the PCCI method and improved PCCI method to solve the system, the orders of PC expansion and Chebyshev series are set as \(k = 1\) and \(q = 1\), so the number of sampling points is (\(k+1\))2(\(q+1\))\(^{2} = 16\). To obtain the reference results, the LHS is 1% Scanning method is used, by setting \(N=100\) and \(p=10\), so the number of sampling points is \(Np ^{2} = 10000\).

The interval mean and interval error bar of the reaction forces at joint A under the hybrid uncertainty are shown in Figs. 9 and 10, where the “UB” and “LB” denote the “upper bound” and “lower bound”, respectively. The interval mean and interval error bar reflect the uncertain extent of the reaction forces changing with time. The interval is quite narrow in the initial stage, but it becomes wider and wider with the increase of time, especially after the time of 0.4 s. The interval error bar is wider than the interval mean since it includes the information of both the mean and standard deviation. Both the PCCI method and improved PCCI method have high accuracy before the time of 0.2 s, while their deviations from the reference results obtained by the LHS–Scanning method become obvious after 0.4 s. The PCCI method gives a wider interval mean and interval error bar compared to the reference results, while the improved PCCI method produces more narrow results related to the reference results, which is affected by the different sampling points of interval variables.

Fig. 9
figure 9

(a) Interval mean of \(F_{{X}}\) (\(k=1\), \(q=1\)); (b) interval error bar of \(F_{{X}}\) (\(k=1\), \(q=1\))

Full size image
Fig. 10
figure 10

(a) Interval mean of \(F_{{Y}}\) (\(k=1\), \(q=1\)); (b) interval error bar of \(F_{{Y}}\) (\(k=1\), \(q=1\))

Full size image

To compare the accuracy of the PCCI method and improved PCCI method more intuitively, the relative error can be computed by integrating their deviation from the reference results in the whole time domain. Increasing the order of PC expansion and Chebyshev series, the accuracy of PCCI method and improved PCCI method becomes higher. The relative error of the PCCI method and improved PCCI method changing with the number of sampling points is provided in Figs. 11 and 12.

Fig. 11
figure 11

(a) Error of interval mean for \(F_{{X}}\); (b) error of interval error bar for \(F_{{X}}\)

Full size image
Fig. 12
figure 12

(a) Error of interval mean for \(F_{{Y}}\); (b) error of interval error bar for \(F_{{Y}}\)

Full size image

The sample sizes in the figures are 16, 36, 81, and 256, which correspond to the order of PC expansion and Chebyshev series with \((k, q) = (1, 1)\), \((1, 2)\), \((2, 2)\), and \((3, 3)\), respectively. It can be found that the error convergence rate of the improved PCCI method is much higher than that of the PCCI method. For all the evaluation indexes, the relative error of the improved PCCI method using 81 sampling points is lower by 5%, which is even lower than the relative error of the PCCI method using 256 sampling points, so the improved PCCI method has both higher accuracy and efficiency compared to PCCI method.

The interval mean and interval error bar when \(k = 3\) and \(q = 3\) are shown in Figs. 13 and 14, which indicate that the results of improved PCCI method are highly in line with those of the LHS–Scanning method during the whole simulation period, while the PCCI method shows some deviation during the final 0.2 s simulation period.

Fig. 13
figure 13

(a) Interval mean of \(F_{{X}}\) (\(k=3\), \(q=3\)); (b) interval error bar of \(F_{{X}}\) (\(k=3\), \(q=3\))

Full size image
Fig. 14
figure 14

(a) Interval mean of \(F_{{Y}}\) (\(k=3\), \(q=3\)); (b) interval error bar of \(F_{{Y}}\) (\(k=3\), \(q=3\))

Full size image

It is worth noting that the improved PCCI method only needs 256 sampling points to get similar accuracy of the LHS–Scanning method that uses 10000 sampling points. Each sampling point requires solving the dynamic equation of the rigid–flexible multibody system, which takes about 40 s. As a result, the total computational time for the LHS–Scanning method is about 111 hours, while the improved PCCI method only takes about 2.8 hours, which is much shorter than for the LHS–Scanning method.

To show the performance of the proposed method under the low stiffness, we change the mean of Young’s modulus to be 6.9 GPa and keep the standard deviation as 1% of its mean, i.e., \(\sigma _{G} = 0.069\) GPa. Due to the low stiffness of the link, it is discretized by 5 ANCF elements, so each element length is 0.09 m. Using the PCCI method and improved PCCI method to solve the system, the orders of the PC expansion and Chebyshev series are set as \(k = 1\) and \(q = 1\). The displacements of the midpoint of the link in the \(X\) and \(Y\) directions are shown in Figs. 15 and 16, respectively. For the displacement in the \(X\) direction, both the PCCI method and improved PCCI method have high accuracy. After 0.5 s, the difference between the results of proposed methods and the LHS–Scanning method appears. Due to the small standard deviation of Young’s modulus, the standard deviation of response is quite small compared to it mean value. As a result, the interval error bar is quite close to the interval mean. The displacement in the \(Y\) direction has lower accuracy than in the \(X\) direction, especially after 0.45 s. It can be found that the improved PCCI method is closer to reference results than the PCCI method for both displacements in the \(X\) and \(Y\) directions.

Fig. 15
figure 15

Displacement of link midpoint in the \(X\) direction (\(k=1\), \(q=1\))

Full size image
Fig. 16
figure 16

Displacement of link midpoint in the \(Y\) direction (\(k=1\), \(q=1\))

Full size image

The relative error of the PCCI method and improved PCCI method changing with the sample size is provided in Figs. 17 and 18. The sample sizes in the figures are 16, 81, and 256, which correspond to the orders of the PC expansion and Chebyshev series with \((k, q) = (1, 1)\), \((2, 2)\), and \((3, 3)\), respectively. It can be found that the trend of the relative error in displacement is the same as for the reaction forces shown in Figs. 11 and 12, but the error of displacement is much smaller than for the reaction forces. The error convergence rate of the improved PCCI method is much higher than that of the PCCI method. For the displacement in the \(X\) direction, the relative error of the improved PCCI method using 81 sampling points is lower by 0.1%, which is close to the relative error of the PCCI method using 256 sampling points. For the displacement in the \(Y\) direction, the relative error of the improved PCCI method using 81 sampling points is lower by 0.2%, which is close to the relative error of the PCCI method using 256 sampling points. Therefore, the improved PCCI method has a higher accuracy than the PCCI method for the displacement of the link midpoint.

Fig. 17
figure 17

Error of interval mean (left) and interval error bar (right) in the \(X\) direction

Full size image
Fig. 18
figure 18

Error of interval mean (left) and interval error bar (right) in the \(Y\) direction

Full size image

The interval mean when \(k = 3\) and \(q = 3\) is shown in Fig. 19, which demonstrates that the results of the PCCI method and improved PCCI method are highly in line with the LHS–Scanning method during the whole simulation period.

Fig. 19
figure 19

Displacement of the link midpoint in the \(X\) direction (left) and \(Y\) direction (right) (\(k=3\), \(q=3\))

Full size image

6 Conclusions

This paper proposes a new dynamic computational method, which systematically integrates the ANCF-based dynamic modeling method, random field discretization method, and hybrid uncertain analysis method to solve the rigid–flexible multibody systems with hybrid uncertain factors. Two evaluation indexes, which are the interval mean and interval error bar, are proposed to demonstrate the hybrid uncertain extent of system response. The rigid–flexible multibody systems are modeled by using ANCF-based method. The geometric size and external load of rigid components are considered to be interval variables, while the material properties (Young’s modulus and Poisson’s ratio) of flexible components are considered to be random fields. The random fields are discretized to independent Gaussian random variables by using the EOLE method. An improved PCCI method is proposed to handle both random and interval variables simultaneously. It effectively combines the PC expansion method solving the probabilistic uncertain problems and improved Chebyshev interval method. Compared to the original PCCI method, the sampling points of interval variables for improved PCCI method are scaled to the bounds of interval variables, which improves the accuracy of estimating the interval bounds of output. A numerical example of rigid–flexible slider–crank mechanism demonstrates that the improved PCCI method has much higher accuracy and efficiency compared to the PCCI method and only takes 1/40 computational time of the reference method (LHS–Scanning method) to achieve similar accuracy.