1 Introduction

The multibody dynamics model is widely applied to mechanical systems, such as aircraft, vehicles, and robotics. Such dynamics models are usually formulated through the so-called differential algebraic equations (DAEs). The modeling methods and specialized numerical techniques for multibody dynamic systems have attracted much attention over the past, and are well established now. The past research usually assumes that the structure and variables involved in the multibody system are deterministic. However, in practical systems, a variety of uncertainties associated with material properties, environmental factors, exterior loads, and dimensional tolerances are ubiquitous. These uncertainties will inevitably lead to the uncertainty of the final system performance and might cause significant fluctuations of the dynamic responses.

The most mature tool to analyze the multibody systems with uncertainties is the probabilistic model, where the stochastic variables or processes are described by the precise probability distribution functions. Among the various probabilistic methods, the Monte Carlo method may be the most accurate and most versatile; however, it suffers from a considerable computational burden. To overcome this drawback, Proppe and Wetzel [1] introduced an efficient risk assessment procedure using the variance-reducing Monte Carlo technique. Referred to as the stochastic perturbation, Choi et al. [2] adopted the Taylor series to predict the response bounds for the multibody systems with probabilistic properties. Moreover, Batou and Soize [3] obtained the prior probability distributions of the stochastic multibody system dynamics model using the maximum entropy principle under the constraints defined by the available information. In the benchmarking study by Strickland et al. [4], three platforms (two finite element models and one multibody body dynamics model) were run to compare the performance difference in precision and efficiency of three probabilistic methods, i.e., the so-called advanced mean value, response surface method, and standard Monte Carlo. Another efficient tool for stochastic dynamics problems is the polynomial chaos expansion (PCE) [5,6,7], due to its strong power in functional representations of stochastic parameters. Using this theory, Xiu and Karniadakis [5] presented the solving techniques for stochastic differential equations. Sandu et al. [8] evaluated the uncertainty quantification capability of PCE in the time and frequency domains and first presented the stochastic DAEs formulations of multibody dynamics. Ryan et al. [9] proposed a novel multibody dynamics automation process using polynomial chaos theory and variational work for the uncertainty propagation analysis of a multibody dynamic system. Sandu et al. [10, 11] introduced generalized PCE to the modeling and analysis of a complicated multibody dynamic system with random uncertainties. Overall speaking, the generalized PCE has a widespread application in various dynamics analyses, such as robot-arm-type manipulator dynamics [12], vehicle dynamics [13], and flexible multibody system dynamics [14].

The aforementioned probabilistic methods are effective, but must assume that the statistical knowledge of uncertainty parameters is known. Unfortunately, the required experimental data are generally insufficient and expensive to collect, as a result, the objective stochastic information is usually unavailable. In this context, the nonprobabilistic methods represented by the fuzzy model and interval model were incorporated into the uncertain dynamics of multibody systems. For instance, Pivovarov et al. [15] considered the uncertainty of the material properties in a multibody dynamics model, and described them using fuzzy theory. Whereas numerical solutions for stochastic dynamic systems can be traced back more than half a century and have been relatively mature, techniques for interval dynamics problems are a comparatively short history. Interval methods only require the upper and lower bounds instead of other stochastic knowledge to depict uncertainty. Therefore, they are considered to be effective alternatives to the probabilistic methods and have been perfectly applied to various uncertain dynamics.

Among the various interval methods, the scanning method [16] may be the simplest, but is computationally expensive. The interval arithmetic operation [17, 18] was another effective tool earlier applied to dynamics problems. Alefeld and Mayer [17] systematically studied the applications of interval arithmetic in uncertain linear equations, algebraic eigenvalue problems, ODEs, and partial differential equations (PDEs). Despite the simplicity and high efficiency, it suffers from producing a larger range enclosure than the actual value, and such overestimation is referred to as the wrapping effect [19,20,21] and is more serious in nonlinear dynamics. To this end, the Taylor expansion-based interval methods were developed to calculate the range enclosure closer to the true solution. Such interval perturbation methods can deal with the large overestimation caused by the interdependence of multiple interval parameters; therefore, it has drawn much attention in the last two decades. For example, Ref. [22,23,24,25,26,27] introduced the application of the interval perturbation method in structural mechanics problems, structural vibration control problems, acoustic field, and composite-laminated plates. Makino and Berz [28], Revol et al. [29], and Lin and Stadtherr [30] applied the Taylor methods to solve the wrapping effect of the interval ODEs, Wu et al. [31] further employed such method to solve the interval DAEs. However, Taylor-based methods have inherent deficiencies. One drawback is that the computing results have significant errors for the large uncertainty problems. To end this, the subinterval method [32, 33] that divided the large intervals into some subintervals was presented to increase the precision. The second deficiency is that the solving process of the Taylor-based methods requires partial derivative information. However, most real-life multibody dynamics models are large systems with high rigidity, nonlinearity, and discontinuity, which makes commercial software the almost essential tool for numerical simulation. For these complicated dynamics models, the partial derivative information may be unavailable. Moreover, the major intrinsic drawback associated with the Taylor-based methods remains their limited ability in reducing the large overestimation [22, 23, and 31].

Some other interval-based interval analysis methods have been proposed to avoid these deficiencies. Xia et al. [34] presented a dynamic interval propagation method for time response using the vertex solution theorem and thus obtained a more accurate range enclosure than the interval perturbation method. However, it is only suitable for monotonous cases and thus is not capable of complicated multibody dynamic systems. Liu et al. [35] applied the particle swarm optimization algorithm to the prediction of the time response of the vehicle–bridge interaction system with interval uncertainty. Although this method is quite accurate, the huge computational burden limits its wide engineering application. Moreover, Wu et al. [36] presented the Chebyshev polynomial expansion to predict the range enclosure of the multibody system with interval uncertainty. Wang et al. [37, 38] further applied such Chebyshev polynomials-based method to estimate the response bounds of rigid–flexible multibody systems and flexible multibody systems with interval uncertainty. Through the combination of Chebyshev orthogonal polynomial and Taylor series expansion, Wang et al. [39] developed an interval tool to produce the tighter range enclosure. Moreover, Wang et al. [40] proposed an RBF-based uncertainty propagation approach to handle the distributed dynamic force reconstruction issue with multisource uncertainty, whereby the interval bounds of dynamic forces are obtained using Taylor expansion combined with the subinterval technique.

This paper investigates a nonintrusive Legendre polynomial approach to predict the response bounds of multibody dynamic systems under interval uncertainty. The motivation for this effort is twofold. First, the traditional methods using the Taylor inclusion function and interval arithmetic are easy to result in the wrapping effect. Second, most real-life multibody dynamics models are large systems with high rigidity, nonlinearity, and discontinuity, which makes commercial software the almost essential tool for numerical simulation. However, many conventional, intrusive methods are not suitable for such large dynamic systems. To end these, a novel PCE-based approach is presented to effectively reduce the large overestimation. This method employs the Legendre orthogonal basis to approximate the range enclosure of an interval function, where the Legendre coefficients are obtained using Galerkin projection. Based on this, an interval uncertainty propagation method for multibody dynamic systems described by DAEs is further introduced. Through sampling, the nonintrusive algorithm expresses the original multibody dynamics system with interval uncertainty as the deterministic DAEs, followed by calculation using the general numerical integration method. The response bounds at each time step are predicted using the truncated Legendre polynomial expansion. PCE has been widely applied to the multisource uncertainty quantification in robot dynamics and vehicle dynamics, but has not yet been tried in artillery dynamics. Therefore, an artillery multibody dynamics model is specifically investigated.

The remainder of this paper is structured as follows. Section 2 generally describes the multibody dynamics system with interval uncertainty. The Legendre polynomial expansion approach for interval functions is then proposed in Sect. 3, and an example is given to show its great advantages in providing a tighter enclosure than the Taylor inclusion function and the direct evaluation using interval arithmetic. In Section 4, the Legendre polynomial approach for multibody system dynamics with interval uncertainty is introduced. A benchmark test based on three methods is analyzed to demonstrate the superiority of this method in relation to precision and efficiency. In Sect. 5, an artillery multibody dynamics model is modeled in commercial software ADAMS/Solver®, and a suite of measurements is employed to verify its rationality. It is then specifically investigated to prove the superiority of the proposed approach in large, complicated multibody dynamic systems. Finally, we summarize the conclusions in Sect. 6.

2 Multibody dynamics system with interval uncertainty

2.1 General equations of multibody dynamics system

Without losing any generality, the multibody system dynamics can be described by DAEs [31]:

$$ \left\{ \begin{gathered} {\mathbf{M}}\left( {\mathbf{q}} \right){\ddot{\mathbf{q}}} + {{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} \left( {{\mathbf{q}},t} \right){{\varvec{\uplambda}}} - {\mathbf{Q}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}},t} \right) = 0 \hfill \\ {{\varvec{\Phi}}}\left( {{\mathbf{q}},t} \right) = 0 \hfill \\ \end{gathered} \right., $$
(1)

where \({\mathbf{q}} \in R^{n}\), \({\dot{\mathbf{q}}} \in R^{n}\), and \({\ddot{\mathbf{q}}} \in R^{n}\) are, respectively, the generalized coordinates, velocities, and accelerations. The matrix \({\mathbf{M}}\left( {\mathbf{q}} \right) \in R^{n \times n}\) is the generalized mass matrix, \({{\varvec{\uplambda}}} \in R^{m}\) is the Lagrange multipliers, \({\mathbf{Q}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}},t} \right) \in R^{n}\) is the generalized force vector, and \({{\varvec{\Phi}}}\left( {{\mathbf{q}},t} \right) \in R^{m}\) is the set of m holonomic constraints, i.e., position-level kinematic constraints. \({{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} \left( {{\mathbf{q}},t} \right)\) is the Jacobian matrix of the constraint equations, which reflects the partial derivatives of \({{\varvec{\Phi}}}^{{\mathbf{T}}}\) with respect to the generalized coordinate \({\mathbf{q}}\). \(t \subseteq \left[ {t^{0} ,\;t^{e} } \right]\) is the time range.

Equation (1) is an index-3 DAE. Differentiating Eq. (1) twice with respect to time t results in the additional velocity, and acceleration constraints, respectively:

$$ {\dot{\mathbf{\Phi }}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}},t} \right) = {{\varvec{\Phi}}}_{{\mathbf{q}}} \left( {{\mathbf{q}},t} \right){\dot{\mathbf{q}}} + {{\varvec{\Phi}}}_{{\mathbf{t}}} \left( {{\mathbf{q}},t} \right) = 0, $$
(2)
$$ {\ddot{\mathbf{\Phi }}}\left( {{\mathbf{q}},{\dot{\mathbf{q}}},{\ddot{\mathbf{q}}},t} \right) = {{\varvec{\Phi}}}_{{\mathbf{q}}} \left( {{\mathbf{q}},t} \right){\ddot{\mathbf{q}}} + \left( {{{\varvec{\Phi}}}_{{\mathbf{q}}} \left( {{\mathbf{q}},t} \right){\dot{\mathbf{q}}}} \right)_{{\mathbf{q}}} {\dot{\mathbf{q}}} + 2{{\varvec{\Phi}}}_{{{\mathbf{q}}t}} \left( {{\mathbf{q}},t} \right){\dot{\mathbf{q}}} + {{\varvec{\Phi}}}_{tt} \left( {{\mathbf{q}},t} \right) = 0. $$
(3)

By this, Eq. (1) is transformed into an index-1 DAE problem, which assumes the following form:

$$ \left[ {\begin{array}{*{20}c} {\mathbf{M}} & {{{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} } \\ {{{\varvec{\Phi}}}_{{\mathbf{q}}} } & 0 \\ \end{array} } \right]\left[ {\begin{array}{*{20}c} {{\ddot{\mathbf{q}}}} \\ {{\varvec{\uplambda}}} \\ \end{array} } \right] = \left[ {\begin{array}{*{20}c} {\mathbf{Q}} \\ {{\varvec{\upgamma}}} \\ \end{array} } \right], $$
(4)

where \({{\varvec{\upgamma}}} = - \left( {{{\varvec{\Phi}}}_{{\mathbf{q}}} {\dot{\mathbf{q}}}} \right)_{{\mathbf{q}}} {\dot{\mathbf{q}}} - 2{{\varvec{\Phi}}}_{{{\mathbf{q}}t}} {\dot{\mathbf{q}}} - {{\varvec{\Phi}}}_{tt}\). Equation (4) forms an overdetermined system that consists of \(n + m\) variables and n + 3 m differential–algebraic equations.

Different from the well-established, solving technologies of ODEs, DAEs still have difficulties in numerical calculations. When solving the DAEs in Eqs. (1) and (4), most numerical methods will experience many challenges, such as the numerical drift of the constraint equations, the compatibility of initial value and constraints, and the difficulties for solving stiff problems.

2.2 Numerical solving methods for DAEs

At present, many specialized numerical computing algorithms have been proposed on this topic. According to the different treatments of generalized coordinates and Lagrange multipliers, these algorithms can be divided into the state-space method, the augmented method, as well as the direct integration method. The state-space method transforms the DAEs to a set of smaller-dimensional ODEs, which is further solved by usual ODEs solvers. However, the biggest deficiency of this category of algorithms is the computationally intensive conversion process from DAEs to ODEs, which becomes more obvious and severe in implicit integration.

Alternatively, the augmented method reduces the index of DAEs from 3 to 1 through the kinematic constraints in Eqs. (2) and (3), thus benefits from the usual ODEs, numerical solvers. However, the original constraint equations are rapidly violated, since the differentiated constraint equations are unstable and numerical errors during computation continuously disturb the system. To attack the numerical violation of system kinematical constraints, many types of constraint violation stabilization methods (CVSM) have been reported. Furthermore, the direct integration method discretizes the constrained equations in Eq. (1) into the algebraic equations at each integration step, and solves the index-3 DAEs directly by some numerical algorithms, such as Newmark method, BDF method, HHT-I3, and generalized α-method.

Referred to as NSTIFF-SI2 [41], the DAEs solver used herein is a stabilized index-2 algorithm that relies on the second-order BDF formulas. Introducing the intermediate variables \({\mathbf{v}} = {\dot{\mathbf{q}}}\), Eq. (1) is transformed as

$$ \begin{aligned} &{\dot{\mathbf{q}}} = {\mathbf{v}}, \hfill \\ & {\mathbf{M}}\left( {\mathbf{q}} \right){\dot{\mathbf{v}}} + {{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} \left( {{\mathbf{q}},t} \right){{\varvec{\uplambda}}} - {\mathbf{Q}}\left( {{\mathbf{q}},{\mathbf{v}},t} \right) = 0, \hfill \\ & {{\varvec{\Phi}}}\left( {{\mathbf{q}},t} \right) = 0. \hfill \\ \end{aligned} $$
(5)

NSTIFF-SI2 explicitly accounts for the velocity kinematic constraint equations and relies on an extra set of Lagrange multipliers \({{\varvec{\upmu}}}\) to enforce these constraints. At each time point, discretization of Eq. (5) using the second-order BDF formula and scaling of \({{\varvec{\Phi}}}\left( {{\mathbf{q}},t} \right) = 0\) by \(3/2h\) result in the following equations:

$$ \begin{aligned} & {\mathbf{M}}\left( {{\mathbf{q}}_{j + 1} } \right){\dot{\mathbf{v}}}_{j + 1} + {{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} \left( {{\mathbf{q}}_{j + 1} ,t_{j + 1} } \right){{\varvec{\uplambda}}}_{j + 1} - {\mathbf{Q}}\left( {{\mathbf{q}}_{j + 1} ,{\mathbf{v}}_{j + 1} ,t_{j + 1} } \right) = 0, \hfill \\ &{\mathbf{v}}_{j + 1} - {\dot{\mathbf{q}}}_{j + 1} + {{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} \left( {{\mathbf{q}}_{j + 1} ,t_{j + 1} } \right){{\varvec{\upmu}}}_{j + 1} = 0, \hfill \\ &\frac{3}{2h}{{\varvec{\Phi}}}\left( {{\mathbf{q}}_{j + 1} ,t_{j + 1} } \right) = 0, \hfill \\ &\frac{3}{2h}{{\varvec{\Phi}}}_{{\mathbf{q}}} \left( {{\mathbf{q}}_{j + 1} ,t_{j + 1} } \right){\mathbf{v}}_{j + 1} + \frac{3}{2h}{{\varvec{\Phi}}}_{t} \left( {{\mathbf{q}}_{j + 1} ,t_{j + 1} } \right) = 0. \hfill \\ \end{aligned} $$
(6)

where h denotes integral step size, the subscript j denotes the jth integral step, and

$$ \begin{aligned} &{\mathbf{q}}_{j + 1} = \frac{4}{3}{\mathbf{q}}_{j} - \frac{1}{3}{\mathbf{q}}_{j - 1} + \frac{2}{3}h{\dot{\mathbf{q}}}_{j + 1} , \hfill \\ & {\mathbf{v}}_{j + 1} = \frac{4}{3}{\mathbf{v}}_{j} - \frac{1}{3}{\mathbf{v}}_{j - 1} + \frac{2}{3}h{\dot{\mathbf{v}}}_{j + 1} . \hfill \\ \end{aligned} $$
(7)

Equation (6) is a nonlinear system with respect to the variable \({\mathbf{w}}_{j + 1} = \left[ {{\ddot{\mathbf{q}}}_{j + 1} ,\;{{\varvec{\uplambda}}}_{j + 1} ,{\dot{\mathbf{v}}}_{j + 1} ,{{\varvec{\upmu}}}_{j + 1} } \right]^{\rm T}\). Using the Newton-type method to solve Eq. (6) for \({\mathbf{w}}_{j + 1}\), the associated Jacobian assumes the following form:

$$ {\mathbf{J}}_{{\text{NSTIFF - SI2}}} = \left[ {\begin{array}{*{20}c} {\mathbf{M}} & {\frac{2h}{3}\left( {{\mathbf{M\dot{v}}} + {{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} {{\varvec{\uplambda}}} - {\mathbf{Q}}} \right)_{{\mathbf{q}}} } & {{{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} } & 0 \\ {\frac{2h}{3}{\mathbf{I}}} & { - {\mathbf{I}} - \frac{2h}{3}\left( {{{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} {{\varvec{\upmu}}}} \right)_{{\mathbf{q}}} } & 0 & {{{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} } \\ {{{\varvec{\Phi}}}_{{\mathbf{q}}} } & 0 & 0 & 0 \\ {\left( {{{\varvec{\Phi}}}_{{\mathbf{q}}} {\mathbf{v}}} \right)_{{\mathbf{q}}} + {{\varvec{\Phi}}}_{{{\mathbf{q}}t}} } & {{{\varvec{\Phi}}}_{{\mathbf{q}}} } & 0 & 0 \\ \end{array} } \right]. $$
(8)

If \({\mathbf{M}}\left( {\mathbf{q}} \right)\) is symmetric and nonsingular and the constraint \({{\varvec{\Phi}}}\left( {{\mathbf{q}},t} \right)\) is independent, JNSTIFF_SI2 is proven to be nonsingular when h tends to 0. Substitution of \({\mathbf{w}}_{i + 1}\) in Eq. (7) gets the generalized coordinate \({\mathbf{q}}\) and velocity \({\dot{\mathbf{q}}}\). Similarly, the solution of each integration step can be obtained in turn.

2.3 DAEs with interval uncertainty parameters

Equation (1) represents a deterministic DAEs problem and can be calculated using the numerical algorithms in Sect. 2.2 to obtain the variations of generalized coordinates and velocities with time. Assuming that there is a d-dimensional uncertainty vector \({\mathbf{x}}\) in Eq. (1) and is described by the interval model, given by

$$ {\mathbf{x}} \in {\mathbf{x}}^{{\mathbf{I}}} = \left[ {x_{1}^{I} ,x_{2}^{I} ,\;...\;,x_{d}^{I} } \right],\;\;x_{i}^{I} = \left[ {\underline {x}_{i} ,\;\overline{x}_{i} } \right],\;\;i = 1,2,\;...\;,d, $$
(9)

where the superscript I denotes interval, \(\underline {x}_{i}\) and \(\overline{x}_{i}\) denote the lower and the upper bounds of the ith interval parameter, respectively, such that the original DAEs become a set of interval DAEs, which is rewritten as:

$$ \left\{ \begin{gathered} {\mathbf{M}}\left( {{\mathbf{q}},{\mathbf{x}}} \right){\ddot{\mathbf{q}}} + {{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} \left( {{\mathbf{q}},{\mathbf{x}},t} \right){{\varvec{\uplambda}}} - {\mathbf{Q}}\left( {{\mathbf{q}},{\mathbf{x}},{\dot{\mathbf{q}}},t} \right) = 0 \hfill \\ {{\varvec{\Phi}}}\left( {{\mathbf{q}},{\mathbf{x}},t} \right) = 0. \hfill \\ \end{gathered} \right. $$
(10)

Due to the uncertainty propagation of Eq. (9), the solution of Eq. (10) such as the generalized coordinate \({\mathbf{q}}\) will be an interval uncertainty vector. Upon simplification, \({\mathbf{q}}\) is written as a functional equation with respect to \({\mathbf{x}}\), \({\mathbf{q}}\left( {\mathbf{x}} \right)\); thus, the interval bounds of \({\mathbf{q}}\) are given by

$$ {\mathbf{\underline {q} }} = \mathop {\min }\limits_{{{\mathbf{x}} \in {\mathbf{x}}^{{\mathbf{I}}} }} \left\{ {{\mathbf{q}}\left( {\mathbf{x}} \right),\;\;{\mathbf{x}} \in {\mathbf{x}}^{{\mathbf{I}}} } \right\},\;{\overline{\mathbf{q}}} = \mathop {\max }\limits_{{{\mathbf{x}} \in {\mathbf{x}}^{{\mathbf{I}}} }} \left\{ {{\mathbf{q}}\left( {\mathbf{x}} \right),\;\;{\mathbf{x}} \in {\mathbf{x}}^{{\mathbf{I}}} } \right\}. $$
(11)

Generally speaking, Eq. (11) is impossible to be directly obtained through Eq. (10) and it must rely on some uncertainty propagation methods. The scanning method is recognized as the simplest and most versatile method; however, it suffers from a considerable computational burden. Interval arithmetic and low-order Taylor models are also implemented to establish the solving framework for interval DAEs. Despite the simplicity and high efficiency, they suffer from producing a larger range enclosure than the actual value. Such a wrapping effect is more serious in nonlinear dynamics. To end this, the Legendre orthogonal basis will be employed to approximate the range enclosure of an interval function.

3 Legendre polynomial expansion for range enclosure prediction of interval functions

3.1 The wrapping effect of interval arithmetic

If the function f is defined in the real number set \(R^{n}\) to \(R^{m}\), the interval function \(f^{I}\) from the real interval \(IR^{n}\) to \(IR^{m}\) can be defined as the inclusion function of f, which can be expressed as

$$ \forall \;{\mathbf{x}}^{{\mathbf{I}}} \in IR^{n} ,\;\;f\left( {{\mathbf{x}}^{{\mathbf{I}}} } \right) \subset f^{I} \left( {{\mathbf{x}}^{{\mathbf{I}}} } \right). $$
(12)

Note that the interval inclusion function is defined as a range enclosure containing all possible f. This proposition of most continuous functions can be directly evaluated by the so-called interval arithmetic; however, it suffers from producing a larger range enclosure than the actual value. To show it more intuitively, we consider a simple mathematical case defined by

$$ f\left( x \right) = x^{3} - 2x^{2} + x,\;\;x^{I} = [0,\;1]. $$
(13)

As shown in Fig. 1, the direct evaluation using interval arithmetic needs to divide f(x) into three interval functions about x (\(f_{1} \left( x \right) = x^{3}\), \(f_{2} \left( x \right) = - 2x^{2}\), and \(f_{3} \left( x \right) = x\)) to calculate separately and then performs the addition operation of interval number. The two previous interval arithmetic operations are summed as [-2, 2]. However, it can be easily shown that the exact interval of Eq. (16) is [0, 4/27]. This phenomenon of large overestimation is very obvious in this nonmonotonic problem. Another point worth noting is that the range enclosure obtained by interval arithmetic is not unique and highly relies on the specific decomposition form of a function.

Fig. 1
figure 1

Wrapping effect of interval arithmetic

Full size image

3.2 Legendre polynomial inclusion function

PCE theory is relatively mature, and many specialized researches have been developed on this topic. A general polynomial chaos expansion, viewed as an uncertainty function y(x) of uncertainty events ξ, can be formulated as:

$$ y({\mathbf{x}}) = \alpha_{0} \psi_{0} + \sum\limits_{{i_{1} = 1}}^{\infty } {\alpha_{{i_{1} }} \psi_{1} \left( {\xi_{{i_{1} }} } \right)} + \sum\limits_{{i_{1} = 1}}^{\infty } {\sum\limits_{{i_{2} = 1}}^{{i_{1} }} {\alpha_{{i_{1} i_{2} }} \psi_{2} \left( {\xi_{{i_{1} }} ,\;\xi_{{i_{2} }} } \right)} } + \sum\limits_{{i_{1} = 1}}^{\infty } {\sum\limits_{{i_{2} = 1}}^{{i_{1} }} {\sum\limits_{{i_{3} = 1}}^{{i_{2} }} {\alpha_{{i_{1} i_{2} i_{3} }} \psi_{3} \left( {\xi_{{i_{1} }} ,\;\xi_{{i_{2} }} ,\;\xi_{{i_{3} }} } \right)} } } + ...\;, $$
(14)

where \({{\varvec{\upalpha}}} = \left[ {\alpha_{0} ,\;\alpha_{{i_{1} }} ,\;...\;,\;\alpha_{{i_{1} i_{2} ...i_{n} }} } \right]\) is the polynomial coefficient, \(\psi_{n} \left( {\xi_{{i_{1} }} ,\;\xi_{{i_{2} }} ,\;...\;,\;\xi_{{i_{n} }} } \right)\) is an nth-order generalized polynomial chaos basis function for d-dimensional uncertain parameters \({{\varvec{\upxi}}} = \left[ {\xi_{1} ,\;\xi_{2} ,\;...\;,\;\xi_{d} } \right]\).

The Legendre basis satisfies the orthogonality of L2(Ω)-norm inner product in the interval [−1,1], while the other orthogonal bases, such as the Hermite basis for Gaussian variables, the Laguerre basis for gamma distributed stochastic variables, the Jacobi basis for beta distributed stochastic variables, are all orthogonal to the weight function. Therefore, the Legendre polynomial \(\phi_{n} \left( \xi \right)\) is employed herein to estimate the range enclosure of an interval function, which is given by

$$ \phi_{n} \left( \xi \right) = {}_{2}F_{1} \left( { - n,n + 1;\;1;\frac{1 - x}{2}} \right). $$
(15)

The (n + 1)th-order Legendre polynomial satisfies the following relation:

$$ \phi_{n + 1} \left( \xi \right) = \frac{2n + 1}{{n + 1}}\xi \phi_{n} \left( \xi \right) - \frac{n}{n + 1}\phi_{n - 1} \left( \xi \right); $$
(16)

therefore, the first few-order Legendre polynomials can be expressed as:

$$ \begin{aligned} & \phi_{0} \left( \xi \right) = 1, \\&\phi_{1} \left( \xi \right) = \xi , \\& \phi_{2} \left( \xi \right) = \frac{1}{2}\left( {3\xi^{2} - 1} \right),\\&\phi_{3} \left( \xi \right) = \frac{1}{2}\left( {5\xi^{3} - 3\xi } \right),\\&\phi_{4} \left( \xi \right) = \frac{1}{8}\left( {35\xi^{4} - 30\xi^{2} + 3} \right), \\&... \end{aligned}$$
(17)

Legendre polynomials satisfy the orthogonality relation, and the inner product of two Legendre polynomials can be formulated as

$$ \left\langle {\phi_{m} \left( \xi \right),\phi_{n} \left( \xi \right)} \right\rangle = \int_{ - 1}^{1} {\phi_{m} \left( \xi \right)\phi_{n} \left( \xi \right)} W\left( \xi \right)d\xi = \frac{1}{2n + 1}\delta_{mn} , $$
(18)

where \(\delta_{mn}\) is the Kronecker delta function, W(ξ) is the weight function which is equal to 1 for Legendre basis, and \(\left\langle {\;,\;} \right\rangle\) is the inner product operation.

Equation (14) is the summation of the polynomial basis of different orders. For convenience, we renumber it by the lower-order polynomial counted first and thus obtain the simplified form:

$$ y = \sum\limits_{i = 0}^{\infty } {a_{i} \varphi_{i} \left( {{\varvec{\upxi}}} \right)} \;, $$
(19)

where \(a_{i}\) and \(\varphi_{i} \left( {{\varvec{\upxi}}} \right)\) are the polynomial coefficients and bases of the simplified expression, respectively.

To reduce the computational cost, we use the maximum expansion terms S to truncate the summation of infinite terms in Eq. (19) and thus obtain

$$ y \approx \tilde{y} = \sum\limits_{i = 0}^{S} {a_{i} \varphi_{i} \left( {{\varvec{\upxi}}} \right)} \;. $$
(20)

S depends on the dimensions (d) of ξ and the highest order (p) of the polynomials \(\varphi \left( {{\varvec{\upxi}}} \right)\) [5], which can be calculated by

$$ S = \sum\limits_{j = 1}^{p} {\frac{1}{j!}\prod\limits_{r = 0}^{j - 1} {\left( {d + r} \right)} } = \frac{{\left( {d + p} \right)!}}{d!p!}\;. $$
(21)

Moreover, the multidimensional, hypergeometric polynomials \(\varphi_{i} \left( {{\varvec{\upxi}}} \right)\) in Eq. (20) are the tensor product of the corresponding univariate polynomial basis:

$$ \varphi_{i} \left( {{\varvec{\upxi}}} \right) = \prod\limits_{k = 1}^{d} {\phi_{k}^{i} \left( {\xi_{k} } \right)} \;. $$
(22)

where \(\phi_{k}^{i} \left( {\xi_{k} } \right)\) is the univariate Legendre basis of k-th dimension interval parameter \(\xi_{k}\).

Once the polynomial coefficients, \(a_{i}\), are obtained, we can directly define the Legendre polynomial inclusion function through the characteristics of PCE:

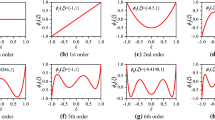
$$ f_{PC}^{I} \left( {{\mathbf{x}}^{{\mathbf{I}}} } \right) = a_{0} + \sum\limits_{i = 1}^{S} {a_{i} \varphi_{i} \left( {{\varvec{\upxi}}} \right)} \;,\;\;{{\varvec{\upxi}}} \in \left[ { - 1,\;1} \right]. $$
(23)

Since \({{\varvec{\upxi}}} \in \left[ { - 1,\;1} \right]\), the accurate range enclosure of the univariate Legendre polynomial basis in Eq. (17) is directly given by

$$ \begin{aligned} & \phi_{0} \left( \xi \right) = 1,\;\; \\& \phi_{1}^{I} \left( \xi \right) = \left[ { - 1,\;1} \right],\;\; \\& \phi_{2}^{I} \left( \xi \right) = \left[ { - 0.5,\;1} \right],\;\; \\& \phi_{3}^{I} \left( \xi \right) = \left[ { - 1,\;1} \right],\;\; \\& \phi_{4}^{I} \left( \xi \right) = \left[ { - 0.4286,\;1} \right],\;\; \\& \phi_{5}^{I} \left( \xi \right) = \left[ { - 1,\;1} \right], \\& \cdots . \end{aligned}$$
(24)

For instance, the univariate Legendre basis and the accurate intervals are given in Fig. 2.

Fig. 2
figure 2

Univariate Legendre basis

Full size image

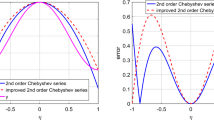
Substituting the exact intervals of univariate Legendre basis into Eq. (23) and followed by interval arithmetic, the range enclosure of an interval function can be obtained. To illustrate the performance of the presented inclusion function in interval evaluation, Eq. (13) is revisited. The third-order Legendre polynomial expansion can be written as:

$$ f_{{PC_{3} }} (x^{I} ) = \frac{1}{12} - \frac{1}{20}\xi - \frac{1}{12}\left( {\frac{3}{2}\xi^{2} - \frac{1}{2}} \right) + \frac{1}{20}\left( {\frac{5}{2}\xi^{3} - \frac{3}{2}\xi } \right),\;\;\xi \in [ - 1,1]. $$
(25)

The third-order Taylor expansion can be expressed as

$$ f_{{T_{3} }} \left( {x^{I} } \right) = f\left( \frac{1}{2} \right) + f^{\prime}\left( \frac{1}{2} \right)\left[ { - \frac{1}{2}\;,\;\frac{1}{2}} \right] + \frac{1}{2!}f^{\prime\prime}\left( \frac{1}{2} \right)\left[ { - \frac{1}{2}\;,\;\frac{1}{2}} \right]^{2} + \frac{1}{3!}f^{\left( 3 \right)} \left( \frac{1}{2} \right)\left[ { - \frac{1}{2}\;,\;\frac{1}{2}} \right]^{3} . $$
(26)

Thus, the predicted range enclosures of Legendre and Taylor include functions are given by

$$ f_{{PC_{3} }}^{I} (x^{I} ) = \left[ { - \frac{1}{10},\;\frac{9}{40}} \right],\;\;f_{{T_{3} }}^{I} \left( {x^{I} } \right) = \left[ { - \frac{1}{4},\;\frac{3}{8}} \right]. $$
(27)

The results show that the proposed method can provide a tighter enclosure than using the Taylor inclusion function and interval arithmetic for evaluation.

3.3 Coefficients calculation using Galerkin projection

An important factor for the success of interval evaluation using the proposed Legendre-based approach is the calculation of the expansion coefficient. The method, called hereafter Galerkin projection, is adopted to calculate the expansion coefficient. By projecting both sides of Eq. (20) onto the orthogonal polynomial \(\varphi_{j} \left( {{\varvec{\upxi}}} \right)\), we obtain for each \(j = 0,1,...,S\),

$$ \left\langle {y\left( {{\varvec{\upxi}}} \right),\;\varphi_{j} \left( {{\varvec{\upxi}}} \right)} \right\rangle = \left\langle {\sum\limits_{i = 0}^{S} {a_{i} \varphi_{i} \left( {{\varvec{\upxi}}} \right)} ,\;\varphi_{j} \left( {{\varvec{\upxi}}} \right)} \right\rangle \;. $$
(28)

Considering the definition of inner product and employing the orthogonality relation,

$$ \left\langle {\varphi_{i} \left( {{\varvec{\upxi}}} \right),\;\varphi_{j} \left( {{\varvec{\upxi}}} \right)} \right\rangle = \left\langle {\varphi_{i}^{2} \left( {{\varvec{\upxi}}} \right)} \right\rangle \delta_{ij} \;, $$
(29)

the expansion coefficient ai is obtained analytically as

$$ a_{i} = \frac{{\left\langle {y\left( \xi \right),\;\varphi_{i} \left( {{\varvec{\upxi}}} \right)} \right\rangle }}{{\left\langle {\varphi_{i} \left( {{\varvec{\upxi}}} \right),\;\varphi_{i} \left( {{\varvec{\upxi}}} \right)} \right\rangle }},\;\;i = 0,1,...,S. $$
(30)

Note that the denominator term can be calculated by the tensor product of the corresponding one-dimensional orthogonal polynomial basis, which is given by

$$ \left\langle {\varphi_{i}^{2} \left( {{\varvec{\upxi}}} \right)} \right\rangle = \prod\limits_{k = 1}^{d} {\left\langle {\left( {\phi_{k}^{i} \left( {\xi_{k} } \right)} \right)^{2} } \right\rangle } \;, $$
(31)

where \(\left\langle {\left( {\phi_{k}^{i} \left( {\xi_{k} } \right)} \right)^{2} } \right\rangle\) is easily obtained through Eq. (18).

Besides, the numerator term of Eq. (30) can be regarded as computing the expectation of \(y\left( \xi \right)\;\varphi_{i} \left( {{\varvec{\upxi}}} \right)\), which can be expressed as follows:

$$ \left\langle {y\left( \xi \right),\;\varphi_{i} \left( {{\varvec{\upxi}}} \right)} \right\rangle = \int_{ - 1}^{1} {y\left( {{\varvec{\upxi}}} \right)\varphi_{i} \left( {{\varvec{\upxi}}} \right)f\left( {{\varvec{\upxi}}} \right)d{{\varvec{\upxi}}}} ,\;\;i = 0,1,...,S, $$
(32)

where \(f\left( {{\varvec{\upxi}}} \right)\) is the joint probability density function. Without affecting the original equation \(y\left( {{\varvec{\upxi}}} \right)\), Eq. (32) can be approximated by some numerical integration methods, such as full-factorial numerical integration (FFNI). Through the Gaussian integral formulas, we can rewrite the above multidimensional integral as a weighted discrete sum

$$ \left\langle {y\left( \xi \right),\;\varphi_{i} \left( {{\varvec{\upxi}}} \right)} \right\rangle = \int_{ - 1}^{1} {{}_{1}..._{d} } \int_{ - 1}^{1} {y\left( {{\varvec{\upxi}}} \right)\varphi_{i} \left( {{\varvec{\upxi}}} \right)f\left( {{\varvec{\upxi}}} \right)d{{\varvec{\upxi}}}} \approx \sum\limits_{{i_{1} = 1}}^{{N_{1} }} {w_{{i_{1} }} ...} \sum\limits_{{i_{j} = 1}}^{{N_{j} }} {w_{{i_{j} }} ...} \sum\limits_{{i_{d} = 1}}^{{N_{d} }} {w_{{i_{d} }} y\left( {l_{{i_{1} }} ,...,l_{{i_{j} }} ,...,l_{{i_{d} }} } \right)} \prod\limits_{k = 1}^{d} {\phi_{k}^{i} \left( {\xi_{k} } \right)} , $$
(33)

where \({{\varvec{\upxi}}} = \left[ {\xi_{1} ,\;\xi_{2} ,\;...\;,\;\xi_{d} } \right]\), \(l_{{i_{j} }}\) and \(w_{{i_{j} }}\) (\(i_{j} = 1,...,N_{j}\)) are the collocation nodes and the corresponding weights of the \(N_{j}\)th integral point of the jth dimension uncertainty variable, respectively. Note that Eq. (33) is the tensor product of the one-dimensional Gaussian integral. As we use the Legendre orthogonality polynomials to evaluate interval functions, the one-dimensional integral nodes and integral weight in Eq. (33) can be generally computed by Gaussian–Legendre quadrature formulas.

Undoubtedly, the choice of the sampling points has a significant impact on the success of the Galerkin projection framework. The Gaussian integral accuracy needs to match the highest order of PCE, p; therefore, the collocation nodes in each parameter dimension, Nj (j = 1,2,…,d), should be no less than (p + 1)/2. To improve the precision and robustness of expansion coefficient calculation, (p + 1) collocation nodes in each parameter dimension are used in the case studies presented here. Moreover, tensor product formulas, e.g., Gauss quadrature, are the most effective but are rather inefficient and cumbersome in medium- and high-dimensional parameter spaces. The sparse grid collocation strategy is recommended for these situations; the interested reader is referred to Ref. [42]. It performs the tensor product only on the one-dimensional integral nodes that satisfy an additional constraint, thereby effectively removes the integral points that have not significantly improved the integration accuracy and avoids the "dimension disaster." The two-dimensional sparse grids of Gaussian–Legendre abscissas are displayed in Fig. 3.

Fig. 3
figure 3

Two-dimensional sparse grids of Gaussian–Legendre abscissas

Full size image

Upon simplification, defining the d-dimensional collocation nodes \(\left\{ {{\mathbf{L}}_{1} ,...,{\mathbf{L}}_{l} ,...,{\mathbf{L}}_{N} } \right\}\) and the corresponding weights \(\left\{ {w_{1} ,...,w_{l} ,...,w_{N} } \right\}\), we can rewrite Eq. (33) as follows

$$ \left\langle {y\left( \xi \right),\;\varphi_{i} \left( {{\varvec{\upxi}}} \right)} \right\rangle \approx \sum\limits_{l = 1}^{N} {\left( {w_{l} y\left( {{\mathbf{L}}_{l} } \right)\prod\limits_{k = 1}^{d} {\phi_{k}^{i} \left( {\xi_{k} } \right)} } \right)} ,\;\;i = 0,1,...,S. $$
(34)

Substitution of Eqs. (31) and (34) in Eq. (30) results in the expansion coefficient ai.

4 Legendre polynomial method for solving interval uncertain multibody dynamics system

4.1 Computational procedure of the Legendre polynomial approach

Wu et al. [31] formulated the Taylor expansion-based approach for solving interval DAEs. Its key technology is the Taylor series expansion of the position kinematic constraint equations \({{\varvec{\Phi}}}\left( {{\mathbf{q}},{\mathbf{x}}} \right)\) to derive the partial derivative constraint equations of \({\mathbf{q}}\) with respect to \({\mathbf{x}}\). This process is complicated and requires a lot of preprocessing. In some large, complex multibody dynamic systems, however, the derivative may be unavailable or cumbersome. Further, such treatment greatly increases the numbers of variables and equations of DAEs and hence may have more difficulties in numerical calculations for large multibody systems.

To avoid the aforementioned deficiencies, a Legendre polynomial-based uncertainty propagation method is proposed to solve the DAEs in Eq. (10). We first select an appropriate number of collocation nodes, \({\mathbf{L}} = \left\{ {{\mathbf{L}}_{1} ,...,{\mathbf{L}}_{j} ,...,{\mathbf{L}}_{N} } \right\}\), in Gaussian–Legendre abscissas, according to the dimensions (d) of interval parameters and the highest order (p) of PCE. For the optimal order of PCE, a second-order approximation is recommended as a first attempt; this approximation can be refined further using higher-order terms, depending on the accuracy needs and available computational resources. Discretizing the time range \(t \subseteq \left[ {t^{0} ,\;t^{e} } \right]\) into a set of integration steps (t0,t1,…,ti,…,te), and substituting all the collocation nodes \({\mathbf{L}} = \left\{ {{\mathbf{L}}_{1} ,...,{\mathbf{L}}_{j} ,...,{\mathbf{L}}_{N} } \right\}\) into the original deterministic DAEs at each integration step \(t^{i}\), we have

$$ \left\{ \begin{gathered} {\mathbf{M}}\left( {{\mathbf{q}},{\mathbf{L}}} \right){\ddot{\mathbf{q}}} + {{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} \left( {{\mathbf{q}},{\mathbf{L}},t} \right){{\varvec{\uplambda}}} = {\mathbf{Q}}\left( {{\mathbf{q}},{\mathbf{L}},{\dot{\mathbf{q}}},t} \right) \hfill \\ {{\varvec{\Phi}}}\left( {{\mathbf{q}},{\mathbf{L}},t} \right) = 0 \hfill \\ \end{gathered} \right., $$
(35)

and obtain the solutions, i.e., \({\mathbf{q}}\left( {t^{i} } \right) = \left[ {{\mathbf{q}}\left( {{\mathbf{L}}_{1} } \right),...,\;{\mathbf{q}}\left( {{\mathbf{L}}_{j} } \right),...,{\mathbf{q}}\left( {{\mathbf{L}}_{N} } \right)} \right]^{\rm T}\) and \({\dot{\mathbf{q}}}\left( {t^{i} } \right) = \left[ {{\dot{\mathbf{q}}}\left( {{\mathbf{L}}_{1} } \right),...,\;{\dot{\mathbf{q}}}\left( {{\mathbf{L}}_{j} } \right),...,{\dot{\mathbf{q}}}\left( {{\mathbf{L}}_{N} } \right)} \right]^{\rm T}\).

At the integration step \(t^{i}\), the uncertain generalized coordinates \({\mathbf{q}}\) and velocities \({\dot{\mathbf{q}}}\) can be estimated using Legendre polynomial expansion, which is given by

$$ {\mathbf{q}}\left( {{\mathbf{L}},\;t^{i} } \right)\;{\text{and}}\;{\dot{\mathbf{q}}}\left( {{\mathbf{L}},\;t^{i} } \right) = a_{0} + \sum\limits_{k = 1}^{S} {a_{k} \varphi_{k} \left( {{\varvec{\xi}}} \right)} \;,\;\;{{\varvec{\xi}}} \in \left[ { - 1,\;1} \right]. $$
(36)

After the expansion coefficients are obtained, the interval bounds of \({\mathbf{q}}^{{\mathbf{I}}}\) and \({\dot{\mathbf{q}}}^{{\mathbf{I}}}\) at the integration step \(t^{i}\) are further evaluated by the defined Legendre polynomial inclusion function. The coefficients computation is completed through sampling and Galerkin projection without intruding the original DAEs. Therefore, it has no special restrictions on numerical methods for solving the DAEs. The computational procedure shown in Fig. 4 mainly includes the following steps:

  • Step I Determine the necessary parameters, including the highest order of Legendre polynomials expansion, the numerical algorithm parameters for solving DAEs (the step size h, termination time te, et al).

  • Step II Compute the required number of collocation nodes N. Sample the d-dimensional collocation nodes \(\left\{ {{\mathbf{L}}_{1} ,...,{\mathbf{L}}_{j} ,...,{\mathbf{L}}_{N} } \right\}\) and the corresponding weights \(\left\{ {w_{1} ,...,w_{j} ,...,w_{N} } \right\}\) in the Gaussian–Legendre abscissas, and initialize the count index i = 0 for counting time iterations.

  • Step III Initialize the count index j=1 for counting the iterations of the collocation nodes.

  • Step IV Substitute the collocation nodes \({\mathbf{L}}_{j}\) into the original deterministic DAEs and then solve it by a numerical technique, and thus obtain the solutions at the integration step \(t^{i}\), \({\mathbf{q}}\left( {t^{i} } \right)\) and \({\dot{\mathbf{q}}}\left( {t^{i} } \right)\).

  • Step V If j > N, continue. Else, set j = j+1, then return Step IV.

  • Step VI Compute the polynomial coefficients using the Galerkin projection method, and thus obtain the Legendre PCE model at the integration step \(t^{i}\).

  • Step VII Evaluate the range enclosure of \({\mathbf{q}}^{{\mathbf{I}}}\) and \({\dot{\mathbf{q}}}^{{\mathbf{I}}}\) at the integration step \(t^{i}\) through the Legendre polynomial inclusion function.

  • Step VIII If i > te/h, output the response bounds of \({\mathbf{q}}^{{\mathbf{I}}}\) and \({\dot{\mathbf{q}}}^{{\mathbf{I}}}\). Otherwise, set i = i + 1, and return Step III.

Fig. 4
figure 4

Computational procedure of the Legendre PCE approach for interval DAEs (fixed step solver)

Full size image

The aforementioned computational procedure is established based on a fixed step size solver. An inherent assumption is that the variation in the parameters used does not affect the time at which discontinuities occur, and this assumption is detrimental in the use of PCE as it may cause stiff DAEs that are unable to be integrated. The adaptive step size solvers are widely used in multibody dynamics. For such cases, we can first substitute collocation nodes into the original deterministic DAEs, then solve them by a numerical technique, and thus obtain the solutions \({\mathbf{q}}\left( {{\mathbf{L}}_{j} } \right)\) and \({\dot{\mathbf{q}}}\left( {{\mathbf{L}}_{j} } \right)\). Discretizing \({\mathbf{q}}\left( {{\mathbf{L}}_{j} } \right)\) and \({\dot{\mathbf{q}}}\left( {{\mathbf{L}}_{j} } \right)\) according to a series of time points (t1,…,te), the Legendre PCE model at time ti can be obtained using the Galerkin projection method, followed by evaluating the range enclosure of \({\mathbf{q}}^{{\mathbf{I}}} \left( {t^{i} } \right)\) and \({\dot{\mathbf{q}}}^{{\mathbf{I}}} \left( {t^{i} } \right)\) with the defined Legendre polynomial inclusion function. The detailed computational procedure is depicted in Fig. 5. This treatment can separate the interval bounds estimation from the DAEs solver and thereby applies to more cases, such as the multibody systems with unilateral collisions which are difficult to simulate due to discontinuities associated with gaining and losing contacts and stick–slip transitions.

Fig. 5
figure 5

Computational procedure of the Legendre PCE approach for interval DAEs (adaptive step size solver)

Full size image

A remarkable superiority of the Legendre polynomial method over the Taylor-based method is that it is nonintrusive. It expresses the original DAEs with interval uncertainty as the deterministic differential algebraic equations through sampling, without deriving the partial derivative constraint equations, such that it greatly reduces the difficulty and complexity of the solution strategy and liberates the users from the complicated preprocessing. Further, it has no special restrictions on numerical methods for solving the DAEs and is also applicable to any multibody system dynamics, including the large, complex multibody dynamics which must be modeled and solved in commercial software. Besides, Eqs. (25–27) have proven the fine performance of the polynomial chaos inclusion function in attacking large overestimation; hence, such application in the proposed approach has the potential to improve the precision of the Taylor-based method.

4.2 Benchmark test: a double-pendulum multibody dynamics model

A schematic of a double-pendulum multibody dynamics model [31] depicted in Fig. 6 is used as the benchmark test to compare the differences of three methods in relation to precision and efficiency, including the Legendre PCE approach which is hereafter abbreviated as PCEM, the Taylor method (TM), and Monte Carlo (MC). Relatively described, \(xoy\) is the global coordinate system, and the local coordinate systems of the two rods are established at their centroids, i.e., \(O_{1}\) and \(O_{2}\). Both rods are homogeneous, the nominal values of rod length \(l_{1}\) and \(l_{2}\) are 1.0 m, and the nominal values of rod mass \(m_{1}\) and \(m_{2}\) are 1.0 kg. Choosing the two rods centroids and the angle of the two rods between y axis as the generalized coordinates \({\mathbf{q}} = \left[ {x_{1} ,y_{1} ,\theta_{1} ,x_{2} ,y_{2} ,\theta_{2} } \right]^{\rm T}\), thus we can obtain this multibody dynamics model, which is specifically expressed as

$$ \left\{ \begin{array}{l} {\mathbf{M\ddot{q}}} + {{\varvec{\Phi}}}_{{\mathbf{q}}}^{{\mathbf{T}}} {{\varvec{\lambda}}} = {\mathbf{Q}} \hfill \\ {{\varvec{\Phi}}} = 0 \hfill \\ \end{array} \right., $$
(37)
Fig. 6
figure 6

Schematic of a double-pendulum multibody dynamics model

Full size image

where \({\mathbf{M}} = {\text{diag}}\left[ {m_{1} ,m_{1} ,I_{1} ,m_{2} ,m_{2} ,I_{2} } \right]\), the rotational inertias are \(I_{1} = m_{1} l_{1}^{2} /12\) and \(I_{2} = m_{2} l_{2}^{2} /12\), respectively, the generalized force is \({\mathbf{Q}} = \left[ {0,m_{1} g,0,0,m_{2} g,0} \right]^{\rm T}\), the position kinematic constraint equations and its Jacobian matrix are given by

$$ {{\varvec{\Phi}}} = \left\{ \begin{gathered} x_{1} - \frac{{l_{1} }}{2}\sin \theta_{1} = 0 \hfill \\ y_{1} - \frac{{l_{1} }}{2}\cos \theta_{1} = 0 \hfill \\ x_{2} - l_{1} \sin \theta_{1} - \frac{{l_{2} }}{2}\sin \theta_{2} = 0 \hfill \\ y_{2} - l_{1} \cos \theta_{1} - \frac{{l_{2} }}{2}\cos \theta_{2} = 0 \hfill \\ \end{gathered} \right.,\;\;{{\varvec{\Phi}}}_{{\mathbf{q}}} = \left[ {\begin{array}{*{20}c} 1 & 0 & { - \frac{{l_{1} }}{2}\cos \theta_{1} } & 0 & 0 & 0 \\ 0 & 1 & {\frac{{l_{1} }}{2}\sin \theta_{1} } & 0 & 0 & 0 \\ 0 & 0 & { - l_{1} \cos \theta_{1} } & 1 & 0 & { - \frac{{l_{2} }}{2}\cos \theta_{2} } \\ 0 & 0 & {l_{1} \sin \theta_{1} } & 0 & 1 & {\frac{{l_{2} }}{2}\sin \theta_{2} } \\ \end{array} } \right]. $$
(38)

For this set of numerical experiments, \(l_{1}\) and \(l_{2}\) are considered as interval parameters, and their uncertainty level is set as ± 5.0%. As the two rods are homogeneous, \(m_{1}\) and \(m_{2}\) are correlated with \(l_{1}\) and \(l_{2},\) respectively. Assuming the initial angles and the angular velocities are \(\left[ {\theta_{1} ,\;\theta_{2} ,\;\dot{\theta }_{1} ,\;\dot{\theta }_{2} } \right] = \left[ {\pi /4,\;\pi /3,\;0,\;0} \right]\), thus the initial conditions of the DAEs are given by

$$ \left\{ \begin{gathered} {\mathbf{q}}_{{\mathbf{0}}} = \left[ {\frac{{l_{1} }}{2}\sin \frac{\pi }{4},\;\frac{{l_{1} }}{2}\cos \frac{\pi }{4},\;\frac{\pi }{4},\;l_{1} \sin \frac{\pi }{4} + \frac{{l_{2} }}{2}\sin \frac{\pi }{3},\;l_{1} \cos \frac{\pi }{4} + \frac{{l_{2} }}{2}\cos \frac{\pi }{3},\;\frac{\pi }{3}} \right]^{\rm T} \hfill \\ {\dot{\mathbf{q}}}_{{\mathbf{0}}} = \left[ {0,\;0,\;0,\;0,\;0,\;0} \right]^{\rm T} \hfill \\ \end{gathered} \right.. $$
(39)

The second-order PCEM and TM are employed to solve the above interval multibody dynamics model, and a brute force MC is adopted to yield benchmark solutions, where the total number of samples is 10,000. The numerical algorithm, NSTIFF-SI2, is implemented in MATLAB®. All calculations in this paper, unless explicitly stated, are completed on the same computer. The partial numerical calculation results are given in Fig. 7.

Fig. 7
figure 7

Interval response bounds of a double-pendulum multibody dynamics model

Full size image

Figure 7 shows that TM does not produce the wrapping effect in the initial time, and the calculation results are almost inside the reference solution, such as 2.0–8.0 s in Fig. 7d, 2.0–7.5 s in Fig. 7e, and 2.0–5.0 s in Fig. 7f. Such range enclosures are smaller than the reference solutions; as time increases, TM produces a large overestimation, its calculation results have great deviations, and \(\theta_{1}\) and \(\dot{\theta }_{2}\) even have a trend of numerical divergence. This may be caused by the fact that TM greatly increases the variables and equations of DAEs and hence a greater probability of numerical divergence and computational instability for large systems. In sharp contrast, PCEM can always enclose the reference solution with fine precision. Although PCEM also produces overestimation at certain time points, such as 9.5–10.0 s in Fig. 7a, 9.0–10.0 s in Fig. 7d, and 8.0–10.0 s in Fig. 7f, it can effectively control the phenomenon of wrapping effect, and its computational accuracy is much better than that of TM.

The range of the interval in relation to the nonlinearity of the function will greatly affect the quality of the approximation, thus another three cases with different uncertainty levels, i.e., 10%, 15%, 20%, are analyzed, and the results of \(\dot{x}_{2}\) are given in Fig. 8. It shows that the computational precision of the TM and the PCEM decreases with the increase in uncertainty level. In comparison, the PCEM provides more accurate interval bounds estimation than TM, especially for the large uncertainty levels. We can summarize that the proposed PCEM can effectively attack the computational challenges of TM in large uncertainty problems.

Fig. 8
figure 8

Interval bounds of \(\dot{x}_{2}\) versus different uncertainty levels

Full size image

Regarding efficiency, the computing times of TM and MC are 232 s and 3784 s, respectively, while that of PCEM is only 13 s. This indicates that the presented PCEM for interval multibody dynamics system can improve the computational efficiency while ensuring the computational precision compared with TM.

5 Computation of an artillery multibody system dynamics with interval uncertainty

5.1 An artillery multibody dynamics model

An artillery rigid–flexible multibody dynamics model is presented in Fig. 9. In the modeling process, we ignored the coupling effect of the projectile in the barrel during the shooting process, and the elevating gear and the traversing gear were regarded as locked; thus, the artillery was in a static equilibrium state before shooting. The actual, complicated hydraulic and gas pressure devices, such as the interior ballistic, the recoil mechanism, and the counter-recoil mechanism, were simplified into load computing models. The barrel, cradle, and top carriage are treated as the flexible body and are structured through a finite element modal neutral file, while the other parts are rigid, through which the rigid–flexible multibody dynamics model of this artillery is created based on the modal synthesis method. According to the modal contribution factor theory, ignoring the modal parameters with small modal contribution factors can decrease the computational burden and assure computing precision. Owing to the complexity of this multibody model, we considered the first 20 modalities herein.

Fig. 9
figure 9

An artillery rigid–flexible, coupling multibody dynamics model

Full size image

The artillery model is a large system and forms a typical, complex multibody dynamics problem. The governing equations are complicated and cumbersome, and thus its solutions are only available from some commercial MBS software. Therefore, we built it and established the connections between the parts in ADAMS/Solver®. The required exterior loads, such as barrel resulting force, recoil absorber force, balance force, and soil reaction force, are calculated through the dynamic link library file which is compiled by FORTRAN® and imported by the ADAMS® user-defined module. Details on the aforementioned loads computing formulas are reported elsewhere [43].

5.2 Model test verification

A suite of measurements was employed to verify the rationality of the artillery multibody dynamics modeling. The projectiles used in the test were hollow base cartridges, and the charge scheme is full charge composed of six unit modules. Direct measure of the breech pressure was performed after trepanning in the chamber and installing pressure sensors. The used piezoelectric crystal pressure sensor was KISTLER 6229A seen in Fig. 10, and the DEWETRON 1201 data acquisition system was employed to record the pressure history. A high-speed photography system captured the recoil movement of the breech during and after the launching transient. The major components of IDT3–S2 high-speed photography system seen in Fig. 11 were Phantom V710 high-speed camera, Nikkor AF-S 400 mm F2.8D ED lens, camera quick-release plate bracket, Kangrinpoche NB1-A tripod video head, Gitzo GT5531S tripod, trigger signal line, etc. Analysis was done on the Xcitex company's image processing software, Pro Analyst, to obtain the recoil displacement with time; further differentiating the measured recoil displacement curve could obtain the recoil velocity with time.

Fig. 10
figure 10

Pressure sensor (left) and its locations on the test section (right)

Full size image
Fig. 11
figure 11

High-speed photography system for artillery recoil movement

Full size image

Another measurement is the nonlinear dynamic responses, such as the muzzle vibration parameters, to evaluate the artillery’s tactical level. The key sensor of the muzzle vibration test section as shown in Fig. 12 was an SDI-ARG-720 angular velocity gyroscope. A protective box wrapping the gyroscope was necessary to attack the muzzle strong impact and was fastened on the bracket by screws. The two elastic brackets were further fixed on the barrel (located nearly the tail of the muzzle brake) by bolts.

Fig. 12
figure 12

Schematic diagram of muzzle vibration test

Full size image

The comparisons between measured and simulated breech pressure history, recoil displacement history, and muzzle vertical angular displacement history are given in Fig. 13a–c, respectively, and the important indicators are given in Table 1. Simulated solutions in Fig. 13 and Table 1 were obtained using the commercial MBS software ADAMS®, where the DAE solver is a BDF stiff integral method, WSTIFF-SI2. Figure 13a shows that in addition to the time delay of the calculated breech pressure curve, the maximum pressure, as well as the entire pressure curve match the actual measured result well, especially during the pressure rise period. Figures 13b and 12c and Table 1 also show that the dynamic characters of the simulation perfectly match the measured responses. The few relative errors demonstrate that the established artillery multibody dynamics model has a good ability to simulate the artillery launching process. It provides a reliable model basis for the later interval uncertainty analysis of the artillery dynamic responses. These results prove that the established artillery multibody dynamics model has high precision, and provides an accurate model basis for subsequent interval uncertainty analysis.

Fig. 13
figure 13

Comparison between simulated and actual measured results of artillery dynamic responses

Full size image
Table 1 Comparison between measured and simulated values
Full size table

5.3 Interval uncertainty analysis results

The sensitivity analysis in reference [43] demonstrated that the vertical and horizontal mass eccentricities of recoiling parts, ey and ez, are sensitive parameters to muzzle vibration. Therefore, they are regarded as interval parameters, and their interval values are [−5, 5] mm, and [−3, 3] mm, respectively. As the explicit DAEs are too complex to be derived, the Taylor-based method is not suitable for this type of complex multibody system dynamics problems that require commercial MBS software simulation. Besides, the software simulation of the artillery model is computation-intensive; thus, the direct MC will suffer from a sky-high computational burden. The second-order PCEM and the scanning method (SM) are employed to solve the above interval artillery multibody dynamics model. SM is adopted to yield benchmark solutions, where ten samples are uniformly taken in each interval uncertainty space; thus, it requires 102 = 100 runs of the artillery dynamics model in ADAMS®. The interval bounds of the artillery dynamics responses, including the firing stability parameters and the muzzle vibration parameters, are displayed in Figs. 14 and 15.

Fig. 14
figure 14

Interval bounds of firing stability parameters

Full size image
Fig. 15
figure 15

Interval bounds of muzzle vibration parameters

Full size image

Figures 14 and 15 show that the proposed PCEM cannot completely avoid the small wrapping effect, which is caused by the interval arithmetic operations. Nonetheless, the proposed PCEM can enclose the reference solution and its results favorably match the interval bounds yielded by SM in most integration steps. The presented approach has high accuracy even in large, complex multibody dynamics. In regard to efficiency, using no less than (p + 1) collocation nodes in each parameter dimension, the second-order PCEM requires at least nine runs of the artillery dynamics model in ADAMS®. This is far less than that of the scanning method, but their results are similar. Considering that the artillery rigid–flexible, coupling dynamics model is computationally intensive, the saving in computational cost is of great practical engineering significance. We can conclude that the PCE method has obvious advantages in the interval bound evaluation, especially for the large, complex multibody dynamics model that the explicit DAEs are difficult to be derived.

6 Conclusions

This paper investigates a nonintrusive Legendre polynomial expansion approach to predict the response bounds of multibody dynamics systems under interval uncertainty. The motivation for this effort is twofold. First, the traditional methods using the Taylor inclusion function and interval arithmetic are easy to result in wrapping effect. Second, most real-life multibody dynamics models are large systems with high rigidity, nonlinearity, and discontinuity, such as the artillery multibody model investigated in this paper, which makes commercial software the almost essential tool for numerical simulation. Many conventional, intrusive methods are not suitable for such large dynamic systems. To end these, a polynomial chaos inclusion function using Legendre orthogonal basis is presented for analyzing such multibody dynamics models with interval uncertainty, where the Galerkin projection method is adopted to compute the Legendre polynomial coefficients. The capacity of the Legendre polynomial inclusion function to alleviate the wrapping effect is proved by a mathematical example. Based on this, an interval uncertainty propagation method for multibody dynamic systems described by DAEs is further introduced. Through sampling, the nonintrusive algorithm expresses the original multibody dynamics system with interval uncertainty as the deterministic differential algebraic equations, followed by calculation using the general numerical integration method. The response bounds at each time step are predicted using the truncated Legendre polynomial expansion. A benchmark test based on three methods is analyzed to illustrate the superiority of this method, and an artillery multibody dynamics model is specifically investigated.

Compared with the Taylor-based method and the scanning method, the Legendre method proposed herein is robust and straightforward to implement. The numerical results have proven the much better performance of the polynomial chaos approach in attacking large overestimation than the Taylor method, and the much higher computational efficiency than the scanning method. Thus, the Legendre polynomial-based algorithm can improve computational efficiency while ensuring computational precision, especially for some large, complicated multibody dynamic systems. However, the polynomial chaos cannot completely avoid the small wrapping effect, which is caused by interval arithmetic operations. Another remarkable advantage is that it is nonintrusive, such that it greatly reduces the difficulty and complexity of the solution strategy and liberates the users from the complicated preprocessing of the Taylor method. Further, it has no special restrictions on numerical methods for solving the DAEs and is also applicable to any multibody system dynamics, especially for the large, complex multibody systems that must be modeled and solved in commercial software.