Dynamics of a three-module vibration-driven system with non-symmetric Coulomb’s dry friction

Abstract

In the present paper, a three-module vibration-driven system moving on a rough horizontal plane is modeled to investigate the relation among the system’s steady-state motion, external Coulomb’s dry friction force and internal excitations. Each module of the system represents a vibration-driven system composed of a rigid body and a movable internal mass. Major attention is focused on the primary resonance situation that the excitation frequency is close to the first-order natural frequency of the system. In the case that the external friction is low, the internal excitation is weak and the stick–slip motion is negligible, both methods of averaging and modal superposition are employed to study the steady-state motion of the system. Through a set of algebraic equations, an approximate value of the system’s average steady-state velocity is obtained. Several numerical examples are calculated to verify the validity of the analytical results both qualitatively and quantitatively. It is seen that big quantitative errors will appear if stick–slip motions occur. Then, two mechanisms for the possible stick–slip motions are put forward, which explain the errors on the average steady-state velocity. Numerical simulations verify our analysis on the stick–slip effects and their mechanisms. Finally, to maximize the average steady-state velocity of the system, optimal control problem is studied. It is shown that, in addition to modifying the friction coefficients, the improvement of the system’s efficiency can be provided by changing the initial phase shifts among the three internal excitations.

1 Introduction

Currently, legged or wheeled robots are gradually out of style in the field of micro-robots. The difficulty on further minimization, the restriction on working environment as well as the possible harm to the contact surface are the great faults of legged and wheeled robots. Rather, the research focus in recent years has inclined more and more to legless locomotion system inspired by the motions of snakes and worms [1–3]. The application fields of such system are widespread, including the diagnosis in engineering pipeline system, inspection in human cardiovascular system and the rescue of survivors in disasters (like earthquakes). These expected applications lead to extensive studies on feasible models of legless locomotion systems.

One possible model is based on such an idea that the snake-like or worm-like system is combined with discrete distributions. Some mechanical components, such as linear or nonlinear springs, viscous dampers and kinematic constraints, are used to connect each two distributions. One or more distributions act as actuators, which drive the whole system moving forward. In general, some kinds of friction exist at the contact surface between the system and the environment. The physical properties of both the system and the environment may affect the characters of the friction. Typically, the friction may be anisotropic, i.e., the friction coefficients depend on the orientation of the relative velocity. The reason for this anisotropism may lie in two folds: one is the non-symmetric Coulomb’s dry friction property of the contact surface; and the other is the scales or bristles fixed on the outer edge of the system, which can prevent system’s backward motions. A number of micro-robot models are put forward in use of the above ideas [4–7]. The current experimental studies on legless locomotion systems have mainly focused on single-module and two-module systems [6–8].

Vibration-driven system is a kind of dynamic model of the actuator mentioned above and has attracted great attention from researchers. It can move in various environments without propelling components (such as wheels, legs, oars, jets, screws and other outward devices). The propulsion of this system is provided due to the vibrations of internal masses and the interaction of the system with the resistive media. Such systems have a number of advantages over conventional systems, they are simple in design and can be fabricated into very small size, and thus can serve as the dynamic models of certain micro-robots and bionic robots.

System with movable internal mass is a typical vibration-driven system. F.L. Chernousko is the precursor for studying the rectilinear motion of a rigid body with a controlled internal mass [9–12]. When a designated excitation force is applied to the internal mass, the reaction force exerts on the rigid body and changes its velocity. Due to the anisotropism of the resistance force between the body and rough medium, the system can thus move forward under control. Mechanisms based on this principle do not require complicated gear case and can be made hermetic and smooth, i.e., without external moving parts. Possible applications of these mechanisms include the manufacture of capsule-type micro-robots, which have a wide applicability in restricted places and vulnerable media, for example, robots for inspection in narrow tubes and self-propelled endoscopes in human vessels [14].

The issue of optimal control of the rectilinear motion of a rigid body with one internal mass along a rough horizontal plane was considered in [9, 10]. Anisotropic Coulomb’s dry friction was assumed to act between the body and the plane. The internal mass was allowed to move within a fixed limit along a line parallel to the line of motion of the rigid body. Two novel control modes of the internal mass, namely, velocity-controlled mode and acceleration-controlled mode were constructed to realize a steady-state motion (velocity-periodic motion) of the rigid body. Close attention was paid to the average velocity of the steady-state motion of the system as a whole. For both control modes, optimal parameters were obtained to maximize the average velocity of the steady-state motion. In [11, 12], for velocity-controlled mode, the resistance force between the system and the environment was extended to piecewise-linear and quadratic-law resistances. Work [13] obtained the optimal and practical values of control parameters when acceleration-controlled mode is applied to the internal mass, and non-symmetric viscous (piecewise-linear) friction works. Some experimental progress, including a pendulum-driven cart, a vibro-robot in a tube and a capsubot, was made by Li, Furuta and Chernousko [14–16].

The rectilinear motions of chain of bodies connected to one another by means of some types of mechanical component have been studied by a number of authors [1, 17–26]. Work [17] devoted to the forward rectilinear motion of a system consisting of two rigid bodies along a horizontal line. Dry friction force was assumed to act between the system and the plane. The motion was controlled by internal forces of interaction between the bodies. The optimum parameters of the system and a control law were found corresponding to the maximum mean velocity of the system as a whole. The authors in work [18] considered a one-dimensional motion of two mass points in a resistive medium. The mass points were interconnected with a kinematic constraint or a linear spring. The friction force was described as non-symmetric viscous friction. The average velocity of the steady-state motion of the system as a whole was obtained through method of averaging. Reference [19] dealt with a system composed of two identical modules with unbalanced vibration exciters. A spring with linear characteristic was used to connect the two modules. The steady-state motion was mainly considered and a nearly resonant excitation mode was investigated. Method of averaging was adopted in the case that the friction is small and the stick–slip motion is negligible. It was shown that the steady-state motion can be controlled by changing the phase shift between the two exciters and the sign of the resonant detuning. In [20, 21], under the action of small non-symmetric Coulomb’s dry friction, the motion of a system that consists of two equal mass points connected by a nonlinear spring with cubical nonlinearity was considered. Small periodical force acted between the two mass points to drive the system. Similarly, without considering the stick–slip effect, method of averaging was employed to study the approximate steady-state motion of the system with a const “on the average” velocity. The algebraic equation for this constant velocity was found. For different parameters of the model, it was found that at most three regions of motion with a constant average velocity exist, but only one or two of them are stable.

As for system composed of more than two modules (or mass points), only a little work has been carried out by K. Zimmermann, I. Zeidis, etc. The motion of a straight chain of three equal mass points interconnected with kinematical constraints was considered in [8, 22]. The ground contact obeys the Coulomb’s dry friction law (discontinuous) or viscous friction law (continuous). The controls were assumed in the form of periodic function with zero average, shifted on a phase one concerning each other. It was shown that motion is possible even in the case of isotropic coefficient of friction and constant normal force when special control algorithms are used. The problem of the motion of a chain of n point masses along a rough straight line in the case of synchronous control of the interaction between the point masses and the problem of the undulatory motion of a chain of three point masses were studied by K. Zimmermann, N. Bolotnik, etc. [1, 24–26]. In [6, 23], some theoretical and experimental investigations on worm-like system were presented. The system was modeled in form of a straight chain of n mass points interconnected by springs, but only the mass point at the center of the chain was excited. The ground contact was described by non-symmetric dry friction.

Our research motivations come from the following two aspects. On one hand, by observing the real motions of worms, one knows that every part of a worm’s body plays a significant role in the propulsion of motion. Hence, with the progress of the research on worm-like systems and worm-like robots that take the earthworms as live prototypes, system consisting of more than two modules (or two mass points) is the developing trend. Each of the modules can serve as an actuator. However, the current studies on three-module and N-module systems have been subjected to several restriction. Either the connecting components are kinematical constraints with specially designated control [8, 22], or only one module works as an actuator [6, 23]. On the other hand, vibration-driven system (system with movable internal mass) provide a better simulation of a worm’s rectilinear motion than conventional actuators. Besides, it is more easily to be minimized, and hence, more easily to be realized in practice. Based on the above two reasons, the study on a three-module vibration-driven system, with each module modeled as a system with a movable internal mass, is not only a breakthrough of the previous studies but also the demands for the development of legless worm-like robots. Moreover, much of the existing research has assumed that the dry friction force at the contact is low, and the possible stick–slip motion of the system is absent or negligible. However, in the case that the system is fabricated into small size, the friction force may be no longer a small value in comparing with other forces. Hence, stick–slip effect can be a remarkable characteristic of such system with dry friction. Some types of stick–slip motion can be even used to further optimize the system to obtain a higher average steady-state velocity [29]. For these reasons, it is necessary for one to consider the stick–slip motions in multi-module vibration-driven systems. The mechanisms of the stick–slip effects can give hints for the design of worm-like robots, either avoiding or making use of the stick–slip motions.

In this paper, the rectilinear motion of a three-module vibration-driven system on a rough horizontal plane is considered. Each module as an actuator is a system with movable internal mass and is interconnected through linear springs. The relative motions of the internal masses are specified as sinusoidal periodic motions. Non-symmetric Coulomb’s dry friction (piecewise constant) is assumed to act between the system and the environment. Firstly, assuming that the friction is small, the excitation is weak and the stick–slip motion is negligible, both methods of averaging and modal superposition are employed to study the steady-state motion of the system as a whole. Major attention is given to the primary resonance situation that the excitation frequency is close to the first-order natural frequency of the system’s relative oscillation. An approximate value of the average steady-state velocity of the system is obtained through a set of algebraic equations. By numerical simulations, we will show that under our assumption, the analytical results are in acceptable agreement with the numerical ones. However, for some values of parameters, big quantitative errors exist. Putting the stick–slip effect into consideration, we will explain that the big errors are induced by stick–slip motions. Then, the mechanisms of the stick–slip motions are analyzed from the view point of mechanics, with numerical examples as verification. We will point out that the phase shifts among the internal excitations play a significant role in the appearance of stick–slip motions. Finally, in order to maximize the average steady-state velocity of the system, two optimal strategies are raised. By applying these two strategies, the efficiency of the system is much improved.

2 Dynamic model

2.1 Description of the dynamic system

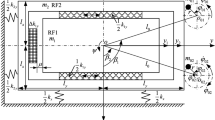
The system under consideration consists of three identical modules interconnected by linear springs. Each module is composed of a rigid body and a movable internal mass, and can move along a same straight line on a rough horizontal plane. The internal masses also move along a horizontal line parallel to the line of motions of the rigid bodies (see Fig. 1). All of the three internal masses are assumed to perform sinusoidal oscillations, whose amplitudes are limited so as to avoid collision with the rigid body. We assume that the three internal masses vibrate with the same frequency and the same amplitude, but are shifted in phase. The resistance force at the contact surface between the system and the rough horizontal plane is described as non-symmetric Coulomb’s dry friction.

Fig. 1

Three-module vibration-driven system

In what follows, for the sake of brevity, the three modules will be referred as module 1, module 2 and module 3, respectively. The following notations are introduced: M is the mass of each of the rigid bodies and m is the mass of each of the internal masses; c is the stiffness coefficient of the linear spring; R _i (i=1,2,3) is the external friction force acting on module i. Let x _i (i=1,2,3) denote the absolute coordinates measuring the displacement of module i relative to the plane, ξ _i (i=1,2,3) denote the coordinate measuring the displacement of each internal mass relative to its container body. Then the corresponding velocities and accelerations of each body and internal mass can be expressed into the first-order derivatives and second-order derivatives of x _i and ξ _i (i=1,2,3).

2.2 Equation of motion

The equations governing the motion of the system are

$$ \begin{aligned} (M+m)\ddot{x}_1&=-m\ddot{\xi}_1+c(x_2-x_1)-R_1,\\(M+m)\ddot{x}_2&=-m\ddot{\xi}_2+c(x_3-x_2)-c(x_2-x_1)-R_2,\\(M+m)\ddot{x}_3&=-m\ddot{\xi}_3-c(x_3-x_2)-R_3.\end{aligned}$$

(1)

Since the internal motions have the sinusoidal form

$$\xi_i=b\sin \varphi_i,\quad i=1,2,3,$$

we have

$$ \ddot{\xi}_i=-b\omega^2\sin \varphi_i ,\quad i=1,2,3,$$

(2)

where φ _i (i=1,2,3) is the phase of internal motion and can be expressed as

$$ \varphi_i=\omega t+\phi_{i0},\quad i=1,2,3.$$

(3)

In the above equations, ω is the excitation frequency, ϕ _i0 (i=1,2,3) is the initial phase (ϕ _i0∈[0,2π]) of each internal mass. In this study, the initial phases ϕ _i0 (i=1,2,3) are assumed to be non-identical.

The non-symmetric Coulomb’s dry friction is defined as

$$ R_i=\begin{cases}F_+, & \text{if}\ \dot{x}_i>0,\\F_0, & \text{if}\ \dot{x}_i=0,\\-F_-, & \text{if}\ \dot{x}_i<0,\end{cases} \quad i=1,2,3,$$

(4)

where

$$ F_+=(M+m)f_+g,\qquad F_-=(M+m)f_-g.$$

(5)

Here, F ₀ is the friction force at the state of rest, g is the acceleration due to gravity, f ₊ and f ₋ are the coefficients of dry friction at the motion in forward and backward directions, respectively. Both f ₊ and f ₋ are non-negative constants and are assumed to be different in magnitudes. This difference implies the anisotropism of the interface or the non-symmetry of the configuration of the container bodies. Without loss of generality, we assume

$$ f_+<f_-,$$

(6)

which means that the friction for forward motion is lower than that for the backward motion.

2.3 A remark on F ₀ and stick–slip effect

Let us denote F _i (i=1,2,3) the resultant of all forces applied to module i except the friction force, i.e.,

$$ \begin{aligned} F_1&=-m\ddot{\xi}_1+c(x_2-x_1),\\F_2&=-m\ddot{\xi}_2+c(x_3-x_2)-c(x_2-x_1),\\F_3&=-m\ddot{\xi}_3-c(x_3-x_2).\end{aligned}$$

(7)

Then we have

$$ F_0=\begin{cases}F_+, & \text{if}\ \dot{x}_i=0\ \mbox{and}\ F_i>(M+m)f_+g,\\F_i, & \text{if}\ \dot{x}_i=0\ \mbox{and}\ -(M+m)f_-g\leq F_i\leq (M+m)f_+g,\\-F_-, & \text{if}\ \dot{x}_i=0\ \mbox{and}\ F_i<-(M+m)f_-g,\quad i=1,2,3.\end{cases}$$

(8)

Sticking (stick–slip motion) is a characteristic feature of dynamical systems with Coulomb’s dry friction. It relates to the friction force of rest F ₀. As long as the magnitude of the resultant force F _i (i=1,2,3) does not exceed the given maximal value of the friction force at rest ((M+m)f ₊ g or (M+m)f ₋ g), module i will remain at a static state (sticking). Such situation can arise not only at the beginning but also during the movement as well as at the end. The sticking state will be destroyed only if the magnitude of the force F _i (i=1,2,3) outstrips one of the maximal values of the friction force at rest. A large series of publication were devoted to the problem of contact and collision with friction [27, 28] as well as the stick–slip motion under the action of Coulomb’s dry friction [29–33].

In this paper, assuming that the stick–slip effect is negligible, we will firstly try to use method of averaging to investigate the steady-state motion of the system (see Sect. 3). An average steady-state velocity of the system can be obtained. However, the adopted assumption does not mean that the system cannot undergo a steady-state motion when the stick–slip effect exists, but that such steady-state motions cannot be acquired by first-order approximation of method of averaging. Therefore, the reason why method of averaging does not work everywhere will be given, and the mechanisms of the possible stick–slip motions will be explained (see Sects. 4 and 5).

2.4 Non-dimensionalization

Introduce the following dimensionless parameters (labeled by asterisk):

$$ \begin{aligned} x_i^{\ast}&=\frac{x_i}{L},\qquad t^{\ast}=t\sqrt{\frac{c}{M+m}},\qquad \varepsilon=\frac{f_-(M+m)g}{cL}\\\varOmega&=\omega\sqrt{\frac{M+m}{c}},\qquad \beta=\frac{mcb}{(M+m)^2gf_-},\qquad r^{\ast}\bigl(\dot{x}_i^{\ast}\bigr)=\frac{R_i}{(M+m)f_-g}, \end{aligned}$$

(9)

where L is a unit of length for non-dimensionalization and can be set arbitrarily.

Proceeded to the dimensionless variables in (1) and then omit the asterisks, to obtain the dimensionless governing equations

$$ \begin{aligned} \ddot{x}_1&=\varepsilon \beta \varOmega^2 \sin \varphi_1+(x_2-x_1)-\varepsilon r(\dot{x}_1),\\\ddot{x}_2&=\varepsilon \beta \varOmega^2 \sin \varphi_2+(x_3-x_2)-(x_2-x_1)-\varepsilon r(\dot{x}_2),\\\ddot{x}_3&=\varepsilon \beta \varOmega^2 \sin \varphi_3-(x_3-x_2)-\varepsilon r(\dot{x}_3). \end{aligned}$$

(10)

Here,

$$ r(\dot{x}_i)=\begin{cases}k, & \text{if}\ \dot{x}_i>0,\\r_0, & \text{if}\ \dot{x}_i=0,\\-1, & \text{if}\ \dot{x}_i<0,\end{cases} \quad i=1,2,3,$$

(11)

in which, $k=\frac{f_{+}}{f_{-}}\in[0,1]$ and r ₀∈[−1,k]. The expression for the dimensionless parameter r ₀ is

$$ r_0=\begin{cases}k, & \text{if}\ \dot{x}_i=0\ \mbox{and}\ F_i>\varepsilon k,\\\frac{F_i}{\varepsilon}, &\text{if}\ \dot{x}_i=0\ \mbox{and}\ -\varepsilon\leq F_i \leq \varepsilon k,\\-1,& \text{if}\ \dot{x}_i=0\ \mbox{and}\ F_i<-\varepsilon,\end{cases} \quad i=1,2,3.$$

(12)

The resultant forces F _i (i=1,2,3) in expression (12) have been transformed into dimensionless form, which give

$$ \begin{aligned} F_1&=\varepsilon \beta \varOmega^2 \sin\varphi_1+(x_2-x_1),\\F_2&=\varepsilon \beta \varOmega^2 \sin \varphi_2+(x_3-x_2)-(x_2-x_1),\\F_3&=\varepsilon \beta \varOmega^2 \sin \varphi_3-(x_3-x_2). \end{aligned}$$

(13)

3 Analysis on steady-state motion

In this section, under the assumption that the stick–slip effect is absent or the portion of the excitation period during which sticking may occur on at least one module is negligible small [34], the steady-state motion in the vicinity of the resonance will be studied. For the sake of brevity, only the primary resonance situation that the excitation frequency is close to the first-order natural frequency of the relative oscillation will be considered. The second-order resonance situation can be analyzed similarly and is omitted in this paper due to limited space. In the case that both the excitation forces and the friction forces are lower compared with the maximal elastic forces developed in the springs, the steady-state solutions of the system will be analytically investigated through method of averaging.

3.1 Modal coordinate equations

Subtracting the first equation of (10) from its second equation, and the second equation of (10) from its third equation, the relative oscillations of the system’s bodies can be expressed as

$$ \left ( \begin{array}{c@{\quad}c}1\, & 0 \\0\; & 1 \\\end{array} \right )\left ( \begin{array}{c}\ddot{\eta}_1 \\\ddot{\eta}_2 \\\end{array} \right )+\left (\begin{array}{c@{\quad}c}2 & -1 \\-1 & 2 \\\end{array} \right )\left ( \begin{array}{c}\eta_1 \\\eta_2 \\\end{array} \right )=\varepsilon \left ( \begin{array}{c}\beta\varOmega^2(\sin\varphi_2-\sin\varphi_1)-(r(\dot{x}_2)-r(\dot{x}_1)) \\\beta\varOmega^2(\sin\varphi_3-\sin\varphi_2)-(r(\dot{x}_3)-r(\dot{x}_2)) \\\end{array}\right ),$$

(14)

where η ₁=x ₂−x ₁ and η ₂=x ₃−x ₂. Through a modal transformation

$$ \left ( \begin{array}{c}\eta_1 \\\eta_2 \\\end{array} \right )=\varPsi \left ( \begin{array}{c}y_1 \\y_2 \\\end{array}\right ),$$

(15)

(14) can be transformed into mass-normalized modal coordinate equations

$$ \left ( \begin{array}{c}\ddot{y}_1 \\\ddot{y}_2 \\\end{array} \right )+\left ( \begin{array}{c@{\quad}c}1\; & 0 \\0\; & 3 \\\end{array} \right )\left (\begin{array}{c}y_1 \\y_2 \\\end{array} \right )=\frac{\varepsilon}{\sqrt{2}} \left ( \begin{array}{c}\mathcal{G}_1-\mathcal{F}_1 \\\mathcal{G}_2-\mathcal{F}_2 \\\end{array} \right ).$$

(16)

Here, y ₁ and y ₂ are modal coordinates, $\mathcal{G}_{1},\mathcal{G}_{2}$ and $\mathcal{F}_{1}, \mathcal{F}_{2}$ can be written as

$$\begin{aligned} \mathcal{G}_1&=\beta\varOmega^2(\sin \varphi_3-\sin \varphi_1),\qquad \mathcal{F}_1=r(\dot{x}_3)-r(\dot{x}_1),\\\mathcal{G}_2&=\beta\varOmega^2(2\sin \varphi_2-\sin \varphi_1-\sin \varphi_3),\qquad \mathcal{F}_2=2r(\dot{x}_2)-r(\dot{x}_1)-r(\dot{x}_3). \end{aligned}$$

The transformation matrix Ψ in (15) is the matrix of mass-normalized modal shape, which gives

$$ \varPsi=\frac{1}{\sqrt{2}}\left ( \begin{array}{c@{\quad}c}1 & 1 \\1 & -1 \\\end{array} \right ).$$

(17)

The natural oscillations are governed by the modal coordinate equation (16) with zero right-hand side, corresponding to the relative oscillations of the system’s bodies in the absence of friction and excitation (i.e., ε=0 in (16)). The first- and second-order natural frequencies are

$$ \omega_{10}=1,\qquad \omega_{20}=\sqrt{3}.$$

(18)

The general solutions of the natural oscillations have the form

$$ \begin{aligned} y_{1n}=a_1\sin(\omega_{10}t+\theta_1),\\y_{2n}=a_2\sin(\omega_{20}t+\theta_2),\\\end{aligned}$$

(19)

where a ₁, a ₂ and θ ₁, θ ₂ are the amplitudes and initial phases of the natural oscillations, respectively, and are all arbitrary constants.

For the purpose of estimating the order of magnitudes of the quantities y ₁ and y ₂, we will ignore the dry friction terms $\mathcal{F}_{1}$ and $\mathcal{F}_{2}$ in (16) and construct the partial solutions of the resulting linear nonhomogeneous equation that correspond to the forced oscillations. For Ω≠ω ₁₀ and Ω≠ω ₂₀, the solutions yield

$$ \begin{aligned} y_{10}&=\frac{1}{\sqrt{2}(\varOmega^2-1)} \bigl[\varepsilon\beta\varOmega^2 ( \sin \varphi_1-\sin \varphi_3 ) \bigr],\\y_{20}&=\frac{1}{\sqrt{2}(\varOmega^2-3)} \bigl[ \varepsilon\beta \varOmega^2 ( \sin \varphi_1+\sin \varphi_3-2\sin \varphi_2 ) \bigr]. \end{aligned}$$

(20)

In the resonance cases where Ω=ω ₁₀ or Ω=ω ₂₀, bounded solutions of (16) with $\mathcal{F}_{1}=0$ and $\mathcal{F}_{2}=0$ do not exist.

3.2 Outline of the analysis through method of averaging

According to the theory of vibration mechanics [35], we know that in a linear multi-degree-of freedom (MDOF) system, all modes of the system are independent of each other. If a harmonic external excitation of frequency Ω acts on a linear MDOF system with positive damping, the system will oscillate with the excitation frequency after the system enter into the steady state, if, none of the natural frequency is equal or close to the excitation frequency. The general solution of the natural oscillation will soon dissipate because of the damping. When the excitation frequency equals or approaches to one of the natural frequencies of the system, resonance may occur. In the present study, the nonlinearity of the system is contained in the friction terms, which have piecewise constant forms. Except the discontinuous points at $\dot{x}_{i}=0\ (i=1,2,3)$, the friction terms are linear. Thus, unless the stick–slip phenomena induced by discontinuous points appear, the studied system behaves as a linear system.

In view of the above analysis, it is essential for us to consider how the steady-state solutions of the system (14) are constructed. On one hand, since the excitation frequency is close to the first-order natural frequency, in the case of no stick–slip motion, the general solution corresponding to the second mode of the natural oscillations (i.e., y _2n in (19)) will soon dissipate on account of the friction, but the partial solution (i.e., y ₂₀ in (20)) will still work. On the other hand, the first mode will behave in the neighborhood of the primary resonance. Its solution should be obtained via method of averaging. Consequently, two parts play a vital role in the solutions of η ₁ and η ₂: one is the solution of the first-order modal equation corresponding to the primary resonance, which should be obtained through method of averaging; the other is the partial solution of the second-order modal equation (i.e., y ₂₀).

Therefore, we will use method of averaging to deal with the first-order modal equation. To that end, we assume

$$ \varepsilon\ll1,\qquad \beta\varOmega^2\sim O(1),\qquad y_1\sim O(1).$$

(21)

The relation y ₂∼O(1) is not required, for the reason that in the second mode, only the partial solution of the resulting linear nonhomogeneous equation that corresponds to the forced oscillation works. According to the definitions in (9), the first two relations of (21) can be rewritten as

$$ \frac{f_-(M+m)g}{cL}\ll1,\qquad \frac{mcb\varOmega^2}{(M+m)^2gf_-}\sim O(1).$$

(22)

The estimation on the order of magnitude of the quantity y ₁ can be given by the maximum of the absolute value of y ₁₀, which is given by

$$ |y_{10}|_{\max}=\frac{\sqrt{2}}{|\varOmega^2-1|}\varepsilon \beta\varOmega^2 \biggl|\sin\frac{\phi_{10}-\phi_{30}}{2} \biggr|.$$

(23)

Substituting the expressions (9) for ε, β and Ω into (23) yields

$$ |y_{10}|_{\max}=\frac{\sqrt{2}}{|(M+m)\omega^2-c|}\frac{mb\omega^2}{L} \biggl|\sin\frac{\phi_{10}-\phi_{30}}{2} \biggr|.$$

(24)

To provide the relation |y ₁₀|∼O(1) in the dimensionless unit, we will choose the length scale L such that |y ₁₀|_max=1, i.e.,

$$ L=\frac{\sqrt{2}mb\omega^2}{|(M+m)\omega^2-c|}\biggl|\sin\frac{\phi_{10}-\phi_{30}}{2} \biggr|.$$

(25)

Hence, the conditions (22) that ε≪1 and βΩ ²∼O(1) become

$$ \frac{f_-(M+m)g|(M+m)\omega^2-c|}{\sqrt{2}mcb\omega^2 |\sin\frac{\phi_{10}-\phi_{30}}{2} |}\ll1,\qquad \frac{mb\omega^2}{(M+m)gf_-}\sim O(1).$$

(26)

To analyze the response of the system near the primary resonance, we assume that the difference of the excitation frequency Ω from the first-order natural frequency ω ₁₀ has an order of magnitude ε, i.e.,

$$ \varOmega^2=\omega_{10}^2(1+\varepsilon\sigma),$$

(27)

where σ is a const and σ∼O(1). Then the first-order modal coordinate equation can be transformed into

$$ \ddot{y}_1+\varOmega^2y_1=\varepsilon \biggl[\frac{1}{\sqrt{2}} (\mathcal{G}_1-\mathcal{F}_1)+\sigma y_1 \biggr].$$

(28)

When ε≠0, we assume that the solution of y ₁ still has the form as y _1n in (19), which yields

$$ \begin{aligned} y_1&=a_1\sin(\varOmega t+\theta_1),\\\dot{y}_1&=a_1\varOmega\cos(\varOmega t+\theta_1), \end{aligned}$$

(29)

where a ₁ and θ ₁ are functions of t. Then with respect to the analysis on the construction of the solutions as well as the modal transformation (15), the steady-state solutions of η ₁ and η ₂ can be written as

$$ \begin{aligned} \eta_1&=\frac{1}{\sqrt{2}}\bigl[a_1\sin (\varOmega t+\theta_1 )+y_{20}\bigr],\\\eta_2&=\frac{1}{\sqrt{2}} \bigl[a_1\sin (\varOmega t+\theta_1 )-y_{20} \bigr]. \end{aligned}$$

(30)

The following changes of variables are introduced:

$$ \begin{aligned} x_1&=X-\frac{1}{3}(2\eta_1+\eta_2),\qquad x_2=X+\frac{1}{3}(\eta_1-\eta_2),\qquad x_3=X+\frac{1}{3}(\eta_1+2\eta_2),\\\dot{x}_1&=V-\frac{1}{3}(2\dot{\eta}_1+\dot{\eta}_2),\qquad \dot{x}_2=V+\frac{1}{3}(\dot{\eta}_1-\dot{\eta}_2),\qquad \dot{x}_3=V+\frac{1}{3}(\dot{\eta}_1+2\dot{\eta}_2),\\V&=\dot{X},\qquad X=\frac{x_1+x_2+x_3}{3}, \end{aligned}$$

(31)

where X and V are the absolute displacement and velocity of the center of mass of the three rigid bodies, respectively.

Adding the three equations of (10) together, the equation for the absolute velocity of the center of mass yields

$$ \dot{V}=\frac{\varepsilon\beta\varOmega^2}{3} (\sin \varphi_1+\sin \varphi_2+\sin \varphi_3 )-\frac{\varepsilon}{3} \bigl(r(\dot{x}_1)+r(\dot{x}_2)+r(\dot{x}_3) \bigr).$$

(32)

Differentiating the first equation of (29) with respect to t, one can eliminate the second equation of (29) and obtain

$$ \dot{a}_1\sin(\varOmega t+\theta_1)+\dot{\theta}_1a_1\cos(\varOmega t+\theta_1)=0.$$

(33)

Differentiating the second equation of (29) and substituting the result into (28) yields

$$ \dot{a}_1\cos(\varOmega t+\theta_1)-a_1\dot{\theta}_1\sin(\varOmega t+\theta_1)=\frac{\varepsilon}{\varOmega} \biggl[\frac{1}{\sqrt{2}}(\mathcal{G}_1-\mathcal{F}_1)+\sigma y_1 \biggr].$$

(34)

Solving (33) and (34), one obtain

$$ \begin{aligned} \dot{a}_1&=\frac{\varepsilon}{2\sqrt{2}\varOmega} \bigl[2\cos(\varOmega t+\theta_1) \bigl(r(\dot{x}_1)-r(\dot{x}_3) \bigr)\\&\quad {}+\beta\varOmega^2 \bigl(\sin(\phi_{30}-\theta_1)-\sin(\phi_{10}-\theta_1) \bigr)\\&\quad {}+\beta\varOmega^2 \bigl(\sin(2\varOmega t+\phi_{30}+\theta_1)-\sin(2\varOmega t+\phi_{10}+\theta_1) \bigr)\\&\quad {}+\sqrt{2}a_1\sigma_1\sin(2\varOmega t+2\theta_1) \bigr],\\\dot{\theta}_1&=\frac{\varepsilon}{2\sqrt{2}a_1\varOmega} \bigl[-2\sin(\varOmega t+\theta_1) \bigl(r(\dot{x}_1)-r(\dot{x}_3)\bigr)\\&\quad {}-\beta\varOmega^2 \bigl(\cos(\phi_{30}-\theta_1)-\cos(\phi_{10}-\theta_1) \bigr)\\&\quad {}+\beta\varOmega^2 \bigl(\cos(2\varOmega t+\phi_{30}+\theta_1)-\cos(2\varOmega t+\phi_{10}+\theta_1) \bigr)\\&\quad {}+\sqrt{2}a_1\sigma_1\cos(2\varOmega t+2\theta_1)-\sqrt{2}a_1\sigma_1 \bigr].\end{aligned}$$

(35)

Keeping only the slowly varying parts in (32) and (35), we obtain a series of standard form equations in terms of the method of averaging

$$ \begin{aligned} \dot{a}_1=\varepsilon f_a&=\frac{\varepsilon}{2\sqrt{2}\varOmega} \bigl[2\cos(\varOmega t+\theta_1)\bigl(r(\dot{x}_1)-r(\dot{x}_3) \bigr)\\&\quad {}+\beta\varOmega^2 \bigl(\sin(\phi_{30}-\theta_1)-\sin(\phi_{10}-\theta_1) \bigr) \bigr],\\\dot{\theta}_1=\varepsilon f_\theta&= \frac{\varepsilon}{2\sqrt{2}a_1\varOmega}\bigl[-2\sin(\varOmega t+\theta_1) \bigl(r(\dot{x}_1)-r(\dot{x}_3) \bigr)\\&\quad {}-\beta\varOmega^2 \bigl(\cos(\phi_{30}-\theta_1)-\cos(\phi_{10}-\theta_1) \bigr)-\sqrt{2}a_1\sigma_1 \bigr],\\\dot{V}=\varepsilon f_V &=\frac{\varepsilon}{3} \bigl[\beta \varOmega^2 (\sin \varphi_1+\sin \varphi_2+\sin \varphi_3 )\\&\quad {}- \bigl(r(\dot{x}_1)+r(\dot{x}_2)+r(\dot{x}_3) \bigr) \bigr]. \end{aligned}$$

(36)

Average the right-hand side of system (36) with respect to the fast variable t from 0 to $\frac{2\pi}{\varOmega}$ to obtain

$$ \dot{a}=\varepsilon \overline{f}_a,\qquad \dot{\theta}=\varepsilon \overline{f}_\theta,\qquad \dot{V}=\varepsilon \overline{f}_V,$$

(37)

where $\overline{f}_{a},\, \overline{f}_{\theta}$ and $\overline{f}_{V}$ are the averages of f _a , f _θ and f _V in a period of $\frac{2\pi}{\varOmega}$, respectively, i.e.,

$$ \begin{aligned} \overline{f}_a&=\frac{\varOmega}{2\pi}\int_0^{\frac{2\pi}{\varOmega}}f_a(t)\,\text{d}t,\\\overline{f}_\theta&=\frac{\varOmega}{2\pi}\int_0^{\frac{2\pi}{\varOmega}}f_\theta(t)\,\text{d}t,\\\overline{f}_V&=\frac{\varOmega}{2\pi}\int_0^{\frac{2\pi}{\varOmega}}f_V(t)\,\text{d}t. \end{aligned}$$

(38)

Special attention should be paid that the integrations need to be performed piecewise because of the existence of non-smooth factor in the friction terms $r(\dot{x}_{i})$, i=1,2,3.

Since any unsteady process approaches to a steady state after the transient state is over, in what follows, the steady-state motion of the system as a whole will be of our interest. The variable V will be used to characterize the velocity of the system as a whole. In the steady state, the velocity is constant “on the average” with periodic oscillation imposed on. We define the system carry out a steady-state motion if V=const, a=const and θ= const, i.e., $\dot{V}=0$, $\dot{a}=0$ and $\dot{\theta}=0$. Thus, the analysis of the steady-state motion is reduced to studying the solutions of the algebraic equations:

$$ \overline{f}_a=0,\qquad \overline{f}_\theta=0,\qquad \overline{f}_V=0.$$

(39)

3.3 More details of the analysis

In (36), $r(\dot{x}_{i})\ (i=1,2,3)$ have piecewise constant forms. In order to find out the discontinuous points, the following transformations are performed in accordance with (31):

$$ \begin{aligned} \dot{x}_1=V-\frac{\sqrt{2}}{6}d_1\cos(\varOmega t-\psi_1),\\\dot{x}_2=V-\frac{\sqrt{2}}{6}d_2\cos(\varOmega t-\psi_2),\\\dot{x}_3=V-\frac{\sqrt{2}}{6}d_3\cos(\varOmega t-\psi_3). \end{aligned}$$

(40)

In the above transformations,

$$\begin{aligned} &\psi_1=\arctan\frac{-d_{12}}{d_{11}},\qquad \psi_2=\arctan\frac{-d_{22}}{d_{21}},\qquad\psi_3=\arctan \frac{-d_{32}}{d_{31}},\\&d_1=\sqrt{d_{11}^2+d_{12}^2},\qquad d_2=\sqrt{d_{21}^2+d_{22}^2},\qquad d_3=\sqrt{d_{31}^2+d_{32}^2},\end{aligned}$$

and

$$\begin{aligned} d_{11}&=3a_1\varOmega\cos \theta_1+\frac{\varepsilon\beta\varOmega^2}{\sqrt{2}(\varOmega^2-3)} (\cos\phi_{10}+\cos \phi_{30}-2\cos\phi_{20} ),\\-d_{12}&=3a_1\varOmega\sin\theta_1+\frac{\varepsilon\beta\varOmega^2}{\sqrt{2}(\varOmega^2-3)} (\sin\phi_{10}+\sin\phi_{30}-2\sin \phi_{20} ),\\d_{21}&=\frac{\sqrt{2}\varepsilon\beta\varOmega^2}{\varOmega^2-3} (\cos\phi_{10}+\cos \phi_{30}-2\cos\phi_{20} ),\\-d_{22}&=\frac{\sqrt{2}\varepsilon\beta\varOmega^2}{\varOmega^2-3} (\sin\phi_{10}+\sin \phi_{30}-2\sin\phi_{20} ),\\d_{31}&=3a_1\varOmega\cos\theta_1-\frac{\varepsilon\beta\varOmega^2}{\sqrt{2}(\varOmega^2-3)} (\cos\phi_{10}+\cos\phi_{30}-2\cos \phi_{20} ),\\-d_{32}&=3a_1\varOmega\sin\theta_1-\frac{\varepsilon\beta\varOmega^2}{\sqrt{2}(\varOmega^2-3)} (\sin\phi_{10}+\sin\phi_{30}-2\sin \phi_{20} ). \end{aligned}$$

According to relations (21) and noting that Ω is far away from the second-order natural frequency $\omega_{20}=\sqrt{3}$, the terms $\frac{\varepsilon\beta\varOmega^{2}}{\varOmega^{2}-3} (\cos\phi_{10}+\cos\phi_{30}-2\cos\phi_{20} )$ and $\frac{\varepsilon\beta\varOmega^{2}}{\varOmega^{2}-3} (\sin\phi_{10}+\sin\phi_{30}-2\sin\phi_{20} )$ are on the order of ε, while the terms a ₁ Ωsinθ ₁ and a ₁ Ωcosθ ₁ are on the order of O(1). Hence, it follows that

$$ d_1\gg d_2,\qquad d_3\gg d_2,\qquad d_1\approx d_3.$$

(41)

In this study, requiring that the velocity of the steady-state motion is positive, only the situation that V>0 will be considered. Letting

$$ u=\frac{V}{\sqrt{2}/6},$$

(42)

we have u>0. Based on whether the value of u is greater than d _i (i=1,2,3), eight possible ranges of u can be given, which are listed in Table 1. Then, on the basis of the definition of non-symmetric Coulomb’s dry friction ((11) and (12)), the integrations (38) will be performed for the eight different situations, respectively.

Table 1 The eight possible ranges of u

In situation (I), $\dot{x}_{i}\ (i=1,2,3)$ is always positive and the average results (38) yield

$$ \begin{aligned} &\overline{f}_a=\frac{\beta\varOmega}{2\sqrt{2}}\bigl(\sin(\phi_{30}-\theta_1)-\sin(\phi_{10}-\theta_1) \bigr),\\&\overline{f}_\theta=\frac{\beta\varOmega}{2\sqrt{2}a_1} \bigl(\cos(\phi_{30}-\theta_1)-\cos(\phi_{10}-\theta_1) \bigr)-\frac{\sigma}{2\varOmega},\\&\overline{f}_V=-k. \end{aligned}$$

(43)

Noting that $\overline{f}_{V}=-k$ is always negative, we know that the steady-state motion cannot be realized in this situation.

In situation (II), u≤d ₁, u≤d ₃ and u>d ₂. The average results give

$$ \begin{aligned} \overline{f}_a&=\frac{1}{2\sqrt{2}\pi\varOmega}\biggl[\pi\beta\varOmega^2 \bigl(\sin(\phi_{30}-\theta_1)-\sin(\phi_{10}-\theta_1) \bigr)\\&{}\quad -2 \biggl(\sqrt{1- \biggl(\frac{u}{d_1} \biggr)^2}k\cos(\theta_1+\psi_1)+\sqrt{1- \biggl(\frac{u}{d_3}\biggr)^2}\cos(\theta_1+\psi_3) \biggr)\\&\quad {}+k \biggl(\sin \biggl(\theta_1-\arccos \biggl(\frac{u}{d_3} \biggr)+\psi_3 \biggr)-\sin \biggl(\theta_1+\arccos \biggl(\frac{u}{d_3} \biggr)+\psi_3\biggr) \biggr)\\&\quad {}- \biggl(\cos \biggl(\theta_1+\arcsin \biggl(\frac{u}{d_1}\biggr)+\psi_1 \biggr)+\sin \biggl(\theta_1+\arccos \biggl(\frac{u}{d_1} \biggr)+\psi_1 \biggr) \biggr) \biggr],\\\overline{f}_\theta&=\frac{1}{2\sqrt{2}a\pi\varOmega} \biggl[\pi\beta \varOmega^2 \bigl(\cos(\phi_{10}-\theta_1)-\cos(\phi_{30}-\theta_1) \bigr)-\sqrt{2}a\pi\theta \\&\quad {}+2 \biggl(\sqrt{1- \biggl(\frac{u}{d_1} \biggr)^2}k\sin(\theta_1+\psi_1)+\sqrt{1- \biggl(\frac{u}{d_3}\biggr)^2}\sin(\theta_1+\psi_3) \biggr)\\&\quad {}+k \biggl(\cos \biggl(\theta_1-\arccos \biggl(\frac{u}{d_3} \biggr)+\psi_3 \biggr)-\cos \biggl(\theta_1+\arccos \biggl(\frac{u}{d_3} \biggr)+\psi_3\biggr) \biggr)\\&\quad {}- \biggl(\cos \biggl(\theta_1+\arccos \biggl(\frac{u}{d_1} \biggr)+\psi_1 \biggr)-\cos \biggl(\theta_1-\arccos \biggl(\frac{u}{d_1} \biggr)+\psi_1\biggr) \biggr) \biggr],\\\overline{f}_V&=\frac{1}{3\pi} \biggl[-3k\pi+(1+k) \biggl(\arccos \biggl(\frac{u}{d_1} \biggr)+\arccos \biggl(\frac{u}{d_3}\biggr) \biggr) \biggr]. \end{aligned}$$

(44)

From the equation $\overline{f}_{V}=0$, the derivative $\frac{\text{d}k}{\text{d}u}<0$ can be derived. According to relations (41), when u=d ₂, the maximal value of k equals approximately $\frac{1}{2}$, and when u=d ₁≈d ₃, the minimal value of k equals 0. Therefore, the steady-state motion can be realized in this situation only if k locates inside the range $(0, \frac{1}{2})$.

One should be noted that in situation (III), the conditions u>d ₁, u>d ₃ and u≤d ₂ contradict with relations (41) (i.e., d ₁≫d ₂, d ₃≫d ₂). Being similarly with situation (III), in situations (IV) and (V), the ranges of u are inconsistent with relations (41) either. As a result, situations (III–V) are leaved out from consideration.

In situation (VI), the average $\overline{f}_{V}$ gives

$$ \overline{f}_V=\frac{1}{3\pi} \biggl[-3k\pi+(1+k)\arccos \biggl(\frac{u}{d_3} \biggr) \biggr].$$

(45)

The derivative $\frac{\text{d}k}{\text{d}u}<0$ can also be obtained from $\overline{f}_{V}=0$. Considering the conditions d ₁≈d ₃≫d ₂ from relations (41) and u>d ₁,u≤d ₃,u>d ₂ in this situation, one obtains that both the minimal and maximal values of k equal approximately to 0, i.e., situation (VI) can only be valid when k=0. Hence, it will not be considered.

Similarly, the average $\overline{f}_{v}$ of situation (VII) is

$$ \overline{f}_V=\frac{1}{3\pi} \biggl[-3k\pi+(1+k)\arccos \biggl(\frac{u}{d_1} \biggr) \biggr].$$

(46)

Through the same analysis as in situation (VI), we need not to take it into consideration either.

The average results for situation (VIII) yield

$$ \begin{aligned} \overline{f}_a&=\frac{1}{2\sqrt{2}\pi\varOmega}\biggl[\pi\beta\varOmega^2 \bigl(\sin(\phi_{30}-\theta_1)-\sin(\phi_{10}-\theta_1) \bigr)\\&\quad {}-2 \biggl(\sqrt{1- \biggl(\frac{u}{d_1} \biggr)^2}k\cos(\theta_1+\psi_1)+\sqrt{1- \biggl(\frac{u}{d_3}\biggr)^2}\cos(\theta_1+\psi_3) \biggr)\\&\quad {}+k \biggl(\sin \biggl(\theta_1-\arccos \biggl(\frac{u}{d_3}\biggr)+\psi_3 \biggr)-\sin \biggl(\theta_1+\arccos \biggl(\frac{u}{d_3} \biggr)+\psi_3 \biggr) \biggr)\\&\quad {}- \biggl(\cos \biggl(\theta_1+\arcsin \biggl(\frac{u}{d_1}\biggr)+\psi_1 \biggr)+\sin \biggl(\theta_1+\arccos \biggl(\frac{u}{d_1} \biggr)+\psi_1 \biggr) \biggr) \biggr],\\\overline{f}_\theta&=\frac{1}{2\sqrt{2}a\pi\varOmega} \biggl[\pi\beta \varOmega^2 \bigl(\cos(\phi_{10}-\theta_1)-\cos(\phi_{30}-\theta_1) \bigr)-\sqrt{2}a\pi\theta \\&\quad {}+2 \biggl(\sqrt{1- \biggl(\frac{u}{d_1} \biggr)^2}k\sin(\theta_1+\psi_1)+\sqrt{1- \biggl(\frac{u}{d_3}\biggr)^2}\sin(\theta_1+\psi_3) \biggr)\\&\quad {}+k \biggl(\cos \biggl(\theta_1-\arccos \biggl(\frac{u}{d_3}\biggr)+\psi_3 \biggr)-\cos \biggl(\theta_1+\arccos \biggl(\frac{u}{d_3} \biggr)+\psi_3 \biggr) \biggr)\\&\quad {}- \biggl(\cos \biggl(\theta_1+\arccos \biggl(\frac{u}{d_1}\biggr)+\psi_1 \biggr)-\cos \biggl(\theta_1-\arccos \biggl(\frac{u}{d_1} \biggr)+\psi_1 \biggr) \biggr) \biggr],\\\overline{f}_V&=\frac{1}{3\pi} \biggl[-3k\pi+(1+k) \biggl(\arccos \biggl(\frac{u}{d_1} \biggr)+\arccos \biggl(\frac{u}{d_2}\biggr)+\arccos \biggl(\frac{u}{d_3} \biggr) \biggr) \biggr]. \end{aligned}$$

(47)

By similar procedure as in situation (II), we can also obtain the range of k for the steady-state motion in this situation. The result is $k\in(\frac{1}{2},1)$.

We then list the results of the averaging procedure in Table 2. From Table 2, one may find that the steady-state motion can only be realized in two situations of the eight, i.e., situations (II) and (VIII). Moreover, for situations (II) and (VIII), the ranges of k for the steady-state motion are also listed in Table 2.

Table 2 The average results for the eight different situations

Therefore, in the later discussion, when $k\in(0,\frac{1}{2})$, the algebraic equations (44) will be used to study the steady-state motion, and when $k\in(\frac{1}{2},1]$, algebraic equations (47) will be used. By numerically solving the three steady-state values of a,θ and u from (44) or (47), one may obtain the approximate average steady-state velocity V _s of the system as a whole by relation (42). Besides, the solutions η ₁ and η ₂ can be expressed also by substituting the steady-state values a _s and θ _s into (30).

4 Numerical simulation

In order to verify the correctness on the construction of the solutions η ₁ and η ₂ as well as the approximate results based on method of averaging, several numerical examples are calculated in this section. Although the values of parameters taken in this section do not have relations with practice, they all locate inside feasible regions, and hence, they are meaningful in guiding experiments on three-module vibration-driven systems. The fourth-order Runge–Kutta method will be employed in this and the following sections. If an appropriate time step is chosen (in this paper, the time step is specialized to be 0.01), the applied method will be able to capture both the fast and slow motion efficiently, and the results will be of acceptable accuracy.

4.1 Numerical examples for $k\in(0,\frac{1}{2})$

With reference to the experiment in [19], the following parameters are firstly taken:

$$ M=1.0\text{ kg},\qquad m=0.3\text{ kg},\qquad c=130\text{ N/m},\qquad b=1\text{ m}.$$

(48)

Corresponding to the dimensionless natural frequencies (18), the dimensional first-order and second-order natural frequencies of this system are

$$ \omega_{10}=10\text{ rad/s},\qquad \omega_{20}=17.32\text{ rad/s}.$$

(49)

The excitation frequency of the internal masses is given as

$$ \omega=11 \text{ rad/s}.$$

(50)

The friction coefficients are given as follows:

$$ f_+=0.1,\qquad f_-=0.4.$$

(51)

Then the dimensionless value k equals 0.25 and locates inside the interval $(0,\frac{1}{2})$. Therefore, to study the steady-state motion, (44) will be employed here.

The length scale L and the dimensionless parameters ε,β in (9) yield

$$ L=1.88 \biggl|\sin\frac{\phi_{10}-\phi_{30}}{2} \biggr| \text{ m},\qquad \varepsilon=\frac{0.0213}{ |\sin\frac{\phi_{10}-\phi_{30}}{2} |},\qquad \beta=5.77.$$

(52)

With reference to (27),

$$ \sigma=\frac{\frac{\varOmega^2}{\omega_{10}^2}-1}{\varepsilon}=9.86 \biggl|\sin\frac{\phi_{10}-\phi_{30}}{2} \biggr|.$$

(53)

In order to use the method of averaging, we will verify whether the three conditions in expression (21) can be fulfilled. The value of βΩ ² equals 6.98, which satisfies the condition βΩ ²∼O(1) in (21). However, according to expressions (23) and (26), when the quantity $|\sin\frac{\phi_{10}-\phi_{30}}{2} |$ takes small values, the conditions y ₁∼O(1) and ε≪1 will be violated, and hence, method of averaging will lose efficacy. Moreover, such situation corresponds to some kinds of stick–slip motion, which will be discussed in detail in Sect. 5.

In what follows, we assume $|\sin\frac{\phi_{10}-\phi_{30}}{2} |=1$ for non-dimensionalization. Then the length scale L=1.88 m, and the dimensionless parameters ε=0.0213, σ=9.86.

Due to the periodicity of the excitation, we notice that instead of the absolute values of the three initial phases, it is the relative values of every two initial phases that affect the steady-state motion of the system. Without loss of generality, we assume ϕ ₂₀ equals zero. To verify the correctness of our analysis through method of averaging, two examples are calculated.

Example 1

k=0.25, ϕ ₂₀=0, ϕ ₃₀=3, and let ϕ ₁₀ vary from 0 to 2π.

Example 2

k=0.25, ϕ ₂₀=0, ϕ ₁₀=2, and let ϕ ₃₀ vary from 0 to 2π.

The approximate dimensionless average steady-state velocities for these two examples are obtained and illustrated in Fig. 2(a) and (b) with solid lines, respectively. Meanwhile, we simulate the exact equations of the system (i.e., (10)) with zero initial displacements and zero initial velocities for all modules. The numerical average steady-state velocities are shown in Fig. 2(a) and (b) with dots.

Fig. 2

The dimensionless average stead-state velocity V _s resulting from numerical simulation (dots) of the exact equation (10) and the approximate solution (solid curve) for k=0.25: (a) ϕ ₂₀=0, ϕ ₃₀=3, ϕ ₁₀ varies from 0 to 2π; (b) ϕ ₁₀=2, ϕ ₂₀=0, ϕ ₃₀ varies from 0 to 2π

It follows from Fig. 2 that the approximate average steady-state velocities based on method of averaging are qualitatively in accordance with the numerical results for both examples. Moreover, in quantitative, they are also in good agreement. Except the very small regions A ₁ and A ₂ near ϕ ₁₀=ϕ ₃₀, the relative errors for almost the whole range are small. As explained above, the big relative errors near ϕ ₁₀=ϕ ₃₀ come from the ineffectiveness of method of averaging, which is induced by the violation of conditions y ₁∼O(1) and ε≪1. Besides, it is worthy mention that the big relative errors correspond to a kind of stick–slip motion, whose mechanism will be discussed in Sect. 5.

Additionally, two groups of parameters are taken to verify the correctness of our construction on solutions η ₁ and η ₂. In Example 1, ϕ ₁₀=1, ϕ ₂₀=0, ϕ ₃₀=3, and in Example 2, ϕ ₁₀=2, ϕ ₂₀=0, ϕ ₃₀=4. For these two cases, the phase diagrams $\eta_{1}-\dot{\eta}_{1}$, $\eta_{2}-\dot{\eta}_{2}$ and the time histories of η ₁ and η ₂ are shown in Figs. 3 and 4, respectively. The analytical solutions obtained through method of averaging are indicated by solid lines, and the numerical solutions are indicated by dot lines. It follows from Figs. 3 and 4 that the solutions we constructed in (30) are correct, and the method of averaging used here is effective and is of high precision when the stick–slip motion is absent.

Fig. 3

The phase diagrams and time histories of η ₁ and η ₂ resulting from numerical simulation (dots) and the approximate solution (solid lines) for k=0.25, ϕ ₁₀=1, ϕ ₂₀=0 and ϕ ₃₀=3: (a) phase diagram $\eta_{1}-\dot{\eta}_{1}$; (b) time history of η ₁; (c) phase diagram $\eta_{2}-\dot{\eta}_{2}$; (d) time history of η ₂

Fig. 4

The phase diagrams and time histories of η ₁ and η ₂ resulting from numerical simulation (dots) and the approximate solution (solid lines) for k=0.25, ϕ ₁₀=2, ϕ ₂₀=0 and ϕ ₃₀=4: (a) phase diagram $\eta_{1}-\dot{\eta}_{1}$; (b) time history of η ₁; (c) phase diagram $\eta_{2}-\dot{\eta}_{2}$; (d) time history of η ₂

4.2 Numerical example for $k\in(\frac{1}{2},1)$

The parameters in expressions (48)∼(50) remain unchanged here, while the friction coefficients are given as follows:

$$ f_+=0.3,\qquad f_-=0.4.$$

(54)

Then the dimensionless value k equals 0.75 and locates inside the interval $(\frac{1}{2},1)$. Equations (47) will be adopted here to study the steady-state motion of the system.

The length scale L and the dimensionless parameters ε,β and σ keep the same as expressions (52) and (53). Similarly, we still assume $|\sin\frac{\phi_{10}-\phi_{30}}{2} |=1$ here, and as in the case $k\in(0,\frac{1}{2})$, L=1.88 m, ε=0.0213 and σ=9.86.

Likewise, two examples, namely, Examples 3 and 4, are calculated:

Example 3

k=0.75, ϕ ₂₀=0, ϕ ₃₀=3, and let ϕ ₁₀ vary from 0 to 2π.

Example 4

k=0.75, ϕ ₂₀=0, ϕ ₁₀=2, and let ϕ ₃₀ vary from 0 to 2π.

Comparisons between the analytical results and numerical results of the dimensionless average steady-state velocity are shown in Fig. 5. Compared with Fig. 2, it can be seen that the magnitudes of the average steady-state velocity have a remarkable decline. Although the trends of the analytical results and numerical results on dimensionless average steady-state velocity are coincident, big quantitative errors exist at the regions B ₁, B ₂ (near ϕ ₁₀=ϕ ₃₀) and region C (near |ϕ ₃₀−ϕ ₁₀|=π). In reigns B ₁ and B ₂, one knows that it is the violation of conditions y ₁∼O(1) and ε≪1 that leads to the invalidation of method of averaging. While in region C, the error is due to the appearance of another kind of stick–slip motion. The detail mechanisms of this stick–slip motion will also be explained in Sect. 5.

Fig. 5

The dimensionless average stead-state velocity V _s resulting from numerical simulation (dots) of the exact equation (10) and the approximate solution (solid curve) for k=0.75: (a) ϕ ₂₀=0, ϕ ₃₀=3, ϕ ₁₀ varies from 0 to 2π; (b) ϕ ₁₀=2, ϕ ₂₀=0, ϕ ₃₀ varies from 0 to 2π

5 Stick–slip effect

Stick–slip effect is an important characteristic of dynamic system with Coulomb’s dry friction. According to the discussion in Sects. 2.3 and 2.4, one knows that module i (i=1,2,3) may conduct a stick–slip motion if the force F _i does not exceed the given maximum value of the friction forces of rest (i.e., ε or εk). The expressions for F _i (i=1,2,3) are shown in (13). Substituting the solutions of η ₁ and η ₂ into expressions (13), we obtain

$$ \begin{aligned}F_1&=\varepsilon \beta \varOmega^2 \sin\varphi_1+\frac{1}{\sqrt{2}}(y_1+y_{20}),\\F_2&=\varepsilon \beta \varOmega^2 \sin \varphi_2-\sqrt{2}y_{20},\\F_3&=\varepsilon \beta \varOmega^2 \sin \varphi_3-\frac{1}{\sqrt{2}}(y_1-y_{20}).\end{aligned}$$

(55)

In what follows, the detail mechanisms for the possible stick–slip motions will be studied. Numerical simulations will be carried out to verify our analysis on the mechanisms. In this section, parameters (48)∼(50) as well as the friction coefficients (51) or (54) will still be used. Without loss of generality, we still assume that ϕ ₂₀=0 here.

5.1 Mechanism 1

Noting that when ϕ ₁₀≈ϕ ₃₀ is hold, $\sin |\frac{\phi_{10}-\phi_{30}}{2} |\approx 0$. In such case, as mentioned in Sect. 4, the conditions y ₁∼O(1) and ε≪1 in expression (21) cannot be satisfied by the first-order modal equation, and hence, method of averaging cannot be adopted any more. This explains the big quantitative errors in regions A ₁, A ₂ of Fig. 2 and regions B ₁, B ₂ of Fig. 5.

According to expression (23), |y ₁₀|_max→0 when ϕ ₁₀≈ϕ ₃₀. Therefore, the amplitude of the first mode is so small that it has little influence on η ₁ and η ₂. Instead, the spatial solution of the second mode plays a leading role y ₂₀. Hence, the solution of η ₁ and η ₂ can be rewritten as

$$ \begin{aligned} \eta_1&\approx\frac{1}{\sqrt{2}}y_{20}=\frac{2\varepsilon \beta \varOmega^2}{\varOmega^2-3}\cos \biggl(\varOmega t+\frac{\phi_{10}}{2} \biggr)\sin\biggl(\frac{\phi_{10}}{2}\biggr),\\\eta_2&\approx-\frac{1}{\sqrt{2}}y_{20}=-\frac{2\varepsilon \beta \varOmega^2}{\varOmega^2-3}\cos \biggl(\varOmega t+\frac{\phi_{10}}{2} \biggr)\sin\biggl(\frac{\phi_{10}}{2}\biggr). \end{aligned}$$

(56)

Then it can speculated from the above equations that η ₁ and η ₂ will evolve anti-synchronously.

Through (13) or (55), the forces F _i (i=1,2,3) can be expressed as

$$ \begin{aligned} F_1&=\varepsilon \beta \varOmega^2 \sqrt{1+ \biggl[ \biggl(\frac{\varOmega^2-1}{\varOmega^2-3}\biggr)^2-1 \biggr]\sin^2 \biggl(\frac{\phi_{10}}{2}\biggr)}\sin \biggl(\varOmega t+\frac{\phi_{10}}{2}+s_1 \biggr),\\F_2&=\frac{\varOmega^2+1}{\varOmega^2-3}\varepsilon \beta \varOmega^2\sin \varOmega t,\\F_3&=\varepsilon \beta \varOmega^2 \sqrt{1+ \biggl[\biggl(\frac{\varOmega^2-1}{\varOmega^2-3} \biggr)^2-1 \biggr]\sin^2\biggl(\frac{\phi_{10}}{2} \biggr)}\sin \biggl(\varOmega t+\frac{\phi_{10}}{2}+s_1\biggr), \end{aligned}$$

(57)

where s ₁ is a constant used for transformations.

As stated in (27), the difference of the excitation frequency Ω from the first natural frequency ω ₁₀ has a magnitude of ε, i.e., Ω ²−1=εσ. Hence, when $\sin^{2}(\frac{\phi_{10}}{2})\rightarrow 1$, the order of F _i (i=1,2,3) can be derived as

$$ |F_1|\sim \varepsilon^2,\qquad |F_2|\sim \varepsilon,\qquad |F_3|\sim \varepsilon^2.$$

(58)

As a result, for a large time interval of a period, the magnitudes of F ₁ and F ₃ are much smaller than the maximal friction forces (i.e., ε or εk), while the magnitude of F ₂ has the same order with the maximal friction forces. As a result, stick–slip motions may happen to modules 1 and 3.

However, when $\sin^{2}(\frac{\phi_{10}}{2})\rightarrow 0$, all the three magnitudes of force F _i (i=1,2,3) have an order of ε. Predictably, although method of averaging does not work here either, no obvious stick–slip motion will take place on modules 1 and 3.

As numerical examples, we firstly take ϕ ₁₀=2.95 and ϕ ₃₀=3, which satisfies the condition ϕ ₁₀≈ϕ ₃₀. This group of values locates insider the region A ₁ of Fig. 2 and region B ₁ of Fig. 5. The value of $\sin^{2}(\frac{\phi_{10}}{2})$ equals 0.99. The time histories of the velocity of each module for k=0.25 and k=0.75 are drawn in Figs. 6 and 7, respectively. The time histories of η ₁ and η ₂ are plotted in Fig. 8 with solid lines and dot-dashed lines, respectively.

Fig. 6

The time histories of $\dot{x}_{i}\ (i=1,2,3)$ for k=0.25, ϕ ₁₀=2.95, ϕ ₂₀=0 and ϕ ₃₀=3: (a) $\dot{x}_{1}-t$; (b) $\dot{x}_{2}-t$; (c) $\dot{x}_{3}-t$

Fig. 7

The time histories of $\dot{x}_{i}\ (i=1,2,3)$ for k=0.75, ϕ ₁₀=2.95, ϕ ₂₀=0 and ϕ ₃₀=3: (a) $\dot{x}_{1}-t$; (b) $\dot{x}_{2}-t$; (c) $\dot{x}_{3}-t$

Fig. 8

The time histories of η ₁ (solid line) and η ₂ (dot-dashed line) for ϕ ₁₀=2.95, ϕ ₂₀=0 and ϕ ₃₀=3: (a) k=0.25; (b) k=0.75

Figures 6 and 7 show that, when the values of ϕ ₁₀ and ϕ ₃₀ lie inside the region A ₁ of Fig. 2 and region B ₁ of Fig. 5, obvious stick–slip motions occur on modules 1 and 3. Solutions of such stick–slip motions cannot be derived by first-order approximation of method of averaging, which as a result, lead to the big quantitative errors in the regions near ϕ ₁₀≈ϕ ₃₀. Besides, it can be seen from Fig. 8 that the time histories of η ₁ and η ₂ are anti-synchronized indeed. This phenomenon coincides with (56) and supports out analysis that the second mode plays a leading role in the situation that ϕ ₁₀≈ϕ ₃₀.

Then, to observe the tendency of the emergence of stick–slip motion with respect to the value of ϕ ₁₀, the following two groups of values are taken, ϕ ₁₀=1.95,ϕ ₃₀=2 and ϕ ₁₀=1,ϕ ₃₀=1, such that the values of $\sin^{2}(\frac{\phi_{10}}{2})$ equal 0.68 and 0.23, respectively. When k=0.25, the time histories of the velocity of each module for ϕ ₁₀=1.95,ϕ ₃₀=2 and ϕ ₁₀=1,ϕ ₃₀=1 are drawn in Figs. 9 and 10, respectively. It reads from Fig. 9 that module 1 does not execute a stick–slip motion, while module 3 still has a sticking state in a very short interval of every period. While from Fig. 10, we find that neither module 1 nor module 3 has stick–slip motion. The above phenomena coincide well with out analysis that modules 1 and 3 will not execute obvious stick–slip motions when $\sin^{2}(\frac{\phi_{10}}{2})\rightarrow 0$.

Fig. 9

The time histories of $\dot{x}_{i}\ (i=1,2,3)$ for k=0.25, ϕ ₁₀=1.95, ϕ ₂₀=0 and ϕ ₃₀=2: (a) $\dot{x}_{1}-t$; (b) $\dot{x}_{2}-t$; (c) $\dot{x}_{3}-t$

Fig. 10

The time histories of $\dot{x}_{i}\ (i=1,2,3)$ for k=0.25, ϕ ₁₀=1, ϕ ₂₀=0 and ϕ ₃₀=1: (a) $\dot{x}_{1}-t$; (b) $\dot{x}_{2}-t$; (c) $\dot{x}_{3}-t$

5.2 Mechanism 2

Notice that when |ϕ ₃₀−ϕ ₁₀|≈π, the conditions y ₁∼O(1) and ε≪1 in expression (21) can be fulfilled by the first-order modal equation. Hence, method of averaging is effective in this case. With reference to (20) and (29), we have

$$\begin{aligned} y_1&=a_1\sin(\varOmega t+\theta_1),\\y_{20}&=-\frac{\sqrt{2}\varepsilon \beta \varOmega^2}{\varOmega^2-3}\sin \varOmega t. \end{aligned}$$

The orders of y ₁ and y ₂₀ yield

$$ y_1\sim O(1),\qquad y_{20}\sim \varepsilon.$$

(59)

It reads that the amplitude of the spatial solution of the second mode y ₂₀ is much smaller than that of y ₁. Hence, we believe that y ₁ plays a leading role in η ₁ and η ₂, and y ₂₀ can be omitted. As a result, the solutions of η ₁ and η ₂ yield

$$ \eta_1\approx \eta_2\approx \frac{1}{\sqrt{2}}a_1\sin(\varOmega t+\theta_1),$$

(60)

and

$$ \eta_2-\eta_1=\frac{2 \varepsilon \beta \varOmega^2}{\varOmega^2-3}\sin \varOmega t.$$

(61)

Hence, it can be speculated that the difference between η ₁ and η ₂ has an order of ε, and η ₁, η ₂ will evolve synchronously.

According to (13) or (55), the forces F _i (i=1,2,3) can be expressed as

$$ \begin{aligned} F_1& \approx \frac{1}{\sqrt{2}}a_1\sin(\varOmega t+\theta_1),\\F_2&=\frac{\varOmega^2-1}{\varOmega^2-3}\varepsilon \beta \varOmega^2\sin \varOmega t,\\F_3& \approx -\frac{1}{\sqrt{2}}a_1\sin(\varOmega t+\theta_1). \end{aligned}$$

(62)

Then, based on (27), the orders of F _i (i=1,2,3) can be determined as

$$ |F_1|\sim O(1),\qquad |F_2|\sim \varepsilon^2,\qquad |F_3|\sim O(1).$$

(63)

Therefore, the magnitudes of F ₁ and F ₃ are much larger than the maximal friction forces (ε or εk) for almost the whole period. On the contrary, the magnitude of F ₂ is smaller than the maximal friction forces. Stick–slip motion may happen to module 2 as a result. This explain the big quantitative error in region C of Fig. 5.

As an example, we select ϕ ₁₀=0 and ϕ ₃₀=3 to verify our analysis on the occurrence of stick–slip motion on module 2. Such values locate inside the region C of Fig. 5(a). Figures 11 and 12 show the time histories of the velocity of each module for k=0.25 and k=0.75, respectively. From Figs. 11 and 12, we can see clearly that module 2 executes an obvious stick–slip motion when k=0.75, while no stick–slip motion appear on any module when k=0.25. The above phenomena not only support our prediction on the stick–slip motion of module 2, but also suggest that the stick–slip motion is also associated with the parameter k (to be discussed later). Moreover, the time histories of η ₁ and η ₂ are shown in Fig. 13 with solid line and dot-dashed line, respectively. Notice that η ₁ and η ₂ are almost synchronized. Hence, the analysis on the solutions of η ₁ and η ₂, as well as (60) and (61) are verified.

Fig. 11

The time histories of $\dot{x}_{i}\ (i=1,2,3)$ for k=0.25, ϕ ₁₀=0, ϕ ₂₀=0 and ϕ ₃₀=3: (a) $\dot{x}_{1}-t$; (b) $\dot{x}_{2}-t$; (c) $\dot{x}_{3}-t$

Fig. 12

The time histories of $\dot{x}_{i}\ (i=1,2,3)$ for k=0.75, ϕ ₁₀=0, ϕ ₂₀=0 and ϕ ₃₀=3: (a) $\dot{x}_{1}-t$; (b) $\dot{x}_{2}-t$; (c) $\dot{x}_{3}-t$

Fig. 13

The time histories of η ₁ (solid line) and η ₂ (dot-dashed line) for ϕ ₁₀=0, ϕ ₂₀=0 and ϕ ₃₀=3: (a) k=0.25; (b) k=0.75

5.3 Effect of k on the stick–slip motion

As is shown in Figs. 11 and 12, the emergence of stick–slip motion is related to the coefficient k. In this section, we will discuss the effect of k on the stick–slip motions.

On one hand, when the value of k is small, the friction for forward motion is relatively low (assuming that f ₋ remains the same). It leads to a larger magnitude of average steady-state velocity of the system as a whole. This can be clearly observed through comparison between Figs. 2 and 5. Besides, according to (60), it can be found that $\dot{\eta}_{1}\approx \dot{\eta}_{2}$. Then it follows from $\dot{x}_{2}=V-\frac{1}{3}(\dot{\eta}_{1}-\dot{\eta}_{2})$ that the velocity of module 2 can be always positive. This result is demonstrated well through Fig. 11, from which we can see that the curve of $\dot{x}_{2}$ locates above zero always. Hence, the stick–slip motion is impossible on module 2, for the reason that $\dot{x}_{2}=0$ cannot be realized. Consequently, we obtain the first result about the effect of k on stick–slip motions.

Result (1): For fixed values of initial phases ϕ _i0 (i=1,2,3) that satisfying |ϕ ₁₀−ϕ ₃₀|≈π, stick–slip motion on module 2 is more difficult to be realized for smaller values of k.

On the other hand, provided that ϕ ₁₀≈ϕ ₃₀ is satisfied, the magnitudes of F ₁ and F ₃ in (57) increase if $\sin^{2}(\frac{\phi_{10}}{2})\rightarrow 0$. If the magnitudes of F ₁ and F ₃ are larger than the maximal friction forces (εk or ε), sticking state cannot be triggered. Hence, it can be predicted that stick–slip motion is easier to be realized on modules 1 and 3 if we take a smaller value of k. We put two examples with the same values of initial phases (ϕ ₁₀=2.5,ϕ ₂₀=0ϕ ₃₀=2.5) but different values of k into comparison. One is k=0.25, and the other is k=0.75. The time histories of the velocity of each module are shown in Figs. 14 and 15, respectively.

Fig. 14

The time histories of $\dot{x}_{i}$ (i=1,2,3) for k=0.25, ϕ ₁₀=2.5, ϕ ₂₀=0 and ϕ ₃₀=2.5: (a) $\dot{x}_{1}-t$; (b) $\dot{x}_{2}-t$; (c) $\dot{x}_{3}-t$

Fig. 15

The time histories of $\dot{x}_{i}\ (i=1,2,3)$ for k=0.75, ϕ ₁₀=2.5, ϕ ₂₀=0 and ϕ ₃₀=2.5: (a) $\dot{x}_{1}-t$; (b) $\dot{x}_{2}-t$; (c) $\dot{x}_{3}-t$

From Figs. 14, we find that modules 1 and 3 perform obvious stick–slip motions for k=0.25. Rather, in Fig. 15, for k=0.75, no stick–slip motion appears. Therefore, our prediction is verified, and the second result about the effect of k on stick–slip motion is given as follows:

Result (2): For fixed values of initial phases ϕ _i0 (i=1,2,3) that satisfying ϕ ₁₀≈ϕ ₃₀, it is easier for modules 1 and 3 to perform stick–slip motions for smaller value of k.

6 Optimal control

As a possible dynamic model of worm-like robot, average steady-state velocity of the system is one of the key characters and is our optimizing object in this research. Larger magnitude of the average steady-state velocity of the system implies higher efficiency and less energy input, which is of great significance in robot industries.

Firstly, the effects of friction coefficients on the average steady-state velocity will be studied. Parameters (48)∼(50) are used in this section again, and the friction coefficient f ₋=0.8 remains unchanged. Similarly with Sects. 4.1 and 4.2, two examples are calculated for $k\in(0, \frac{1}{2})$ and $k\in (\frac{1}{2}, 1)$ respectively, i.e.,

Example 5

$k\in(0, \frac{1}{2})$, ϕ ₂₀=0,ϕ ₃₀=3.1, and let ϕ ₁₀ vary from 0 to 2π.

Example 6

$k\in (\frac{1}{2}, 1)$, ϕ ₂₀=0,ϕ ₃₀=3.1, and let ϕ ₁₀ vary from 0 to 2π.

For different values of k, the dimensionless average steady-state velocities of the system are numerically obtained and are shown in Fig. 16(a). To observe the variation of the average steady-state velocity with the parameter k more clearly, plots for $k\in(0, \frac{1}{2})$ and $k\in(\frac{1}{2}, 1)$ are shown in Figs. 16(b) and (c), respectively.

Fig. 16

The average steady-state velocities for different values of k when ϕ ₂₀=0, ϕ ₃₀=3.1 and ϕ ₁₀ varies from 0 to 2π: (a) k∈(0,1); (b) $k\in (0, \frac{1}{2})$; (c) $k\in (\frac{1}{2}, 1)$

It follows from Fig. 16 that the average steady-state velocity decreases significantly when we enlarge the magnitude of k. Such a phenomenon is predictable, since the resistance force for forward motion will be much smaller than that for backward motion if a small value of k is taken. Moreover, no matter what values of ϕ ₁₀ are taken, we find that all the dimensionless average steady-state velocities for k>0.5 are almost smaller than 0.1. In such situation, the average steady-state velocities are so small that can be hardly utilized in practice. Based on the above analysis, we conclude the first optimal control strategy.

Strategy (1): The dimensionless friction coefficient k ($k=\frac{f_{+}}{f_{-}}$) should be taken as small as possible, so as to achieve a higher average steady-state velocity of the system as a whole.

Then, we will study the effects of initial phases on the average steady-state velocity. Provided that the value of k is small (e.g., k<0.45), we notice from Fig. 16 that the maximum value of the average steady-state velocity is always obtained in the region near |ϕ ₁₀−ϕ ₃₀|≈π. Such a phenomenon does not occur when k>0.45 due to the stick–slip motions on module 2 when |ϕ ₁₀−ϕ ₃₀|≈π. Hence, the second optimal control strategy is derived as follows:

Strategy (2): Provided that Strategy (1) is applied, the values of initial phases ϕ ₁₀ and ϕ ₃₀ should satisfy the condition that |ϕ ₁₀−ϕ ₃₀|≈π so as to increase the average steady-state velocity of the system as a whole. Extra energy input is not required in the process of this optimal control.

To observe the effects of control, we put the uncontrolled situation and the optimal-controlled situation into comparison. When there is no control, we have ϕ ₁₀=ϕ ₂₀=ϕ ₃₀=0; and when the optimal control is applied according to Strategy (2), we have ϕ ₁₀=0, ϕ ₂₀=0, ϕ ₃₀=3.1. k is assumed to be 0.25 here. The time histories of the variable V are shown in Fig. 17(a) and (b) for the two situations, respectively.

Fig. 17

The time histories of V for the uncontrolled situation and optimal-controlled situation when k=0.25: (a) uncontrolled situation ϕ ₁₀=ϕ ₂₀=ϕ ₃₀; (b) optimal-controlled situation ϕ ₁₀=0, ϕ ₂₀=0, ϕ ₃₀=3.1

It follows from Fig. 17 that the average steady-state velocity has a remarkable increase due to our optimal control. The dimensionless average steady-state velocity equals 0.107 for the uncontrolled situation, while equals 0.45 for the optimal-controlled situation. Besides, the velocity amplitude has a significant decline to about 0.09 for the optimal control situation from 0.27 for the uncontrolled situation. Thus, by utilizing control strategy (2), without extra energy input, a higher average steady-state velocity can be obtained. The efficiency of the system is improved.

Figures 18(a) and (b) show the time histories of the velocity of each module of the two situations, respectively. It is clear that modules 1, 2 and 3 move synchronously in the uncontrolled situation, with a low velocity on average. No elastic force is generated on the springs, i.e., the three modules move independently. However, in the optimal-controlled situation, it is noticed that the three modules oscillate with a larger average steady-state velocity. Especially, module 2 has an always positive velocity, with very little up-and-down fluctuation. Instead, the velocities of modules 1 and 3 oscillate with a large amplitude. A half cycle difference exists between their velocities, and it seems that modules 1 and 3 conduct an anti-synchronized motion. Such anti-synchronization phenomenon can be explained as follows. As mentioned in (61) and (62), when |ϕ ₁₀−ϕ ₃₀|≈π, $\eta_{1}\approx\eta_{2}\approx\frac{1}{\sqrt{2}}a_{1}\sin(\varOmega t+\theta_{1})$ and $\eta_{2}-\eta_{1}=\frac{2 \varepsilon \beta \varOmega^{2}}{\varOmega^{2}-3}\sin\varOmega t$. Putting (61) and (62) into (31), one obtain

$$ \begin{aligned} \dot{x}_1&\approx V-\frac{1}{\sqrt{2}}a_1\varOmega\cos(\varOmega t+\theta_1),\\\dot{x}_2&\approx V+\frac{2\varepsilon \beta \varOmega^3}{3(3-\varOmega^2)}\cos\varOmega t,\\\dot{x}_3&\approx V+\frac{1}{\sqrt{2}}a_1\varOmega\cos(\varOmega t+\theta_1). \end{aligned}$$

(64)

Hence, we know that modules 1 and 3 do carry out an anti-synchronized motion. Some elastic forces will generate on the springs owing to the relative displacement between two adjacent modules. It seems that each module “pushes” or “pulls” the neighboring module.

Fig. 18

The time histories of $\dot{x}_{1}$ (dashed lines), $\dot{x}_{2}$ (solid lines) and $\dot{x}_{3}$ (dotted lines) for the two situations when k=0.25: (a) uncontrolled situation ϕ ₁₀=ϕ ₂₀=ϕ ₃₀; (b) optimal-controlled situation ϕ ₁₀=0, ϕ ₂₀=0, ϕ ₃₀=3.1

7 Conclusion

The dynamics of a three-module vibration-driven system is studied in this paper. Each module serves as an actuator and represents a system with a movable internal mass. Such system accords with the developing trend of modern robots, since it has the earthworm as prototype and is promisingly to be further minimized. Therefore, the study on the dynamics of such vibration-driven system is of great significance in robots design and manufacture. In this research, non-symmetric Coulomb’s dry friction is assumed to act between the system and the medium, and sinusoidal excitations are applied to the internal masses.

Our paper consists of two parts. In the first part, the mechanical system is established, whose equations of motion are transformed into a nondimensional form. Particular attention is paid to investigate the steady-state behaviors of the system when stick–slip effect is negligible. By studying the modal coordinate equations, both methods of averaging and modal superposition are employed to construct the steady-state solutions of the system. A series of algebraic equations are obtained, from which, the average steady-state velocity of the system as a whole can be derived. For relatively small value of k, numerical simulation shows that the approximate average steady-state velocities based on method of averaging coincide with the numerical results in acceptable accuracy. However, when k is relatively large, the magnitudes of the average steady-state velocity are very small, and there exist big quantitative errors between the analytical results and numerical results. These errors are caused by the invalidation of the method of averaging and the possible stick–slip motions.

In the second part of our paper we focus firstly on the mechanisms for the possible stick–slip motions. Two mechanisms associated with the initial phases of the internal excitations are put forward, which explains the big quantitative errors on the approximate average steady-state velocity of the system. Numerical examples are calculated to verify our analysis on the mechanisms of stick–slip motions. Moreover, we point out that the stick–slip motions are k-dependent. Then the optimal control problem is analyzed, whose object is to realize the maximization of the average steady-state velocity of the system as a whole. Starting from the effect of friction coefficient on the average steady-state velocity, by control strategy (1) it is seen that small values of k should be taken so as to achieve a large magnitude of the average steady-state velocity. Special attention is also paid to the initial phases of the internal excitations, and control strategy (2) is raised: the values of initial phases ϕ ₁₀ and ϕ ₃₀ should satisfy the condition |ϕ ₁₀−ϕ ₃₀|≈π so as to increase the average steady-state velocity of the system without extra energy input.