Abstract
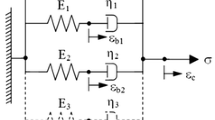
This study investigates the role of a breathing crack on a viscoelastic composite rotor-shaft system supported at the ends by journal bearings. A finite element-based mathematical formulation is developed to model the breathing crack. The geometry of the crack configuration is used to derive a time-dependent stiffness matrix. This matrix is then incorporated into the equation of motion for the composite shaft, derived with the Equivalent Modulus Theory (EMT). The equation of motion is of higher order due to the inclusion of the material’s internal damping behavior, modeled using an operator-based viscoelastic model. Upon validating the mathematical model of the breathing crack, we analyzed its effects over one complete shaft rotation. This analysis further compared the strain energy and orbit plots of the cracked shaft with those of an intact shaft.
Similar content being viewed by others
Explore related subjects
Discover the latest articles, news and stories from top researchers in related subjects.Avoid common mistakes on your manuscript.
1 Introduction
A rotating machine consists of several parts, but the rotating module, i.e., the shaft or rotor, is responsible for the key cause of vibration in the structure. Heavy loading of these machines eventually leads to an asymmetrical defect or final failure, resulting in equipment and loss of life. Out of several failures in rotating structures, vibration and fatigue cracks are considered the major failure causes, propagating in due sequence of operation. Eventually, to solve the vibration issue in rotating structures, the conventional materials used for modeling the shaft system are replaced with materials with lesser density and higher strength, like composites. Under conditions when unconventional materials are used to construct the rotating module, proper modeling of the material damping properties is necessary, which tends to generate a rotating damping force tangential to whirl orbit, destabilizing the rotor shaft system (Dimentberg 1961).
Several researchers have published works depicting different modeling techniques and experimental procedures for predicting the dynamic behavior of the shaft made of composite materials. Zinberg and Symonds (1970) performed experiments on the composite shaft and compared the critical speed by modeling the shaft using the Equivalent Modulus Beam Theory (EMBT). Bert (1993) analyzed a composite shaft incorporating the effects of bending and torsion coupling as well as gyroscopic moment modeled using the Euler–Bernoulli beam theory. Kim and Bert (1993) developed the equation of motion for cylindrical hollow composite shaft using the Sanders first-order approximation. Singh and Gupta (1994) used First-Order Shear Deformation Theory (FSDT) to formulate the equation of motion and perform the eigenvalue analysis of a composite shaft. Singh and Gupta (1996) performed the dynamic analysis of composite shaft employing Layered Beam Theory (LBT) and EMBT. It was perceived that EMBT had limitations to symmetric stacking sequences. Gubran et al. (2000) used modified EMBT and Rayleigh-Ritz displacement method for stress analysis of fiber-reinforced thin composite shaft subjected to steady torque and unbalanced excitation. Kam and Liu (1998) applied a nondestructive evaluation approach to determine the distribution of bending stiffness along the span of a composite shaft. Kim et al. (1999) used the general Galerkin method to study the effect of shaft tapering and the use of filament-wound composite shaft for high-speed cutting tool operations. Chang et al. (2004) adopted the Mori–Tanaka mean field theory to study the vibration behavior of the composite shaft embedded with randomly oriented reinforcements. Gubran and Gupta (2005) used EMBT to model a composite tubular shaft integrating the effect of shear deformation, rotary inertia, and gyroscopic effect and performed a parametric study over different stacking sequences. Alwan et al. (2010) performed experimental as well as numerical analysis over composite tube and solid shafts made of different materials such as carbon-epoxy, glass-epoxy, and boron-epoxy to determine system eigen frequencies and damping characteristics. Yongsheng et al. (2014) used the Galerkin method to solve the governing equation and carry out the dynamic analysis of a thin-walled, internally damped rotating composite shaft. Further, Irani et al. (2016) applied the Differential Quadrature numerical Method (DQM) to derive the governing equation of a composite Timoshenko rotor considering longitudinal-transverse vibration. The authors studied the effects of spin speed, lamination angles, and boundary conditions over the system’s natural frequencies and instability speed limits.
Viscoelastic composites are known for their superior damping characteristics, crucial in mitigating vibrations and reducing noise in rotor-shaft systems. These properties enhance the stability and longevity of rotor shafts, particularly in high-speed and high-performance applications. Roy and Dutt (2016) applied a constitutive relationship based on an operator-based approach to developing a higher-order Finite Element (FE) model of the viscoelastic composite rotor using an ADF (Anelastic displacement field) approach after assuming the viscoelastic nature of both fiber and matrix materials. Mendonça et al. (2017) studied the effect of internal damping present in the composite shaft over the rotors mounted on it. The authors simulated different composite shaft layup to present its influence on the rotor’s behavior. Most recently, Ben Arab et al. (2017, 2018) used Equivalent Single Layer Theory (ESLT) to formulate the equation of motion and perform vibration analysis of an operating composite shaft considering the effects of stacking sequence, fiber alignments, and normal-shear coupling and hysteretic damping. The authors recognized ESLT as a fairly appropriate approach for the dynamic analysis of rotating composite shafts in symmetric and nonsymmetric stacking arrangements. Following this, Ganguly and Roy (2021a) proposed the Equivalent Modulus Technique (EMT) to include the effect of viscoelastic properties of different composite layers while deriving the equation of motion of the rotating shaft and performing its dynamic analysis.
Along with the modeling of evolving new materials for shafts such as composites, proper modeling and execution of dynamic analysis of operating shafts detected with cracks due to cyclic loading or manufacturing fault early to circumvent catastrophic failure is also important. The presence of a crack adversely affects the stiffness of a structure as complex as rotating shafts and its mechanical behavior. Several researches show that it is important to study the dynamics in such conditions so as to determine the operation limits of the structure.
Though literature provides an abundant study on modeling cracks of varying nature using different techniques and further incorporated in structures to investigate its effects, a perfect modeling technique resembling the breathing behavior, i.e., closing and opening of a crack, is approximated. Precisely, the breathing crack model on a rotating shaft is entirely different, which, however, was estimated by a few researchers through different unique techniques. Mayes and Davies (1984) formulated the time-dependent stiffness of a cracked rotor, showing its breathing nature using classical breathing function, and performed a dynamic analysis of the cracked rotor system. Jun et al. (1992) applied the concepts of fracture mechanics to derive a simplified model for breathing crack by assuming the crack to behave as switching in nature and studied its effect on the vibration characteristics of a simple rotor system. Green and Casey (2005) and Jun and Gadala (2008) studied the breathing crack behavior on the crack responses and harmonic characteristics of a rotating shaft using the Transfer Matrix Method. Papadopoulos (2008) approached modeling switching and breathing cracks in a rotor shaft by applying the strain energy release rate approach. Patel and Darpe (2008) performed a comparative study on the nonlinear dynamics of a rotor, considering both switching and breathing crack models formulated using a response-dependent flexibility matrix. Al-Shudeifat and Butcher (2011) modeled a breathing crack and derived the time-dependent moment of inertia on the basis of geometry and objective functions. Guo et al. (2013) worked on approximating and detecting the breathing crack and its propagation in a Jeffcott rotor using the empirical mode decomposition method. A methodical 3-D computational approach was presented by El Arem and Ben Zid (2017) to identify the breathing crack nature based on the unilateral contact conditions on the crack lips and further study the shaft dynamics. Varney and Green (2017) performed a stability analysis on an overhung rotor to study the effect of a breathing crack modeled using Floquet stability analysis. The authors concluded that with increasing crack depth, the thick shaft rotating at a lower speed tends to reach unstable regions. Prawin et al. (2019) performed a novel experiment using a single sensor based on the zero strain energy node concept to locate the exact position of a breathing crack in space. Most recently, Ganguly and Roy (2021b) presented an optimization-based novel mathematical model based on the crack geometry to exactly replicate the breathing behavior of the crack on a composite rotor system.
The current analysis emphasizes presenting a methodology to model the breathing nature of a crack and investigate its effect on the journal-bearing mounted viscoelastic laminated composite shaft. The breathing behavior of a crack over one complete shaft rotation is generated based on closed-loop relations derived from the crack geometry. The geometric relations are used to derive the time-dependent uncracked area, centroidal positions, and, finally, the area moment of inertia. On further formulating the time-dependent stiffness and mass matrix, which also tends to imitate the opening and closing behaviors of the crack, it is assembled in the respective global matrices of the FE model of the laminated composite shaft. A comparative study of the intact shaft with that of the crack shaft for one complete rotation is presented to show the impact of the breathing crack for different stacking sequences in terms of strain energy, mode shapes, time response, and orbit plot.
2 Mathematical modeling
2.1 Geometric modeling of breathing crack
In general, the breathing behavior implies the opening and closing of the crack during one complete rotation of the cracked cross-section. In rotating machinery, the breathing mechanism of the crack mainly appears due to the shaft weight. Among all types of cracks, breathing crack models closely resemble the practical situation (Liu and Barkey 2018).
Numerous methodologies are cited in the literature asserting diverse modeling methods to efficiently replicate the genuine breathing nature of a crack in a circular cross-section of a rotor system (Al-Shudeifat and Butcher 2011; Guo et al. 2013). However, this segment describes a much easier and equally effective method to depict the closing and opening phenomenon of a breathing crack, specifically in a dynamic rotor system. The breathing behavior, which depends on shaft rotation, is modeled using its geometry.
The following are the assumptions considered for modeling the breathing behavior of the shaft and performing the analysis of the cracked viscoelastic composite shaft.
-
Linear Viscoelastic Material: The shaft material is assumed to be linearly viscoelastic, meaning that the stress-strain relationship follows the Hooke law, and the material deforms proportionally to the applied load. Linear viscoelastic models are used to represent the viscoelastic behavior of the material.
-
Small Deformations: Deformations are assumed to be small, allowing the use of linear theories of elasticity and beam theory. This means that the changes in geometry due to deformation are negligible.
-
Symmetric Geometry: The shaft is assumed to be perfectly circular in cross-section and symmetric about its longitudinal axis, except for the presence of the crack.
-
Breathing Crack Behaviour: The crack is assumed to exhibit breathing behavior, meaning it opens and closes periodically during rotation. The crack opens due to tensile stress and closes under compressive stress. The modeling of such behavior is done using the geometry that the cross-section follows throughout one full shaft rotation.
-
Crack Location and Orientation: The location, size, and orientation of the crack are precisely defined. The crack is typically assumed to be transverse (perpendicular to the shaft axis) and located at a specific position along the length and circumference of the shaft.
-
Uniform Rotational Speed: The shaft rotates at a constant angular velocity, and the effects of acceleration and deceleration are neglected. This simplifies the dynamic analysis.
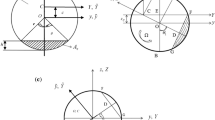
The labeled diagram at different instances of the cracked circular cross-section depicting breathing behavior is represented in Fig. 1. The crack with the maximum crack depth ratio \(\mu = \frac{h}{r}\) subtends an angle \(\gamma = 2\cos ^{ - 1}\left ( 1 - \mu \right )\) to the center. The crack divides the cross-section into two areas, i.e., \(A_{1}\) the constant uncrack area and the maximum crack area denoted by \(A_{c}\). The expressions for these variables can be derived using basic geometrical relations. For any instant of rotation of the cross-section with breathing crack varying between \(0 \le \theta \le 2\pi \) where \(\theta = \Omega t\), point C denotes the time-dependent centroid coordinates while the cracked area \(A_{c}\) becomes \(\theta \) dependent.
The zoomed-in view of Fig. 1(c), which focuses on the instant of time, where the crack is partially closed, is shown in Fig. 2. The labeling clearly indicates that the time-dependent closed portion is further divided into two geometrically known areas denoted as \(A_{2}(t)\) and \(A_{3}(t)\). However, the coordinates of the centroid C for the range of time while the crack is fully open are given by,
For the range of \(\theta \) where the crack starts to close (\(\theta _{1}\)) to the instant when the crack fully closes (\(\theta _{2}\)), it is known that the geometrical parameters related to the total circular cross-section, such as total uncracked area, centroid position and moment of inertia becomes time-dependent. In this case, all the variables used to define the instantaneous area and respective moment of inertia are a function of \(\gamma \), \(r\), and \(z_{\mathrm{C}}\). Out of these \(\alpha \) and \(r\) are the known quantities, while \(z_{\mathrm{C}}\) is the instantaneous centroid coordinate, which remains unknown throughout shaft rotation.
Following Ganguly and Roy (2021b), the equations of the labels in Fig. 2 are expressed in terms of \(z_{\mathrm{C}}\).
Similarly, the areas \(A_{2}\) and \(A_{3}\) and their respective centroid coordinates \(\left ( y_{2},z_{2} \right )\) and \(\left ( y_{3},z_{3} \right )\) can also be derived using the above relations,
where, \(e_{3} = \frac{4r\left ( \sin \left ( \frac{\beta}{2} \right ) \right )^{3}}{3\left ( \beta - \sin \beta \right )}\) is the centroid distance of area \(A_{3}\) from \(O\).
Since the expressions for individual segments of the total uncracked area are now obtained, a conventional formula based on geometrical decomposition can be used to determine the centroid distance of the total closed area (\(z_{\mathrm{C}}\)) in the following form,
On substituting the equation for \(z_{1}\) (Eq. (1)) as well as all other variables from Eq. (2a)–(2d) and Eq. (3a)–(3d), Eq. (4) is formed to be nonlinear in nature for \(z_{\mathrm{C}}\) and dependent on \(\theta \). A nonlinear equation solver is used to solve for \(z_{\mathrm{C}}\) at any value of \(\theta \).
Once the value of \(z_{\mathrm{C}}\) is in hand, all the labels (Eq. (2a)–(2d) and Eq. (3a)–(3d)) are now reassessed. Therefore, at any \(\theta \) instant, the centroid coordinate \(y_{\mathrm{C}}\) can be regenerated using the similar conventional equation.
Further, to find the area moment of inertia of the entire closed region at any point of time between \(\theta _{1}\) and \(\theta _{2}\), the area moment of inertia of each area, i.e., \(A_{1}\), \(A_{2}\), and \(A_{3}\) are found out individually.
Further following Ganguly et al. (2021), the total area moment of inertia about the centroid axis can be calculated as,
The above expression for moment of inertia is ultimately used in the FE-based bending stiffness and circulatory stiffness matrix of the crack element of the shaft continuum, making it a function of time.
2.2 Viscoelastic crack composite shaft: FE model
This segment concisely represents the FE modeling of cracked composite shaft considering material damping. The composite shaft encompasses concentric laminas of unidirectional fiber reinforced into the matrix material. The structure being 1-dimensional in nature and dominant longitudinal strain, the 1-D constitutive relationship is considered through plane stress condition.
Applying EMT (Ganguly et al. 2021), the stiffness matrix \(\left [ \mathbf{K} \right ]\) of the composite laminated shaft considering Timoshenko beam theory is given by,
Where \(A_{i}\) is the uncracked area of the \(i\)th layer of the laminated composite rotor. As the crack depth increases, the crack tends to reach consecutive layers of the rotor, resulting in a decrease in the uncracked area of the \(i\)th layer. In contrast, the moment of inertia denoted by \(I\) is replaced by the time-dependent relation derived in the previous section. Hence, the equivalent modulus of the composite structure happens to be dependent on the area and the moment of inertia of the uncracked lamina, which is further a function of the crack depth.
The higher-order equation of motion of the laminated composite shaft element can be written as (Ganguly and Roy 2021a),
where,
The bending stiffness \(\left [ \bar{\mathbf{K}}_{B} \right ]\), circulatory matrices \(\left [ \bar{\mathbf{K}}_{C} \right ]\), and mass matrix \(\left [ \mathbf{M} \right ]\) used in the above equation of motion are for the intact element of the shaft. However, these matrices are replaced with the matrices derived for crack element in the shaft system and further assembled according to the finite element procedure depending upon the crack element position.
3 Results and discussion
3.1 Problem statement
The composite is fabricated by reinforcing carbon fiber into the epoxy matrix. A single lamina composite sample fabricated using unidirectional carbon fibers embedded into epoxy resin is experimented with in DMA to acquire their storage and loss modulus properties. For numerical illustration, a rotor shaft of continuum length 1 m and diameter 0.048 m is considered to be mounted over two journal bearings at its two extreme ends, as shown in Fig. 3, to closely relate to realistic models. The stiffness coefficients \(K_{b_{yy}}\), \(K_{b_{yz}}\), \(K_{b_{zy}}\), \(K_{b_{zz}}\) and damping coefficients \(C_{b_{yy}}\), \(C_{b_{yz}}\), \(C_{b_{zy}}\), \(C_{b_{zz}}\) for the journal bearing are determined based on the methodology described by Friswell et al. (2010). The parameters for calculating these coefficients include a bearing length-to-diameter ratio \(L_{brg}/D_{brg} = 0.3\), a bearing diameter \(D_{brg} = 0.048m\), an oil viscosity of 0.1 Pa-s, and a radial clearance of 0.0001 m between the journal and the bearing. The static thrust forces on the left and right bearings, resulting from the self-weight of the system, generate different bearing coefficients at the two ends. Equivalent Modulus Theory is applied to configure the composite modeling of the shaft while the FE model based on Euler–Bernoulli beam theory is formulated after meshing the shaft continuum into ten 1-D 2-noded elements, with each node having 4 degrees of freedom, i.e., two translational and two rotational. The detailed properties of the composite material are tabulated in Table 1, while Table 2 provides the details of the discs mounted on the rotor at two different nodal positions, i.e., nodes 4 and 8, following Ganguly and Roy (2021a).
3.2 Strain energy
The strain energy stored in the laminated composite shaft due to deformation is given by,
Considering longitudinal strain \(\varepsilon _{xx}\) subjected to bending, the deformation energy can be written as
For the finite element formulation, the total strain energy stored can be represented as the summation of elemental deformation energy to which the system continuum is discretized, i.e., the total strain energy of the system with \(E\) number of discretized elements can be signified as
The expression of the deformation energy for the \(e\)th element having \(n\) number of layers is given as,
Following Fig. 4(a) and Fig. 4(b), the nodal degrees of freedom of the shaft element \(\left \{ q_{v}^{e} \right \}\) and \(\left \{ q_{w}^{e} \right \}\) mentioned in the above equation can be arranged in the following manner;
On solving the above equation of deformation energy and substituting in Eq. (7), the total strain energy stored due to deformation is given by,
The matrix \(\left [ \mathbf{K}^{\mathbf{e}} \right ]\) in the above equation is derived and globalized for \(E\) number of elements while modeling the viscoelastic laminated composite shaft using EMT. Hence, the globalized matrix is represented by the matrix \(\left [ \mathbf{A}_{\mathbf{0}} \right ]\) from Eq. (8).
As the \(\left [ \mathbf{A}_{\mathbf{0}} \right ]\) matrix is a function of \(\Omega t\), as a result ofresulting from the breathing phenomenon, the strain energy stored can be represented for one complete rotation (\(0 \le \Omega t \le 2\pi \)) of the cracked composite shaft at a spin speed within a stable range. The study is performed considering four different laminate stack sequences of the 8-layer composite shaft as tabulated in Table 3, considering a breathing crack of depth ratio \(\mu = 0.5\) in the fifth element of the discretized continuum of the shaft.
Figure 5 represents the strain energy stored in an uncracked composite shaft and compares it with the same composite shaft system, considering a breathing crack for all four sequences, as mentioned in Table 3. The plot represents the strain energy stored for one full rotation of both cracked and uncracked composite shaft, i.e., from 0 to \(2\pi \) at a spin speed of \(\Omega = 1000 rpm\), below the stability limit of spin speed. For certain region, within one full rotation of the cracked shaft, as the breathing crack tends to close or open, the energy stored is observed to be increasing and decreasing, depending on the rise and fall of the stiffness due to the breathing phenomenon.
Compared with the uncracked shaft for any sequence, the cracked shaft with a fully open condition shows the maximum loss in energy. Although the deflection \(\left \{ \mathbf{q} \right \}\) for the fully open cracked shaft is more than the deflection in the uncracked shaft, the stiffness, i.e., \(\left [ \mathbf{A}_{\mathbf{0}} \right ]\), which is \(> > \left \{ \mathbf{q} \right \}\), varies inversely for the cracked and uncracked shaft system. However, for the part of the rotation when the crack is in fully closed condition, the energy stored matched for both cracked and uncracked system. Hence, a loss in stored energy is observed to follow such a pattern for one full rotation.
When it comes to the stacking sequences, the maximum energy loss in Sequence 1 is minimal, while Sequence 4 (Fig. 5(d)) shows that the maximum loss in energy is the highest among all the sequences. Considering the fact that as the 0̊ fiber laminas move outwards (Sequence 3) and also increase in number (Sequence 4), the system tends to exhibit more stored energy. For the considered crack depth ratio \(\mu = 0.5\), which cracks the first four laminas of each sequence from outside, Sequence 4 is observed to crack down two 0̊ fibre laminas resulting in maximum loss in energy when compared to uncracked shaft among all the sequences. Table 4 represents the maximum percentage error in the energy storage during one full shaft rotation for all the considered sequences.
3.3 Mode shapes
The mode shape represents the shape of the composite shaft by indicating the path traveled by all the points throughout the continuum at different modes. The eigenvectors of the composite shaft system are used to plot the 3D forward and backward mode shapes owing to forward (F) and backward (B) whirling, respectively, at a spin speed of 1000 rpm. Figure 6 shows the first four bending modes of the uncracked composite shaft and is further compared with the composite shaft considering the breathing crack of in \(\mu = 0.5\). The locus of each node starts with a (*) mark and is kept unfinished to demonstrate the direction. Clockwise rotations of the circles present in the figure are considered backward whirl, while the forward whirl is determined by counterclockwise rotation of the circles. The first two modes, 1B (Fig. 6(a)) and 3F (Fig. 6(b)), respectively, signify the backward and forward whirl corresponding to the first mode of vibration, while 2B (Fig. 6(c)) and 4F (Fig. 6(d)) denotes the backward and forward whirl corresponding to the second mode of vibration. A clear distortion in the mode shapes for all modes is observed under crack conditions.
3.4 Time response and orbit plot
This section delves into the dynamic behavior of the crack over time, as illustrated by the time response and orbit plot. Specifically, in Sect. 3.1, we conduct a numerical study of a cracked composite rotor shaft and compare its responses to those of an uncracked shaft. This comparison is made for the fourth stacking sequence at the second disc position from the left end of the shaft (node 7), operating within a stable speed region (\(\Omega = 3200\) rpm).
The Y- and Z-direction time response patterns, depicted in Fig. 7, exhibit the steady-state vibration characteristics of both the uncracked and cracked shafts. For enhanced clarity, a magnified view of the comparative time response is presented in Fig. 7(a). This zoomed-in perspective highlights the periodic deviations between the responses of the cracked and uncracked shafts, which are indicative of the crack’s breathing action — the opening and closing of the crack over time.
Figure 7(b) features the orbit plot, which illustrates the trajectory of the shaft’s rotation over one complete cycle. This plot provides further insight into the dynamic behavior of the shaft. During the phases when the crack closes, the response of the cracked shaft aligns closely with that of the uncracked shaft, demonstrating similar vibration patterns. This alignment occurs because the closing of the crack temporarily restores the structural integrity of the shaft, making its dynamic response resemble that of an uncracked shaft. The periodic nature of these deviations, as shown in the time response and orbit plot, underscores the repetitive opening and closing of the crack, which is a critical aspect of the shaft’s dynamic behavior under operational conditions.
4 Conclusions
The presented study is carried out to model a breathing crack and show its effect on the composite rotor-shaft system. A surface breathing crack is integrated into the continuum of the shaft, the mechanism of which is derived on the basis of closed-loop time-dependent geometric parameters. Geometry-based systems of closed nonlinear equations are derived and solved to find the accurate time-dependent geometric variables, viz. centroidal location, uncrack area, and moment of inertia. FE formulation of the viscoelastic laminated composite shaft is modified after incorporating those derived time-dependent geometric parameters. A comparison between the intact and cracked composite shaft is performed to study the loss in a reduction in strain energy for one complete shaft rotation. The mode shapes are compared between the intact and cracked shaft for the first four bending modes to show the effect of crack. Finally, the time responses are depicted to show the breathing behavior with time.
Data Availability
No datasets were generated or analysed during the current study.
Abbreviations
- \(h\) :
-
Depth of the crack
- \(r\) :
-
Radius of the cross-section of the shaft
- \(\mu \) :
-
Crack depth ratio
- O:
-
Origin
- C:
-
Centroid
- \(\gamma \) :
-
Angle subjected at the origin by the crack
- \(A_{1}\) :
-
Constant Uncrack Area
- \(A_{c}\) :
-
Maximum Crack Area
- \(\theta \) :
-
Angle by which the cross-section rotated
- \(\theta _{1}\) :
-
Angle at which the crack starts to close
- \(\theta _{2}\) :
-
Angle at which the crack is fully closed
- \(\Omega \) :
-
Spin speed of the shaft
- \(t\) :
-
Time
- \(y\), \(z\) :
-
Original stationary plane
- \(\tilde{y}\), \(\tilde{z}\) :
-
Original rotating plane
- \(\mathrm{Y}\), \(\mathrm{Z}\) :
-
Centroidal stationary plane
- \(\tilde{\mathrm{Y}}\), \(\tilde{\mathrm{Z}}\) :
-
Centroidal rotating plane
- e:
-
Eccentricity (Vertical distance between y-axis and Y-axis)
- \(\mathrm{y}_{c}\) :
-
Time-dependent y-coordinate of the centroid C
- \(z_{c}\) :
-
Time-dependent z-coordinate of the centroid C
- A2 :
-
Time-dependent area of the closing crack (Triangle Part)
- A3 :
-
Time-dependent area of the closing crack (Segment Part)
- \(A\) eff :
-
Effective uncrack area (\(A_{1}+A_{2}\)(t)+\(A_{3}\)(t))
- \(I\) :
-
Area moment of inertia
- \(\beta \) :
-
Angle subtended at the origin by segment \(A_{3}\)
- \(\mathrm{y}_{1}\) :
-
y-coordinate of the centroid of time-dependent area \(A_{1}\)
- \(z_{1}\) :
-
z-coordinate of the centroid of time-dependent area \(A_{1}\)
- \(\mathrm{y}_{2}\) :
-
y-coordinate of the centroid of time-dependent area \(A_{2}\)
- \(\mathrm{y}_{3}\) :
-
y-coordinate of the centroid of time-dependent area \(A_{3}\)
- \(z_{2}\) :
-
z-coordinate of the centroid of time-dependent area \(A_{2}\)
- \(z_{3}\) :
-
z-coordinate of the centroid of time-dependent area \(A_{3}\)
References
Al-Shudeifat, M.A., Butcher, E.A.: New breathing functions for the transverse breathing crack of the cracked rotor system: approach for critical and subcritical harmonic analysis. J. Sound Vib. 330(3), 526–544 (2011)
Alwan, V., Gupta, A., Sekhar, A.S., Velmurugan, R.: Dynamic analysis of shafts of composite materials. J. Reinf. Plast. Compos. 29(22), 3364–3379 (2010)
Arab, S.B., Rodrigues, J.D., Bouaziz, S., Haddar, M.: A finite element based on Equivalent Single Layer Theory for rotating composite shafts dynamic analysis. Compos. Struct. 178, 135–144 (2017)
Arab, S.B., Rodrigues, J.D., Bouaziz, S., Haddar, M.: Stability analysis of internally damped rotating composite shafts using a finite element formulation. C. R. Mecanique 346(4), 291–307 (2018)
Bert, C.W.: The effect of bending-twisting coupling on the critical speed of a driveshaft. In: Japan-U. S. Conference on Composite Materials, 6 th, Orlando, FL, pp. 29–36 (1993)
Chang, C.Y., Chang, M.Y., Huang, J.H.: Vibration analysis of rotating composite shafts containing randomly oriented reinforcements. Compos. Struct. 63(1), 21–32 (2004)
Dimentberg, F.M.: Flexural vibrations of rotating shafts. Butterworths’. (1961)
El Arem, S., Ben Zid, M.: On a systematic approach for cracked rotating shaft study: breathing mechanism, dynamics and instability. Nonlinear Dyn. 88(3), 2123–2138 (2017)
Friswell, M.I., Penny, J.E.T., Garvey, S.D., Lees, A.W.: Rotor Dynamics: Modelling and Analysis of Rotating Machines. Cambridge University Press, Cambridge (2010)
Ganguly, K., Roy, H.: Modelling and analysis of viscoelastic laminated composite shaft: an operator-based finite element approach. Arch. Appl. Mech. 91(1), 343–362 (2021a)
Ganguly, K., Roy, H.: A novel geometric model of breathing crack and its influence on rotor dynamics. J. Vib. Control 28(21–22), 3411–3425 (2021b)
Ganguly, K., Raj, A., Roy, H.: Modelling and comparative study of viscoelastic laminated composite beam–an operator based finite element approach. Mech. Time-Depend. Mater. 25(4), 691–710 (2021)
Green, I., Casey, C.: Crack detection in a rotor dynamic system by vibration monitoring—part I: analysis. J. Eng. Gas Turbines Power 127(2), 425–436 (2005)
Gubran, H.B.H., Gupta, K.: The effect of stacking sequence and coupling mechanisms on the natural frequencies of composite shafts. J. Sound Vib. 282(1–2), 231–248 (2005)
Gubran, H.B.H., Singh, S.P., Gupta, K.: Stresses in composite shafts subjected to unbalance excitation and transmitted torque. Int. J. Rotating Mach. 6(4), 235–244 (2000)
Guo, C., Al-Shudeifat, M.A., Yan, J., Bergman, L.A., McFarland, D.M., Butcher, E.A.: Application of empirical mode decomposition to a Jeffcott rotor with a breathing crack. J. Sound Vib. 332(16), 3881–3892 (2013)
Irani, R.M., Mohebbi, A., Afshari, H.: Longitudinal-torsional and two plane transverse vibrations of a composite Timoshenko rotor. J. Solid Mech. 8(2), 418–434 (2016)
Jun, O.S., Gadala, M.S.: Dynamic behavior analysis of cracked rotor. J. Sound Vib. 309(1–2), 210–245 (2008)
Jun, O.S., Eun, H.J., Earmme, Y.Y., Lee, C.W.: Modelling and vibration analysis of a simple rotor with a breathing crack. J. Sound Vib. 155(2), 273–290 (1992)
Kam, T.Y., Liu, C.K.: Stiffness identification of laminated composite shafts. Int. J. Mech. Sci. 40(9), 927–936 (1998)
Kim, C.D., Bert, C.W.: Critical speed analysis of laminated composite, hollow drive shafts. Compos. Eng. 3(7–8), 633–643 (1993)
Kim, W., Argento, A., Scott, R.A.: Free vibration of a rotating tapered composite Timoshenko shaft. J. Sound Vib. 226(1), 125–147 (1999)
Liu, W., Barkey, M.E.: The effects of breathing behaviour on crack growth of a vibrating beam. In: Shock and Vibration (2018). 2018
Mayes, I.W., Davies, W.G.R.: Analysis of the response of a multi-rotor-bearing system containing a transverse crack in a rotor. J. Vib. Acoust. 106(1), 139–145 (1984)
Mendonça, W.R.D.P., De Medeiros, E.C., Pereira, A.L.R., Mathias, M.H.: The dynamic analysis of rotors mounted on composite shafts with internal damping. Compos. Struct. 167, 50–62 (2017)
Papadopoulos, C.A.: The strain energy release approach for modeling cracks in rotors: a state of the art review. Mech. Syst. Signal Process. 22(4), 763–789 (2008)
Patel, T.H., Darpe, A.K.: Influence of crack breathing model on nonlinear dynamics of a cracked rotor. J. Sound Vib. 311(3–5), 953–972 (2008)
Prawin, J., Lakshmi, K., Rao, A.R.M.: A novel vibration based breathing crack localization technique using a single sensor measurement. Mech. Syst. Signal Process. 122, 117–138 (2019)
Roy, H., Dutt, J.K.: Dynamics of polymer and polymer composite rotors–an operator based finite element approach. Appl. Math. Model. 40(3), 1754–1768 (2016)
Singh, S.P., Gupta, K.: Free damped flexural vibration analysis of composite cylindrical tubes using beam and shell theories. J. Sound Vib. 172(2), 171–190 (1994)
Singh, S.P., Gupta, K.: Composite shaft rotordynamic analysis using a layerwise theory. J. Sound Vib. 191(5), 739–756 (1996)
Varney, P., Green, I.: Comparing the Floquet stability of open and breathing fatigue cracks in an overhung rotordynamic system. J. Sound Vib. 408, 314–330 (2017)
Yongsheng, R., Xingqi, Z., Yanghang, L., Xiulong, C.: Vibration and instability of rotating composite thin-walled shafts with internal damping. Shock Vib. 2014, 123271 (2014)
Zinberg, H., Symonds, M.F.: The development of an advanced composite tail rotor driveshaft. In: Proceedings of the 26th Annual Forum of the American Helicopter Society, Washington, United States (1970)
Funding
The author(s) received no financial support for the research, authorship, and/or publication of this article.
Author information
Authors and Affiliations
Contributions
S.K.S. and K.G. were involved in building Methodology, Conceptualization, Investigation, Visualization, Software, Validation, Writing, Review & Editing – Original draft, Revision. S. K. P. and R.P. were involved in building the Methodology, Conceptualization and provided Supervision.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Springer Nature or its licensor (e.g. a society or other partner) holds exclusive rights to this article under a publishing agreement with the author(s) or other rightsholder(s); author self-archiving of the accepted manuscript version of this article is solely governed by the terms of such publishing agreement and applicable law.
About this article
Cite this article
Sutar, S.K., Ganguly, K., Pradhan, S.K. et al. The effect of a geometry-based breathing crack model on a viscoelastic composite rotor-shaft system. Mech Time-Depend Mater (2024). https://doi.org/10.1007/s11043-024-09730-3
Received:
Accepted:
Published:
DOI: https://doi.org/10.1007/s11043-024-09730-3