Introduction

Rotating machines are widely used in engineering applications such as aircrafts, pumps, compressors, turbines, power plants, etc. In practice, most rotors operate under heavy loading conditions that may result in undesirable defects. Crack is one of these defects which is considered the most dangerous one as it may cause serious damage and loss of the machine operating lifetime. Numerous review papers summarize the various modelling and identification techniques of cracks in stationary and rotating shafts studied in previous research works [1,2,3]. Most recently, Kushwaha et al. [4] provided a rich survey on various modelling approaches and crack detection techniques adopted by previous researches.

Several research works provided helpful crack indicators. Al-Shudeifat et al. [5] employed the harmonic balance approach verified by experimental work to study the effect of crack depth on the steady state dynamic behavior of a cracked rotor system. It was found that the unique behavior of the whirl orbit during passage through subcritical speeds is an indicator of presence of breathing crack in the shaft. The results showed that as the crack depth increases, resonance peaks at subcritical speeds increase. Compared with [5], Al-Shudeifat et al. [6] developed new breathing functions that accurately model the crack breathing mechanism. Then, Al-Shudeifat [7] introduced the finite element modelling of asymmetric open cracked rotor. Distinguishing features between open and breathing crack were revealed via the whirl orbits at the vicinity of the first subcritical speeds. A further improvement in the modeling of the breathing behavior of transverse cracks in rotating shafts was developed by Spagnol et al. [8]. Since the breathing crack causes asymmetry in the shaft cross section, the principle of unsymmertic bending should be utilized for accurate modeling of the breathing behavior, in which the neutral axis will be inclined with changing the rotational angles, instead of the assumed horizontal neutral axis as developed in Ref. [6]. Sinou [9] used the harmonic balance method to investigate the evolution of the super harmonic frequency components (2X, 3X) in the subcritical response region as a crack presence indicator. However, it was demonstrated that these frequency components are affected by other factors such as unbalance orientation, crack depth and location. Empirical mode decomposition (EMD) was employed by Guo et al. [10] to track the change of amplitudes of the super harmonic frequency components and whirl orbits in the vicinity of 1/2 and 1/3 of the critical speed. Variation of these components’ amplitudes can be considered as a crack indicator. However, noise may cause a limitation to the proposed method.

More crack indicators have been obtained through the investigation of the coupling phenomenon of the vibration modes due to presence of cracks [11,12,13,14,15,16,17,18,19,20,21]. According to this, due to crack presence, excited vibration in one direction results in vibration interaction in other directions. In Ref. [13], Darpe et al. investigated the coupling of longitudinal, torsional and lateral vibrations. Numerical work by Darpe et al. [22], and parametric experimental work by El-Mongy et al. [23] analyzed the coupling of the longitudinal and lateral steady state vibrations of a cracked Jeffcott rotor system subjected to axial excitation. Presence of axial excitation frequencies in the lateral vibration spectra represents the vibration coupling and thus a crack presence indicator. Moreover, numerical and experimental investigation of the dynamic behavior of a cracked rotor system during start-up was carried out by El-Mongy et al. [24, 25] for sub-critical analysis. It was concluded that the presence of subcritical resonances in the system’s sub-critical response can be considered as a good crack detector. As the crack depth increases, more sub-critical resonances appear in the response. Darpe et al. [26] numerically and experimentally studied the breathing behavior of a cracked rotor while passing through critical speed and subharmonic resonances. Three different crack models were considered (open, switching and breathing). Higher harmonic components and orbit orientation change during passage through these subharmonic resonances provided reliable crack indicators. The effect of crack on the nonlinear response of a rotating shaft was analyzed by Sinou et al. [27] using the alternate frequency/time domain approach and path-following procedure were the crack breathing was modeled as a truncated Fourier series.

Most of the previous research on cracked rotors considered the crack front to be straight edged. However, the actual crack front usually takes an elliptical profile. Hence, the results achieved using the straight edge assumption reflect the behaviour of the idealized crack shape not the real crack behaviour. Earliest work on semi-elliptical cracks in round bars was focused on determining the stress intensity factors under bending loading [28,29,30,31,32] and studying fatigue crack growth under specific loading conditions as in Ref. [33]. Fonte and Freitas [34, 35] constructed an experimental rig to study fatigue crack growth of semi-elliptical cracks under bending and steady torsion loading and observed the elliptical crack shape evolution. Rubio et al. [36] presented closed form flexibility coefficients for bending and tension taking into account the size and shape of the whole elliptical crack front. These obtained expressions were validated via calculation of static transverse displacement due to a point load. In a series of papers, Rubio et al. [37,38,39] presented different approaches for evaluation of the stress intensity factors of an elliptical breathing crack in a rotating shaft. Also, the dynamic behavior of rotors with elliptical cracks were investigated. Han et al. [40] studied the steady state response and dynamic instability regions of an elliptically cracked shaft. The crack was modelled using the local flexibility method. The crack front shape had significant effect on the instability regions. Di et al. [41] studied the vibration response of a rotor system with an elliptical crack. The cracked element stiffness was estimated based on the strain energy density approach that was described for the straight fronted crack in Ref. [42]. They considered the coupling of bending and torsional vibrations. The study was limited to the frequency spectra and harmonics amplitudes variation with the crack depth. Muñoz-Abella et al. [43] studied the influence of unbalance mass position on the breathing mechanism of elliptical crack on a rotating shaft. Then, in Ref. [44] they introduced an analytical expression to evaluate the first four bending natural frequencies of a nonrotating pinned–pinned Euler–Bernoulli shaft. And as an inverse problem, they proposed a genetic algorithm technique to identify elliptical crack using these known natural frequencies. Wei et al. [45] analyzed the breathing behavior of the elliptical crack and derived the cracked element stiffness matrix based on the time changing area and area moments of inertia. Spagnol et al. [46] further improved the work done in Ref. [45] to study cracks with a range of elliptical-front crack curvatures. A four-degree-of–freedom Jeffcott rotor model with massless shaft was considered by Spagnol et al. in Ref. [47]. The dynamic response was computed using Runge–Kutta numerical integration of the equations of motions in state-space form. Significant differences were found between the straight-front and elliptical front models in transverse trajectories at one-third and one-half of the critical speed.

To date, research works are still ongoing to reach closed-form expressions for flexibility coefficients of the elliptical crack (i.e. the real crack front shape). The effect of crack parameters (such as crack depth, shape factor and crack location) combined with system parameters (such as unbalance amount and orientation) needs further extensive numerical and experimental investigations. The breathing models used for the elliptical crack investigations needs further refinement to obtain more realistic results that accurately represent the dynamic behavior of elliptically cracked rotor systems.

In this paper, the dynamic behavior of a rotor system with a transverse elliptical breathing crack is studied numerically using finite element analysis. The crack is modeled using the moment of inertia reduction approach. The present breathing model not only accounts for the real crack shape but also for the real asymmetry of the cracked cross-section where the neutral axis orientation change is taken into account rather than being assumed constantly horizontal as in Refs. [46, 47]. Harmonic balance method is used to solve the system’s equations of motion. Whirl orbits of the shaft rotating at constant speeds during crack propagation considering the effect of shape factor are studied. In addition, whirl orbits during passage through subcritical speeds are presented. Significant differences between the real elliptical front versus the assumed straight front may help in earlier crack diagnosis and in turn prevent misdiagnosis to avoid component failure.

Finite Element Modelling of Rotor System

Modeling of the Shaft

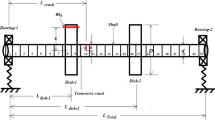
The shaft of length L is discretized into N elements with N + 1 nodes. Each node has four degrees of freedom consisting of two translational displacements in the X and Y directions and two rotational displacements about the X and Y directions (Fig. 1).

Fig. 1
figure 1

Shaft finite element model

Full size image

On assembling the equations of motion of each element, the finite element equation of motion of the whole shaft can be written as [48]:

$$\mathbf{M}\ddot{\mathbf{q}}\left(t\right)+\left(\mathbf{C}-\Omega \mathbf{G}\right)\dot{\mathbf{q}}\left(t\right)+\mathbf{K}\mathbf{q}\left(t\right)=\mathbf{Q}\left(t\right)+{\mathbf{F}}_{\mathrm{g}},$$
(1)

where \(\mathbf{M}\), \(\mathbf{C}\), \(\mathbf{G}\) and \(\mathbf{K}\) are the shaft mass, damping, gyroscopic and stiffness matrices, respectively. Expressions of these matrices for each element can be found in Refs. [48, 49]. The vector \(\mathbf{q}(\mathrm{t})= {\left[\begin{array}{cccccc}{\mathbf{q}}_{1}^{\mathrm{T}}& {\mathbf{q}}_{2}^{\mathrm{T}}& \dots & {\mathbf{q}}_{\mathrm{i}}^{\mathrm{T}}& \dots & {\mathbf{q}}_{N+1}^{\mathrm{T}}\end{array}\right]}^{\mathrm{T}}\) is the nodal displacements vector in which \({\mathbf{q}}_{\mathrm{i}}^{\mathrm{T}}(t)=\boldsymbol{ }\left[\begin{array}{cccc}{u}_{i}& {v}_{i}& {\varphi }_{i}^{x}& {\varphi }_{i}^{y}\end{array}\right]\) is the displacement vector of a single node. Here, the excitation vector \(\mathbf{Q}\left(t\right)\) is the unbalance force vector due to the unbalance mass located on the disk. The vector \({\mathbf{F}}_{\mathrm{g}}\) is the gravity force vector of the rotor system.

Disk Modelling

The disk is assumed to be a rigid concentrated mass in which its mass center is assumed to lie at the intersection node of two elements as shown in Fig. 2. Therefore, the disk mass center has the same displacement vector as this node.

Fig. 2
figure 2

Disk at node i on the shaft

Full size image

The equation of motion of the rigid disk at node i is expressed as [5]:

$${\mathbf{M}}^{d}\ddot{\mathbf{q}}\left(t\right)-\Omega {\mathbf{G}}^{d}\dot{\mathbf{q}}\left(t\right)=0,$$
(2)

where \({\mathbf{M}}^{d}\), \({\mathbf{G}}^{d}\) are the rigid disk mass and gyroscopic matrices, respectively whose expressions can be found in Refs. [5, 48].

The unbalance force vector due to the unbalance mass attached to the disk can be expressed as:

$${\mathbf{F}}_{u} = \left\lceil {\begin{array}{*{20}c} {me\Omega ^{2} {\text{cos}}\left( {\Omega t + \phi } \right)} \\ {me\Omega ^{2} {\text{sin}}\left( {\Omega t + \phi } \right)} \\ 0 \\ 0 \\ \end{array} } \right\rceil ,$$
(3)

where \(me\) is the unbalance amount in (kg m), \(\Omega\) is the spinning speed in (rad/s) and \(\phi\) is the initial unbalance angle with respect to the positive \(X\) axis.The system damping matrix \(\mathbf{C}\) is assumed to be proportional damping matrix and can be calculated as [50]:

$$\mathbf{C}={\alpha }_{d}\mathbf{M}+{\beta }_{d}\mathbf{K},$$
(4)

where the parameters \({\alpha }_{d},{\beta }_{d}\) are calculated using the first two natural frequencies and first two modal damping ratios.

Crack Modelling

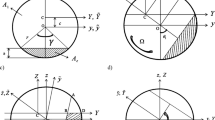
The crack is introduced at a cross section at the middle of the shaft. The crack front realistic shape is considered as the intersection of an ellipse with the shaft’s circular circumference [45] (Fig. 3).

Fig. 3
figure 3

Shaft cross section with a fully open elliptical crack

Full size image

Here, this ellipse has a major axis \(b\) which represents the crack depth and a minor axis \(a\). The major centerline of that ellipse is always tangent to the shaft cross-section. The crack depth ratio is taken as \(\mu =b/R\) and the crack front shape factor is defined as \(\beta =b/a\). The shape factor gives an indication of the crack front curvature such that, as β increases, the front becomes more curved and as it decreases, the front becomes more flattened. Hence, the straight-front transverse crack is a special case of the elliptical crack where β = 0. The crack is assumed to be fully open at t = 0 (before rotation). In this case, the area of the crack segment \({A}_{c}\) is composed of two areas \({A}_{c1}\) and \({A}_{c2}\), meanwhile, the uncracked portion of the cross section has an area \({A}_{1}\). The Y-coordinate of the centroids of the areas \({A}_{c1}\), \({A}_{c2}\) and \({A}_{1}\) are denoted respectively as \({Y}_{c}^{{A}_{c1}}\), \({Y}_{c}^{{A}_{c2}}\) and \({y}_{ce}\). The moments of inertia of the area components \({A}_{c1}, {A}_{c2}\) about the X and Y axes are denoted as \({I}_{X}^{Ac1}\),\({{I}_{Y}}^{Ac1}\), \({{I}_{X}}^{Ac2}\) and \({{I}_{Y}}^{Ac2}\). Then, the moments of inertia of the area \({A}_{1}\) about the X and Y axes are denoted as \({I}_{X}^{{A}_{1}}\) and \({I}_{Y}^{{A}_{1}}\). The moments of inertia of \({A}_{1}\) about the centroidal \(\overline{X }\) and \(\overline{Y }\) axes are denoted as \({I}_{\overline{X} }^{{A}_{1}}\) and \({I}_{\overline{Y} }^{{A}_{1}}\). Mathematical calculations of these areas, centroid coordinates and moments of inertia at t = 0 are found in Refs. [45, 46].

Crack Breathing

Due to the heavy weight of the rotor in which the static deflection dominates the deflection due to vibration, the crack was found to open and close synchronously with the shaft rotation. In other words, as the shaft rotates, the angular orientation of the neutral axis of the cross section of the cracked element keeps changing. So, at some instants, part of the crack segment becomes in the compressive stress region and so it is closed, while the other part lies in the tensile stress region and hence it remains open. This process of gradual closing and opening is called crack breathing. The angular regions where the crack closes or opens gradually and remains fully open or fully closed are described in Fig. 4.

Fig. 4
figure 4

Crack breathing process and the neutral axis inclination during shaft rotation

Full size image

The values of the breathing angles \({\theta }_{1}\) and \({\theta }_{2}\) can be calculated as:

$${\theta }_{1}={\mathrm{tan}}^{-1}\left(\frac{{I}_{\overline{Y} }^{{A}_{1}}}{{I}_{\overline{X} }^{{A}_{1}}}.\frac{{y}_{ce}+R\mathrm{cos}\psi }{R\mathrm{sin}\psi }\right),{\theta }_{2}=\frac{\pi }{2}+\psi .$$
(5)

Accordingly, the time varying moments of inertia of the cracked element cross section about the fixed centroidal axes \(\overline{X }\) and \(\overline{Y }\) can now be expressed as [8, 51]:

$${\widehat{I}}_{\overline{X} }\left(t\right)=I-{I}_{11}{f}_{1}\left(t\right)$$
(6)
$${\widehat{I}}_{\overline{Y} }\left(t\right)=I+{f}_{1}\left(t\right){I}_{11}+{f}_{2}\left(t\right){I}_{22}$$
(7)
$${\widehat{I}}_{\overline{X }\overline{Y} }\left(t\right)={I}_{33}{f}_{3}\left(t\right),$$
(8)

where \({f}_{1}\left(t\right)\), \({f}_{2}\left(t\right)\) and \({f}_{3}\left(t\right)\) are the breathing functions that model the crack breathing mechanism. Expressions of these functions are found in Ref. [51]. The parameters, \({I}_{11}\), \({I}_{22}\) and \({I}_{33}\) are expressed as:

$${I}_{11}=I-\left({I}_{X}^{Ac1}+{I}_{X}^{Ac2}+{A}_{1}{{y}_{ce}}^{2}\right),{I}_{22}=I-\left({I}_{Y}^{Ac1}+{I}_{Y}^{Ac2}\right),{I}_{33}=\frac{{I}_{\overline{Y} }^{{A}_{1}}-{I}_{\overline{X} }^{{A}_{1}}}{2}.$$
(9)

Then, the time varying cracked element stiffness matrix can be expressed as:

$${\mathbf{k}}_{ce}\left(t\right)=\mathbf{k}+{\mathbf{k}}_{1}{f}_{1}\left(t\right)+{\mathbf{k}}_{2}{f}_{2}\left(t\right)+{\mathbf{k}}_{3}{f}_{3}\left(t\right),$$
(10)

where \({\mathbf{k}}_{1}\), \({\mathbf{k}}_{2}\) and \({\mathbf{k}}_{3}\) are the secondary stiffness matrices due to crack presence. Expressions of \({\mathbf{k}}_{1}\), \({\mathbf{k}}_{2}\) can be found in Ref. [6] and expression of \({\mathbf{k}}_{3}\) is found in Ref. [8]. Hence, the finite element equation of motion for an unbalanced rotor system with breathing crack is written as:

$$\mathbf{M}\ddot{\mathbf{q}}\left(t\right)+\left(\mathbf{C}-\Omega \mathbf{G}\right)\dot{\mathbf{q}}\left(t\right)+\left(\mathbf{K}+{f}_{1}\left(t\right){\mathbf{K}}_{1}+{f}_{2}\left(t\right){\mathbf{K}}_{2}+{f}_{3}\left(t\right){\mathbf{K}}_{3}\right)\mathbf{q}\left(t\right)={\mathbf{F}}_{1}\mathrm{cos}\Omega t+{\mathbf{F}}_{2}\mathrm{sin}\Omega t+{\mathbf{F}}_{\mathrm{g}},$$
(11)

where \({\mathbf{K}}_{1}\), \({\mathbf{K}}_{2}\), \({\mathbf{K}}_{3}\) are the secondary stiffness matrices of zero entries except for those corresponding to the cracked element where the entries equal to \({\mathbf{k}}_{1}\), \({\mathbf{k}}_{2}\), \({\mathbf{k}}_{3}\) respectively; \({\mathbf{F}}_{1}\), \({\mathbf{F}}_{2}\) are the unbalance force amplitude vectors of zero entries except for those corresponding to the disk node. Expressions of \({\mathbf{F}}_{1}\), \({\mathbf{F}}_{2}\) can be found in Ref. [5].

Steady State Solution of the System

The harmonic balance method is used to get the steady state solution of the cracked rotor system represented by Eq. (11) and shown in Fig. 5. The disk is located at the shaft midspan where the elliptical crack is located in the most adjacent element to the disk.

Fig. 5
figure 5

Finite element model of the rotor system assembly

Full size image

The solution is expressed as a finite Fourier series as:

$${\mathbf{q}}\left( t \right) = {\mathbf{A}}_{o} + \sum\limits_{{k = 1}}^{n} {\left( {{\mathbf{A}}_{k} {\text{cos}}\left( {k\Omega t} \right) + {\mathbf{B}}_{k} {\text{sin}}\left( {k\Omega t} \right)} \right)} ,$$
(12)

where n is the number of harmonics used. The breathing functions can be rewritten as:

$${f}_{1}\left(t\right)={a}_{o}+\sum_{j=1}^{m}{a}_{j}\mathrm{cos}\left(j\Omega t\right), {f}_{2}\left(t\right)={b}_{o}+\sum_{j=1}^{2n}{b}_{j}\mathrm{cos}\left(j\Omega t\right), {f}_{3}\left(t\right)=\sum_{j=1}^{2n}{\gamma }_{j}\mathrm{sin}\left(j\Omega t\right).$$
(13)

Inserting this solution into Eq. (11) yields:

$$\left[\begin{array}{ccccccccc}\widetilde{\mathbf{C}}& {0.5\mathbf{C}}_{2}^{\left(1\right)}& {0.5\mathbf{C}}_{22}^{\left(1\right)}& {0.5\mathbf{C}}_{2}^{\left(2\right)}& {0.5\mathrm{C}}_{22}^{\left(2\right)}& {0.5\mathbf{C}}_{2}^{\left(3\right)}& {0.5\mathbf{C}}_{22}^{\left(3\right)}& \cdots & {0.5\mathbf{C}}_{22}^{\left(n\right)}\\ {\mathbf{C}}_{2}^{\left(1\right)}& {\mathbf{C}}^{\left(1\right)}& {\mathbf{C}}_{1}^{\left(1\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{1,1}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{1,1}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{1,2}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{1,2}\right)}& \cdots & {\mathbf{C}}_{33}^{\left(1,n-1\right)}\\ {\mathbf{C}}_{22}^{\left(1\right)}& {\mathbf{C}}_{11}^{\left(1\right)}& {\mathbf{C}}^{\left(2\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{2,1}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{2,1}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{2,2}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{2,2}\right)}& \ddots & {\mathbf{C}}_{3}^{\left(2,n-1\right)}\\ {\mathbf{C}}_{2}^{\left(2\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{1,1}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{2,1}\right)}& {\mathbf{C}}^{\left(3\right)}& {\mathbf{C}}_{1}^{\left(2\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{3,1}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{3,1}\right)}& \ddots & {\mathbf{C}}_{33}^{\left(3,n-2\right)}\\ {\mathbf{C}}_{22}^{\left(2\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{1,1}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{2,1}\right)}& {\mathbf{C}}_{11}^{\left(2\right)}& {\mathbf{C}}^{\left(4\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{4,1}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{4,1}\right)}& \ddots & {\mathbf{C}}_{3}^{\left(4,\mathrm{n}-2\right)}\\ {\mathbf{C}}_{2}^{\left(3\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{1,2}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{2,2}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{3,1}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{4,1}\right)}& {\mathbf{C}}^{\left(5\right)}& {\mathbf{C}}_{1}^{\left(3\right)}& \ddots & {\mathbf{C}}_{33}^{\left(5,n-3\right)}\\ {\mathbf{C}}_{22}^{\left(3\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{1,2}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{2,2}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{3,1}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{4,1}\right)}& {\mathbf{C}}_{11}^{\left(3\right)}& {\mathbf{C}}^{\left(6\right)}& \ddots & \vdots \\ {\mathbf{C}}_{2}^{\left(4\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{1,3}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{2,3}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{3,2}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{4,2}\right)}& {\mathbf{C}}_{3}^{\left(\mathrm{5,1}\right)}& {\mathbf{C}}_{33}^{\left(\mathrm{5,1}\right)}& \ddots & {\mathbf{C}}_{3}^{\left(2n-\mathrm{2,1}\right)}\\ \vdots & \vdots & \ddots & \ddots & \ddots & \ddots & \ddots & {\mathbf{C}}^{\left(2n-1\right)}& {\mathbf{C}}_{1}^{\left(n\right)}\\ {\mathbf{C}}_{22}^{\left(n\right)}& {\mathbf{C}}_{33}^{\left(1,n-1\right)}& {\mathbf{C}}_{3}^{\left(2,n-1\right)}& {\mathbf{C}}_{33}^{\left(3,n-2\right)}& {\mathbf{C}}_{3}^{\left(4,n-2\right)}& {\mathbf{C}}_{33}^{\left(5,n-3\right)}& \cdots & {\mathbf{C}}_{11}^{\left(n\right)}& {\mathbf{C}}^{\left(2n\right)}\end{array}\right]\lceil\begin{array}{c}{\mathbf{A}}_{o}\\ {\mathbf{A}}_{1}\\ {\mathbf{B}}_{1}\\ {\mathbf{A}}_{2}\\ {\mathbf{B}}_{2}\\ \vdots \\ {\mathbf{A}}_{n-1}\\ {\mathbf{B}}_{n-1}\\ {\mathbf{A}}_{n}\\ {\mathbf{B}}_{n}\end{array}\rceil=\lceil\begin{array}{c}{\mathbf{F}}_{g}\\ {\mathbf{F}}_{1}\\ {\mathbf{F}}_{2}\\ 0\\ 0\\ 0\\ 0\\ 0\\ \vdots \\ 0\end{array}\rceil,$$
(14)

where \(\widetilde{\mathbf{C}}=\mathbf{K}+{a}_{o}{\mathbf{K}}_{1}+{b}_{o}{\mathbf{K}}_{2}\) and \({\mathbf{C}}^{\left(i\right)}=\widetilde{\mathbf{C}}-{\left(\left(i+1\right)\Omega /2\right)}^{2}\mathbf{M}+\frac{1}{2}\left({a}_{i+1}{\mathbf{K}}_{1}+{b}_{i+1}{\mathbf{K}}_{2}\right)\) for odd values of \(i\) \((i=\mathrm{1,3},5,\dots \dots ,2n-1)\) and \({\mathbf{C}}^{\left(i\right)}=\widetilde{\mathbf{C}}-{\left(i\Omega /2\right)}^{2}\mathbf{M}-\frac{1}{2}\left({a}_{i}{\mathbf{K}}_{1}+{b}_{i}{\mathbf{K}}_{2}\right)\) for even values of \(i\) \((i=\mathrm{2,4},6,\dots \dots ,2n)\) and \({\mathbf{C}}_{1}^{\left(i\right)}=i\Omega \left(\mathbf{C}-\Omega \mathbf{G}\right)+\frac{1}{2}{\gamma }_{i}{\mathbf{K}}_{3}\) for \((i=\mathrm{1,2},\cdots ,n)\) and \({\mathbf{C}}_{11}^{\left(i\right)}=-i\Omega \left(\mathbf{C}-\Omega \mathbf{G}\right)+\frac{1}{2}{\gamma }_{i}{\mathbf{K}}_{3}\) and \({\mathbf{C}}_{2}^{\left(i\right)}={a}_{i}{\mathbf{K}}_{1}+{b}_{i}{\mathbf{K}}_{2}\) for \((i=\mathrm{1,2},\cdots ,n)\) and \({\mathbf{C}}_{22}^{\left(i\right)}={\gamma }_{i}{\mathbf{K}}_{3}\) and \({\mathbf{C}}_{3}^{\left(k,i\right)}=\frac{1}{2}\left[\left({a}_{i+k+1}+{a}_{i}\right){\mathbf{K}}_{1}+\left({b}_{i+k+1}+{b}_{i}\right){\mathbf{K}}_{2}\right]\) for odd values of \(k\) \((k=\mathrm{1,3},5,\dots \dots ,2n-3)\) and \({\mathbf{C}}_{3}^{\left(k,i\right)}=\frac{1}{2}\left[\left({a}_{i}-{a}_{i+k}\right){\mathbf{K}}_{1}+\left({b}_{i}-{b}_{i+k}\right){\mathbf{K}}_{2}\right]\) for even values of \(k(k=\mathrm{2,4},6,\dots \dots ,2n-2)\) and \({\mathbf{C}}_{33}^{\left(k,i\right)}=\frac{1}{2}\left({\gamma }_{i+k+1}+{\gamma }_{i}\right){\mathbf{K}}_{3}\) for odd values of \(k\) \((k=\mathrm{1,3},5,\dots \dots ,2n-3)\) and \({\mathbf{C}}_{33}^{\left(k,i\right)}=\frac{1}{2}\left({\gamma }_{i}-{\gamma }_{i+k}\right){\mathbf{K}}_{3}\) for even values of \(k\) \((k=\mathrm{2,4},6,\dots \dots ,2n-2)\).

Note that, in this case the \({\varvec{Z}}\) matrix is of size \(((2 n+1 ) \times S, (2 n+1 ) \times S ))\).

Results and Discussion

Geometrical and material data of the rotor system are given in Table 1. A MATLAB® code is used to build the finite element model of the system and perform the numerical calculations. The shaft is divided into 22 Euler–Bernoulli beam elements. Steady state response is evaluated using the harmonic balance method with 8 harmonics.

Table 1 Parameters of the rotor system
Full size table

The horizontal and vertical vibration responses (denoted as \(u\) and\(v\), respectively) are calculated at the node where the disk is located. The whirl amplitude is then calculated as \(\sqrt{{u}^{2}+{v}^{2}}\). From the eigen value analysis of the uncracked simply supported system, the first bending natural frequency Ωcr1 is obtained as ≈ 124 Hz.

To validate the model, the Newmark integration method (with parameters αN = 0.25 and δN = 0.5 [50]) was used to obtain the response and compare with the results obtained from the Harmonic balance method (HBM). Arbitrary different cases of crack depth, shape factor and spinning speed were chosen for the validation process. The spinning speeds were chosen around the subcritical speed zones.

For a low crack depth (μ = 0.2), validation was made for both straight crack front (i.e. β = 0) as shown in Fig. 6; and elliptical front with β = 0.5 as shown in Fig. 7. Speeds were chosen during passage through 1/4th, 1/3rd and 1/2 of the respective first critical speed of the rotor. Similarly, Figs. 8 and 9 present the validation results for crack depth μ = 0.3 (with β = 0 and β = 1) but with the same set of rotating speeds (during passage through 1/4th and 1/5th of the first critical speed). Validation for moderately high crack depths is also presented in Fig. 10 for μ = 0.4 and β = 1/3; and Fig. 11 for μ = 0.5 and β = 0.5, at arbitrarily chosen rotational speeds. As shown in the figures, the two solution methods showed very good agreement with different values of system and crack parameters.

Fig. 6
figure 6

Comparison of whirl orbits for straight crack front for μ = 0.2 using harmonic balance method and Newmark method during passing the fourth and third of the first critical speed

Full size image
Fig. 7
figure 7

Comparison of whirl orbits for elliptical crack front for μ = 0.2 and β = 0.5 using harmonic balance method and Newmark method during passing the third and half of the first critical speed

Full size image
Fig. 8
figure 8

Comparison of whirl orbits for straight crack front for μ = 0.3 using harmonic balance method and Newmark method during passing the fourth and fifth of the first critical speed

Full size image
Fig. 9
figure 9

Comparison of whirl orbits for elliptical crack front for μ = 0.3 and β = 1 using harmonic balance method and Newmark method during passing the fourth and fifth of the first critical speed

Full size image
Fig. 10
figure 10

Comparison of whirl orbits for elliptical crack front for μ = 0.4 and β = 1/3 using harmonic balance method and Newmark method at different speeds

Full size image
Fig. 11
figure 11

Comparison of whirl orbits for elliptical crack front for μ = 0.5 and β = 0.5 using harmonic balance method and Newmark method at different speeds

Full size image

Effect of the Shape Factor on the Subcritical Resonances

Results of the whirl amplitudes versus the rotational speed revealed the subcritical resonance speeds in the form of emerging peaks which are considered an indicator of breathing crack presence as shown in Fig. 12. Each case is drawn by varying the value of the shape factor at constant crack depth to show the crack front curvature effect on the system critical speeds. Here, this effect can be noticed as the existing shift in critical speeds compared with the straight front assumption (i.e. β = 0). It can be noticed also that as the shape factor increases, shifting in peaks increases. Also, as the crack depth increases, more sub-resonance peaks appear as shown in Fig. 12c. It can be seen that relying on the crack indicator related to the subcritical speeds corresponding to the straight front can lead to crack misdiagnosis which in turn may expose the system to failure especially at deeper cracks.

Fig. 12
figure 12

Peaks of subcritical speeds at different values of crack depths and shape factors: a μ = 0.3, b μ = 0.5, c μ = 0.8. at \(m.e=1\times {10}^{-6}\) kg m

Full size image

Whirl Orbits at Different Crack Depths and Shape Factors at Constant Rotational Speeds

The constant rotational speeds are chosen here as integer submultiples of the first critical speed of an intermediate case of crack depth and shape factor from the cases shown in Fig. 12. The effect of the crack shape factor and crack depth is shown in Figs. 13 and 14 at speeds (1847.4 rpm) and (3694 rpm) respectively.

Fig. 13
figure 13

Evolution of the system whirl orbits at different values of crack depths and shape factors at \(\Omega =1847.4\) rpm, \(m.e=2.5\times {10}^{-4}\) kg m

Full size image
Fig. 14
figure 14

Evolution of the system whirl orbits at different values of crack depths and shape factors at \(\Omega =3694\) rpm, \(m.e=2.5\times {10}^{-4}\) kg m

Full size image

Variation of the whirling response can be witnessed in the orbit plots in Fig. 13 as the crack propagates at different shape factors. It is observed that at this speed with small crack depth (μ = 0.2), no loops are formed in the whirl orbits. At μ = 0.3 and μ = 0.5, it can be noticed that both orientation and shape of the orbits are varied with changing the shape factor β which indicates corresponding change in the amplitude and phase of the vibration response. The loops appearing in the orbits clearly indicate the presence of higher harmonics in the crack response which is a well-known crack signature [10, 26, 52]. At higher crack depth, μ = 0.8, it can be observed that the change in the orbit becomes less pronounced.

Figure 14 shows the evolution of whirl orbits at half the first critical speed for different crack depths and shape factors. The inner loop indicating the presence of second harmonic component is observed clearly which is a known crack indicator at this speed. However, the shape factor has an obvious effect on the shape of the orbits. For μ = 0.2, the inner loop is getting smaller with the increase of the shape factor and it disappears for β = 1. It is also noticed that at a constant shape factor, the orbit experiences a change in its orientation by about π rad as the crack propagates (see Fig. 14f, i) which agrees well with previous literature as [26]. All these changes demonstrate the variations that occur in the amplitude and phase of the vibration response of the cracked rotor when the crack shape is taken into consideration.

Whirl Orbits During Passage Through Subcritical Resonances

The whirl orbits of the system while passing through the subcritical speeds are plotted in Figs. 15 and 16 at crack depth μ = 0.3 for two shape factors β = 0.5 and β = 1 respectively. The orbit plots corresponding to the straight crack front (β = 0) are plotted on the same axes of other shape factor values for comparison. The stiffness variation due to breathing of the elliptical crack in the rotating coordinate system gives rise to higher harmonics in the nonlinear system response as can be seen in the orbit shapes in both Figs. 15 and 16. This stiffness variation affects the frequency content of the response during passage through the sub-critical speeds [9, 26]. For example, the forward whirl orbits at μ = 0.3, β = 0.5 while crossing 1/5th of the first critical speed Ωcr1 (in this case 1/5 Ωcr1 ≈ 1480.6 rpm) shown in Fig. 15a–c, the 5X harmonic component dominates the system response. This is also indicated by formation of the four inner loops in the orbits. It can be noticed that the size of the inner loops gets larger as the speed approaches the subcritical speed, and then gets smaller as the speed increases away from the subcritical speed. Orbit orientation change can be observed while crossing the subcritical speed. Meanwhile, significant different orbit shape, size and direction is noticed in case of the assumed straight crack front. Here the orbit has five outer loops whose size decays earlier as the speed increases.

Fig. 15
figure 15

Whirl orbits at μ = 0.3, β = 0.5 during passage through the subcritical speeds, a–c through 1/5 Ωcr1 ≈ 1480.6 rpm, d–f through 1/3Ωcr1 ≈ 2468 rpm, g–i through 1/2Ωcr1 ≈ 3702 rpm. for \(m.e=2.5\times {10}^{-4}\) kg m

Full size image
Fig. 16
figure 16

Whirl orbits at μ = 0.3, β = 1 during passage through the subcritical speeds, a–c through 1/5Ωcr1 ≈ 1484 rpm, d–f through 1/4Ωcr1 ≈ 1856 rpm for \(m.e=2.5\times {10}^{-4}\) kg m

Full size image

Similar observations can be seen in case of 1/3rd the first critical speed as in Fig. 15d–f. Here, the response is dominated by the 3X frequency component. The orbit has two inner loops and rotates by about π/2 rad as it crosses the subcritical speed. In this case, the difference between the elliptical and straight crack is less noticeable compared with the previous case. In Fig. 15g–i, orbits during passage through 1/2 the first critical speed where the response is dominated by the 2X component. The forward whirl orbit is characterized by the inner loop and rotates by about π/2 rad as it crosses the subcritical speed. In this case, difference between the models is less noticeable compared with the previous two cases except that the orbit rotates by a smaller amount (≈ π/4 rad). It can be noticed that the orbit size of the elliptical crack is smaller than that of the straight crack before the subcritical speed zone as shown in Fig. 15a, d, g; and larger at the subcritical speed zone (Fig. 15b, e, h); then slightly larger after the subcritical speed zone (Fig. 15c, f, i).

Figure 16 shows the whirl orbits during passage through the 1/5th and 1/4th of the first critical speed at μ = 0.3 for the case β = 1 (i.e. circular front). The orbits in Fig. 16a–c show similar observations as those in Fig. 15a–c in case of β = 0.5 except for the relative orientation of the orbit loops among the two cases. Figure 16d–f presents forward whirl orbits while passage through 1/4th of the first critical speed. Here the 4X component is dominant but on a narrow range of rotational speeds as evident by the three inner loops. In addition, the relative orientation of the orbit inner loops gets distorted to some extent while crossing the subcritical speed. Meanwhile, for the straight front model, different whirl direction is observed. In this case, the orbit is backward with five outer loops with decreasing size with the speed.

Conclusions

In this paper, the finite element model of a rotor system with a transverse elliptical breathing crack is developed to investigate the system’s steady state response using the harmonic balance method. Crack breathing mechanism is modeled through the time varying area moments of inertia approach taking into account the neutral axis inclination change. The major findings of this work are summarized as follows. Presence of the breathing elliptical crack can be tracked using the super harmonic frequency components in the system subcritical response. Whirl orbits in the vicinity of the subcritical speeds introduced unique shapes and orientation and in turn serve as a key detector of crack presence. Compared to the assumed straight crack front, shape factors can affect the whirl orbit characteristics such as the size of the inner or outer loops and the amount by which the orbits rotate while crossing the subcritical speeds. The present breathing model that considers the effects of the elliptical crack shape, the non-symmetric cracked cross section and the neutral axis inclination angle provides closer simulation of real cracked rotors. Hence, consideration of these effects may help in earlier crack diagnosis and better modelling of crack effects on the vibration response.