1 Introduction

It is now well acknowledged that the usage of the internet is rapidly growing in all walks of life like engineering, medical, military, educational, political, banking, marketing and vice versa. Everyone wants their data and information to be secured over the internet while transmission third party don’t have unauthorized access to the communication between two people. In [7], Shannon proposed the concept of block cipher. Block cyphers such as the Data Encryption Standard (DES) and Advanced Encryption Standard (AES) are the critical components of multimedia security. DES [32] like cryptosystem break easily due to its short 56 bit key and more complicated due to 16 Feistel rounds. AES like cryptosystem used 128, 192 and 256-bits keys for 10, 12 and 14 rounds respectively for encryption. In 2001 NIST introduced AES and modern cryptography based on it [10]. AES is a type of block cypher that encrypts and decrypts data with the same key using the substitution permutation network (SP-network). The substitution box is still the most crucial part of block cyphers, including AES (S-box). This is because this ingredient is the sole source of the nonlinearity effect. Furthermore, according to Shannon's pioneering work [36], S-Box is consistent with the influence of confusion, which obscures the statistical relationship between the plain text and the private keys.

S-box is a vectorial Boolean function that is defined mathematically as: \(\varphi :{\mathbb{Z}}_{2}^{u}\to {\mathbb{Z}}_{2}^{v}\) which map \(u\) input bit into \(v\) output bit. The algebraic and statistical features of the S-box, such as NL, BIC, SAC, DU, LAP, and MLC, are used to assess its validity. Substitution boxes are essential in symmetric key cryptography because they are used to perform substitutions. S-boxes are commonly used in block ciphers to conceal the relation among the cipher text and the key. Because of the usage of algebraically weak S-boxes, cryptosystems are unsecure and unstandardized. Similarly, constructing an efficient and safe cryptosystem requires the creation of a robust algebraic S-box. Many methods have been developed as a result of these significant applications to create more reliable S-boxes that will be used for robust block encryption. For these reasons, researchers are currently concentrating on developing new algorithms for constructing more secure and trustworthy S-boxes. Zhang et al. utilized I-Ching operators to create an S-box in [43]. The nature of the created S-Box was assessed using various techniques, with great results showing the scheme's resilience. [21] Introduces a novel approach for constructing key dependent S-boxes. Firdousi et al. [16] created a modified S-box using quantum maps. The recommended S-box is strong enough to meet the needed requirement of secure encryption technique. [26] Presents a powerful image encryption technique based on a newly developed S-box. Shafique et al. [35] created a secure S-box using Cubic-Logistic mapping. With the use of integer multiplication, a safe and efficient chaotic map [23] is created, which is then used to generate a strong S-box. In [44], authors devised an approach using the combination of chaotic systems. In [37], the authors have investigated matrix action on the Galois field and created an S-box with good cryptographic features.

The symmetric group \({S}_{n}\) is utilised to enhance the nonlinearity value of S-box. Rows and columns of 8 × 8 S-boxes are rearranged using permutations of the S16 group, whereas cells of S-boxes are rearranged using permutations of the S256 symmetric group. A function's Taylor series is used to express a function in the form of the sum of infinite terms of the function's derivative at a point. Taylor's series, which is named after Brook Tayler, extends a function in terms of Polynomial. The McLaurin series is a special form of the Taylor series at \(x = 0\) [1]. Mellin transformation is a type of integral transformation that is similar to Laplace and Fourier transformations. Hjalmar Mellin [25], a mathematician, describes this transformation. It is employed in number theory, asymptotic expansion theory, and mathematical statistics. The literature contains various publications on the Mellin transform based cryptography technique [33, 34]. Mellin transformation was utilised by Bhatti et al. in [8] for encryption and decryption, however the building of S-boxes using Mellin transformation has never been mentioned before. In this study, we introduce a unique, efficient, and creative method for building robust S-boxes utilizing the Mellin transformation.

The following is the main contribution of our work in this manuscript:

  • A new S-box construction process based on the McLaurin and Mellin transformation.

  • Permutation of symmetric group \({S}_{256}\) are used to generate the recommended S-box which have an average non-linearity of 112.5.

  • The recommended S-box is utilized for image encryption, and its validity in image encryption is assessed using various tests.

  • Compare the proposed encrypted image with different algorithm, which shows that our S-box gives the best encryption scheme for the security of image data.

The body of this article is structured as follows: Basic definitions are provided in Section 2. In Section 3, a mathematical algorithm is described for the construction of S-box using the McLaurin series and Mellin transformation. Additionally, the nonlinearity of the initial S-box, which has an average nonlinearity of 112.5 and is higher than the AES NL score, is increased using a special permutation of the symmetric group \({S}_{256}\). In Section 4, the proposed S-box is examined using several tests, including NL, BIC, DP, and SAC, and it is compared to existing boxes from the literature. In Section 5, the recommended S-box is employed for image encryption, and the encryption strength is assessed using various tests and the proposed algorithm's conclusion is provided in Section 5.

2 Preliminaries

2.1 Mellin Transformation

It is an integral transformation that was named by the mathematician Hjalmar Mellin. It is defined as,

$$M\left[g\left(x\right);h\right]={\int_0^\infty}g\left(x\right){x}^{h-1} dx$$

Hjalmar Mellin also define inverse Mellin transformation as:

$${M}^{-1}\left[g\left(x\right);h\right]=\frac{1}{2\lambda i}{\int_{c+i\infty}^{c-i\infty}}g\left(x\right){x}^{(-h)} dx$$

which is the line integral in complex plane.

2.2 Taylor series

The formula for Tayler series of a real or complex-valued function is defined as

$$f\left(a\right)+\frac{{f}^{{}^{\prime}}\left(a\right)}{1!}(x-a)+\frac{{f}^{{}^{\prime}}\left(a\right)}{2!}{\left(x-a\right)}^{2}+\frac{{f}^{{}^{\prime\prime\prime}}\left(a\right)}{3!}{(x-a)}^{3}+\dots +\frac{{f}^{n}(a)}{n!}+\dots$$

In sigma notation;

$$f\left(a\right)=\sum\nolimits_{n=0}^{\infty }\frac{{f}^{n}\left(\alpha \right)}{n!}{\left(x-a\right)}^{n}$$

where \(n!\) denotes factorial of n and \(a\in R,C\). McLaurin series is the special case of Taylor series for which \(a=0\)

3 Algebraic Structure of S-box

  • Step 1: Let S indicates a Set of integers ranging from 0 to 255.

    $$S=\left\{k|k\in Z\wedge 0\le k\le 255\right\}$$

A function \(f\left(x\right)=1/(1-x)\) whose McLaurin series is

$$f\left(x\right)=\sum_{n=0}^{\infty }{x}^{n}$$

Series is the sum of elements of the sequence

$$\left\{{x}^{n}\right\} n=\mathrm{0,1}, 2, 3,$$

Write down all of the components of \(S\) in ascending order and multiply with the first 256 terms of \(\left\{{x}^{n}\right\}\) such that \(k.{x}^{n}\) is possible if \(k=n\).

The outcomes will be as follows:

$$\mathrm{0,1}x,2{x}^{2},3{x}^{3},\dots ,255{x}^{255}$$

Now we will develop a new sequence, as seen below.

$$\left\{n{x}^{n}\right\} n=\mathrm{0,1}, 2, 3,\dots ,255$$

This sequence can be extended by multiplying \({x}^{2}\) with each term of the sequence \(\left\{n{x}^{n}\right\} 0\le n\le 255\) as

$$\left\{n{x}^{n+2}\right\} n=0, 1, 2, 3,\dots ,255.$$

If we apply the Mellin transformation to the \({n}^{th}\) term of the sequence while neglecting limitations, we get the following formula:

$$M\left[n{x}^{n+2},h\right]=n\frac{{\left(x\right)}^{n+h+2}}{n+h+2} n=0, 1, 2, 3\dots 255$$

When we apply the above formula to each term in the sequence \(\left\{n{x}^{n+2}\right\}\), we get the new sequence shown below

$$\left\{n\frac{{(x)}^{n+h+2}}{n+h+2}\right\}n=0, 1, 2, 3\dots 255$$

Here we will use \(h=3\) then the sequence will become \(\left\{n\frac{{(x)}^{n+5}}{n+5}\right\}\) \(n=0, 1, 2, 3\dots 255\)

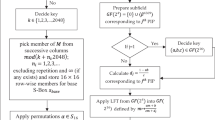
  • Step 2: Since an S-box \({S:\{\mathrm{0,1}\}}^{n}\to {\{\mathrm{0,1}\}}^{n}\) is basically any rearrangements of the elements of set \(S=\left\{k|k\in Z\wedge 0\le k\le 255\right\}\). We used \(mod\;257\) to solve the coefficients of all sequence terms. As we determined that the \({127}^{th}\) coefficient is equal to 256, which does not belong to set S, and the \({253}^{th}\) coefficient is equal to \(\infty\), these coefficients are replaced by 64 and 1 respectively. Put all of these results in the \(16\times 16\) table, which is our initial S-box and has an average non-linearity of 102.5. (See Table 1).

Table 1 Initial S-box 1
Full size table
Table 2 Permutation of \({S}_{256}\)
Full size table
Table 3 Proposed S-box
Full size table

A flow chart for the mathematical construction of initial S-box:

figure a

  • Step 3: Since our data is shown in a \(16\times 16\) table with 256 cells, we may improve the randomization by swapping the placements of these cells. For this reason, a particular type of permutation from Symmetric group \({S}_{256}\), as shown in Table 2, is applied on Table 1, and the new S-box, which is our suggested S-box with an average non-linearity of 112.5, is shown in Table 3.

4 Security analysis

Within this part, a number of tests have been provided to assess the effectiveness of suggested S-box. Non-linearity test (NL), Bit Independent Criterion (BIC), Strict Avalanche Criterion (SAC), Linear Approximation Probability (LAP), and differential Uniformity (DU) of Substitution box are a few examples. Table 9 compares the algebraic characteristics of S-boxes to those of many other S-boxes.

4.1 Non-linearity

In 1988, Pieprzyk and Finkelstein proposed the non-linearity test [31]. It is quite helpful in determining the effectiveness of the S-box. If the correspondence from plain text to cypher is linear, S-box is regarded weak, and attackers may easily perform a linear attack on cypher text. The mathematical formula for determining the non-linearity of S-box is defined as follows:

$${N}_{f}={\left(2\right)}^{n-1}[1-{\left(2\right)}^{-n}max\left|{W}_{f}\left(a\right)\right|$$
(1)

where \({W}_{f}(a)\) is the value of Walsh Spectrum

$${W}_{f}\left(a\right)=\sum\nolimits_{a\in {F}_{2}^{n}}{\left(-1\right)}^{f\left(x\right)\oplus a.x}$$
(2)

and \(a.x\) is dot product defined by

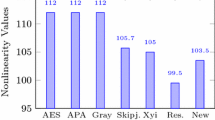
$${a}_{1}{.x}_{1}\oplus {a}_{2}{.x}_{2}\oplus \dots \oplus {a}_{n}{.x}_{n}$$
(3)

Table 4 presents the non-linearity values of eight balanced Boolean functions of constructed S-Boxes and Fig. 1 compares the non-linearity values of the proposed S-box to those of several previously developed S-boxes in the literature.

Table 4 Non- linearity values
Full size table
Fig. 1
figure 1

A comparison between the non-linearity values of suggested S-box and various other S-boxes

Full size image

4.2 Bit independent criterion

A Vectorial Boolean \(S:{\{\mathrm{0,1}\}}^{n}\to {\{\mathrm{0,1}\}}^{n}\) function meets BIC requirements if \(\forall i,j,k\in \{\mathrm{1,2},3,\dots ,n\}\) the inversion of \({i}^{th}\) input modifies output \({j}^{th}\) and \({k}^{th}\) separately [41]. Tables 5 and 6 provide the results of the BIC non-linearity values and the BIC SAC values of the recommended S-box, respectively. Where the relationship is discovered when we modify the \({i}^{th}\) input and the corresponding change in the \({j}^{th}\) and \({k}^{th}\) output bits. Our S-box has a BIC nonlinearity score of 103.79, and a BIC-SAC score of 0.4992, which is quite near to the ideal value of 0.5. As a consequence, our S-box satisfies the BIC's requirements. Table 9 compares the BIC non-linearity values of the recommended S-boxes to those of numerous other S-boxes.

Table 5 BIC Nonlinearity Values of S-box 2
Full size table
Table 6 BIC SAC Values of S-box 2
Full size table

4.3 Strict avalanche criterion

This is a critical requirement for determining the algebraic characteristics of the S-box [41]. This S-box feature assures that the output bit changes by 50% or 1/2 probability after altering a single input bit. This criteria asserts that if a single input bit is changed, each output bit will change with a chance of 1/2. [31, 41] provide a strong approach for calculating SAC of S-boxes using a dependency matrix. The S-Box has an average SAC value of 0.4995, indicating that the recommended S-Box meets the SAC criteria adequately. Table 7 shows the SAC values of the recommended S-box and Table 9 compares them to other S-boxes.

Table 7 SAC values of recommended S-box
Full size table

4.4 Differential Uniformity

Biham E and Shamir A [40] proposed this analysis. The differential uniformity of a Boolean function is calculated by requiring that the XOR values of each output have the same probability as the XOR values of each input. The following is the mathematical formula for calculating differential uniformity.

$$DU={max}_{\Delta x\ne 0,\Delta y}\left(\#\{x\in X|f(x)\oplus f(x\oplus \Delta x)=\Delta y\}\right)$$
(4)

Table 8 shows the differential uniformity values of the recommended S-box, and Table 9 shows a comparison of the differential probability values of the proposed S-box and many other existing S-boxes in the literature. Figure 2 depicts a graphical comparison between DU values of the recommended S-box and several existing S-boxes.

Table 8 Input / Output XOR Distribution Table
Full size table
Table 9 The comparison between LP, DP, BIL-NL, and SAC values of S-Boxes
Full size table
Fig. 2
figure 2

A comparison between DU scores of different S-boxes

Full size image

4.5 Linear approximation probability

The present block cypher's cryptologist seeks to create enough unpredictability and bit diffusion to protect the data from cryptanalytic efforts. An S-box with a low linear probability (LP) denotes a mapping that is more nonlinear and resists linear cryptanalysis. This analysis is performed to determine the event's greatest value of imbalance. Matsui [28] proposed this approach, and the mathematical formula is as follows,

$$LP={max}_{{a}_{1,}{a}_{2}\ne 0}\left|\frac{\#\{x\in X|x.{a}_{1}=f\left(x\right).{a}_{2}\}}{{2}^{n}}-\frac{1}{2}\right|$$
(5)

Table 9 illustrates the LP values of the proposed S-box and compares them to other S-boxes.

5 Applications of s-box in image encryption

In this phase, we apply the recommended S-box for image encryption scheme using Advanced Encryption Standard algorithm. MLC specifies a methodology for assessing the findings of various statistical studies, such as energy, homogeneity, contrast, entropy and correlation. This evaluation determined the validity of S-box for image encryption Figs. 3 and 4.

Fig. 3
figure 3

Original Lena Image

Full size image
Fig. 4
figure 4

Encrypted Lena Image

Full size image

5.1 Contrast

Contrast is the change in color that sorts an image different from other image within the similar field of view. The contrast is high means that disorderness in encrypted image increased. Contrast is related with the amount of confusion which is produced by the s-box to the plan image. The mathematical form of contrast is,

$$Contrast=\sum {\left|k-m\right|}^{2}p(k,m)$$

Here \(k, m\) denotes the pixels of the image.

5.2 Correlation

Correlation expands the link among the pixels of the cipher image. This assessment is divided into three categories.

  1. a.

    General correlation

  2. b.

    Diagonal formats

  3. c.

    Vertical and horizontal

If G, H represents two matrices, the correlation is,

$$Correlation=\sqrt{\frac{{\sum }_{m}{\sum }_{n}({G}_{mn}-\overline{G })({H}_{mn}-\overline{H })}{{\sum }_{m}{\sum }_{n}{({G}_{mn}-\overline{G })}^{2}{\sum }_{m}{\sum }_{n}{({H}_{mn}-\overline{H })}^{2}}}$$

Two distinct images may have similar correlation but dispersal of colors of the pixels may be totally different as shown in Fig. 3.

5.3 Energy

The Grey-level co-occurrence matrix is applied to calculate energy. If energy is nearly equal to zero then encryption scheme is better. The mathematical form of the energy is Fig. 5,

Fig. 5
figure 5

Encrypted image Correlation

Full size image
$$Energy=\sum P{(k,l)}^{2}$$

5.4 Homogeneity

We put into practice the homogeneity that calculates how closely the scattered components are together. This is called Grey-tone spatial dependency matrix. The homogeneity close to zero ensured that encrypted image is good. The GLCM table radiates the frequency of Grey levels.

The mathematical form of homogeneity is

$$Homogeneity=\sum\nolimits_{kl}\frac{p(k,l)}{1+\left|k-l\right|}$$

Here grey level co-occurrence matrices in the GLCM is mentioned by \(P (k, l).\)

5.5 Entropy

Entropy measures the randomness in the picture. Mathematically its denoted as,

$$Entropy=-\sum\nolimits_{j=1}^{n}(p\left({x}_{j}\right){\mathrm{log}}_{b}p({x}_{j}))$$

where \(p({x}_{j })\) have the histogram count. Figure 6 shows that assessment of lower and higher entropy. If entropy is close to 8 then encryption quality is better.

Fig. 6
figure 6

Lower vs higher entropy

Full size image

Here the Table 10 describes the MLC of s-boxes which fulfill all the conditions up to the mark.

Table 10 Pseudocode of Proposed Image Encryption Scheme
Full size table

5.6 Complexity analysis

This section explores the computational complexity of the proposed encryption scheme, which involves dividing the image into Most Significant Bits (MSBs) and Least Significant Bits (LSBs). Each pixel in the image is split into two sub-blocks using a constant time complexity of \(O(1).\) The initial step requires \(O(M\times N)\) bit operations. Next, the scheme maps each element of the image onto proposed S-box in constant time since the image data lies within a fixed range. The preprocessing step requires \(O(M\times N)\) bit operations to execute. The substitution module is also performed in linear time. As all modules of the algorithm operate in linear time, the overall computational complexity of the scheme is \(O(M\times N),\) which is linear time. \((M\times N)\) represents the dimension of the plain image. Comparing the computational time complexities of the proposed encryption scheme with those of existing algorithms [30], the computational time complexity for generating the cross-coupled chaotic sequence for one round operation is \(O(2 \times {M}_{x})\),where \({M}_{x}\) is the maximum value of \({M}_{1}\) and \({M}_{2}\) respectively. The time complexity for the row-column permutation stage is\(O({M}_{1}\times {N}_{1})\), while the computational complexity for the row-column diffusion operation is\(8( {M}_{1}+{N}_{1})\). Therefore, the overall total computational time complexity of the encryption algorithm [30] is \(O(2Mx+9({M}_{1}+{N}_{1})\) which is almost equal to that of the proposed algorithm.

5.7 Pseudocode of encoding of proposed image data

The pseudocode for proposed image encryption scheme is explain in Table 10.

6 Analysis and comparison

In this part, we have applied statistical analysis to proposed encrypted Lena image Fig. 4. We have computed entropy, contrast, correlation, energy, and homogeneity of the ciphered image. Table 10 shows the comparison of recommended S-box encryption scheme with other algorithms. This ensures that our highly non-linear S-box is favorable for the image's encryption reliability (Fig. 5).

Table 11 shows that entropy is nearly equal to 8, contrast is higher. Because if entropy is close to 8 then encryption scheme is good and contrast higher also ensure the quality of the image encryption scheme. The energy and correlation is close to zero and homogeneity is also declines. For better encryption quality energy also nearly equal to zero. From these analysis and comparisons, we can say that proposed S-boxes for image encryption are good.

Table 11 Comparison of MLC
Full size table

7 Conclusion

In this manuscript, we provided an innovative technique to construct the S-box by using Maclaurin series of logarithmic function and apply Mellin transformation on it to erect the initial S-box. After that, specific permutations of \({S}_{256}\) utilized to enhance the nonlinearity of preliminary S-box and generate the final S-box. The effectiveness of our suggested S-box is then compared to other famous S-boxes in the literature. We apply statistical and algebraic tests to evaluate the efficiency of our final S-box. NL, SAC, DU, LAP and BIC are all part of the algebraic test. Because our final S-box meet all of the conditions of these analyses, regarded as strong S-box for secure communication. We use the Majority Logic Criterion in the statistical test to evaluate the effectiveness of the final S-box in an image encryption application. In this context, statistical tests such as contrast, energy, homogeneity and entropy are applied. The output result show that S-box consider more secure and effective against invaders attacks. In future, we can construct the S-boxes by using other transformations such as Sumudu and Fourier transformations and further those S-boxes can be utilized in audio, video, and text encryption schemes.