1 Introduction

In today’s environment protection of data is essential. Information should be delivered in such a way that any third person would not have approach to alter the data. To overcome the problem of security of information cryptographic techniques are used to transfer data in secret form or back in readable form. It is separated into two branches, symmetric key cryptography and asymmetric key cryptography [1] Symmetric key comprised on the use of single key for encryption and decryption. While in asymmetric key the key is used for encryption cannot be used for decryption. Symmetric key has two main branches block ciphers and stream ciphers. Stream cipher encrypt one byte of plain text at a time while block cipher encrypts one block at a time. In block cipher the size of block may be of one byte or more or less. DES, Triple DES, IDEA and AES use symmetric block key algorithms. ECC and RSA are asymmetric key algorithms.

A novel scheme based on modified Pascal’s triangle and elliptic curve [2] is proposed in this paper. We have to construct S-box [3] using this technique so that we can apply our proposed S-boxes for different encryption schemes as well for other applications. Before this technique some researchers have done work on elliptic curve cryptography, several approaches to construct S-box using ECC have been proposed in the literature [4,5,6,7]. No one yet utilized the combination of ECC and Modified Pascal’s Triangle to construct S-box. We have measured strength of our proposed S-box by different analysis such as LP, DP, BIC, SAC and NL. We compare our proposed S-boxes with the existing S-boxes in literature. Also we have two applications of our proposed S-boxes first one is image encryption and second one is noise removal.

In first section we discus some basics of S-box, elliptic curve and modified Pascal’s triangle. In second section we have steps to construct our proposed S-box. In third section we have results and analysis of proposed S-box and comparison with existing S-boxes. In last we have application of newly created S-box.

2 Preliminaries

In this section, we elaborate some basics of substitution-box, elliptic curve and modified Pascal’s triangle.

2.1 S-Box

In 1949, Claude Shannon gave the concept of substitution-box [8]. The substitution box (S-box) is indispensable resource in cryptography. Substitution-boxes are responsible for the protection of information, a strong S-box have more secure cryptosystem [9]. S-boxes have been used in almost all cryptosystem such as DES, AES. Before using any S-box in cryptosystem we have to measure its strength by different analysis.

2.2 Elliptic Curve

An elliptic curve is a cubic curve and is defined over a finite field by an Eq. (1)

$$y^{2} = (x^{3} + ax + b)modp$$
(1)

where \(p\) is a prime and \(a,b \in F\) be constants and

$$\left( {4a^{3} + 27b^{2} } \right)modp \ne 0$$

It requires that the curve should be non-singular means that the curve has no self-intersection, and it is achieved when discriminant is non-zero [10].

The concept of elliptic curve in cryptography has been given by Miller [11] and Koblitz [12] in 1985. ECC provide us more security of the data with small key size then other cryptosystems.

2.3 Modified Pascal’s Triangle

In Pascal’s Triangle numbers are arranged in such a way that they are coefficients of binomial expansion and these numbers are arranged in a triangle. In Pascal’s triangle the first and the last element of each row is 1 and other numbers are obtained by adding two numbers that lies above it [13] (Figs. 1, 2).

Fig. 1
figure 1

Pascal’s Triangle

Full size image
Fig. 2
figure 2

Modified Pascal’s Triangle

Full size image

It is obtained by mathematical expression

$$pt\left( {m,n} \right) = pt\left( {m - 1,n - 1} \right) + pt\left( {m - 1,n} \right)$$
$$pt\left( {m,0} \right) = 1$$
$$pt\left( {0,n} \right) = 1$$

In modified Pascal’s triangle the first and the last elements are generated by sequences and given by the mathematical expression

$$pt\left( {m,n} \right) = pt\left( {m,n - 1} \right) + pt\left( {m - 1,n} \right)$$
$$pt\left( {m,0} \right) = a_{m}$$
$$pt\left( {0,n} \right) = b_{n}$$

where \(a_{m}\) and \(b_{n}\) are sequences and defined as

$$a_{m} = 2m\;{\text{and}}\;b_{n} = n^{2} + 1$$

3 The Proposed Scheme

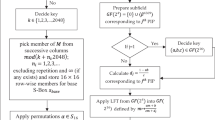
The procedure to construct new Substitution-box is following as

3.1 Step-1

For the construction of S-box first we consider the relation of Modified Pascal’s Triangle defined in Eqs. (2), (3) and (4)

$$pt\left( {m,n} \right) = pt\left( {m,n - 1} \right) + pt\left( {m - 1,n} \right)$$
(2)
$$pt\left( {m,0} \right) = a_{m}$$
(3)
$$pt\left( {0,n} \right) = b_{n}$$
(4)

where \(a_{m}\) and \(b_{n}\) are sequences and defined as

$$a_{m} = 2m\;{\text{and}}\;b_{n} = n^{2} + 1$$

3.2 Step-2

Now we apply “loop” on m and n such that m varies from 2 to 127 and n varies from 3 to 127.

Using the relation of Modified Pascal’s Triangle, we construct a 16 × 16 matrix. But we have some numbers in sequence which do not gives us better result for strong S-box.

3.3 Step-3

To overcome problem of above step we consider equation of elliptic curve [14]

$$y^{2} = (x^{3} + ax + b)modp$$

where \(p\) is a prime and \(a,b \in F\) be constants. Choose \(a = 2320,\;b = 1174\;{\text{and}}\;p = 2851\)

P should be a prime number and the condition \(\left( {4a^{3} + 27b^{2} } \right)modp \ne 0\) must be satisfied.

We can change the value of \(a\) and \(b\), every time when we change the value of \(a\) and \(b\) we obtain a new S-box. The value of \(p\) should be greater then 289 and \(a\) > \(b\).

3.4 Step-4

We take output of Step-2 and then applying elliptic curve on it and we get 16 × 16 S-box. This S- box gives us better results as compared to S-box of step-2 (Tables 1, 2).

Table 1 Proposed S-box 1
Full size table
Table 2 Proposed S-box 2
Full size table

4 Results, Analysis and Comparison of S-Boxes

First, we investigate the properties of newly constructed S-box. We apply different analyses such as NL, SAC, BIC, DP and LP [15]. In addition, we compare proposed S-boxes with some existing S-boxes available in literature, presented in [2, 16,17,18,19,20,21,22,23,24].

Brief explanation of some analysis that are tested to S-boxes is given below.

4.1 Non-linearity

In non-linearity method the number of bits must be changed in order to reach close to the affine function. The maximum value of the non-linearity is given as \(N\left( f \right) = 2^{n - 1} - 2^{n/2 - 1}\) for the S-boxes in \(GF\left( {2^{n} } \right)\) [9], which is \(N = 120\).

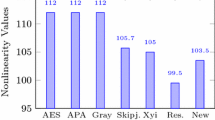
The results and comparison for the test of non-linearity analysis is given below in Table 3. The proposed S-box 1 shows maximum non-linearity = 108, minimum non-linearity = 104 and average non-linearity = 105. While the proposed S-box 2 shows maximum non-linearity = 108, minimum non-linearity = 102 and average non-linearity = 104. Also, we have graphically comparison of non-linearity which is given below in Fig. 3.

Table 3 Non-linearity analysis
Full size table
Fig. 3
figure 3

Non-linearity comparison

Full size image

4.2 Bit Independence Criterion

In this criterion the output bits b and c necessarily to be change when an individual input bit a is altered ∀ a, b and c, with bit independence it becomes more difficult to approach the cryptosystem. It means that BIC is a desirable property in cryptography.

The results of BIC of newly created S-boxes is shown in Table 4 and comparison with some S-boxes that are available in literature also shown in table below. Our proposed S-box 1 shows average and minimum value 103.5 and 94 respectively with square deviation 3.404. While Average, minimum and square deviation of proposed S-box 2 is 103.14, 96 and 2.870 respectively. Graphically comparison of BIC is shown below in Fig. 4.

Table 4 BIC analysis
Full size table
Fig. 4
figure 4

BIC comparison

Full size image

4.3 Strict Avalanche Criterion

The strict avalanche criterion is an obligatory ingredient for S-boxes it states that if single input bit changed then with this single change half of output bits must be changed means that it causes avalanche of changes [9]. The concept of SAC was presented by Webster and Tavares [25].

Results and analysis are listed in Table 5 it can be viewed from table that SAC analysis of proposed S-boxes is approximately 0.5, also we have graphically representation of S-boxes in Fig. 5.

Table 5 SAC analysis
Full size table
Fig. 5
figure 5

SAC comparison

Full size image

4.4 Differential Approximation Probability

In this method we analyze the attitude of input and output bit. For a desirable situation S-boxes shows differential consistency. For this, input differential necessarily to be mapped to unique output differential. DP is expressed as

$$DP_{{\left( {\Delta {\text{x}} \to \Delta {\text{y}}} \right)}} = \left[ {\frac{{\# \{ x \in X/S\left( x \right) \oplus S\left( {x + \Delta {\text{x}}} \right) = \Delta {\text{y}}}}{{2^{m} }}} \right]$$

where \(\Delta x\) is input and Δy is output differential operator and \(2^{m}\) is total elements.

Results and comparison of DP in given in Table 6, it can be viewed from table that differential approximation probability of proposed S-boxes is comparatively better than skipjack, Xyi and residue prime. Graphical representation is shown in Fig. 6.

Table 6 DP analysis
Full size table
Fig. 6
figure 6

DP comparison

Full size image

4.5 Linear Approximation Probability

Linear approximation probability is defined as maximum value of inequality that is occur. The consistency of input and output bit must be alike. LP is defined as

$$LP = max_{\psi x,\psi y \ne 0} \left| {\frac{{\# \left\{ {x \in X/x .\psi x = S\left( x \right) .\psi y} \right\}}}{{2^{n} }} - \frac{1}{2}} \right|$$

where set X defines all possible inputs and \(2^{n}\) is total elements.

In Table 7, the results and analysis of proposed S-boxes are shown also we have comparison with some S-boxes. Maximum value of both proposed S-boxes is 160. Graphical comparison is shown in Fig. 7.

Table 7 LP analysis
Full size table
Fig. 7
figure 7

LP comparison

Full size image

5 Image Encryption

Confidential image protection became one of the most important research area of cryptography. In particular, the standard data protection systems with a single S-box are not reasonably better to ensure the image security [26]. Some novel cryptosystems must be required that can withstand image safety attacks effectively. Here we use our proposed S-boxes for the encryption of an image. We used capsicum image as a sample for encryption. We apply two rounds of encryption for better results.

5.1 Image Encryption Algorithm

Here we have algorithm how we encrypt the image:

  1. 1.

    First we take a capsicum image of pixel values from 0 to 255 shown in Figs. 8 and 9.

    Fig. 8
    figure 8

    a Original image. b One round. c Two round

    Full size image
    Fig. 9
    figure 9

    a Original image. b. One round. c. Two round

    Full size image
  2. 2.

    Then we take our Proposed S-boxes which also have values from 0 to 255.

  3. 3.

    We apply our Proposed S-box on image.

  4. 4.

    Substitute each value of S-box too each corresponding value of image.

  5. 5.

    In this way we get encrypted image which is shown in Figs. 8 and 9, this is one round to encrypt the image.

  6. 6.

    We apply second round of same steps to again encrypt Figs. 8 and 9.

  7. 7.

    Then we get our final encrypted image shown in Figs. 8 and 9.

6 Noise Removal

The performance of the proposed S-box is access in terms of its bit error rate (BER) as a function of length of burst errors for numerous values of SNR in combination with single error correcting code. The performance of the proposed S-box is compared with conventional random S-boxes, such as AES, Skipjack, Gray and Residue prime in terms of bit error rate as a function of length of burst error. For this, we use MATLAB software.

For size N = 256 we take 100 block of random data. The data is encrypted using linear block hamming code. The message to code word length is chosen as (7, 4). Any existing message to code word length can be taken with least hamming space of 3 so that a single error can be corrected. To calculate the performance against burst errors, burst of errors with several lengths are presented manually and exclusive OR (XOR) with modified data [27].

At receiver, bit error rate is calculated for proposed S-box, Gray, Skipjack, and Residue prime and AES to compare the performance of these S-box in burst errors environment. This comparison is shown in tables. In tables we have shown BER for the different values of SNR. We calculate BER of SNR = 5, SNR = 10, SNR = 15 and SNR = 20.

Here are four different tables for the comparison of BER for different values of SNR (Tables 8, 9, 10).

Table 8 BER for SNR = 05
Full size table
Table 9 a. BER for SNR = 10, b. BER for SNR = 15
Full size table
Table 10 BER for SNR = 20
Full size table

7 Conclusion

In this paper, we construct the new S-boxes using the methodology of Modified Pascal’s Triangle and Elliptic Curve. To measure the strength of proposed S-boxes we have some analyses like Non-linearity, Strict Avalanche Criterion, Bit Independence criterion, Differential approximation probability and linear approximation probability. We used our proposed S-boxes for image encryption and noise removal, it can be seen that proposed S-boxes shows better results as compare with some commonly used S-boxes.