Paracatadioptric camera calibration based on the projecting relationship of the relative position between two spheres

Abstract

We discuss how the projecting relationship of the relative position between two spheres in space can be used to calibrate paracatadioptric cameras. The projections of two spheres under a paracatadioptric camera are classified into three cases: Intersection, tangency, and separation. Methods for obtaining the principal point are proposed for each case. When the principal point is known, an analysis of the geometric relationship of the two spheres on the unit viewing sphere model shows that their tangent lines at the antipodal points are parallel. Based on this geometric relationship, the vanishing line of the plane containing the projection circle can be determined to yield the imaged circular points and obtain the remaining intrinsic camera parameters. When the principal point is unknown, the intersection points of two groups of parallel projection circles of the two spheres on the unit viewing sphere model combine with their corresponding antipodal points to form a rectangle; hence, the vanishing point in the orthogonal directions can be determined. Finally, the intrinsic camera parameters can be obtained by applying the constraints of the vanishing points in orthogonal directions to the absolute conic. Simulation results and real image data demonstrate the effectiveness of our methods.

1 Introduction

Any computer vision application, such as robot navigation, surveillance, three-dimensional measurement, 3D reconstruction, or virtual reality, requires large field-of-view (FOV) images [12, 18, 33]. Modifying a traditional camera with a specially shaped mirror effectively enhances the FOV, and such a camera is called a catadioptric camera. Catadioptric cameras employ many types of surface shapes such as planar, spherical, conical, and rotational quadric surfaces [12, 18, 19]. Baker and Nayar [2] classified catadioptric cameras into central and non-central types, depending on whether there is a fixed single viewpoint.

A central catadioptric camera has a fixed single viewpoint and a large FOV, and an image captured by such a camera can be easily converted into a perspective image. Therefore, central catadioptric cameras are widely used in computer vision applications. A central catadioptric camera uses one of four types of mirror surface shapes: paraboloidal, hyperboloidal, ellipsoidal, or planar. Geyer and Daniilidis [9] proposed a generalized projection model for a central catadioptric camera, the imaging process of which is equivalent to a two-step mapping via a unit viewing sphere. The unit sphere model of a central catadioptric camera provides a mathematical basis for the theoretical study of its calibration. Camera calibration plays a significant role in computer vision and makes it possible to extract metric information in the real world from projections on the image plane [8, 36]. The calibration of a central catadioptric camera is categorized into five primary types according to the entity used in the calibration:

• (a) Calibration based on 2D patterns [7]: These methods use 2D calibration patterns with control points (e.g., corners, dots, or arbitrary features), and the image points of these control points are easily extracted.

• (b) Calibration based on 3D points [21, 23]: These methods determine the 3D world coordinates, and the image points of these 3D points are easily extracted.

• (c) Self-calibration [13]: These methods directly use the image of a scene and employ constraints among corresponding points in multiple views to calibrate the camera.

• (d) Calibration based on lines [3, 10, 28, 29, 32]: These methods use only an image of lines in a scene without any metric information.

• (e) Calibration based on spheres [5, 29, 30, 32, 35]: These methods use only an image of spheres in a scene without any metric information.

In this paper, we mainly discuss the calibration of a paracatadioptric camera based on the projecting relationship of the relative position between two spheres.

Using an image of a sphere to calibrate a catadioptric camera has definitive research value and practical significance. A sphere is a common geometric object, the most important advantage of which is a lack of self-occlusion; moreover, from any direction, the closed contour of a sphere is observed as a circle [31]. Because a sphere has abundant visual geometric properties, camera calibration methods that employ images of spheres are attracting considerable attention.

Several authors have introduced methods that employ an image of a sphere for traditional camera calibration [1, 4, 20, 22, 24,25,26, 31, 34]. Lu and Payandeh [15] discussed the sensitivity of traditional camera calibration using images of spheres. Ying and Hu [29] were the first to propose central catadioptric camera calibration using sphere images. In the above-mentioned studies, the authors demonstrated that the image of a sphere in space taken with a central catadioptric camera is conic under a unit sphere projection model. Further, they proved that in the non-degradation case, the projection of a sphere can provide only two invariants. Theoretically, the projections of at least three spheres are required to achieve catadioptric camera calibration in the non-degenerate case. A calibration method [29] that uses fractional steps to reduce the complexity of the solution requires the projections of at least four spheres; however, this method is nonlinear, its computation is relatively complex, and it obtains only some of the intrinsic parameters of the paracatadioptric camera.

Ying and Zha [32] were the first to discover the modified image of the absolute conic (MIAC) and its application to the central catadioptric camera. Furthermore, they discovered that each sphere image has the geometric property of double contact with the MIAC, and they proposed a linear calibration method for central catadioptric cameras. Ying and Zha [30] further studied the geometric and algebraic relationships between the MIAC and sphere images. They used the double-contact theorem [6] to explain the relationship between the MIAC and sphere images, and their conclusion holds for the dual form of the sphere images. In addition, they proposed a linear calibration method. However, in the case of the paracatadioptric camera, previously proposed theories and calibration methods [30, 32] are degenerate. In order to overcome this problem, the properties of an antipodal sphere image under a paracatadioptric camera have been investigated, and an optimum estimation algorithm has been proposed for a sphere image and its antipodal sphere image. Further, a linear method for calibrating the paracatadioptric camera has been established using two parallel projection circles on the unit viewing sphere [5]. A calibration method based on two parallel circles was initially proposed for a pinhole camera, but the selection of the imaged circular points is complicated [27].

Zhao and Wang [35] were the first to use two spheres overlapping each other within the image plane for paracatadioptric camera calibration. They used real intersections of the images and antipodal images of the two spheres to obtain the orthogonal vanishing points and calibrate the intrinsic camera parameters. However, this calibration method requires at least five views of the two spheres; moreover, it considers neither imaginary intersections of the images with antipodal images of the two spheres, nor cases in which the two spheres contact with or separate from each other within the image plane.

Based on the studies mentioned above [5, 29, 30, 32, 35], this paper mainly discusses how to use the projecting relationship of the relative position between two spheres to calibrate a paracatadioptric camera. Through analysis of the projections of the two spheres on the unit viewing sphere for a paracatadioptric camera, three cases are found by adjusting the position between them. For each condition, a method for calculating the principal point is proposed. When the principal point is given, analysis of the geometric relationship between two groups of parallel projection circles on the unit viewing sphere indicates that the tangent lines of the circles at the antipodal points are parallel. The vanishing points of the plane containing the projection circle can be obtained from the relationship that determines the vanishing line containing the projection circle. Further, the imaged circular points can be obtained by solving the equations of the vanishing line and sphere image. As a result, the other intrinsic parameters of the camera can be obtained from their relationship with the imaged circular points. When the principal point is unknown, the intersection points (including real or virtual points) of two groups of parallel projection circles of the two spheres on the unit viewing sphere combine with their corresponding antipodal points to form a rectangle. Thus, the orthogonal vanishing points can be obtained by the orthogonal directions formed by the rectangle. As a result, the intrinsic camera parameters can be obtained using the relationship between the orthogonal vanishing points and the intrinsic camera parameters as constraint conditions.

The remainder of this paper is organized as follows. Section 2 reviews the unit viewing sphere model for a central catadioptric camera as well as some related studies. Section 3 provides a detailed description of paracatadioptric camera calibration using images of the relative position between two spheres. Section 4 presents the experimental results. Finally, Section 5 concludes the paper.

2 Preliminaries

In this section, we briefly describe the central catadioptric projection model, the antipodal image points, and their properties. Subsequently, we discuss the projection process of a sphere under a paracatadioptric camera.

2.1 Central catadioptric projection model

Baker and Nayar [2] showed that only four types of reflecting mirror surface shapes exist for a central catadioptric camera: paraboloidal, hyperboloidal, ellipsoidal, and planar. Geyer and Daniilidis [9] proposed a generalized projection model for a central catadioptric camera. The generalized projection model of the imaging process of a central catadioptric camera is equivalent to a two-step mapping via a unit sphere (see Fig. 1).

• Step 1. Point M is projected in 3D space to two points M_S+ and M_S− on the unit viewing sphere, where M_S+ and M_S− are two intersection points of the unit sphere and the line joining its center O and the 3D point M. {M_S+, M_S−} is called a pair of antipodal points [28].

• Step 2. Two points M_S+, M_S− on the unit viewing sphere are projected to two corresponding points m₊, m₋ in the catadioptric image plane Π_I using 3D point O_c as the projection center. {m₊, m₋} is called a pair of antipodal image points [28].

Fig. 1

Projection process of a 3D point M under the unit sphere model

The intrinsic parameters of the virtual camera with optical center O_c are estimated, while the intrinsic parameters of the central catadioptric camera are known. The intrinsic matrix of the virtual camera is

$$ {K}_c=\left[\begin{array}{ccc}r{f}_e& s& {u}_0\\ {}0& {f}_e& {v}_0\\ {}0& 0& 1\end{array}\right], $$

(1)

where r is the aspect ratio, f_e is the effective focal length, s is the skew factor, and [u₀ v₀ 1]^T are the homogeneous coordinates of principal point p, which is the projection of center O of the unit viewing sphere. As shown in Fig. 1, the homogeneous coordinates of a 3D point M be [x_w y_w z_w 1]^T under the world coordinate system O − x_wy_wz_w. The homogeneous coordinates of its projection points m_± in catadioptric image plane Π_I can then be represented as:

$$ {\lambda}_{\pm }{m}_{\pm }={K}_c\left(\pm \frac{\overset{\sim }{M}}{\left\Vert M\right\Vert }+\xi e\right), $$

(2)

where λ₊, λ₋ are two unknown scale factors, $\left\Vert M\right\Vert =\sqrt{x_w^2+{y}_w^2+{z}_w^2}$, $\overset{\sim }{M}={\left[{x}_w\ {y}_w\ {z}_w\right]}^T$, e = [0 0 1]^T, and parameter ξ(ξ=| OO_c| ) is a mirror parameter. The value of ξ corresponds to the different types of mirrors; the mirror is a paraboloid if ξ = 1, an ellipsoid or a hyperboloid if 0 < ξ < 1, and a plane if ξ = 0.

2.2 Projection process of a sphere under the paracatadioptric camera

For the unit sphere model, Duan and Wu [5] suggested that the projection process of a sphere in space under the paracatadioptric camera can be divided into two steps. First, a sphere Q in space can be projected to two parallel circles S₊ and S₋ on the unit viewing sphere; circle S₊ is called the projection circle of sphere Q, circle S₋ is called the antipodal circle of projection circle S₊, and the two planes containing circles S₊ and S₋are called their respective base planes. The two base planes are parallel, and their elements at infinity are the same [29]. Next, the two parallel circles S₊ and S₋ are respectively projected to two conics C₊ and C₋in the paracatadioptric image plane Π_I through the optical center O_c of a virtual camera. Conic C₊ (i.e., the sphere image) is visible, and conicC₋ (i.e., the antipodal sphere image) is not visible. This projection process is shown in Fig. 2. The following conclusions can be drawn from this projection process:

Fig. 2

Sphere projection via the unit viewing sphere under a paracatadioptric camera

Proposition 1

In Fig. 2, if B₁₊is any point on projection circle S₊ of Q, the antipodal point B₁₋ of B₁₊is on the antipodal circle S₋ of S₊.

This can easily be proved according to the projection principle of the unit sphere model and three-dimensional geometry of space-related knowledge. From Proposition 1, the following corollary can be deduced.

Corollary 1

In Fig. 2, if n different points B_k+ and B_k−(k = 1, 2, ⋯, n)are on circles S₊and S₋, respectively, and {B_k+, B_k−}(k = 1, 2, ⋯, n) are n pairs of antipodal points, then (i) the tangent lines l_k+of circleS₊ at points B_k+ are parallel to the tangent lines l_k−of circle S₋ at points B_k−, where l_k+lies on the base plane of S₊and l_k−lies on the base plane of S₋; and (ii) when n ≥ 2, the vanishing line $\overset{\sim }{l}$on the base plane of S₊ can be determined by n pairs of antipodal points {B_k+, B_k−}, and thus, the imaged circular points m_I, m_Jon the base plane of S₊ can be obtained.

Proof

(i) As shown in Fig. 2, from the properties of the tangent of a circle, there existO₊B_k+ ⊥ l_k+, O₋B_k− ⊥ l_k−. Then, from O₊O₋ ⊥ O₊B_k+, O₊O₋ ⊥ O₋B_k−, and the coplanarity of the four points O₊, O₋, B_k+, B_k+, we haveO₊B_k+ ∥ O₋B_k−. Further, the plane containing l_k+ and the plane containing l_k− are parallel; hence, l_k+ ∥ l_k−. (ii) For an arbitrary k, the intersection point of l_k+and l_k− is a point at infinity on the base plane of S₊from conclusion (i) of Corollary 1, denoted asD_k∞.The images of points B_k+andB_k− are denoted as b_k+ and b_k−, respectively; {b_k+, b_k−}is a pair of antipodal image points. The images of lines l_k+and l_k− are denoted as ${\overset{\sim }{l}}_{k+}$and ${\overset{\sim }{l}}_{k-}$, respectively, and the intersection point of ${\overset{\sim }{l}}_{k+}$and ${\overset{\sim }{l}}_{k-}$ is d_k. According to the properties of projective transformation, ${\overset{\sim }{l}}_{k+}$is a tangent line of sphere image C₊at point b_k+, ${\overset{\sim }{l}}_{k-}$is a tangent line of antipodal sphere image C₋ at pointb_k−, and d_kis the image of D_k∞. According to the definition of a vanishing point [11], d_k is a vanishing point on the base plane of S₊; hence, a vanishing point on the base plane of S₊ can be determined by a pair of antipodal points {B_k+, B_k−}.Then,n vanishing points on the base plane of S₊ can be determined by n pairs of antipodal points {B_k+, B_k−}; thus, n ≥ 2. Thesen vanishing points can determine the line of Π_I, which is a vanishing line $\overset{\sim }{l}$on the base plane of S₊. According to the definition of circular points and the combination characteristic of the projective transformation, vanishing line S₊ and conics C₊ and C₋have the same intersection points, which are the imaged circular points m_I, m_J on the base plane of S₊.

3 Using the projecting relationship of the relative position between two spheres to calibrate the paracatadioptric camera

In this section, we discuss the projection of two spheres under the imaging model of the paracatadioptric camera and investigate how the projecting relationship of the relative position between two spheres can be used to calibrate the paracatadioptric camera.

3.1 Projection of two spheres under the paracatadioptric camera

First, the following definition is introduced before studying the projection properties of two spheres under the unit sphere model of the paracatadioptric camera.

Definition 1

Two viewing cones formed by taking a point in space as a viewpoint to observe two spheres in 3D space cannot contain each other. If the two viewing cones intersect two common generatrices, the two spheres are mutually occluding in this viewpoint. If the two viewing cones only intersect in one common generatrix, the two spheres are tangential in this viewpoint. If the two viewing cones do not intersect, the two spheres are separated in this viewpoint.

In Definition 1, the case in which the projection cone of one sphere contains the other one will not be discussed. Consider the projections of two spheres Q₁, Q₂ under the unit sphere model for the paracatadioptric camera. Here, take the ith(i ∈ ℕ₊) view of the two spheres Q₁, Q₂ as an example, where the elements in the ith view are denoted by the superscript letter i. By Definition 1, two arbitrary spheres in 3D space can be classified into three types: mutually occluding spheres, tangential spheres, and separated spheres. For each of type, the following proposition is true.

Proposition 2

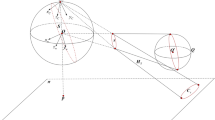
Taking the center of the unit viewing sphere as a viewpoint, the projection of two mutually occluding spheres under the unit sphere model for the paracatadioptric camera has the following properties (see Fig. 3): (i) Projection circles ${S}_{1+}^i,{S}_{2+}^i$ of two spheres Q₁, Q₂ have two real points ${A}_{1+}^i,{A}_{2+}^i$ on the unit viewing sphere. Their antipodal circles${S}_{1-}^i,{S}_{2-}^i$also have two real intersection points ${A}_{1-}^i,{A}_{2-}^i$ on the unit viewing sphere, and $\left\{{A}_{1+}^i,{A}_{1-}^i\right\}$and$\left\{{A}_{2+}^i,{A}_{2-}^i\right\}$are two pairs of antipodal points. (ii) Images ${C}_{1+}^i,{C}_{2+}^i$ of two spheres Q₁, Q₂ have two real intersection points ${a}_{1+}^i,{a}_{2+}^i$and two imaginary intersection points ${a}_{3+}^i,{a}_{4+}^i$. Their antipodal sphere images ${C}_{1-}^i$ and ${C}_{2-}^i$ also have two real intersection points${a}_{1-}^i,{a}_{2-}^i$ and two imaginary intersection points ${a}_{3-}^i,{a}_{4-}^i$. Further,$\left\{{a}_{j+}^i,{a}_{j-}^i\right\}\left(j=1,2,3,4\right)$ are four pairs of antipodal image points, where two pairs of imaginary antipodal image points $\left\{{a}_{3+}^i,{a}_{3-}^i\right\}$ and $\left\{{a}_{4+}^i,{a}_{4-}^i\right\}$ can be regarded as the images of two pairs of imaginary antipodal points $\left\{{A}_{3+}^i,{A}_{3-}^i\right\}$ and $\left\{{A}_{4+}^i,{A}_{4-}^i\right\}$, respectively. (iii) The lines passing through points ${a}_{j+}^i,{a}_{j-}^i\left(j=1,2,3,4\right)$intersect at principal point p.

Fig. 3

Projection of two mutually occluding spheres under the unit sphere model of the paracatadioptric camera: a The projection circles ${S}_{1+}^i$ and ${S}_{2+}^i$ intersect at two real points${A}_{1+}^i$and ${A}_{2+}^i$on the unit viewing sphere for the paracatadioptric camera; their antipodal circles${S}_{1-}^i$and ${S}_{2-}^i$also intersect at two real points ${A}_{1-}^i$and${A}_{2-}^i$. b The corresponding projection of (a) in the image planeΠ_I

Proof

(i) As shown in Fig. 3a, let two viewing cones formed by viewing point O and two spheres Q₁, Q₂ be ${V}_1^i,{V}_2^i$, respectively. Because Q₁, Q₂are mutually occluding, according to Definition 1, ${V}_1^i,{V}_2^i$ have two common generatrices, and the two common generatrices and the viewing sphere intersect at four real intersection points. The viewing sphere and ${V}_1^i$, ${V}_2^i$ intersect in${S}_{1+}^i$, ${S}_{1-}^i$and ${S}_{2+}^i$, ${S}_{2-}^i$, respectively; thus, two of the four abovementioned intersection points are the intersection of ${S}_{1+}^i$ and ${S}_{2+}^i$, denoted as ${A}_{1+}^i,{A}_{2+}^i$, respectively, and the other two intersection points are the intersection of ${S}_{1-}^i$and${S}_{2-}^i$, denoted as ${A}_{1-}^i,{A}_{2-}^i$, respectively. By definition, $\left\{{A}_{1+}^i,{A}_{1-}^i\right\}$ and $\left\{{A}_{2+}^i,{A}_{2-}^i\right\}$are two pairs of antipodal points. (ii) From Section 2.2, under the optical centerO_cof a virtual camera, ${C}_{1+}^i$ and ${C}_{2+}^i$ are the projections of ${S}_{1+}^i$and${S}_{2+}^i$, and ${C}_{1-}^i$and ${C}_{2-}^i$ are the projections of ${S}_{1-}^i$and${S}_{2-}^i$. From conclusion (i) of Proposition 2 and the combination characteristic of the projective transformation, ${C}_{1+}^i$and ${C}_{2+}^i$ have two real intersection points, denoted as ${a}_{1+}^i,{a}_{2+}^i$, respectively; ${C}_{1-}^i$ and ${C}_{2-}^i$ also have two real intersection points, denoted as ${a}_{1-}^i,{a}_{2-}^i$, respectively. Further, ${a}_{1+}^i,{a}_{2+}^i,{a}_{1-}^i,{a}_{2-}^i$are the projections of ${A}_{1+}^i,{A}_{2+}^i,{A}_{1-}^i,A$under O_c. According to conclusion (i) of Proposition 2 and Definition 1, $\left\{{a}_{1+}^i,{a}_{1-}^i\right\}$ and $\left\{{a}_{2+}^i,{a}_{2-}^i\right\}$are two pairs of antipodal image points. Every two different conics on the same plane have two imaginary intersection points; hence, the two imaginary intersection points of ${C}_{1+}^i$and ${C}_{2+}^i$ are denoted as ${a}_{3+}^i,{a}_{4+}^i$, respectively, and the two imaginary intersection points of ${C}_{1-}^i$and ${C}_{2-}^i$ are denoted as ${a}_{3-}^i,{a}_{4-}^i$, respectively. Further, $\left\{{a}_{3+}^i,{a}_{3-}^i\right\}$ and $\left\{{a}_{4+}^i,{a}_{4-}^i\right\}$ are two pairs of imaginary antipodal image points that can be regarded as the images of two pairs of imaginary antipodal points $\left\{{A}_{3+}^i,{A}_{3-}^i\right\}$and $\left\{{A}_{4+}^i,{A}_{4-}^i\right\}$, respectively, as shown in Fig. 3b. (iii) According to properties of the antipodal image points [28], any pair of antipodal image points and p are collinear, and combined with conclusion (ii) of Proposition 2, the lines passing through points ${a}_{j+}^i,{a}_{j-}^i\left(j=1,2,3,4\right)$intersect at principal point p, as shown in Fig. 3b.

Proposition 3

Taking the center of the unit viewing sphere as a viewpoint, the projection of two tangential spheres under the unit sphere model for the paracatadioptric camera has the following properties (see Fig. 4): (i) Projection circles ${S}_{1+}^i,{S}_{2+}^i$ of two spheres Q₁, Q₂ have a real point${A}_{1+}^i$ on the unit viewing sphere. Their antipodal circles ${S}_{1-}^i,{S}_{2-}^i$also have a real intersection point ${A}_{1-}^i$ on the unit viewing sphere, and $\left\{{A}_{1+}^i,{A}_{1-}^i\right\}$ is a pair of antipodal points. (ii) Images ${C}_{1+}^i,{C}_{2+}^i$ of two spheres Q₁, Q₂have a real intersection point ${a}_{1+}^i$and two imaginary intersection points ${a}_{2+}^i,{a}_{3+}^i$.Their antipodal sphere images ${C}_{1-}^i$ and ${C}_{2-}^i$ also have a real intersection point${a}_{1-}^i$ and two imaginary intersection points ${a}_{2-}^i,{a}_{3-}^i$; hence, $\left\{{a}_{j+}^i,{a}_{j-}^i\right\}\left(j=1,2,3\right)$ are three pairs of antipodal image points, where two pairs of imaginary antipodal image points $\left\{{a}_{2+}^i,{a}_{2-}^i\right\}$ and $\left\{{a}_{3+}^i,{a}_{3-}^i\right\}$ can be regarded as the images of two pairs of imaginary antipodal points $\left\{{A}_{2+}^i,{A}_{2-}^i\right\}$ and $\left\{{A}_{3+}^i,{A}_{3-}^i\right\}$, respectively. (iii) The lines passing through points $\left\{{a}_{j+}^i,{a}_{j-}^i\right\}\left(j=1,2,3\right)$intersect at principal point p.

Fig. 4

Projection of two tangential spheres under the unit sphere model of the paracatadioptric camera: a The projection circles ${S}_{1+}^i$ and ${S}_{2+}^i$ intersect at a real intersection point ${A}_{1+}^i$on the unit viewing sphere for the paracatadioptric camera; their antipodal circles ${S}_{1-}^i$and${S}_{2-}^i$ also intersect at a real intersection point${A}_{1-}^i$. b The corresponding projection of (a) in the paracatadioptric image planeΠ_I

Proposition 4

Taking the center of the unit viewing sphere as a viewpoint, the projection of two separated spheres under the unit sphere model for the paracatadioptric camera has the following properties (see Fig. 5): (i) Projection circles ${S}_{1+}^i,{S}_{2+}^i$ of two spheres Q₁, Q₂ have no real intersection point; their antipodal circles ${S}_{1-}^i,{S}_{2-}^i$also have no real intersection point. (ii) Images ${C}_{1+}^i,{C}_{2+}^i$ of two spheres Q₁, Q₂ have four imaginary intersection points ${a}_{j+}^i$. Their antipodal sphere images ${C}_{1-}^i$ and ${C}_{2-}^i$ also have four imaginary intersection points ${a}_{j-}^i$, and$\left\{{a}_{j+}^i,{a}_{j-}^i\right\}$are four pairs of antipodal image points, which can be regarded as the images of four pairs of imaginary antipodal points$\left\{{A}_{j+}^i,{A}_{j-}^i\right\}$, respectively, where j = 1, 2, 3, 4. (iii) The lines passing through points ${a}_{j+}^i,{a}_{j-}^i\left(j=1,2,3,4\right)$intersect at principal point p.

Fig. 5

Projection of two separated spheres under the unit sphere model of the paracatadioptric camera: a The projection circles ${S}_{1+}^i$and${S}_{2+}^i$ have no real intersection points; their antipodal circles${S}_{1-}^i$and ${S}_{2-}^i$ also have no real intersection points on the unit viewing sphere. b The corresponding projection of (a) in the paracatadioptric image plane Π_I

The proofs of Propositions 4 and 5 follow the same procedure as the proof of Proposition 2; hence, they are omitted. Propositions 3, 4, and 5 describe the projection properties of three different cases of two spheres under the unit sphere model of the paracatadioptric camera. For the sake of discussion, the projection types that correspond to Propositions 3, 4, and 5 are referred to as the first projection, the second projection, and the third projection, respectively.

3.2 Obtaining the principal point of the paracatadioptric camera by a view of two spheres

On the basis of Section 3.1, we discuss how to obtain the principal point of the paracatadioptric camera using three different cases of two spheres. According to Propositions 3, 4, and 5, the following corollary is true.

Corollary 2

In each type of projection, the principal point of the paracatadioptric camera can be determined using only one view of the two spheres.

From the conclusions and proofs of Propositions 3, 4, and 5, it is easy to deduce the correctness of Corollary 2; hence, its proof is omitted.

With only one view of two spheres, there are two pairs of conics${C}_{n\pm}^1$in the paracatadioptric image plane:

$$ {C}_{n\pm}^1=\left[\begin{array}{ccc}{a}_{n\pm}^1& {b}_{n\pm}^1& {d}_{n\pm}^1\\ {}{b}_{n\pm}^1& {c}_{n\pm}^1& {e}_{n\pm}^1\\ {}{d}_{n\pm}^1& {e}_{n\pm}^1& {f}_{n\pm}^1\end{array}\right],n=1,2, $$

(3)

where conic ${C}_{n+}^1$is the image of sphere Q_nand conic ${C}_{n-}^1$is the antipodal sphere image of sphere Q_n. The equations of conics ${C}_{n+}^1,{C}_{n-}^1$can be estimated, as discussed in [5]. The method for obtaining the principal point of each projection type is as follows.

In the first projection, images ${C}_{1+}^1$and ${C}_{2+}^1$of two spheres have two real intersection points and two imaginary intersection points, the homogeneous coordinates of which are denoted as ${a}_{j+}^1={\left[{u}_{aj+}^1\ {v}_{aj+}^1\ 1\right]}^T\left(j=1,2\right)$and ${a}_{j+}^1={\left[{u}_{aj+}^1\ {v}_{aj+}^1\ 1\right]}^T\left(j=3,4\right)$, respectively. Their antipodal spheres images ${C}_{1-}^i$ and ${C}_{2-}^i$ also have two real intersection points and two imaginary intersection points, the homogeneous coordinates of which are denoted as ${a}_{j-}^1={\left[{u}_{aj-}^1\ {v}_{aj-}^1\ 1\right]}^T\left(j=1,2\right)$ and ${a}_{j-}^1={\left[{u}_{aj-}^1\ {v}_{aj-}^1\ 1\right]}^T\left(j=3,4\right)$, respectively, as shown in Fig. 3b. From the simultaneous equations of conics ${C}_{n+}^1\left(n=1,2\right)$, we have:

$$ \left[{u}^1\ {v}^1\ 1\right]{C}_{n+}^1{\left[{u}^1\ {v}^1\ 1\right]}^T=0,\kern0.3em n=1,2. $$

(4)

Similarly, from the simultaneous equations of conics ${C}_{1-}^1,{C}_{2-}^1$, we have:

$$ \left[{u}^1\ {v}^1\ 1\right]{C}_{n-}^1{\left[{u}^1\ {v}^1\ 1\right]}^T=0,n=1,2, $$

(5)

where [u¹ v¹ 1]^T represents a pixel coordinate of the first view in the paracatadioptric image plane, and it is the same in the following part. According to the discussion in Section 3.1, ${a}_{j+}^1={\left[{u}_{aj+}^1\ {v}_{aj+}^1\ 1\right]}^T\left(j=1,2\right)$ is a pair of real solutions and ${a}_{j+}^1={\left[{u}_{aj+}^1\ {v}_{aj+}^1\ 1\right]}^T\left(j=3,4\right)$is a pair of conjugate imaginary solutions in Eq. (4). Further, ${a}_{j-}^1={\left[{u}_{aj-}^1\ {v}_{aj-}^1\ 1\right]}^T\left(j=1,2\right)$is a pair of real solutions and ${a}_{j-}^1={\left[{u}_{aj-}^1\ {v}_{aj-}^1\ 1\right]}^T\left(j=3,4\right)$ is a pair of conjugate imaginary solutions in Eq. (5). At the same time, $\left\{{a}_{j+}^1,{a}_{j-}^1\right\}\left(j=1,2,3,4\right)$are four pairs of antipodal image points. Principal pointp is the intersection point of the lines passing through points ${a}_{j+}^1,{a}_{j-}^1\left(j=1,2,3,4\right)$. Hence, principal point p = [u₀ v₀ 1]^T is a solution of the following linear equations:

$$ {\left({a}_{j+}^1\times {a}_{j-}^1\right)}^T{\left[{u}^1\ {v}^1\ 1\right]}^T=0,j=1,2,3,4. $$

(6)

In the second projection, principal point p = [u₀ v₀ 1]^Tcan be determined by solving the linear equations:

$$ {\left({a}_{j+}^1\times {a}_{j-}^1\right)}^T{\left[{u}^1\ {v}^1\ 1\right]}^T=0,j=1,2,3, $$

(7)

where ${a}_{1+}^1={\left[{u}_{a1+}^1\ {v}_{a1+}^1\ 1\right]}^T$is the real intersection point of ${C}_{1+}^1$and ${C}_{2+}^1$, and ${a}_{j+}^1={\left[{u}_{aj+}^1\ {v}_{aj+}^1\ 1\right]}^T\left(j=2,3\right)$ are two imaginary intersection points of ${C}_{1+}^1$ and ${C}_{2+}^1$.

In the third projection, principal point p = [u₀ v₀ 1]^T can be determined by solving the linear equations

$$ {\left({a}_{j+}^1\times {a}_{j-}^1\right)}^T{\left[{u}^1\ {v}^1\ 1\right]}^T=0,j=1,2,3,4, $$

(8)

where${a}_{j+}^1={\left[{u}_{aj+}^1\ {v}_{aj+}^1\ 1\right]}^T\left(j=1,2,3,4\right)$ are four imaginary intersection points of ${C}_{1+}^1$ and ${C}_{2+}^1$, and ${a}_{j-}^1=\left[{u}_{aj-}^1\ {v}_{aj-}^1\ 1\right]\left(j=1,2,3,4\right)$ are four imaginary intersection points of ${C}_{1-}^1$ and ${C}_{2-}^1$.

In theory, linear equations have unique solutions, but because of the effects of noise, their solutions may be non-unique. The solutions of Eqs. (6), (7), and (8) can be obtained by singular value decomposition (SVD).

3.3 Obtaining the other intrinsic camera parameters using the imaged circular points

As discussed in Section 3.2, by the analysis of the three projection types under the paracatadioptric camera, the solution for the principal point of the camera can be obtained from a view of two spheres. In this section, we discuss how the projection of the two spheres can be used to obtain the other intrinsic camera parameters for the three projection types. Based on Corollary 1, a pair of imaged circular points can be obtained from a view of a sphere; hence, two pairs of imaged circular points can be obtained from a view of two spheres. Because a pair of imaged circular points can provide two constraints of the intrinsic camera parameters, the other intrinsic camera parameters can be obtained using the two imaged circular points.

3.3.1 Obtaining the imaged circular points

Conclusion (ii) of Corollary 1 and its proof provide the basis for obtaining the imaged circular points by a view of a sphere. A view of two spheres can be considered as two views of a sphere in the same image plane. On the basis of Corollary 1, we discuss the implementation for obtaining the imaged circular points.

As there are three projection cases of two spheres Q₁, Q₂ under the paracatadioptric camera, and their solutions of the imaged circular points are nearly the same, taking the first projection as an example, the method for obtaining the imaged circular points is given. The imaged circular points ${m}_{2I}^i,{m}_{2J}^i$ on the base plane of projection circle ${S}_{2+}^i$ of sphere Q₂are obtained in a similar manner as the imaged circular points ${m}_{1I}^i,{m}_{1J}^i$on the base plane of projection circle ${S}_{1+}^i$of sphere Q₁. Given k(k ≥ 1) views of two spheres Q₁, Q₂ in the paracatadioptric image plane Π_I, there are 2k pairs of conics${C}_{n\pm}^i$:

$$ {C}_{n\pm}^i=\left[\begin{array}{ccc}{a}_{n\pm}^i& {b}_{n\pm}^i& {d}_{n\pm}^i\\ {}{b}_{n\pm}^i& {c}_{n\pm}^i& {e}_{n\pm}^i\\ {}{d}_{n\pm}^i& {e}_{n\pm}^i& {f}_{n\pm}^i\end{array}\right],i=1,2,\cdots, k;n=1,2, $$

(9)

where conic ${C}_{n+}^i$ is the image of sphere Q_n and conic ${C}_{n-}^i$ is the antipodal image of sphere Q_n in the ith view. The equations of conics ${C}_{n+}^i,{C}_{n-}^i$can be estimated as discussed in [5]. Select ${N}_1^i$different points ${b}_{nm+}^i$on conic ${C}_{n+}^i$, the homogeneous coordinates of which are represented as ${\left[{u}_{bnm+}^i\ {v}_{bnm+}^i\ 1\right]}^T$, and these points are known. Let the antipodal image points of ${b}_{nm+}^i$be ${b}_{nm-}^i$, the homogeneous coordinates of which are ${\left[{u}_{bnm-}^i\ {v}_{bnm-}^i\ 1\right]}^T$, and ${b}_{nm-}^i$ are on conic ${C}_{n-}^i$from the previous analysis. From properties of the antipodal image points [28], the points ${b}_{nm-}^i$are along the lines $p-{b}_{nm+}^i$and on ${C}_{n-}^i$; hence, the points ${b}_{nm-}^i$ are intersection points of the lines $p{b}_{nm+}^i$ and the conic ${C}_{n-}^i$. From the simultaneous equations of lines $p{b}_{nm+}^i$and conics ${C}_{n-}^i$, we have:

$$ \Big\{{\displaystyle \begin{array}{l}{\left(p\times {b}_{nm+}^i\right)}^T{\left[{u}^i\ {v}^i\ 1\right]}^T=0\\ {}\left[{u}^i\ {v}^i\ 1\right]{C}_{n-}^i{\left[{u}^i\ {v}^i\ 1\right]}^T=0\end{array}}, $$

(10)

where[uⁱ vⁱ 1]^Trepresents a pixel coordinate of the ith view in the paracatadioptric image. The homogeneous coordinates of the principal point pcan be obtained by the method described in Section 3.2. According to the analysis presented above, ${b}_{nm-}^i={\left[{u}_{bnm-}^i\ {v}_{bnm-}^i\ 1\right]}^T$are the solutions of Eq. (10). In general, there exist two groups of solutions for Eq. (10). Obtaining the initial values of the intrinsic camera parameters as discussed in [29], ${b}_{nm-}^i={\left[{u}_{bnm-}^i\ {v}_{bnm-}^i\ 1\right]}^T$ can be selected using properties of the antipodal image points [28]. By definition of the tangent line, the tangential point of which is on a conic [11], the equations of tangent lines ${\overset{\sim }{l}}_{nm+}^i$ at points ${b}_{nm+}^i$ on conic ${C}_{n+}^i$are:

$$ {\left({b}_{nm+}^i\right)}^T{C}_{n+}^i{\left[{u}^i\ {v}^i\ 1\right]}^T=0. $$

(11)

Similarly, the equations of tangent lines ${\overset{\sim }{l}}_{nm-}^i$ at points ${b}_{nm-}^i$ on conic${C}_{n-}^i$are:

$$ {\left({b}_{nm-}^i\right)}^{\mathrm{T}}{C}_{n-}^i{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0. $$

(12)

From the simultaneous Eqs. (11) and (12), linear equations can be obtained:

$$ \Big\{{\displaystyle \begin{array}{l}{\left({b}_{nm+}^i\right)}^T{C}_{n+}^i{\left[{u}^i\ {v}^i\ 1\right]}^T=0\\ {}{\left({b}_{nm-}^i\right)}^T{C}_{n-}^i{\left[{u}^i\ {v}^i\ 1\right]}^T=0\end{array}}. $$

(13)

Let points ${d}_{nm}^i$be the vanishing points of lines ${l}_{nm+}^i$, the homogeneous coordinates of which are ${\left[{u}_{bnm-}^i\ {v}_{bnm-}^i\ 1\right]}^T$; hence, ${d}_{nm}^i={\left[{u}_{dnm}^i\ {v}_{dnm}^i\ 1\right]}^T$are solutions of Eq. (13), and ${d}_{nm}^i$ are images of ${N}_1^i\left({N}_1^i\ge 2\right)$points at infinity on the plane containing circle ${S}_{n+}^i$. When ${N}_1^i=2$, the equation of vanishing line ${\overset{\sim }{l}}_n^i$on the base plane of circle ${S}_{n+}^i$ is:

$$ {\left[{d}_{n1}^i\times {d}_{n2}^i\right]}^T{\left[{u}^i\ {v}^i\ 1\right]}^T=0. $$

(14)

When ${N}_1^i\ge 3$, the equation of vanishing line ${\overset{\sim }{l}}_n^i$on the base plane of circle ${S}_{n+}^i$ can be obtained by least squares fitting [16]. To simplify the description, let the equation of vanishing line ${\overset{\sim }{l}}_n^i$ be:

$$ {\left({\overset{\sim }{l}}_n^i\right)}^T{\left[{u}^i\ {v}^i\ 1\right]}^T=0, $$

(15)

where ${\overset{\sim }{l}}_n^i={\left[{u}_{ln}^i\ {v}_{ln}^i\ 1\right]}^T$ denotes the homogeneous line coordinates of vanishing line ${\overset{\sim }{l}}_n^i$. Let the conjugate imaginary points ${m}_{nI}^i,{m}_{nJ}^i$ be the imaged circular points of the base plane of circle ${S}_{n+}^i$ with homogeneous coordinates ${\left[{a}_n^i+{b}_n^ii\ {c}_n^i+{d}_n^ii\ 1\right]}^T$of points ${m}_{nI}^i$ and homogeneous coordinates ${\left[{a}_n^i-{b}_n^ii\ {c}_n^i-{d}_n^ii\ 1\right]}^T$of points ${m}_{nJ}^i$. By the simultaneous equations of vanishing line ${\overset{\sim }{l}}_n^i$ and conic ${C}_{n+}^i$, we have:

$$ \Big\{{\displaystyle \begin{array}{l}{\left({\overset{\sim }{l}}_n^i\right)}^T{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0\\ {}\left[{u}^i\ {v}^i\ 1\right]{C}_{n+}^i{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0\end{array}}. $$

(16)

Similarly, by the simultaneous equation system of vanishing line ${\overset{\sim }{l}}_n^i$ and conic ${C}_{n-}^i$, we have:

$$ \Big\{{\displaystyle \begin{array}{l}{\left({\overset{\sim }{l}}_n^i\right)}^{\mathrm{T}}{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0\\ {}\left[{u}^i\ {v}^i\ 1\right]{C}_{n-}^i{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0\end{array}}. $$

(17)

In theory, Eqs. (16) and (17) have the same solutions, which are ${m}_{nI}^i={\left[{a}_n^i+{b}_n^ii\ {c}_n^i+{d}_n^ii\ 1\right]}^{\mathrm{T}}$ and ${m}_{nJ}^i={\left[{a}_n^i-{b}_n^ii\ {c}_n^i-{d}_n^ii\ 1\right]}^{\mathrm{T}}$. However, because of the effect of noise, not all of their solutions may be the same. Let the solutions of Eq. (16) be ${\left[{a}_{n1}^i+{b}_{n1}^ii\ {c}_{n1}^i+{d}_{n1}^ii\ 1\right]}^{\mathrm{T}}$and${\left[{a}_{n1}^i-{b}_{n1}^ii\ {c}_{n1}^i-{d}_{n1}^ii\ 1\right]}^{\mathrm{T}}$, and let the solutions of Eq. (17) be ${\left[{a}_{n2}^i+{b}_{n2}^ii\ {c}_{n2}^i+{d}_{n2}^ii\ 1\right]}^{\mathrm{T}}$and${\left[{a}_{n2}^i-{b}_{n2}^ii\ {c}_{n2}^i-{d}_{n2}^ii\ 1\right]}^{\mathrm{T}}$.Then,

$$ \Big\{{\displaystyle \begin{array}{l}{m}_{nI}^i={\left[\frac{a_{n1}^i+{a}_{n2}^i}{2}+\frac{b_{n1}^i+{b}_{n2}^i}{2}i\kern0.5em \frac{c_{n1}^i+{c}_{n2}^i}{2}+\frac{d_{n1}^i+{d}_{n2}^i}{2}i\kern0.5em 1\right]}^{\mathrm{T}}\\ {}{m}_{nJ}^i={\left[\frac{a_{n1}^i+{a}_{n2}^i}{2}-\frac{b_{n1}^i+{b}_{n2}^i}{2}i\kern0.5em \frac{c_{n1}^i+{c}_{n2}^i}{2}-\frac{d_{n1}^i+{d}_{n2}^i}{2}i\kern0.5em 1\right]}^{\mathrm{T}}\end{array}}. $$

(18)

Thus, we have obtained a pair of imaged circular points ${m}_{nI}^i,{m}_{nJ}^i$on the plane containing circle ${S}_{n+}^i$.

3.3.2 Obtaining the other intrinsic camera parameters

The principal point p can be obtained by the method described in Section 3.2, and the algorithm can be simplified using a method presented in the literature [17]. First, via translation of transformation matrix T_p, move the origin of the image coordinate system to the principal point p, with:

$$ {T}_p=\left[\begin{array}{ccc}1& 0& -{u}_0\\ {}0& 1& -{v}_0\\ {}0& 0& 1\end{array}\right]. $$

(19)

In the new coordinate system, the intrinsic matrix K_c can be simplified as:

$$ {K}_c^{\prime }={T}_p{K}_c=\left[\begin{array}{ccc}r{f}_e& s& 0\\ {}0& {f}_e& 0\\ {}0& 0& 1\end{array}\right]. $$

(20)

Therefore, ωcan be simplified as:

$$ {\omega}^{\prime }={\left({K}_c^{\prime}\right)}^{-\mathrm{T}}{\left({K}_c^{\prime}\right)}^{-1}:= \left[\begin{array}{ccc}{\omega}_1^{\prime }& {\omega}_2^{\prime }& 0\\ {}{\omega}_2^{\prime }& {\omega}_3^{\prime }& 0\\ {}0& 0& {\omega}_4^{\prime}\end{array}\right]. $$

(21)

In this case, ω^′can be obtained using at least three linear constraints (i.e., three degrees of freedom); hence, at least two pairs of imaged circular points are required to obtainω^′. In the new coordinate system, the imaged circular points ${m}_{nI}^i,{m}_{nJ}^i$ on the plane containing circle ${S}_{n+}^i$ transform into:

$$ \Big\{{\displaystyle \begin{array}{l}{\overset{\sim }{m}}_{nI}^i={T}_p{m}_{nI}^i:= {\left[{\overset{\sim }{a}}_n^i+{\overset{\sim }{b}}_n^ii\kern0.5em {\overset{\sim }{c}}_n^i+{\overset{\sim }{d}}_n^ii\kern0.5em 1\right]}^{\mathrm{T}}\\ {}{\overset{\sim }{m}}_{nJ}^i={T}_p{m}_{nJ}^i:= {\left[{\overset{\sim }{a}}_n^i-{\overset{\sim }{b}}_n^ii\kern0.5em {\overset{\sim }{c}}_n^i-{\overset{\sim }{d}}_n^ii\kern0.5em 1\right]}^{\mathrm{T}}\end{array}}, $$

(22)

where ${\overset{\sim }{a}}_n^i={a}_n^i-{u}_0,{\overset{\sim }{b}}_n^i={b}_n^i,{\overset{\sim }{c}}_n^i={c}_n^i-{v}_0,{\overset{\sim }{d}}_n^i={d}_n^i$. Further, 2k pairs of imaged circular points can be obtained from k(k ≥ 1) views of two spheres Q₁, Q₂. Applying the constraints of the imaged circular points to the image of the absolute conic (IAC), linear equations for the elements of ω^′can be established:

$$ \Big\{{\displaystyle \begin{array}{l}\operatorname{Re}\left[{\left({\overset{\sim }{m}}_{nI}^i\right)}^{\mathrm{T}}{\omega}^{\prime }{\overset{\sim }{m}}_{nI}^i\right]=0\ \\ {} \operatorname {Im}\left[{\left({\overset{\sim }{m}}_{nI}^i\right)}^{\mathrm{T}}{\omega}^{\prime }{\overset{\sim }{m}}_{nI}^i\right]=0\ \end{array}},i=1,2,\cdots, k;n=1,2, $$

(23)

where ω^′is given by Eq. (21). Eq. (23) includes 2k linear equations for the elements of ω^′; the solution of Eq. (23) can be obtained using SVD to get ω^′. Finally, via Cholesky decomposition of the known ω^′, the simplified intrinsic matrix ${K}_c^{\prime }$ under the new coordinate system can be obtained directly by the inverse solution of the decomposition matrix.

The calibration algorithm by utilizing the imaged circular points is as follows:

• Input: The images of two spheres in k(k ≥ 1) views.

• Output: The camera intrinsic matrix K_c.

• 1): Extract the pixel coordinates of the images of two spheres in k(k ≥ 1) views to estimate equations ${C}_{n+}^i$ (i = 1, 2, ⋯, k; n = 1, 2) of the sphere images, and equations ${C}_{n-}^i$ of their antipodal sphere images according to [5].

• 2): Take the i(i = 1, 2, ⋯, k) th view and solve the principal pointp of the camera according to section 3.2.

• 3): Solve the imaged circular points ${m}_{nI}^i,{m}_{nJ}^i$ (i = 1, 2, ⋯, k; n = 1, 2) on the plane containing circle ${S}_{n+}^i$according to section 3.3.1.

• 4): Move the coordinate origin point of the image coordinate system to the principal point p via translation of transformation matrix T_p, and get ${K}_c^{\prime }$, ω^', ${\overset{\sim }{m}}_{n\;I}^i,{\overset{\sim }{m}}_{nJ}^i$(i = 1, 2, ⋯, k; n = 1, 2) from (20), (21), (22), respectively.

• 5): Solve ω^′ from (23) by SVD. With Cholesky decomposition of the known ω^′ matrix, ${K}_c^{\prime }$ can be obtained directly by inverse solving for the decomposition matrix. Finally, K_ccan be obtained by (20).

3.4 Obtaining the intrinsic camera parameters using orthogonal vanishing points

In this section, we discuss how the three projection types of two spheres can be used to obtain the intrinsic camera parameters when the principal point is unknown. The method for obtaining the intrinsic camera parameters is proposed using only orthogonal vanishing points.

The following corollary can be obtained from definition of the antipodal points.

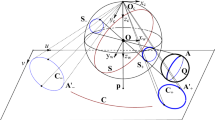
Corollary 3

If {M_S1+, M_S1−}and {M_S2+, M_S2−} are two pairs of antipodal points, the directions of the straight line passing through points M_S1+and M_S2+, and the straight line passing through points M_S1+ and M_S2− are orthogonal.

Proof

According to definition of the antipodal points, M_S1+M_S1−and M_S2+M_S2−are two diameters on the unit viewing sphere; hence, quadrilateralM_S1+M_S2+M_S1−M_S2− is a rectangle. Thus, the directions of the straight line passing through points M_S1+and M_S2+, as well as the straight line passing through points M_S1+ and M_S2−, are orthogonal.

Corollary 3 establishes the relationship between the antipodal points and orthogonal direction and provides a theoretical basis for using the orthogonal vanishing point to obtain the intrinsic camera parameters. Next, we discuss how the intrinsic camera parameters can be obtained using the orthogonal vanishing points for the three projection types.

For the first projection, from Corollary 3 and Proposition 2, we have the following corollary.

Corollary 4

The six groups of orthogonal vanishing points can be determined by a view of two mutually occluding spheres Q₁, Q₂, and the intrinsic camera parameters can be handled linearly by at least one view.

Proof

From the conclusion of Proposition 2, four pairs of antipodal points $\left\{{A}_{j+}^i,{A}_{j-}^i\right\}\left(j=1,2,3,4\right)$ are obtained from a view of two spheres Q₁, Q₂ in the first projection, where $\left\{{A}_{j+}^i,{A}_{j-}^i\right\}\left(j=1,2\right)$ are two pairs of real antipodal points, and$\left\{{A}_{j+}^i,{A}_{j-}^i\right\}\left(j=3,4\right)$ are two pairs of imaginary antipodal points. According to Corollary 3, the four pairs of antipodal points can provide six groups of orthogonal directions ${A}_{j_1+}^i{A}_{j_2+}^i$ and${A}_{j_1+}^i{A}_{j_2-}^i$, where j₁, j₂ = 1, 2, 3, 4, j₁ ≠ j₂. A group of orthogonal vanishing points exists in the group of orthogonal directions in space; hence, six groups of orthogonal vanishing points can be determined by the above six groups of orthogonal directions. According to the relationship between the orthogonal vanishing points and the IAC [11], ω can be determined by at least five groups of orthogonal vanishing points to obtain the intrinsic camera parameters, in other words, the paracatadioptric camera calibration requires at least a view of two spheres Q₁, Q₂ in this case.

We present the solution procedure in detail in this case. Given k(k ≥ 1) views of two spheres Q₁, Q₂ in paracatadioptric image plane Π_I, there are 2k pairs of conics, denoted for simplicity as ${C}_{n\pm}^i\left(n=1,2;i=1,2,\cdots, k\right)$, which can be estimated, as discussed in [5]. Let the homogeneous coordinates ${a}_{j\pm}^i={\left[{u}_{aj\pm}^i\ {v}_{aj\pm}^i\ 1\right]}^{\mathrm{T}}$ be the images of points ${A}_{j\pm}^i$with (j = 1, 2, 3, 4); hence, $\left\{{a}_{j+}^i,{a}_{j-}^i\right\}\left(j=1,2,3,4\right)$ are four pairs of antipodal image points from the definition of the antipodal image points. According to Proposition 2, points ${a}_{1+}^i$,${a}_{2+}^i$ are two real intersection points of two conics ${C}_{1+}^i$,${C}_{2+}^i$, points ${a}_{3+}^i$,${a}_{4+}^i$ are two imaginary intersection points of two conics ${C}_{1+}^i$,${C}_{2+}^i$, points ${a}_{1-}^i$,${a}_{2-}^i$ are two real intersection points of two conics ${C}_{1-}^i$,${C}_{2-}^i$, and points ${a}_{3-}^i$,${a}_{4-}^i$ are two imaginary intersection points of two conics ${C}_{1-}^i$,${C}_{2-}^i$. The following equation can be obtained from the simultaneous equations of conics ${C}_{1+}^i,{C}_{2+}^i$:

$$ \left[{u}^i\ {v}^i\ 1\right]{C}_{n+}^i{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0,n=1,2. $$

(24)

Eq. (25) can be similarly obtained from the simultaneous equations of conics ${C}_{1-}^1,{C}_{2-}^1$:

$$ \left[{u}^i\ {v}^i\ 1\right]{C}_{n-}^i{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0,n=1,2. $$

(25)

From the above analysis, ${a}_{j+}^i={\left[{u}_{aj+}^i\ {v}_{aj+}^i\ 1\right]}^{\mathrm{T}}\left(j=1,2\right)$ is a pair of real solutions and ${a}_{j+}^i={\left[{u}_{aj+}^i\ {v}_{aj+}^i\ 1\right]}^{\mathrm{T}}\left(j=3,4\right)$ is a pair of conjugate imaginary solutions in Eq. (24). Further, ${a}_{j-}^i={\left[{u}_{aj-}^i\ {v}_{aj-}^i\ 1\right]}^{\mathrm{T}}\left(j=1,2\right)$ is a pair of real solutions and ${a}_{j-}^i={\left[{u}_{aj-}^i\ {v}_{aj-}^i\ 1\right]}^{\mathrm{T}}\left(j=3,4\right)$is a pair of conjugate imaginary solutions in Eq. (25). The points at infinity in ${A}_{j_1+}^i{A}_{j_2+}^i$, ${A}_{j_1+}^i{A}_{j_2-}^i$directions are denoted as ${U}_{j_1{j}_2\infty}^i$,${V}_{j_1{j}_2\infty}^i\left({j}_1,{j}_2=1,2,3,4;{j}_1\ne {j}_2\right)$, respectively, and ${A}_{j_1+}^i{A}_{j_2+}^i$as well as ${A}_{j_1+}^i{A}_{j_2-}^i$ are orthogonal from the above analysis. The images of points ${U}_{j_1{j}_2\infty}^i$,${V}_{j_1{j}_2\infty}^i$ are denoted as ${u}_{j_1{j}_2}^i$,${v}_{j_1{j}_2}^i$, respectively; hence, ${u}_{j_1{j}_2}^i$, ${v}_{j_1{j}_2}^i$are orthogonal vanishing points in the plane Π_I. According to the combination characteristic of the projective transformation, ${u}_{j_1{j}_2}^i$is the intersection point of line ${a}_{j_1+}^i{a}_{j_2+}^i$ and line ${a}_{j_1-}^i{a}_{j_2-}^i$, and ${v}_{j_1{j}_2}^i$ is the intersection point of line ${a}_{j_1+}^i{a}_{j_2-}^i$ and line ${a}_{j_1-}^i{a}_{j_2+}^i$. Let the homogeneous coordinates of points ${u}_{j_1{j}_2}^i$, ${v}_{j_1{j}_2}^i$be ${\left[{u}_{u{j}_1{j}_2}^i\ {v}_{u{j}_1{j}_2}^i\ 1\right]}^{\mathrm{T}}$, ${\left[{u}_{v{j}_1{j}_2}^i\ {v}_{v{j}_1{j}_2}^i\ 1\right]}^{\mathrm{T}}$, respectively, which are the solutions of two linear equations, respectively:

$$ \Big\{{\displaystyle \begin{array}{l}{\left({a}_{j_1+}^i\times {a}_{j_2+}^i\right)}^{\mathrm{T}}{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0\\ {}{\left({a}_{j_1-}^i\times {a}_{j_2-}^i\right)}^{\mathrm{T}}{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0\end{array}}, $$

(26)

$$ \Big\{{\displaystyle \begin{array}{l}{\left({a}_{j_1+}^i\times {a}_{j_2-}^i\right)}^{\mathrm{T}}{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0\\ {}{\left({a}_{j_1-}^i\times {a}_{j_2+}^i\right)}^{\mathrm{T}}{\left[{u}^i\ {v}^i\ 1\right]}^{\mathrm{T}}=0\end{array}}, $$

(27)

where j₁, j₂ = 1, 2, 3, 4; j₁ ≠ j₂, and there exist 6k pairs of orthogonal vanishing points in k views. Therefore, a linear equation can be given using the constraints of the orthogonal vanishing points and the IAC [11]:

$$ {\left({u}_{j_1{j}_2}^i\right)}^{\mathrm{T}}\omega {v}_{j_1{j}_2}^i=0,i=1,2,\cdots, k;{j}_1,{j}_2=1,2,3,4;{j}_1\ne {j}_2, $$

(28)

with

$$ \omega =\left[\begin{array}{ccc}{\omega}_1& {\omega}_2& {\omega}_4\\ {}{\omega}_2& {\omega}_3& {\omega}_5\\ {}{\omega}_4& {\omega}_5& {\omega}_6\end{array}\right], $$

(29)

where ω is the IAC equation coefficient matrix. Eq. (28) consists of 6k linear equations of the elements of ω. The solution of Eq. (28) can be obtained by SVD to giveω. Finally, via Cholesky decomposition of ω, the intrinsic matrix ω can be obtained.

For the second projection, from Corollary 3 and Proposition 3, we have the following corollary.

Corollary 5

The three groups of orthogonal vanishing points can be determined by a view of two tangential spheres Q₁, Q₂ with viewpoint O; hence, the intrinsic camera parameters can be handled by at least two views.

The proof of Corollary 5 follows the same procedure as the proof of Corollary 4; hence, it is omitted. Furthermore, the solutions of the orthogonal vanishing points and the intrinsic camera parameters are the same as those in the first projection. In the second projection, the major difference is that a view of the two spheres only can obtain three pairs of antipodal points; hence, three groups of orthogonal directions can be provided to determine three groups of orthogonal vanishing points. Therefore, the camera calibration requires at least two views of the two spheres. The points${A}_{1+}^i$ and ${A}_{2+}^i$ are regarded as the same point in the first projection; hence, the solution process can be obtained in the second projection.

In the third projection, from Corollary 3 and Proposition 4, we have the following corollary.

Corollary 6

The six groups of orthogonal vanishing points can be determined by a view of two separated spheres Q₁, Q₂ with viewpoint O; hence, the intrinsic camera parameters can be handled by at least one view.

The proof of Corollary 6 follows the same procedure as the proof of Corollary 4; hence, it is omitted. Furthermore, the solutions of the orthogonal vanishing points and the intrinsic camera parameters are the same as those in the first projection. In the third projection, the major difference is that a view of the two spheres can obtain four pairs of imaginary antipodal points, and two pairs of four pairs of antipodal points in the first projection only belong to the imaginary antipodal points. The real points ${A}_{1+}^i,{A}_{2+}^i$ in the first projection are regarded as two imaginary points; hence, the solution process can be obtained in the third projection.

For three projection types of two spheres, the methods using the constraints of vanishing points in orthogonal directions to solve the camera intrinsic parameters are essentially the same. The calibration steps are as follows:

• Input: The images of two spheres in k views.

• if it is the first or third projection, then k ≥ 1.

• else it is the second projection, then k ≥ 2.

• Output: The camera intrinsic matrix K_c

• 1): Extract the pixel coordinates of the images of two spheres in k views to estimate equations for the ${C}_{n+}^i$ of the sphere images and equations for the ${C}_{n-}^i$ of their antipodal sphere images [5].

• 2): Solve intersection points ${a}_{j+}^i$ and ${a}_{j-}^i$ of their antipodal sphere images ${C}_{n-}^i$ in the ith view using Eqs. (27) and (28), where i = 1, 2, ⋯, k; j = 1, 2, 3, 4; and n = 1, 2.

• if it is the first projection, then points ${a}_{1+}^i$ and ${a}_{2+}^i$ are two different real points and points ${a}_{1-}^i$ and ${a}_{2-}^i$ are also two different real points.

• else if it is the second projection, then points ${a}_{1+}^i$ and ${a}_{2+}^i$ are the same real point and points ${a}_{1-}^i$ and ${a}_{2-}^i$ are also the same real point.

• else it is the third projection, then points ${a}_{1+}^i$ and ${a}_{2+}^i$ are two different imaginary points of images ${C}_{n+}^i$ of the two spheres. Points ${a}_{1-}^i$ and ${a}_{2-}^i$ are also two different imaginary points.

• 3): Solve the orthogonal vanishing points in the ith view according to Section 3.4.

• 4): Obtain ω using SVD for Eq. (31), perform a Cholesky decomposition and its inverse to obtain K_c.

4 Experiments

In order to verify the effectiveness of the calibration methods and test their sensitivity to noise, a number of computations were performed using both simulation data and real experimental data. Through analysis of the geometric projective property of a ball under the unit viewing sphere model, the calibration method for the paracatadioptric camera can be present by using the vanishing point, the vanishing line and parallel circles recently [14], which are denoted as [36]1, [36]2, [36]3, respectively, and are added to the experiments. The two types of calibration methods discussed in this study, i.e., using imaged circular points (ICP) and orthogonal vanishing points (OVP), were compared with the three calibration methods of Li and Zhao [14], Duan and Wu [5], and the initial estimation method based on the paraboloidal mirror contour projection (Initial) [29].

4.1 Experimental results with simulated data

Let the mirror parameter of the simulated paracatadioptric camera be ξ = 1, and let its FOV be180^∘. The matrix of the intrinsic parameters is ${K}_c=\left[\begin{array}{ccc}800& 0.8& 450\\ {}0& 750& 380\\ {}0& 0& 1\end{array}\right]$, where[450 380 1]^Tare the homogeneous coordinates of principal point p, 16/15 is the value of the aspect ratio r, 750 is the value of the effective focal length f_e, and 0.8 is the value of the skew factor s.

When the principal point is unknown, the camera calibration with OVP requires two views of the two spheres in the second projection, and the calibration method of Duan and Wu [5] requires at least three views of one sphere. We generate two views of two spheres in each of the three projections: two separated spheres, two tangential spheres, and two intersection spheres. The views of two spheres under the three different projection cases are shown in Fig. 6, where the bold conic represents the projected contour of the paraboloid mirror, the two conics inside the projected contour represent the images of the two spheres, and the two conics outside the projected contour represent the antipodal sphere images of the two spheres. Both the images of the two spheres and their antipodal sphere images in the catadioptric image plane show the following probable results: intersection, tangency, and separation, as shown in Fig. 6a, b, and c, respectively.

Fig. 6

Three categories of images of two simulated spheres and their antipodal spheres: a two real intersection points, (b) one real intersection point, and (c) no real intersection point

Further, 100 points are chosen on each conic. In the simulated experiment, Gaussian noise with zero mean and standard deviation σ was added to these points on the conics, and the noise level of σ varied from 0 to 3.5 pixels. For each noise level, we performed 100 independent trials, and the absolute errors of these recovered parameters were computed over each run. The effect of the change in the absolute errors of the estimated intrinsic camera parameters is shown in Fig. 7 for ICP and OVP. According to the discussion in Section 3.3, regardless of the type of projection of the two spheres under the paracatadioptric camera, the solutions using ICP are similar. Here, taking the first projection as an example, the change in the absolute error of the intrinsic camera parameters with ICP is shown in Fig. 7a. According to the discussion in Section 3.4, OVP is different for the three projection cases of two spheres under the paracatadioptric camera, i.e., intersection, tangency, and separation, represented by OVP1, OVP2, and OVP3, respectively. The effect on the absolute errors of the estimated intrinsic camera parameters is shown in Fig. 7b, c, and d for OVP1, OVP2, and OVP3, respectively. More importantly, the results of our methods (ICP, OVP1, OVP2, and OVP3), the method of Li and Zhao [14], Duan and Wu [5], and Initial [29] are compared in Fig. 8. Because the performances ofu₀ and v₀are very similar, only the estimated results for u₀ are shown here. Asσincreases, the absolute error of the intrinsic camera parameters decreases, implying that our methods are more accurate than other methods, while the methods of Li and Zhao [14] are more accurate than Duan and Wu [5] and Initial [29], and the method of Duan and Wu [5] is more accurate than Initial [29]. In our methods, the process for obtaining the imaged circular points and vanishing points is simple; hence, our results are more precise. In some views, if the mirror contour projection is not very clear, the calibration results, which mainly depend on the mirror contour projection, are relatively poor. The absolute error of the intrinsic camera parameters obtained by ICP, OVP1, OVP3, and OVP2 increases gradually, implying that their precise decreases gradually, but the differences are insignificant.

Fig. 7

Absolute errors of the intrinsic camera parameters obtained by different methods under different noise levels. a, (b), (c), and (d) show the results of ICP, OVP1, OVP2, and OVP3, respectively

Fig. 8

Comparison of the results of our methods, the method of Li and Zhao [14] ([36]1, [36]2, [36]3 denoted respectively as the vanishing point, the vanishing line and parallel circles), the method of Duan and Wu [5], and Initial [29] for a camera with different noise levels: (a) r, (b) f_e, (c) u₀, and (d) s

4.2 Experimental results with real data

In the real experiment, we used two yellow table tennis balls as the calibration model. We used a central catadioptric camera with a hyperboloidal mirror designed by the Center for Machine Perception at the Czech Technical University; the FOV and mirror parameter of the camera are 212° and ξ = 0.966 (approximately equal to 1), respectively.

In the experiment, the two balls were moved so that they met, and based on their relative position, three projection cases were considered: intersection, tangency, and separation. Two different pictures were captured by the catadioptric camera in each case. Six images that meet the stipulated conditions are shown in Fig. 9a–f; each image has a resolution of 1063 × 1033. Because the processing is similar for each image in Fig. 9, here, only Fig. 9a is discussed as an example. First, the Canny edge detector is used to extract the edges of the sphere image and the contour projection of the paraboloidal mirror, as shown in Fig. 10a. Next, the equation of the sphere image and the contour projection are obtained by least squares fitting (see Fig. 10b). The initial values of the intrinsic camera parameters can be obtained by the equation for the paraboloidal mirror contour projection [29]. On this basis, the equations of the sphere image and its antipodal sphere image are estimated using the method of Duan and Wu [5], as shown in Fig. 10b, where the thickest conic is the projected contour of the paraboloidal mirror, the two thin conics are the images of the two spheres, and the two remaining conics are the images of the antipodal spheres. Finally, the intersection points of the two sphere images and their antipodal sphere images in each image can be obtained, as discussed in Section 3.2. In particular, the tangent point of the two tangential sphere images needs to obey the following rules: (i) if the two spheres have no real intersection point, the midpoint of the closest two points between the two sphere images is used as their tangent point and (ii) if the two spheres have two close real intersection points, the midpoint between the two real intersection points is used as their tangent point. The tangent point of the two antipodal tangential sphere images is determined similarly.

Fig. 9

Six images of two spheres in the real experiment: (a), (b) images of two intersecting spheres; (c), (d) images of two tangential spheres; (e), (f) images of two separated spheres

Fig. 10

a Edges of the image in Fig. 9a are extracted using the Canny edge detector. b Corresponding to Fig. 10a, the contour projection of the paraboloidal mirror is obtained through least squares fitting, and the images of the two spheres and their antipodal sphere images are obtained by the method of Duan and Wu [5]

Using the results of the above operation, the intrinsic camera parameters are obtained using our methods presented in Section 3 as well as the methods of Li and Zhao [14], Duan and Wu [5], and Initial [29]. Because the method of Li and Zhao [14] and Duan and Wu [5] requires three images of a ball, the three images were chosen arbitrarily from those shown in Fig. 9a–f. The average calibration results with real data are listed in Table 1. We find that the calibration results using these methods are similar to one another, which implies that the calibration methods in this paper are effective. In order to further verify the effectiveness of the calibration methods proposed in this paper, we use the obtained intrinsic camera parameters (see Table 1) to rectify the images shown in Fig. 9 to obtain their perspective images. Here, only the rectified results of Fig. 9a, c, and e and are shown in Fig. 11, which only displays the vanishing point ([36]1) for the literature [14]. These results indicate that our methods are very effective.

Table 1 Calibration Results with Real Data

Fig. 11

Rectified images of the images shown in Fig. 9a, c, and e: (a), (f), (k) using the initial parameters [29]; (b), (g), (l) using the method of Duan and Wu [5] to obtain the intrinsic camera parameters; (c), (h), (m) using the vanishing point ([36]1) to obtain the intrinsic camera parameters; (d), (i), (n) using ICP to obtain the intrinsic camera parameters; (e), (j), (o) using OVP to obtain the intrinsic camera parameters

5 Discussion and conclusions

In this study, we mainly discussed how to make use of the relative position between the projections of two spheres to calibrate a paracatadioptric camera. From the analysis of the relative projections of two spheres in the paracatadioptric image plane, there are three cases for which methods for obtaining the principal point are given. Based on the principal point obtained, the geometric relationship between the two groups of parallel circles for which two spheres are projected on the unit viewing sphere is analyzed, and the tangent lines at the antipodal points are found to be parallel. The vanishing points on the plane of the projection circle can be obtained to determine the vanishing line, and the imaged circular points can be calculated by the equations of the vanishing line and the projection circle. Hence, the other intrinsic camera parameters can be obtained using the imaged circular points. When the principal point is unknown, the orthogonal directions can be established to determine the orthogonal vanishing points on the basis of a rectangle having the (real or imaginary) intersection points of the circles for which two spheres are projected on the unit viewing sphere and their corresponding antipodal points as the vertices, and the intrinsic camera parameters can be obtained. In addition, the method of applying two spheres to calibration theories can be extended to n(n ≥ 3) spheres in a view; and the only difference is that their projection cases have various combinations (as the number of combinations increases with the number of spheres), and higher accuracy can be achieved. Furthermore, n(n ≥ 2) spheres in a view may be regarded as n(n ≥ 2) combination views of one sphere at different locations; hence, n(n ≥ 2) views of one sphere for camera calibration are equivalent to spheres at different locations.