A calibration method for paracatadioptric cameras based on circular sections

Abstract

Camera calibration is a crucial step in 3D reconstruction. To improve the reconstruction accuracy, we propose a calibration method for the paracatadioptric camera based on the projective properties of spheres. The starting point of the method is to consider the three great circles that are parallel to the projection of the sphere onto the unit viewing sphere in the imaging model of the paracatadioptric camera. The absolute conic is determined from the orthogonal vanishing points obtained from the intersections of the projections of the three great circles on the image plane. Then, the intrinsic parameters are obtained from the algebraic constraints on the image of the absolute conic. Compared with results obtained by Zhao’s, Yu’s and Li′s methods, 3D reconstruction using our method appears more accurate.

1 Introduction

Camera calibration is the essential step of 3D reconstruction algorithms [24, 25]. Catadioptric cameras are widely employed since they overcome the shortcoming of small imaging angle. They are currently employed in two versions: the non-central catadioptric cameras and the central catadioptric cameras [17]. In this paper, we focus on central catadioptric cameras since the algebraic constraints may be obtained by using the unit viewing sphere model, making the calibration method easier to obtain from geometric constraints [11].

According to type of mirrors, central catadioptric cameras could be divided into four categories: planar, ellipsoidal, hyperboloidal and paraboloidal [3]. The line and point are used to calibrate the central catadioptric camera [23, 32]. Under the central catadioptric camera, a cluster of line images may be fitted [9]. Duan et al. [8] have found the algebraic constraints between the projection of the circle on image plane and the image of absolute conic (IAC) to calibrate central catadioptric camera. Compared with the above common geometry, the projection of the sphere may be fitted more accurately, so the sphere is often chosen for calibration [1, 2, 10, 13, 26]. The projection of the sphere onto the image of central catadioptric cameras has double contact with modified image of IAC. Two methods of central catadioptric camera calibration have been presented based on IAC [19, 28]. Zhang et al. [31] have discussed the relationship between the dual sphere image and the dual absolute conic. Based on this, a novel central catadioptric camera calibration method has been derived. They also proposed two calibration algorithms according to the apparent contour of the projection of the three spheres [30]. The geometric invariants have been then applied to calibrate the central catadioptric camera [27]. Those geometric invariants are not suitable for the paracatadioptric camera calibration. Two calibration methods for paracatadioptric camera by using lines were presented [4, 12]. Based on the sphere, Duan et al. [5, 6] have presented two different methods for paracatadioptric camera calibration based on the antipodal sphere images. Projections of two spheres on the image plane were used to calibrate the paracatadioptric camera [20, 21]. Zhao et al. [14, 15] used properties of the polar of a point at infinity with respect to a circle and antipodal sphere images to obtain the imaged circular points. Yu et al. [34] have suggested a method exploiting self-polar triangles to calibrate paracatadioptric camera. Wang et al. [22] have presented three methods to calibrate paracatadioptric camera by pole-polar relationship and the antipodal sphere image.

Ying et al. [28] have found that the projection of the sphere onto the unit viewing sphere is a special case of the line, but this relationship was not applied to calibrate the paracatadioptric camera. Duan et al. [5, 6] have presented a method that it is necessary to fit the projective contour of the parabolic mirror and need a lot of pictures of the sphere. In order to reduce the demand for photos of the sphere, three different cases of two spheres were used to calibrate the paracatadioptric camera [20, 21]. However, they need to be in the proper place when taking photos, and projections of two spheres onto the image plane were hard to fit. Based on three pictures of a sphere, Zhao et al. [14, 15, 22, 34] have proposed the calibration methods that obtain the camera intrinsic parameter based on pole-polar relationship and the antipodal point images. These methods all need to acquire the antipodal sphere images, because antipodal point images were obtained based on the antipodal sphere images. Thus, the self-polar triangles and the pole-polar could be used to calibrate the paracatadioptric camera. These calibration methods are complex due to obtaining the formulation of antipodal sphere images. Once the antipodal sphere images are computed wrongly, the intrinsic parameters would be inaccurate. Therefore, they are sensitive to the noise.

To improve abovementioned calibration methods for paracatadioptric camera, we propose a calibration method using the sphere image directly instead of antipodal sphere images. Firstly, the projection of a sphere onto the unit viewing sphere is a small circle. Additionally, we may calculate the great circle which passes through the center of the unit viewing sphere and is parallel with the small circle. This may be regarded as the projection of a line onto the unit viewing sphere. Overall, a pair of orthogonal vanishing points is determined by the intersections of the projection of the great circles on the image plane. Based on constraints between the vanishing points and the absolute conic (IAC), the intrinsic parameters of the paracatadioptric camera can be obtained using three sphere images. The proposed method is simpler, so the performance is better against the noise.

In this paper, we use the relationship between the projection of the sphere and the line onto the unit viewing sphere to calibrate paracatadioptric camera. In this way, the calibration methods using the line would connect with that using the sphere. However, the mirror parameter for other types of the central catadioptric cameras is unknown. The formulation of the sphere image will contain an unknown mirror parameter constant ξ which cannot be solved directly in our method. Due to the sphere image is still a conic, the principle in this paper is also suitable for solving ξ by adding the sphere image.

This paper is organized as follows. Section 2 reviews the unit viewing sphere model for the paracatadioptric camera, the calibration method using the line, and the geometric properties of the line and the sphere under the paracatadioptric camera. Section 3 describes that our calibration algorithm using the projection properties of three spheres in detail. Section 4 illustrates the results for simulated and real experiments, confirming the effectiveness of the algorithms. Section 5 closes the paper with some concluding remarks.

2 Preliminaries

In this section, we review the geometric properties of the line and the sphere with central catadioptric camera [28]. The imaging and calibration processes for the line based on the paracatadioptric camera also are discussed [33].

2.1 Paracatadioptric camera projection model

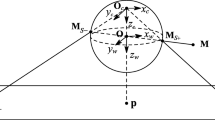
Geyer et al. [11] have presented the unit viewing sphere model for central catadioptric camera calibration. There are two coordinate systems, as shown in Fig. 1. One is the global coordinate system O-x_wy_wz_w, where the origin O is placed at the center of the unit viewing sphere, and the z_w- axis is perpendicular to the image plane. The other coordinate system is that of the virtual camera O_c-x_cy_cz_c, whose z_c- axis coincides with z_w- axis. They are both referred to as optical axis. Based on the unit viewing sphere model, Ying and Zha [27] have suggested a projective process of the sphere for the paracatadioptric camera. This consists of two steps, as follows.

• Step 1: The projection of the sphere Q onto the unit viewing sphere, which is the small circle s.

• Step 2: By the perspective projection of the virtual camera, the projection of the small circle s into the image plane∏, i.e., the conic C_s is obtained.

Fig. 1

Sphere projection with a paracatadioptric camera

Let the intrinsic parameter matrix of the virtual camera be K. It can be expressed as

$$ K=\left[\begin{array}{ccc}r{f}_e& s& {u}_0\\ {}0& {f}_e& {v}_0\\ {}0& 0& 1\end{array}\right] $$

(1)

where f_e, r, s are the effective focal length, the aspect radio, and the skew factor, respectively. [u₀v₀ 1]^T is the homogeneous coordinate of the principal point P.

2.2 Geometric properties of the line and the sphere under the central Catadioptric camera

Ying et al. [28] have introduced the projective geometric properties of the line and the sphere, whose properties are as follows:

Proposition 1

In Fig. 1, the projection of the sphere onto the unit viewing sphere is the small circle s, it can be written as:

$$ {n}_x{x}_w+{n}_y{y}_w+{n}_zz{}_w+{d}_0=0 $$

(2)

where [n_xn_yn_z]^T is the unit normal vector and |d₀| is the distance from the origin O to the plane. [x_wy_wz_w]^T is a point on s. Thus, there is the great circle S that is parallel to the small circle and placed across the origin O. It can be regarded as projection of the line onto the unit viewing sphere. By setting d₀ = 0, it can be written as:

$$ {n}_x{x}_w+{n}_y{y}_w+{n}_z{z}_w=0 $$

(3)

The projection of the line may be considered as a special case of the projection of the sphere onto the image.

Proposition 2

In Fig. 1, H_s is referred to as the viewing conic which is formed by projection of the sphere onto the image plane C_s and the center of the visual camera O_C.

2.3 Using the line to calibrate the Paracatadioptric camera

Gu et al. [33] have proposed a method to calibrate the central catadioptric camera using the line. On the unit viewing sphere, projection of the line is the great circle across the origin O. Because a point on the circle outside the diameter is perpendicular to the line at both ends of the diameter, the orthogonal vanishing points can be determined by the line. The intrinsic parameters of camera may be obtained from the algebraic constraints between the orthogonal vanishing points and IAC.

3 Method of calibrating the intrinsic parameters of the PARACATADOIPTRIC camera

This section discusses how to use the sphere to calibrate the paracatadioptric camera in details.

3.1 Solution of the equation of the small circle

Proposition 3

In Fig. 1, H_s is formed by the projection of the sphere onto the image C_s and the center of the visual camera O_C. The equation of H_s is

$$ \left[x\;y\;z\;1\right]\left[\begin{array}{cccc}{\left(\frac{f_e+2}{z+1}\right)}^2{\beta}_{11}& {\left(\frac{f_e+2}{z+1}\right)}^2{\beta}_{12}& 0& \frac{f_e+2}{z+1}{\beta}_{14}\\ {}{\left(\frac{f_e+2}{z+1}\right)}^2{\beta}_{21}& {\left(\frac{f_e+2}{z+1}\right)}^2{\beta}_{22}& 0& \frac{f_e+2}{z+1}{\beta}_{24}\\ {}0& 0& 0& 0\\ {}\frac{f_e+2}{z+1}{\beta}_{41}& \frac{f_e+2}{z+1}{\beta}_{42}& 0& {\beta}_{44}\end{array}\right]{\left[x\;y\;z\;1\right]}^T=0 $$

(4)

where f_e is the effective focal length, and β_ij (i, j = 1, 2, 3, 4) are non-zero constants.

Proof

In homogeneous coordinate, C_s can be rewritten as

$$ \left[{x}_1\;{y}_1\;{z}_1\;1\right]\left[\begin{array}{cccc}{\beta}_{11}& {\beta}_{12}& 0& {\beta}_{14}\\ {}{\beta}_{21}& {\beta}_{22}& 0& {\beta}_{24}\\ {}0& 0& 0& 0\\ {}{\beta}_{41}& {\beta}_{42}& 0& {\beta}_{44}\end{array}\right]{\left[{x}_1\;{y}_1\;{z}_1\;1\right]}^T=0 $$

(5)

where β_ij = β_ji (i, j = 1, 2, 3, 4), and [x₁y₁z₁ 1]^T is the homogeneous coordinate of a point on C_s. The global coordinate of the z_w axis is f_e+1. C_s can be also expressed as

$$ \left[{x}_1\;{y}_1\;{f}_e+1\;1\right]\left[\begin{array}{cccc}{\beta}_{11}& {\beta}_{12}& 0& {\beta}_{14}\\ {}{\beta}_{21}& {\beta}_{22}& 0& {\beta}_{24}\\ {}0& 0& 0& 0\\ {}{\beta}_{41}& {\beta}_{42}& 0& {\beta}_{44}\end{array}\right]{\left[{x}_1\;{y}_1\;{f}_e+1\;1\right]}^T=0 $$

(6)

where β_ij = β_ji (i, j = 1, 2, 3, 4). It is expressed as F^′(x₁, y₁, z₁) = 0.

The line formed by the point m on C_s and O_C is called the generating line, where O_C = [0 0–1 1]^T. The parametric equation of the generating line is

$$ \Big\{{\displaystyle \begin{array}{c}{x}_1= x\lambda \\ {}{y}_1= y\lambda \\ {}{z}_1+1=\left(z+1\right)\lambda \end{array}}. $$

(7)

Thus, the equation of the viewing cone H_s can be obtained by merging Eqs. (6) and (7).

$$ \Big\{{\displaystyle \begin{array}{c}F\left({x}_1,{y}_1,{z}_1\;1\right)=0\\ {}{x}_1= x\lambda \\ {}{y}_1= y\lambda \\ {}{z}_1+1=\left(z+1\right)\lambda \end{array}} $$

(8)

from which we have

$$ \left[x\;y\;z\;1\right]\left[\begin{array}{cccc}{\left(\frac{f_e+2}{z+1}\right)}^2{\beta}_{11}& {\left(\frac{f_e+2}{z+1}\right)}^2{\beta}_{12}& 0& \frac{f_e+2}{z+1}{\beta}_{14}\\ {}{\left(\frac{f_e+2}{z+1}\right)}^2{\beta}_{21}& {\left(\frac{f_e+2}{z+1}\right)}^2{\beta}_{22}& 0& \frac{f_e+2}{z+1}{\beta}_{24}\\ {}0& 0& 0& 0\\ {}\frac{f_e+2}{z+1}{\beta}_{41}& \frac{f_e+2}{z+1}{\beta}_{42}& 0& {\beta}_{44}\end{array}\right]{\left[x\;y\;z\;1\right]}^T=0 $$

(9)

where β_ij = β_ji (i, j = 1, 2, 3, 4). It also can be written as F^′(x, y, z) = 0.

Proposition 4

If the equation of C_s is known, equation of the small circle s can be obtained.

Proof

From Fig. 1, one may see that the small circle s is the intersection of the right cone and the viewing cone.

In the global coordinate system, the unit viewing sphere can be re-expressed as

$$ \left[{x}_w\;{y}_w\;{z}_w\;1\;\right]\left[\begin{array}{cccc}1& 0& 0& 0\\ {}0& 1& 0& 0\\ {}0& 0& 1& 0\\ {}0& 0& 0& -1\end{array}\right]{\left[{x}_w\;{y}_w\;{z}_w\;1\right]}^T=0 $$

(10)

It also can be expressed as F^′(x_w, y_w, z_w) = 0.

Thus, the equation of the small circle s can be obtained from

$$ \Big\{{\displaystyle \begin{array}{c}{F}^{\prime}\left(x,y,z\right)=0\\ {}{F}^{\prime}\left({x}_w,{y}_w,{z}_w\right)=0\end{array}} $$

(11)

3.2 Calculating of the great circle on the unit viewing sphere

Proposition 5

From Fig. 1, one sees that if the small circle s is known, then the great circle S can be written as

$$ \Big\{{\displaystyle \begin{array}{c}{n}_x{X}_s+{n}_y{Y}_s+{n}_z{Z}_s=0\\ {}{X_s}^2+{Y_s}^2+{Z_s}^2=1\end{array}} $$

(12)

Proof

The equation of the small circle s can be described as

$$ {n}_x\left({x}^{\prime}\hbox{-} {x}_s\right)+{n}_y\left({y}^{\prime }-{y}_s\right)+{n}_z\left({z}^{\prime }-{z}_s\right)=0 $$

(13)

where n = [n_xn_yn_z 1]^T is the normal direction of s. If we choose three points at random on the small circle s, the normal direction n can be calculated by Eq. (13). The distance of the small circle s from the center of the origin O = [0 0 0 1]^T can be computed as

$$ {d}_0=\frac{\mid {n}_x{x}_{s1}+{n}_y{y}_{s1}+{n}_z{z}_{s1}\mid }{\sqrt{{n_x}^2+{n_y}^2+{n_z}^2}} $$

(14)

The equation of the great circle S is then given by

$$ \Big\{{\displaystyle \begin{array}{c}{n}_x{X}_s+{n}_y{Y}_s+{n}_z{Z}_s=0\\ {}{X_s}^2+{Y_s}^2+{Z_s}^2=1\end{array}} $$

(15)

Proposition 6

If the normal direction of the small circle s is known, the projection of the line onto the image plane C_L can be written as

$$ {C}_L=\left[\begin{array}{ccc}{n_z}^2& 0& -{f}_e{n}_z{n}_x\\ {}0& {n_z}^2& -{f}_e{n}_z{n}_y\\ {}-{n}_z{n}_x& -{n}_z{n}_y& -{f_e}^2{n_z}^2\end{array}\right] $$

(16)

where f_e is the effective focal length.

Proof

The sphere image C_s satisfies

$$ \lambda {\boldsymbol{C}}_S={{\boldsymbol{K}}_C}^{\hbox{-} \mathrm{T}}{\boldsymbol{H}}_S{{\boldsymbol{K}}_C}^{-1} $$

(17)

where ${K}_C=\left[\begin{array}{ccc}{f}_x& s& {u}_0\\ {}0& {f}_y& {v}_0\\ {}0& 0& 1\end{array}\right]$ describes the intrinsic parameters of the virtual camera.

$$ {H}_S=\left[\begin{array}{ccc}{\left({d}_0-{n}_z\right)}^2& 0& \left({d}_0-{n}_z\right){n}_x\\ {}0& {\left({d}_0-{n}_z\right)}^2& \left({d}_0-{n}_z\right){n}_y\\ {}\left({d}_0-{n}_z\right){n}_x& \left({d}_0-{n}_z\right){n}_y& {d_0}^2-{n_z}^2\end{array}\right]. $$

(18)

It is the equation of the viewing cone, where d₀ is the distance of the origin O from the small circle s. The great circle S can be regarded as the projection of the line onto the unit viewing sphere. The projection of the line onto the image plane C_L also can be obtained from (17) and rewritten as

$$ \lambda {\boldsymbol{C}}_L={{\boldsymbol{K}}_C}^{\hbox{-} \mathrm{T}}{\boldsymbol{H}}_S^{\prime }{{\boldsymbol{K}}_C}^{-1} $$

(19)

where ${H}_S^{\prime }=\left[\begin{array}{ccc}{n_z}^2& 0& -{n}_z{n}_x\\ {}0& {n_z}^2& -{n}_z{n}_y\\ {}-{n}_z{n}_x& -{n}_z{n}_y& -{n_z}^2\end{array}\right]$.

3.3 Calibrating the Paracatadioptric camera by the projection of the small circle onto the image

Starting from the projection of three great circles onto the image plane, the vanishing points would be obtained by the intersections of two of them. This allows one to calibrate the paracatadioptric camera. To prove this statement, let us start from the following proposition.

Proposition 7

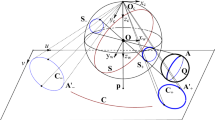
The vanishing points can be determined from the three small circles s_i(i = 1,2,3).

Proof

As shown in Fig. 2, one sees that for every small circle s_i may determine the unique great circle S_i(i = 1,2,3). Intersection of them on the image plane is obtained from.

$$ {\overline{H}}_{ij}\ast {\overline{K}}_{ij}={C}_{Li}\wedge {C}_{Lj} $$

(20)

where the C_Li(i, j = 1, 2, 3) is the projection of the great circle onto the image plane, and “˄“represents the intersection of two conics. $\overline{\boldsymbol{H}}$*$\overline{\boldsymbol{K}}$ is the intersection of them on image plane [33].

Fig. 2

Projection of the sphere and corresponding great circle onto the unit viewing sphere

As shown in Fig. 2, there are total six intersections, according to the geometric properties of the circle. Thus, three pairs of orthogonal vanishing points can be determined on image plane. The intersection of ${\overline{\boldsymbol{H}}}_{12}{\overline{\boldsymbol{H}}}_{13}$ and ${\overline{\boldsymbol{K}}}_{12}{\overline{\boldsymbol{K}}}_{13}$ (see in Fig. 3) can be obtained from

$$ {f}_{23}=\left({\overline{H}}_{12}\wedge {\overline{H}}_{13}\right)\wedge \left({\overline{K}}_{13}\wedge {\overline{K}}_{12}\right) $$

(21)

and the intersection of ${\overline{\boldsymbol{H}}}_{12}{\overline{\boldsymbol{K}}}_{13}$ and ${\overline{\boldsymbol{H}}}_{13}{\overline{\boldsymbol{K}}}_{12}$ can be obtained from

$$ {u}_{23}=\left({\overline{H}}_{12}\wedge {\overline{K}}_{13}\right)\wedge \left({\overline{H}}_{13}\wedge {\overline{K}}_{12}\right) $$

(22)

where f₂₃ and u₂₃ are the intersections. They also are a pair of the orthogonal vanishing points. Other two pairs of orthogonal vanishing points are f₂₄ and u₂₄, f₃₄ and u₃₄. They can be computed in same way.

Fig. 3

A pair of orthogonal vanishing points in image plane

In Fig. 4, ${\overline{\boldsymbol{H}}}_{12}{\overline{\boldsymbol{K}}}_{12}$, ${\overline{\boldsymbol{H}}}_{13}{\overline{\boldsymbol{K}}}_{13}$ and ${\overline{\boldsymbol{H}}}_{23}{\overline{\boldsymbol{K}}}_{23}$ intersect at a point P = (w_xw_y) which is the principal point. It can be obtained from

$$ P={\overline{H}}_{12}{\overline{K}}_{12}\wedge {\overline{H}}_{13}{\overline{K}}_{13}\wedge {\overline{H}}_{23}{\overline{K}}_{23} $$

(23)

Fig. 4

Coordinate of principal point

If the center of coordinate system of the image plane is moved to principal point P, all image points also would be moved. This shift is obtained by multiplying by the matrix T₀

$$ {T}_0=\left[\begin{array}{ccc}1& 0& -{w}_X\\ {}0& 1& -{w}_y\\ {}0& 0& 1\end{array}\right] $$

(24)

In the new coordinate system, the coordinates of ${\overline{\boldsymbol{H}}}_{ij}{\overline{\boldsymbol{K}}}_{ij}$ can be obtained from.

$$ {{\overline{H}}^{\prime}}_{ij}={T}_o{\overline{H}}_{ij},{{\overline{K}}^{\prime}}_{ij}={T}_o{\overline{K}}_{ij} $$

(25)

The new coordinates for the orthogonal vanishing points are obtained from

$$ {f}_{23}^{\prime }=\left({{\overline{H}}^{\prime}}_{12}\wedge {{\overline{H}}^{\prime}}_{13}\right)\wedge \left({{\overline{K}}^{\prime}}_{12}\wedge {{\overline{K}}^{\prime}}_{13}\right) $$

(26)

$$ {u}_{23}^{\prime }=\left({{\overline{H}}^{\prime}}_{12}\wedge {{\overline{K}}^{\prime}}_{13}\right)\wedge \left({{\overline{H}}^{\prime}}_{13}\wedge {{\overline{K}}^{\prime}}_{12}\right) $$

(27)

Because f^′_ij (i, j = 1,2,3) and u^′_ij (i, j = 1,2,3) is a pair of the orthogonal vanishing points, the algebraic constraint of IAC may be written.

$$ {{\boldsymbol{f}}_{ij}^{\prime}}^{\boldsymbol{T}}{{\boldsymbol{\omega}}^{\prime }{\boldsymbol{u}}^{\prime}}_{ij}=0\left(i,j=1,2,3\right) $$

(28)

The image of IAC is written as

$$ {\boldsymbol{\omega}}^{\prime }={K^{\prime}}^{-T}{K^{\prime}}^{-1} $$

(29)

where K^′ = T₀K.

A pair of the orthogonal vanishing points provides a constraint for the IAC, whereas the projection of a sphere onto the unit viewing sphere can only provide a great circle. Since ω^′ has five degrees of freedom, at least the projection of three spheres is necessary to obtain ω^′. In order to calculate K^′-1, one may decompose using Cholesky decomposition, and the matrix K^′ can be obtained by solving for the inverse of K^′-1. If the principal point _P is known, the intrinsic parameter matrix K can be obtained.

According to the above analysis, we may summarize the algorithm in six steps.

• Step 1: Use the projection of k (k ≥ 3) spheres onto the image plane as input, and extract the pixel coordinates of the conics C_s and projective contour of the mirror. Solve the equation of the C_s [19].

• Step 2: Select the points on the C_s, and evaluate the effective focal length f_e [7].

• Step 3: Solve the equation of the viewing conic H_s by Proposition 1 and the small circle s, which is the intersection between the viewing conic and the unit viewing sphere. It may be obtained by Proposition 2.

• Step 4: Obtain the image of the great circle S that is parallel to the s on the surface of the unit viewing sphere by Proposition 3 and Proposition 5. The orthogonal vanishing points may be obtained from Eqs. (21) and (22).

• Step 5: Determine the principal point P by Eq. (23). Moving the origin of coordinate system of the image plane to principal point P. Obtain the new coordinates of a pair of the vanishing points by multiplying by a matrix T₀, according to Eqs. (26) and (27).

• Step 6: Find ω^′ by using Eq. (29). K^′ may then be calculated by decomposing ω^′ which obtained using Cholesky decomposition. The matrix K^′ can be obtained by solving the inverse of K^′-1. Since the principal point P is known, the intrinsic parameter matrix K can be obtained.

4 Experiments

In order to assess the performance of the proposed method, we have performed experiments with simulated and real data.

4.1 Experiment with simulated data

The principal point of the simulated paracatadioptric camera were assumed as P = (400,300 1). We have generated three views to calibrate the camera. Figure 5 shows the projection of the sphere onto the image plane. The blue small conic and the great conic represent the projection of the sphere onto the image plane, the projected contour of the paraboloidal mirror, respectively. In Fig. 6, the blue small circle represents the projection of the sphere onto the unit viewing sphere, and the green great circle represents the great circle that is parallel with them, regarded as projection of the line onto the unit viewing sphere. The red great circle represents the contour circle of the unit viewing sphere.

Fig. 5

The projection of the sphere onto the image plane, and the projected contour of the paraboloidal mirror

Fig. 6

(a)-(c) Projection of the spheres onto the unit viewing sphere and the corresponding great circles

To test the steady of our method, we have compared the steady of our method to that of Li’s method, Yu’s and Zhao’s methods with the same noise. We used 100 points from each image to added Gaussian noise which sampled from a distribution with zero mean and a standard deviation σ. The noise level σ was varied from 0 to 4 pixels. For each noise level, we have performed 100 independent trials to obtain the absolute errors of the five intrinsic parameters. The experimental results are as shown in Figs. 7(a)-(e).

Fig. 7

Variations in the absolute errors of (a) fe, (b) r, (c) s, (d) v0, (e) u0 obtained by our calibration method and by those of Zhao [22], Li [15], and Yu [34], for different amount of Gaussian noise

As it is apparent from those plots, the absolute errors increase linearly with the noise. However, the projection of the sphere onto the unit viewing sphere is used directly in our method. It’s easier than others based on the antipodal sphere image, so our method is more robust against the noise. Although other methods are all linear too, the performance of Zhao’s [22] methods is better using the simpler pole-polar relationship. The absolute error variation trend of three methods presented in Zhao’s study [22] is mostly the same due to the similar geometric relationship. Yu’s [34] method involves additional steps. Moreover, the common self-polar triangles highly depend on four imaginary intersection points from the pair of antipodal circles and great circle. Therefore, the robustness is less than that of the Zhao’s methods. Li’s [15] methods are necessary to acquire two pairs of antipodal image points on every sphere image. In addition, the vanishing line passing through the orthogonal vanishing points would be inaccurate due to the added noise. Therefore, the absolute error of Li’s methods [15] is slightly larger than that of other methods, and there are no obvious distinctions from Figs. 7(a)-(e) based on the Li’s methods [15]. The results state that our method has the superior robustness.

4.2 Experiment with real images

To measure whether our method can estimate the intrinsic parameters successfully, the five intrinsic parameters have been obtained using our method, Zhao’s [22] methods, Li’s [15], and Yu’s methods [34]. The results are presented in Table 1. Although other methods are linear too, these methods highly rely on the antipodal sphere images. Compared to our method which directly obtains the intrinsic parameters using the sphere images, these methods are complex to obtain the antipodal sphere image. Moreover, the common self-triangles would be inaccurate in Yu’s method [34], due to the four imaginary intersection points are obtianed diffcultly umder the influence of the noise. In Zhao’s method [22], the sphere image contour is acquried inaccurate due to the noise. Therefore, the intrinsic parameters obtained by our method are closer to the ground truths as shown in Table 1. The results state that the intrinsic parameters are more accurate obtained by our method.

Table 1 Calibration results with real data (Unit: Pixel)

In our experiment, we have employed a central catadioptric camera designed by the Center for Machine Perception at Czech Technical University and used a yellow table tennis ball as the calibration model. The paraboloidal mirror parameter is ξ = 0.966. The table tennis has been placed on a checkerboard in different positions (see the images in Figs. 8(a)-(c)), and the resolution is 1204 × 1176 pixels. The edge points of the sphere images and the mirror contour projection have been acquired by Canny edge detector, as shown in Figs. 9(a)-(c). The projection of the spheres and mirror contour onto the image plane has been obtained by least-square fitting.

Fig. 8

(a)-(c) Three images of a table tennis ball in different position on the checkerboard

Fig. 9

(a)-(c) Edges of the three images above, extracted with Canny edge detector

To further assess the performance of our methods, we have used the intrinsic parameters obtained by our method to correct images of Figs. 8(a)-(c). The corrected results are shown in Figs. 10(a)-(c), which all the deformed lines were straightened. The real information is displayed by corrected images well. To perform the more detailed verification, we checked the orthogonal lines on the checkerboard. The orthogonal intersections of the projection for two corresponding parallel lines on to the image plane have been detected by Hough transformation [16]. Results are shown in Figs. 11(a)-(c). In principle, a vanishing line can be determined by a pair of orthogonal vanishing points, which should be coincident. In practice, they do not intersect at a single point due to the noise, as shown in Figs. 12(a)-(c). Results clearly show that our method is convincing and accurate.

Fig. 10

(a)-(c) A group of the corrected images in three positions using our method

Fig. 11

(a)-(c) Results of extracting lines from Fig. 10(a)-10(c) by Hough transform, respectively

Fig. 12

(a)-(c) Vanishing lines are obtained by the Hough transform using Fig. 11(a)-11(c)

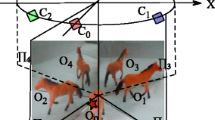
To further verify the accuracy of the intrinsic parameters obtained by our method, we have performed the 3D reconstruction [18] for the checkerboard of Fig. 8 using the parameters reported in Table 1. Fifty points of the checkerboard using Harris corner detection [29] have been selected from each image as shown in Figs. 13(a)-(c). The results are shown in Figs. 14(a)-(g) using our method, Zhao’s [22] methods, Yu’s [34] and Li’s [15] methods. As shown Figs. 14(a)-(g), the 3D reconstruction results are similar. To measure the performance of 3D reconstruction based on the different methods, the parallelism and orthogonality of the 3D reconstruction results would be test. To obtain the equation for each line and column as shown in Figs. 14(a)-(g), the angles between any two lines in parallel directions have been calculated and then averaged by least-square fitting. The average angle in the orthogonal directions may be analogously computed. The angle results as Table 2 shown. The angles for parallel and orthogonal lines are 0° and 90° in the checkerboard, respectively. Therefore, the closer the angles for the parallelity and orthogonality of 3D reconstruction are to 0°, 90°, respectively, the better the performance of the method. More antipodal image points and the projective contour of the mirror are obtained in Li’s methods [34], so the results of Li’s methods [34] are not good as others. Common self-polar triangles highly depend on four imaginary intersection points obtained more difficultly, so the performance of Yu’s methods [15] is not competitive with that of Zhao’s methods [22]. Only a pair of antipodal image points is obtained in Zhao’s methods [22], so the results of their three methods are similar and better than Li’s [34] and Yu’s [15] methods. Different from these methods, our method is only based on the projection of sphere onto the unit viewing sphere directly without using the pole-polar relationship and properties of the antipodal sphere image, so it is simpler. It demonstrates that the reliability of our method and the enhancement in precision compared to other six methods.

Fig. 13

(a)-(c) Results of the Harris corner detector in Fig. 8(a)-8(c), respectively

Fig. 14

Reconstruction results with the intrinsic parameters in Table 1 for (a) our method, (b)-(d) Zhao [22], (e)-(f) Li [15], (g) Yu [34]

Table 2 Testing results of the Parallelity and Orthogonality of 3D Reconstruction with Real Data (Unit: Degree)

5 Conclusion

In this paper, we propose a calibration method for paracatadioptric camera. According to the unit viewing sphere model, the projection of the spatial sphere is the small circle onto the unit viewing sphere. There exists a great circle which is parallel to the corresponding small circle, representing the projection of a line onto the unit viewing sphere. Based on a point of the circle outside the diameter is perpendicular to the line at both ends of the diameter on the great circle, the orthogonal vanishing points may be obtained using the geometric invariance on the image plane. Therefore, the intrinsic parameters of paracatadioptric camera are obtained from the algebraic constraints between the vanishing points and intrinsic parameters. The experimental results state that our method can estimate the intrinsic parameters accurately.

The calibration methods [15, 22, 34] for paracatadioptric camera using the sphere are all based on the antipodal sphere image. Li et al. [15] used the antipodal sphere image to obtain polar and corresponding point at infinity. However, the vanishing lines cannot intersect at circular points due to the noise. Yu et al. [34] used the antipodal sphere image to acquire the self-polar triangles, but the imaginary intersection points are obtained difficultly. Zhao et al. [22] acquired the symmetry axis according to the antipodal sphere image, but the sphere image contour is obtained inaccurate due to the noise. To improve the abovementioned methods, we obtained the intrinsic parameters by exploiting the properties of the projection of the sphere onto the unit viewing sphere. Our method makes indeed use of the geometric properties of the projection of the line and the sphere onto the unit viewing sphere directly. This also allows that the calibration method using lines may be also applied to cases where spheres are used as calibration model.