A new approach for image encryption and watermarking based on substitution box over the classes of chain rings

Abstract

The meanings of passing information from one side to other side by a conventional way is been changed because of internet and communication technology. The issues of the security and the uprightness of information increase due to fast developments in digital world. Presently digital communication has become an important part of transmission of information securely. There are various internet applications which are utilized to convey covertly. As an outcome, the security of data against unapproved access has turned into a prime target. This leads to parts of advancement of different systems for information hiding. Cryptography and watermarking are famous techniques for hiding information accessible to conceal information safely. Our main goal here is to develop an innovative algebraic structures for the construction of nonlinear components of block cipher namely substitution boxes (S-boxes); and also use these components in image encryption and watermarking applications. Different types of S-boxes were introduced in literature based on Galois field and chaos theory in order to add confusion in any cryptosystems. The present construction is entirely based on Galois ring which enrich the existing algebraic structures of S-box theory.

1 Introduction

Information is exceptionally significant to any organization or for any individual. None of us prefers our discussion being caught as it contains the capability of being abused. Same is the situation with the information of any association or of any individual. The trading of information among two potential gatherings must be done in secured system to maintain a strategic distance from any altering. Two sorts of dangers exist amid any data trade. The unintended client who may attempt to catch this discussion can either alter with this information to change its unique importance or it can attempt to listen to the message with proposition to decipher it. Both these attacks disregarded the secrecy and trustworthiness of the communication passed.

Giving planned get to and dodging unintended access is an exceptionally testing undertaking. Information hiding has been since long time. In past, individuals utilized concealed images or undetectable ink to pass on confidential data. But nowadays, we are living in the era of digital world where information security systems depends extensively on binary Boolean functions. Keeping in view the growing demands of digital security mechanism, we have devised a novel technique of image encryption and watermarking based on classes of finite chain ring to enrich existing information hiding scheme that rely on Galois field.

For valuable application and a new role, maximal cyclic subgroup of the group of units of a Galois extension ring attains a keen interest in algebraic cryptography and coding theory. In this respect, initially Shankar [30] presented a construction technique of BCH (Bose Chaudhuri Hocquenghem) codes over local commutative rings with the help of maximal cyclic subgroup of the group of units of a Galois extension of a local commutative ring ${\mathbb{Z}}_{p^k}.$ The construction of this maximal cyclic subgroup is based on a mod − p reduction map from commutative ring ${\mathbb{Z}}_{p^k}$ to ℤ _p (see Shankar [30]). However, the exponential sums over Galois rings and an upper bound for the hybrid sum over the Galois rings by using maximal cyclic subgroups of the groups of units of these Galois rings in a series of papers Cohen [12] and Shanbhag et al. [29]. Further, Andrade and Palazzo gave the construction of BCH codes over the Galois rings by means of maximal cyclic subgroup. In this sequel, Shah et al. [28] used maximal cyclic subgroups of the chain of groups of units in the chain of finite Galois rings to produce new class of S-boxes. In this correspondence, the proposed work presents a construction technique of a substitution box (S-box) using this maximal cyclic subgroup of the group of units in Galois rings and chain ring [3–8, 11, 12, 18–21, 28, 30]. The complexity of the problem is to construct bijective Boolean functions over this maximal cyclic subgroup adjoining zero, with the extension 0 → 0 and then apply permutation in order to increase the number of S-boxes in a databased to add confusion in the selection of appropriate S-boxes. These S-boxes are not so simple as compared to S-boxes which are based on Galois field. These proposed S-boxes are small in nature but having much enrich statistical and algebraic properties [9, 10, 13–15, 25, 31, 32]. The second part of this article is to utilize these structures in image encryption and data hiding techniques namely watermarking [16, 17, 22–24, 26, 27].

The paper is organized as follows: In Section 2, the algebraic structure of the maximal cyclic subgroup is presented. Section 3 consists of the algebraic expression of the proposed S-boxes over maximal cyclic subgroups of groups of units of Galois ring extensions GR(4, 2), GR(4, 4), GR(8, 4), GR(16, 4) and GR(32, 4) of ℤ ₄. In Section 4, we have added construction of S-boxes with Galois ring extensions. In Section 5, we discussed another class of chain ring and S-box construction. In Section 6, we examine the security of the projected S-box with first order texture analysis, second order texture analysis, image quality measures and image similarity metrics and section 7 is about conclusions and future directions.

2 Galois rings and their groups of unit elements

In this section, we discuss some elementary concepts, for instance; Local commutative ring with identity, Galois extension ring, unit elements, and maximal cyclic subgroup of group of invertible elements of a Galois ring.

2.1 Galois rings

We begin with some basic definitions of unitary (local) commutative rings.

Let R be a commutative ring with unity. An element u is unit in R if there exists an element v in R such that u. v = 1, where 1 is the identity of R.

A commutative ring R with unity is said to be local if and only if its all non-unit elements form an additive Abelian group. For instance ${\mathbb{Z}}_{p^k}$, p is a prime integer and k is any positive integer, is a local ring.

Let R be a commutative ring with unity. A non-zero element a is a zero divisor in R if there exists a non-zero element b in R such that a. b = 0.

Let (R, M) be a local commutative ring with unity. An irreducible polynomial f(x) ∈ R[x] over R is said to be a basic irreducible polynomial if it is irreducible over the corresponding residue field K, where (K = R/M).

Consider the finite local ring ${\mathbb{Z}}_{p^k}$, where p is prime and k is a positive integer with corresponding residue field ℤ _p . Now ${\mathbb{Z}}_{p^k}\left[x\right]=\left\{{a}_0+{a}_1x+{a}_2{x}^2+\dots +{a}_n{x}^n:{a}_i\in {\mathbb{Z}}_{p^k},n\in {\mathbb{Z}}^{+}\right\}$ is the polynomial extension of ${\mathbb{Z}}_{p^k}$ in the variable x and ℤ _p [x] = {a ₀ + a ₁ x + … + a _n x ⁿ : a _i  ∈ ℤ _p , n ∈ ℤ ⁺} is the polynomial extension of ℤ _pk in the variable x. Let $f(x)\in {\mathbb{Z}}_{p^k}\left[x\right]$ be a basic irreducible polynomial with degree h. Ideal generated by f(x) is denoted as 〈f(x)〉 and defined as $\left\langle f(x)\right\rangle =\left\{a(x).f(x):a(x)\in {\mathbb{Z}}_{p^k}\left[x\right]\right\}.$ Let $R={\scriptscriptstyle \frac{{\mathbb{Z}}_{p^k}\left[x\right]}{\left\langle f(x)\right\rangle }}=\left\{{a}_0+{a}_1x+{a}_2{x}^2+\dots +{a}_{h-1}{x}^{h-1}:{a}_i\in {\mathbb{Z}}_{p^k}\right\}$ denote the set of residue classes of polynomial in x over ${\mathbb{Z}}_{p^k}$, modulo the polynomial f(x). This ring, denoted by GR(p ^k, h), is a commutative ring with identity and is called the Galois extension of ${\mathbb{Z}}_{p^k}$. Also GR(p ^k, 1) is isomorphic to ${\mathbb{Z}}_{p^k}$ and $GR\left(p,h\right)={\scriptscriptstyle \frac{{\mathbb{Z}}_{p^k}\left[x\right]}{\left\langle f(x)\right\rangle }}=K$ is isomorphic to GF(p ^h), a Galois field extension of ${\mathbb{Z}}_{p^k}$ having p ^h elements, where $\overline{f}={r}_p(f)$ polynomial f which has coefficient modulo p.

2.2 Maximal cyclic subgroup of group of units of Galois rings

Let K ^∗ and R ^∗ be the multiplicative group of units of field and the ring K and R, respectively. Then R ^∗ is an abelian group and can be written in the direct product of cyclic subgroups. By the following Theorem from [1, Theorem 2], between these cyclic subgroups, there is only one cyclic subgroup of order p ^h − 1.

R ^∗ has one and only one cyclic subgroup of order relatively prime to p. This cyclic subgroup has order p ^h − 1. The cyclic subgroup of order p ^h − 1 can be generated by the generator of the corresponding finite field. This cyclic subgroup is denoted by G _n , where n = p ^h − 1. Since the order of K ^∗ and G _n is the same, i.e., p ^h − 1 and both will be cyclic. Therefore G _n is isomorphic to K ^∗.

3 Construction of S-boxes based on maximal cyclic subgroups

In order to create confusion in a data many techniques can be used to do so. One of these techniques is using an S-box. The strongest S-boxes are constructed through mathematical formulas and systematic calculations. In order to improve the quality many have worked in the Galois fields GF(2ⁿ), 1 ≤ n ≤ 8 and created numerous S-boxes. In [1], a 4 × 4 S-box over maximal cyclic subgroup of group of units of Galois ring GR(4, 4) is constructed with its application in watermarking. However, as an extension to [1], in this section, a novel construction technique of 4 × 4 S-boxes with the utility of maximal cyclic subgroups of groups of units of the Galois rings GR(4, 4), GR(8, 4) and GR(32, 4) is given. While, in each three cases the maximal cyclic subgroups G ₁₅ of orders 15 are, respectively, isomorphic to the cyclic Galois group GF(2, 4)^∗. The association of maximal cyclic subgroups with admiring cyclic Galois group GF(2, 4)^∗, which are caused by the mod- 2 reduction maps from local commutative rings ℤ ₄, ℤ ₈ and ℤ ₃₂ to their common residue field ℤ ₂, supports in construction of the 4 × 4 S-boxes over maximal cyclic subgroups. Of course these newly designed S-boxes are increasing complexity during encryption and decryption.

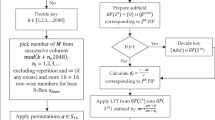
3.1 S-box construction algorithm on Galois ring $GR\left({\mathbb{Z}}_{2^m},\;4\right)$

Given below is the procedure, defining the S-box in 4 steps:

• Step.1: Inversion function I : G _n  ∪ {0} → G _n  ∪ {0},

• Step.2: Linear scalar multiple function f : G _n  ∪ {0} → G _n  ∪ {0},

• Step.3: Take composition of I ∘ f to get (n + 1) × (n + 1) S-box,

• Step.4: Apply permutations S _n to each element of S-box obtained in step 3, which gives us n ! S-boxes.

The map described above is nothing more than a substitution within the set G _n  ∪ {0}. An element of the set is substituted with the element next to its respective inverse. (In this case we define this direction with increasing power of the generator) or in other words the scalar multiplied with the inverse. In the examples below we discuss and analyze this construction method for S-boxes of size 4 × 4.

Let us consider the local rings ℤ ₄ = {0, 1, 2, 3}, ℤ ₈ = {0, 1, 2, …, 7}, ℤ ₁₆ = {0, 1, 2, …, 15} and ℤ ₃₂ = {0, 1, 2, …, 31}, whereas ℤ ₂ = {0, 1}, is their common residue field. The monic polynomial f(x) = x ⁴ + x + 1 is basic irreducible over the local rings ℤ ₄, ℤ ₈, ℤ ₁₆ and ℤ ₃₂ such that f(x) = f(x) mod 2 = x ⁴ + x + 1 is irreducible polynomial over ℤ ₂.

3.2 S-box on GF(2⁴)

Take the polynomial ring ℤ ₂[x] = {a ₀ + a ₁ x + a ₂ x ² + ⋯ + a _n x ⁿ : a _i  ∈ ℤ ₂, n ∈ ℤ ⁺} in one indeterminate x over binary field ℤ ₂. Let < f(x) > = {a(x). f(x) : a(x) ∈ ℤ ₂[x]} be the principal ideal in ℤ ₂[x], generated by f(x). Then elements of Galois extension field K = ℤ ₂[x])/(< f(x) >), of order 16 are given in Table 1.

Table 1 Elements of Galois field GF(2⁴)

Now, let us construct the S-box on the Galois field extension GF(2⁴) (Table 1). It can be seen in Table 2 that it is the most basic S-box and it satisfies all the fundamental properties being an S-box.

Table 2 S-box on GF(2⁴)

3.3 S-box on GR(4, 4)

Let ℤ ₄[x] = {a ₀ + a ₁ x + a ₂ x ² + ⋯ + a _n x ⁿ : a _i  ∈ ℤ ₄, n ∈ ℤ ⁺} is the polynomial ring with one indeterminate x and < f(x) > = {a(x). f(x) : a(x) ∈ ℤ ₄[x]} is a principal ideal generated by f(x). Thus R = (ℤ ₄[x])/(< f(x) >) = {a ₀ + a ₁ x + a ₂ x ² + ⋯ a _{(4 − 1)} x ^{(4 − 1)} : a _i  ∈ ℤ ₄} is the Galois ring extension of order 256 with corresponding Galois field extension K = (ℤ ₂[x])/(< f(x) >) of order 16, whose elements are given in Table 1.

K ^∗ = K\{0} becomes the multiplicative group of units of the field K. Now, let R ^∗ be the multiplicative group of units of the Galois ring R. Then the maximal cyclic subgroup of R ^∗, isomorphic to the cyclic Galois group K ^∗, of order 15 is denoted by G ₁₅ and it is given in Table 3.

Table 3 Elements of G ₁₅ ∪ {0} in GR(4, 4)

Followed by the construction algorithm 3.1 and using maximal cyclic subgroup of Table 3. We obtain S-box given in the Table 4.

Table 4 S-box on GR(4, 4)

3.4 S-box on GR(ℤ ₈, 4)

ℤ ₈[x] = {a ₀ + a ₁ x + a ₂ x ² + ⋯ + a _n x ⁿ : a _i  ∈ ℤ ₈, n ∈ ℤ ⁺} is the polynomial ring with one indeterminate x and < f(x) > = {a(x). f(x) : a(x) ∈ ℤ ₈[x]} is principal ideal generated by f(x). Thus R = (ℤ ₈[x])/(< f(x) >) = {a ₀ + a ₁ x + a ₂ x ² + ⋯ a _{(4 − 1)} x ^{(4 − 1)} : a _i  ∈ ℤ ₈} is the Galois ring extension of order 4096 with corresponding Galois field extension K = (ℤ ₂[x])/(< f(x) >) of order 16, whose elements are given in Table 1.

K ^∗ = K\{0} becomes the multiplicative group of the field K. Now, let R ^∗ be the multiplicative group of units of R. Then the cyclic subgroup of R ^∗, isomorphic to K ^∗ , of order 15 is denoted by c and is given in Table 5.

Table 5 Elements of G ₁₅ ∪ {0} in GR(8, 4)

Followed by the construction algorithm 3.1 and using maximal cyclic subgroup of Table 5, we obtain S-box given in the Table 6.

Table 6 S-box on GR(8, 4)

3.5 Nonexistence of S-box on GR(ℤ ₁₆, 4)

ℤ ₁₆[x] = {a ₀ + a ₁ x + a ₂ x ² + ⋯ + a _n x ⁿ : a _i  ∈ ℤ ₁₆, n ∈ ℤ ⁺}is the polynomial ring with one indeterminate x and < f(x) > = {a(x). f(x) : a(x) ∈ ℤ ₁₆[x]} is principal ideal generated by f(x). Thus R = (ℤ ₁₆[x])/(< f(x) >) = {a ₀ + a ₁ x + a ₂ x ² + ⋯ a _{(4 − 1)} x ^{(4 − 1)} : a _i  ∈ ℤ ₁₆} is the Galois ring extension of order 65535 with corresponding Galois field extension K = (ℤ ₂[x])/(< f(x) >) of order 16, whose elements are given in Table 1.

K ^∗ = K\{0} becomes the multiplicative group of the field K. Now, let R ^∗ be the multiplicative group of units of R. Then the cyclic subgroup of R ^∗, isomorphic to K ^∗, of order 15 is denoted by G ₁₅ and is given in Table 5.

Followed by the construction algorithm 3.1 and using maximal cyclic subgroup of Table 7, we obtain S-box given in the Table 8.

Table 7 Elements of G₁₅ ∪ {0} in GR(16,4)

Table 8 S-box on GR(16, 4)

The structure in Table 8 is not an S-Box as repetition of 1 on two positions. So, this gives us a counter example that, not every maximal cyclic subgroup of the group of units of Galois ring extension generates an S-box.

3.6 S-box on GR(ℤ ₃₂, 4)

ℤ ₃₂[x] = {a ₀ + a ₁ x + a ₂ x ² + ⋯ + a _n x ⁿ : a _i  ∈ ℤ ₃₂, n ∈ ℤ ⁺} is the polynomial ring with one indeterminate x and < f(x) > = {a(x). f(x) : a(x) ∈ ℤ ₃₂[x]} is principal ideal generated by f(x). Thus R = (ℤ ₃₂[x])/(< f(x) >) = {a ₀ + a ₁ x + a ₂ x ² + ⋯ a _{(h − 1)} x ^{(h − 1)} : a _i  ∈ ℤ ₃₂} is the Galois ring extension of order 1048576 with corresponding Galois field extension K = (ℤ ₂[x])/(< f(x) >) of order 16, whose elements are given in Table 1.

K ^∗ = K\{0} becomes the multiplicative group the field K. Now, let R ^∗ be the multiplicative group of units of R. Then the cyclic subgroup of R ^∗, isomorphic to K ^∗ of order 15 is denoted by G ₁₅ and is given in Table 9.

Table 9 Elements of G₁₅ ∪ {0} in GR(32, 4)

Followed by the construction algorithm 3.1 and using maximal cyclic subgroup of Table 9, we obtain S-box given in the Table 10.

Table 10 S-box on GR(32, 4)

So, we are not certain if G _s of every Galois ring will generate an S-box for us. This implies that with a certain polynomial and Galois ring structure we are not sure if we will get an S-box over it or not. It shows that, the method discussed in [1] is not an efficient technique to get S-boxes for use in different applications. Even though these newly designed S-boxes are increasing encryption and decryption difficulty as compare to the S-boxes constructed over Galois field GF(2, 4).

4 Basic primilanaries of finite chain ring of the type ${\scriptscriptstyle \frac{{\mathsf{F}}_2\left[u\right]}{<{u}^k>}}={\mathsf{F}}_2+u{\mathsf{F}}_2+{u}^2{\mathsf{F}}_2+\cdots +{u}^{k-1}{\mathsf{F}}_2$

Let R be a ring. An element v is unit in R if there exists an element w in R such that vw = 1, where 1 is the identity of R. Unit elements of a ring form a multiplicative group. A non-zero element a is a zero divisor in R if there exists a non-zero element b in R such that ab = 0. A nonzero element a is said to be nilpotent element in R if there exists a positive integer k such that a ^k = 0. The least positive integer k with this property is known as the nilpotency index a.

A ring R is local if and only if its all non-unit elements form an additive Abelian group. More unambiguously a local ring R has a unique maximal ideal M and the factor ring ${\scriptscriptstyle \frac{R}{M}}$ is its residue field.

A local finite ring R is a chain ring if and only if the radical M of R is a principal ideal (consists of all multiples of a fixed element of R, and this fixed element is called the generator of the ideal), and therefore the factor ring $\frac{\mathbf{R}}{\mathbf{M}}$ is a field. Thus ideals of a chain ring form a chain. The famous examples of such rings are ${\mathbb{Z}}_{p^n}\left[x\right]$ the ring of integers modulo p ⁿ where p is prime, and the Galois field $GF\left({p}^n\right)={\mathsf{F}}_q$ with q = p ⁿ elements. Another large class of finite chain rings is the Galois rings $GR\left({p}^n,\;r\right)={\scriptscriptstyle \frac{{\mathsf{Z}}_{p^n}\left[x\right]}{<f(x)>}}$, where f(x) ∈ ${\mathbb{Z}}_{p^n}\left[x\right]$ is monic irreducible polynomial of degree r generates the principal ideal < f(x) >, however f(x) is also irreducible modulo the prime p, i.e. f(x) is the basic irreducible polynomial. Whereas the Galois ring R = GR(p ⁿ, r) has p ^nr number of elements and an element ā(x) in GR(p ⁿ, r) has the representation ā ₀ + ā ₁ x + … + ā _r − 1 x ^r − 1, ā ₀, ā ₁, …, ā _r − 1 ∈ ${\mathbb{Z}}_{p^n}$. The radical M is the set of nilpotent elements of R and the residue field $\frac{\mathbf{R}}{\mathbf{M}}$ of R is the Galois extension field GF(p ^r). One of the typical class of chain rings is the factor ring ${\scriptscriptstyle \frac{GF\left({p}^r\right)\left[x\right]}{<{x}^k>}}$ of Euclidean domain GF(p ^r)[x]. The finite chain ring ${\scriptscriptstyle \frac{GF\left({p}^r\right)\left[x\right]}{<{x}^k>}}\left(={\scriptscriptstyle \frac{{\mathsf{F}}_{p^r}\left[x\right]}{<{x}^k>}}\right)$ has the representation ${\mathsf{F}}_{p^r}+x{\mathsf{F}}_{p^r}+\cdots +{x}^{k-1}{\mathsf{F}}_{p^r}.$

Let R _k be the representation of finite chain ring ${\scriptscriptstyle \frac{{\mathsf{F}}_2\left[u\right]}{<{u}^k>}}={\mathsf{F}}_2+u{\mathsf{F}}_2+{u}^2{\mathsf{F}}_2+\cdots +{u}^{k-1}{\mathsf{F}}_2.$ The ring R _k has 2^k number of elements. The element u is the nilpotent element with nilpotency index k (i.e., u ^k = 0 ). Thus it follows that < 0 > = u ^k R _k  ⊂ u ^k − 1 R _k  ⊂ ⋯ ⊂ u ² R _k  ⊂ uR _k  ⊂ R _k is the ascending chain of ideals in R _k and therefore R _k is a local ring with only maximal ideal uR _k . Whereas, ${\scriptscriptstyle \frac{R_k}{u{R}_k}}\simeq {\mathsf{F}}_2$ is the residue field of the chain ring R _k . The ideals u ⁱ R _k and u ^i + 1 R _k , where i = 0, 1, 2, ⋯, k − 1, respectively have the cardinality 2^k − i and 2^{k − i + 1}. Thus the cardinality of u ⁱ R _k is 2 times the cardinality of u ^i + 1 R _k .

Amongst the rings of four elements, earlier the Galois field ${\mathsf{F}}_4$ , and later the integers modulo 4 ring ℤ ₄, are frequently used in algebraic coding theory. Recently, Abualrub and Siap [2] studied cyclic codes of an arbitrary length n over the rings ${\mathsf{F}}_2+u{\mathsf{F}}_2=\left\{0,\;1,\;u,\;\overline{u}=1+u\right\}$, with u ² = 0, and ${\mathsf{F}}_2+u{\mathsf{F}}_2+{u}^2{\mathsf{F}}_2=\left\{0,\;1,\;u,\;{u}^2,\;1+u,\;1+{u}^2,\;u+{u}^2,\;1+u+{u}^2\right\}$, with u ³ = 0. However, Al-Ashker and Hamoudeh [7] extend these results to more general rings of the form ${R}_k={\mathsf{F}}_2+u{\mathsf{F}}_2+\cdots +{u}_2^{k-1}{\mathsf{F}}_2$ , with u ^k = 0. The ring ${\mathsf{F}}_2+u{\mathsf{F}}_2$ share some good properties of both ℤ ₄ and ${\mathsf{F}}_4.$ The alphabet in the ring ${\mathsf{F}}_2+u{\mathsf{F}}_2$ is given to all binary polynomials in indeterminate u of degree at most 1, and is closed under binary polynomial addition and multiplication modulo u ². The multiplication and addition tables for the ring ${\mathsf{F}}_2+u{\mathsf{F}}_2$ are given in Table 11. The multiplication table of the ring ${\mathsf{F}}_2+u{\mathsf{F}}_2$ coincides with that of ℤ₄, when u and ū are replaced by 2 and 3 respectively. In this sense ${\mathsf{F}}_2+u{\mathsf{F}}_2$ is analogous to ℤ₄ and here u plays the role of 2. Whereas the addition table is different and is similar to that of the Galois field ${\mathsf{F}}_4=\left\{0,\;1,\;\beta,\;{\beta}^2=1+\beta \right\}$, where ū and u are replaced by β and β ², respectively (Table 12).

Table 11 × and + Tables for F₂ + uF₂

Table 12 Elements in chain ring R ₃

Table 13 Elements in $f\circ g\left({M}_{g_3}\right)$

Table 14 S - box over R ₃ = F₂ + uF₂ + u ²F₂

Table 15 Elements in chain ring R ₄

5 Construction of S-box through finite chain rings ${\mathsf{F}}_2+u{\mathsf{F}}_2+\cdots +{u}^{k-1}{\mathsf{F}}_2$

The chain ring ${R}_k={\scriptscriptstyle \frac{{\mathsf{F}}_2\left[u\right]}{<{u}^k>}}={\mathsf{F}}_2+u{\mathsf{F}}_2+\dots +{u}^{k-1}{\mathsf{F}}_2$ has cardinality 2^k. As u is a nilpotent element with nilpotency index k, it follows that < 0 > = u ^k R _k  ⊂ u ^k − 1 R _k  ⊂ … ⊂ uR _k  ⊂ R _k . Accordingly the residue field of R _k is ${\scriptscriptstyle \frac{R_k}{u{R}_k}}\simeq {\mathsf{F}}_2$. The ring R _k shares some properties of the local ring ℤ${}_{2^k}$ and the Galois field ${\mathsf{F}}_{2^k}$. More explicitly the multiplication binary operation of R _k coincides with of ℤ${}_{2^k}$, whereas the addition binary operation is similar to that of ${\mathsf{F}}_{2^k}$.

A significant S-box with wide-ranging cryptographic features is of ultimate worth for the development of resilient cryptographic system. Constructing cryptographically strong S-boxes is a basic challenge. In this study we propose a method to amalgam an efficient 4 × 4 S-box based on unit elements of the chain rings ${\mathsf{F}}_2+u{\mathsf{F}}_2+\cdots +{u}^{k-1}{\mathsf{F}}_2$. For the purpose we fix k to 2, 3, 4, 5, 6, 7 and 8.

The 4 × 4 S-box construction steps are given bellow:

• 1) Table ${M}_{G_k},$ the multiplicative group of unit elements of the ring R _k .

• 2) If the cardinality of ${M}_{G_k}$ is a perfect square and less than or equal to 16, define an inversion map $f:{M}_{G_k}\to {M}_{G_k}$ and a linear scalar multiple function g :${M}_{G_k}\to {M}_{G_k}$. Otherwise choose a subgroup ${H}_{G_k}$ of ${M}_{G_k}$ of desired size 16 and then define these two bijective maps f and g from ${H}_{G_k}$to ${H}_{G_k}$. The selection of subgroups and defined maps for each ring are explicitly explained in subsections.

• 3) Take the composition of the maps f and g.

• 4) Generate 4 × 4 S-box by arranging them row wise.

• 5) Apply permutations S _n to each elements of S-box obtained in step 4 which result in n ! S-boxes.

5.1 Construction of S-box through multiplicative group of R ₃

The chain ring ${R}_3={\scriptscriptstyle \frac{{\mathsf{F}}_2\left[u\right]}{<{u}^3>}}={\mathsf{F}}_2+u{\mathsf{F}}_2+{u}^2{\mathsf{F}}_2$ has 8 number of elements. The chain of ideals of this ring is < 0 > = u ³ R ₃ ⊂ u ² R ₃ ⊂ uR ₃ ⊂ R ₃ and ${\scriptscriptstyle \frac{R_3}{u{R}_3}}\simeq {\mathsf{F}}_2$ is its residue field. The multiplication binary operation of R ₃ coincides with of ℤ₈ , whereas the addition binary operation is similar to that of ${\mathsf{F}}_8$.

The multiplicative group of unit elements of the ring R ₃ is

$$ {M}_{G_3}=\left\{1,\kern0.28em 1+u,\kern0.28em 1+{u}^2,\kern0.28em 1+u+{u}^2\right\}. $$

Define $f:{M}_{G_3}\to {M}_{G_3}$ by f(a) = a ^− 1 and $g:{M}_{G_3}\to {M}_{G_3}$ by $g(a)={a}^{\prime }a,$ where ${a}^{\prime }=1+u.$ Thus $f\circ g(a)={\left({a}^{\prime }a\right)}^{-1}.$

5.2 Construction of S-box through multiplicative group of R ₄

The chain ring ${R}_4={\scriptscriptstyle \frac{{\mathsf{F}}_2\left[u\right]}{<{u}^4>}}={\mathsf{F}}_2+u{\mathsf{F}}_2+{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2$ has 16 elements. Its chain of ideals is < 0 > = u ⁴ R ₄ ⊂ u ³ R ₄ ⊂ u ² R ₄ ⊂ uR ₄ ⊂ R ₄, whereas the residue field of this ring is ${\scriptscriptstyle \frac{R_4}{u{R}_4}}\simeq {\mathsf{F}}_2.$ The ring R ₄ shares some properties of the local ring ℤ₁₆ and the Galois field F₁₆. The multiplication and addition binary operations of R ₄ coincides with ℤ₁₆ and F₁₆ respectively.

Multiplicative group of unit elements of the ring R ₄ is

$$ {M}_{G_4}=\left\{1,\kern0.28em 1+u,\kern0.28em 1+{u}^2,\kern0.28em 1+{u}^3,\kern0.28em 1+u+{u}^2,\kern0.28em 1+u+{u}^3,\kern0.28em 1+{u}^2+{u}^3,\kern0.28em 1+u+{u}^2+{u}^3\right\}. $$

Take a subgroup ${H}_{G_4}=\left\{1,\;1+u,\;1+{u}^2,\;1+u+{u}^2+{u}^3\right\}$ of index 2 of the group ${M}_{G_4}$ and apply given procedure on subgroup rather than group ${M}_{G_4}$. Define $f:{H}_{G_4}\to {H}_{G_4}$ by f(a) = a ^− 1 and $g:{H}_{G_4}\to {H}_{G_4}$ by $g(a)={a}^{\prime }a,$ where ${a}^{\prime }=1+u,f\circ g(a)={\left({a}^{\prime }a\right)}^{-1}.$ The following Table 16 is of $f\circ g\left({H}_{G_4}\right)$ in binary and decimal form, which is in fact the S-box constructed over the chain ring ${R}_4={\mathsf{F}}_2+u{\mathsf{F}}_2+{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2$.

Table 16 S - box over R ₄

5.3 Construction of S-box through multiplicative group of R ₅

The chain ring ${R}_5={\scriptscriptstyle \frac{{\mathsf{F}}_2\left[u\right]}{<{u}^5>}}={\mathsf{F}}_2+u{\mathsf{F}}_2++{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2+{u}^4{\mathsf{F}}_2$ has 32 number of elements. The chain of ideals is, < 0 > = u ⁵ R ₅ ⊂ u ⁴ R ₅ ⊂ u ³ R ₅ ⊂ u ² R ₅ ⊂ uR ₅ ⊂ R ₅ and its residue field is ${\scriptscriptstyle \frac{R_5}{u{R}_5}}\simeq {\mathsf{F}}_2.$ The multiplication binary operation of R ₅ coincides with of ℤ${}_{2^5}$, whereas the addition binary operation is similar to that of ${\mathsf{F}}_{2^5}$.

Multiplicative group of unit elements of the ring R ₅ is

$$ {M}_{G_5}=\left\{\begin{array}{c}1,\;1+u,\;1+{u}^2,\;1+{u}^3,\;1+{u}^4,\;1+u+{u}^2,\;1+u+{u}^3,\;1+u+{u}^4,\;1+{u}^2+{u}^3,\\ {}1+{u}^2+{u}^4,\;1+{u}^3+{u}^4,\;1+u+{u}^2+{u}^3,\;1+u+{u}^2+{u}^4,\;1+u+{u}^3+{u}^4,\\ {}1+{u}^2+{u}^3+{u}^4,\;1+u+{u}^2+{u}^3+{u}^4\end{array}\right\}. $$

Define $f:{M}_{G_5}\to {M}_{G_5}$ by f(a) = a ^− 1 and $g:{M}_{G_5}\to {M}_{G_5}$ by g(a) = a′a , where a′ = 1 + u. Thus (f ∘ g)(a) = (a′a)^− 1.

The following Table 17 is of $f\circ g\left({H}_{G_5}\right)$ in binary and decimal form, which is in fact the S-box constructed over the chain ring ${R}_5={\mathsf{F}}_2+u{\mathsf{F}}_2++{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2+{u}^4{\mathsf{F}}_2$.

Table 17 S-box over R ₅

5.4 Construction of S-box through multiplicative group of R ₆

The chain ring ${R}_6={\mathsf{F}}_2\left[u\right]/<{u}^6>={\mathsf{F}}_2+u{\mathsf{F}}_2++{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2+{u}^4{\mathsf{F}}_2+{u}^5{\mathsf{F}}_2$ has cardinality 64. As u is a nilpotent element with nilpotency index 6 , it follows that < 0 > = u ⁶ R ₆ ⊂ u ⁵ R ₆ ⊂ u ⁴ R ₆ ⊂ u ³ R ₆ ⊂ u ² R ₆ ⊂ uR ₆ ⊂ R ₆ and the residue field of R ₆ is ${\scriptscriptstyle \frac{R_6}{u{R}_6}}\simeq {\mathsf{F}}_2$. The addition and multiplication binary operation of R ₆ coincides with ${\mathsf{F}}_{2^6}$ and ℤ${}_{2^6}$ respectively.

Multiplicative group of the ring R ₆ is

$$ {M}_{G_6}=\left\{\begin{array}{c}1,\;1+u,\;1+{u}^2,\;1+{u}^3,\;1+{u}^4,\;1+{u}^5,\;1+u+{u}^2,\;1+u+{u}^3,\;1+u+{u}^4,\;1+u+{u}^5,\\ {}1+{u}^2+{u}^3,\;1+{u}^2+{u}^4,\;1+{u}^2+{u}^5,\;1+{u}^3+{u}^4,\;1+{u}^3+{u}^5,\;1+{u}^4+{u}^5,\;1+u+{u}^2+{u}^3,\\ {}1+u+{u}^2+{u}^4,\;1+u+{u}^2+{u}^5,\;1+u+{u}^3+{u}^4,\;1+u+{u}^3+{u}^5,\;1+u+{u}^4+{u}^5,\\ {}1+{u}^2+{u}^3+{u}^4,\;1+{u}^2+{u}^3+{u}^5,\;1+u+{u}^2+{u}^3+{u}^4,\;1+u+{u}^2+{u}^3+{u}^5,\;1+u+{u}^2+\\ {}{u}^4+{u}^5,\;1+u+{u}^3+{u}^4+{u}^5,\;1+{u}^2+{u}^3+{u}^4+{u}^5,\;1+u+{u}^2+{u}^3+{u}^4+{u}^5\end{array}\right\} $$

The multiplicative subgroup ${M}_{G_6}$ contains 32 elements, sixteen elements of order 8, 8 elements of order 4, 7 elements of order 2, and one element of order 1. Since our interest is in the subgroups of cardinality 16, so we combine these cyclic subgroups in such a way that they generate subgroups of order 16. We take subgroups ${H}_{G_6}=\left\langle 1+{u}^2,1+{u}^3+{u}^4,1+{u}^3+{u}^5\right\rangle$ of cardinality 16 of the multiplicative group ${M}_{G_6}$. Define the maps $f:{H}_{G_6}\to {H}_{G_6}$ by f(a) = a ^− 1 and $g:{H}_{G_6}\to {H}_{G_6}$ by g(a) = a′a, where a′ = 1 + u ⁴. Thus, $\left(g\circ f\right)(a)={\left({a}^{\prime }a\right)}^{-1}$. The following Table 18 is of $f\circ g\left({H}_{G_6}\right)$ in binary and decimal form, which is in fact the S-box designed over the chain ring R ₆.

Table 18 S-box over R ₆

5.5 Construction of S-box through multiplicative group of R ₇

The size of chain ring ${R}_7={\scriptscriptstyle \frac{{\mathsf{F}}_2\left[u\right]/}{<{u}^7>}}={\mathsf{F}}_2+u{\mathsf{F}}_2++{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2+{u}^4{\mathsf{F}}_2+{u}^5{\mathsf{F}}_2+{u}^6{\mathsf{F}}_2$ is 128. The chain of ideals is < 0 > = u ⁷ R ₇ ⊂ u ⁶ R ₇ ⊂ u ⁵ R ₇ ⊂ u ⁴ R ₇ ⊂ u ³ R ₇ ⊂ u ² R ₇ ⊂ uR ₇ ⊂ R ₇. Accordingly the residue field of R ₇ is ${\scriptscriptstyle \frac{R_7}{u{R}_7}}\simeq {\mathsf{F}}_2$. The ring R ₇ shares some properties of the local ring ℤ${}_{2^7}$ and the Galois field ${\mathsf{F}}_{2^7}$. The multiplicative subgroup ${M}_{G_7}$ contains 64 elements, with 32 elements of order 8, 24 elements of order 4, 7 elements of order 2 and 1 element of order 1. Since we require the subgroups of size 16 , it follows that we can fulfill our requirement by above explained availability for ${M}_{G_7}$. For this purpose we choose a subgroup ${H}_{G_7}=\left\langle 1+{u}^3,\;1+{u}^2+{u}^3\right\rangle$ of cardinality 16 of the multiplicative group ${M}_{G_7}$.

Define the maps $f:{H}_{G_7}\to {H}_{G_7}$ by f(a) = a ^− 1 and $g:{H}_{G_7}\to {H}_{G_7}$ by g(a) = a′a , where a′ = 1 + u ³. Thus, (g ∘ f)(a) = (a′a)^− 1. The following Table 19 is of $f\circ g\left({H}_{G_7}\right)$ in decimal form, which is in fact the S-box constructed over the chain ring ${R}_7={\mathsf{F}}_2+u{\mathsf{F}}_2++{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2+{u}^4{\mathsf{F}}_2+{u}^5{\mathsf{F}}_2+{u}^6{\mathsf{F}}_2.$

Table 19 S-box over R ₇

5.6 Construction of S-box through multiplicative group of R ₈

The ring ${R}_8={\scriptscriptstyle \frac{{\mathsf{F}}_2\left[u\right]}{<{u}^8>}}={\mathsf{F}}_2+u{\mathsf{F}}_2++{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2+{u}^4{\mathsf{F}}_2+{u}^5{\mathsf{F}}_2+{u}^6{\mathsf{F}}_2+{u}^7{\mathsf{F}}_2$ is a commutative chain ring of 2⁸ elements. Since u is nilpotent with nilpotency index 8, it follows that < 0 > = u ⁸ R ₈ ⊂ u ⁷ R ₈ ⊂ u ⁶ R ₈ ⊂ u ⁵ R ₈ ⊂ u ⁴ R ₈ ⊂ u ³ R ₈ ⊂ u ² R ₈ ⊂ uR ₈ ⊂ R ₈ and ${\scriptscriptstyle \frac{R_8}{u{R}_8}}\simeq {\mathsf{F}}_2$ is the residue field of R ₈. The ring R ₈ shares some properties of the local ring ℤ${}_{2^8}$ and the Galois field ${\mathsf{F}}_{2^8}$. The multiplication binary operation of R ₈ coincides with of ℤ${}_{2^8}$, whereas the addition binary operation is similar to that of ${\mathsf{F}}_{2^8}$. We choose a subgroup ${H}_{G_8}=\left\langle 1+{u}^3+{u}^6,\;1+{u}^2+{u}^4+{u}^5+{u}^7\right\rangle$ of the group ${M}_{G_8}$ having cardinality 16. Define the maps $f:{H}_{G_8}\to {H}_{G_8}$ by f(a) = a ^− 1 and $g:{H}_{G_8}\to {H}_{G_8}$ by g(a) = a′a , where we take a′ = 1 + u ⁴ + u ⁶. Thus, (g ∘ f)(a) = (a′a)^− 1. The following Table 20 is of $f\circ g\left({H}_{G_8}\right)$ in decimal form, which is in fact the S-box designed over the chain ring ${R}_8={\mathsf{F}}_2+u{\mathsf{F}}_2++{u}^2{\mathsf{F}}_2+{u}^3{\mathsf{F}}_2+{u}^4{\mathsf{F}}_2+{u}^5{\mathsf{F}}_2+{u}^6{\mathsf{F}}_2+{u}^7{\mathsf{F}}_2$.

Table 20 S-box over R ₈

6 Applications of proposed substitution box in image encryption and watermarking

As digital image plays an important role in multimedia technology, it becomes more important for the user’s to maintain privacy. And to provide such security and privacy to the user, encryption and watermarking is very important to protect from any unauthorized user access. The encryption and watermarking have applications in various fields, including internet communication, multimedia systems, medical imaging, Telemedicine and military communication. Nowadays, the prominent share of the multimedia fabrication and dissemination is carried out digitally. The rapid growth of digital media like Internet and Compact Discs has ushered in a wonderful era where the flow, duplication and modification of digital images have become all the more easier and simpler. Mega distribution of flawless replicas of multimedia data at an accelerated degree has become the order of the day. And this phenomenon has unfortunately resulted in tremendous threats to multimedia safety and copyright security. This has the effect of ringing an alarm bell for authors, when the stark reality dawned upon them, convincing that conservative safety systems, like encryption were incapable of affording the much-needed shelter. This has motivated many investigators to devise alternate methods, one of which is known by the term ’digital watermarking’ which is nothing but the art of concealing data in a healthy way and without being noticed by pirates or others of the sort [29]. The classifications of information hiding techniques are cryptography, watermarking and steganography. Here we will only focus on encryption that belongs to cryptography and watermarking. Encryption protects content during the transmission of the data from the sender to receiver. However, after receipt and subsequent decoding, the data is no longer protected and is in the clear. Watermarking compliments encryption by embedding a signal directly into the data. Thus, the goal of a watermarking is to always remain present in the data. The algorithms for image encryption and watermarking schemes are presented in Figs. 1 and 2.

Fig. 1

Proposed image encryption algorithmbased on Galois ring

Fig. 2

Algorithm for image watermarking based on Galois ring

The results after applying the proposed image encryption and watermarking schemes are given in Figs. 3, 4, 5 and 6 respectively.

Fig. 3

(a) Plain Lena image, (b) Encrypted image using GR(4,4), (c) Encrypted image using GR(8,4), (d) Encrypted image using GR(32,4)

Fig. 4

(a) Plain Lena image, (b) Encrypted image using R₅, (c) Encrypted image using R₆, (d) Encrypted image using R₇, (e) Encrypted image using R₈

Fig. 5

(a) Cover Lena image, (b) Watermarked image using GR(4,4), (c) Watermarked image using GR(8,4), (d) Watermarked image using GR(32,4)

Fig. 6

(a) Cover Lena image, (b) Watermarked image using R₅, (c) Watermarked image using R₆, (d) Watermarked image using R₇, (e) Watermarked image using R₈

The statistical analysis plays an important role in estimating good quality information hiding. We have applies first order texture image analysis that deals with the histograms of an image which includes mean, standard deviation (Std.), skewness and kurtosis [27]. The GLCM (Gray-Level Co-Occurrence Matrix) analysis of an image consists of entropy, contrast, homogeneity, energy and correlation [15]. The correlation based statistical analyses consists of structure content, normalized cross correlation. The human visual system (HVS) fundamentally deals with the human perceptions. These analyses include universal image quality index, structure content and structure similarity index metric.

First-order statistics are quite straightforward. They are computed from a function that measures the probability of a certain pixel occurring in an image. The interpretations of first order texture analysis of an image are quite straightforward. They are computed from the mechanism which measures the pixel probabilities in an image. The analysis of first order textures like mean, standard deviation, skewness and kurtosis reflects that there are significant changes in these features for plain and encrypted images in case of Galois rings and finite chain rings (see Tables 21, 22, 23, 24, 25, 26 and 27) whereas in the case of watermarking these parameter values will remain constant with some minute changes for original and watermarked images (see Tables 56, 57, 58, 59, 60, 61 and 62).

Table 21 First order texture analysis of proposed encryption scheme based on S-box of GR(4,4)

Table 22 First order texture analysis of proposed encryption scheme based on S-box of GR(8,4)

Table 23 First order texture analysis of proposed encryption scheme based on S-box of GR(32,4)

Table 24 First order texture analysis of proposed encryption scheme based on S-box of R₅

Table 25 First order texture analysis of proposed encryption scheme based on S-box of R₆

Table 26 First order texture analysis of proposed encryption scheme based on S-box of R₇

Table 27 First order texture analysis of proposed encryption scheme based on S-box of R₈

Table 28 Second order texture analysis of proposed encryption scheme based on S-box of GR(4,4)

Table 29 Comparison of second order texture analysis of proposed encryption scheme based on S-box of GR(4,4) with some existing algorithm

Table 30 Second order texture analysis of proposed encryption scheme based on S-box of GR(8,4)

Table 31 Comparison of second order texture analysis of proposed encryption scheme based on S-box of GR(8,4) with some existing algorithm

Table 32 Second order texture analysis of proposed encryption scheme based on S-box of GR(32,4)

Table 33 Comparison of second order texture analysis of proposed encryption scheme based on S-box of GR(32,4) with some existing algorithm

Table 34 Second order texture analysis of proposed encryption scheme based on S-box of R₅

Table 35 Second order texture analysis of proposed encryption scheme based on S-box of R₁ with some well known algorithm

Table 36 Second order texture analysis of proposed encryption scheme based on S-box of R₆

Table 37 Comparison of second order texture analysis of proposed encryption scheme based on S-box of R₆ with some well known algorithm

Table 38 Second order texture analysis of proposed encryption scheme based on S-box of R₇

Table 39 Comparison of second order texture analysis of proposed encryption scheme based on S-box of R₇ with some well known algorithm

Table 40 Second order texture analysis of proposed encryption scheme based on S-box of R₈

Table 41 Comparison of second order texture analysis of proposed encryption scheme based on S-box of R₈

Table 42 Image error measurements of proposed encryption scheme based on S-box of GR(4,4)

Table 43 Image error measurements of proposed encryption scheme based on S-box of GR(8,4)

Table 44 Image error measurements of proposed encryption scheme based on S-box of GR(32,4)

Table 45 Image error measurements of proposed encryption scheme based on S-box of R₅

Table 46 Image error measurements of proposed encryption scheme based on S-box of R₆

Table 47 Image error measurments of proposed encryption scheme based on S-box of R₇

Table 48 Image error measurments of proposed encryption scheme based on S-box of R₈

Table 49 Image similarity measurements of proposed encryption scheme based on S-box of GR(4,4)

Table 50 Image similarity measurements of proposed encryption scheme based on S-box of GR(8,4)

Table 51 Image similarity measurements of proposed encryption scheme based on S-box of GR(32,4)

Table 52 Image similaritymeasurments of proposed encryption scheme based on S-box of R₅

Table 53 Image similarity measurments of proposed encryption scheme based on S-box of R₆

Table 54 Image similaritymeasurments of proposed encryption scheme based on S-box of R₇

Table 55 Image similaritymeasurments of proposed encryption scheme based on S-box of R₈

Table 56 First order texture analysis of proposed watermarking scheme based on S-box of GR(4,4)

Table 57 First order texture analysis of proposed watermarking scheme based on S-box of GR(8,4)

Table 58 First order texture analysis of proposed watermarking scheme based on S-box of GR(32,4)

Table 59 First order texture analysis of proposed watermarking scheme based on S-box of R₅

Table 60 First order texture analysis of proposed watermarking scheme based on S-box of R₆

Table 61 First order texture analysis of proposed watermarking scheme based on S-box of R₇

Table 62 First order texture analysis of proposed watermarking scheme based on S-box of R₈

The second order texture analysis generally deals with contrast, homogeneity, entropy, correlation and energy. The contrast measures the amount of local variations present in the image. Contrast is zero when the neighboring pixels have constant values. The values second order characteristics for plain and encrypted images are different from each other and for watermarking through Galois rings and finite chain rings are remain same or tend to cover image second order texture features (see Tables 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72 and 73).

Table 63 Second order texture analysis of proposed watermarking scheme based on S-box of GR(4,4)

Table 64 Second order texture analysis of proposed watermarking scheme based on S-box of GR(8,4)

Table 65 Second order texture analysis of proposed watermarking scheme based on S-box of GR(32,4)

Table 66 Second order texture analysis of proposed watermarking scheme based on S-box of R₅

Table 67 Second order texture analysis of proposed watermarking scheme based on S-box of R₆

Table 68 Second order texture analysis of proposed watermarking scheme based on S-box of R₇

Table 69 Second order texture analysis of proposed watermarking scheme based on S-box of R₈

Table 70 Image error measurements of proposed watermarking scheme based on S-box of GR(4,4)

Table 71 Image error measurements of proposed watermarking scheme based on S-box of GR(8,4)

Table 72 Image error measurements of proposed watermarking scheme based on S-box of GR(32,4)

Table 73 Image error measurments of proposed watermarking scheme based on S-box of R₅

The image error measurements and image similarity analysis in case of image encryption and watermarking are quite different. The values of the means square error and mean absolute error increases, whereas peak signal to noise ratio decreases for image encryption. As far as watermarking is concerned, these analyses are entirely changed (Table 41). The value of mean square error and mean absolute error decreases, and peak signal to noise ratio decreases (see Tables 42, 43, 44, 45, 46, 47, 48, 70, 71, 72, 73, 74, 75 and 76).

Table 74 Image error measurments of proposed watermarking scheme based on S-box of R₆

Table 75 Image error measurments of proposed watermarking scheme based on S-box of R₇

Table 76 Image error measurments of proposed watermarking scheme based on S-box of R₈

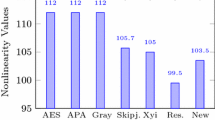
The structural similarity image quality standard is grounded on the notion that the human visual system is extremely modified for extracting structural information from the scene, and therefore a measure of structural similarity can provide a good approximation to perceived image quality. The standard similarity measurement tests which include structure content, universal image quality index and structure similarity index metric (SSIM). The similarity coefficients values for image encryption and watermarking are computed (see Tables 49, 50, 51, 52, 53, 54, 55, 77, 78, 79, 80, 81, 82 and 83). The readings of similarity measures discloses the quality of encryption using proposed algorithms for image encryption, which is based on chain rings. The structure content values in case of image encryption are higher than unity which reveals that two images are completely different. Similarly, structure similarity index and universal image quality index measure far away from unity backwardly which guarantee the authentication of the proposed image encryption algorithm. In case of watermarking similarity coefficients are closed to one which elucidates the robustness of suggested watermarking algorithm constructed on the classes of chain rings (Tables 56, 57, 58, 59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73, 74, 75, 76, 77, 78, 79, 80, 81, 82 and 83).

Table 77 Image similarity measurements of proposed watermarking scheme based on S-box of GR(4,4)

Table 78 Image similarity measurements of proposed watermarking scheme based on S-box of GR(8,4)

Table 79 Image similarity measurements of proposed watermarking scheme based on S-box of GR(32,4)

Table 80 Image similaritymeasurments of proposed watermarking scheme based on S-box of R₅

Table 81 Image similaritymeasurments of proposed watermarking scheme based on S-box of R₆

Table 82 Image similaritymeasurments of proposed watermarking scheme based on S-box of R₇

Table 83 Image similaritymeasurments of proposed watermarking scheme based on S-box of R₈

7 Conclusion

In this article, we developed new schemes for image encryption and watermarking independently that soundly depends on classes of finite chain rings. The readings of test images in case of encryption and watermarking are closed to optimal values that reflect the endorsement of our suggested data hiding technique. In future, we will combine encryption and watermarking due to the fact that cryptography provides no protection once the content is decrypted, which is required for human perception, whereas watermarking complements cryptography by embedding a message within the content.