1 Introduction

Layout problems [4, 12] study how to put objects into limited space reasonably under given constraints (for example, no interference, increasing space utilization ratio). There are also lots of complex problems in various engineering fields, such as layout design of spacecraft modules and plant equipment. As for complex layout problems, some additional behavioral constraints need to be taken into account, such as the requirements for equilibrium, connectivity and adjacent states. These layout problems are of great importance. But unfortunately, due to their NP-Complete complexity, it is hard to solve them satisfactorily.

Relevant references [1, 4, 34] summarized the common approaches to solving layout problems, including mathematical programming and criterion methods, heuristic algorithms, graph theory, expert systems and algorithms based on swarm intelligence and natural laws. Mathematical programming and criterion methods possess relatively well-developed theoretical systems. Since these methods usually have the property of local convergence, it is rather difficult for them to solve large-scale problems. As a rule, we can obtain satisfactory solutions by heuristic algorithms. But every heuristic algorithm has its own scope of application and it is only effective for a restricted kind of problems. Some spatial relationships such as “adjacent” and “distance” are used in graph theory. These relationships can be adopted to cut out some search branches and relax “combination explosion” in search space. But several new questions (e.g., incomplete solution space) appear. Besides, the descriptive method of the solution space by graph theory is quite complicated. The limitation on solving complex layout problems by expert systems lies in that it is not easy to acquire expert knowledge and create inference engines. In accordance with the algorithm trend and solution quality, the robust universal algorithms based on swarm intelligence have significant advantages. They are particularly fit to solve medium or large-scale complex layout problems, compared with other traditional methods [35, 46]. Meanwhile, these algorithms also have several defects with regard to themselves, including premature and slow convergence rate. In this paper, some measures are taken and a novel swarm-based intelligent optimization algorithm is presented on the basis of PGA [9, 20]. We hope our work can benefit solving complex layout problems satisfactorily.

2 Presented Swarm-Based Intelligent Optimization Algorithm

2.1 Chaos Initialization

The purpose of adopting chaos initialization is to improve the quality of initial individuals. Chaos is a nonlinear phenomenon, which extensively exists in nature [33, 36]. Chaos systems possess the characteristics, such as randomness, ergodicity and sensibility to initial conditions [24]. By means of these characteristics, we can initialize population superiorly. The basic idea of chaos initialization can be stated as follows. First of all, generate the same number of chaos variables as many as decision variables. Then introduce chaos into decision variables and map the ergodic range of chaos variables onto the definition ranges of decision variables. Here we select the following Logistic mapping as chaos generator.

$$ {Z_k}_{+1}=f\left(\mu, {Z}_k\right)=\mu {Z}_k\left(1-{Z}_k\right)k=0,1,2,\dots $$
(1)

where μ is a control parameter and the system is in chaotic state when μ = 4.

The concrete procedure of chaos initialization is as follows. Assume that the number of decision variables is n. Firstly assign n original values Z i0 (i = 1, 2,…, n) to Z k in formula (1), which are all between 0 and 1. So it can generate n different sequences of chaos variables, i.e., {Z ik , i = 1, 2,…, n}. Then introduce every chaos variable into its corresponding decision variable by (2).

$$ {x}_{ik}={a}_i+\left({b}_i-{a}_i\right){Z}_{ik} $$
(2)

where b i and a i are the upper and lower bounds of decision variable x i respectively.

For a given k, decision vector X k  = (x 1k , x 2k ,…, x nk )T represents a solution (an individual) to the problem. Along with increase in the value of k, we can obtain a series of initial individuals. Finally, we calculate the fitness of every obtained individual, select superior individuals to form initial population and divide it into initial subpopulations.

2.2 Interpolating rank-based selection with pressure

In traditional rank-based selection operator of genetic algorithms, a probability assignment table should be preset. But there is no deterministic rule for design of the table. And it is difficult for traditional rank-based model to make the selection probabilities of individuals adaptively changed along with evolution process. So some research works have been devoted to the improvement of traditional rank-based selection for these years [3, 37]. In this paper, based on the mathematical concept of interpolation method, we introduce interpolating rank-based selection with pressure and its relevant formulas. It can overcome the above-stated shortcomings of traditional rank-based selection operator.

2.2.1 Parameter decision

There are three control parameters in this kind of selection. They are selection pressure, distribution of interpolation points corresponding to individuals and probabilistic interpolating function.

Selection pressure α denotes the ratio of the maximal individual selection probability P max to the minimal individual selection probability P min within a generation, i.e., P max = αP min. This parameter indicates the priority that the better individuals are reproduced into the next generation during selection process and it is changeable along with the evolution process of the algorithm. Because the fitness values of individuals within a population are usually not much different from one another in the final stage of genetic algorithms and traditional proportional selection model can’t assign higher selection probability values to superior individuals, it usually takes a long time to converge to final results for genetic algorithms. However the proposed concept of changeable selection pressure α can overcome this difficulty effectively. In the early stage, lesser selection pressure α can keep population diversity and avoid early premature; while in the late stage, greater selection pressure α helps to speed up algorithm convergence.

Let α = f (K), K and f denote the generation number and an increasing function respectively. f can be multiple forms and we adopt linear increasing function for the sake of simplicity. Let α max and α min denote the maximum and minimum of selection pressure respectively, then

$$ \alpha =\frac{\left(K-1\right)\left({\alpha}_{\max }-{\alpha}_{\min}\right)}{K_{\max }-1}+{\alpha}_{\min } $$
(3)

where K max is the maximal generation number set in a algorithm. And our numerical experiments show that α max and α min may be chosen in the interval [38, 46] and [1.5, 5] respectively [21].

To calculate the selection probability of every individual, we should arrange all the individuals within a population in descending order based on their fitness values at first. And then determine every interpolation point corresponding to every individual. Interpolation points can be denoted by x k+1 = x k  + h k , k = 1, 2, …, M-1, where M is the population size. x k is the kth interpolation point corresponding to the kth individual within the descending order arrangement. h k is the step size of interpolation. If h k  = c (k = 1, 2, …, M-1), c is a constant, then the distribution of individual interpolation points is equidistant. Otherwise, it is inequidistant. The concrete distribution types should be determined according to the requirement of actual computational condition. For example, under the circumstances of the same α and P(x) (see the next paragraph), comparing the equidistant distribution shown in Fig. 1a to the inequidistant distribution with more compact ends shown in Fig. 1b, we know that the latter lays more emphasis on the function of the superior individuals with greater fitness values.

Fig. 1
figure 1

Distribution types of individual interpolation points

Full size image

P(x) is called probabilistic interpolating function and it is a decreasing function. The selection probability of the kth individual is P k  = P(x k ). And there exist P min = P(x M ) and P max = P(x 1). P max and P min are the maximal and minimal selection probability respectively. P(x) can be linear or nonlinear functions.

2.2.2 Realization process

Assume that the probabilistic interpolating function is linear and the distribution of individual interpolation points is equidistant. We present derived formulas of calculating selection probabilities of individuals in this case as follows. The relevant formulas in other cases can be derived similarly.

As it’s shown in Fig. 1a, let δ k  = P(x k )-P(x k+1), k = 1,2, …, M-1. And assume that the difference between P max and P min is Δ = (α-1)P min. Because P(x) is a linear function and h k  = x k+1-x k  = c (k = 1, 2, …, M-1), δ k (k = 1,2,…, M-1) is a constant, denoted by δ. And there exists δ = Δ /(M-1) =[(α-1)P min]/(M-1). Therefore the selection probability of the kth individual is

$$ {P}_k=\alpha {P}_{min}+\left[\left(1-\alpha \right){P}_{min}\left(k-1\right)\right]/\left(M-1\right) $$
(4)

The sum of all the individual selection probability is 1, i.e.,

$$ {\displaystyle \sum_{k=1}^M\left[\alpha \cdot {P}_{\min }+\frac{\left(1-\alpha \right)\cdot P \min \cdot \left(k-1\right)}{M-1}\right]}=1 $$
(5)

Therefore we obtain

$$ {P}_{\min }=\frac{2}{M\left(\alpha +1\right)} $$
(6)

Substituting above formula into formula (4), it is easy to find that

$$ \begin{array}{cc}\hfill {P}_k=\frac{2\alpha \cdot \left(M-k\right)+2\left(k-1\right)}{M\cdot \left(\alpha +1\right)\cdot \left(M-1\right)}\hfill & \hfill k=1,2,\dots, M\hfill \end{array} $$
(7)

Proposed selection operation can be described as follows. We first reproduce the best individual of current generation and put its copy into the next generation directly based on elitist model. Then calculate selection probabilities of all the individuals according to formula (7). Finally generate the other M-1 individuals of the next generation by fitness proportional model. The advantage of proposed selection operation is that it can conveniently change the selection probabilities of individuals by changing selection pressure during the evolution process. Therefore, the selection operation can be more adaptive to the algorithm run.

2.3 Improved adaptive crossover and mutation

To avoid early premature of genetic algorithms effectively and protect superior individuals from untimely destruction, the idea of adaptive crossover and mutation is proposed by Srinivas and Patnaik [38], see (8) and (9) and shown in Fig. 2. Here P c and P m denote crossover and mutation rate respectively.

Fig. 2
figure 2

Adaptive crossover & mutation operators by Srinivas and Patnaik [38]

Full size image
$$ {P}_c\left\{\begin{array}{ll}{k}_1\left({F}_{\max }-F\right)/\left({F}_{\max }-{F}_{avg}\right),\hfill & F^{\prime}\ge {F}_{avg}\hfill \\ {}{k}_3,\hfill & F^{\prime }<{F}_{avg}\hfill \end{array}\right. $$
(8)
$$ {P}_{\mathrm{m}}\left\{\begin{array}{ll}{k}_2\left({F}_{\max }-F\right)/\left({F}_{\max }-{F}_{avg}\right),\hfill & F^{\prime}\ge {F}_{avg}\hfill \\ {}{k}_4,\hfill & F^{\prime }<{F}_{avg}\hfill \end{array}\right. $$
(9)

In formula (8) and (9), F max and F avg denote the maximal and average fitness of current population. F′ denotes the greater fitness of the two individuals that participate in crossover operation. F denotes the fitness of the individual under mutation operation. k 1, k 2, k 3, k 4 are constants. And there exist 0 < k 1, k 2, k 3, k 4 ≤ 1.0, k 1 < k 3, k 2 < k 4.

But according to these operators, crossover and mutation rate of the best individual among a population are both zero. It may lead to rather slow evolution in the early stage. To avoid its occurrence, it’s better to let the individuals have due crossover and mutation rates, whose fitness values are equal or approximate to the maximal fitness. Therefore, improved adaptive crossover rate P c and mutation rate P m are presented as follows and shown in Fig. 3.

Fig. 3
figure 3

Improved adaptive crossover & mutation operators

Full size image
$$ {P}_c\left\{\begin{array}{ll}{k}_1 \exp \left[\frac{\left({F}_{\max }-F^{\prime}\right)}{F_{\max }-{F}_{avg}}\left( \ln {k}_3- \ln {k}_1\right)\right],\hfill & F^{\prime}\ge {F}_{avg}\hfill \\ {}{k}_3,\hfill & F^{\prime }<{F}_{avg}\hfill \end{array}\right. $$
(10)
$$ {P}_{\mathrm{m}}\left\{\begin{array}{ll}{k}_2 \exp \left[\frac{\left({F}_{\max }-F\right)}{F_{\max }-{F}_{avg}}\left( \ln {k}_4- \ln {k}_2\right)\right],\hfill & F\ge {F}_{avg}\hfill \\ {}{k}_4,\hfill & F<{F}_{avg}\hfill \end{array}\right. $$
(11)

The basic idea of the improved adaptive operators can be described as follows. When the fitness value of an individual is less than the average fitness of the whole population, this individual is assigned greater crossover and mutation rates. It contributes to further exploration of solution space and prevention the algorithm from premature. While when the fitness value of an individual is greater than the average fitness of the whole population, the crossover and mutation rate of this individual decline exponentially with the increase of its fitness value. It can help the algorithm to enforce the exploitation ability and consolidate local search around superior individuals.

2.4 Multi-subpopulation evolution

It is well known that both exploration and exploitation are necessary for the optimization algorithms of swarm intelligence. Exploration denotes the ability to investigate the various unknown regions in the solution space; while exploitation refers to the ability to apply the knowledge of the previous good solutions to find better solutions. In order to achieve excellent performance, the two abilities of one swarm-based algorithm should be well balanced. Therefore, we classify subpopulations of proposed algorithm into two classes (named class A and B) according to their crossover and mutation rates (P c and P m). Suppose that there is only one subpopulation within every class, named class A and B subpopulation respectively. Their parametric features are shown in Table 1.

Table 1 Parametric features of two classes of subpopulations
Full size table

In the light of their properties of initial fitness as well as crossover and mutation rates, we can see that it is easier for class A subpopulation to explore new parts of solution space and guard against premature. Class B subpopulation is mainly to consolidate local search around superior solutions. Obviously, class A subpopulation is for exploration and Class B subpopulation is for exploitation. After chaos initialization, presented algorithm arranges all the generated individuals according to their fitness values. The initial individuals with greater fitness are allocated to class B subpopulation; the initial individuals with smaller fitness are allocated to class A subpopulation.

The individual migration strategy between subpopulations of presented algorithm is as follows. At intervals of given migration cycle, the algorithm copies the best individuals in class A and saves them into class B subpopulation, then update class B subpopulation (eliminate the inferior individuals from it) and keep the same subpopulation size. Meanwhile, it selects some individuals from class B subpopulation and makes them migrate to class A subpopulation respectively. The migration individuals will replace inferior individuals in above subpopulations respectively as well. This migration strategy can accelerate convergence. In addition, we set control parameter K m. When generation number K is multiples of K m, the algorithm merges all the subpopulations together and arrange all individuals according to their fitness. Then it reallocates individuals to two subpopulations respectively according to their fitness values.

2.5 PSO update operators

Particle Swarm Optimization (PSO) was originally developed by Kennedy and Eberhart [19]. In PSO, each particle as an individual in genetic algorithms represents a potential solution. There are mainly two forms of PSO at present, i.e., global version and local version.

With regard to global version of PSO, in the n-dimensional search space, M particles are assumed to consist of a population. The position and velocity vector of the ith particle are denoted by X i  = (x i1 , x i2 , . . ., x in )T and V i  = (v i1 , v i2 , . . ., v in )T respectively. Then its velocity and position are updated according to the following formulas.

$$ {v}_{id}^{k+1}=w\cdot {v}_{id}^k+{c}_1\cdot rand\left(\right)\cdot \left({p}_{id}^k-{x}_{id}^k\right)+{c}_2\cdot rand\left(\right)\cdot \left({p}_{gd}^k-{x}_{id}^k\right) $$
(12)
$$ {x}_{id}^{k+1}={x}_{id}^k+{v}_{id}^{k+1} $$
(13)

where i = 1,2,…, M; d = 1,2,…, n; k and k + 1 are iterative numbers. p i  = (p i1 , p i2,…, p in )T is the best previous position that ith particle searched so far and p g  = (p g1, p g2, …, p gn )T is the best previous position for whole particle swarm. rand() denotes a uniform random number between 0 and 1. Acceleration coefficients c 1 and c 2 are positive constants (usually c 1 = c 2 = 2.0). w is inertia weight and it showed that w decreases gradually along with iteration can enhance entire algorithm performance effectively [32].

It is usually set limitation to a particle velocity. Without loss of generality, assume that relevant following intervals are symmetrical. There exists v k id ∈ [−v d,max, +v d,max]. v d,max (d = 1,2,…, n) determine the resolution with which regions between present position and target position are searched. If v d,max is too high, particles may fly past good solutions. While, if it is too small, the algorithm may be stuck to local optima. Suppose that the range of definition for the dth dimension of a position vector is [−x d,max, +x d,max], i.e., x k id ∈ [−x d,max, +x d,max]. Usually let ± v d,max = ± kx d,max, 0.1 ≤ k ≤1.

In local version of PSO, particle i keeps track of not only the best previous position of itself, but also the best position p li  = (p li,1, p li,2,…, p li,n )T attained by its local neighbor particles rather than that of the whole particle swarm. Typically, the circle-topology neighborhood model is adopted [11]. Its velocity update formula is

$$ {v}_{id}^{k+1}=w\cdot {v}_{id}^k+{c}_1\cdot rand\left(\right)\cdot \left({p}_{id}^k-{x}_{id}^k\right)+{c}_2\cdot rand\left(\right)\cdot \left({p}_{li,d}^k-{x}_{id}^k\right) $$
(14)

And its position update formula is same as that of the global version of PSO. Compared with global version of PSO, local version of PSO has a relatively slower convergence rate but it is not easy to be stuck to local optima.

In addition to global and local version of PSO, we propose an additional new version, named random version of PSO. In random version, the neighborhood N i of particle i is composed of s particles. Apart from particle i itself, the other s-1 particles are randomly selected from the whole population. That is to say, particle i keeps track of the best previous position of itself and the best position attained within its random neighborhood N i . In the broad sense, random version PSO can be regarded as a special kind of local version PSO. Merely its topology structure of neighborhood is dynamic and stochastic. Therefore it helps to explore solution space thoroughly and prevent from premature. The position update formula of random version is also same as that of the global version of PSO.

PSO has been applied to many fields and results are satisfactory [18]. It is easy to be implemented and has quite fast convergence rate among evolutionary algorithms. We noticed that both genetic algorithms and PSO are based on swarm intelligence and can match each other fairly well. To make full use of outstanding convergence characteristic of PSO and global search ability of genetic algorithms, we propose this hybrid algorithm. Specifically, let velocity and position update formulas together serve as a new operator (PSO update). After conventional genetic operation, individuals go on with PSO update operation. It hopes to make hybrid algorithm possess more superior global performance.

In presented algorithm, different versions of PSO update operator are introduced into different subpopulations. Global version PSO update operator is introduced into class B subpopulation in order to speed up the convergence of its individuals to global optima. While, random version PSO update operator is introduced into class A subpopulation. The reason lies in that it matches the function of exploring solution space of class A subpopulation and helps to prevent algorithm from premature.

We lay emphasis on two parameters in PSO update operator, i.e., inertia weight w and maximal velocity V max. Usually there exist w∈ [0.3, 1.5], ±v d,max = ± kx d,max (0.1 ≤ k ≤1.0). If they select greater values, the update operator is more likely to find out new parts of solution space. Otherwise the update operator is good at local search. According to characteristics of different subpopulations, we set the range of w and V max of every mode of update operator in Table 2. Based on adaptation idea [32], we let w and k (coefficient of maximal velocity) decrease linearly along with evolution from their maximal values to the minimal values.

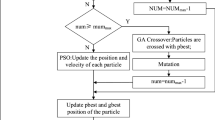
Table 2 Relevant settings of PSO update operators for two classes of subpopulations
Full size table

2.6 The procedure of presented algorithm

Flow chart of the presented swarm-based intelligent optimization algorithm is shown in Fig. 4.

Fig. 4
figure 4

Flow chart of the presented swarm-based intelligent optimization algorithm

Full size image

3 Numerical example

The engineering background of this example is the layout design of printed circuit boards (PCB) and plant equipment. Assume that there are n objects named A 1, A 2, …, A n and the weight between A i and A j is w ij , i, j = 1,2,…, n. Try to locate each object such that the value of expression S+ λ w C of a layout scheme is as small as possible and the constraints of no interference between any two objects are satisfied. Here S is the area of enveloping rectangle of a layout scheme. λ w is a weight factor and C is the sum of the products of d ij multiplied by w ij , i.e.,

$$ C={\displaystyle \sum_{i=1}^{n-1}{\displaystyle \sum_{j=i+1}^n{d}_{ij}{w}_{ij}}} $$
(15)

where d ij is the distance between object A i and A j . w ij may possess different meanings in different engineering problems. For example, in PCB layout design problems, w ij denotes the connectivity between integrated devices. While in the layout design problems of plant equipment, w ij denotes the adjacent requirement between equipment.

Suppose that (x i , y i ) is the coordinates of the center of the object A i . The mathematical model for this problem is given by

$$ \begin{array}{l}\mathrm{Find}X={\left({x}_i,{y}_i\right)}^T,i\in \left\{1,2,\dots, n\right\}\hfill \\ {} \min f(X)=S+{\lambda}_wC\hfill \\ {}\mathrm{s}.\mathrm{t}.\operatorname{int}{A}_i\cap int{A}_j=\mathrm{\O}\kern0.5em i\ne j,\ i,j\in \left\{1,2,\dots, n\right\}\hfill \end{array} $$
(16)

where intA i presents the interior of object A i .

Quoted from Ref. [22], 15 circular objects are contained in this example. Let λ w  = 1. The radii of objects are r 1 = r 3 = r 10 = 12, r 2 = r 4 = 3, r 5 = r 13 = r 14 = 9, r 6 = r 12 = r 15 = 10, r 7 = 7, r 8 = 8, r 9 = 4, r 11 = 6 mm. The weight matrix is

$$ \boldsymbol{W}=\left(\begin{array}{ccccccccccccccc}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 98\hfill & \hfill 98\hfill & \hfill 0\hfill & \hfill 81\hfill & \hfill 0\hfill & \hfill 92\hfill & \hfill 93\hfill & \hfill 45\hfill & \hfill 61\hfill & \hfill 99\hfill & \hfill 84\hfill & \hfill 27\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 34\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 93\hfill & \hfill 44\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 33\hfill & \hfill 60\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 56\hfill \\ {}\hfill 0\hfill & \hfill 34\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 85\hfill & \hfill 0\hfill & \hfill 65\hfill & \hfill 39\hfill & \hfill 0\hfill & \hfill 50\hfill \\ {}\hfill 98\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 91\hfill & \hfill 50\hfill & \hfill 5\hfill & \hfill 24\hfill & \hfill 73\hfill & \hfill 0\hfill & \hfill 4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 31\hfill & \hfill 23\hfill \\ {}\hfill 98\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 91\hfill & \hfill 0\hfill & \hfill 37\hfill & \hfill 0\hfill & \hfill 16\hfill & \hfill 78\hfill & \hfill 95\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 73\hfill & \hfill 32\hfill & \hfill 0\hfill \\ {}\hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 50\hfill & \hfill 37\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 35\hfill & \hfill 0\hfill & \hfill 31\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 48\hfill & \hfill 0\hfill \\ {}\hfill 81\hfill & \hfill 93\hfill & \hfill 0\hfill & \hfill 5\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 94\hfill & \hfill 33\hfill & \hfill 34\hfill & \hfill 26\hfill & \hfill 61\hfill & \hfill 0\hfill & \hfill 87\hfill & \hfill 87\hfill \\ {}\hfill 0\hfill & \hfill 44\hfill & \hfill 0\hfill & \hfill 24\hfill & \hfill 16\hfill & \hfill 35\hfill & \hfill 94\hfill & \hfill 0\hfill & \hfill 91\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 59\hfill & \hfill 39\hfill & \hfill 0\hfill \\ {}\hfill 92\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 73\hfill & \hfill 78\hfill & \hfill 0\hfill & \hfill 33\hfill & \hfill 91\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 30\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 93\hfill & \hfill 0\hfill & \hfill 85\hfill & \hfill 0\hfill & \hfill 95\hfill & \hfill 31\hfill & \hfill 34\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 45\hfill & \hfill 33\hfill & \hfill 0\hfill & \hfill 4\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 26\hfill & \hfill 0\hfill & \hfill 30\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 21\hfill & \hfill 35\hfill & \hfill 2\hfill \\ {}\hfill 61\hfill & \hfill 60\hfill & \hfill 65\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 61\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 56\hfill & \hfill 0\hfill & \hfill 43\hfill \\ {}\hfill 99\hfill & \hfill 0\hfill & \hfill 39\hfill & \hfill 0\hfill & \hfill 73\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 59\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 21\hfill & \hfill 56\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill \\ {}\hfill 84\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 31\hfill & \hfill 32\hfill & \hfill 48\hfill & \hfill 87\hfill & \hfill 39\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 35\hfill & \hfill 0\hfill & \hfill 1\hfill & \hfill 0\hfill & \hfill 0\hfill \\ {}\hfill 27\hfill & \hfill 56\hfill & \hfill 50\hfill & \hfill 23\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 87\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 2\hfill & \hfill 43\hfill & \hfill 0\hfill & \hfill 0\hfill & \hfill 0\hfill \end{array}\right) $$
(17)

To compare the performance of presented algorithm with that of traditional PGA objectively, we adopt presented algorithm and the PGA that possesses two subpopulations (same as presented algorithm) to solve this example respectively and the subpopulation sizes of both algorithms are identical. Moreover, any relevant contents of the two algorithms, such as encoding scheme, fitness function and migration cycle, that may be identical are selected as the same. All computation is performed on PC with CPU at 2.1GHz and RAM size of 2GB.

Both algorithms are calculated 20 times respectively. The best layouts among 20 optimal results by them are in Table 3 and the corresponding best geometric layout patterns are shown in Fig. 5. The comparison of obtained results of the best layouts is given in Table 4. In Table 4, ΔS and t denote the interference area and computation time respectively.

Table 3 The best layouts by two algorithms of the example
Full size table
Fig. 5
figure 5

The obtained best layout patterns of the example by two algorithms

Full size image
Table 4 Comparison of obtained results of the best layouts by two algorithms of the example
Full size table

As the data presented in Table 4, for the best layout by PGA, S, C and computation time t are 5996.46 mm2, 89779.16 and 29.79 s; for the best layout by presented algorithm, S, C and t are 5258.63 mm2, 79082.28 and 27.53 s. When obtained S ≤ 5996.46 mm2, C ≤ 89779.16 by presented algorithm, it takes 22.91 s. So in the sense of best results, to reach the same precision, presented algorithm reduces the cost of time by 23.10 % compared with PGA.

Table 5 lists relevant average values of obtained twenty optimal results of the example by two algorithms. In this table, K represents elapsed generation number for an optimal result.

Table 5 Comparison of average values of optimal results by two algorithms of the example
Full size table

Table 5 shows that compared with PGA, on an average, presented algorithm reduces the area of enveloping rectangle S, the parameter C and elapsed generation number K by 12.05, 9.17 and 27.38 %, i.e., from 6153.83 to 5412.23 mm2, from 95739.06 to 86962.57 and from 705 to 512 respectively.

4 Conclusions

In order to solve complex layout problems more effectively, on the basis of PGA, we take several measures and propose a novel swarm-based intelligent optimization algorithm. These measures involve introducing chaos initialization, interpolating rank-based selection with pressure as well as multi-subpopulation evolution based on improved adaptive crossover and mutation into proposed algorithm. And more importantly, the idea of particle swarm optimization is introduced and PSO update operators can improve the global performance of the proposed algorithm. A numerical example shows that presented algorithm is feasible and effective for this kind of problems. It is really superior to PGA in accuracy and convergence rate. Our work is expected to provide inspiration and reference for solving layout problems satisfactorily. In addition, because presented algorithm is a universal algorithm, it also can be applied to solve other complex engineering optimization problems. The proposed optimization approach is able to be applied in some related research fields, such as network [13–17, 31], image processing [2, 7, 26–28, 39, 47], computer graphics [30], grid [5, 6, 23], cloud computing [40–43], multimedia [10, 25, 29, 45], optimization algorithms [8, 44, 48, 49].