1 Introduction

In the fields of engineering and science, many practical problems can be regarded as optimization problems. The mathematical models of these problems are often complicated. The traditional algorithms are limited in solving these problems and cannot obtain ideal results (Garg 2016). Therefore, a series of metaheuristic algorithms came into being (Garg 2014); scholars around the world used their optimization algorithms to solve multi-constraint optimization problems in practical engineering. For example, the improved gradient-based optimization algorithm (IGBO) was used to accurately define the static model of photovoltaic panel characteristics under various environmental conditions (Abd Elaziz et al. 2022; Jamei et al. 2022); arithmetic optimization algorithm (AOA) and its improved algorithms such as improved algorithm optimization algorithm (IAOA), logarithmic spiral algorithm optimization algorithm (LS-AOA), chaotic quasi-oppositional arithmetic optimization algorithm (COAOA) were applied to wind power prediction (Al-qaness et al. 2022), optimized solar cell (Abbassi et al. 2022), power grid design (Kharrich et al. 2022), thermal economy optimization of shell-tube condenser with mixed refrigerant (Turgut et al. 2022), control of electric system (Ekinci et al. 2022) and other practical engineering problems; Hernan et al. (2021) proposed DOA to solve the optimization problem of PID control parameters. Mirjalili et al. proposed WOA (2016) and GWO (2014) to solve traditional engineering problems such as tension/compression spring design; He et al. (2004) and He and Wang (2007) proposed an improved PSO to solve the optimization of multi-constraint mechanical design problem; Dimopoulos (2006) used GA to solve mixed-integer engineering design optimization problems; Zhang et al. (2019) proposed an algorithm to predict financial time series based on improved GA and neural network.

Among the above optimization algorithms, the swarm intelligence (SI) algorithm represented by PSO and the evolutionary algorithm (EA) represented by GA are widely used in practical engineering. Compared with various new algorithms, GA and PSO have extremely distinct advantages and disadvantages, such as GA has strong global optimization capability, but it has no memory and is easy to lose the optimal solution; moreover, the operation time is long and the efficiency is low (Coello 2000; Coello and Montes 2002); PSO has memory and high efficiency, but it is easy to fall into local optimum (Liu et al. 2015; Abdelhalim et al. 2019; Rahman et al. 2020). In view of the complementary advantages and disadvantages of GA and PSO, scholars are studying the hybrid algorithm of GA and PSO, namely GPSO, hoping to integrate the advantages of the two algorithms perfectly and get an algorithm that is most suitable for solving problems in practical engineering (Zhang 2021; Song 2018; Alrufaiaat and Althahab 2021; Zhao et al. 2019; Guan et al. 2019; Guo et al. 2018). However, the proposed GPSO is all serial algorithms, that is, on the basis of PSO algorithm, PSO and GA are used to update the particles at the same time. Although such GPSO algorithm can solve the problem that the traditional PSO is easy to fall into local optimum in the iterative process, due to the serial connection of GA, there are also problems such as the decrease of optimization efficiency and the large operation overhead.

Aiming at the above problems in the existing GPSO algorithm, this paper fully combines the efficiency of PSO with the global optimization ability of GA and proposes a new parallel GPSO optimization algorithm to better solve the multi-constrained optimization problem. This algorithm takes PSO as the main body, and GA as a means of updating particles in parallel to complete the optimization task. The parallel relationship refers to that when the algorithm does not fall into local optimum, PSO is used to update the particles alone. When the algorithm falls into local optimum, GA is used to select, crossover and mutation of the particles alone to update the particles, which helps the algorithm jump out of local optimum. Once the algorithm jumps out of local optimum, PSO is continued to be used for optimization. Since PSO has memory, GA does not destroy the found optimal value. The parallel structure gives full play to the advantages of PSO efficiency and GA global optimization ability, avoids the disadvantages of PSO easily falling into local optimum and GA low optimization efficiency. Moreover, to solve the multi-constrained optimization problem better and faster, this GPSO uses adaptive inertia weight, adaptive mutation parameters and multi-point crossover operation between particles and pbest to improve the global optimization ability of the algorithm. In Sect. 4, a classical nonlinear constrained optimization problem and three classical structural optimization problems are used to test the performance of the algorithm. The results show that the proposed GPSO can perform very well in solving multi-constrained optimization problems. The following points can summarize the main contributions of the paper:

  • A new parallel GPSO algorithm is proposed, which fully integrates the efficiency of PSO and the global optimization ability of GA.

  • Evaluation the proposed GPSO algorithm’s efficiency and its performance on Himmelblau’s nonlinear optimization problem.

  • Evaluation of the proposed GPSO algorithm’s efficiency and its performance on the structural optimization problems (pressure vessel design problem, welded beam design problem and gear train design problem).

  • In order to verify the optimization performance of the proposed GPSO algorithm, the algorithm is compared with the latest GPSO algorithm and several other latest algorithms. The performance evaluation of the proposed algorithm is carried out by using the evaluation indexes such as best value, mean value, median value, worst value, standard deviation, operation time and convergence speed.

The rest of the paper is organized as follows: Sect. 2 introduces the GPSO algorithm proposed in recent years; Sect. 3 presents the proposed GPSO algorithm; Sect. 4 presents the results and discussions of the function test; Sect. 5 summarizes the conclusions of this paper and future work.

2 Relative work

In practice, we are often faced with many optimization problems. EA and SI algorithm are the two most commonly used algorithms to solve practical engineering problems, because these two types of algorithms are simple and easy to implement and do not require high resolution of the objective function. The most representative of them are GA and PSO. However, as mentioned above, GA has strong global optimization ability but low efficiency; PSO has high efficiency, but it is easy to fall into local optimum. So many scholars are studying GPSO, hoping to integrate the advantages of the two algorithms perfectly.

Zhang (2021) proposed GPSO to introduce crossover and mutation operations of GA into PSO. The fitness values of the particles are calculated and sorted, and then, the particles with lower fitness are eliminated, and the remaining particles are crossed and mutated. Particles with better fitness are crossed with pbest or gbest until the total number of particles reaches the total number of particles before elimination. This can fully improve the quality of particles, which improved the ability to search for optimization. Song et al. (2018) proposed a GPSO algorithm based on differential evolution. On the basis of PSO, the differential evolution of each three particles is carried out to replace the existing particles to improve the quality of particles. Su et al. (2021) integrated the ant colony algorithm (AC) on the basis of GPSO algorithm, used the high efficiency of GPSO to update the velocity and position of particles, and used the global optimization ability of AC to update the fitness value of particles. The GPSO algorithms proposed by Sheng et al. (2021) and Aravinth et al. (2021) are similar to the algorithm proposed by Zhang (2021). The difference is that the parent generations of the crossover operation are randomly selected in the current population, which can improve the diversity of the population and avoided falling into local optimum. The GPSO algorithm proposed by Salaria et al. (2021) is based on PSO, while the inertia weight is optimized by the algorithm, and the quasi-oppositional population-based global particle swarm optimizer is used to update and evolve the particles, which greatly improves the optimization ability of the algorithm. The GPSO algorithm proposed by Chen and Li (2021) has made two improvements based on GPSO. Firstly, the global inertia weight is introduced to improve the global search ability in the whole optimization process. Second, using a small probability mutation operation, GPSO algorithm is easy to jump out of local optimum. Alrufaiaat and Althahab (2021) proposed the GPSO algorithm, where a new update formula is innovated by combing the GPSO with the gradient ascent/descent algorithm, so that the update of particle position can be completed faster and better. GPSO algorithm proposed by Allawi et al. (2020) uses greedy algorithm to select and optimize pbest and gbest, which can avoid falling into local optimum. Gao et al. (2020) proposed a GPSO algorithm using binary coding system and gradient penalty. In this algorithm, the particles are arranged in gradient according to the size of the fitness value, so that the particles with high quality are updated preferentially. This purpose is to solve the problem that when the number of particles in PSO is large, PSO cannot judge the priority of particle update, which leads to low convergence efficiency. Mir et al. (2020) proposed a GPSO algorithm, which made two improvements based on PSO. The first is to change inertia weight into adaptive parameters. The second is to use Gaussian function to optimize the particle update formula, which can accelerate the particle update and improve the optimization speed and quality. Zhao et al. (2019) proposed a grouping GPSO algorithm, in which the population is composed of several groups. For each iteration, an elite group is constructed to replace the worst group. Grouping is conducive to improving the diversity of solutions, thereby enhancing the global search ability of the algorithm. Guan et al. (2019) proposed a GPSO algorithm, which integrates the crossover and mutation operation of GA into the optimization iteration process of PSO and adaptively processes the crossover parameters, mutation parameters, inertia weight and learning factor parameters to enhance the ability of population to jump out of local optimum. Guo et al. (2018) proposed a grouping GPSO-PG algorithm based on individual best position guidance, which maintains the diversity of population by preserving the diversity of samples. On the one hand, the uniform random allocation strategy is used to assign particles to different groups, and the loser in each group will learn from the winner. On the other hand, the pbest of each particle in social learning is used to replace the gbest. This not only increases the diversity of samples, but also eliminates the dominant influence of gbest on optimization and prevents falling into local optimum. Al-Bahrani and Patra (2018) proposed an OPSO algorithm. The algorithm uses the orthogonal diagonalization between the particles with good performance and the residual particles to replace the crossover operation of GA to update the particles. All the GPSO algorithms mentioned above are series algorithms. Although they can also ensure the optimization ability of the algorithm, the series algorithm will reduce the optimization efficiency of the algorithm and increase the overhead of the algorithm. Therefore, parallel GPSO algorithm is required to improve the optimization efficiency and reduce the algorithm overhead while ensuring the optimization ability. Table 1 shows the similarities and differences between the proposed GPSO algorithm and the other GPSO algorithm (except the differences in parallel architecture).

Table 1 Similarities and differences between the proposed GPSO and the other GPSO
Full size table

3 GPSO

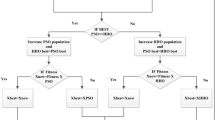
The GPSO proposed in this paper takes PSO as the main body and GA as a means of updating particles in parallel to complete the optimization task. The algorithm can fully combine the advantages of PSO efficiency and GA excellent global optimization ability. The operation of the algorithm can be divided into the following three stages:

  1. 1.

    First stage

In the first stage, in order to ensure the efficiency of optimization, GA does not participate in the updating of particles and only uses PSO to update particles, so that gbest quickly approaches the optimal value. During this period, the velocity and position of particles are updated by Eqs. (1) and (2) as follows:

$$ v_{k + 1}^{i} = w \cdot v_{k}^{i} + c_{1} \cdot {\text{rand}}_{1} \cdot \left( {p_{k}^{i} - x_{k}^{i} } \right) + c_{2} \cdot {\text{rand}}_{2} \cdot \left( {p_{k}^{g} - x_{k}^{i} } \right) $$
(1)
$$ x_{k + 1}^{i} = x_{k}^{i} + v_{k + 1}^{i} $$
(2)

where \(v_{k}^{i}\) is the particle velocity,\( x_{k}^{i}\) is the particle position, w is the inertia weight, c1 and c2 are constants known as the social and cognitive parameters, rand1 and rand2 are random numbers in the range of [0,1], \(p_{k}^{i}\) is pbest, \(p_{k}^{g}\) is gbest.

The right side of Eq. (1) consists of three terms: The first item is the "inertia" part, which represents the tendency of particles to maintain their own speed; the second item is the "cognition" part, which indicates that the particle has a tendency to approach the best position in its own history; the third item is the "social" part, which represents the tendency of the particle to approach the best position in the history of the group or neighborhood. The first item guarantees the global convergence performance of the algorithm, and the second and third items guarantee the ability of local convergence. Therefore, in order to ensure the global search capability of the algorithm, w is dynamically adjusted during the search process in Eq. (3):

$$ w = w_{\max } - \frac{{\left( {w_{\max } - w_{\min } } \right) \cdot t}}{{T_{\max } }} $$
(3)

where wmax and wmin are the maximum and minimum of the inertia weight; t is the current number of iterations; Tmax is the maximum number of iterations.

  1. 2.

    Second stage

When the continuous nummax generation of gbest does not change, the algorithm assumes that it falls into the local optimum (It may also find the optimal value, while since the particle swarm algorithm has memory, it will not destroy the optimal value). At this time, it is difficult to help the algorithm jump out of the local optimum by continuing to use the PSO update particles in the first stage. Therefore, the algorithm enters the second stage, that is, the selection, crossover and mutation of GA are used to help the algorithm jump out of the local optimum. In the crossover operation, multi-point crossover operation between particles and pbest can quickly improve the quality of the population and improve the optimization efficiency. In the second stage, once gbest changes, it indicates that GA has completed its mission and has helped the algorithm jump out of local optimum, so the algorithm jumps back to the first stage to continue optimization. Equations (4) and (5) for updating particles by GA are as follows:

$$ x_{k + 1}^{{i\left( {{\text{rand}} < p_{c} } \right)}} = {\text{rand}}i_{D} \cdot x_{k}^{{i\left( {{\text{rand}} < p_{c} } \right)}} + \left( {1 - {\text{rand}}i_{D} } \right) \cdot p_{k}^{{i\left( {{\text{rand}} < p_{c} } \right)}} $$
(4)
$$ x_{{k + 1}}^{{i\left( {\left\lceil {N \cdot {\text{rand}}} \right\rceil } \right)}} {\mkern 1mu}{}_{{\left\lceil {{\text{rand}} \cdot D} \right\rceil }} = x_{{k + 1_{{\left\lceil {{\text{rand}} \cdot D} \right\rceil _{{\max }} }} }}^{i} - {\text{rand}} \cdot \left( {x_{{k + 1_{{\left\lceil {{\text{rand}} \cdot D} \right\rceil _{{\max }} }} }}^{i} - x_{{k + 1_{{\left\lceil {{\text{rand}} \cdot D} \right\rceil _{{\min }} }} }}^{i} } \right) $$
(5)

where pc is probability of crossover, \(x_{k}^{{i\left( {{\text{rand}} < p_{c} } \right)}}\) are the crossing particles, D is the dimension of the particles, \({\text{rand}}i_{D}\) is the binary vector with length D, \(p_{k}^{{i\left( {{\text{rand}} < p_{c} } \right)}}\) is the pbest of crossing particle, N is the number of particle swarm, ⌈ ⌉ represents an upward integer, \(x_{{k + 1}}^{{i\left( {\left\lceil {N \cdot {\text{rand}}} \right\rceil } \right)}}{}_{{\left\lceil {{\text{rand}} \cdot D} \right\rceil }}\) represents the random particles in the particle swarm participating in the mutation operation, Mutation operation N·pm times, pm is the mutation probability. \(x_{{k + 1_{{\left\lceil {{\text{rand}} \cdot D} \right\rceil_{\max } }} }}^{i}\) and \(x_{{k + 1_{{\left\lceil {{\text{rand}} \cdot D} \right\rceil_{\min } }} }}^{i}\) are the maximum and minimum values of the particle.

  1. 3.

    Third stage

When the continuous NUMmax generation of gbest does not change, it indicates that the operation in the second stage of the algorithm cannot help the algorithm jump out of the local optimum. Moreover, after several generations of evolution, most of the particles have been trapped in the local optimum. At this time, the population structure needs to be greatly changed. By using Eqs. (6) and (7), the mutation probability is greatly improved, so that the individuals in most particles are randomly updated and the maximum possible jump out of local optimum. Once gbest changes, it indicates that GA has completed its mission and has helped the algorithm jump out of the local optimum. Therefore, the algorithm jumps back to the first stage for further optimization, otherwise, it will always use GA to update particles.

$$ p_{m} = \left( {\frac{t}{{T_{\max } }}} \right)^{\gamma } \cdot p_{{m_{\max } }} $$
(6)
$$ \gamma = \left\{ {\begin{array}{*{20}l} 1 \hfill & {{\text{NUM}} < {\text{NUM}}_{{{\text{MAX}}}} } \hfill \\ {0.5} \hfill & {{\text{NUM}} \ge {\text{NUM}}_{{{\text{MAX}}}} } \hfill \\ \end{array} } \right. $$
(7)

where \(p_{{m_{\max } }}\) is the maximum probability of mutation, γ is the coefficient of mutation.

Through the above steps, the whole process of GPSO optimization is completed. The GPSO flowchart is shown in Fig. 1:

Fig. 1
figure 1

Flowchart of GPSO

Full size image

3.1 Time complexity analysis

Since the running time of an algorithm is greatly affected by computer performance, the time complexity of an algorithm is generally used to evaluate the execution efficiency of an algorithm. Time complexity can also be understood as a relative measure of the running time of an algorithm, usually described by the big O notation, that is, \(T\;\left( n \right)\; = \;O\;\left( {f\left( n \right)} \right)\).

Because PSO and GA are included in the algorithm, there are many iterations in the algorithm. The time complexity of the algorithm is estimated by taking the frequency of the most repeated sentences in the algorithm. The most frequently executed statement in the algorithm is the judgment statement in PSO whether the velocity and position of the particle after updating exceed the boundary. Three loops are needed to execute the statement. The first loop is the iteration of the whole algorithm, the second loop is the PSO population updating, and the third loop is to determine whether the velocity and position of each particle exceed the boundary. Since the algorithm has three loops, its time complexity is \(T\;\left( n \right)\; = \;O\;\left( {n^{{3}} } \right)\). The time complexity of other serial GPSO algorithms is also \(O\;\left( {n^{{3}} } \right)\). However, since GA is always involved in the operation in the serial GPSO algorithm, and the parallel GPSO only participates in the operation when the algorithm falls into local optimum, the operation overhead of the parallel GPSO is lower than that of the serial GPSO. The analysis of time complexity is only a rough estimate of the efficiency and overhead of the algorithm. The comparison of the running time of the specific algorithm is shown in Sect. 4.

4 Verification and analysis of algorithm performance

In order to verify the effectiveness of the proposed GPSO, this paper selects several classical multi-constrained optimization problems to test the algorithm. In order to eliminate the influence of computer performance on the algorithm, this paper reproduces several latest GPSO algorithms and tests them under the same computer; in order to eliminate the influence of algorithm stability on the results, this paper takes the best value, mean value, median value, worst value, standard deviation, operation time and convergence speed of each algorithm in 100 experiments as the evaluation indexes of algorithm performance, so as to fully eliminate the contingency of the results and ensure that the results have statistical significance.

4.1 Constrained optimization problem

4.1.1 Himmelblau’s nonlinear optimization problem

The performance of the proposed GPSO is verified by Himmelblau's nonlinear optimization problem. The problem was first proposed by Himmelblau and is now widely used to validate nonlinear constrained optimization algorithms. This problem contains five optimization variables and six nonlinear constraints, as follows:

$$ x = \left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right] $$
(8)
$$ {\text{Min}}f\left( x \right) = 5.3578547x_{3}^{2} + 0.8356891x_{1} x_{5} + 37.293239x_{1} - 40792.141 $$
(9)

s.t.

$$ 0 \le g_{1} \left( x \right) \le 92 $$
(10)
$$ 90 \le g_{2} \left( x \right) \le 110 $$
(11)
$$ 20 \le g_{3} \left( x \right) \le 25 $$
(12)

where

$$ g_{1} \left( x \right) = 85.334407 + 0.0056858x_{2} x_{5} + 0.0006262x_{1} x_{4} - 0.0022053x_{3} x_{5} $$
(13)
$$ g_{2} \left( x \right) = 80.51249 + 0.0071317x_{2} x_{5} + 0.0029955x_{1} x_{2} - 0.0021813x_{3}^{2} $$
(14)
$$ g_{3} \left( x \right) = 9.300961 + 0.0047026x_{3} x_{5} + 0.0012547x_{1} x_{3} + 0.0019085x_{3} x_{4} $$
(15)
$$ 78 \le x_{1} \le 102 $$
(16)
$$ 33 \le x_{2} \le 45 $$
(17)
$$ 27 \le x_{3} ,x_{4} ,x_{5} \le 45 $$
(18)

This paper uses this problem to test the performance of the proposed GPSO algorithm and compares it with several latest GPSO algorithms. The comparison results are shown in Tables 2 and 3.

Table 2 Comparison of the optimal value for Himmelblau's nonlinear optimization problem found by different algorithms
Full size table
Table 3 Performance of different algorithms for Himmelblau’s nonlinear optimization problem
Full size table

In Table 2, different algorithms have achieved good results in optimizing this problem, but there are small differences in the results of the optimal value. The optimal value of GPSO proposed in this paper is − 30,659.81, which is closer to the real optimal value compared with other results in the table. At this time, the parameter is: [x1, x2, x3, x4, x5] = [78.01, 33.01, 30.01, 44.94, 36.78], which is within the constraint range of the parameter and meets the parameter requirements. The constraint result obtained by substituting the parameters into the constraint equations is: [g1, g2, g3] = [91.99, 98.85, 20.00], which also satisfies the constraint condition. Through comparative analysis, it is proved that the optimization algorithm proposed in this paper can obtain a better optimal value to Himmelblau’s nonlinear optimization problem.

Table 3 shows the algorithm performance of each algorithm in solving Himmelblau’s nonlinear optimization problem. The optimal value of GPSO proposed in this paper is − 30,659.81, which is closer to the real optimal value compared with other results in the table; it shows that the GPSO proposed in this paper can get a better optimal value. The average value of the optimal value obtained by 100 experiments is − 30,597.25, which is smaller than the optimal value of − 30,595.62 in the above algorithm. It shows that the algorithm can obtain better results in many repeated experiments and proves that the algorithm has a better stability. The standard deviation is 59.54, which is smaller than the minimum deviation of 60.26 in the above algorithm, indicating that the stability of the algorithm is better. The time of 100 experimental results is only 2.62 s. Compared with the shortest time of 2.85 s in the above algorithm, the time can be shortened by 8%, indicating that the algorithm has high optimization speed and low time complexity. Through the comparative analysis of the above performance, it is proved that the GPSO proposed in this paper can obtain better optimal value and has good performance in stability and efficiency.

In addition, Fig. 2 shows the convergence performance of each algorithm in solving Himmelblau's nonlinear optimization problem. It can be seen from Fig. 2 that the GPSO proposed in this paper has a higher convergence speed compared with other algorithms. Through the comparative analysis of the above performance, it is proved that the GPSO proposed in this paper can get a better optimal value and has good performance in stability, convergence speed and time overhead.

Fig. 2
figure 2

The convergence performance of each algorithm in solving Himmelblau's nonlinear optimization problem

Full size image

4.2 Structural optimization problems

In order to verify the effectiveness of the algorithm in solving multi-objective optimization problems in practical engineering, comparative tests were carried out on three classic practical engineering problems, including pressure vessel design problem, the welded beam design problem and the gear train design problem.

4.2.1 Pressure vessel problem

The objective of pressure vessel design problem is to minimize the cost of pressure vessel fabrication (matching, forming and welding). The design of the pressure vessel is shown in Fig. 3. Both ends of the pressure vessel have a cover top. The cover at one end of the head is hemispherical. The maximum working pressure is 2000 psi, and the maximum volume is 750 ft3. L is the section length of the cylinder part without considering the head, R is the inner wall diameter of the cylinder part, Ts and Th represent the wall thickness of the cylinder part and the head. L, R, Ts and Th are the four optimization variables of the pressure vessel design problem. The objective function and constraints of the problem are expressed as follows:

$$ x = \left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right] = \left[ {T_{s} ,T_{h} ,R,L} \right] $$
(19)
$$ {\text{Min}}f\left( x \right) = 0.6224x_{1} x_{3} x_{4} + 1.7781x_{1} x_{3}^{2} + 3.1661x_{1}^{2} x_{4} + 19.84x_{1}^{2} x_{3} $$
(20)
Fig. 3
figure 3

The design of the pressure vessel

Full size image
$$ \begin{aligned}&{\text{s.t.}}\\&g_{1} \left( x \right) = - x_{1} + 0.0193x_{3} \le 0 \end{aligned}$$
(21)
$$ g_{2} \left( x \right) = - x_{2} + 0.00954x_{3} \le 0 $$
(22)
$$ g_{3} \left( x \right) = - \pi x_{3}^{2} - \frac{4}{3}\pi x_{3}^{2} + 1296000 \le 0 $$
(23)
$$ g_{4} \left( x \right) = x_{4} - 240 \le 0 $$
(24)
$$ 1 \times 0.0625 \le x_{1} ,x_{2} \le 99 \times 0.0625 $$
(25)
$$ 10 \le x_{3} ,x_{4} \le 200 $$
(26)

This paper uses this problem to test the performance of the proposed GPSO algorithm and compares it with several latest GPSO algorithms. The comparison results are shown in Tables 4 and 5.

Table 4 Comparison of the optimal value for pressure vessel design problem found by different algorithms
Full size table
Table 5 Performance of different algorithms for pressure vessel design problem
Full size table

In Table 4, different algorithms have achieved good results in optimizing this problem, but there are small differences in the results of the optimal value. The optimal value of GPSO proposed in this paper is 5881.0474, which is closer to the real optimal value compared with other results in the table. At this time, the parameter is: [x1, x2, x3, x4] = [0.7782, 0.3831, 40.3199, 199.9980], which is within the constraint range of the parameter and meets the parameter requirements. The constraint result obtained by substituting the parameters into the constraint equations is: [g1, g2, g3, g4] = [− 3.8027e−6, − 1.0516e−4, − 8.6355, − 40.0020], which also satisfies the constraint condition. Through comparative analysis, it is proved that the optimization algorithm proposed in this paper can obtain a better optimal value to pressure vessel design problem.

Table 5 shows the algorithm performance of each algorithm in solving pressure vessel design problem. The optimal value of GPSO proposed in this paper is 5881.0474, which is closer to the real optimal value compared with other results in the table, and it shows that the GPSO proposed in this paper can get a better optimal value. The average value of the optimal value obtained by 100 experiments is 6001.3177, which is smaller than the optimal value of 6006.4589 in the above algorithm. It shows that the algorithm can obtain better results in many repeated experiments and proves that the algorithm has a better stability. The median value of the optimal value obtained from 100 experiments is 5882.6562, which is smaller than the minimum median value of 5892.4465 in the above algorithm, indicating better stability of the algorithm. The time of 100 experimental results is only 2.3047 s. Compared with the shortest time of 2.5270 s in the above algorithm, the time can be shortened by 9%, indicating that the algorithm has high optimization speed and low time complexity. Through the comparative analysis of the above performance, it is proved that the GPSO proposed in this paper can obtain better optimal value and has good performance in stability and efficiency.

In addition, Fig. 4 shows the convergence performance of each algorithm in solving pressure vessel design problem. It can be seen from Fig. 4 that the GPSO proposed in this paper has a higher convergence speed compared with other algorithms. Through the comparative analysis of the above performance, it is proved that the GPSO proposed in this paper can get a better optimal value and has good performance in stability, convergence speed and time overhead.

Fig. 4
figure 4

The convergence performance of each algorithm in solving pressure vessel design problem

Full size image

4.2.2 Welded beam problem

The welded beam design problem is also a classic optimization problem. The objective is to find the minimum fabricating cost of the welded beam subject to constraints on shear stress (τ), bending stress in the beam (θ), buckling load on the bar (Pc), the end deflection of the beam (δ), and side constraint; the design of welded beam is shown in Fig. 5. This problem has four variables that need to be optimized, namely the thickness of the welded layer h, the length of the welded layer l, the width of the beam t, and the thickness of the beam b. The objective function and constraints of the problem are expressed as follows:

$$ x = \left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right] = \left[ {h,l,t,b} \right] $$
(27)
$$ {\text{Min}}f\left( x \right) = 1.10471x_{1}^{2} x_{2} + 0.04811x_{3} x_{4} \left( {14 + x_{2} } \right) $$
(28)
Fig. 5
figure 5

The design of the welded beam

Full size image

s.t.

$$ g_{1} \left( x \right) = \tau \left( x \right) - \tau_{\max } \le 0 $$
(29)
$$ g_{2} \left( x \right) = \sigma \left( x \right) - \sigma_{\max } \le 0 $$
(30)
$$ g_{3} \left( x \right) = x_{1} - x_{4} \le 0 $$
(31)
$$ g_{4} \left( x \right) = 0.125 - x_{1} \le 0 $$
(32)
$$ g_{5} \left( x \right) = \delta \left( x \right) - 0.25 \le 0 $$
(33)
$$ g_{6} \left( x \right) = P - P_{c} \left( x \right) \le 0 $$
(34)
$$ g_{7} \left( x \right) = 0.10471x_{1}^{2} + 0.04811x_{3} x_{4} \left( {14 + x_{2} } \right) - 5 \le 0 $$
(35)
$$ 0.1 \le x_{1} ,x_{4} \le 2 $$
(36)
$$ 0.1 \le x_{2} ,x_{3} \le 10 $$
(37)

where \(\tau \left( x \right)\) is the shear stress in the weld, \(\tau_{\max }\) is the allowable shear stress of the weld (= 13600 psi), \(\sigma \left( x \right)\) is the normal stress in the beam, \(\sigma_{\max }\) is the allowable normal stress for the beam material (= 30000 psi), \(P_{c} \left( x \right)\) is the bar buckling load, P is the load (= 6000 lb), and \(\delta \left( x \right)\) is the beam end deflection:

$$ \tau \left( x \right) = \sqrt {\tau_{1}^{2} + 2\tau_{1} \tau_{2} \left( {\frac{{x_{2} }}{2R}} \right) + \tau_{2}^{2} } $$
(38)
$$ \tau_{1} = \frac{P}{{\sqrt 2 x_{1} x_{2} }} $$
(39)
$$ \tau_{2} = \frac{MR}{J} $$
(40)
$$ M = P\left( {L + \frac{{x_{2} }}{2}} \right) $$
(41)
$$ J = 2\left\{ {\sqrt 2 x_{1} x_{2} \left[ {\frac{{x_{2}^{2} }}{2} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } \right]} \right\} $$
(42)
$$ R = \sqrt {\frac{{x_{2}^{2} }}{4} + \left( {\frac{{x_{1} + x_{3} }}{2}} \right)^{2} } $$
(43)
$$ \sigma \left( x \right) = \frac{6PL}{{Ex_{3}^{3} x_{4} }} $$
(44)
$$ P_{c} \left( x \right) = \frac{{4.013E\sqrt {\frac{{x_{3}^{2} x_{4}^{6} }}{36}} }}{{L^{2} }}\left( {1 - \frac{{x_{3} }}{2L}\sqrt{\frac{E}{4G}} } \right) $$
(45)
$$ G = 12 \times 10^{6} \;{\text{psi}}, E = 30 \times 10^{6} \;{\text{psi}},P = 6000\;{\text{lb}},L = 14\;{\text{in}} $$
(46)

This paper uses this problem to test the performance of the proposed GPSO algorithm and compares it with several latest GPSO algorithms. The comparison results are shown in Tables 6 and 7.

Table 6 Comparison of the optimal solution for welded beam design problem found by different algorithms
Full size table
Table 7 Performance of different algorithms for welded beam design problem
Full size table

In Table 6, the optimal value of GPSO proposed in this paper is 1.7249; this value is the same as the optimal value obtained by the existing algorithm, indicating that the algorithm can get a good optimal value. At this time, the parameter is: [x1, x2, x3, x4] = [0.2057, 3.4705, 9.0366, 0.2057], which is within the constraint range of the parameter and meets the parameter requirements. The constraint result obtained by substituting the parameters into the constraint equations is: [g1, g2, g3, g4, g5, g6, g7] = [0, − 7.2760e−12, − 2.2204e−16, − 3.4330, − 0.0807, − 0.2355, 0], which also satisfies the constraint condition. Through comparative analysis, it is proved that the optimization algorithm proposed in this paper can obtain a better optimal value to welded beam design problem.

Table 7 shows the algorithm performance of each algorithm in solving welded beam design problem. The optimal value, average value and median value of GPSO proposed in this paper are all 1.7249, which are the same as the optimal value obtained by the existing algorithm, indicating that the algorithm can get a good optimal value and have a good stability. The standard deviation is 6.6979e−6, which is smaller than the minimum deviation of 3.4796E−05 in the above algorithm, indicating that the stability of the algorithm is better. The worst value of the optimal value obtained from 100 experiments is 1.7251, which is smaller than the minimum worst value of 1.7255 in the above algorithm, indicating better accuracy of the algorithm. The time of 100 experimental results is only 5.1190 s. Compared with the shortest time of 5.2413 s in the above algorithm, the time can be shortened by 2.3%, indicating that the algorithm has high optimization speed and low time complexity. Through the comparative analysis of the above performance, it is proved that the GPSO proposed in this paper can obtain better optimal value and has good performance in stability and efficiency.

In addition, Fig. 6 shows the convergence performance of each algorithm in solving welded beam design problem. It can be seen from Fig. 6 that the GPSO proposed in this paper has a higher convergence speed compared with other algorithms. Through the comparative analysis of the above performance, it is proved that the GPSO proposed in this paper can get a better optimal value and has good performance in stability, convergence speed and time overhead.

Fig. 6
figure 6

The convergence performance of each algorithm in solving welded beam design problem

Full size image

4.2.3 Gear train problem

Gear train design problem is also a common optimization problem in engineering. The optimization goal is to make the gear transmission ratio reach or close to the given transmission ratio by optimizing the number of gear teeth. The optimized variable is the number of teeth of 4 gears (gear range [12, 60]). The objective function and constraints of the problem are expressed as follows:

$$ x = \left[ {x_{1} ,x_{2} ,x_{3} ,x_{4} } \right] = \left[ {T_{1} ,T_{2} ,T_{3} ,T_{4} } \right] $$
(47)
$$ {\text{Min}}f\left( x \right) = \left( {\frac{1}{6.931} - \frac{{x_{1} x_{2} }}{{x_{3} x_{4} }}} \right)^{2} $$
(48)
$$ \begin{aligned}&{\text{s.t.}}\\& 12 \le x_{1} ,x_{2} ,x_{3} ,x_{4} \le 60\end{aligned} $$
(49)
$$ x_{i} \in Z^{ + } $$
(50)

This paper uses this problem to test the performance of the proposed GPSO algorithm and compares it with several latest GPSO algorithms. The comparison results are shown in Tables 8 and 9.

Table 8 Comparison of the optimal solution for gear train design problem found by different algorithms
Full size table
Table 9 Performance of different algorithms for gear train design problem
Full size table

In Table 8, the result of using the GPSO proposed in this paper to optimize the problem is: 2.7009e−12, the parameter is: [x1, x2, x3, x4] = [19, 16, 43, 49]. Since the parameters of this problem are finite integers, the optimal value is known. The significance of solving this optimization problem is to compare the advantages and disadvantages of the algorithms by comparing the performance of the algorithms.

Table 9 shows the algorithm performance of each algorithm in solving gear train design problem. The optimal value and median value of GPSO proposed in this paper are all 2.7009E−12, which are the same as the optimal value obtained by the existing algorithm, the average value is 5.1431E−11 which is smaller than the minimum optimal value of 1.9522E−10 in the above algorithm, indicating that the algorithm can get a good optimal value and have a good stability. The standard deviation is 8.8063E−11, which is smaller than the minimum deviation of 4.1787E−10 in the above algorithm, indicating that the stability of the algorithm is better. The worst value of the optimal value obtained from 100 experiments is 2.3576E−09, which is the same as the optimal value obtained by the existing algorithm, indicating good accuracy of the algorithm. The time of 100 experimental results is only 2.3258 s. Compared with the shortest time of 2.3780 s in the above algorithm, the time can be shortened by 2.2%, indicating that the algorithm has high optimization speed and low time complexity. Through the comparative analysis of the above performance, it is proved that the GPSO proposed in this paper can obtain better optimal value and has good performance in stability and efficiency.

In addition, Fig. 7 shows the convergence performance of each algorithm in solving gear train design problem. It can be seen from Fig. 7 that the GPSO proposed in this paper has a higher convergence speed compared with other algorithms. Through the comparative analysis of the above performance, it is proved that the GPSO proposed in this paper can get a better optimal value and has good performance in stability, convergence speed and time overhead.

Fig. 7
figure 7

The convergence performance of each algorithm in solving gear train design problem

Full size image

In summary, through the comparative analysis of the results of the classical nonlinear multi-constrained optimization problem and the classical multi-constrained optimization problems in practical engineering, GPSO proposed in this paper has obvious advantages over other GPSO algorithms in solving the multi-constrained optimization problem in terms of accuracy, stability, convergence speed and time overhead.

5 Conclusion

In this paper, a parallel GPSO algorithm is proposed based on the high efficiency of PSO and the global optimization ability of GA. This algorithm takes PSO as the main body, only when gbest has not changed for many generations, GA is enabled to replace PSO to update the particles and help the particles jump out of the local optimum. Since PSO has memory, GA does not destroy the found optimal value. In addition, this paper compares the performance of GPSO algorithm with several newly proposed algorithms on several multi-constrained optimization problems (Himmelblau’s nonlinear optimization problem, pressure vessel design problem, welded beam design problem and gear train design problem) and evaluates the performance of the proposed algorithms with optimal value, average value, median value, worst value, standard deviation, time overhead and convergence speed. The results show that the GPSO proposed in this paper can get a better optimal value and has good performance in stability, convergence speed and time overhead. It shows that GPSO can ensure the effectiveness of solving multi-constrained optimization problems, ensure the accuracy of optimization results and the high speed of convergence.

This algorithm is only a basic version of the parallel GPSO algorithm. In fact, due to the high compatibility of the GPSO algorithm, it can continue to integrate other latest algorithms to improve the optimization performance and speed of the algorithm. In the future, the algorithm will continue to be developed and studied to improve its performance and speed, and the algorithm will be applied to various complex engineering optimization design to solve various problems in practice.