1 Introduction

Composite media have been widely used because of the high performance demands of engineering devices. However, in the interface of two different materials there exists stress concentration occurred by the mismatch of material properties, especially in the environment of high-temperature change. Therefore, the concept of Functional Graded Material (FGM) was introduced to simultaneously reduce thermal expansion mismatch [1], increase interface bonding strength [2, 3], and enhance coating toughness [4].

Literatures corresponding to FGM plates subjected to thermal loads have been rapidly increased recently. Lee and Erodgan [5] studied the exponentially metal-rich, ceramic-rich, and linear FGMs under uniform thermal loading and showed that the metal-rich has the lowest stress singularity. Chi and Chung [6] evaluated the stress intensity factors of cracked coating–substrate composite media by the finite element method, and indicated if the material strength of the coating is weaker than that of the substrate, although the use of the S-type functionally graded material can eliminate the stress singularity on the interfaces, the S-type functionally graded material that behaves like a bridge connecting the material difference of the coating and substrate will help the crack further extends into the substrate. Based on the classical plate theory and Fourier series expansion, Chung and Chang [7] obtained the series solutions for power-law FGM, sigmoid FGM, and exponential FGM plates with the coefficient of thermal expansion varying continuously throughout the thickness direction subjected to linear temperature change in the z direction. The mechanical behaviors of simply supported beams made of functionally graded materials (FGM) under an in-plane loading was investigated by Ma and Lee [8], indicating that the response of load–frequency for the beams is quite different from what was observed in the analysis for beams made of pure materials when effects of both the transverse shear deformation and the temperature dependent material properties are simultaneously taken into account. Chareonsuk [9] used a high-order control volume finite element method to explore thermal stress analysis for FGM structural components subjected to steady-state thermal and mechanical loads at steady state with the unstructured mesh capability for arbitrary-shaped domain. Ghannadpour [10] applied a finite strip method to analyze the buckling behavior of rectangular functionally graded plates (FGPs) under thermal loadings, and discussed the effects of geometrical parameters and material properties on the FGPs’ buckling temperature difference. Thermal effect on buckling and free vibration behavior of functionally graded (FG) microbeams based on classical and first order shear deformation beam theories to count for the effect of shear deformations is presented by Nateghi [11], indicating that higher temperature changes signify size dependency of FG microbeam. Tahvilian [12] examined the thermal residual stress distribution in a functionally graded cemented tungsten carbide (FG WC– Co) hollow cylinder with an emphasis on the effects of key variables, such as gradient profile and gradient thickness on the magnitude and distribution of the stress field, and pointed that the effect of gradient thickness. By the investigation of two-dimensional thermoelastic sliding frictional contact of functionally graded material (FGM) coated half-plane under the plane strain deformation, Liu [13] showed that the distribution of the contact stress can be altered and therefore the thermoelastic contact damage can be modified by adjusting the gradient index, Peclet number and friction coefficient. To gain better understanding of the thermo-mechanical behavior of layered structures, Liu [14] investigated the problem of a finite line bond between two orthotropic functionally graded strips under thermal loading, by using Fourier transforms technique. Zhang et al. [15] applied to study the mechanical and thermal buckling behaviors of ceramic–metal functionally grade plates and to investigate the influences of volume fraction exponent, boundary condition, length-to-thickness ratio and loading type on the buckling behaviors of functionally grade plates. Taking into account the effects of transverse shear strains as well as the transverse normal strain, Zenkour [16] refined plate theory as well as different plate theories to study the thermoelastic response of multilayered cross-ply laminates and angle-ply sandwich plates resting on Pasternak’s or Winkler’s elastic foundation. Assuming that the material properties depended on the temperature vary in the thickness direction by a simple power law distribution, Parandvar and Farid [17] studied large amplitude vibration of functionally graded material (FGM) plates subjected to combined random pressure and thermal load using finite element modal reduction method. Kulikov and Plotnikova [18] developed the method of sampling surfaces and its implementation for the three-dimensional steady-state problem of thermoelasticity for laminated functionally graded plates subjected to thermomechanical loading and indicated that sampling surfaces method can be applied efficiently to the 3D stress analysis for thermoelastic laminated FG plates with a specified accuracy utilizing the sufficient number of sampling surfaces. Trabelsi, et al. [19] investigated geometrically nonlinear post-buckling responses of Functionally Graded Material shell structures exposed to uniform, linear and nonlinear temperature distributions through the thickness direction based on a modified first order shear deformation theory. And the effect the geometrical parameters, the volume fraction index and boundary conditions on nonlinear responses are performed. A hybrid genetic algorithm with the complex method is developed by Ding and Wu [20] for the optimization of the material composition of a multi-layered functionally graded material plate with temperature-dependent material properties in order to minimize the thermal stresses induced in the plate when it is subjected to steady-state thermal loads. Sator et al. [21] presented the development of completely 2D formulation for bending of functionally graded plates subjected to stationary thermal loading. Zhang et al. [22] investigated the dynamic thermal buckling and postbuckling of imperfect functionally graded material (FGM) annular plates based on the nonlinear plate theory. And the effects of the loads, the material gradient and the initial geometric imperfections on the dynamic responses and the buckling critical temperatures of the FGM annular plates are analyzed in detail. Liew et al. [23] delt with the linear and nonlinear vibration analysis of a three-layercoating-FGM-substrate cylindrical panel with general boundary conditions and subjected to a temperature gradient across the thickness due to steady heat conduction. Wu et al. [24] investigated the parametric instability of functionally graded graphene reinforced nanocomposite plates that undergo a periodic uniaxial in-plane force and a uniform temperature rise, and found that the addition of a small amount of graphene nanoplatelets (GPLs) reinforcements considerably increases the critical buckling load and natural frequencies. Consequently, thermoelastic analysis of functionally graded material reinforced with graphene nanoplatelet (GPLs) was further studied by Yang et al. for circular and annular plates [25], for elliptical plates [26], and for rectangular plates [27].

FGMs may be utilized to plate structures in engineering applications as a thermal barrier. Hence understanding the mechanical behavior of the thermal barrier is important in assessing the safety of FGM plate structures. It is well known that the closed-form solutions can provide a much better understanding of the thermo-mechanical behavior of FGM plates. In this study, based on the Fourier series expansion, the closed-form solutions to the problem of simply-supported rectangular FGM plates subjected to temperature distribution change in the x- or z-direction is developed and proved by finite element calculation. To the authors’ best knowledge, the closed-form solutions to the problem concerned that is not found in the literature.

2 Governing equations of FGM plates under thermal Loading

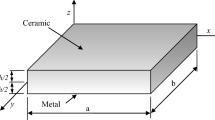
Consider a simply-supported, medium-thick, rectangular FGM plate with uniform thickness exposed to a temperature change \(T(x,y,z)\). It is assumed that the thickness of the medium-thick FGM plate is in the range \(\frac{1}{20}\) ~ \(\frac{1}{100}\) of its span approximately. Then the plate is thick enough to carry the transverse load, and the plate is not so thick that the transverse shear deformation can be neglected [28]. Further assume that the through-thickness functionality of material properties is graded. For the non-homogeneous elastic FGM plate, the stress–strain relation under thermal loading \(T(x,y,z)\) based on the assumptions of small deformation is [7]:

$$\begin{aligned} \left\{ {\begin{array}{*{20}c} {\sigma _{x} } \\ {\sigma _{y} } \\ {\tau _{{xy}} } \\ \end{array} } \right\} = & \frac{{E(z)}}{{1 - \nu (z)^{2} }}\left[ {\begin{array}{*{20}c} 1 & {\nu (z)} & 0 \\ {\nu (z)} & 1 & 0 \\ 0 & 0 & {(1 - \nu (z))/2} \\ \end{array} } \right]\left\{ {\begin{array}{*{20}c} {\varepsilon _{x} } \\ {\varepsilon _{y} } \\ {\gamma _{{xy}} } \\ \end{array} } \right\} \\ - & \frac{{E(z)\alpha (z)T(x,y,z)}}{{1 - \nu (z)}}\left\{ {\begin{array}{*{20}c} 1 \\ 1 \\ 0 \\ \end{array} } \right\} \\ \end{aligned}$$
(1)

By the definitions of the in-plane axial forces \((N_{x} ,N_{y} ,N_{xy} ) = \int_{{ - h_{2} }}^{{h_{{ 1}} }} {(\sigma_{x} ,\sigma_{y} ,\tau_{xy} )dz}\) and the bending moments \((M_{x} ,M_{y} ,M_{xy} ) = \int_{{ - h_{2} }}^{{h_{{ 1}} }} {(z\sigma_{x} ,z\sigma_{y} ,z\tau_{xy} )dz}\), the in-plane axial forces and the bending moments expressed in matrix forms are:

$$\left\{ N \right\} = [A]\left\{ {\varepsilon_{0} } \right\} + [B]\left\{ \kappa \right\} - \{ N^{\Delta T} \}$$
(2)
$$\left\{ M \right\} = [B]\left\{ {\varepsilon_{0} } \right\} + [C]\left\{ \kappa \right\} - \{ M^{\Delta T} \}$$
(3)

where \(\{ N\} = \{ N_{x} ,N_{y} ,N_{xy} \}^{T}\); \(\{ M\} = \{ M_{x} ,M_{y} ,M_{xy} \}^{T}\); \(\{ \varepsilon_{0} \} = \{ \varepsilon_{x0} ,\varepsilon_{y0} ,\gamma_{xy0} \}^{T}\) are the strains at the neutral surface; \(\{ \kappa \} = \{ \kappa_{x} ,\kappa_{y} ,\kappa_{xy} \}^{T}\) are curvatures of the FGM plate; \(\{ N^{\Delta T} \} = \{ N^{\Delta T} ,N^{\Delta T} ,0\}^{T}\) and \(\{ M^{\Delta T} \} = \{ M^{\Delta T} ,M^{\Delta T} ,0\}^{T}\) are temperature dependent quantities in which the entries \(N^{\Delta T}\), \(M^{\Delta T}\) are of the following forms:

$$N^{\Delta T} = \int_{{ - h_{2} }}^{{h_{1} }} {\frac{E(z)\alpha (z)}{{1 - \nu (z)}}T(x,y,z)dz}$$
(4)
$$M^{\Delta T} = \int_{{ - h_{2} }}^{{h_{1} }} {\frac{zE(z)\alpha (z)}{{1 - \nu (z)}}} T(x,y,z)dz$$
(5)

where \(h_{1}\) and \(h_{2}\) are the distances of the neutral surface to the bottom and top surfaces of the FGM plate. The entries of \([A], \, [B], \, [C]\) in Eqs. (2) and (3) are the integration of the material properties of the FGM plate:

$$(A_{ij} ,B_{ij} ,C_{ij} ) = \int_{{ - h_{2} }}^{{h_{1} }} {(1,z,z^{2} )\frac{E(z)}{{1 - v(z)^{2} }}dz}$$
(6)

By introducing the stress function \(\phi \left( {x,y} \right)\) such that

$$N_{x} = \frac{{\partial^{2} \phi }}{{\partial y^{2} }},N_{y} = \frac{{\partial^{2} \phi }}{{\partial x^{2} }},N_{xy} = - \frac{{\partial^{2} \phi }}{\partial x\partial y}$$
(7)

the consequently gives zero under thermal loading is expressed in terms of the deflection \(w\) and the stress function \(\phi \left( {x,y} \right)\) as followings [29]:

$$\begin{aligned} Q_{{12}} \frac{{\partial ^{4} \phi }}{{\partial x^{4} }} + & \left( {2Q_{{11}} - 2Q_{{66}} } \right)\frac{{\partial ^{4} \phi }}{{\partial x^{2} \partial y^{2} }} + Q_{{12}} \frac{{\partial ^{4} \phi }}{{\partial y^{4} }} + S_{{11}} \frac{{\partial ^{4} w}}{{\partial x^{4} }} \\ + & \,\left( {2S_{{12}} + 4S_{{66}} } \right)\frac{{\partial ^{4} w}}{{\partial x^{2} \partial y^{2} }} + S_{{11}} \frac{{\partial ^{4} w}}{{\partial y^{4} }} \\ = & - (Q_{{11}} + Q_{{12}} )\left( {\frac{{\partial ^{2} N^{T} }}{{\partial x^{2} }} + \frac{{\partial ^{2} N^{T} }}{{\partial y^{2} }}} \right) - \left( {\frac{{\partial ^{2} M^{T} }}{{\partial x^{2} }} + \frac{{\partial ^{2} M^{T} }}{{\partial y^{2} }}} \right) \\ \end{aligned}$$
(8)

And the compatibility equation of an FGM plates, \(\frac{{\partial^{2} \varepsilon_{x} }}{{\partial y^{2} }} + \frac{{\partial^{2} \varepsilon_{y} }}{{\partial x^{2} }} = \frac{{\partial^{2} \gamma_{xy} }}{\partial x\partial y}\), can be rewritten in terms of stress function \(\phi \left( {x,y} \right)\) and the deflection \(w\) as:

$$\begin{gathered} P_{{11}} \frac{{\partial ^{4} \phi }}{{\partial x^{4} }} + \left( {2P_{{12}} - P_{{66}} } \right)\frac{{\partial ^{4} \phi }}{{\partial x^{2} \partial y^{2} }} + P_{{11}} \frac{{\partial ^{4} \phi }}{{\partial y^{4} }} - Q_{{12}} \frac{{\partial ^{4} w}}{{\partial x^{4} }} - 2\left( {Q_{{11}} - Q_{{66}} } \right)\frac{{\partial ^{4} w}}{{\partial x^{2} \partial y^{2} }} - Q_{{12}} \frac{{\partial ^{4} w}}{{\partial y^{4} }} \hfill \\ = - (P_{{11}} + P_{{12}} )\left( {\frac{{\partial ^{2} N^{T} }}{{\partial x^{2} }} + \frac{{\partial ^{2} N^{T} }}{{\partial y^{2} }}} \right) \hfill \\ \end{gathered}$$
(9)

where the definitions of quantities \(Q_{ij}\), \(S_{ij}\) and \(P_{ij}\) can be found in Chi and Chung [29]. The equilibrium equations, Eq. (8), and the compatibility equation, Eq. (9), provide the simultaneous equations to solve for the stress function \(\phi \left( {x,y} \right)\) and the deflection \(w\) for an FGM plate subjected to thermal loads.

3 Series solution of simply-supported FGM plates under thermal loading

Consider a simply-supported rectangular FGM plate with length \(a\), width \(b\), and uniform thickness \(h\) subjected to a temperature change \(T(x,y,z)\). Further assume that the temperature change \(T(x,y,z)\) can be expressed as \(T(x,y,z) = F(z)G(x,y)\) where \(F(z)\) and \(G(x,y)\) are the temperature change in the z-direction and x–y plane, respectively. For the simply-supported FGM plates, the transverse and tangential components of displacements are restricted to move but the axial components are allowed on all four edges. Therefore, the boundary conditions of the simply supported rectangular FGM plate are:

$$\left\{ {\begin{array}{*{20}c} {\upsilon = w = 0} \\ {N_{x} = M_{x} = 0} \\ \end{array} } \right.\begin{array}{*{20}c} {} & {at} & {x = 0} & {and} & {x = a} \\ \end{array}$$
(10a)
$$\left\{ {\begin{array}{*{20}c} {u = w = 0} \\ {N_{y} = M_{y} = 0} \\ \end{array} } \right.\begin{array}{*{20}c} {} & {at} & {y = 0} & {and} & {y = b} \\ \end{array}$$
(10b)

First, expanding the thermal load \(T(x,y,z)\) into Fourier series as follows:

$$T(x,y,z) = F(z)G(x,y) = F(z)\sum {\sum {T_{mn} } } \sin (k_{1} x)\sin (k_{2} y)$$
(11a)

where

$$T_{mn} = \frac{4}{ab}\int {\int {G\left( {x,y} \right)} } \sin (k_{1} x)\sin (k_{2} y)dxdy$$
(11b)

and \(k_{1} = m\pi /a\), \(k_{2} = n\pi /b\). Then, substituting Eq. (11) into Eqs. (4) and (5) yields the temperature dependent quantities \(N^{\Delta T}\) and \(M^{\Delta T}\):

$$N^{\Delta T} = N^{*} \sum\limits_{m} {\sum\limits_{n} {T_{mn} } } \sin (k_{1} x)\sin (k_{2} y)$$
(12a)
$$M^{\Delta T} = M^{*} \sum\limits_{m} {\sum\limits_{n} {T_{mn} } } \sin (k_{1} x)\sin (k_{2} y)$$
(12b)

where

$$N^{*} = \int_{{ - h_{2} }}^{{h_{1} }} {\frac{E(z)\alpha (z)F(z)}{{1 - \nu (z)}}} dz$$
(13a)
$$M^{*} = \int_{{ - h_{2} }}^{{h_{1} }} {\frac{zE(z)\alpha (z)F(z)}{{1 - \nu (z)}}} dz$$
(13b)

The quantities \(N^{*}\), \(M^{*}\) represent axial force and bending moment caused by temperature change, called thermal axial force and thermal bending moment in this study. To satisfy the loading condition in Eq. (11) and the boundary conditions in Eq. (10), the deflection function \(w\) and the stress function \(\phi \left( {x,y} \right)\) of the FGM plate can be expressed in the forms of:

$$w(x,y) = \sum\limits_{m} {\sum\limits_{n} {} } w_{mn} \sin (k_{1} x)\sin (k_{2} y)$$
(14a)
$$\phi (x,y) = \sum\limits_{m} {\sum\limits_{n} {} } \phi_{mn} \sin (k_{1} x)\sin (k_{2} y)$$
(14b)

where \(w_{mn}\) and \(\phi_{mn}\) are unknown constants. By substituting Eq. (14) into the equilibrium as well as the compatibility equations in Eqs. (8), (9), and then solving the simultaneous equations, one can obtain the coefficients \(w_{mn}\) and \(\phi_{mn}\):

$$w_{mn} = \left( {\frac{\xi J - K\eta }{{K^{2} + HJ}}} \right)T_{mn}$$
(15a)
$$\phi_{mn} = \left( {\frac{\xi K + H\eta }{{K^{2} + HJ}}} \right)T_{mn}$$
(15b)

where

$$H = S_{11} k_{1}^{4} + 2\left( {S_{12} + 2S_{66} } \right)k_{1}^{2} k_{2}^{2} + S_{11} k_{2}^{4}$$
(15c)
$$J = P_{11} k_{1}^{4} + \left( {2P_{12} - P_{66} } \right)k_{1}^{2} k_{2}^{2} + P_{11} k_{2}^{4}$$
(15d)
$$K = Q_{12} k_{1}^{4} + 2\left( {Q_{11} - Q_{66} } \right)k_{1}^{2} k_{2}^{2} + Q_{12} k_{2}^{4}$$
(15e)
$$\xi = \left[ {\left( {Q_{11} + Q_{12} } \right)N^{ * } + M^{ * } } \right]\left( {k_{1}^{2} + k_{2}^{2} } \right)$$
(15f)
$$\eta = N^{ * } (P_{11} + P_{12} )\left( {k_{1}^{2} + k_{2}^{2} } \right)$$
(15g)

Consequently, the strains at neutral surface are:

$$\begin{gathered} \varepsilon _{{x_{0} }} = \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{{mn}} }}{{K^{2} + HJ}}} } \left\{ {\left[ { - P_{{12}} \left( {\xi K + H\eta } \right) + Q_{{11}} \left( {\xi J - K\eta } \right)} \right]k_{1}^{2} } \right. \hfill \\ \left. {\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \,\left[ { - P_{{11}} \left( {\xi K + H\eta } \right) + Q_{{12}} \left( {\xi J - K\eta } \right)} \right]k_{2}^{2} } \right\}\sin (k_{1} x)\sin (k_{2} y) \hfill \\ \,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\, + \left( {P_{{11}} + P_{{12}} } \right)N^{ * } \sum\limits_{m} {\sum\limits_{n} {T_{{mn}} \sin (k_{1} x)\sin (k_{2} y)} } \hfill \\ \end{gathered}$$
(16a)
$$\begin{gathered} \varepsilon _{{y_{0} }} = \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{{mn}} }}{{K^{2} + HJ}}} } \left\{ {\left[ { - P_{{11}} \left( {\xi K + H\eta } \right) + Q_{{12}} \left( {\xi J - K\eta } \right)} \right]k_{1}^{2} } \right. \hfill \\ {\text{ }}\,\,\,\left. {\,\,\,\,\,\,\,\,\, + \left[ { - P_{{12}} \left( {\xi K + H\eta } \right) + Q_{{11}} \left( {\xi J - K\eta } \right)} \right]k_{2}^{2} } \right\}\sin (k_{1} x)\sin (k_{2} y) \hfill \\ {\text{ }}\,\,\,\,\,\,\,\,\,\,\,\, + \left( {P_{{11}} + P_{{12}} } \right)N^{ * } \sum\limits_{m} {\sum\limits_{n} {T_{{mn}} \sin (k_{1} x)\sin (k_{2} y)} } \hfill \\ \end{gathered}$$
(16b)
$$\gamma_{{xy_{0} }} = \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{mn} }}{{K^{2} + HJ}}\left[ {P_{66} \left( {\xi K + H\eta } \right) - 2Q_{66} \left( {\xi J - K\eta } \right)} \right]} } \times k_{1} k_{2} \cos (k_{1} x)\cos (k_{2} y)$$
(16c)

And the strain and stress fields of the FGM plate under thermal loads are found as:

$$\begin{gathered} \varepsilon _{x} = \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{{mn}} }}{{K^{2} + HJ}}} } \left\{ {\left[ { - P_{{12}} \left( {\xi K + H\eta } \right) + \left( {Q_{{11}} + z} \right)\left( {\xi J - K\eta } \right)} \right]k_{1}^{2} } \right. \hfill \\ {\text{ }}\left. {\,\,\,\,\,\,\,\,\,\,\, + \left[ { - P_{{11}} \left( {\xi K + H\eta } \right) + Q_{{12}} \left( {\xi J - K\eta } \right)} \right]k_{2}^{2} } \right\}\sin (k_{1} x)\sin (k_{2} y) \hfill \\ {\text{ }}\,\,\,\,\,\,\,\,\,\,\, + \left( {P_{{11}} + P_{{12}} } \right)N^{ * } \sum\limits_{m} {\sum\limits_{n} {T_{{mn}} \sin (k_{1} x)\sin (k_{2} y)} } {\text{ }} \hfill \\ \end{gathered}$$
(16d)
$$\begin{gathered} \varepsilon _{y} = \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{{mn}} }}{{K^{2} + HJ}}} } \left\{ {\left[ { - P_{{11}} \left( {\xi K + H\eta } \right) + Q_{{12}} \left( {\xi J - K\eta } \right)} \right]k_{1}^{2} } \right. \hfill \\ {\text{ }}\left. {\,\,\,\,\,\,\,\,\,\, + \left[ { - P_{{12}} \left( {\xi K^{ * } + H\eta } \right) + \left( {Q_{{11}} + z} \right)\left( {\xi J - K\eta } \right)} \right]k_{2}^{2} } \right\}\sin (k_{1} x)\sin (k_{2} y) \hfill \\ {\text{ }}\,\,\,\,\,\,\,\,\,\, + \left( {P_{{11}} + P_{{12}} } \right)N^{ * } \sum\limits_{m} {\sum\limits_{n} {T_{{mn}} \sin (k_{1} x)\sin (k_{2} y)} } {\text{ }} \hfill \\ \end{gathered}$$
(16e)
$$\gamma_{xy} = \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{mn} }}{{K^{2} + HJ}}\left[ {P_{66} \left( {\xi K + H\eta } \right) - 2\left( {Q_{66} + z} \right)\left( {\xi J - K\eta } \right)} \right]} } \times k_{1} k_{2} \cos (k_{1} x)\cos (k_{2} y$$
(16f)

and

$$\begin{gathered} \sigma _{x} = \frac{{E(z)}}{{1 - \nu (z)^{2} }}\sum\limits_{m} {\sum\limits_{n} {\frac{{T_{{mn}} }}{{K^{2} + HJ}}} } \left\{ {\left[ { - P_{{12}} \left( {\xi K + H\eta } \right) + \left( {Q_{{11}} + z} \right)\left( {\xi J - K\eta } \right)} \right]\left[ {k_{1}^{2} + \nu (z)k_{2}^{2} } \right]} \right. \hfill \\ {\text{ }}\left. {\,\,\,\,\,\,\,\,\,\, + \left[ { - P_{{11}} \left( {\xi K + H\eta } \right) + Q_{{12}} \left( {\xi J - K\eta } \right)} \right]\left[ {k_{2}^{2} + \nu (z)k_{1}^{2} } \right]} \right\}\sin (k_{1} x)\sin (k_{2} y) \hfill \\ {\text{ }}\,\,\,\,\,\,\,\,\,\, + \frac{{E(z)\alpha (z)}}{{1 - \nu (z)}}\left[ {\left( {P_{{11}} + P_{{12}} } \right)N^{ * } - F(z)} \right]\sum\limits_{m} {\sum\limits_{n} {T_{{mn}} \sin (k_{1} x)\sin (k_{2} y)} } \hfill \\ {\text{ }} \hfill \\ \end{gathered}$$
(16g)
$$\begin{gathered} \sigma _{y} = \frac{{E(z)}}{{1 - \nu (z)^{2} }}\sum\limits_{m} {\sum\limits_{n} {\frac{{T_{{mn}} }}{{K^{2} + HJ}}} } \left\{ {\left[ { - P_{{11}} \left( {\xi K + H\eta } \right) + Q_{{12}} \left( {\xi J - K\eta } \right)} \right]\left[ {k_{1}^{2} + \nu (z)k_{2}^{2} } \right]} \right. \hfill \\ {\text{ }}\left. {{\text{ }}\,\,\,\,\,\,\,\, + \left[ { - P_{{12}} \left( {\xi K + H\eta } \right) + \left( {Q_{{11}} + z} \right)\left( {\xi J - K\eta } \right)} \right]\left[ {k_{2}^{2} + \nu (z)k_{1}^{2} } \right]} \right\}\sin (k_{1} x)\sin (k_{2} y) \hfill \\ {\text{ }}\,\,\,\,\,\,\,\,\,\,\, + \frac{{E(z)}}{{1 - \nu (z)}}\left[ {\left( {P_{{11}} + P_{{12}} } \right)N^{ * } - F(z)} \right]\sum\limits_{m} {\sum\limits_{n} {T_{{mn}} \sin (k_{1} x)\sin (k_{2} y)} } \hfill \\ {\text{ }} \hfill \\ \end{gathered}$$
(16h)
$$\sigma_{{xy}} = \frac{{E(z)}}{2({1 - \nu (z) })}\sum\limits_{m} {\sum\limits_{n} {\frac{{T_{mn} }}{{K^{2} + HJ}}\left[ {P_{66} \left( {\xi K + H\eta } \right) - 2(Q_{66} + z)\left( {\xi J - K\eta } \right)} \right]} } \times k_{1} k_{2} \cos (k_{1} x)\cos (k_{2} y)$$
(16i)

With the aid of Eq. (7), the in-plane axial forces and the bending moments of the FGM plate subjected to thermal loads are also obtained:

$$\begin{gathered} N_{x} = \frac{{\partial ^{2} \phi }}{{\partial y^{2} }} \hfill \\ = - \sum\limits_{m} {\sum\limits_{n} {\left( {\frac{{\xi K + H\eta }}{{K^{2} + HJ}}} \right)k_{2}^{2} } } T_{{mn}} \sin (k_{1} x)\sin (k_{2} y) \hfill \\ \end{gathered}$$
(16j)
$$\begin{gathered} N_{y} = \frac{{\partial ^{2} \phi }}{{\partial x^{2} }} \hfill \\ = - \sum\limits_{m} {\sum\limits_{n} {\left( {\frac{{\xi K + H\eta }}{{K^{2} + HJ}}} \right)} } {\text{ }}k_{1}^{2} T_{{mn}} \sin (k_{1} x)\sin (k_{2} y) \hfill \\ \end{gathered}$$
(16k)
$$\begin{gathered} N_{{xy}} = - \frac{{\partial ^{2} \phi }}{{\partial x\partial y}} \hfill \\ = - \sum\limits_{m} {\sum\limits_{n} {\left( {\frac{{\xi K + H\eta }}{{K^{2} + HJ}}} \right)k_{1} k_{2} } } T_{{mn}} \cos (k_{1} x)\cos (k_{2} y) \hfill \\ \end{gathered}$$
(16l)

and

$$\begin{gathered} M_{x} = \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{{mn}} }}{{K^{2} + HJ}}} } \left\{ {\left[ {Q_{{12}} \left( {\xi K + H\eta } \right) + S_{{11}} \left( {\xi J - K\eta } \right)} \right]k_{1}^{2} } \right. \hfill \\ {\text{ }}\left. {{\text{ }}\,\,\,\,\,\,\,\,\,\, + \left[ {Q_{{11}} \left( {\xi K + H\eta } \right) + S_{{12}} \left( {\xi J - K\eta } \right)} \right]k_{2}^{2} } \right\}\sin (k_{1} x)\sin (k_{2} y) \hfill \\ {\text{ }}\,\,\,\,\,\,\,\,\,\,\,\, - \left[ {\left( {Q_{{11}} + Q_{{12}} } \right)N^{ * } + M^{ * } } \right]\sum\limits_{m} {\sum\limits_{n} {T_{{mn}} \sin (k_{1} x)\sin (k_{2} y)} } {\text{ }} \hfill \\ \end{gathered}$$
(16m)
$$\begin{gathered} M_{y} = \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{{mn}} }}{{K^{2} + HJ}}} } \left\{ {\left[ {Q_{{11}} \left( {\xi K + H\eta } \right) + S_{{12}} \left( {\xi J - K\eta } \right)} \right]k_{1}^{2} } \right. \hfill \\ {\text{ }}\left. {{\text{ }}\,\,\,\,\,\,\,\,\,\, + \left[ {Q_{{12}} \left( {\xi K + H\eta } \right) + S_{{11}} \left( {\xi J - K\eta } \right)} \right]k_{2}^{2} } \right\}\sin (k_{1} x)\sin (k_{2} y) \hfill \\ {\text{ }}\,\,\,\,\,\,\,\,\,\,\,\, - \left[ {\left( {Q_{{11}} + Q_{{12}} } \right)N^{ * } + M^{ * } } \right]\sum\limits_{m} {\sum\limits_{n} {T_{{mn}} \sin (k_{1} x)\sin (k_{2} y)} } {\text{ }} \hfill \\ \end{gathered}$$
(16n)
$$M_{xy} = \sum\limits_{m} {\sum\limits_{n} {\frac{{ - T_{mn} }}{{K^{2} + HJ}}\left[ {Q_{66} \left( {\xi K + H\eta } \right) + 2S_{66} \left( {\xi J - K\eta } \right)} \right]} } \times k_{1} k_{2} \cos (k_{1} x)\cos (k_{2} y)$$
(16o)

4 The solution of the FGM plate with constant Poisson’s ratio

Delale and Erdogan [30] indicated that the influence of the Poisson’s ratio on the deformation of the FGM plates will be much less than that of Young’s modulus. The same conclusion also obtained by Chi and Chung [31]. Therefore, this paragraph will derive the solutions for the FGM plates with Poisson’s ratio and the coefficient of thermal expansion being constant, but Young’s modulus varying in the thickness direction. Consequently, the relations of the quantities \(A_{ij}\),\(B_{ij}\), \(C_{ij}\), \(Q_{ij}\), \(S_{ij}\) and \(P_{ij}\) for the material with \(\alpha\),\(\nu =\) constant but \(E = E(z)\) can be simplified as follows:

$$A_{12} = \nu A_{11} ,A_{66} = (1 - \nu )A_{11} /2, B_{12} = \nu B_{11}$$
$$B_{66} = (1 - \nu )B_{11} /2,C_{12} = \nu C_{11} ,\,C_{66} = (1 - \nu )C_{11} /2$$
$$P_{11} = \frac{1}{{(1 - \nu^{2} )A_{11} }},P_{12} = - \nu P_{11} ,\,P_{66} = - 2(1 + \nu )P_{11}$$
$$Q_{11} = - \frac{{B_{11} }}{{A_{11} }},Q_{12} = 0,Q_{66} = Q_{11}$$
$$S_{11} = B_{11} Q_{11} + C_{11} , S_{12} = \nu S_{11} , S_{66} = (1 - \nu )S_{11} /2$$
(17)

Substituting Eq. (17) into Eq. (15) gives:

$$H = S_{11} \left( {k_{1}^{2} + k_{2}^{2} } \right)^{2} ,J = P_{11} \left( {k_{1}^{2} + k_{2}^{2} } \right)^{2} ,K = 0$$
(18)

Notably, if the origin of the z-axis of the FGM plates is located on the neutral surface, one can obtain \(B_{11} = 0\) and then eliminate stretching–bending coupling in FGM plates, indicated by Chung and Chen [32, 33]. Subsequently, the condition of \(B_{11} = 0\) further provides \(B_{12} = B_{66} = 0\), \(Q_{11} = Q_{12} = Q_{66} = 0\), and \(S_{11} = C_{11}\).

4.1 linear temperature change in the x–y plane

Assume that the temperature change of the FGM plate varies only in the x–y plane, i.e.,

$$T(x,y,z) = G(x,y) = \sum\limits_{m} {\sum\limits_{n} {T_{mn} } } \sin (k_{1} x)\sin (k_{2} y)$$
(19)

where \(T_{mn}\) can be evaluated from Eq. (11b). For the assumption of \(\alpha (z) = \alpha\), \(\nu (z) = \nu\), and \(F(z)\) = 1, the thermal axial force \(N^{*}\) and thermal bending moment \(M^{*}\) defined in Eq. (13) are simplified as:

$$N^{*} = (1 + \nu )\alpha A_{11} ,M^{*} = (1 + \nu )\alpha B_{11} = 0$$
(20)

and the parameters \(\xi\) and \(\eta\) are:

$$\xi = 0,\eta = \alpha \left[ {k_{1}^{2} + k_{2}^{2} } \right]$$
(21)

It is noted that the thermal bending moment \(M^{*} = 0\), Eq. (20), coincides with the phenomenon of FGM plates subjected to thermal change in the x–y plane. And the thermal axial force \(N^{*}\) is independent of Young’s modulus. By the use of Eqs. (14), (15), (18), (20) and (21), the deflection and the stress functions of the FGM plates with constant Poisson’s ratio and constant thermal expansion coefficient subjected to temperature change in the x–y plane are then found as:

$$w(x,y) = 0$$
(22a)
$$\phi (x,y) = (1 - \nu^{2} )\alpha A_{11} \sum\limits_{m} {\sum\limits_{n} {\frac{{T_{mn} }}{{k_{1}^{2} + k_{2}^{2} }}} } \sin (k_{1} x)\sin (k_{2} y)$$
(22b)

Finally, the strains, stresses, axial forces and the bending moments of the FGM plates with the material of \(E = E(z)\) are:

$$\varepsilon_{x} = \left( {1 + \nu } \right)\alpha \sum\limits_{m} {\sum\limits_{n} {k_{aa} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(23a)
$$\varepsilon_{y} = \left( {1 + \nu } \right)\alpha \sum\limits_{m} {\sum\limits_{n} {k_{bb} } } T_{mn} \sin (k_{1} x)\sin (k_{2} y)$$
(23b)
$$\gamma_{xy} = - 2\left( {1 + \nu } \right)\alpha \sum\limits_{m} {\sum\limits_{n} {k_{ab} } } T_{mn} \cos (k_{1} x)\cos (k_{2} y)$$
(23c)
$$\sigma_{x} = - \alpha E\left( z \right)\sum\limits_{m} {\sum\limits_{n} {k_{bb} } } T_{mn} \sin (k_{1} x)\sin (k_{2} y)$$
(23d)
$$\sigma_{y} = - \alpha E\left( z \right)\sum\limits_{m} {\sum\limits_{n} {k_{aa} } } T_{mn} \sin (k_{1} x)\sin (k_{2} y)$$
(23e)
$$\sigma_{xy} = - \alpha E\left( z \right)\sum\limits_{m} {\sum\limits_{n} {k_{ab} } } T_{mn} \cos (k_{1} x)\cos (k_{2} y)$$
(23f)
$$N_{x} = - (1 - \nu^{2} )\alpha A_{11} \sum\limits_{m} {\sum\limits_{n} {k_{bb} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(23g)
$$N_{y} = - (1 - \nu^{2} )\alpha A_{11} \sum\limits_{m} {\sum\limits_{n} {k_{aa} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(23h)
$$N_{xy} = - (1 - \nu^{2} )\alpha A_{11} \sum\limits_{m} {\sum\limits_{n} {k_{ab} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(23i)
$$M_{x} = M_{y} = M_{xy} = 0$$
(23j)

where

$$k_{aa} = \frac{{k_{1}^{2} }}{{k_{1}^{2} + k_{2}^{2} }},k_{bb} = \frac{{k_{2}^{2} }}{{k_{1}^{2} + k_{2}^{2} }},k_{ab} = \frac{{k_{1}^{{}} k_{2}^{{}} }}{{k_{1}^{2} + k_{2}^{2} }}$$
(23k)

The closed-form solution in Eq. (23) reveals if an FGM plate with constant \(\alpha {\text{ and }}\nu\) is subjected to temperature change in the x–y plane, the strains and axial forces are independent of Young’s modulus. The bending moment \(M_{x} = M_{y} = M_{xy} = 0\), as expected. Moreover, the stresses in Eq. (23) indicate that the stresses are a function of \(E(z)\), and hence the stresses along the thickness of the FGM plate have the same shapes as the corresponding variations of Young’s moduli.

4.2 linear temperature change in the z-direction

Consider the situation that the temperature change of the FGM plate varies in the z-direction, i.e.

$$T(x,y,z) = F(z)G(x,y) = F(z){\text{ with }}G(x,y) = 1$$
(24)

The temperature change \(\, G(x,y)\) equal to one gives \(T_{mn} = 16/mn\pi^{2}\) for \(m, \, n = 1, \, 3, \, 5, \, ....\). For the FGM plates with constant Poisson’s ratio \(\nu\) and constant thermal expansion coefficient \(\alpha\), the quantities \(H, \, J, \, K\) are the same as those given in Eqs. (15c–e), however the parameters \(\xi {\text{ and }}\eta\) become:

$$\xi = M^{*} (k_{1}^{2} + k_{2}^{2} ),\, \eta = \frac{{N^{*} }}{{(1 + \nu )A_{11} }}(k_{1}^{2} + k_{2}^{2} )$$
(25)

With the aid of Eqs. (14a) and (15a–b), the deflection of FGM plates with \(E = E(z)\) subjected to temperature change in the z-direction is:

$$w(x,y) = \frac{{M^{*} }}{{C_{11} }}\sum\limits_{m} {\sum\limits_{n} {\frac{{T_{mn} }}{{k_{1}^{2} + k_{2}^{2} }}} } \sin (k_{1} x)\sin (k_{2} y)$$
(26)

Consequently, the strain, stress, axial force, and bending moment fields are:

$$\varepsilon_{x} = \left( {\frac{{N^{*} }}{{A_{11} }} + \frac{{zM^{*} }}{{C_{11} }}} \right)\sum\limits_{m} {\sum\limits_{n} {k_{aa} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(27a)
$$\varepsilon_{y} = \left( {\frac{{N^{*} }}{{A_{11} }} + \frac{{zM^{*} }}{{C_{11} }}} \right)\sum\limits_{m} {\sum\limits_{n} {k_{bb} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(27b)
$$\gamma_{xy} = - 2\left( {\frac{{N^{*} }}{{A_{11} }} + \frac{{zM^{*} }}{{C_{11} }}} \right)\sum\limits_{m} {\sum\limits_{n} {k_{ab} T_{mn} \cos (k_{1} x)\cos (k_{2} y)} }$$
(27c)
$$\sigma_{x} = \frac{E(z)}{{(1 - \nu^{2} )}}\sum\limits_{m} {\sum\limits_{n} {\left\{ {\left( {\frac{{N^{*} }}{{A_{11} }} + \frac{{zM^{*} }}{{C_{11} }}} \right)k_{\nu b} - (1 + \nu )\alpha F(z)} \right\}} } T_{mn} \sin (k_{1} x)\sin (k_{2} y)$$
(27d)
$$\sigma_{y} = \frac{E(z)}{{(1 - \nu^{2} )}}\sum\limits_{m} {\sum\limits_{n} {\left\{ {\left( {\frac{{N^{*} }}{{A_{11} }} + \frac{{zM^{*} }}{{C_{11} }}} \right)k_{\nu a} - (1 + \nu )\alpha F(z)} \right\}} } T_{mn} \sin (k_{1} x)\sin (k_{2} y)$$
(27e)
$$\tau_{xy} = - \frac{E(z)}{{(1 + \nu )}}\sum\limits_{m} {\sum\limits_{n} {\left( {\frac{{N^{*} }}{{A_{11} }} + \frac{{zM^{*} }}{{C_{11} }}} \right)k_{ab} } } T_{mn} \cos (k_{1} x)\cos (k_{2} y)$$
(27f)
$$N_{x} = - (1 - \nu )N^{*} \sum\limits_{m} {\sum\limits_{n} {k_{bb} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(27g)
$$N_{y} = - (1 - \nu )N^{*} \sum\limits_{m} {\sum\limits_{n} {k_{aa} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(27h)
$$N_{xy} = - (1 - \nu )N^{*} \sum\limits_{m} {\sum\limits_{n} {k_{ab} T_{mn} \cos (k_{1} x)\cos (k_{2} y)} }$$
(27i)
$$M_{x} = - (1 - \nu )M^{*} \sum\limits_{m} {\sum\limits_{n} {k_{bb} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(27j)
$$M_{y} = - (1 - \nu )M^{*} \sum\limits_{m} {\sum\limits_{n} {k_{aa} T_{mn} \sin (k_{1} x)\sin (k_{2} y)} }$$
(27k)
$$M_{xy} = - (1 - \nu )M^{*} \sum\limits_{m} {\sum\limits_{n} {k_{ab} T_{mn} \cos (k_{1} x)\cos (k_{2} y)} }$$
(27l)

where \(k_{\nu b} = \frac{{k_{1}^{2} + \nu k_{2}^{2} }}{{k_{1}^{2} + k_{2}^{2} }}\), \(k_{\nu a} = \frac{{\nu k_{1}^{2} + k_{2}^{2} }}{{k_{1}^{2} + k_{2}^{2} }}\). It is noted from Eq. (27) that the strains and stresses along the thickness of the FGM plate with constant \(\alpha {\text{ and }}\nu\) subjected to temperature change in the z-direction are functions of z and \(zE(z)\), respectively, and herein the stress curves along the thickness of the FGM plate will be the shapes of \(zE(z)\). Furthermore, the axial forces and the bending moment are functions of thermal axial force \(N^{*}\) and thermal bending moment \(M^{*}\) respectively. The quantities \(N^{*}\) and \(M^{*}\) are temperature-dependent and will be evaluated in Sect. 5.2 for given temperature change.

4.3 Material gradation

The Young’s modulus of the considered FGM plates is assumed to vary continuously in the thickness direction (z-axis) based on power-law function (simply called P-FGM), sigmoid function (S-FGM), or exponential function (E-FGM).

4.3.1 P-FGM plates

The Young’s modulus of P-FGM plates is defined by:

$$E\left( z \right) = g(z)E_{1} + \left[ {1 - g(z)} \right]E_{2} ,{\text{with }}g\left( z \right) = \left( {\frac{{z + h_{2} {\kern 1pt} }}{h}} \right)^{p}$$
(28)

where \(E_{1}\) and \(E_{2}\) are Young’s moduli of the lowest (\(z = h_{1}\)) and top surfaces (\(z = - h_{2}\)) of the FGM plate, respectively. The quantity \(p\) is the material parameter. By solving the simultaneous equations of \(B_{11} = 0\) and \(h = h_{1} + h_{2}\) yields

$$\begin{gathered} h_{1} = \frac{{hE_{2} \left[ {2\left( {\overline{E} - 1} \right) + \left( {p + 1} \right)\left( {p + 2} \right)} \right]}}{{2\left( {p + 2} \right)(\overline{E} + p)}} \hfill \\ h_{2} = \frac{{hE_{2} \left( {p + 1} \right)\left[ {2\left( {\overline{E} - 1} \right) + \left( {p + 2} \right)} \right]}}{{2\left( {p + 2} \right)(\overline{E} + p)}} \hfill \\ \end{gathered}$$
(29)

Then the coefficients \(A_{11}\) and \(C_{11}\) of the P-FGM plates evaluated from Eq. (6) are:

$$A_{11} = \frac{{hE_{2} (\overline{E} + p)}}{{(1 - \nu^{2} )(1 + p)}}$$
(30a)
$$C_{11} = \frac{{E_{2} h^{3} }}{{12(1 - v^{2} )}}\left\{ {12(\overline{E} - 1)\left[ {\frac{1}{p + 3} - \frac{{2\overline{h}_{2} }}{p + 2} + \frac{{\left( {\overline{h}_{2} } \right)^{2} }}{p + 1}} \right] + 4\left[ {\left( {\overline{h}_{1} } \right)^{3} + \left( {\overline{h}_{2} } \right)^{3} } \right]} \right\}$$
(30b)

Where \(\overline{E} = E_{1} /E_{2}\), \(\overline{h}_{1} = h_{1} /h\), \(\overline{h}_{2} = h_{2} /h\) are dimensionless quantities. The term \(\frac{{E_{2} h^{3} }}{{12(1 - \nu^{2} )}}\) is the stiffness of homogeneous plate with Young’s modulus \(E_{2}\). Thus the characteristic of \(C_{11}\) is the stiffness of FGM plates.

4.3.2 S-FGM plates

The Young’s modulus of S-FGM plates can be calculated by:

$$E(z) = g_{1} (z)E_{1} + [1 - g_{1} (z)]E_{2} {\text{ for}} - h_{2} \le z \le - h_{2} + h/2$$
(31a)
$$E(z) = g_{2} (z)E_{1} + [1 - g_{2} (z)]E_{2} {\text{for}} - h_{2} + h/2 \le z \le h_{1}$$
(31b)

with \(g_{1} (z) = \frac{1}{2}\left( {\frac{{h_{2} + z}}{h/2}} \right)^{p}\) for \(- h_{2} \le z \le - h_{2} + h/2\), and \(g_{2} (z) = 1 - \frac{1}{2}\left( {\frac{{h_{1} - z}}{h/2}} \right)^{p}\) for \(- h_{2} + h/2 \le z \le h_{1}\). Hence, with the aid of \(B_{11} = 0\) and \(h = h_{1} + h_{2}\), the quantities \(h_{1}\) and \(h_{2}\) of S-FGM plates can be evaluated as:

$$h_{1} = \frac{{h\left( {\overline{E} + 3} \right)}}{{4\left( {\overline{E} + 1} \right)}} + \frac{{h\left( {\overline{E} - 1} \right)}}{{2\left( {p + 1} \right)\left( {p + 2} \right)\left( {\overline{E} + 1} \right)}}$$
(32a)
$$h_{2} = \frac{{h\left( {3\overline{E} + 1} \right)}}{{4\left( {\overline{E} + 1} \right)}} - \frac{{h\left( {\overline{E} - 1} \right)}}{{2\left( {p + 1} \right)\left( {p + 2} \right)\left( {\overline{E} + 1} \right)}}$$
(32b)

Consequently, the coefficients \(A_{11}\) and \(C_{11}\) of S-FGM plates expressed in terms of material properties and the plate thickness are found as:

$$A_{11} = \frac{{hE_{2} (\overline{E} + 1)}}{{2(1 - \nu^{2} )}}$$
(33a)
$$C_{11} = \frac{{E_{2} h^{3} }}{{12\left( {1 - v^{2} } \right)}}\left\{ {3(\overline{E} - 1)\left[ {\frac{{\left( {\overline{h}_{2} } \right)^{2} - \left( {\overline{h}_{1} } \right)^{2} }}{{\left( {p + 1} \right)\left( {p + 2} \right)}}} \right] + 12\overline{E}\left( {\frac{1}{12} - \frac{{\overline{h}_{1} }}{2} + \left( {\overline{h}_{1} } \right)^{2} } \right)} \right.\left. { + 12\left( {\frac{1}{12} - \frac{{\overline{h}_{2} }}{2} + (\overline{h}_{2} )^{2} } \right)} \right\}$$
(33b)

4.3.3 E-FGM plates

The Young’s modulus of E-FGM plates is specified as

$$E(z) = E_{2} e^{{B(z + h_{2} )}} ,{\text{ where }}Bh = \ln (\overline{E})$$
(34)

With the manner similar with P-FGM plates, the quantities \(h_{1}\), \(h_{2}\), \(A_{11}\) and \(C_{11}\) of the E-FGM plates are:

$$h_{1} = \frac{h}{{1 - \overline{E}}} + \frac{h}{{\ln \overline{E}}},$$
(35a)
$$h_{2} = \frac{{h\overline{E}}}{{\overline{E} - 1}} - \frac{h}{{\ln \overline{E}}}$$
(35b)
$$A_{11} = \frac{{hE_{2} (\overline{E} - 1)}}{{(1 - \nu^{2} )\ln (\overline{E})}}$$
(35c)
$$C_{11} = \frac{{E_{2} h^{3} }}{{12(1 - v^{2} )}}\left[ {12\overline{E}\left( {\frac{{(\overline{h}_{1} )^{2} }}{{\ln \overline{E}}} - \frac{{2\overline{h}_{1} }}{{(\ln \overline{E})^{2} }} + \frac{2}{{(\ln \overline{E})^{3} }}} \right) - 12\left( {\frac{{(\overline{h}_{2} )^{2} }}{{\ln \overline{E}}} + \frac{{2\overline{h}_{2} }}{{(\ln \overline{E})^{2} }} + \frac{2}{{(\ln \overline{E})^{3} }}} \right)} \right]$$
(35d)

5 Numerical results

The dimensions of the FGM plate are taken as \(a = b = 100\) cm and \(h = 2\) cm. The Poisson’s ratio and the coefficient of thermal expansion are \(v = 0.3\) and \(\alpha = 1 \times 10^{ - 5} /^{ \circ } C\). The Young’s modulus at the top (\(z = - h_{2}\)) of the FGM plate is fixed to \(E_{2} = 21GPa\) and that at the bottom of the plate varies according to the ratio of \({{E_{2} } \mathord{\left/ {\vphantom {{E_{2} } {E_{1} }}} \right. \kern-\nulldelimiterspace} {E_{1} }}\) = 1, 2, 5, 10, 20 and 50, while Young’s modulus inside the FGM plate is determined based on the material gradation defined in Sect. 4.3. The theoretical solutions are obtained according to the closed-form solutions and compared with the finite element analysis.

5.1 linear temperature change in the x-direction

Simply assume that the temperature change of the FGM plate linearly varies in the x-direction from \(T_{0}\) at \(x = 0\) to \(T_{a}\) at \(x = a\).The distribution of the temperature change \(T(x,y,z)\) is expressed as:

$$T(x,y,z) = T_{H} (x,y) = \left( {T_{a} - T_{0} } \right)\left( \frac{x}{a} \right) + T_{0}$$
(36)

Then \(T_{mn} = 8[T_{0} - T_{a} \cos (m\pi )]/mn\pi^{2}\) with \(m, \, n = 1, \, 3, \, 5, \, .....\). Hence, substituting \(T_{mn}\) into Eq. (23) gives the solutions of strains, stresses, axial forces and the bending moments for the FGM plates with the material of \(E = E(z)\) subjected to the temperature change in x-directions. Taking \(T_{0}\) = \(10^{ \circ } C\) and \(T_{a}\) = \(100^{ \circ } C\). The strains \(\varepsilon_{x} , \, \varepsilon_{y} , \, \gamma_{xy}\) at \(x = a/2\), \(y = b/2\) of the FGM plate versus the aspect ratio \(a/b\) for \(T_{a} /T_{0} = 10\) is plotted in Fig. 1(a), implying that strain \(\varepsilon_{x}\) decreases rapidly for increasing aspect ratio \(a/b\), stain \(\varepsilon_{y}\) increases with an increase of \(a/b\), and the strain \(\gamma_{xy} = 0\), as expected. The strain \(\varepsilon_{x}\) at \(x = a/2\), \(y = b/2\) of the FGM plate for \(T_{a} /T_{0} = 10\), \(30\), \(100\), \(200\), \(500\) displayed in Fig. 1(b) shows that the strain \(\varepsilon_{x}\) vanishes for small as well as large temperature changes as the aspect ratio \(a/b \approx 3\). The stresses \(\sigma_{x}\) at the central points of the P-FGM (\(p = 2\)), S-FGM (\(p = 2\)), and E-FGM plates for \(E_{2} /E_{1} =\) 1, 2, 5, 10, 20, 50 are illustrated in Fig. 2, showing the decrease of the compressive stress \(\sigma_{x}\) with the increase of \(E_{2} /E_{1}\). This phenomenon is attributed to that the increase \(E_{2} /E_{1}\) for fixed \(E_{2}\) means the decrease of the overall strength of the FGM plate, causing a decreases of the stresses. Moreover, it can be seen from Fig. 2 that the stress distribution along the thickness direction exhibits \(E(z)\) curves for P-, S-, and E-FGM plates. The distribution of axial force \(N_{x}\) along y-direction at \(x = a/2\) are plotted in Fig. 3 for different aspect ratio \(a/b\). Figure 3 reveals that the axial force \(N_{x}\) appears peaks near the edges of \(y = 0\) and \(y = b\) for small aspect ratio. This event is attributed to the simply-supported edges. Moreover, the axial force \(N_{x}\) increases as \(a/b\) increases.

Fig. 1
figure 1

The strains at central point (\(x = a/2\),\(y = b/2\)) of FGM plate under linear temperature change in the x-direction versus the aspect ratio \(a/b\)

Full size image
Fig. 2
figure 2

The stresses \(\sigma_{x}\) at the central point of FGM (\(p = 2\)) plate under linear temperature change in the x-direction for \(E_{2} /E_{1} =\) 1, 2, 5, 10, 20, 50 for a P-FGM, b S-FGM, c E-FGM

Full size image
Fig. 3
figure 3

The axial forces \(N_{x}\) at points \((a/2,y)\) of P-FGM plates under linear temperature change in the x-direction for different aspect ratios \(a/b\)

Full size image

5.2 Linear temperature change in the z-direction

Assume that the temperature change varies linearly in the z-direction from \(T(x,y,z) = T_{1}\) at the bottom surface to \(T(x,y,z) = T_{2}\) at the top surface:

$$T(x,y,z) = T_{V} (z) = \left( {T_{1} - T_{2} } \right)\frac{{z - h_{1} }}{h} + T_{1}$$
(37)

Then the quantities \(N^{*}\) and \(M^{*}\) defined in Eq. (13) are evaluated as:

$$N^{*} = \frac{{\alpha hE_{2} T_{2} }}{2(1 - \nu )}\left[ {\frac{{(\overline{T} + 1)(p + \overline{E})}}{(p + 1)} + \frac{{p(\overline{T} - 1)(\overline{E} - 1)}}{(p + 1)(p + 2)}} \right]$$
(38a)
$$M^{*} = \frac{{\alpha h^{2} E_{2} T_{2} }}{4(1 - \nu )}\left\{ {\frac{{p(\overline{T} + 1)(\overline{E} - 1)}}{(p + 1)(p + 2)} + \frac{{(\overline{T} - 1)\left[ {3(p^{2} + p + 2)\overline{E} + p(p^{2} + 3p + 8)} \right]}}{3(p + 1)(p + 2)(p + 3)}} \right\}$$
(38b)

for P-FGM plates,

$$N^{*} = \frac{{\alpha hE_{2} T_{2} }}{4(1 - \nu )}\left[ {(\overline{T} + 1)(\overline{E} + 1) + \frac{{p(p + 3)(\overline{T} - 1)(\overline{E} - 1)}}{2(p + 1)(p + 2)}} \right]$$
(39a)
$$M^{*} = \frac{{\alpha h^{2} E_{2} T_{2} }}{8(1 - \nu )}\left[ {\frac{{p(p + 3)(\overline{T} + 1)(\overline{E} - 1)}}{2(p + 1)(p + 2)} + \frac{{(\overline{T} - 1)(\overline{E} + 1)}}{3}} \right]$$
(39b)

for S-FGM plates, and

$$N^{*} = \frac{{\alpha hE_{2} T_{2} }}{2(1 - \nu )}\left\{ {\frac{{(\overline{T} + 1)(\overline{E} - 1)}}{{\ln \overline{E}}} + \frac{{(\overline{T} - 1)\left[ {(\overline{E} + 1)\ln \overline{E} - 2(\overline{E} - 1)} \right]}}{{(\ln \overline{E})^{2} }}} \right\}$$
(40a)
$$M^{*} = \frac{{\alpha h^{2} E_{2} T_{2} }}{4(1 - \nu )}\left\{ {\frac{{(\overline{T} + 1)\left[ {(\overline{E} + 1)\ln \overline{E} - 2(\overline{E} - 1)} \right]}}{{\left[ {\ln (E_{1} /E_{2} )} \right]{\kern 1pt}^{2} }} + \frac{{(\overline{T} - 1)\left[ {(\overline{E} - 1)[(\ln \overline{E})^{2} + 8] - 4(\overline{E} + 1)\ln \overline{E}} \right]}}{{(\ln \overline{E})^{3} }}} \right\}$$
(40b)

for E-FGM plates, where \(\overline{T} = T_{1} /T_{2}\). By the Substitution Eqs. (38–40) to Eq. (27), one can obtain the closed-form solutions of the FGM plates with the material property of \(E = E(z)\) subjected to the temperature linearly change in the z-direction.

Taking \(T_{1} = 100\,^{ \circ } {\text{C}}\) and \(T_{2} = 10\,^{ \circ } {\text{C}}\), the deflections at \(y = b/2\) of S-FGM plates for different \(E_{2} /E_{1}\) ratios are illustrated in Fig. 4. Notably, it can be seen from Fig. 4 that the deflection \(w \to 0\) as \(E_{2} /E_{1} \approx 5\). This indicates that for FGM plates under temperature change in the thickness direction, one can choose the ratio of \(E_{2} /E_{1}\) to a certain value such that no deflection occurs. This occurrence can be easily achieved by setting \(M^{*} = 0\). Herein, with the aid of Eq. (39b), the material steep

$$\frac{{E_{2} }}{{E_{1} }} = \frac{{3p(p + 3)(\overline{T} + 1) + 2(p + 1)(p + 2)(\overline{T} - 1)}}{{3p(p + 3)(\overline{T} + 1) - 2(p + 1)(p + 2)(\overline{T} - 1)}}$$
(41)
Fig. 4
figure 4

The deflections at the points \((x, \, b/2)\) of S-FGM plate under linear temperature change in the z-direction for different \(E_{2} /E_{1}\) ratios

Full size image

provides \(M^{*} = 0\), and consequently gives zero deflection for S-FGM plates. Taking \(p = 2\), \(\overline{T} = 10\) in Eq. (41) yields \(E_{2} /E_{1} = 4.789\), closely corresponding to the result in Fig. 4. Similarly,

$$\frac{{E_{2} }}{{E_{1} }} = \frac{{p(p + 3)(\overline{T} + 1) + 3(2 + p + p^{2} )(\overline{T} - 1)}}{{p(p + 3)(\overline{T} + 1) - p(8 + 3p + p^{2} )(\overline{T} - 1)}}$$
(42)

gives zero deflection for P-FGM plates. The maximum deflections \(w_{\max }\) of the S-FGM plates versus the aspect ratio is displayed in Fig. 5 for different \(E_{2} /E_{1}\) ratios and in Fig. 6 for different \(T_{1} /T_{2}\) ratios, revealing that the maximum deflections \(w_{\max }\) increase as the aspect ratio, or material gradient, or temperature steep increases.

Fig. 5
figure 5

The maximum deflections of S-FGM plate (\(p = 2\),\(T_{1} /T_{2} = 10\)) under linear temperature change in the z-direction versus the aspect ratio \(a/b\) for different \(E_{2} /E_{1}\) ratios

Full size image
Fig. 6
figure 6

The maximum deflections of S-FGM plate (\(p = 2\)) under linear temperature change in the z-direction versus the aspect ratio \(a/b\) for different \(T_{1} /T_{2}\) ratios, a \(E_{2} /E_{1} = 0.1\), b \(E_{2} /E_{1} = 10\)

Full size image

The stress distributions at the center of P-FGM, S-FGM, and E-FGM plates under linear temperature change in the z-direction are represented in Fig. 7, indicating that the maximum stress of FGM plates, except E-FGM plates, is in the inner portion of the FGM plates for \(E_{2} /E_{1} \ne 1\) instead of locating at the top or the bottom surface for the homogeneous plates. Notably, it also can be seen from Fig. 7 that the maximum stress of the FGM plates is much smaller than that of the homogeneous plate (\(E_{2} /E_{1} = 1\)). Thus, the use of FGM moves the maximum stress from the top or bottom surface to the inner portion of the FGM plate concerned, and significantly reduces the maximum stress of the plates.

Fig. 7
figure 7

The stress distributions at central point of P-FGM plate (\(p = 2\)) under linear temperature change in the z direction for different \(E_{2} /E_{1}\) ratios

Full size image

The comparison of the different kind of FGM plates are illustrated in Fig. 8 for \(E_{2} /E_{1} = 2, \, 5, \, 20, \, 50\), respectively. For the objectivity of comparison, the P-FGM plates with material parameters \(p = 1/2\),\(p = 1\), and \(p = 2\), and the S-FGM plates with \(p = 1/2\) and \(p = 2\) are analyzed and discussed. For convenience, the P-FGM plate with \(p = 1/2\), \(p = 1\) and \(p = 2\) are simply denoted as \(P_{1/2} - {\text{FGM}}\), \(P_{1} - {\text{FGM}}\) and \(P_{2} - {\text{FGM}}\), respectively. And the S-FGM plate with \(p = 1/2\) and \(p = 2\) are simply symbolized as \(S_{1/2} - {\text{FGM}}\) and \(S_{2} - {\text{FGM}}\). Figure 8 depict that the maximum stresses of \(P_{2} - {\text{FGM}}\) and \(S_{1/2} - {\text{FGM}}\) plates are much larger than those of E-FGM,\(P_{1/2} - {\text{FGM}}\), and \(S_{2} - {\text{FGM}}\) plates. Therefore, among the comparison, \(P_{2} - {\text{FGM}}\) and \(S_{1/2} - {\text{FGM}}\) are worse material distributions. Moreover, as \(E_{2} /E_{1}\) ratio increases, the stress at the bottom surface (\(z = h_{1}\)) decreases.

Fig. 8
figure 8

The comparison of the stress distributions for the different FGM plates under linear temperature change in the z-direction for \(T_{2} /T_{1} = 1/10\), \(E_{2} /E_{1} = 2, \, 5, \, 20, \, 50\)

Full size image

6 Conclusion

Based on the medium-thick plate assumption, the closed-form solutions of the simply-supported FGM plates under thermal loading by Fourier series expansion has been successfully developed and leads to the following conclusion:

  1. (1)

    Under the assumption of constant Poisson’s ratio and constant thermal expansion coefficient, the closed-form solutions of the FGM plates with through-the-thickness Young’s modulus under temperature change in the radial and thickness directions are evaluated, and give a complete insight into the thermal–mechanical behavior of FGM plates.

  2. (2)

    For the situation that the temperature change linearly varies in the x-direction, the strains and axial forces are independent of Young’s modulus, the bending moments are zero, and the stresses along the thickness of the FGM plate have the same shapes as the corresponding variations of Young’s moduli.

  3. (3)

    If the temperature change is linear in the z-direction, the strains and stresses along the thickness of the FGM plate are functions of z and \(zE(z)\), respectively. And, the axial force and the bending moment are functions of thermal axial force \(N^{*}\) and thermal bending moment \(M^{*}\), respectively.

  4. (4)

    The steep of material gradation for which the deflection of the FGM plate subjected to temperature change in the thickness direction is zero can been easily evaluated from the obtained closed-form solutions.

  5. (5)

    Among E-FGM,\(P_{1/2} - {\text{FGM}}\), \(P_{1} - {\text{FGM}}\), \(S_{1/2} - {\text{FGM}}\) and \(S_{2} - {\text{FGM}}\), the maximum stresses of \(P_{2} - {\text{FGM}}\) and \(S_{1/2} - {\text{FGM}}\) plates are much larger than those of E-FGM, \(P_{1/2} - {\text{FGM}}\), and \(S_{2} - {\text{FGM}}\) plates, and thus \(P_{2} - {\text{FGM}}\) and \(S_{1/2} - {\text{FGM}}\) are worse material distributions when the temperature change is linear in the z-direction.