Nonlinear vibration absorbers applied on footbridges

Abstract

This paper deals with the performance of linear and nonlinear dynamic vibration absorbers (DVAs) to suppress footbridges vertical vibrations. The walking pedestrian vertical force is modeled as a moving time-dependent force and mass. The partial differential equations govern the dynamics of the system; such equations are reduced to a set of ordinary differential equations by means of the Bubnov–Galerkin method with an accurate multimode expansion of the displacement field. The optimal vibration absorber parameters are determined using two objective functions: maximum footbridge deflection and the transferred energy from the footbridge to the DVA. The most suitable nonlinear DVA is proposed for the investigated footbridge. The results show that the DVAs with quadratic nonlinearity are the most performant DVAs.

1 Introduction

The reduction of human-induced vibrations is a serviceability and safety issue in footbridges. Under a moving pedestrian load, in near resonance condition, the structure of the footbridge may suffer from large deflections. The resonance occurs when a natural frequency of the structure is within the range of pedestrian pacing frequencies and cause damages. There are several methods to reduce the vibrations of the footbridges including, the selection of structural material, general end conditions, and the most promising of them, dynamic vibration absorber (DVA). In Ref [1] human-structure interaction models for the vertical vibration under pedestrian excitation are considered. In the mentioned paper, the beam equation is modeled employing the modal coordinates and finite element method. Pedersen and Frier [2, 3] worked on the footbridge response under pedestrian load models and investigated the sensitivity of the footbridge vibrations to walking parameters. They represent the excessive vibrations and serviceability problems of slender footbridges under pedestrian traffic. In Ref.[2], it was shown that walking parameters such as step frequency, pedestrian mass, dynamic load factor are essentially stochastic. Pedersen and Frier [3] were focused on estimating the vertical structural response to single person loading. In Ref [4] a literature review of experimental and analytical pedestrian forces on the footbridges are brought. They investigated human-structure, dynamic interaction, and pedestrian synchronization during walking. In the past years, a large amount of investigations has been carried out on moving mass models, see, for instance, Refs.[5,6,7]. The effect of pedestrian mass has been considered by these models; hence the Coriolis and centripetal forces were usually disregarded. Pfeil et al. [8], estimated human-induced vibration amplitudes of vertical bending in footbridges. They investigated a single DOF model to simulate the walking pedestrian—structure interaction, which was developed based upon the vertical accelerations.

DVAs have been used to reduce structural vibrations. Samani et al. [9] showed the performances of linear and nonlinear DVAs applied to the specific problem of moving loads or vehicles. They found that the cubic stiffness shows better performance concerning the linear one. They conclude that using higher power for the nonlinear stiffness leads to a more effective reduction of the beam deflection. Wu [10] suggested using the DVA in the middle of a beam span under the force exerted by a moving load. On the other hand, considering moving mass instead of moving load seems to be feasible; in Refs [1, 11] was shown that the time response of a beam under either moving masses or moving loads is almost similar. Wu [10] followed Den Hartog’s method [12] to determine the optimized values of stiffness and damping ratio of the DVA. Pun and Liu [13] explored the potential of the nonlinear vibration absorber in a system subjected to harmonic loading. They showed that a hardening absorber can deliver a wider bandwidth range of frequency, with respect to the linear one. Ding and Chen [14] provided a comprehensive review of the researches on the nonlinear vibration absorber. Their work emphasizes on designs, analysis, conclusion, and applications of nonlinear vibration absorber devices to enhance vibration reduction in engineering fields. Lievens et al. [15] propose an optimization approach based upon the worst-case for the design of a TMD which accounts for uncertainties in the modal parameters. The goal was the minimization of the mass of the TMD, by tuning the mass, stiffness, and damping values. They have considered limit values for acceleration, deflection, and upper and lower limit for the stiffness and damping. In [16], Jiang et al. worked theoretically and experimentally on the effects of a nonlinear vibration absorber with cubic stiffness, on the steady-state vibration of a linear primary system. They illustrated the ability of a nonlinear vibration absorber in absorbing the vibrations over a relatively wide frequency range. It is an attractive advantage over classical linear vibration absorbers. Gourdon et al. [17, 18] applied experimentally a cubic nonlinearity with implementing two linear springs. Gatti [19] has been worked on the performance of a nonlinear TMD with cubic stiffness behavior. By using an analytical formulation, the effect of nonlinearity and mass ratio of the attachment is investigated for both softening and hardening stiffness. A. Alhassan et al. [20] have investigated the effect of human-induced vibrations on a special footbridge in Jordan. They have used ETABS software to identify footbridge properties. They showed that by using a tuned mass damper (TMD), the fundamental vibration frequency of the mentioned footbridge will be decreased to a stable value less than human excitation frequencies, after attaching of a TMD to the footbridge. They concluded that the footbridge will be stable under a pedestrian excitation. They used the Den Hartog values for the mechanical characteristics of the TMD. Ferreira et al. [21] used a semi-active damper between the structure and TMD to control synchronous lateral excitations in footbridges. By proposing a numerical method, they have evaluated the effectiveness of the new semi-active TMD with the conventional passive one. The main conclusion was that by using the new procedure, a lower mass for the semi-active TMD was required to achieve the same performance as that of the passive one. Moutinho et al. [22] have proposed the implementation of a semi-active TMD to reduce vibrations in a specific footbridge. The semi-active TMD was including a magnetorheological damper; which was controlled by phase control law. Because the mentioned footbridge had several critical vibration modes with natural frequencies close to 2 Hz, only a conventional passive linear TMD cannot act efficiently on all of the modes. In these cases, a semi-active TMD seems to be appropriate, where the capability of self-tuning and the possibility of performing multimode control are given. Maslanka [23] presented a semi-active TMD with acceleration and relative motion feedbacks optimized in the frequency domain. This type of semi-active tuned mass damper with a mass of one-seventh of an equivalent TMD optimized with Den Hartog formulation has the same vibration damping efficiency respect to a TMD with Den Hartog values. The displacement due to the proposed semi-active TMD is not greater than a Den Hartog one. This type of semi-active TMD has a magnetorheological controllable viscous damper. Parseh et al. [24], considered the dynamics of linear, Euler–Bernoulli beam with an attached nonlinear energy sink (NES), considering cubic nonlinear stiffness, subjected to harmonic excitation. They claimed that to achieve better performance for NES in comparison with tuned mass damper, NES must be designed for maximum amplitude of exciting force. Samani and Pellicano [25], investigated the performance of DVA in suppressing the vibrations of a simply supported beam subjected to an infinite sequence of regularly spaced concentrated moving loads. It was shown that there is more beam deflection reduction by using nonlinear DVAs comparing with linear type. They investigated the performance of several types of nonlinear DVAs on the beam including, piecewise linear stiffness, cubic stiffness, 5 order monomial stiffness, linear-quadratic damping, cubic damping.

Nonlinear vibration absorbers are applied to reduce vibrations of structures, bridges, and various engineering fields. The following references are brought to show the effectiveness of nonlinearity for various applicable cases. Yang and Wang [26] modeled a cantilever beam embedded with the impact damper. The impact damper causes momentum exchange between the beam and impact mass. Experimental results show a robust reduction in the velocity amplitude of the investigated beam. In another research, Gourc et al. [27] showed the effectiveness of using a nonlinear vibration absorber in controlling the chatter instability in turning processes. Finally, the experimental results showed a significant reduction of the tool amplitude by using a nonlinear vibration absorber. Wang et al. [28] proposed a nonlinear passive mass damper, to mitigate the unwanted responses of building structures. The vibration absorber consists of a mass connected to the primary structure through a linear and a cubic nonlinear spring. The proposed vibration absorber showed high performance in the mitigation of structural response.

In the present paper, the dynamics of the Euler–Bernoulli beam subjected to a moving pedestrian is studied. The major contribution is offering the best nonlinear DVA for pedestrian footbridges, to minimize deflection of the footbridge and to damp the vibration in the shortest possible time. A classical linear DVA is limited in that it reduces the vibration of a bridge over a narrow excitation frequency; while a nonlinear one can be applied under a wide range of excitation frequency. To solve the governing partial differential equations (PDE) of the beam, the Bubnov–Galerkin approach was applied to transform the PDE into a set of ordinary differential equations. The dynamics are studied numerically by integrating the ordinary equations using the Gauss–Kronrod method. The time response results with an attached DVA are compared with the bare footbridge time history results. By applying different types of nonlinear DVAs on the footbridges and comparing them with the linear DVA, characterized by Den Hartog formulation, the effectiveness of nonlinearity in DVAs is presented.

2 System description and basic formulations

Due to the walking or running of a pedestrian on a footbridge, three force components produced in vertical, horizontal, and longitudinal directions. The vertical one is the most noteworthy of those. The vertical component, due to its high amplitude, has been considered by researchers during the distant past. The force model exerted by a single pedestrian within one step is illustrated in Fig. 1; it represents the forces produced from the left and right foot that overlap in time while walking, just as there is always one foot on the footbridge [6, 29]. Unlike spatially discrete forces at the foot placement position, walking can be described by spatially continuous footfall forces [30].

Fig. 1

Vertical force and approximated model force [1]

The ground natural reaction force from successive footfalls can be described by the following series, [1], see Fig. 2:

$$G\left( t \right) = W + \sum\limits_{k = 1}^{h} {W\eta_{k} \cos \left( {2\pi kf_{p} t + \varphi_{k} } \right)}$$

(1)

where, W = m_pg is the pedestrian weight while standing, g is the gravity acceleration; m_p is the pedestrian mass; f_p is pacing frequency (variable with the velocity of the pedestrian; i.e. the number of footfalls per second [31]); η_k is the coefficient of Fourier series which is named “dynamic load factor”; φ_k is the phase angle of the harmonic; h represents the number of harmonics.

Fig. 2

A footbridge model with the attached DVA subjected to a moving mass

In the past, researchers used different numbers of harmonics and coefficients in the Fourier series to represent the vertical force [31,32,33]. The mean values of the first four harmonics, used in this study, are as follows [5]:

$$\begin{aligned} \eta_{1} = &\, 0.37\left( {f_{p} - 0.95} \right) \le 0.5 \\ \eta_{2} = &\, 0.054 + 0.0044f_{p} \\ \eta_{3} = &\, 0.026 + 0.0050f_{p} \\ \eta_{4} = &\, 0.010 + 0.0051f_{p} \\ \end{aligned}$$

(2)

2.1 Pedestrian simulated as moving mass/force

In this section, the passing pedestrian is modeled as either a moving mass or a moving force with the amplitude of G(t). A solid passing velocity of ν is considered for the pedestrian. The following general equation is intended to simulate the moving mass model, which is a function of time and position:

$$F\left( {x,t} \right) = \left[ {G\left( t \right) - m_{p} w_{,tt} } \right] \delta \left( {x - vt} \right)\left[ {H\left( {\frac{L}{v} - t} \right)} \right]$$

(3)

where, G(t) is the footfall force amplitude exerted by a pedestrian and is represented by Eq. (1); w is the deflection response of the beam. δ is the Dirac delta function and defines the location of moving mass during the passing time, and H(t) is the Heaviside function [34]. The moving force model can be written as the following equation:

$$F\left( {x,t} \right) = G\left( t \right) \delta \left( {x - vt} \right)\left[ {H\left( {\frac{L}{v} - t} \right)} \right]$$

(4)

2.2 Footbridge with attached DVA

The model consists of a simply supported linear Euler–Bernoulli beam excited with moving force/mass. As it is shown in Fig. 2, a DVA is connected to the footbridge to reduce the vibrations.

The partial differential equation of the dynamics of the footbridge with boundary and initial conditions are as follows:

$$EIw_{,xxxx} \left( {x,t} \right) + \rho Aw_{,tt} \left( {x,t} \right) + \left[ {f\left( u \right) + g\left( {u_{,t} } \right)} \right]\delta \left( {x - d} \right) = F\left( {x,t} \right)\;\;\;x \in \left( {0,L} \right), t > 0$$

(5)

$$w\left( {0,t} \right) = 0,\;w\left( {L,t} \right) = 0,\;w_{,xx} \left( {0,t} \right) = 0,\;w_{,xx} \left( {L,t} \right) = 0$$

(6)

$$w\left( {x,0} \right) = 0,\;w_{,t} \left( {x,0} \right) = 0,\;u\left( t \right) = w\left( {d,t} \right) - z\left( t \right)$$

(7)

$$w_{,t} = \frac{\partial w}{{\partial t}},\;\;w_{,tt} = \frac{{\partial^{2} w}}{{\partial t^{2} }},\;\;w_{,xxxx} = \frac{{\partial^{4} w}}{{\partial x^{4} }}$$

(8)

where, I is the moment of inertia of the cross-sectional area of the beam; ρ is the material density; A is the cross-sectional area of the beam; F(x, t) is taken from Eq. (4), in which the reaction force amplitude obtain from Eq. (1), $g\left( {u_{,t} } \right) = \lambda u_{,t} \left( t \right)$ is the viscous damping force; f(u) is the stiffness force in Eq. (5); the term $\left[ {f\left( u \right) + g\left( {u_{,t} } \right)} \right]\delta \left( {x - d} \right)$ represents the force exerted by the dynamic damper; d represents the location of the damper on the beam, which is equal to $\frac{L}{2}$ and λ is the damping coefficient of the viscous damper. The dynamics of the DVA is governed by the following equations:

$$m_{0} z_{,tt} - ku - \lambda u_{,t} \left( t \right) = 0,\;\;t > 0$$

(9)

$$z\left( 0 \right) = 0,\;\;z_{,t} \left( 0 \right) = 0,\;\;\;t > 0$$

(10)

where, m₀ is the mass of the DVA and, z(t) is the position of the mass of DVA, m₀. By using the Bubnov-Galerkin method the displacement function of the footbridge is as Eq. (11):

$$w\left( {x,t} \right) = \sum\limits_{r = 1r = 1}^{N} {q_{r} \left( t \right)\varphi_{r} \left( x \right)}$$

(11)

thus:

$$w_{,tt} = \sum\limits_{r = 1r = 1}^{N} {\ddot{q}_{r} \left( t \right)\varphi_{r} \left( x \right)}$$

(12)

q_r(t) are unknown functions of time (modal coordinates), φ_r(x) are the normalized eigenfunctions and N is the number of modes of the system. The eigenfunctions are defined as:

$$\varphi_{r} \left( x \right) = \left( \frac{2}{mL} \right)^{\frac{1}{2}} \sin \left( {\frac{r\pi x}{L}} \right),\;\;\omega_{r} = \left( {r\pi } \right)^{2} \left( {\frac{EI}{{mL^{4} }}} \right)^{\frac{1}{2}} ,\;\;\;r = 1,2,3, \ldots$$

(13)

m = ρA is the mass per unit length of the footbridge and ω_r is the natural circular frequency of the r^th mode. The footbridge is subjected to a single moving mass. By substituting Eqs. (11–12) into Eqs. (5–10), applying Eq. (3) in the right-hand of Eq. (5), using the orthogonality conditions in Ref [34] and assuming constant velocity, the j^th modal equation can be derived as follows:

$$\ddot{q}_{j} + 2\xi_{j} \omega_{j} \dot{q}_{j} + \omega_{j}^{2} q_{j} + \left\{ {K\left( t \right) + C\left( t \right)} \right\}\varphi_{j} \left( d \right) = \varphi_{j} \left( {vt} \right)\left\{ {G\left( t \right) - m_{p} \left[ {\sum\limits_{r = 1}^{N} {\ddot{q}_{r} \left( t \right)\varphi_{r} \left( {vt} \right)} } \right]} \right\}$$

(14)

where, G(t) is satisfied by Eq. (1); K(t) and C(t) are described by Eqs. (15) and (16):

$$K\left( t \right) = k\left[ {\sum\limits_{r = 1}^{N} {q_{r} \left( t \right)\varphi_{r} \left( d \right) - z\left( t \right)} } \right]^{\alpha } \left| {\sum\limits_{r = 1}^{N} {q_{r} \left( t \right)\varphi_{r} \left( d \right) - z\left( t \right)} } \right|^{\beta } \;\;\left( {{\text{stiffness}}\;{\text{function}}} \right)$$

(15)

and

$$C\left( t \right) = \lambda \left[ {\sum\limits_{r = 1}^{N} {\dot{q}_{r} \left( t \right)\varphi_{r} \left( d \right) - \dot{z}\left( t \right)} } \right]^{\gamma } \left| {\sum\limits_{r = 1r = 1}^{N} {\dot{q}_{r} \left( t \right)\varphi_{r} \left( d \right) - \dot{z}\left( t \right)} } \right|^{\delta } \;\;\;\left( {{\text{damping}}\;{\text{function}}} \right)$$

(16)

where, α, β, γ and, δ are integer powers defined based upon the type of stiffness and damping (linear or nonlinear) used in various DVAs. In the system described above, a moving mass pedestrian was considered. The formulations can be extended to a moving force model, as well. Governing equations under moving force excitation is the same as moving mass ones; where, m_p in the right-hand side of Eq. (14) should be replaced by zero, which means the absence of inertial effects.

2.3 Classical linear DVA

To decrease the resonance phenomenon of a beam subjected to a periodic load, the equivalent mass of the beam should be defined, which depends on the position of the DVA [12]. The optimal position to attach a DVA to a simply supported beam, to suppress the first mode is the middle of the beam [25]. The related optimal values of the stiffness and damping of the linear DVA, attached to a simply supported beam, are as follows:

$$k = m_{0} \left( {\frac{{\omega_{1} }}{1 + \mu }} \right)^{2}$$

(17)

$$\lambda = 2m_{0} \omega_{1} \sqrt {\frac{3\mu }{{8\left( {1 + \mu } \right)^{3} }}}$$

(18)

where, ω₁ is the fundamental natural frequency of the beam, $\mu = \frac{{m_{0} }}{{m_{e} }}$ is the mass ratio, and $m_{e} = \frac{mL}{{2\left( {\sin \frac{\pi d}{L}} \right)^{2} }}$ is the beam equivalent mass.

3 Validation

To evaluate the accuracy of the present results, the case of a footbridge without DVA is investigated and results compared with Ref. [1]. Consider the system of Eqs. (14–16), with m_p, k, and λ equal to zero. A simply-supported footbridge with the following parameters brought in Table 1, is subjected to a moving single pedestrian force:

Table 1 Footbridge characteristics

The pedestrian weight is 724 N, which moves with a velocity of 1.25 m/s and a frequency of 2 Hz. The pedestrian force exerted to the footbridge by the pedestrian feet is shown in Fig. 3. Due to the bridge length, and the pedestrian velocity, the force exerted to the footbridge is truncated after 40 s, while the pedestrian passed the footbridge.

Fig. 3

Exerted force to the footbridge, a short period, b long period

Figures 4 and 5 show the acceleration time history and corresponding RMS (root mean square) of the footbridge mid-span under moving pedestrian force and mass, respectively. The difference between the maximum RMS of acceleration of the beam under moving mass (1.178 m/s) and moving force (1.218 m/s) is about 4%. Moreover, the difference between the maximum deflection of the beam under moving mass (9.1 mm) and moving force (11 mm) is about 9%. Consequently, at the excitation frequency (2 Hz), for the selection of performant DVA the equations of the beam under moving force, is considered. Notably, the pedestrian frequency is within the normal pacing frequency range of 1.8–2.2 Hz [31]. Four modes Bubnov–Galerkin expansion is selected after truncation evaluation; error is less than 1%. In Table 2 the difference between present study and Ref.[1], compared.

Fig. 4

Footbridge mid-span acceleration subjected to moving pedestrian force; yellow line: time response result of the present model; blue filled circle RMS of the Ref.[1], blue line: RMS of the present result. a time history during 40 s. b time history during 120 s

Fig. 5

Footbridge mid-span acceleration subjected to moving pedestrian mass; yellow line: time response result of the present model; blue filled circle: RMS of Ref.[1], blue line: RMS of the present result. a time history during 40 s. b time history during 120 s

Table 2 Maximum values of RMS of acceleration time response

To verify the effectiveness of the nonlinearity of DVAs, in the case of moving loads, further verification is done; data are used from Ref [34] for this aim. By considering the system of Fig. 2, where the integer powers of the elastic and damping forces [related to Eqs. (15) and (16)] are: α = 3, β = 0, γ = 1, δ = 0. The system parameters in Ref [34] are brought in Table 3.

Table 3 Footbridge characteristics of Ref [34]

Figure 6a, b show the maximum deflection of the mid-span of the beam against the stiffness of the nonlinear absorber (linear damping and nonlinear stiffness). Notably, the moving excitation is not due to pedestrian walking, and it is a moving force with a constant amplitude as mentioned in Ref.[34].

Fig. 6

Comparison of beam subjected to moving load with an attached nonlinear DVA; red line: present results and blue filled circle: Ref.[34]; a 1-mode expansion and b 5-modes expansion

In Fig. 6a, b, 1-mode and 4-mode expansions are used, respectively. Moreover, by using four mode expansions, good agreement with Ref [34] is found. Notably, transformation of the PDE to ODEs is done analytically.

4 Passive nonlinear DVA formulation

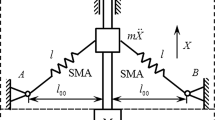
In this study, different types of nonlinear DVAs with quadratic and cubic nonlinearity are applied on the footbridges. The effect of the attached nonlinear DVAs is investigated in Sects. 5.2 through 5.7. The reason for choosing the mentioned nonlinearity for the DVAs in the present study is due to the custom use of nonlinear mathematical models in the attached DVAs applied on the vehicle bridges, in recent years [9, 16,17,18, 25, 34,35,36,37]. Although the piece-wise linear stiffness or damping types as mentioned by [25], and nonlinear impact absorber modeled by [26] can be added to the nonlinear DVAs, the mentioned ones in this study are the most common types of nonlinear DVAs for simply supported bridges. For the sake of brevity, six common nonlinear DVAs in two objective optimization goals are investigated in the following section. These nonlinear DVAs and the linear ones which are compared with each other are including sixteen cases in the following sections. In Fig. 7, a schematic of a nonlinear attachment vibration absorber for the bridge is illustrated. Although the attached stiffness and damper are linear individually, the whole attachment DVA is nonlinear.

Fig. 7

Schematic of the geometrically nonlinear DVA

To investigate the order of nonlinearity, for the mentioned nonlinear configuration for the attached system in Fig. 7, the following procedure is done. It is notable to say that, in Ref.[38], A similar model is proposed for the configuration of a cubic passive vibration absorber for a structure. In this section by applying little changes to the mentioned model [38] and modifying it for an attached nonlinear DVA to a footbridge, a new model is proposed. By supposing the blue spring shown in Fig. 8, as the spring with its free length L, located in position 1. By attaching the mass, m₀ to the linear springs, m₀ will be placed in its static position 2. The Newton equation in the vertical direction is as the following; which is due to the free body diagram of position 2 in Fig. 8.

$$2R_{2} \sin \alpha = m_{0} g$$

(19)

R₂ is the spring force in position 2. As shown in Fig. 8, δ_st is the static location of the mass (m₀). The force R₂ is created in the spring due to the static displacement of the DVA mass. m₀g is the weight of the DVA mass, m₀. α is the angle between position 1 and position 2. α and R₂ are defined as the following equations:

$$\alpha = \frac{{\delta_{st} }}{{\sqrt {\delta_{st}^{2} + L_{0}^{2} } }}$$

(20)

where, L₀ is the free length of each of the springs.

$$R_{2} = k\left[ {\sqrt {\delta_{st}^{2} + L_{0}^{2} } - L_{0} } \right]$$

(21)

Fig. 8

Cubic configuration of the springs

By exerting the external force,${\text{F}}$ the mass of the DVA will be located in position 3. Due to Eqs. (19) to (21), the weight vector of m₀, in the body diagram of position 3 is omitted which is shown in Fig. 8. So the following equations can be written for Newton’s law in the vertical direction in position 3.

$$F = 2R_{3} \sin \theta$$

(22)

and,

$$R_{3} = k\left[ {\sqrt {v^{2} + L_{0}^{2} } - L_{0} } \right]$$

(23)

where, ν is the displacement of the mass due to exerted force F, and

$$\sin \theta = \frac{v}{{\sqrt {v^{2} + L_{0}^{2} } }}$$

(24)

thus, Eq. (22), will be reformed as:

$$F = 2k\left[ {\sqrt {v^{2} + L_{0}^{2} } - L_{0} } \right]\frac{v}{{\sqrt {v^{2} + L_{0}^{2} } }} = 2kv\left[ {1 - \frac{{L_{0} }}{{\sqrt {v^{2} + L_{0}^{2} } }}} \right]$$

(25)

By writing the Taylor expansion of relation $\frac{1}{{\sqrt {v^{2} + L_{0}^{2} } }}$, about ν = 0, the following equation will be achieved:

$$F = 2kv\left[ {1 - L_{0} \left( {\frac{1}{{L_{0} }} - \frac{{v^{2} }}{{2L_{0}^{3} }} + 3\frac{{v^{4} }}{{8L_{0}^{5} }} - \frac{{v^{6} }}{{4L_{0}^{7} }} + \ldots } \right)} \right]$$

(26)

which is summarized to:

$$F = \frac{k}{{L_{0}^{2} }}v^{3} + O\left( {v^{5} } \right) = Kv^{3} + O\left( {v^{5} } \right)$$

(27)

So the geometric nonlinearity of the attached system in Fig. 7, produces a cubic stiffness nonlinearity.

The above-mentioned procedure can be done for any type of nonlinear configurations of the stiffness and damping, which is not in the aims of this study.

5 Optimization of the DVA parameters

In this section, for various types of DVAs, the optimal stiffness and damping of the linear DVA of the beam are optimized. The position of the DVA also affects the beam deflection [39]. Ref [25] shows that the optimal position of the DVA for a simply supported beam under periodic excitation is the middle of the beam.

Two objective functions for the presented optimization investigate in this paper. The first objective function is the minimization of the maximum beam deflection. The second goal function is the maximization of the amount of energy dissipated by the DVA (η), computed by Eq. (28); see Ref. [40].

$$\eta = \frac{{E_{{{\text{DVA}}}} }}{{E_{{{\text{in}}}} }} = \frac{{\int\limits_{0}^{{t_{1} }} {\lambda \left[ {\dot{z}(t) - \sum\limits_{r = 1}^{N} {\dot{q}_{r} (t)\varphi_{r} (d)} } \right]^{m} \left| {\dot{z}(t) - \sum\limits_{r = 1}^{N} {\dot{q}_{r} (t)\varphi_{r} (d)} } \right|^{n} {\text{d}}t} }}{{\int\limits_{0}^{{t_{0} }} {F_{i} \left[ {\dot{q}_{r} (t)\varphi_{r} (x_{F} )} \right]{\text{d}}t} }}$$

(28)

where, F_i is the pedestrian force, which is defined by Eqs. (3 and 4); x_F = νt, is the position of the pedestrian on the footbridge. E_DVA is the energy absorbed by DVA; E_in represents the input energy exerted by pedestrian feet on the footbridge. The integer powers m and n are defined depending on the type of damper (linear or nonlinear) used in various DVAs. $t_{1}$ is the assumed time, large enough to be sure that the transient response is damped; and t₀ is the duration of the load acting on the footbridge. This approach is focused on the maximization of the energy dissipated by the DVA [34].

5.1 Optimal design of the linear DVA

The optimum values λ and k, obtained by Den Hartog's method [Eqs. (17) and (18)] for the present numerical model are 5293 Ns/m and 164 kN/m, respectively. Following the approaches considered above, the optimum values related to both goal functions will be achieved. Under a moving pedestrian force, after focusing on the region where the maximum η and minimum deflection are located, the ranges of λ and k are 0 to 10 kNs/m and 50 kN/m to 300 kN/m, respectively. By sampling the viscous damping and stiffness on a 50 × 50 grid, meaning that the damping and stiffness resolutions are 0.2 kNs/m and 5 kN/m, respectively, the minimum deflection is obtained. The optimized λ and k for the deflection approach are the values that offer the minimum value of the maximum deflection in each frequency. The minimum deflection of 0.96 mm for the gained optimum parameters: λ = 6 kNs/m and k = 180 kN/m is achieved in an overall search using the deflection objective function which is shown in Fig. 9a. The optimized λ and k for energy objective function are the values in which the DVA dissipates the maximum energy. In Fig. 10b peaks A, B, and C show the minimum values of the optimized DVA with energy approach. These peaks present the worst situation of the optimized DVA for the probable excitation frequency range. By choosing m = 2 and n = 0 in Eq. (28), the η = 92.80%, for λ = 6.4 kNs/m and k = 145 kN/m is achieved which is shown in Fig. 9b. It is notable that the integer powers in Eqs. (15) and (16) are: α = 1, β = 0, γ = 1 and δ = 0. The difference between the two mentioned optimization approaches is that, in the energy approach, the time response of the footbridge would be damped faster, whereas in the deflection approach the maximum deflection of the footbridge would be minimum.

Fig. 9

DVA optimized parameters. a deflection approach optimization method; b energy approach optimization method

Fig. 10

a Maximum deflection of footbridges subjected to linear DVAs in frequency domain; b The amount of dissipated energy by linear DVAs

Note that, the common range of pedestrian walking frequency is 1.6–2.4 Hz [31]; hence it is noticeable to find the maximum deflection of the footbridge and the amount of energy absorbed by DVA in a wide range of low frequencies. The importance of using a frequency domain illustration is due to the fact, that walking parameters such as pedestrian frequencies are stochastic [2]. In Fig. 10, a comparison of DVAs optimized by energy and deflection approach to DVA with Den Hartog values, in a frequency domain is illustrated.

In the subsequent figures, peak points A, B and C are presented for curves related to the deflection approach optimized DVA, linear DVA with Den Hartog values, and energy approach optimized DVA. These points give the critical frequencies which affect the selection of the optimized parameters for each linear or nonlinear DVAs. Note that, these points for deflection (w) graphs are correlated to frequencies that present the maximum deflections and similarly, for dissipated energy (η) graphs are associated with frequencies that present the minimum dissipated energy.

Peak A, in Fig. 10a, shows the minimum deflection of 0.96 mm in the deflection approach method, which is smaller than peaks B and C. In Fig. 10b, peak C illustrates the η = 92.82% related to the energy approach optimization, which is higher than peaks A and B related to the deflection approach and the Den Hartog method. The anti-peak at frequency 2 Hz, in Fig. 10b, is due to a resonance phenomenon.

Notably, the optimal parameters of the attached DVA to the footbridge under moving pedestrian mass have also been checked. The results were very close to those gained under moving pedestrian force. So, in the following sections, the moving force model is only used to investigate the acceleration and deflection of the footbridge. In the subsequent sections, different types of nonlinear DVAs are going to be analyzed. When the frequency of the applied excitation is not fixed, taking advantage of the nonlinear DVAs is proposed.

5.2 Nonlinear DVA with quadratic damping

To minimize the deflection of the system, subjected to periodic excitation some researchers suggested the use of quadratic damping, e.g., Starovetsky investigated a system with nonlinear energy sink with quadratic damping characteristics [41]. By considering a linear stiffness and quadratic damping, by choosing α = 1, β = 0, γ = 1, and δ = 1 in Eqs. (15) and (16), the maximum deflection of the footbridge and the absorbed energy by the DVA, are illustrated in Fig. 11a, b, respectively. By using the energy approach method and employing Eq. (28) with m = 2 and n = 1, the following optimal values are obtained: λ = 1000 kNs²/m² and k = 146kN/m. The maximum value of the minimum dissipated energy by DVAs is 92.77%, Fig. 11b, peak C. The minimum deflection of 0.95 mm which is demonstrated by peak A, for the achieved optimum parameters: λ = 415kNs²/m² and k = 183 kN/m, Fig. 11a. These optimal values are obtained in an overall search using the deflection approach optimization method. The peak points A, B, and C corresponding to the critical frequencies are shown in Fig. 11.

Fig. 11

a Maximum deflection of footbridges subjected to DVAs with quadratic damping and linear stiffness in comparison with DVA with Den Hartog values; b The absorbed energy by the mentioned DVAs

5.3 Nonlinear DVA with quadratic stiffness

In this section a nonlinear DVA with quadratic stiffness and linear damping is investigated; where the integer powers of the elastic and damping forces [related to Eqs. (15) and (16)] are α = 1, β = 1, γ = 1, and δ = 0. Minaei and Ghorbani [42] have been presented a new variable stiffness mechanism which can be extended as an applicable nonlinear one in engineering. To determine the optimal parameters for the present nonlinear DVA, the energy approach method is considered. By defining m = 2 and n = 0 in Eq. (28), the optimal set is defined as λ = 9900Ns/m and k = 2.4 × 10⁸ N/m². Then, by applying the deflection approach, the following λ and k are found 4750 Ns/m and 1.55 × 10⁸ N/m². A detailed comparison between different optimization results under moving load excitation is brought in Table 4, at the end of Sect. 5.7. The maximum deflection of the beam and the absorbed energy by DVA is represented in Fig. 12. The interesting result is that for the considered nonlinear DVA with quadratic stiffness and linear damping there is a perceptible anti-peak for energy approach, Fig. 12b, point C. While, for the case with linear DVA with Den Hartog optimized values and case with nonlinear DVA with quadratic stiffness and linear damping, optimized with deflection approach optimization method, no anti-peak is observed.

Table 4 Comparison between various optimization results under pedestrian excitation

Fig. 12

a Maximum deflection of footbridge with an attached DVA with quadratic stiffness and linear damping in frequency domain; b The amount of dissipated energy by DVA

Peak A, in Fig. 12a, shows the minimum deflection of 0.97 mm in the deflection approach method, which is smaller than peaks B and C, which means DVA with quadratic stiffness and linear damping performance is better concerning linear DVA. As it is illustrated in Fig. 12a, a nonlinear DVA with quadratic stiffness (dashed black line) which is optimized based upon the deflection approach optimization method, approximately in the whole range of frequency (1.5 Hz- 2.5 Hz) performs better than a linear DVA with Den Hartog values. In Fig. 12b, peak B (Den Hartog values) presents η = 90.68%, which is higher than peaks C and A, corresponding to energy and deflection approach methods. The anti-peaks at frequency 2 Hz, are due to a resonance phenomenon. It means that this particular type of nonlinear DVA is not a more efficient concerning the linear DVA from the energy approach point of view.

Figure 13 is presented to check the correctness of the peak and anti-peak observed in Fig. 12; points C in Fig. 12a, b. For this purpose, the deflection of the footbridge and the relative velocity of the DVA in the critical frequency (1.86 Hz), and a frequency beside the critical frequency (1.97 Hz) in the time domain are investigated. Figure 13a–h present the deflection time response of the footbridge; where Fig. 13i–n present relative velocity time response of the mass of the DVA. In Fig. 13, two excitation frequencies are considered (1.86 Hz and 1.97 Hz). The attached linear DVA with Den Hartog values and nonlinear DVA with quadratic stiffness and linear damping (for both above-mentioned optimization approaches) are considered. The beam with an attached nonlinear DVA, optimized by the energy approach method, introduces more significant maximum deflection (2.6 mm) respect to the bare beam at the frequency of 1.86 Hz. The frequency of 1.86 Hz is the frequency in which a peak in Fig. 12a or an anti-peak in Fig. 12b is appeared (illustrated with point C on the green lines). One important point is that the beam deflection possessing nonlinear DVA, optimized by the energy approach method, introduces more significant maximum deflection (2.6 mm) respect to the bare beam at the frequency of 1.86 Hz. The beam with linear DVA does not show any anti-peak for this frequency; this is investigated in time history results in Fig. 13g, too. The DVA mass velocity respect to beam $(\dot{u})$ is presented in Fig. 13k for the frequency of 1.86 Hz (frequency of anti-peak). Similar time responses are presented in Fig. 13b, d, f, and h for comparison. This frequency (1.97 Hz) is close to the primary resonance, which is less critical for the considered cases. These time response results verify the results presented in Fig. 12.

Fig. 13

Time responses of the footbridge mid-span a, b bare beam deflections, c, d beam with nonlinear DVA optimized by deflection approach, e, f beam with nonlinear DVA optimized for energy approach, g, h beam with DVA with Den Hartog values, i, j relative velocity of mass of DVA optimized by deflection approach, k, l relative velocity of mass of DVA optimized by energy approach, m, n relative velocity of mass of DVA with Den Hartog values, Note: at t = 40 s the pedestrian leaves the footbridge

5.4 Nonlinear DVA with quadratic damping and quadratic stiffness

The performance of nonlinear DVA with quadratic stiffness and quadratic damping characteristics is evaluated in this section. The optimal parameters are listed in Table 4; the maximum deflection of the beam and the absorbed energy by DVA is represented in Fig. 14. It is apparent from Fig. 14b that by using this type of DVA, optimized by the energy approach method the minor anti-peak in the frequency of 1.88 Hz occurs. At the same frequency in the deflection graph, Fig. 14a point C, the peak is observable. The integer powers for elastic and damping forces in Eqs. (15) and (16) are α = 1, β = 1, γ = 1, and δ = 1. The integer powers in Eq. (28) are: m = 2 and n = 1.

Fig. 14

Footbridge with an attached DVA with quadratic stiffness and quadratic damping in frequency domain a maximum deflection, b the amount of dissipated energy by DVA

Peak A, in Fig. 14a, shows the minimum deflection of 0.97 mm in the deflection approach method, which is smaller than peaks B and C; which means DVA with quadratic stiffness and quadratic damping perform better respect to linear DVA. The optimal values λ = 230 kNs²/m² and k = 150 × 10⁶ N/m² are obtained in an overall search using the deflection approach optimization method. These optimal values for the energy approach method are λ = 1350 kNs²/m² and k = 265 × 10⁶ N/m². As shown in Fig. 14a, a nonlinear DVA with quadratic damping and stiffness (dashed black line), in the whole considered range of frequency, except the ranges of [1.78 Hz- 1.83 Hz] and [2.3 Hz–2.4 Hz] performs better than a linear one with Den Hartog values. In Fig. 14b, peaks B and C illustrate the η = 90.68% related to Den Hartog and energy approach optimization values, which are higher than peak A, of the deflection approach method. The anti-peaks at frequency 2 Hz, are due to a resonance phenomenon. It means that this type of nonlinear DVA is not a more efficient concerning the linear DVA from the energy approach point of view.

5.5 Nonlinear DVA with cubic damping

As it is mentioned in the introduction section of the present study, in Ref [9] concluded that using the higher power of nonlinearity for stiffness leads to a more effective reduction of beam deflection. So, in the following subsections, the higher power of nonlinearity for damping and stiffness are investigated. In this section a cubic damping and linear stiffness for the DVA is considered. By choosing α = 1, β = 0, γ = 3, δ = 0 in Eqs. (15) and (16), the maximum deflection of the footbridge and the absorbed energy by the DVA, are illustrated in Fig. 15a, b, respectively. By using the energy approach method and employing Eq. (28) with m = 4 and n = 0, the following optimal values are obtained as λ = 9.5 × 10⁷ Ns³/m³ and k = 1.48 × 10⁵ N/m. The maximum value of the minimum dissipated energy by DVAs is 92% which is shown by Fig. 15b by peak C. The minimum deflection of 0.96 mm, which is shown by peak A, for the achieved optimum parameters: λ = 2.75 × 10⁷ Ns³/m³ and k = 1.85 × 10⁵ N/m, is obtained in an overall search using the deflection approach optimization method; results are shown in Fig. 15a. The peak points A, B, and C corresponding to the critical frequencies are shown in Fig. 15. Decreasing in absorbed energy due to deflection approach optimization values (frequencies lower than 1.75 Hz) is not due to resonance or superharmonic resonance; in fact, it is because of the method of optimization and the mechanical values achieved from this method. The interesting result is that for the considered nonlinear DVA with cubic damping and linear stiffness, there is a perceptible anti-peak at the frequency of 1.95 Hz for the energy approach shown in Fig. 15b; which introduces maximum deflection (1.8 mm) at the frequency of 1.95 Hz that is shown in Fig. 15a.

Fig. 15

DVA with cubic damping and linear stiffness; a Maximum deflection of footbridge; b the energy absorbed by DVA

5.6 Nonlinear DVA with cubic stiffness

This section investigates cubic stiffness performance for the nonlinear DVA. The integer powers of the elastic and damping forces [related to Eqs. (15) and (16)] are α = 3, β = 0, γ = 1, δ = 0. To determine the optimal parameters for the present nonlinear DVA, the energy approach method is considered. By defining m = 2 and n = 0 in Eq. (28), the optimal set is defined as λ = 11700Ns/m and k = 2.57 × 10¹¹ N/m³. Then, by applying the deflection approach, the following λ and k are found as 7750Ns/m and 1.29 × 10¹¹ N/m³. A detailed comparison between different optimization results under moving load excitation is listed in Table 4, at the end of Sect. 5.7. The maximum deflection of the beam and the absorbed energy by DVA is illustrated in Fig. 16. The interesting result is that for the considered nonlinear DVA with cubic stiffness and linear damping there is a perceptible anti-peak for energy approach; while for the case of linear DVA with Den Hartog values, and DVA with cubic stiffness and linear damping, which is optimized by deflection approach optimization method, no anti-peak is observed, Fig. 16b, point C.

Fig. 16

DVA with cubic stiffness and linear damping attached to the footbridge; a Maximum deflection of footbridge; b the energy absorbed by DVA

5.7 Nonlinear DVA cubic damping and cubic stiffness

In this section, the behavior of the system with cubic damping and cubic stiffness has been studied. By applying energy and deflection approach optimization methods, the mechanical characteristics of the DVA are defined; which listed in Table 4. The maximum deflection of the beam and the absorbed energy by the DVA is illustrated in Fig. 17. It is apparent from Fig. 17b that by using a DVA with cubic stiffness and cubic damping, optimized by the energy approach method the anti-peak in the frequency of 1.9 Hz occurs. At the same frequency in the deflection graph, Fig. 17a, point C, the peak is observable. The integer powers for elastic and damping forces in Eqs. (15) and (16) are α = 3, β = 0, γ = 3, δ = 0. The integer powers in Eq. (28) are: m = 4 and n = 0.

Fig. 17

a Maximum deflection of footbridge; b the energy absorbed by DVA

The issue is apparent from Fig. 17 is that for cubic damping and cubic stiffness, the DVA optimized for the deflection approach behave suitably for both approaches for the frequency range of 1.8–2.2 Hz. Table 4 summarizes results for a bare beam and beam subjected to DVAs (linear and nonlinear); these results are for the frequency range of 1.5–2.5 Hz.

The Sects. 5.2 to 5.7 show that the optimal parameters for the approach of minimum deflection and approach of maximum absorbed energy are not necessarily similar; i.e., it is essential to specify the goal of using DVA and then decide for suitable DVA. In Ref.[9], using higher power for the nonlinear stiffness leads to a more effective reduction of the beam deflection which is subjected to the vehicles; wherein this study, quadratic nonlinearities show better performance for the case of pedestrian excitation. In this research higher-order in stiffness and damping nonlinearities is studied. However, no improvement is found; so, for the sake of brevity, such results are omitted in this paper.

6 Discussion

In this section, the results of the previous sections are discussed. The performance of different types of linear and nonlinear DVAs is analyzed with two approaches. The first approach is the minimization of the maximum footbridge deflection. Smaller footbridge deflection leads to smaller stress and finally longer structure lifetime. The second approach maximization of the energy transferred from the footbridge to the DVA. Bigger dissipation energy by DVA means that the footbridge vibration damps faster, i.e., less vibrational motion. One interesting result of this paper arises from Fig. 12a. It is shown that utilizing the DVA with quadratic stiffness and linear damping, optimized by the deflection approach, within 92% of the investigated frequency range (1.5–2.5 Hz), the deflection of the footbridge is smaller concerning a footbridge with a linear attached DVA. It means that this type of nonlinear DVA leads to better performance over a wide range of frequency. Another interesting result arises from Fig. 14a; by using a nonlinear DVA with quadratic stiffness and quadratic damping optimized by deflection approach over 86% of the investigated frequency range (1.5–2.5 Hz), the deflection of the footbridge is smaller concerning the footbridge with optimized linear DVA. This later type of DVA is the most effective DVA type for a critical frequency value. The rest of the other investigated types of DVAs could not make sensible improvements. It is notable by using: (1) nonlinear DVA with quadratic damping and linear stiffness (2) nonlinear DVA with cubic damping and linear stiffness, the maximum deflection of 0.96 mm achieved. The maximum absolute deflection for the footbridge without DVA is 11.4 mm; for the footbridge with optimized linear DVA is 0.96 mm, which is similar to the optimal nonlinear cases. The Den Hartog optimization presents the maximum deflection of 1.1 mm; which means such parameters are not the absolute optimum values. However, the nonlinear DVAs are effective for reducing the maximum deflections over a wider frequency range; it can be observable for different DVA types, Figs. 11a, 10a and 12a. It can conclude that the use of nonlinear (quadratic stiffness and linear damping or quadratic damping and quadratic stiffness) DVAs instead of the classical linear DVA is convenient for the footbridges.

Figure 18 is presented merely to show how the higher modes at the internal resonances can be effective on the nonlinear results of this paper. 20 modes of the footbridge have been considered to investigate the effect of the nonlinearity of the DVAs on the excitation of the other modes. Fro this verification, only two selected DVAs (cases 8 and 10) are investigated. As it is shown in Fig. 18a, b, the continuous red line shows the footbridge response by considering 4-mode expansion; where the black dotted line shows the footbridge response with 20 modes of vibration. The figures show that there is no difference between the two expansions, so the internal resonances would not occur under the excitation frequency in the frequency ranges of 1.5–2.5 Hz. Notably, the internal resonances may occur under the excitation frequencies of more than 3 Hz and less than 1.25 Hz; which is not in the applicable walking excitation frequency ranges of 1.5–2.5 Hz.

Fig. 18

Maximum deflection of footbridges; a DVA with quadratic stiffness and linear damping attached to the footbridge; b DVA with quadratic stiffness and quadratic damping attached to the footbridge

7 Concluding remarks

In this paper, the vertical response of a bare simply-supported footbridge subjected to a single moving pedestrian is studied. The considered frequency range is the applicable frequency range for normal pedestrian (1.5–2.5 Hz). The performance of different types of linear and nonlinear DVAs is analyzed. The main conclusion points of this research are listed as follow:

• Two nonlinear DVA types introduce better performance respect to the optimized linear DVA: (i) nonlinear DVA with quadratic stiffness and linear damping and (ii) nonlinear DVA with quadratic damping and quadratic stiffness; which are optimized with deflection approach optimization method. These two nonlinear DVAs with optimal parameters can decrease footbridge deflection over the walking pedestrian frequency range.

• The present results give approximately 12% smaller deflection for the footbridge with an attached DVA with quadratic nonlinearity in comparison with linear DVA with Den Hartog formulation, under moving single pedestrian.

• With an attached DVA with cubic damping and linear stiffness an 11% reduction will be achieved in comparison with linear DVA with Den Hartog formulation, under moving single pedestrian.

• Even by using a linear DVA optimized by deflection approach method, the maximum deflection of the footbridge will be less than the deflection of the footbridge with an attached linear DVA with Den Hartog formulation. Note that, the excitation type in this research is a kind of transient load with harmonic amplitude considering for 4 expansion modes.

• Results show that using an energy approach optimization method for DVAs, will not help in suppressing the deflection of the footbridge in comparison with Den Hartog formulation. Even, this type of optimization will not affect on the velocity of damping the vibrations by absorbing the energy from the footbridge.

• Nonlinear DVAs with cubic stiffness nonlinearity does not have better performance respect to the linear DVA with Den Hartog formulation in suppressing the footbridge deflection.