Performances of dynamic vibration absorbers for beams subjected to moving loads

Abstract

The goal of this work is a general assessment regarding the performances of linear and nonlinear dynamic vibration absorbers (DVAs) applied to the specific problem of moving loads or vehicles. The problem consists of a simply supported linear Euler–Bernoulli beam excited with a moving load/vehicle; a DVA is connected to the beam in order to reduce the vibrations. The moving vehicle is modeled by a single degree of freedom mass spring system. The partial differential equations governing the beam dynamics is reduced to a set of ordinary differential equations by means of the Bubnov–Galerkin method. A parametric analysis is carried out to find the optimal parameters of the DVA that minimize the maximum vibration amplitude of the beam. For the case of a moving vehicle, the energy absorbed by the DVA is evaluated. Comparisons among the performances of different types of linear and DVAs are carried out. The goal is to clarify if the use of nonlinearities in the DVAs can effectively improve their performances. The study shows that the most effective type of DVA for the test cases considered is the piecewise linear elastic restoring force.

1 Introduction

The dynamic response of the beams subjected to the passage of moving loads or moving vehicles is an interesting topic for structural engineers. Trains or vehicles running on bridges, trolleys of overhead traveling cranes that move on their girders and the airport runways may be modeled as loads, masses or vehicles running on beams with or without contact with an elastic ground. When excessive external loads having high velocity move on bridges (or generically on a flexible slender structure), the structures may suffer from large deflections that can cause damages and danger for human life and structural integrity.

Several techniques can be considered for reducing structural vibrations; among others, the use of dynamic vibration absorbers is very promising.

The dynamic vibration absorbers (DVA) consist of mass–spring–damper systems attached to the main structure; in their simpler linear form, they are widely used in Engineering for reducing vibrations; in particular, they are very effective in the case of harmonic steady excitations. DVAs are preferred to active controls for several reasons: (i) after a good tuning, DVAs work well regardless of the frequency; conversely, active controls are suitable for low frequencies; (ii) DVAs work well regardless of the scaling (nano to macro scale); (iii) there is no need for maintenance or power supply; (iv) DVAs are suitable for big structures (bridges, buildings, skyscrapers) where active controls would need unrealistically huge power. The previous comments explain why in many applications DVAs represent the only way to suppress or reduce the vibration of a structure; therefore, improvements of their performances are welcome.

It is useful to point out that DVAs are called differently in the scientific and technical literature, depending on their nature and behavior: tuned mass dampers (TMD), dynamic dampers, nonlinear energy sinks (NES, only for special nonlinear DVAs displaying irreversible energy transfer from the structure to the DVA).

In [1, 2], it is shown that DVAs can be effective also for structures subjected to moving loads.

For the case of linear vibration absorbers and periodic loading, Den Hartog [3] proved that one can find the optimal linear spring and viscous damper coefficients in order to minimize structural deflection. We have shown [2] that, in the case of transient moving loads on beams, the optimal stiffness and damper coefficients are generally different from those obtained by the classical approach [3] that was developed for periodic excitations.

References [4, 5] are suggested to readers interested in a comprehensive treatise on structures excited by moving loads; these publications report several applications.

In the past, researchers tried to find suitable DVAs able to decrease structural deflections, in order to increase the lifetime of structures subjected to moving loads; most of them used linear vibration absorbers [6–12]. Interesting studies, focused on the performance of nonlinear DVAs, can be found in [13–15]; however, such works did not consider moving loads or moving vehicles; moreover, most of them considered only DVAs having cubic stiffness. In [16, 17], it was shown that, under certain conditions, a local nonlinear attachment, having essential nonlinear stiffness, can passively absorb energy from a linear non-conservative (damped) structure, in essence acting as a nonlinear energy sink (NES).

Jiang et al. [18] showed that the nonlinear DVAs are capable of absorbing steady state vibration energy from the linear oscillator over a relatively broad frequency range [18]; they pointed out that those nonlinear DVAs behave as passive energy pumping, i.e. a one-way irreversible transfer of energy takes place from a linear main system to a nonlinear attachment. Malatkar and Nayfeh [19] explored the rich dynamics exhibited by a harmonically excited linear subsystem coupled with an essentially nonlinear oscillator; they did not find any occurrence of energy transfer via modulation, as indicated in [18]. In the rebuttal [20], Vakakis and Bergman claimed that steady state energy pumping occurs in certain frequency ranges of the coupled system. Finally, in [21], Malatkar and Nayfeh provided more results to disprove what was claimed in [20], they wrote that the addition of the nonlinear DVA leads to an increase in the amplitude of vibration of the linear subsystem and that the name of the so-called nonlinear energy sink (NES) is not suitable for these passive DVAs. The issue seems to be still open.

Recently, Lee et al. [22] studied the performance of vibro-impact DVAs in systems of coupled oscillators; a 1-DOF primary linear oscillator was coupled with a vibro-impact attachment acting as a non-smooth NES. They found that the most efficient mechanism for vibro-impact targeted energy transfers is through the excitation of highly energetic impulsive orbits, i.e. periodic or quasi periodic orbits corresponding to zero initial conditions, except for the initial velocities of the linear oscillators.

Deshpande et al. [23] developed a numerical approach to optimize the performance of a piecewise linear vibration isolation system. They found that the optimal solution depends on the damping coefficients, stiffness ratio, and clearance.

Rüdinger [24] studied the performance of nonlinear viscous damping for DVAs attached to a single-degree-of-freedom system excited by white noise. They found that the structural damping has very little influence on the optimal parameters for a DVA. Moreover, Rüdinger [24] revealed that the optimal linear and nonlinear DVAs have practically the same effect in terms of reducing the structural displacement.

In the present paper, the performances of linear and nonlinear DVAs are studied; the goal is to reduce the vibration of an Euler–Bernoulli beam under transient moving load or moving vehicle. The present work completes and enlarges the analyses carried out in [1, 2]. In [2], only the cubic stiffness is considered as nonlinearity; moreover, the case of moving vehicle excitation (dynamic effects of moving elements) was not studied.

Here, the performances of different types of nonlinear local passive attachments having monomial, polynomial or piecewise linear stiffness are considered. The moving vehicle is modeled considering dynamic effects due to the suspension. The partial differential equation (PDE) governing the beam dynamics is reduced to a set of ordinary differential equations (ODE) by applying the Bubnov–Galerkin method. After expanding the displacement field using the eigenfunctions of the beam without attachments and loads, the PDE is projected using a metric that takes advantage from the orthogonality properties of the eigenfunctions. The resulting ODEs, which are generally nonlinear (and also non-smooth in the case of piecewise linear attachments), are studied numerically using adaptive step size integration method, which automatically switches between BDF (backward differentiation formulas) and Adams multistep methods, depending on the “stiffness” of the equations (Mathematica).

Optimal parameters of linear and nonlinear DVAs are obtained numerically using two strategies: brute force and random search. The DVAs are classified on the base of their performances.

The goal of this paper is to furnish a clear and honest scenario regarding the capability of nonlinear DVAs to reduce and damp out the vibration of a slender structure under moving loads; in addition, the nonlinear DVAs are compared with the classical linear ones, in order to clarify if the use of nonlinearities gives effective improvements.

2 Dynamical systems and basic equations

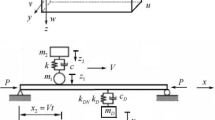
In this section, a model of the beam subjected to a moving vehicle or load (one DOF model, i.e. monocycle) is developed; see Figs. 1 and 2. The model consists of a simply supported beam connected to a small mass through a linear or nonlinear spring and a linear or nonlinear viscous damper. In the case of moving vehicles, Fig. 1, a mass is connected to the beam through a linear spring and a damper; this mass moves along the beam and exerts on it a force depending on the relative motion. In the case of a moving load, Fig. 2, there is a constant load that travels on the beam. The latter one is a simplified model largely used in the literature, even though it neglects the dynamic effects of the vehicle dynamics and the interaction with the beam.

Fig. 1

A beam model subjected to a moving vehicle

Fig. 2

A beam model subjected to a fixed position transient force, see [25]

2.1 Basic Equations

The beam dynamics is modeled through the Euler–Bernoulli theory, a DVA is attached to the beam, it exerts an additional action on the beam. The equations of motion read:

1. Beam

(1a)

(1b)

(1c)

2. Moving load or vehicle

$$ f_{m} = \left\{ \begin{array}{@{}l} \{[k_{v}w(t) + c_{v}w,_{t}(t)]\delta(x - Vt)H ( \frac{L}{V} - t), \\[2mm] \quad\mathrm{moving\ vehicle}\} \\[2mm] - F_{0}\delta(x - Vt)H ( \frac{L}{V} - t ),\quad \mathrm{moving\ load}. \end{array} \right. $$

(1d)

3. DVA

(2a)

$$ u ( t ) = y ( d,t ) - v ( t ). $$

(2b)

For the case of moving vehicle an additional differential equation must be added:

(3a)

$$ w(t) = y(d,t) - z(t). $$

(3b)

The beam dynamics is governed by the PDE represented by (1a) with simply supported boundary conditions (1b) and initial conditions (1c): the term [f(u)+λu, _t (t)]δ(x−d) represents the force exerted by the DVA; x is the longitudinal coordinate measured from left end of the beam; t is the time; f(u) is the elastic restoring force, which can be linear or nonlinear; $\tilde{f}(u,_{t})$ represent the dissipative force of the DVA, which is considered generally linear (λu, _t (t)) if not specified otherwise; F ₀ and V are the magnitude and speed of the moving force, respectively. y(x,t) is the transverse displacement field of the beam (down is positive). E is the Young’s modulus; I is the moment of inertia of the cross-section area; ρ is the material density and A is the cross-section area. Equation (1d) defines f _m , the beam excitation for the moving vehicle or the moving load. Equation (2a) governs the dynamics of the DVA: v(t) is the absolute position of the vibration absorber mass m ₀; x=d represents the location of the DVA on the beam. δ is the Dirac function and H(t) is the Heaviside step function; u(t) is the elongation of DVA spring, which is defined by (2b). Equation (3a) governs the vehicle dynamics; m _v , k _v and c _v are the mass, stiffness and viscous damping of the vehicle suspension, respectively; z(t) is the vertical position of the vehicle (down is positive). w is the elongation of the suspension, which is defined by (3b); g is the acceleration of gravity. Note that, due to the nonlinearity of the vibration absorber, this set of partial differential equations cannot be decoupled.

2.2 Discretization

The dynamics of the system are analyzed by projecting the partial differential equation (1a) into a complete and orthonormal basis. For the present problem, the eigenfunctions of the linear operator representing the simply supported beam without attachments can be used, see [2] for details:

(4a)

φ _r (x) is the normalized eigenfunction and ω _r is the natural frequency of the rth mode. The eigenfunctions satisfy the following orthonormality conditions,

(4b)

where δ _ij is Kronecker’s delta. The transverse vibration of the beam is expanded as follows:

$$ y ( x,t ) = \sum_{r = 1}^{\infty} a_{r} ( t )\varphi_{r} ( x ), $$

(5)

where a _r (t) are unknown functions of time (modal coordinates).

After projecting on the pth eigenfunction and using the orthonormality conditions, one obtains

(6a)

$$ m_{0}\ddot{v} ( t ) - D ( t ) - \tilde{D} ( t ) = 0, $$

(6b)

(6c)

$$ D_{v}(t) = \left\{ \begin{array}{@{}l} \{k_{v} [ z ( t ) - \sum_{r = 1}^{\infty} a_{r} ( t )\phi_{r} ( Vt )] \\[2mm] \quad{}+ c_{v} [ \dot{z} ( t ) - \sum _{r = 1}^{\infty} \dot{a}_{r} ( t ) \phi_{r} ( Vt ) ],\\[2mm] \quad\mbox{moving vehicle}\} \\[2mm] F(t),\quad\mbox{moving load}, \end{array} \right. $$

(6d)

$$ \tilde{D} ( t ) = \left\{ \begin{array}{@{}l} \{\lambda [ \sum_{r = 1}^{\infty} \dot{a}_{r} ( t )\phi_{r} ( d ) - \dot{v} ( t )], \\[2mm] \quad\mbox{if not specified}\} \\[2mm] \lambda_{3} [ \sum_{r = 1}^{\infty} \dot{a}_{r} ( t )\phi_{r} ( d ) - \dot {v} ( t ) ]^{3}. \end{array} \right. $$

(6e)

D(t) represents the restoring force acting on the beam due to the DVA spring:

(7a)

(7b)

(7c)

The transient response of the ODEs represented by Eqs. (6a)–(6e) and (7a)–(7c) is studied numerically.

3 Validation

In order to validate the present model, the case of a beam connected with a nonlinear vibration absorber loaded with a time transient force having fixed position is now investigated; see [25]. Consider the system of Fig. 2, with f(u)=Cu ³, subjected to an impulsive force, a half-sine shock with magnitude F _a ; see Fig. 3.

Fig. 3

Half-sine pulse excitation force

The portion of the input energy absorbed by DVA is called η; the remaining portion of energy, i.e. (1−η), is dissipated inside the main beam structure, η is computed by the following expression:

$$ \eta= \frac{E_{\mathrm{NES}}}{E_{\mathrm{in}}} = \frac{\int_{0}^{t_{1}} \lambda [ \dot{v} ( t ) - \sum_{r = 1}^{n} \dot{a}_{r} ( t )\varphi _{r} ( d ) ]^{2}\,\mathrm{d}t}{\int_{0}^{t_{0}} F_{1} [ \sum_{r = 1}^{n} \dot{a}_{r} ( t )\varphi_{r} ( x_{F} ) ]\,\mathrm{d}t}. $$

(8)

E _in represents the total input energy of the beam due to the excitation; E _NES is the energy that is passively absorbed and locally dissipated by the DVA; t ₁ is assumed large enough to assure that the transient dynamics is damped out; and t ₀=T/2 is the impulse duration.

For the present comparison, the numerical parameters are the following: F _a =10.0 N, T=0.4/π s, EI=1.0 Pa m⁴, ρA=1.0 kg/m, 2ξ _p ω _p =0.05 s⁻¹, L=1.0 m, m ₀=0.1 kg, x _F =0.3 m, λ=0.05 N s/m, d=0.65 m and C=1.322×10³ N/m³, five mode shapes are taken into account in the series (5). Note that in this model the modal damping ratio is not constant for the beam, for example, ξ ₁=0.00253, ξ ₂=0.000633…; t ₁ is set equal to 150 s.

A comparison between the present model and results of [25] is shown in Figs. 4 and 5. Figure 4 shows v(t), i.e. the DVA deflection. Figure 5 presents the portion of energy dissipated by the DVA, η, versus its stiffness coefficient. Good agreement between [25] and the present model is found.

Fig. 4

Transient response of DVA deflection: (—) present results, (•) [25]

Fig. 5

The portion of input energy absorbed and dissipated by the DVA as a function of DVA stiffness (C): (—) present results, (•) [25]

4 Numerical results

The following test case is considered for the numerical model: E=206800 MPa, ρ=7820 kg/m³, A=0.03 m×0.03 m, L=4 m, ξ _p =0.01 (p=1,2,…) and m ₀=1.4076 kg. The vibration absorber is installed near the middle, d=0.55L for linear and piecewise linear vibration absorber and d=0.53L for other kinds of nonlinearities; if not specified otherwise, the damping is linear and viscous with λ=0.1 N s/m, see [3] for explanation. The maximum deflection occurs at different velocities for the case of the moving load and moving vehicle; in each case, the optimization is carried out to find the corresponding critical velocities.

Figure 6 shows the transient response of the beam without attachment, as well as the beam with linear DVA optimized in [6], V=21.5 m/s. The vertical green line shows the time instant for which the moving load leaves the beam (x _F =L); the maximum deflection occurs at the first peak, which happens before the load leaves the beam.

Fig. 6

Transient responses: bare beam (- - -); beam with linear DVA (—)

4.1 DVA optimization under moving load excitation

The beam is now excited by a moving load with constant magnitude, F(t)=F ₀=9.8N, the beam presents an internal dissipation, ξ _p =0.01 (p=1,2,…). The maximum beam deflection occurs at V=21.5 m/s; for such a velocity, the maximum bare beam deflection is 1.6042 mm, see [2].

4.1.1 Performance of the monomial stiffness

Consider a local attachment having monomial stiffness; i.e. f(u)=c _i u ⁱ, i=1,3,5,7,9, see Eq. (1a). The linear (f(u)=c ₁ u) and cubic (f(u)=c ₃ u ³) stiffnesses have been studied in [2]; here we use such cases for comparisons.

For each type of monomial, the nonlinear DVAs are optimized; Figs. 7(a)–7(d) show the maximum beam deflection with DVA versus the coefficient c _i . The optimal coefficients are readily obtained. Note that a unique minimum is present. The optimal (minimum) deflections and the corresponding stiffness coefficients are summarized in Table 1. The reduction percentage for each case is calculated by comparing the maximum beam deflection with the maximum deflection of the bare beam, i.e. Case 1 in Table 1. In [3], it was found that the cubic stiffness shows better performance with respect to the linear one. The results reported in Table 1 show that using higher power for the nonlinear stiffness leads to a more effective reduction of the beam deflection. For example, by using a linear DVA, one can reduce the beam deflection by 6.159 % and using a cubic one, it is possible to reduce the beam deflection by 7.418 %; while if a power-nine stiffness is used, f(u)=c ₉ u ⁹ (c ₉=88×10²⁷ N/m⁹), the DVA is able to reduce the beam deflection up to 8.147 %.

Fig. 7

Moving loads, optimal monomial stiffness: (a) f(u)=c ₃ u ³; (b) f(u)=c ₅ u ⁵; (c) f(u)=c ₇ u ⁷; (d) f(u)=c ₉ u ⁹

Table 1 Comparison of different kinds of DVA, λ=0.1 N s/m

4.1.2 Performance of the polynomial stiffness

Consider a DVA having linear viscous damping and polynomial stiffness, f(u)=c ₁ u+c ₃ u ³+c ₅ u ⁵+c ₇ u ⁷. The optimization is carried out considering a four-parameter space: c ₁, c ₃, c ₅ and c ₇. Such parameters are randomly sampled and the minimum deflection is found. The total number of random samples (sets of parameters) is 1,720,000. The high dimension of the parameter space makes a direct search of the optimum impossible; however, the number of random samples has been set big enough to have acceptable resolution. After carrying out the random search, one obtains a set of values of the objective function (maximum beam deflection) versus four parameters c _i ; this set is projected on sections of the parameter space to allow visualization; see Figs. 8(a)–8(d).

Fig. 8

Moving loads, random optimization of the polynomial stiffness: (a) maximum deflection vs. c ₁; (b) maximum deflection vs. c ₃; (c) maximum deflection vs. c ₅; (d) maximum deflection vs. c ₇

The optimal set is found by means of a suitable code developed for the Mathematica software. However, Figs. 8(a)–8(d) allow quickly finding the minimum and the corresponding parameter set; such a set is presented in Table 1, Case 6; it gives the maximum beam deflection equal to 1.4757 mm (8.01 % reduction with respect to bare beam). Similarly to the previous cases, a linear dissipation is used, λ=0.1 N s/m.

It turns out that the dominant part of this DVA is the seventh power of stiffness (c ₇=46.6(10²¹) N/m⁷); i.e. the effects of linear (c ₁=15.7 N/m), cubic (c ₃=0.49(10⁹) N/m³) and fifth power terms (c ₅=0.56(10¹⁵) N/m⁵) are negligible with respect to the seventh power term. This can be proven by comparing Case 6 of Table 1 with Cases 2–5. By comparing Case 6 of Table 1 with Cases 5, 7, it turns out that a high power monomial stiffness performs better than a polynomial one. Figure 8 shows also that the minimum is located in a flat region, this means that it is robust; moreover, no local minima are visible.

4.1.3 Performance of the piecewise linear stiffness

Now a piecewise linear stiffness for the DVA is considered. This kind of restoring force is relatively simple to realize using linear springs with a gap; moreover, it can be thought as a limiting case of the high power restoring force. Figure 9 shows a schematic representation of this restoring force versus a generic elongation u. When the elongation |u| is smaller than the gap Δ, the restoring force is zero (2Δ is the dead zone). For |u|>Δ, the restoring force varies linearly with u; the slope is given by k.

Fig. 9

Schematic stiffness force versus stiffness deflection for piecewise linear DVA

The optimization is carried out considering two parameters: Δ and k; such parameters are regularly sampled. Figure 10 depicts the maximum beam deflection versus Δ and k; the behavior is extremely regular and the optimum appears robust, the optimal pair is k=37,000 N/m and Δ=0.58 mm, corresponding to a maximum beam deflection equal to 1.4735 mm (8.147 % reduction with respect to the bare beam). Figure 11 is the 3D representation of Fig. 10; it confirms the regularity of the objective function and the flatness of the neighborhood of the optimum. Table 1 shows that the piecewise linear DVA is the most effective for reducing the beam deflection (Case 8).

Fig. 10

Moving loads. Maximum deflection vs. gap Δ and stiffness k of the piecewise linear stiffness; the optimum is k=37,000 N/m and Δ=0.58 mm (1.4735 mm max deflection)

Fig. 11

Moving loads. Maximum deflection vs. gap Δ and stiffness k of the piecewise linear stiffness: 3D presentation

4.2 DVA optimization under moving vehicle excitation: maximum deflection approach

A moving vehicle is considered now; the physical parameters for the beam are the same as in the case of a moving load. Moreover, m _v =1 kg, k _v =980 N/m and c _v =6.26 N s/m are the mass, stiffness and viscous damping of the moving vehicle, respectively, and g=9.81 m/s² is the gravitational acceleration. Note that the weight of the present moving vehicle corresponds to the moving load of the previous section.

For the present case, the maximum deflection of the beam without attachment, 2.498 mm, occurs at V=19.5 m/s; this velocity is slightly less than the critical one for the case of a moving load. The maximum deflection is bigger with respect to the case of the beam under moving load. This is the first proof for the need of replacing a moving load with a more realistic model of the moving vehicle. Now the task is to find the best (optimal) DVA that is able to reduce the beam vibration.

Having in mind the results of the previous section, the best candidate should be the piecewise linear stiffness DVA; in order to give a comprehensive view of the performance, such a DVA is compared with those having linear and cubic stiffness.

4.2.1 Performance of the monomial stiffness (linear and cubic)

The optimal DVAs with linear and cubic stiffnesses are found following the procedure outlined in the previous section. The optimal linear DVA (location, d=0.55L) corresponds to k=2120 N/m and λ=0 N s/m (see Fig. 12), it allows a reduction of the maximum beam deflection by 6.35 % with respect to the bare beam, i.e. 2.3393 mm max deflection; when the DVA is in the middle of the beam, d=0.50L, the optimum is k=2030 N/m, the maximum beam deflection is 2.3427 mm (6.22 % reduction), details are omitted for the sake of brevity.

Fig. 12

Moving vehicle. Verification of optimal damping for linear absorber

In [3], numerical results proved that the use of a vibration absorber without dissipation leads to the best vibration reduction (note that in [3] only moving loads are considered); similar behaviors are found for the moving vehicle as well, see Fig. 12.

Table 2 summarizes the results obtained assuming that the viscous damping is λ=0.1 N s/m (zero damping is unrealistic): using a cubic nonlinear stiffness, one is able to reduce the maximum beam deflection from 2.4980 mm (bare beam) to 2.3393 mm, i.e. 6.35 % reduction; the DVA is more effective compared to the case of the beam under moving load. Figure 13 shows the optimal parameter search for nonlinear cubic stiffness, the behavior is quite smooth, there is a unique minimum and the region is flat.

Fig. 13

Moving vehicle, optimal cubic stiffness of the vibration absorber parameters: (a) optimal stiffness; (b) optimal location

Table 2 Maximum deflection approach: performance of the nonlinear DVA for the beam under moving vehicle, λ=0.1 N s/m

4.2.2 Performance of the piecewise linear stiffness

The nonlinear DVA having a piecewise linear stiffness is now investigated. In order to find the optimal pair Δ and k, a regular sampling is carried out; the position of the attachment is d=0.55L. Figures 14 and 15 show the maximum beam displacement versus Δ and k; similar to the case of the beam under a moving load, the piecewise linear vibration absorber is the most effective kind of DVA, with 8.43 % vibration reduction; see Table 2 (Case 4). The behavior of the objective function is similar to the case of a moving load (see Fig. 10), i.e. it is regular, there are no local minima and the optimum is located in a flat region.

Fig. 14

Moving vehicle, maximum deflection vs. clearance Δ and stiffness k of the piecewise linear stiffness; optimum set: k=28,000 N/m and Δ=0.79 mm (2.2874 mm max deflection)

Fig. 15

Moving vehicle. Maximum deflection vs. clearance Δ and stiffness k of the piecewise linear stiffness; 3D representation

4.3 Energy dissipation, optimal DVA under moving vehicle excitation

Even though the maximum amplitude of vibration is an extremely important indicator for evaluating the structure lifetime, one should consider that after the vehicle transit the structure undergoes several oscillation cycles; the number of cycles and the amplitude depend on the dissipation; they greatly influence the fatigue resistance.

The goal function of the present optimization is the portion of the input energy absorbed by the DVA, η; see (8) for definition. The excitation is a moving vehicle; for the case of a moving load excitation, check [2]. Let us consider linear viscous damping and three types of stiffness for the DVA; its location is d=0.55L. The moving vehicle velocity is constant, V=19.5 m/s. In Equation (8), t ₀ is L/V and t ₁ is set equal to 150 s, other numerical data remain unaltered.

The results of this section are summarized in Table 3; there are two design variables: stiffness (c ₁ for linear stiffness and c ₃ for cubic stiffness) and linear damping, λ. For these two cases, the brute force optimization is carried out. The number of samplings is 81 for each design variable. For the case of cubic stiffness, the portion of input energy absorbed by the DVA, η=η(λ,c ₃), is shown in Fig. 16.

Fig. 16

Moving vehicle, optimal DVA with cubic stiffness vs. η

Table 3 Energy approach: performance of the linear and nonlinear types of DVA stiffness for the beam under moving vehicle; damping behavior is linear. The values inside brackets are for the case of a moving load from [3]

In Fig. 17, the scenario for a DVA having cubic dissipation is presented, the optimum gives 87 % of the structural energy absorbed by the DVA when c ₁=860 N/m and λ ₃=4080 N s³/m³.

Fig. 17

Moving vehicle, optimal DVA with cubic damping vs. η

For the case of a piecewise linear stiffness, Case 3 in Table 3, there are three design variables: the stiffness, k, the gap, Δ, and the linear damping, λ. For this case, the random optimization is carried out, the total number of samplings is 20,000, details are omitted for the sake of brevity.

The results in Table 3 show that the capabilities of the investigated DVAs for absorbing input energy are almost the same.

5 Transient response, piecewise linear vibration absorber

In order to give a clear explanation of the physical behavior of the piecewise linear DVA, the transient responses of the beam and the DVA are shown in Fig. 18; time histories are presented both for the moving load and moving vehicle; the DVAs analyzed are: Case 8 of Table 1, for the moving load; Case 4 of Table 2, for the moving vehicle. Figures 18(a) and 18(b) show the displacement of the beam (x=0.55L) and the DVA mass. Details are presented in Figs. 18(c) and 18(d); the piecewise linear spring elongations (u(t)=y(0.55L,t)−v(t)) are shown as well. Figures 18(e) and 18(f) present the DVA mass velocities and accelerations. Three interesting different conditions deserve to be commented:

• 1. The absolute value of the DVA mass displacement is less than the gap, |u|<Δ (in the case of the moving load Δ=0.58 m and in the case of the moving vehicle Δ=0.79 m); there is no contact or force acting on the mass, i.e. the system is in the dead zone of the piecewise linear spring (note that the damping force with respect to the stiffness force is negligible). In this condition, the mass acceleration (thick green line) is zero, the mass velocity (orange line with diamonds) is constant and the mass displacement (blue line) is linear.

• 2. The elongation u is greater than the gap, u>Δu; the beam is moving down (down is positive), there is contact and the DVA mass is pushed down. The mass acceleration is positive (upward sharp peaks) and the velocity increases suddenly.

• 3. When the elongation u is negative, but it exceeds the gap (u<−Δ), there is contact and a force pushes up the mass; the mass acceleration has a downward sharp peak and the velocity decreases suddenly.

Fig. 18

Moving vehicle, transient responses for the beam and piecewise DVA: (dashed red line) beam deflection above the DVA (x=0.55L) [mm], (solid blue line) DVA mass deflection [mm], (dash–dot purple line) DVA spring elongation u(t)={y(0.55L,t)}−v [mm], (orange color) DVA mass velocity (10⁻²) [m/s], (green and thick) DVA mass acceleration [m/s²]; (a, c and e) under moving load; (b, d and f) under moving vehicle

The last two conditions happen for short periods and the non-contact condition is dominant.

Note that at the beginning the DVA mass remains steady (zero velocity), this is true until the elongation reaches the gap, about t=0.08 s. Initially, after each contact, a subsequent contact happens in the opposite direction, but later two similar contacts (same direction) can happen; this is due to the combination of the beam and DVA mass dynamics, sometimes the restoring force is not big enough to launch the mass across the whole gap, the beam moves more quickly and a “rebound” occurs. This situation is visible from mass acceleration time history when two subsequent peaks occur with the same direction.

6 Conclusions

In this paper, the performance of several kinds of nonlinear dynamic vibration absorbers is studied. Monomial, polynomial and piecewise linear DVA are applied to a simply supported Euler–Bernoulli beam under a transient moving load or a moving vehicle, in order to reduce the beam stresses and increase structural life.

Results show that, for the test cases considered, the DVAs with essentially nonlinear stiffnesses having higher power are more effective than the linear one in reducing the maximum beam deflection; however, DVAs having piecewise linear stiffnesses are the most effective both for moving loads and moving vehicles. Moreover, for the case of the beam under transient moving vehicle, DVAs are slightly more effective compared to the case of the moving load.

For the specific problem investigated in this paper, we can claim that there is no evidence that nonlinear DVAs are much better than linear ones, i.e. there is an improvement, but it is not relevant for engineering applications. It should be pointed out that the present study is fully numeric; therefore, we cannot exclude the possibility that in a remote and narrow region of the parameter space or in the case of a specific kind of excitations, the nonlinear DVAs could exhibit surprisingly good performances in attenuating the vibration of the main structure. However, our feeling is that such a remote possibility is irrelevant from an engineering point of view.

In the future, the present analyses could be improved by considering non-symmetric nonlinear stiffness and/or damping, distribution of DVAs over the structure with a possibility of cross-interactions. Of course, the increment of the complexity would lead to an incommensurably larger number of test cases to analyze; therefore, more sophisticated optimization techniques would be needed.