Semi-analytical analysis of vibrations induced by a mass traversing a beam supported by a finite depth foundation with simplified shear resistance

Abstract

In this paper the new semi-analytical solution for the moving mass problem on massless foundation, published by the author of this paper, is extended to account for inertial foundation modelled by a continuous homogeneous finite depth foundation with simplified shear resistance. Derivations are presented for infinite as well as finite homogeneous beams. Mode expansion method is used to solve the problem on finite beams, thus vibration modes, the corresponding orthogonality condition, reengagement of coupled equations to ensure significant calculation time savings are derived. Methods of integral transforms and contour integration are exploited to obtain the solution on infinite beams. Resulting vibrations are derived as a sum of the steady and unsteady harmonic vibrations and a transient contribution. The unsteady harmonic vibration is proven to be a useful indicator of unstable behaviour through the mass induced frequencies. Besides frequency lines also discontinuity lines are determined and their influence on the proximity of harmonic and full solutions is discussed. Even if the differences between these two versions are larger than for the massless foundation, it is shown that the harmonic solution provides a very good estimate of the full solution (in several cases perfect match is achieved) with the advantage to be obtainable by a simple evaluation of the derived closed-form results. Like for the massless foundation, also here, vibrations on infinite beams can be obtained on long finite beams with eliminated effect of its supports. All mentioned approaches are also validated by the finite element method.

1 Introduction

Several fields of engineering applications have to deal with moving load problems. These problems are specified by a guiding structure, usually in form of a beam, the foundation, which the guiding structure is placed on, and the moving load. Although this kind of applications generally uses the term “moving loads”, it should be clearly stated whether mass and thus inertial forces are included in the moving object or not, in other words, if moving force(s) or moving mass(es), oscillator(s), etc. are being considered.

This paper deals with the moving mass problem, which is inherently a non-linear problem, even if the mechanical properties of the respective parts are linear. Therefore, its solution is more complicated than the solution of the problem with the moving force, and in general there is no possibility of superposition of the results concerning different moving masses.

Moving load problems have attracted the scientific community for more than a century, and therefore a significant amount of works has already been published and it would be quite difficult to summarize all the relevant contributions. Hence, only some fundamental works and some recent trends will be referred with the focus on semi-analytical and analytical methods. In the first place it is necessary to mention Frýba’s monograph [1], where several solutions for finite and infinite structures are summarized, together with references to pioneering contributions in the field of moving loads [2,3,4,5,6].

There are several models used by the researchers to describe the moving load problems. In most of the models, the guiding structure has distributed mass and consequently allows for wave propagation. But wave propagation in the foundation is not always enabled, like in models with massless foundation. Foundations with lumped masses allow for wave propagation in a simplified manner. Only the distributed mass models are capable of full wave propagation. This is another fact that is very important to highlight in the beginning of the model description. Most times models referring “the elastic foundation” are grouped together, but it is quite different when such foundation is composed by Winkler springs or by elastic half-space.

Vibrations generated by moving forces traversing a beam on a massless foundation is still an active research field [7, 8], extension to non-linear behaviour is given in [9,10,11] and other features are analysed in [12,13,14]. Partially inertial foundation is used in classical models with discrete supports [15, 16], that are solved by finite element method (FEM) or other techniques. It is also necessary to mention moving elements, moving window method and spectral elements [17]. Alternatives to Fourier transform are based on wavelet approximations [18] which can be also extended to non-linear behaviour by Adomian decomposition method. Fully inertial models use elastic half-space [19,20,21]. However, because it is possible to assume that the part of the foundation that can be dynamically activated has only a limited depth, there is another group of works that take such assumption into account. This preposition facilitates the introduction of a dynamic interaction between the beam and the foundation, as shown in the critical velocity analysis in [22, 23] and in [24].

The moving mass or moving oscillator problem is generally more complicated than a moving force problem. Akin and Mofid [25] can be included among pioneering works, but there are also more recent developments [26,27,28,29,30,31,32,33,34], mostly related to finite beams. The problem has been solved numerically in [35]. Extensive analyses of conditions for instability are presented in [36,37,38,39]. Dynamic Green’s function is implemented in [40, 41], among recent contributions [42] can be mentioned.

If infinite homogeneous guiding structure supported by a continues homogeneous foundation is assumed, it is also necessary to specify, whether only steady-state solution will be searched for or whether unsteady vibrations will also be under consideration. It should be of general knowledge that the steady-state vibrations induced by a moving mass acted on by a constant force are exactly the same as the ones induced by the moving force only. Some authors associate mass to the moving object and then restrict themselves to the steady-state solution, even if in such a way inertial effects related to the moving mass are removed. This restriction can be hidden in application of multiple Fourier transform [43, 44]. In the absence of damping, the resonance case identifies the critical velocity. If the mass is acted on by a harmonic force, then the resulting steady-state vibrations are not exactly the same as for the moving harmonic force, because the mass value influences the amplitude of the steady-state vibrations, but the frequency is only dictated by the excitation frequency. Then, in the absence of damping it can happen that the amplitude of the resulting vibrations attains an infinite value. This happens when the forcing frequency attains the natural frequency of the system. Then the denominator of the expression for the steady state amplitude as well as for the transient part of the vibrations is zero, and therefore these values are not mathematically defined. This is also a resonance effect. Unstable behaviour is identified by exponential increase of vibration amplitudes with respect to time, which can occur in undamped as well as damped case.

Steady-state solution is unable to detect instability of the moving object, and therefore, when instability is to be analysed, then unsteady part must be included, and the object induced vibrations must be tracked from the very beginning. This marks fundamental difference between the moving inertial object and the moving force, where instability is out of the question, and therefore it is not essential to track the vibrations from the start. In summary, vibrations that arise by actions of moving inertial objects with velocities that can reach or overpass the critical one, should always be considered with their unsteady part. Moreover, it is more realistic to include inertial effects in all involved parts, because the critical velocity is strongly dependent on the wave propagation in the foundation and the critical velocity is closely related to the onset of instability. The unsteady vibrations are important not only for instability analysis of the moving object. Their importance should not be overlooked because (i) in an undamped case they last forever, and steady-state situation is never reached; (ii) any disturbance in load and/or foundation will originate unsteady contribution to the resulting vibrations.

New form for semi-analytical solution of vibrations induced by mass or oscillator traversing a beam on a two-parameter massless foundation is detailed in previous author’s works [45,46,47]. It is shown that there is a very good proximity between vibrations of finite and infinite structures when the load is set to start actuating a little bit further from the support. This implies that, if finite structures can be analysed with the effect of the supports eliminated this way, then it is possible to select for their representation the most advantageous type, which for finite beams are undoubtably simple supports. Vibrations in finite beams will reach the steady-state solution only after significant part of the structure is passed and therefore, inherently include the unsteady part, which is suitable for the validation of unsteady vibrations obtained in infinite beams. However, is not easy to achieve proximity of these solutions in moving force problems. Analysis of special conditions to be applied on moving force to reach stabilized solution in undamped cases is presented in [12].

In this paper, the new form for the semi-analytical solution of vibrations induced by moving mass from [45, 46] will be extended to the foundation model with partial shear resistance. This foundation model has been proven to be an acceptable approximation of reality (see [22, 23]). Neglecting the shear resistance, the model is equivalent to the one presented in [48]. The model is simple enough to be handled by semi-analytical approaches and has a counterpart in modal expansion, which is suitable for finite beams. The model (i) can acceptably approximate vibrations recorded experimentally as shown in [22] and (ii) provides results sufficiently close to the ones obtained on more sophisticated models [23].

In this paper the semi-analytical solution of vibrations induced by moving mass traversing a homogenous beam (finite or infinite) supported by a continues homogenous finite depth foundation with simplified shear resistance is presented. The new contributions for the case of finite beam are:

• (i) identification of vibration modes and orthogonality conditions;

• (ii) reengagement of coupled equations to ensure significant savings of the calculation time.

For the case of an infinite beam, the new contributions are:

• (iii) presentation of resulting vibrations as a sum of their steady-state part, the unsteady harmonic part (through mass induced frequencies) and the transient part;

• (iv) analysis of proximity of the harmonic (steady and unsteady) and the full solutions with the help of frequency and discontinuity lines;

• (v) determination and analysis of mass induced frequencies and their importance for final solution and the onset of instability;

• (vi) identification of several cases where the harmonic solution very well approximates the full solution, which allows to take advantage of closed-form formulas numerically stable even at larger times.

The paper is organized in the following way: in Sect. 2 the problem to be solved is specified on infinite beams and its solution is presented in Sect. 3. The problem definition and solution on finite beams is given in Sect. 4. Section 5 is dedicated to illustrative examples and validations. Conclusions are drawn in Sect. 6.

2 Problem definition on infinite beams

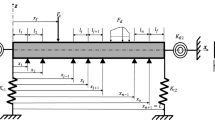
In this section the problem at hand will be defined on infinite beams, together with some simplifying assumptions. Let a uniform movement of a point mass over a homogenous beam supported by a continuous homogeneous finite depth foundation with simplified shear resistance be considered. It is assumed that at zero time the beam is at rest and all deflection fields are measured from static position of the involved parts, excluding from further analysis beam and foundation weight. As the problem has applications in railways, the moving force acting on the point mass may not be coincident with the mass weight. The beam will be treated according to the Euler–Bernoulli theory. Foundation model, as described in [22, 23], corresponds to a foundation strip of a finite width $b$, which is the same as the beam width, and a finite depth $H$. It has zero strain in width’s direction and neglected horizontal displacements. The shear resistance is included in its simplified form by the shear stress originated by vertical displacements. This means that in FEM, the foundation can be modelled by plane strain continuum without horizontal displacements with recalculated foundation properties in order to respect the considered width.

The beam dynamic equilibrium in fixed coordinates $(x,t)$ is given by:

$$\begin{aligned} & EIw_{,xxxx} (x,t) + Nw_{,xx} (x,t) + mw_{,tt} (x,t) \\ & \quad + c_{b} w_{,t} (x,t) + s(x,t) = F(x,t) \\ \end{aligned}$$

(1)

where $w(x,t)$ is the unknown transversal displacement of the beam, positive when oriented downward. $F(x,t)$ is the loading term and $s(x,t)$ is the foundation pressure. $EI$, $m$ and $c_{b}$ stand for the bending stiffness and mass per unit length of the beam, and the external viscous damping coefficient, respectively. $N$ is the normal force considered positive when inducing compression. Here and in what follows derivatives are designated by the respective variable in subscript position, preceded by a comma. Boundary conditions dictate zero displacement and slope at positions corresponding to plus and minus infinity, $x \to \pm \infty$, and the initial conditions are considered homogeneous

$$\left. {w(x,t)} \right|_{t = 0} = 0,\quad \left. {w_{,t} (x,t)} \right|_{t = 0} = 0\quad \forall x .$$

(2)

The loading term with one point mass $M$ acted on by a constant force $P$ with harmonic component of amplitude $P_{0}$, forcing frequency $\omega_{f}$ and phase shift $\varphi_{f}$ is depicted in Fig. 1. Harmonic part of the forcing term is represented by trigonometric sine function. Trigonometric representation of the loading term is important for analysis of finite beams in order to keep the analysis in the real domain. However, exponential function has more advantages in analysis of infinite beams. In order to keep the phase indicated in sine function, it is necessary to add $3\pi /2$ or $- \pi /2$, because the real part of the exponential function with imaginary exponent correspond to the trigonometric function cosine. Therefore, the loading term reads as:

$$F(x,t) = \left( {P + P_{0} {\text{e}}^{{{\text{i}}\left( {\omega_{f} t + \varphi_{f} + 3\pi /2} \right)}} - Mw_{0,tt} (t)} \right)\delta (x - vt)$$

(3)

where $v$ is the velocity, $w_{0}$ is the mass displacement at the contact point and $\delta$ is the Dirac delta function. Rotary inertia of the mass is neglected and it is assumed that the mass is in continuous contact with the beam, thus $w_{0} (t) = w(vt,t)$. In addition, friction acting at the contact between the mass and the beam is not considered. The actual wheel shape is not taken into account, meaning that if in damped and/or supercritical velocity case the slope of the deflection at the force position is not zero, the contact point is not converted to the correct position, which moves slightly forward due to the actual wheel shape. Also, the drag force acting against the moving force in such cases is neglected.

Fig. 1

Infinite beam on elastic foundation of finite depth subjected to a moving load and a normal force

The foundation pressure $s(x,t)$ has to be determined from the analysis of the foundation. The dynamic equilibrium in the vertical direction under plane strain condition reads as:

$$(\lambda + 2\mu )u_{z,zz} \,(x,z,t) + \mu u_{z,xx} (x,z,t) = \rho u_{z,tt} (x,z,t)$$

(4)

where $u_{z} (x,z,t)$ is the unknown vertical displacement of the foundation, $\lambda$ and $\mu$ are the generalized Lame’s constants of the soil and $\rho$ is the soil density. The soil damping is introduced as viscous, but similar derivations could also be performed for hysteretic one, as shown in [23].

$$\lambda = \lambda_{0} \left( {1 + c_{f} \bullet_{,t} } \right),\quad \mu = \mu_{0} \left( {1 + c_{f} \bullet_{,t} } \right)$$

(5)

In Eq. (5) $c_{f}$ is the relative coefficient of viscous damping of the foundation, and $\lambda_{0}$ and $\mu_{0}$ are basic values of Lame’s constants.

Therefore, the foundation equilibrium is given by:

$$\begin{aligned} & \left( {\lambda_{0} + 2\mu_{0} } \right)\left( {u_{z,zz} (x,z,t) + c_{f} u_{z,zzt} (x,z,t)} \right) \\ & \quad + \mu_{0} \left( {u_{z,xx} (x,z,t) + c_{f} u_{z,xxt} (x,z,t)} \right) \\ & \quad - \rho u_{z,tt} (x,z,t) = 0 \\ \end{aligned}$$

(6)

$$\begin{aligned} & {\text{i}} . {\text{e}} .\;\;\;v_{p}^{2} \left( {u_{z,zz} (x,z,t) + c_{f} u_{z,zzt} (x,z,t)} \right) \\ & \quad + v_{s}^{2} \left( {u_{z,xx} (x,z,t) + c_{f} u_{z,xxt} (x,z,t)} \right) \\ & \quad - u_{z,tt} (x,z,t) = 0 \\ \end{aligned}$$

(7)

where

$$v_{p} = \sqrt {\frac{{\lambda_{0} + 2\mu_{0} }}{\rho }} ,\quad v_{s} = \sqrt {\frac{{\mu_{0} }}{\rho }}$$

(8)

are velocities of propagation of the pressure and shear waves, respectively.

Initial conditions are again assumed as homogeneous. One of the boundary conditions states zero displacement at the foundation depth $H$ and the other one is in fact continuity condition, connecting the beam with the foundation by

$$w(x,t) = u_{z} (x,0,t)$$

(9)

In addition, Eqs. (1) and (7) are coupled by the foundation pressure, $s(x,t)$, which is determined from $u_{z}$ by classical equations of elasticity defining the normal stress, which has to be multiplied by the foundation width $b$ in order to obtain a value distributed in line. It is also important to change the sign due to standard sign conventions:

$$s(x,t) = - \sigma_{z} (x,0,t)b.$$

(10)

3 Problem solution on infinite beams

At first, it is necessary to remove the additional unknown $w_{0} (t)$ and express it in terms of the beam deflection $w(x,t)$ with the help of the assumption of continuous (rigid) contact: $w_{0} (t) = w(vt,t)$. The relevant derivatives are obtained by the chain rule

$$\begin{aligned} w_{0,t} (t) & = vw_{,x} (x,t) + w_{,t} (x,t), \\ w_{0,tt} (t) & = v^{2} w_{,xx} (x,t) + 2vw_{,xt} (x,t) \\ & \quad + w_{,tt} (x,t)\;\;\;\; {\text{with}}\;\;\;\;x = vt \\ \end{aligned}$$

(11)

Consequently, the loading term becomes

$$F\left( {x,t} \right) = \left( {P + P_{0} {\text{e}}^{{{\text{i}}\left( {\omega_{f} t + \varphi_{f} + 3\pi /2} \right)}} - M\left( {w_{,tt} \left( {x,t} \right) + 2vw_{,xt} \left( {x,t} \right) + v^{2} w_{,xx} \left( {x,t} \right)} \right)} \right)\delta \left( {x - vt} \right)$$

(12)

Now, the governing Eqs. (1) and (7) are transferred to moving coordinates $r = x - vt$, $z = z$, $t = t$. It is necessary to highlight that the time dependent terms will be kept in order to account for the transient vibrations. For the sake of simplicity, functional dependence will be mainly omitted, unless expression could be ambiguous. The beam equilibrium in moving coordinates is thus

$$\begin{aligned} & EIw_{,rrrr} + Nw_{,rr} + m\left( {w_{,tt} - 2vw_{,rt} + v^{2} w_{,rr} } \right) \\ & \quad \quad \quad + c_{b} \left( {w_{,t} - vw_{,r} } \right) + s \\ & \quad = \left( {P + P_{0} {\text{e}}^{{{\text{i}}\left( {\omega_{f} t + \varphi_{f} + 3\pi /2} \right)}} - Mw_{,tt} } \right)\delta (r) \\ \end{aligned}$$

(13)

and Eq. (7) reads as

$$\begin{aligned} & v_{p}^{2} \left( {u_{z,zz} - vc_{f} u_{z,zzr} + c_{f} u_{z,zzt} } \right) \\ & \quad + v_{s}^{2} \left( {u_{z,rr} - vc_{f} u_{z,rrr} + c_{f} u_{z,rrt} } \right) \\ & \quad - v^{2} u_{z,rr} + 2vu_{z,rt} - u_{z,tt} = 0 \\ \end{aligned}$$

(14)

For the solution method, as well as for presenting and calculating the results, it is convenient to switch to dimensionless coordinates, parameters and unknown displacement fields. The finite depth foundation has the advantage of being able to introduce the equivalent Winkler constant, $k$, which guarantees the connection with the standard dimensionless parameters for massless foundation, therefore:

$$\begin{aligned} k & = \frac{{\left( {\lambda_{0} + 2\mu_{0} } \right)b}}{H},\quad \chi = \sqrt[4]{{\frac{k}{4EI}}}, \\ w_{st} & = \frac{P\chi }{2k},\quad v_{cr} = \sqrt[4]{{\frac{4kEI}{{m^{2} }}}} = \frac{1}{\chi }\sqrt {\frac{k}{m}} \\ \end{aligned}$$

(15)

where $\chi$ is the inverse of the characteristic length, $w_{st}$ is the maximum static displacement exerted by the force $P$ when the beam is posed on foundation with the equivalent Winkler constant and $v_{cr}$ is its critical velocity. Then it is convenient to introduce the velocity and foundation mass ratios, $\alpha$ and $R$, respectively:

$$\alpha = \frac{v}{{v_{cr} }},\quad R = \sqrt {\frac{\rho bH}{m}}$$

(16)

Thus, the mass ratio $R$ corresponds to the square root of the ratio of the dynamically activated foundation mass to the beam mass. Dimensionless coordinates, time and displacements are

$$\begin{aligned} \xi & = \chi r,\quad \zeta = \frac{z}{H}, \\ \tau & = \chi v_{cr} t = t\sqrt {\frac{k}{m}} \;\;\;{\text{and}} \\ \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z} & = \frac{{u_{z} }}{{w_{st} }},\quad \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} = \frac{w}{{w_{st} }} \\ \end{aligned}$$

(17)

Going back to Eq. (13), it is obtained after switching to the dimensionless form (following [45, 46]):

$$\begin{aligned} & \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\xi \xi \xi \xi } + 4\left( {\eta_{N} + \alpha^{2} } \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\xi \xi } + 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\tau \tau } \\ & \quad \quad\; - 8\alpha \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\xi \tau } + 8\eta_{b} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\tau } - \alpha \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\xi } } \right) + 4\frac{s}{{kw_{st} }} \\ & \quad = 4\left( {2\eta_{P} + 2\eta_{{P_{0} }} {\text{e}}^{{{\text{i}}\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} \tau + \varphi_{f} + 3\pi /2} \right)}} - \eta_{{M_{u} }} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\tau \tau } } \right)\delta (\xi ) \\ \end{aligned}$$

(18)

where the additional parameters are

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} & = \frac{{\omega_{f} }}{{\chi v_{cr} }},\quad \eta_{b} = \frac{{{\text{c}}_{b} }}{{2\sqrt {mk} }},\quad \eta_{N} = \frac{N}{{N_{cr} }}, \\ \eta_{P} & = \frac{P}{P} = 1,\quad \eta_{{P_{0} }} = \frac{{P_{0} }}{P},\quad \eta_{M} = \frac{M\chi }{m} \\ \end{aligned}$$

(19)

where $N_{cr} = 2\sqrt {kEI}$ is the static buckling load of beam on Winkler’s foundation, $\eta_{b}$ is the damping ratio and $\eta_{M}$ is the moving mass ratio. Further, Eq. (14) in dimensionless form reads as:

$$\begin{aligned} & v_{p}^{2} \left( {\frac{1}{{H^{2} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\zeta \zeta } - vc_{f} \frac{\chi }{{H^{2} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\zeta \zeta \xi } + c_{f} \frac{{\chi v_{cr} }}{{H^{2} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\zeta \zeta \tau } } \right) \\ & \quad + v_{s}^{2} \left( {\chi^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\xi \xi } - vc_{f} \chi^{3} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\xi \xi \xi } + c_{f} \chi^{3} v_{cr} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\xi \xi \tau } } \right) \\ & \quad - v^{2} \chi^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\xi \xi } + 2v\chi^{2} v_{cr} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\xi \tau } - \chi^{2} v_{cr}^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{u}_{z,\tau \tau } = 0 .\\ \end{aligned}$$

(20)

In conformity with [45, 46], Laplace transform is applied first on the time variable $\tau$ and then Fourier transform on moving spatial coordinate $\xi$.

$$\tilde{F}(\xi ,\bar{q}) = \int\limits_{0}^{\infty } {f(\xi ,\tau ){\text{e}}^{{ - \bar{q}\tau }} d\tau } ,\;\;\;{\text{where}}\;\;\bar{q} = {\text{i}}q$$

(21)

$$F(p,\bar{q}) = \int\limits_{ - \infty }^{\infty } {\tilde{F}(\xi ,\bar{q})e^{ - ip\xi } d\xi }$$

(22)

As in [36], $\bar{q}$ is used in the definition of the Laplace transform in Eq. (21), to be similar to the usual form of the definition integral. Change to $q$ is justified by the fact that the physical meaning of $q$ is a frequency, and it is convenient to use expressions similar to the ones usually used when using the exponential form (compare with Eq. (37) in further text). This does not impose any restriction, both $\bar{q}$ and $q$ are complex.

Let us first deal with Eq. (20). After simplifications using

$$\frac{{Hv_{cr} \chi }}{{v_{p} }} = R\quad {\text{and}}\quad \frac{Hv\chi }{{v_{p} }} = \alpha R$$

(23)

and introducing new foundation damping parameter $\eta_{f}$ and shear ratio $\vartheta_{s}$

$$\eta_{f} = c_{f} \sqrt {\frac{k}{m}} = c_{f} v_{cr} \chi ,\quad \vartheta_{s} = \frac{{v_{s} }}{{v_{cr} }}$$

(24)

one obtains

$$U_{z,\zeta \zeta } + U_{z} \left( {\frac{{C_{f}^{2} }}{{\eta_{d}^{2} }} - p^{2} R^{2} \vartheta_{s}^{2} } \right) = 0$$

(25)

where

$$\eta_{d}^{2} = \left( {1 - {\text{i}}\eta_{f} (\alpha p - q)} \right),\quad C_{f}^{2} = R^{2} (\alpha p - q)^{2}$$

(26)

With introducing

$$\bar{C}_{f}^{2} = \left( {C_{f}^{2} - p^{2} R^{2} \vartheta_{s}^{2} \eta_{d}^{2} } \right)$$

(27)

the solution of Eq. (25) is

$$U_{z} = A\sin \left( {\frac{{\bar{C}_{f} }}{{\eta_{d} }}\zeta } \right) + B\cos \left( {\frac{{\bar{C}_{f} }}{{\eta_{d} }}\zeta } \right)$$

(28)

where in fact, square root was used, but it will be seen further that the sign in front of the square root is immaterial. Integration constants $A$ and $B$ will be determined from the boundary and interface conditions. The boundary condition implies

$$U_{z} (1) = 0 = A\sin \left( {\frac{{\bar{C}_{f} }}{{\eta_{d} }}} \right) + B\cos \left( {\frac{{\bar{C}_{f} }}{{\eta_{d} }}} \right)$$

(29)

and the interface condition gives

$$W = U_{z} (0) = B$$

(30)

In Eq. (18), the term accounting for the foundation pressure is $\frac{4s}{{kw_{st} }}$, which in transformed space corresponds to $\frac{4S}{{kw_{st} }}$. In Eq. (10) it was specified that $s = - \sigma_{z} (0)b$, which in transformed space means $S = - \varSigma_{z} (0)b$. By using classical elasticity equations, one obtains:

$$\frac{4S}{{kw_{st} }} = - 4\eta_{d} \bar{C}_{f} A$$

(31)

then together with Eqs. (29) and (30):

$$\frac{4S}{{kw_{st} }} = - 4\eta_{d} \bar{C}_{f} A = 4\eta_{d} \bar{C}_{f} B/\tan \left( {\bar{C}_{f} /\eta_{d} } \right) = 4W\eta_{d} \bar{C}_{f} /\tan \left( {\bar{C}_{f} /\eta_{d} } \right)$$

(32)

Now, it is seen from Eq. (32) that the sign in front of the square root in both cases, for $\eta_{d}$ and $\bar{C}_{f}$, is immaterial.

In the transformed space then [with the help of Eq. (32)], it holds for the beam

$$\begin{aligned} & W(p,{\text{i}}q)\left[ {p^{4} - 4p^{2} \left( {\eta_{N} + \alpha^{2} } \right) - 4q^{2} + 8\alpha pq + 8{\text{i}}\eta_{b} q - 8{\text{i}}\eta_{b} \alpha p + 4\eta_{d} \bar{C}_{f} /\tan \left( {\bar{C}_{f} /\eta_{d} } \right)} \right] \\ & \quad = \frac{{8\eta_{{P_{u} }} }}{{{\text{i}}q}} + \frac{{8\eta_{{P_{0} }} {\text{e}}^{{{\text{i}}\left( {\varphi_{f} + 3\pi /2} \right)}} }}{{{\text{i}}q - {\text{i}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} }} + 4\eta_{M} q^{2} \tilde{W}(0,{\text{i}}q) \\ \end{aligned}$$

(33)

After that it is possible to proceed as in [45, 46] with the only difference that

$$\begin{aligned} D(p,q) &= p^{4} - 4p^{2} \left( {\eta_{N} + \alpha^{2} } \right) - 4q^{2} \\ & \quad + 8\alpha pq + 8{\text{i}}\eta_{b} q - 8{\text{i}}\eta_{b} \alpha p + 4\eta_{d} \bar{C}_{f} /\tan \left( {\bar{C}_{f} /\eta_{d} } \right) \\ \end{aligned}$$

(34)

has now the last term in form of $4\eta_{d} \bar{C}_{f} /\tan \left( {\bar{C}_{f} /\eta_{d} } \right)$ instead of previous number 4.

The Laplace image of the solution can be solved analytically:

$$\tilde{W}(\xi ,q) = \left( {\frac{{4\eta_{P} }}{{{\text{i}}q}} + \frac{{4\eta_{{P_{0} }} {\text{e}}^{{{\text{i}}\left( {\varphi_{f} + 3\pi /2} \right)}} }}{{{\text{i}}q - {\text{i}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} }}} \right)\frac{K(\xi ,q)}{{\pi - 2\eta_{M} q^{2} K(q)}}$$

(35)

where

$$\pi - 2K(0,q)\eta_{M} q^{2} = 0$$

(36)

is the characteristic equation.

The final solution, expressed as a sum of residues and an additional term representing the additional transient part $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{tr} (\xi ,\tau )$, reads as

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} (\xi ,\tau ) & = \frac{{4\eta_{P} K(\xi ,0)}}{\pi } + \frac{{4\eta_{{P_{0} }} K\left( {\xi ,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} } \right){\text{e}}^{{{\text{i}}\left( {\varphi_{f} + 3\pi /2} \right)}} }}{{\left( {\pi - 2K\left( {0,\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} } \right)\eta_{M} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f}^{2} } \right)}}{\text{e}}^{{{\text{i}}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} \tau }} \\ & \quad + \sum\limits_{j = 0,2,4, \ldots } {\frac{{ - 2\eta_{P} K\left( {\xi ,q_{{M_{j} }} } \right)}}{{\pi + q_{{M_{j} }}^{3} K_{,q} \left( {q_{{M_{j} }} } \right)\eta_{{M_{u} }} }}{\text{e}}^{{{\text{i}}q_{{M_{j} }} \tau }} } \\ & \quad + \sum\limits_{j = 0,2,4, \ldots } {\frac{{ - 2\eta_{{P_{0} }} q_{{M_{j} }} K\left( {\xi ,q_{{M_{j} }} } \right){\text{e}}^{{{\text{i}}\left( {\varphi_{f} + 3\pi /2} \right)}} }}{{\left( {\pi + q_{{M_{j} }}^{3} \eta_{M} K_{,q} \left( {q_{{M_{j} }} } \right)} \right)\left( {q_{{M_{j} }} - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} } \right)}}{\text{e}}^{{{\text{i}}q_{{M_{j} }} \tau }} + \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{tr} (\xi ,\tau )} \\ \end{aligned}$$

(37)

where the relevant functions for results evaluation are defined by

$$K(\xi ,q) = \int\limits_{ - \infty }^{\infty } {\frac{{{\text{e}}^{{{\text{i}}p\xi }} }}{D(p,q)}{\text{d}}p}$$

(38)

and

$$K_{,q} (q) = \int\limits_{ - \infty }^{\infty } { - \frac{ 1}{{D(p,q)^{2} }}{\text{d}}p}$$

(39)

and $q_{{M_{j} }}$ are the mass induced frequencies, identified as complex roots of the characteristic equation (36).

The first two terms in Eq. (37) represent the steady-state part of the solution and the last three terms the transient one. The first term is induced by the constant force and the second one by the harmonic one. The transient part of the solution has two parts: the third and the fourth terms in Eq. (37) can be represented by a closed-form expression and the last term can only be evaluated by numerical integration. This separation a consequence of the Cauchy theorem because the function to be integrated (the Laplace image of the solution) has poles and discontinuities. The poles are representing the natural frequencies of the system (named here as the mass induced frequencies in conformity with [45,46,47]). It was verified numerically that the number of poles is limited, similarly as for the massless foundation. If a pole exists, then the complex conjugate of its opposite value is also a pole. For this reason, the number of poles is always even. Typically, there are only two or four poles, or there can be none. Therefore, the third and the fourth terms of Eq. (37) can be easily evaluated. The other advantage of this separation is that if poles exist, then the third and the fourth terms of Eq. (37) are dominant when compared with the last one. The third term is induced by the constant force and the fourth term by the harmonic one. Except for the last term in Eq. (37), all other terms are harmonic, represented by closed-form expressions obtained from the definition of residues. For the sake of clarity, they will be referred to as the harmonic solution, so that they can be clearly distinguished from the complete solution, which includes all terms from Eq. (37). It was carefully checked by the argument principle, that there are no other poles then the ones presented in examples section and that all of them are simple.

In agreement with [45,46,47] the roots of the characteristic equation (36), named as the mass induced frequencies, can be solved by the two iterative techniques suggested there. These frequencies are in fact poles of the function to be integrated in the inverse Laplace transform and so they are used for residues evaluation that form the unsteady harmonic part of the solution. Mass induced frequencies come always in pairs, thus when $q_{{M_{j} }}$ is a root, then $\left( { - q_{{M_{j} }} } \right)*$ is another root, where * designates complex conjugate value. Justification is the same as for massless foundation presented in [45,46,47]. In this way each pair of roots constitute a harmonic term. When the imaginary part of these frequencies is positive, then the corresponding vibration is stable and will gradually disappear. When they are negative, then vibrations are unstable, and amplitudes will increase exponentially with time. For real frequencies, the unsteady part stays unchanged.

For the unstable behaviour, it is necessary to have at least one pair of induced frequencies with negative imaginary part. This proves that unstable solution cannot be detected by approaches leading directly to the steady-state solution. In this sense such methods are incomplete because they hide important features of the structural behaviour.

For a specific set of problem parameters, smooth change in the velocity ratio originates smooth change in the induced frequency, except when discontinuity in $K(0,q)$ is reached. A set of smoothly varying induced frequencies will be named as a frequency line. From the numerical point of view, the iterative techniques for induced frequencies solution require only repetitive calculation of $K(0,q)$. In the first technique, the complex equation to be solved on a complex plane is intended as if $K(0,q)$ and $q$ were independent. Having some estimate from n-th iteration $q_{n}$, the next iteration is calculated as

$$q_{n + 1} = \beta q_{i} + (1 - \beta )q_{n}$$

(40)

where $q_{i}$ is calculated from

$$\pi - 2K\left( {0,q_{n} } \right)\eta_{M} q_{i}^{2} = 0$$

(41)

and $\beta$ is some adequate weight. This means that $K(0,q)$ is evaluated at the previous estimate $q_{n}$ and then it is easy to get $q_{i}$. Convergence of this procedure depends on the initial estimate $q_{0}$ and on the selected weight $\beta$. If the convergence is achieved, then the root can be determined with the required precision. The initial estimate is conveniently obtained from the general tendency of each frequency line. To start a frequency line, it is advised to select a velocity ratio further from the critical one, where convergence is guaranteed even for estimates not entirely close to the root. For the purpose of this paper $\beta = 0.05$ was used in all cases. If convergence difficulties are experienced, the other technique, named as delimiting search, can be used. Having a reasonable estimate of the induced frequency value, it is possible to identify a rectangle domain in the complex $q$-plane where the real and imaginary parts of $\pi - 2K(0,q)\eta_{M} q^{2}$ are monotonic and change their sign. Zero values identify two lines on $q$-plane. In further iterations it is necessary to reduce the rectangle domain without losing the intersection of the lines just identified. Step by step reduction of the rectangle domain determines the root with the required precision.

In the same way as in massless foundation, real $p$-roots of $D(p,q)$ originate discontinuity in $K(0,q)$. These discontinuities cause that the frequency lines are cut. In massless foundation these cuts can be easily predicted, because they corresponded to the frequency value with imaginary part close to $\eta_{b}$. There is only one line of discontinuity (interrupted for subcritical velocities) and thus the velocity intervals with no induced frequencies are very narrow and occur only in lightly damped cases. The foundation model in this paper is more complicated and thus the discontinuity lines are also more complicated and cuts in frequency lines are not obvious. Much more discontinuities cause that the set of velocities for which induced frequencies do not exist is much larger. This implies that there are less situations when the transient solution can be replaced by simple harmonic function. Discontinuity lines should be eliminated from the contour integration by branch cuts, but it was confirmed numerically that it is sufficient to eliminate only the major discontinuities. All discontinuity lines are located in the upper half-plane, i.e. where the imaginary part of $q$ is positive, which will implicitly ensure that the vibration determined through integration along the branch cuts are stable. The higher the imaginary part the lower the influence of these vibrations on the final result. This also justifies that the roots indicating the onset of instability can be easily found, because there are no discontinuities in their proximity. From this point of view the onset of instability is precisely defined by the method proposed. Nevertheless, the onset of instability was also check by the D-decomposition method introduced with the same purpose in [36].

In summary, the foundation model under consideration when compared to the massless foundation, is characterized by: (i) infinite number of discontinuity lines affecting not only the imaginary part of $K(0,q)$ but also its real part; (ii) discontinuity lines which are not straight; (iii) in some cases, larger differences between the harmonic and full solutions. It will be shown in Sect. 5 that: (i) only the most severe discontinuities in $K(0,q)$ should be avoided; (ii) the region to be avoided can be tested by the agreement with the initial conditions; (iii) in several cases the differences between the full and harmonic solutions are originated by the imaginary part of the induced frequencies, and thus the harmonic solutions looks like being slightly overdamped with respect to the full one. These discrepancies are thus not very important.

The other disadvantage with respect to the massless foundation is that $K(0,q)$ cannot be calculated in an exact way as a sum of residues and must be determined numerically, and therefore, it is necessary to introduce some damping to avoid numerical problems. For the purpose of this article, Matlab predefined numerical integral evaluation was used and both iterative techniques for induced frequencies determination were programmed in Matlab. Results obtained are not compromised by low Matlab numerical precision, because in regions with large gradients, discontinuities are present, and $q_{{M_{j} }}$ do not exist. These regions are usually located around the critical velocity. In this context it is necessary to recall that the critical velocity of a uniformly moving constant force was determined for this foundation model in [22], where also approximate formula given in Eq. (42)

$$\alpha_{cr} = \left( {\sqrt {1 - \eta_{N} } - \vartheta_{s} } \right)\sqrt {\frac{2}{{2 + R^{{2 + \sqrt {\vartheta_{s} } }} }}} + \vartheta_{s}$$

(42)

was derived. $\alpha_{cr} = V_{cr} /v_{cr}$ with $V_{cr}$ as the new value of the critical velocity. Thus, for a low foundation mass ratio, the critical velocity approaches the classical value $v_{cr,N} = v_{cr} \sqrt {1 - \eta_{N} }$ and for a higher foundation mass ratio, it approaches the velocity of propagation of shear waves $v_{s}$ in the foundation, which is the lowest wave-velocity of propagation related to the model adopted, because the Rayleigh velocity $v_{R}$ cannot be developed without proper horizontal displacements contribution. $v_{s}$ and $v_{R}$ are, however, quite close to each other, as shown by the approximate formula [49],

$$\frac{{v_{R} }}{{v_{s} }} = \frac{0.87 + 1.12\upsilon }{1 + \upsilon }$$

(43)

where $\upsilon$ is the soil Poisson ratio.

After frequency lines determination, velocity intervals with and without induced frequencies are known. If induced frequencies exist, then the full solution can be reasonably well approximated by the harmonic solution. For amplitudes calculation it is also necessary to evaluate numerically the integral from Eq. (39). Getting closer to the regions with no induced frequencies, the harmonic solution starts to deviate from the full one and the transient part becomes more important. When there are no induced frequencies, then the full solution must be determined numerically by

$$\begin{aligned} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} (\xi ,\tau ) & = \frac{1}{2\pi }\int\limits_{{ - {\text{i}}a - \infty }}^{{ - {\text{i}}a + \infty }} {\tilde{W}(\xi ,q){\text{e}}^{{{\text{i}}q\tau }} {\text{d}}q} \\ & = \frac{1}{\pi }\int\limits_{{ - {\text{i}}a - \infty }}^{{ - {\text{i}}a + \infty }} {\frac{{ - 2{\text{i}}K(\xi ,q)}}{{q\left( {\pi - 2K(0,q)\eta_{M} q^{2} } \right)}}{\text{e}}^{{{\text{i}}q\tau }} {\text{d}}q} \\ \end{aligned}$$

(44)

with some suitable $a$ as a real number determined in a way that all discontinuities and poles lie above the line specified by $\left\langle { - \infty - {\text{i}}a; + \infty - {\text{i}}a} \right\rangle$ in complex $q$-plane. In several of such cases, the full solution is mainly composed of the steady-state solution and the transient part is only adapting the solution to the initial conditions. Equation (44) was obtained directly from the definition of the inverse Laplace transform and by switching the real and complex parts.

One may argue that Eq. (44) could be used in all cases and that is true. But, numerical evaluation according to Eq. (44) can easily accumulate numerical errors and be numerically compromised as the time is increasing. More importantly, the induced frequencies give a very important information about the unsteady harmonic part of the solution. They are important indicators of the regions of instability and its severity and they also indicate resonance situation for a harmonic force. Evaluation of the unsteady harmonic part with the help of induced frequencies gives thus always numerically confident values for any considered time, because they are obtained from a closed form formula. It will be shown in Sect. 5 that the induced frequencies can be easily found in many situations and, as in [45,46,47], in most cases the harmonic solution stands for a very good and sufficient approximation of the full one.

4 Problem definition and solution on finite beams

This section is concerned with the problem definition and solution on finite beams. Derivations that will be presented can be used generally, however, they will be presented in a way, to fulfil the purpose of this paper, which is related to the validation of results on infinite beams. For this, it is necessary to eliminate the supports influence. Firstly, it is necessary to select some convenient supports and include the corresponding boundary conditions. As justified before, simple supports will be considered. Secondly, it is necessary to assume that the load will start actuating a little bit further from the support.

General derivations start with Eqs. (1) and (2) and modifying Eq. (3) to the real range by

$$F(x,t) = \left( {P + P_{0} \sin \left( {\omega_{f} t + \varphi_{f} } \right) - Mw_{0,tt} (t)} \right)\delta (x - vt) ,$$

(45)

Boundary conditions dictate zero displacement and bending moment at the supports:

$$\left. {w(x,t)} \right|_{x = 0} = 0,\quad \left. {w_{,xx} (x,t)} \right|_{x = 0} = 0,\quad \left. {w(x,t)} \right|_{x = L} = 0,\quad \left. {w_{,xx} (x,t)} \right|_{x = L} = 0\quad \forall t,$$

(46)

where L is the beam length.

The moving coordinates are not convenient in the analysis of finite beams and will not be introduced. By removing $w_{0}$, the loading term becomes

$$F(x,t) = \left( {P + P_{0} \sin \left( {\omega_{f} t + \varphi_{f} } \right) - M\left( {w_{,tt} (x,t) + 2vw_{,xt} (x,t) + v^{2} w_{,xx} (x,t)} \right)} \right)\delta (x - vt)$$

(47)

therefore, in fixed coordinates the dynamic equilibrium in dimensionless form reads

$$\begin{aligned} & \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\xi \xi \xi \xi } + 4\eta_{N} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\xi \xi } + 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\tau \tau } + 8\eta_{b} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\tau } + 4R\theta_{z} \frac{1}{{\tan R\theta_{z} }}\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} \\ & \quad = \left( {8\left( {\eta_{P} + \eta_{{P_{0} }} \sin \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} \tau + \varphi_{f} } \right)} \right) - \eta_{M} \left( {4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\tau \tau } + 8\alpha \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\xi \tau } + 4\alpha^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{,\xi \xi } } \right)} \right)\delta (\xi - \alpha \tau ) \\ \end{aligned}$$

(48)

because soil vertical displacements are governed by

$$f(\zeta ) = \frac{{\sin \left( {R\theta_{z} (1 - \zeta )} \right)}}{{\sin \left( {R\theta_{z} } \right)}}$$

(49)

where

$$\theta_{z} = \sqrt {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }^{2} - \left( {p_{j} \vartheta_{S} } \right)^{2} }$$

(50)

Thus, frequencies of undamped natural modes can be calculated from

$$p_{j}^{4} - 4\eta_{N} p_{j}^{2} - 4\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }^{2} + 4R\theta_{z} \frac{1}{{\tan R\theta_{z} }} = 0$$

(51)

where

$$w_{j} (\xi ) = \sin (p_{j} \xi ),\quad p_{j} = \frac{j\pi }{L\chi }$$

(52)

because the only function that fulfils the boundary conditions stated in Eq. (46) is sine. In Eq. (52), $L\chi$ is the corresponding dimensionless counterpart of the beam length $L$. The undamped vibration modes form a complete space and thus the transient response in the time domain can be expressed as infinite sum $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w} (\xi ,\tau ) = \sum\nolimits_{j = 1}^{\infty } {q_{j} (\tau )w_{j} (\xi )}$, where $q_{j} (\tau )$ are modal coordinates. Orthogonality condition can be defined as

$$\left( {1 + R^{2} \int_{\zeta = 0}^{1} {f\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j,n} } \right)f\left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j,l} } \right)d\zeta } } \right)\int_{\xi = 0}^{L\chi } {\sin^{2} \left( {\frac{j\pi }{L\chi }\xi } \right)d\xi } = \delta_{nl} \quad \forall j,n \ne l$$

(53)

where $\delta_{jk}$ is the Kronecker delta, and the associated norm in square is [50],

$$N_{j,n} = \int_{\xi = 0}^{L\chi } {\left( {1 + R^{2} \int_{\zeta = 0}^{1} {f^{2} \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j,n} } \right)d\zeta } } \right)} \sin^{2} \left( {\frac{j\pi }{L\chi }\xi } \right)d\xi$$

(54)

When only moving force is considered, modal coordinates can be presented in a closed form. For the sake of simplicity, they are shown in Eq. (55) only for an undamped situation and moving constant force [50],

$$\begin{aligned} q_{j} (\tau ) & = \sum\limits_{n} {\frac{{2\eta_{P} }}{{N_{j,n} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j,n}^{2} \left( {1 - \varOmega_{j,n}^{2} } \right)}}\left[ {\sin \left( {\varOmega_{j,n} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j,n} \tau } \right) - \varOmega_{j,n} \sin \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j,n} \tau } \right)} \right]} , \\ \varOmega_{j,n} & = \frac{j\pi \alpha }{{L\chi \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j,n} }} \\ \end{aligned}$$

(55)

However, when moving mass is assumed, the equations for unknown $q_{j} (\tau )$ are coupled in the modal space. This coupling is extended not only over the beam modes, but also over the soil modes. If $\bar{j}$ beam modes and $\bar{n}$ soil modes are taken into account, then there are $\bar{m} = \bar{j}\bar{n}$ coupled equations. A compact matrix form can be presented as

$${\mathbf{M}}(\tau ) \cdot {\mathbf{q}}_{,\tau \tau } (\tau ) + {\mathbf{C}}(\tau ) \cdot {\mathbf{q}}_{,\tau } (\tau ) + {\mathbf{K}}(\tau ) \cdot {\mathbf{q}}(\tau ) = {\mathbf{p}}(\tau )$$

(56)

where square $\bar{m} \times \bar{m}$ matrices ${\mathbf{M}}$, ${\mathbf{C}}$, ${\mathbf{K}}$ are not approximations resulting from some discretization of the problem, like in the FEM, but are defined by vibration modes in their exact analytical form. It is immaterial whether the modes are sorted firstly according to the beam mode number and then by the soil mode number, or vice versa. Matrix components at positions $(i,k)$ are given by

$$M_{ik} = 4\delta_{ik} + 4\eta_{M} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i} (\alpha \tau )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{k} (\alpha \tau )$$

(57)

$$C_{ik} = 8\delta_{ik} \eta_{b} + 8\eta_{M} \alpha \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i} (\alpha \tau )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{k,\xi } (\alpha \tau )$$

(58)

$$K_{ik} = 4\delta_{ik} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j}^{2} + 4\eta_{M} \alpha^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i} (\alpha \tau )\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{k,\xi \xi } (\alpha \tau )$$

(59)

$$p_{i} = 8\left( {\eta_{P} + \eta_{{P_{0} }} \sin \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} \tau + \varphi_{f} } \right)} \right)\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i} (\alpha \tau )$$

(60)

If the viscous damping is to be applied only as external, a correction must be introduced to the term $8\delta_{ik} \eta_{b}$ in the form of $L\chi /2/N_{k}$, because by keeping the original value, damping would be applied on the foundation as well, but in a different way than specified by $\eta_{f}$. As Matlab code has only first order differential equation solvers, the system (56) should be written in the state-space form as

$$\left\{ {\begin{array}{*{20}c} {\mathbf{q}} \\ {{\mathbf{q}}_{,\tau } } \\ \end{array} } \right\}_{,\tau } = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - {\mathbf{M}}^{ - 1} {\mathbf{K}}} & { - {\mathbf{M}}^{ - 1} {\mathbf{C}}} \\ \end{array} } \right] \cdot \left\{ {\begin{array}{*{20}c} {\mathbf{q}} \\ {{\mathbf{q}}_{,\tau } } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\mathbf{M}}^{ - 1} {\mathbf{p}}} \\ \end{array} } \right\}$$

(61)

For higher number of modes, significant calculation time is required, because lower blocks of the main matrix in Eq. (61) are full. It is therefore suggested to reorder these terms by keeping the usual form for uncoupled equations and join together coupled terms in one additional equation. This will in fact increase the number of equations by one, but this increase is compensated by the fact that main parts of the involved matrices is diagonal, and therefore the computational time is much lower. Then

$${\tilde{\mathbf{M}}}\left( t \right) = \left[ {\begin{array}{*{20}c} {\tilde{M}_{ik} } & { - \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{i} (\alpha \tau + d)} \\ {4\eta_{M} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{k} (\alpha \tau + d)} & 1 \\ \end{array} } \right]$$

(62)

$${\tilde{\mathbf{C}}}\left( t \right) = \left[ {\begin{array}{*{20}c} {\tilde{C}_{ik} } & 0 \\ {8\eta_{M} \alpha \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{k,\xi } (\alpha \tau + d)} & 0 \\ \end{array} } \right]$$

(63)

$${\tilde{\mathbf{K}}}\left( t \right) = \left[ {\begin{array}{*{20}c} {\tilde{K}_{ik} } & 0 \\ {4\eta_{M} \alpha^{2} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{k,\xi \xi } (\alpha \tau + d)} & 0 \\ \end{array} } \right]$$

(64)

$${\tilde{\mathbf{p}}} = \left\{ {\begin{array}{*{20}c} 0 \\ {8\left( {\eta_{P} + \eta_{{P_{0} }} \sin \left( {\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{f} \tau + \varphi_{f} } \right)} \right)} \\ \end{array} } \right\}$$

(65)

where the diagonal terms are

$$\tilde{M}_{ik} = 4\delta_{ik} ,\quad \tilde{C}_{ik} = 8\delta_{ik} \eta_{b} ,\quad \tilde{K}_{ik} = 4\delta_{ik} \overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{\omega }_{j}^{2}$$

(66)

For the sake of completeness, the load advance $d$ with respect to the left support is included. $d$-value should be tested numerically. The new unknown vector is now

$${\tilde{\mathbf{q}}} = \left\{ {\begin{array}{*{20}c} {q_{j} } \\ {\bar{q}} \\ \end{array} } \right\}$$

(67)

and

$$\left\{ {\begin{array}{*{20}c} {{\tilde{\mathbf{q}}}} \\ {{\tilde{\mathbf{q}}}_{,\tau } } \\ \end{array} } \right\}_{,\tau } = \left[ {\begin{array}{*{20}c} {\mathbf{0}} & {\mathbf{I}} \\ { - {\tilde{\mathbf{M}}}^{ - 1} {\tilde{\mathbf{K}}}} & { - {\tilde{\mathbf{M}}}^{ - 1} {\tilde{\mathbf{C}}}} \\ \end{array} } \right] \cdot \left\{ {\begin{array}{*{20}c} {{\tilde{\mathbf{q}}}} \\ {{\tilde{\mathbf{q}}}_{,\tau } } \\ \end{array} } \right\} + \left\{ {\begin{array}{*{20}c} {\mathbf{0}} \\ {{\tilde{\mathbf{M}}}^{ - 1} {\tilde{\mathbf{p}}}} \\ \end{array} } \right\}$$

(68)

5 Results

5.1 Validation

For the initial validation, it is assumed that the beam is composed by one standard rail, the constant force is representing a typical axle load with the mass being associated as if the force was its weight using a simplified value for acceleration of gravity: $g = 10\;{\text{m/s}}^{ 2}$, and no harmonic component is added. The effect of the normal force is not included. Four cases from the subcritical velocity range [with respect to the critical velocity defined by Eq. (42)] are selected. The input data are summarized in Table 1. The cases are designated as case 1, 2, 3 and 4, respectively, in the same order as load velocity and the foundation mass ratio are placed in lines of Table 1. For the sake of completeness, the associated critical velocity presented in Table 1 is the exact value obtained numerically by identifying the double pole located on the real Fourier variable axis, as derived in [23]. In such cases it is expected that the harmonic solution will be a good approximation of the full one.

Table 1 Input data for validation examples

All four possibilities: two approaches for finite beams (modal expansion as described in Sect. 4 and FEM in LS-DYNA), and two forms for infinite beams (harmonic and full solutions as derived in Sect. 3) are being compared.

No damping is assumed for vibrations on finite beams in order to visualise clearly the unsteady part. Small damping has to be introduced on infinite beams for numerical reasons. Nevertheless, very small value as indicated in Table 1 was implemented producing no visible differences in the analysed time range. The beam length of finite beams was calculated in the way to ensure valid results within the tested time range.

In Fig. 2, displacement evolution at the contact point is plotted with respect to the dimensionless time. In order to get some acceptable agreement, for modal expansion 120 beam modes and 15 soil modes had to be used; as regard as FEM by LS-DYNA, 1000 elements along the beam and around 40 along the vertical direction of the foundation had to be implemented. By further increase of number of modes and elements, better agreement could be obtained at the expense of calculation time. Nevertheless, it can be concluded that even for this choice the agreement is very good. As already mentioned, the cases were selected in a way to obtain good correlation between the harmonic and full solutions as discussed in Sect. 3, which is confirmed in Fig. 2. In further analysis it will be seen that this is not always the case.

Fig. 2

Displacements at the contact point (full grey—modal expansion, dotted—full, dashed—harmonic, full black—LS-DYNA): a case 1; b case 2; c case 3; d case 4

For better clarity, the relative error of these cases is also presented. As confirmed by the harmonic solution, displacement evolution can be described by one harmonic curse, because there is only one pair of induced frequencies. In Table 2, the steady-state position, the amplitude and the frequency are being compared.

Table 2 Relative error of main characteristics of the validation examples

In Table 2, $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{b}$ corresponds to the steady-state displacement of the contact point, $A_{hr}$ is the amplitude of the harmonic vibration and $q_{hr}$ is its frequency. These values were determined exactly for the harmonic solution and extracted numerically for the other cases. Due to the negligible damping and subcritical velocity, the induced frequency is real. The relative error is expressed with respect to the full solution; however, the steady-state position is better expressed in the harmonic solution by its analytical form. It can be concluded from Table 2 that the relative error is very low.

5.2 Discontinuities in K-function

When $D(p,q)$ has a real root, $p_{t}$, for same particular frequency, $q_{t}$, then there is a discontinuity in $K(0,q)$, as already mentioned in Sect. 3. Smooth change of $q_{t}$ lead to a smooth change of $p_{t}$, and vice versa, and thus each such set of $q_{t}$ delimitates a discontinuity line of $K(0,q)$ in the complex $q$-plane. There is an infinite number of discontinuity lines, nevertheless, only some of them are important for the evaluation of the resulting vibrations. Discontinuity lines can be determined semianalytically, as will be demonstrated further in this section.

For convenience, $D(p,q)$ is separated in the dispersion equation of the beam $D_{b} (p,q)$ and the foundation contribution $D_{f} (p,q)$. For the sake of simplicity, it is assumed $\eta_{N} = \eta_{b} = 0$, then

$$D_{b} (p,q) = p^{4} - 4p^{2} \alpha^{2} - 4q^{2} + 8\alpha pq$$

(69)

$$D_{f} (p,q) = 4\eta_{d} \bar{C}_{f} /\tan \left( {\bar{C}_{f} /\eta_{d} } \right)$$

(70)

From Eqs. (69) and (70) it is clear that each $p_{t}$ will always be associated to two values of frequency with the same imaginary part, because for a medium value $q_{m,\alpha } = \alpha p_{t} + {\text{i}}q_{i}$, both $D_{b} (p,q)$ and $D_{f} (p,q)$ are real and for $q_{t,\alpha } = \alpha p_{t} + \Delta q_{r,\alpha } + {\text{i}}q_{i}$ imaginary parts of $D_{b} (p,q)$ and $D_{f} (p,q)$ are odd and real parts are even with respect to $q_{m,\alpha }$ and variable $\Delta q_{r,\alpha }$. Therefore, $p_{t}$ does not depend on $\alpha$ and to each possible $p_{t}$ it is also feasible to use its negative value $- p_{t}$ leading to total of four frequencies:

$$\begin{aligned} q_{{t_{1} ,\alpha }} & = q_{{r_{1} ,\alpha }} + {\text{i}}q_{i} ,\quad q_{{t_{2} ,\alpha }} = - q_{{r_{2} ,\alpha }} + {\text{i}}q_{i} , \\ q_{{t_{3} ,\alpha }} & = q_{{r_{2} ,\alpha }} + {\text{i}}q_{i} ,\quad q_{{t_{4} ,\alpha }} = - q_{{r_{1} ,\alpha }} + {\text{i}}q_{i} \\ \end{aligned}$$

(71)

where

$$q_{{r_{1} ,\alpha }} = \alpha p_{t} + \Delta q_{r,\alpha } ,\quad q_{{r_{2} ,\alpha }} = - \alpha p_{t} + \Delta q_{r,\alpha }$$

(72)

It is also useful to remark that, by having frequencies for one specific value $\alpha_{1}$, the corresponding values for $\alpha_{2}$ can be simply obtained by

$$q_{{t_{j} ,\alpha_{2} }} = q_{{t_{j} ,\alpha_{1} }} + \left( {\alpha_{2} - \alpha_{1} } \right)p_{t} ,\quad j = 1, \ldots ,4$$

(73)

because then

$$2q_{{m,\alpha_{2} }} = q_{{t_{1} ,\alpha_{2} }} + q_{{t_{2} ,\alpha_{2} }} = q_{{t_{1} ,\alpha_{1} }} + q_{{t_{2} ,\alpha_{1} }} + 2\left( {\alpha_{2} - \alpha_{1} } \right)p_{t} = 2\alpha_{2} p_{t} + 2{\text{i}}q_{i}$$

(74)

and similarly for $j = 3,4$, by exploiting the medium value for negative $- p_{t}$: $q_{{\bar{m},\alpha }} = - \alpha p_{t} + {\text{i}}q_{i}$.

Each discontinuity line has a starting point, that is characterized by $p_{t} = 0$. Then $D(p,q)$ is only a function of $\Delta q_{r,\alpha }$ and $q_{i}$. This defines two equations (imaginary part as well as real part of $D(p,q)$ must be null) for two real unknowns, which can be solved numerically. There are multiple solutions due to the tangent function, each marking a starting point of two lines, inconformity with the previous analysis, $\Delta q_{r,\alpha }$ marks the starting point of $q_{{t_{j} ,\alpha }}$ for $j = 1,3$ and $- \Delta q_{r,\alpha }$ for $j = 2,4$. These starting points are valid for all $\vartheta_{s}$, but further extension of discontinuity lines naturally depends on $\vartheta_{s}$.

Determination of discontinuity lines is straightforward for $\vartheta_{s} = 0$. At first, $q = \alpha p_{t} + \Delta q_{r,\alpha } + {\text{i}}q_{i}$ is substituted, a convenient $\alpha$ is selected and a starting point is calculated by introducing $p_{t} = 0$. Then, it is convenient to separate $D_{b} (p,q)$ and $D_{f} (p,q)$ into their real and imaginary parts:

$$\begin{aligned} \text{Re} \left[ {D_{b} \left( {p,\Delta q_{r,\alpha } } \right)} \right] & = p^{4} - 4\Delta q_{r,\alpha }^{2} + 4q_{i}^{2} , \\ \text{Im} \left[ {D_{b} \left( {p,\Delta q_{r,\alpha } } \right)} \right] & = - 8\Delta q_{r,\alpha } q_{i} \\ \end{aligned}$$

(75)

$D_{f} (p,q)$ needs a little bit more sophisticated approach, but it is generally more convenient for this analysis, because it does not depend on $p$.

$$D_{f} \left( {\Delta q_{r,\alpha } } \right) = \frac{{4R\left( {\Delta q_{r,\alpha } + {\text{i}}q_{i} } \right)\sqrt {1 - \eta_{f} q_{i} + {\text{i}}\eta_{f} \Delta q_{r,\alpha } } }}{{\tan \left( {\frac{{R\left( {\Delta q_{r,\alpha } + {\text{i}}q_{i} } \right)}}{{\sqrt {1 - \eta_{f} q_{i} + {\text{i}}\eta_{f} \Delta q_{r,\alpha } } }}} \right)}}$$

(76)

For the square root it will be used

$$\sqrt {O + {\text{i}}Q} = \sqrt {\frac{{O + \sqrt {O^{2} + Q^{2} } }}{2}} + {\text{i}}\sqrt {\frac{{ - O + \sqrt {O^{2} + Q^{2} } }}{2}}$$

(77)

and for the tangent function

$$\tan (O + {\text{i}}Q) = \frac{\sin O\cos O}{{\cos^{2} O + \sinh^{2} Q}} + {\text{i}}\frac{\sinh Q\cosh Q}{{\cos^{2} O + \sinh^{2} Q}}$$

(78)

Denoting

$$\begin{aligned} O_{1} & = \sqrt {\frac{{1 - \eta_{f} q_{i} + \sqrt {\left( {1 - \eta_{f} q_{i} } \right)^{2} + \left( {\eta_{f} \Delta q_{r,\alpha } } \right)^{2} } }}{2}} , \\ Q_{1} & = \sqrt {\frac{{ - 1 + \eta_{f} q_{i} + \sqrt {\left( {1 - \eta_{f} q_{i} } \right)^{2} + \left( {\eta_{f} \Delta q_{r,\alpha } } \right)^{2} } }}{2}} \\ \end{aligned}$$

(79)

$$\begin{aligned} O_{2} &= \frac{{R\left( {O_{1} \Delta q_{r,\alpha } + Q_{1} q_{i} } \right)}}{{O_{1}^{2} + Q_{1}^{2} }},\\ Q_{2} &= \frac{{R\left( { - Q_{1} \Delta q_{r,\alpha } + O_{1} q_{i} } \right)}}{{O_{1}^{2} + Q_{1}^{2} }} \\ \end{aligned}$$

(80)

$$\begin{aligned} O_{3} &= \frac{{\sin O_{2} \cos O_{2} }}{{\cos^{2} O_{2} + \sinh^{2} Q_{2} }},\\ Q_{3} &= \frac{{\sinh Q_{2} \cosh Q_{2} }}{{\cos^{2} O_{2} + \sinh^{2} Q_{2} }}\\ \end{aligned}$$

(81)

Then

$$\begin{aligned} \text{Re} \left[ {D_{f} \left( {\Delta q_{r,\alpha } } \right)} \right] & = 4R\frac{{\left( {O_{1} \Delta q_{r,\alpha } - Q_{1} q_{i} } \right)O_{3} + \left( {Q_{1} \Delta q_{r,\alpha } + O_{1} q_{i} } \right)Q_{3} }}{{O_{3}^{2} + Q_{3}^{2} }} \\ \text{Im} \left[ {D_{f} \left( {\Delta q_{r,\alpha } } \right)} \right] & = 4R\frac{{ - \left( {O_{1} \Delta q_{r,\alpha } - Q_{1} q_{i} } \right)Q_{3} + \left( {Q_{1} \Delta q_{r,\alpha } + O_{1} q_{i} } \right)O_{3} }}{{O_{3}^{2} + Q_{3}^{2} }} \\ \end{aligned}$$

(82)

After that, further $q_{i}$ is selected, $\Delta q_{r,\alpha }$ is calculated by nulling the imaginary part of $D(p,q)$ and $p_{t}$ is calculated by nulling the real part of $D(p,q)$. It is seen from Eqs. (75) and (82) that there is only one occurrence of $p^{4}$, therefore only roots $\Delta q_{r,\alpha }$ leading to real $p_{t}$ are valid. It can be shown that the lowest $q_{i,1}$ of a starting point is positive and the corresponding discontinuity line extends by increasing $q_{i,1}$. For further starting points $q_{i,j}$, $j = 2, \ldots$, the discontinuity line firstly extends by slight decreasing of $q_{i,j}$ and then by its increasing.

When $\vartheta_{s} \ne 0$, then $D_{f} \left( {p,\Delta q_{r,\alpha } } \right)$ depends on $p$ and therefore either an iterative procedure can be implemented or the two equations can be solved directly by indicating a reasonable estimate for $p_{t}$ and $\Delta q_{r,\alpha }$ obtained from the discontinuity line tendency.

After having discontinuity lines, it is necessary to evaluate their importance. For $\vartheta_{s} = 0$ discontinuity lines are short, with increasing $\vartheta_{s}$, they extend much more.

5.3 Low foundation damping

For illustration of a case with low foundation damping, $\eta_{f} = 0.001$, $\eta_{b} = \eta_{N} = \eta_{{P_{0} }} = 0$, $R = 2$, $\eta_{M} = 70$ and $\vartheta_{s} = 0{:}0.1{:}1.5$ are selected. Here a Matlab designation is used: $a{:}b{:}c$ means that discrete values from $a$ until $c$ by step $b$ will be considered. At first, frequency lines are shown in Fig. 3. They are grouped in three sets: set 1: $\vartheta_{s} = 0{:}0.1{:}0.5$, set 2: $\vartheta_{s} = 0.6{:}0.1{:}1.0$ and set 3: $\vartheta_{s} = 1.1{:}0.1{:}1.5$. In the first set these frequencies are shown until $\alpha = 1.2$, and in the last two ones until $\alpha = 1.5$, to catch well the loops. Only one frequency from each pair is plotted, meaning that other lines would be obtained by reverting the real part.

Fig. 3

Frequency lines: a set 1; b set 2; c set 3 (within the considered sequence, the lines are getting darker with increasing $\vartheta_{s}$)

Frequency lines clearly identify the different regimes as described in Sect. 3. In the first velocity interval starting at almost zero velocity and ending close to the critical velocity, at $\alpha_{{C_{1} }}$, the induced frequencies are well-defined. They start with practically zero, but positive imaginary part, which is then slightly increasing. Getting closer to the critical velocity, discontinuities in $K(0,q)$ are getting more severe and frequency lines are cut at $\alpha_{{C_{1} }}$. Within the next velocity interval $\left( {\alpha_{{C_{1} }} ;\alpha_{{C_{2} }} } \right)$, there are no induced frequencies. After that, for $\alpha > \alpha_{{C_{2} }}$, frequency lines are recovered and they form almost perfectly symmetric loops with very similar real parts and practically opposite imaginary parts. Then frequency lines are interrupted again by no frequency region $\left( {\alpha_{{C_{3} }} ;\alpha_{{C_{4} }} } \right)$ and after that continue further in a similar way. The onset of instability is located very close to $\alpha_{{C_{2} }}$, as can be observed from Fig. 3. Within the no induced frequency interval $\left( {\alpha_{{C_{3} }} ;\alpha_{{C_{4} }} } \right)$ stability is recovered, but it is lost again when the frequency lines are recovered and induced frequencies achieve negative imaginary parts in the next loops. Especially for lower $\vartheta_{s}$, there is a clear region with no induced frequencies $\left( {\alpha_{{C_{3} }} ;\alpha_{{C_{4} }} } \right)$, where the stability is recovered.

As expected, damping shifts the onset of instability into the supercritical velocity range, but as the damping level is low, this shift is not significant. This can be observed in Fig. 4, where the onset of instability is plotted together with the critical velocity.

Fig. 4

Lines identifying the first frequency line cut $\alpha_{{C_{1} }}$ (full grey), second frequency line cut $\alpha_{{C_{2} }}$ (dotted), the critical velocity (full black) and the onset of instability (dashed)

Before showing some particular cases, discontinuity lines are analysed. In conformity with Sect. 5.2, first three starting points are determined as: $q_{i} = 2.000 \times 10^{ - 4} ;\;1.936 \times 10^{ - 3} ;\;5.804 \times 10^{ - 3}$ and $\Delta q_{r} = 0.632;\;1.968;\;3.407$ which are valid for each $\vartheta_{s}$ and $\alpha$. Further, discontinuity lines were determined for each $\vartheta_{s}$ and $\alpha = 1.4$, and recalculated for other $\alpha$ by Eq. (73). Only the cases of $\vartheta_{s} = 0$ and $\vartheta_{s} = 0.8$ are shown here, in Figs. 5 and 6.

Fig. 5

Discontinuity lines for $\vartheta_{s} = 0$ and $\alpha = 0.2{:}0.2{:}1.2$. Black dots represent the induced frequencies

Fig. 6

Discontinuity lines for $\vartheta_{s} = 0.8$ and $\alpha = 0.2{:}0.2{:}1.2$. Black dots represent the induced frequencies (from the first, the second and the third starting point the lines are: full, dashed and dotted, respectively)

Figure 5 confirms that the discontinuity lines for $\vartheta_{s} = 0$ are short, when compared with the ones in Fig. 6 for $\vartheta_{s} = 0.8$, but the starting points are the same for each $\vartheta_{s}$ and $\alpha$ as proven in Sect. 5.2. The induced frequencies are added in Figs. 5 and 6 only when they fall within the scale, in Fig. 5 this happens for $\alpha = 0.2$ and $\alpha = 0.4$, and in Fig. 6 for $\alpha = 0.2{:}0.2{:}0.8$. They also exist for $\vartheta_{s} = 0$ and $\alpha = 0.8,\;1.2$; $\vartheta_{s} = 0.8$ and $\alpha = 1.0$, but lie out of the scale.

As some particular cases, velocities $\alpha = 0.2{:}0.2{:}1.0$ combined with $\vartheta_{s} = 0$, $\vartheta_{s} = 0.8$ and massless foundation ($R = 0$) are selected. Displacements of the contact point are shown in Figs. 7, 8 and 9. Full deflection shapes along the beam are not presented, because many cases were already analysed in previous works. The induced frequencies for $\vartheta_{s} = 0$ exist only for $\alpha = 0.2,\;0.4,\;0.8$, but for $\vartheta_{s} = 0.8$ all selected velocities can be characterized by the induced frequencies. Massless foundation is assumed without damping and therefore $\alpha = 1$ cannot be considered as then the steady-state part of the solution is infinite. Frequencies and steady-state deflections $\overset{\lower0.5em\hbox{$\smash{\scriptscriptstyle\frown}$}}{w}_{b}$ are summarized in Table 3.

Fig. 7

Displacements at the contact point for $\vartheta_{s} = 0$ (full grey—harmonic, dotted—full): a $\alpha = 0.2,\;0.4$; b $\alpha = 0.8$

Fig. 8

Displacements at the contact point for $\vartheta_{s} = 0.8$ (full grey—harmonic, dotted—full): a $\alpha = 0.2{:}0.2{:}0.8$; b $\alpha = 1$

Fig. 9

Displacements at the contact point (full black—$R = 0$, dashed—$\vartheta_{s} = 0$, dotted—$\vartheta_{s} = 0.8$): a $\alpha = 0.2$; b $\alpha = 0.4$; c $\alpha = 0.6$; d $\alpha = 0.8$

Table 3 Induced frequencies and steady-state deflections for the selected cases

Excellent agreement between the harmonic and full solutions is obtained for $\vartheta_{s} = 0$ and each $\alpha = 0.2,\;0.4,\;0.8$, as illustrated in Fig. 7, and as expected from the analysis of discontinuity lines and differences between the initial value of the harmonic solution and the initial conditions.

In Fig. 8, same comparison for $\vartheta_{s} = 0.8$ is shown. Worse agreement is obtained for $\alpha = 0.8$, which could be guessed from the analysis of the discontinuity lines and from the deviation of the initial values of the harmonic solution from the initial conditions.

It can be concluded from the analysis of frequency and discontinuity lines: (i) within the velocity interval until $\alpha_{{C_{1} }}$, full solution is very well approximated by the harmonic one. This is often related to the situation, when the imaginary part of the induced frequencies is lower than $q_{i,1}$ ($\vartheta_{s} = 0$ and $\alpha = 0.2,\;0.4$; $\vartheta_{s} = 0.8$ and $\alpha = 0.2,\;0.4,\;0.6$); (ii) for $\alpha < \alpha_{{C_{1} }}$ but close to $\alpha_{{C_{1} }}$ there are some visible differences between the harmonic and full solutions indicating the importance of the transient part. This is often related to the situation, when the imaginary part of the induced frequencies is higher than $q_{i,1}$ and the initial value of the harmonic solution is deviated from the initial conditions ($\vartheta_{s} = 0.8$ and $\alpha = 0.8$); (iii) when the solution is unstable, than the imaginary part of the induced frequencies is always lower than $q_{i,1}$ because it is negative. In such cases the agreement is again very good. If there is another frequency with high imaginary part, then such frequency usually lies in the discontinuity region and should be disregarded ($\vartheta_{s} = 0$ and $\alpha = 0.8$; $\vartheta_{s} = 0.8$ and $\alpha = 1.0$); (iv) within the velocity interval with no induced frequencies, as e.g. $\left( {\alpha_{{C_{1} }} ;\alpha_{{C_{2} }} } \right)$, but not very close to the extremities, the transient part of the solution smoothly adapts the vibrations from the initial conditions to the steady-state form ($\vartheta_{s} = 0$ and $\alpha = 0.6$, Fig. 9c); (v) within the velocity interval with no induced frequencies but closer to its extremities, full solution looks like that there should be a significant harmonic part, but there is no such induced frequency. In such cases the agreement is not very good; (vi) when the initial values of the harmonic solution are deviated from the initial conditions, then there must be a contribution of the transient part to adapt the solution to the initial conditions ($\vartheta_{s} = 0.8$ and $\alpha = 0.8$). This conclusion has already been drawn in previous works for massless foundation.

Finally, comparison between the previous cases and the massless foundation is shown in Fig. 9. In this comparison, full solution is used. In Fig. 9d related to $\alpha = 0.8$, the case with $\vartheta_{s} = 0$ is not included, because it is unstable and thus the corresponding deflections are much higher.

Differences between displacements in Fig. 9 are mainly due to the different position of selected $\alpha$ with respect to the critical velocity of each case, but it is seen that the inertial foundation with no shear resistance give rise to higher displacements dictated by lower frequencies, while higher shear resistance stiffens the foundation.

5.4 High foundation damping

For illustration of a case with high foundation damping, $\eta_{f} = 0.1$, $\eta_{b} = \eta_{N} = \eta_{{P_{0} }} = 0$, $R = 4$, $\eta_{M} = 60$ and $\vartheta_{s} = 0{:}0.1{:}1.5$ are selected. At first, frequency lines are shown in Fig. 10. They are grouped in three sets as in Sect. 5.3. First two sets show frequencies until $\alpha = 1.5$, the last one is until $\alpha = 1.8$, to catch well the onset of instability.

Fig. 10

Frequency lines: a set 1; b set 2; c set 3 (within the considered sequence the lines are getting darker with increasing $\vartheta_{s}$)

Also here, the frequency lines clearly identify the different regimes as described in Sect. 3. In the first velocity interval starting at almost zero velocity they start with low positive imaginary part, which is then increasing. Getting closer to the critical velocity, discontinuities in $K(0,q)$ are getting more severe and frequency lines are cut at $\alpha_{{C_{1} }}$. Within this velocity range, there are also additional branches with significantly higher frequencies, starting from $\vartheta_{s} = 0.9$, but these frequencies lie in the discontinuity region and should be disregarded from the harmonic solution. Within the next velocity interval $\left( {\alpha_{{C_{1} }} ;\alpha_{{C_{2} }} } \right)$, there are no induced frequencies. After that, for $\alpha > \alpha_{{C_{2} }}$, frequency lines are recovered. In all cases the onset of instability can be easily found by identifying the lowest $\alpha$ for which the frequency has a negative imaginary part. As expected, there is quite significant increase of the velocity at the onset of instability with respect to the critical velocity, especially for low shear ratios. This is further demonstrated in Fig. 11, where the onset of instability is plotted together with the critical velocity.

Fig. 11

Lines identifying the first frequency line cut $\alpha_{{C_{1} }}$ (full grey), second frequency line cut $\alpha_{{C_{2} }}$ (dotted), the critical velocity (full black) and the onset of instability (dashed)

Before showing some particular cases, discontinuity lines are analysed. In conformity with Sect. 5.2, first three starting points are determined as: $q_{i} = 6.832 \times 10^{ - 3} ;\,6.165 \times 10^{ - 2} ;\,1.720 \times 10^{ - 1}$ and $\Delta q_{r} = 0.370;\,1.109;\,1.847$. It is seen that $q_{i}$ of starting points, influenced by the foundation damping, are now much higher than in Sect. 5.3, contrary to $\Delta q_{r}$ that are lower. Also here, discontinuity lines were determined for each $\vartheta_{s}$ and $\alpha = 1.4$, and after that recalculated to other $\alpha$. Cases of $\vartheta_{s} = 0$ and $\vartheta_{s} = 0.2$ and two particular velocities for $\vartheta_{s} = 1.5$ are shown in Figs. 12, 13 and 14.

Fig. 12

Discontinuity lines for $\vartheta_{s} = 0$ and $\alpha = 0.2{:}0.2{:}1.4$. Black dots represent the induced frequencies

Fig. 13

Discontinuity lines for $\vartheta_{s} = 0.2$ and $\alpha = 0.2{:}0.2{:}1.4$. Black dots represent the induced frequencies (from the first, the second and the third starting point the lines are: full, dashed and dotted, respectively)

Fig. 14

Discontinuity lines for $\vartheta_{s} = 1.5$, $\alpha = 1$ and $\alpha = 1.2$. Black dots represent the induced frequencies (from the first, the second and the third starting point the lines are: full, dashed and dotted, respectively)

Figure 12 confirms that the discontinuity lines for $\vartheta_{s} = 0$ are short, when compared with the ones from Figs. 13 and 14. The induced frequencies are added only when they fall within the scale.

Regarding the displacements of the contact point, $\alpha = 0.2{:}0.2{:}1.4$ are considered, combined with $\vartheta_{s} = 0$, $\vartheta_{s} = 0.2$, $\vartheta_{s} = 0.4$, $\vartheta_{s} = 1.2$ and $\vartheta_{s} = 1.5$. All these cases are selected in order to confirm the previous conclusions, nevertheless, due to the extension of the paper, the corresponding graphs of associated deflections are placed in “Appendix”. It is shown that the previous conclusions are maintained, nevertheless, with higher foundation damping the differences between the harmonic and full solutions are aggravated. For this reason, a simplified transient solution can be defined as contour integral eliminating the most severe discontinuities. Summary of induced frequencies and steady-state deflections is presented in Table 4. Frequencies identified by frequency lines in Fig. 10 but falling into discontinuity regions are not included as they should not enter the formula for the harmonic solution. A typical case of such position is shown in Fig. 14 for $\alpha = 1.2$.

Table 4 Induced frequencies and steady-state deflections for the selected cases

Summary of conclusions are for better clarity organized in Table 5, implementing the designations from Sect. 5.3. It is, however, necessary add two more points, that were not required in Sect. 5.3: (vii) when $\alpha > \alpha_{{C_{2} }}$ but still within the stability region, then usually (and especially for values close to $\alpha_{{C_{2} }}$) the imaginary part of the induced frequencies is much higher than $q_{i,1}$. For the harmonic solution it implies that the imaginary part seems to be overestimated (looks like that higher damping than the model is having is acting). Nevertheless, the real part and therefore the frequency of the resulting oscillation matches well; (viii) when $\alpha > \alpha_{{C_{2} }}$, still within the stability region but getting closer to instability and further from $\alpha_{{C_{2} }}$, then the overdamping effect is vanishing and the agreement between the harmonic and full solutions is again excellent. This is sometimes strengthened by that fact that the imaginary part of the induced frequencies falls again below $q_{i,1}$.

Table 5 Induced frequencies and steady-state deflections for the selected cases

The column in Table 5 named as “agreement” stands for the quantification of the agreement between the harmonic and full solutions.

From the previous analysis, it can be concluded that the harmonic solution still provides a very good approximation in majority of cases. The cases with only reasonable agreement have somehow artificial overdamping, but generally the frequency of the unsteady part is correct. Such cases occur more often for lower shear resistance, except when it is completely neglected.

As regard as the instability, it was seen that the induced frequencies always exist in the instability velocity intervals and are therefore simple indicators of such behaviour. It was also seen, that in such cases the agreement between the harmonic and full solutions is always excellent, and therefore the harmonic solution can be exploited for evaluation of the severity of instability, which is important for mitigation measures.

Cases with no induced frequencies are always stable. Unfortunately, within these situations there are some cases with only poor agreement between the harmonic and full solutions. Nevertheless, these cases are rare and do not invalidate the proposed method.

5.5 Low moving mass ratio

Having in mind applications to railways, it is necessary to see whether the method is not affected by a very low moving mass ratio. For illustration, $\eta_{f} = \eta_{b} = 0.1$, $\eta_{N} = \eta_{{P_{0} }} = 0$, $R = 2$, $\eta_{M} = 10$ and $\vartheta_{s} = 0{:}0.1{:}1.5$ are selected, but not so many details as in previous sections will be given due to the extension of the paper. At first, frequency lines are shown in Fig. 15. They are grouped in three sets as in previous sections. First two sets show frequencies until $\alpha = 1.5$, the last one is until $\alpha = 1.8$, to catch well the onset of instability.

Fig. 15

Frequency lines: a set 1; b set 2; c set 3 (within the considered sequence the lines are getting darker with increasing $\vartheta_{s}$)

As expected, there is quite significant increase of the onset of instability with respect to the critical velocity, especially for low shear ratios. This is further demonstrated in Fig. 16, where the onset of instability is plotted together with the critical velocity.

Fig. 16

Lines identifying the first frequency line cut $\alpha_{{C_{1} }}$ (full grey), second frequency line cut $\alpha_{{C_{2} }}$ (dotted), the critical velocity (full black) and the onset of instability (dashed)

Only few cases of comparison between the harmonic and full solutions are shown in “Appendix”.

6 Conclusions

In this papers analysis of moving mass problem is conducted. It is assumed that the mass is traversing uniformly a beam supported by a finite depth foundation with simplified shear resistance. The problem is solved by mode expansion method on finite beams and by integral transforms on infinite beams. Special attention is placed on unsteady harmonic part of the vibration, which is an indicator of unstable behaviour.

Final formula defining deflection shape on infinite beams has a similar form as for the massless foundation. However, in the foundation model considered in this paper the agreement between the harmonic and full solutions is not dictated only by the initial matching with initial conditions, but also by the position of the induced frequencies along the frequency lines with respect to the frequency line cuts. Some cases result in an overdamped solution, suggesting that probably some regularization of the foundation model would be possible. When agreement between the harmonic and full solutions is only approximate, simplified version of transient vibration can be calculated by numerical integration. One may argue that it is not worthwhile to separate the solution into harmonic and transient parts, because full solution can always be calculated directly by numerical integration. Nevertheless, it is necessary to highlight that in the proposed approach the numerical integration is performed only around a limited region, which can be easily controlled numerically. Moreover, main part of resulting vibrations is contained in the harmonic part and therefore the transient one is rapidly decreasing in time. Determination of frequency lines is easy, and this is a secure way how to determine the onset of instability.

Mode expansion method on finite beams can be used for an easy analysis of undamped vibrations, impossible to reach on infinite beams due to numerical reason. Such model has, however, larger applications and can be simply adapted for analysis of abrupt change in foundation stiffness.

Appendix

This appendix summarizes graphs of evolution of the displacement at the contact point for cases tested in Sect. 5.4, namely $\eta_{f} = 0.1$, $\eta_{b} = 0$, $R = 4$, $\eta_{M} = 60$, $\alpha = 0.2{:}0.2{:}1.4$ for $\vartheta_{s} = 0{:}0.2{:}0.4$ and $\alpha = 0.2{:}0.2{:}1.8$ for $\vartheta_{s} = 1.2,\;1.5$. As in the other cases, for the sake of simplicity $\eta_{N} = 0$ and $\eta_{{P_{0} }} = 0$. Few cases from Sect. 5.5 are also included (see Figs. 17, 18, 19, 20, 21, 22).

Fig. 17

Displacements at the contact point for $\vartheta_{s} = 0$ (full grey—harmonic with simplified transient, dashed—harmonic, dotted—full): a $\alpha = 0.2$; b $\alpha = 0.4$; c $\alpha = 0.6$; d $\alpha = 0.8$; e $\alpha = 1.0$; f $\alpha = 1.2$; g $\alpha = 1.4$

Fig. 18

Displacements at the contact point for $\vartheta_{s} = 0.2$ (full grey—harmonic with simplified transient, dashed—harmonic, dotted—full): a $\alpha = 0.2$; b $\alpha = 0.4$; c $\alpha = 0.6$; d $\alpha = 0.8$; e $\alpha = 1.0$; f $\alpha = 1.2$; g $\alpha = 1.4$

Fig. 19

Displacements at the contact point for $\vartheta_{s} = 0.4$ (full grey—harmonic with simplified transient, dashed—harmonic, dotted—full): a $\alpha = 0.2$; b $\alpha = 0.4$; c $\alpha = 0.6$; d $\alpha = 0.8$; e $\alpha = 1.0$; f $\alpha = 1.2$; g $\alpha = 1.4$

Fig. 20

Displacements at the contact point for $\vartheta_{s} = 1.2$ (full grey—harmonic with simplified transient, dashed—harmonic, dotted—full): a $\alpha = 0.2$; b $\alpha = 0.4$; c $\alpha = 0.6$; d $\alpha = 0.8$; e $\alpha = 1.0$; f $\alpha = 1.2$; g $\alpha = 1.4$; h $\alpha = 1.6$; i $\alpha = 1.8$

Fig. 21

Displacements at the contact point for $\vartheta_{s} = 1.5$ (full grey—harmonic with simplified transient, dashed—harmonic, dotted—full): a $\alpha = 0.2$; b $\alpha = 0.4$; c $\alpha = 0.6$; d $\alpha = 0.8$; e $\alpha = 1.0$; f $\alpha = 1.2$; g $\alpha = 1.4$; h $\alpha = 1.6$; i $\alpha = 1.8$

Fig. 22

Displacements at the contact point for $\vartheta_{s} = 0$ (full grey—harmonic, dotted—full): a $\alpha = 0.2$; b $\alpha = 0.4$; c $\alpha = 1.0$; d $\alpha = 1.4$; e $\alpha = 1.5$

Only in part (b) of Fig. 22 it is seen that the harmonic solution is deviated from the full solution due to the difference between the initial values of the harmonic solution and initial conditions.