1 Introduction

The magnetohydrodynamic (MHD) flows of rheological materials have indispensable significance in the industrial and physiological applications related to magnetic abrasive finishing (MAF), blood circulation, magnetic drug targeting (MDT), magnetic fluid hyperthermia (MFH), control of liquid metals in continuous casting, plasma welding, metallurgy, magnetic cell separation, oil exploration, geophysics. Also the interest in peristaltic flow is quite prevalent due to its extensive applications in medical science, engineering and industrial manufacturing. Peristalsis is a mechanism of fluid transport in which a progressive wave of contraction or expansion propagates along the length of a distensible tube containing fluid. It is involved in the movement of chyme in the gastrointestinal tract, transport of spermatozoa in the ductus efferentes of the male reproductive tract, the locomotion of worms, transport of lymph in the lymphatic vessels, fallopian tube, vasomotion of small blood vessels such as arterioles, venules and capillaries. Most sophisticated applications can be seen in early stage embryonic development [1], diabetes pumps [2] and pharmacological delivery system [3].

A number of attempts have been made in recent past to analyze peristaltic motion in various scenarios [4–24]. The impact of curvature on peristaltic transport of fluid is analyzed through the studies [25–36]. These attempts can be broadly classified in terms of Reynolds number, fluid nature, geometry of the vessel and heat transfer mechanism. However very few studies for asymptotic analysis of peristaltic motion exist in the literature. More recently Asghar et al. [37] studied the boundary layer structure in the magnetohydrodynamic peristaltic flow of Sisko fluid in a straight channel using the method of matched asymptotic expansion. Their analysis motived us to look into the same problem by taking into account the impact of curvature of the channel. It is mentioned that this problem has not been yet studied in the literature in any manner. We model the flow problem employing long wavelength and low Reynolds number assumptions. The solution of equation governing the flow is constructed using the method of matched asymptotic expansion for two specific values of power-law index. Our main focus is to highlight the boundary layer character of the solutions. The choice of Sisko model is driven firstly by its effectiveness in describing the flow properties of shear-thinning material over four or five decades of shear rate and secondly due to its superiority over power-law model. Moreover rheology of many materials like commercial fabric softener, aqueous solution of carbopol, polymer liquid crystal and yogurt can be described by Sisko fluid model [38]. Magnetohydrodynamic (MHD) effects have been taken into account because of its numerous applications in bioengineering and medical devices. Specific applications include magnetic wound or cancer tumor treatment, bleeding reduction during surgeries and targeted transport of drugs using magnetic particles as drug carrier. Apart from that bio-fluids like blood is magnetrohydrodynamic because of complex intercellular protein, cell membrane and hemoglobin.

The arrangement of the present paper is as follows: The problem is mathematically formulated with appropriate assumptions in Sect. 2. Asymptotic solutions for large values of Hartmann number and for two specific values of power-law index are obtained in Sect. 3. Graphical illustration of the solutions is also presented in Sect. 3. We compile the main observations of the paper in Sect. 4.

2 Mathematical formulation and rheological constitutive equations

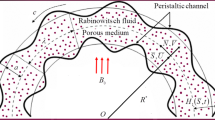
Let us consider two-dimensional incompressible flow of Sisko fluid in a curved channel having width 2a 1 with centre O and R * radius. The flow in the channel is due to sinusoidal waves of amplitude a 2 travelling along the walls. A schematic diagram illustrating the flow geometry is provided in Fig. 1. A curvilinear coordinate system (R, X), in which R is along the radial direction and X is along the axial direction is used. Let V 1 and V 2 be the components of velocity in the radial (R) and axial (X) directions, respectively. The equations describing the geometry of upper and lower walls are:

$$\,H_{1} \left( {X,t} \right) = a_{1} + a_{2} \sin \left( {\left( {\frac{2\pi }{\lambda }} \right)\left( {X - ct} \right)} \right), \quad {\text{Upper}}\,{\text{wall,}}$$
(1)
$$H_{2} \left( {X,t} \right) = - a_{1} - a_{2} \sin \left( {\left( {\frac{2\pi }{\lambda }} \right)\left( {X - ct} \right)} \right), \quad {\text{Lower}}\,{\text{wall,}}$$
(2)

where λ and t represent the wavelength and time, respectively.

Fig. 1
figure 1

Flow diagram of the curved model

Full size image

The velocity field for the flow under consideration is

$$\varvec{V}{ = }\left[ {V_{1} \left( {X,R,t} \right),\,V_{2} \left( {X,R,t} \right),\,0\,} \right].$$
(3)

The flow through the curved channel is governed by the following equations

$$\,{\mathbf{\nabla }} .\varvec{V}{ = }\, 0 ,$$
(4)
$$\rho \frac{{d\varvec{V}}}{dt} = \,\,{\mathbf{\nabla }} .\varvec{T + J} \times \varvec{B} ,$$
(5)

where ρ, T, J and B represent the fluid density, the Cauchy stress tensor, the current density and an applied magnetic field in the radial direction, respectively.

The Cauchy stress tensor is given by

$$\varvec{T}\, = \, - p\varvec{I}\, + \varvec{S},$$
(6)

where p the isotopic pressure, \(\varvec{I}\) is the identity tensor and \(\varvec{S}\) is the extra stress tensor which for Sisko model satisfies [37]

$$\varvec{S} = \left[ {a + b\left( {\sqrt \varPi } \right)^{n - 1} } \right]A_{1} ,$$
(7)

with the expressions

$$A_{1} = {\mathbf{L + L}}^{{\mathbf{t}}},\quad {\mathbf{L = }}\text{ grad} \varvec{V},\quad \varPi = \frac{1}{2}{\text{tr}}\left( {A_{1}^{2} } \right).$$
(8)

In the above equations Π is the second invariant of the symmetric part of the velocity gradient, A 1 is the rate of deformation tensor, n is the power-law index, a is the infinite shear rate viscosity and b is the consistency index. The Sisko model reduces to power-law model by setting a = 0 while the corresponding tensor of Newtonian model can be obtained by either putting b = 0, or a = 0 and n = 1 simultaneously. The model (7) is capable of predicting shear-thinning and shear-thickening effects for n < 1 and n > 1, respectively.

Let us assume that the flow is subject to applied magnetic field in the radial direction. Assuming the magnetic Reynolds number to be small and utilizing Maxwell equations, we obtain [36]

$$\varvec{B}\, = \,\left( {\frac{{B_{0} R^{*} }}{{R + R^{*} }}} \right)\varvec{e}_{\varvec{R}} \text{,}$$
(9)

where B 0 is the characteristic magnetic induction in the limit R * → ∞, and \(\varvec{e}_{\varvec{R}}\) is the unit vector in the radial direction. It is pointed out here that the magnetic field given by Eq. (9) is solenoidal.

Using Eq. (9), the term \(\varvec{J} \times \varvec{B}\) in Eq. (5) is given by [36]

$$\varvec{J} \times \varvec{B} = - \left( {\frac{{\sigma B_{0}^{2} V_{2} R^{*2} }}{{\left( {R + R^{*} } \right)^{2} }}} \right)\varvec{e}_{\varvec{X}} ,$$
(10)

where \(\varvec{e}_{\varvec{X}}\) is the unit vector in the azimuthal direction.

In view of Eq. (6), we can write Eq. (5) as follows:

$$\rho \frac{{d{\mathbf{V}}}}{dt} = \,\, - {\mathbf{\nabla }}p\, + \,{\mathbf{\nabla }}\varvec{.S + J} \times \varvec{B}.\,$$
(11)

For two-dimensional velocity field, Eqs. (4) and (11) yield the following equations:

$$\frac{\partial }{\partial R}\left\{ {\left( {R + R^{*} } \right)V_{1} } \right\} + R^{*} \frac{{\partial V_{2} }}{\partial X} = 0,\,$$
(12)
$$\begin{aligned} \rho \left[ {\frac{{\partial V_{1} }}{\partial t} + V_{1} \frac{{\partial V_{1} }}{\partial R} + \frac{{R^{*} V_{2} }}{{R + R^{*} }}\frac{{\partial V_{1} }}{\partial X} - \frac{{V_{2}^{2} }}{{R + R^{*} }}} \right]\,\, = \, - \frac{\partial p}{\partial R} + \frac{1}{{R + R^{*} }}\,\frac{\partial }{\partial R}\left\{ {\left( {R + R^{*} } \right)\,S^{RR} } \right\} \hfill \\ + \frac{{R^{*} }}{{R + R^{*} }}\frac{\partial }{\partial X}S^{RX} - \frac{{S^{XX} }}{{R + R^{*} }}, \hfill \\ \end{aligned}$$
(13)
$$\begin{aligned} \rho \left[ {\frac{{\partial V_{2} }}{{\partial \text{t}}}\text{ + }V_{1} \frac{{\partial V_{2} }}{\partial R}\text{ + }\frac{{R^{*} V_{2} }}{{R\text{ + }R^{*} }}\frac{{\partial V_{2} }}{\partial X} - \frac{{V_{2} V_{1} }}{{R\text{ + }R^{*} }}} \right]\text{ = } - \left( {\frac{{R^{*} }}{{R\text{ + }R^{*} }}} \right)\frac{\partial p}{\partial X}\text{ + }\frac{\text{1}}{{\left( {\text{R + }R^{*} } \right)^{2} }}\frac{\partial }{{\partial \text{R}}}\left\{ {\left( {\text{R + }R^{*} } \right)^{2} S^{RX} } \right\} \hfill \\ \text{ + }\frac{{R^{*} }}{{\text{R + }R^{*} }}\frac{\partial }{\partial X}S^{XX} - \frac{{\sigma B_{0}^{\text{2}} V_{2} R^{*2} }}{{\left( {\text{R + }R^{*} } \right)^{2} }}. \hfill \\ \end{aligned}$$
(14)

We remark here that curvilinear coordinates (R, X) with scale factor given by h 1 = 1 and h 2 = (R + R *)/R *are used in the derivation of above equations.

The transformations that relates independent variables, velocity components and pressure in fixed frame (R, X) to the corresponding quantities in wave frame \(\left( {r, x} \right)\) which is moving with speed c are:

$$x\, = X - ct,\,\,r\, = \,R,\,\,v_{1} \, = \,\,V_{1} ,\,\,v_{2} \, = \,\,V_{2} - c,\,\,p = p.$$
(15)

Employing (15), Eqs. (12)–(14) in wave frame become

$$\frac{\partial }{\partial r}\left\{ {\left( {r + R^{*} } \right)v_{1} } \right\} + R^{*} \frac{{\partial v_{2} }}{\partial x} = 0,\,$$
(16)
$$\rho \left[ { - c\,\frac{{\partial v_{1} }}{\partial x} + v_{1} \frac{{\partial v_{1} }}{\partial r} + \frac{{R^{*} \left( {v_{2} + c} \right)}}{{r + R^{*} }}\frac{{\partial v_{1} }}{\partial x} - \frac{{\left( {v_{2} + c} \right)^{2} }}{{r + R^{*} }}} \right]\,\, = \, - \frac{\partial p}{\partial r} + \frac{1}{{r + R^{*} }}\,\frac{\partial }{\partial r}\left\{ {\left( {r + R^{*} } \right)\,S^{rr} } \right\}$$
$$+ \frac{{R^{*} }}{{r + R^{*} }}\frac{\partial }{\partial x}S^{rx} - \frac{{S^{xx} }}{{r + R^{*} }},$$
(17)
$$\begin{aligned} \rho \left[ { - c\,\frac{{\partial v_{2} }}{\partial x} + v_{1} \frac{{\partial v_{2} }}{\partial r} + \frac{{R^{*} \left( {v_{2} + c} \right)}}{{r + R^{*} }}\frac{{\partial v_{2} }}{\partial x} - \frac{{\left( {v_{2} + c} \right)v_{1} }}{{r + R^{*} }}} \right] = - \left( {\frac{{R^{*} }}{{r + R^{*} }}} \right)\frac{\partial p}{\partial x} + \frac{1}{{\left( {r + R^{*} } \right)^{2} }}\frac{\partial }{\partial r}\left\{ {\left( {r + R^{*} } \right)^{2} S^{rx} } \right\} \hfill \\ + \frac{{R^{*} }}{{r + R^{*} }}\frac{\partial }{\partial x}S^{xx} - \frac{{\sigma B_{0}^{2} R^{*2} \left( {v_{2} + c} \right)}}{{\left( {r + R^{*} } \right)^{2} }}. \hfill \\ \end{aligned}$$
(18)

The characteristics lengths in radial and transverse directions are λ and a 1, respectively. Similarly, characteristic velocity scale in the problem is the velocity of the peristaltic wave c. Therefore, based on these length and velocity scales, we define [25–27]

$$\begin{aligned} \bar{x}\,\, = \,\,\frac{2\pi }{\lambda }x,\,\bar{\eta }\,\, = \,\,\frac{r}{{a_{1} }},\,\bar{v}_{1} = \,\frac{{v_{1} }}{c},\,\bar{v}_{2} = \,\,\frac{{v_{2} }}{c},\,Re\,\, = \,\,\frac{{\rho ca_{1} }}{{\mu_{0} }},\,\bar{p}\,\, = \,\,\frac{{2\pi a_{1}^{2} }}{{\lambda \mu_{0} c}}p,\,\bar{S}^{ij} \, = \,\,\frac{{a_{1} }}{{\mu_{0} c}}S^{ij} ,\,K\, = \frac{{R^{*} }}{{a_{1} }},\, \hfill \\ \delta \,\, = \,\,\frac{{2\pi a_{1} }}{\lambda },\,Ha = \beta_{0} \sqrt {\frac{\sigma }{{\mu_{0} }}} ,\,a^{*} = \frac{a}{{\mu_{0} }},\,\mu_{0} = \frac{b}{{\left( {\frac{{a_{1} }}{c}} \right)^{n - 1} }}. \hfill \\ \end{aligned}$$
(19)

For simplification we will use bar variables without bar. In view of (19), Eqs. (16)–(18) become

$$\frac{\partial }{\partial \eta }\left\{ {\left( {\eta + K} \right)v_{1} } \right\} + \delta K\frac{{\partial v_{2} }}{\partial x} = 0,$$
(20)
$$\begin{aligned} \delta Re\left[ { - \delta \,\frac{{\partial v_{1} }}{\partial x} + v_{1} \frac{{\partial v_{1} }}{\partial \eta } + \delta \frac{{K\left( {v_{2} + 1} \right)}}{\eta + K}\frac{{\partial v_{1} }}{\partial x} - \frac{{\left( {v_{2} + 1} \right)^{2} }}{\eta + K}} \right]\,\, = \, - \frac{\partial p}{\partial \eta } + \delta \left( {\frac{1}{\eta + K}\,\frac{\partial }{\partial \eta }\left\{ {\left( {\eta + K} \right)\,S^{\eta \eta } } \right\}} \right. \hfill \\ \left. { + \delta \frac{K}{\eta + K}\frac{\partial }{\partial x}S^{\eta \,x} - \frac{{S^{x\,x} }}{\eta + K}} \right), \hfill \\ \end{aligned}$$
(21)
$$\begin{aligned} Re\left[ { - \delta \,\frac{{\partial v_{2} }}{\partial x} + v_{1} \frac{{\partial v_{2} }}{\partial \eta } + \delta \frac{{K\left( {v_{2} + 1} \right)}}{\eta + K}\frac{{\partial v_{2} }}{\partial x} - \frac{{\left( {v_{2} + 1} \right)v_{1} }}{\eta + K}} \right]\,\, = - \left( {\frac{K}{\eta + K}} \right)\frac{\partial p}{\partial x} + \frac{\text{1}}{{\left( {\eta + K} \right)^{2} }}\,\frac{\partial }{\partial \eta }\left\{ {\left( {\eta + K} \right)^{2} S^{\eta x\,} } \right\} \hfill \\ + \delta \frac{K}{\eta + K}\frac{\partial }{\partial x}S^{xx} - \frac{{Ha^{\text{2}} K^{2} \left( {v_{2} \text{ + 1}} \right)}}{{\left( {\eta + K} \right)^{2} }}. \hfill \\ \end{aligned}$$
(22)

In components form, Eq. (7) gives

$$S^{x\,x} \, = \,2\left[ {a^{*} + \left( {\sqrt \varPi } \right)^{n - 1} } \right]\frac{{\partial v_{1} }}{\partial \eta },$$
(23a)
$$S^{x\,\eta } \, = \left[ {a^{*} + \left( {\sqrt \varPi } \right)^{n - 1} } \right]\left( {\frac{{\partial v_{2} }}{\partial \eta } + \frac{K}{\eta + K}\frac{{\partial v_{1} }}{\partial \eta } - \frac{{\left( {1 + v_{2} } \right)}}{\eta + K}} \right),$$
(23b)
$$S^{\eta \,\eta } \, = 2\left[ {a^{*} + \left( {\sqrt \varPi } \right)^{n - 1} } \right]\left( {\frac{K}{\eta + K}\frac{{\partial v_{2} }}{\partial x} + \frac{{v_{1} }}{\eta + K}} \right),\,$$
(23c)
$$\varPi = \frac{1}{2}\left( {\left( {2\frac{{\partial v_{1} }}{\partial \eta }} \right)^{2} + 2\left( {\frac{{\partial v_{2} }}{\partial \eta } + \frac{K}{\eta + K}\frac{{\partial v_{1} }}{\partial \eta } - \frac{{\left( {1 + v_{2} } \right)}}{\eta + K}} \right)^{2} + \left( {\frac{2K}{\eta + K}\frac{{\partial v_{2} }}{\partial x} + \frac{{2v_{1} }}{\eta + K}} \right)^{2} } \right)\,.$$
(24)

In above equations Re, δ and K represent the Reynolds number, the wave number and the dimensionless radius of curvature, respectively. The parameter Ha is the Hartmann number and it is the ratio of magnetic force to the viscous force. Its large values correspond to the case of strong imposed magnetic field. The parameter a * is the generalized ratio of infinite-shear rate viscosity to the consistency index in a Sisko fluid if n ≠ 1. In the case of n = 1, a * = 0 denotes a viscous Newtonian fluid, whilst a * = 0 describes a purely power-law fluid. Moreover, the case n = 1, a * ≠ 0 corresponds to Newtonian fluid with viscosity (1 + a *).

Defining the components of velocity in terms of stream function by the relations

$$v_{1} \,\, = \,\,\delta \frac{K}{K + \eta }\frac{\partial \psi }{\partial x},\,\,\,\,\,v_{2} \,\, = - \frac{\partial \psi }{\partial \eta },$$
(25)

and employing the long wavelength and low Reynolds number approximations [26], Eqs. (20)–(24) reduce to

$$\frac{\partial p}{\partial \eta } = 0,$$
(26)
$$- \frac{\partial p}{\partial x} + \frac{1}{{K\,\left( {K + \eta } \right)}}\,\,\frac{\partial }{\partial \eta }\,\left( {\left( {K + \eta } \right)^{2} S^{\eta \,x} } \right) - \,\frac{{Ha^{2} K}}{{\,\left( {K + \eta } \right)}}\,\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)\, = \,0,\,$$
(27)

where

$$S^{x\,x} \, = \,0,$$
(28a)
$$S^{\eta \,x} \, = \,\left[ {a^{*} + \left( {\sqrt \varPi } \right)^{n - 1} } \right]\left( { - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }} - \frac{1}{\eta + K}\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)} \right),$$
(28b)
$$S^{\eta \eta } \, = \,0,$$
(28c)
$$\varPi = \left( { - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }} - \frac{1}{\eta + K}\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)} \right)^{2} .$$
(28d)

It should be pointed out here that in view of Eq. (25) the continuity Eq. (20) is satisfied identically. Insertion of the expression of S ηx from Eq. (28b) into Eq. (27) yields

$$\begin{aligned} - \frac{\partial p}{\partial x} + \frac{1}{{K\,\left( {K + \eta } \right)}}\,\,\frac{\partial }{\partial \eta }\,\left( {\left( {K + \eta } \right)^{2} \left( {a^{*} + \left( {\left( { - \frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)^{2} } \right)^{{\frac{{^{n - 1} }}{2}}} } \right)\left( { - \frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)} \right.} \right. \hfill \\ \left. { - \left. {\frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)} \right) - \,\frac{{Ha^{2} K}}{{\,\,\left( {K + \eta } \right)}}\,\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)\, = \,0,\, \hfill \\ \end{aligned}$$
(29)

Elimination of pressure between Eqs. (26) and (29) results in the following compatibility equation

$$\begin{aligned} \frac{\partial }{\partial \eta }\left( {\frac{1}{{\,\left( {K + \eta } \right)}}\,\,\frac{\partial }{\partial \eta }\,\left( {\left( {K + \eta } \right)^{2} \left( {a^{*} + \left( {\left( { - \frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)^{2} } \right)^{{\frac{n - 1}{2}}} } \right)\left( { - \frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)} \right)} \right.\, \hfill \\ \left. { - \,\frac{{Ha^{2} K^{2} }}{{\,\,\left( {K + \eta } \right)}}\,\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)} \right) = \,0. \hfill \\ \end{aligned}$$
(30)

Equation (30) is subject to following boundary conditions [25]

$$\left. \begin{aligned} \psi = - \frac{f}{2},\,\frac{\partial \psi }{\partial \eta } = \,\,1,\,\,\,{\text{at}}\,\,\,\eta \,\, = h_{1} = 1 + \varPhi { \sin }x,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(a) \hfill \\ \psi = \,\frac{f}{2},\,\,\,\,\frac{\partial \psi }{\partial \eta } = \,\,1,\,\,\,{\text{at}}\,\,\,\eta \,\, = h_{2} = - 1 - \varPhi { \sin }x,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,(b) \hfill \\ \end{aligned} \right\}$$
(31)

where Φ = a 2/a 1 is the amplitude ratio. The dimensionless mean flow rate Θ, in laboratory frame, and f in wave frame are related according to the following expression [25]:

$$\varTheta = f + 2.$$
(32)

We remark here that boundary conditions ∂ψ/∂η = 1 at η = h 1 and ∂ψ/∂η = 1 at η = h 2 are consequence of no-slip at the surface. However, the boundary conditions ψ = − f/2 at η = h 1 and ψ = f/2 at η = h 2 come from the definition of flow rate f in the wave frame. According to this definition [25]

$$f = - \int\limits_{{h_{2} }}^{{h_{1} }} {\frac{\partial \psi }{\partial \eta }d\eta = \psi \left( {h_{2} } \right) - \psi \left( {h_{1} } \right).}$$
(33)

The above expression furnish the conditions ψ(h 1) = − f/2 and ψ(h 2) = f/2. It is pointed out that for flow problem under consideration, either the pressure difference across one wavelength or the relative flow rate in the wave frame f, (or the absolute flow rate in the laboratory frame, Θ) must be prescribed. In the present analysis, we followed later approach and prescribed f as a constant.

3 Asymptotic solution

Due to the nonlinear nature of Eq. (30), an exact solution is difficult to find. However, it is possible to obtain an asymptotic solution of this equation for large values of Hartmann number. To this end, we rewrite Eq. (30) in the form

$$\begin{aligned} \frac{\partial }{\partial \eta }\left( {\frac{1}{{\,\left( {K + \eta } \right)}}\,\,\frac{\partial }{\partial \eta }\,\left( {\left( {K + \eta } \right)^{2} \left( {a^{*} + \left( {\frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) + \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)^{n - 1} } \right)\,\left( { - \frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)} \right)} \right.\, \hfill \\ \left. { - \,\frac{{Ha^{2} K^{2} }}{{\,\,\left( {K + \eta } \right)}}\,\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)} \right) = \,0. \hfill \\ \end{aligned}$$
(34)

where \({\text{Ha}} = 1/\varepsilon \,{\text{and }}\varepsilon \ll 1.\)

The above equation in terms of small parameter ε becomes

$$\begin{aligned} \frac{\partial }{\partial \eta }\left( {\frac{{\varepsilon^{2} }}{{\,\left( {K + \eta } \right)}}\,\,\frac{\partial }{\partial \eta }\,\left( {\left( {K + \eta } \right)^{2} \left( {a^{*} + \left( {\frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) + \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)^{n - 1} } \right)\,\left( { - \frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)} \right)} \right.\, \hfill \\ \left. { - \,\frac{{K^{2} }}{{\,\,\left( {K + \eta } \right)}}\,\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)} \right) = \,0. \hfill \\ \end{aligned}$$
(35)

Since the small parameter ε multiplies with highest derivative in Eq. (35), therefore Eq. (35) subject to boundary conditions (31) constitute a singular perturbation problem. The singular perturbation problems in fluid mechanics usually exhibit boundary layer phenomena [40]. In such problems the greatest gradients in flow velocity are confined in a thin layer (boundary layer) near the solid surface. Therefore, it is expected that solution of Eq. (30) subject to boundary conditions (31) exhibits boundary character for large values of Hartmann number. The method of matched asymptotic expansion is used to obtain the solution. In this method an inner solution at the location of two walls and an outer solution away from the wall while remaining inside the channel are obtained. Then by defining some intermediate variable each inner and outer solution are matched at the upper and lower walls to determine the unknown constants. Finally based on these solutions a composite solution valid for small values of ε is expressed. We refer the reader to Ref. [37] by Asghar et al. and book by Bush [39] for procedural details.

3.1 The case n = 1 and \(\varvec{a}^{\varvec{*}} \ne 0\)

For n = 1 and a * ≠ 0, Eq. (35) takes the following form

$$\frac{\partial }{\partial \eta }\left( {\frac{{\varepsilon^{2} (a^{*} + 1)}}{{\,\left( {K + \eta } \right)}}\,\,\frac{\partial }{\partial \eta }\,\left( {\left( {K + \eta } \right)^{2} \left( { - \frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)} \right)} \right.\left. { - \,\frac{{K^{2} }}{{\,\,\left( {K + \eta } \right)}}\,\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)} \right) = \,0.$$
(36)

3.1.1 Inner solutions

To find inner solution at η = h 1, let us introduce the stretched variable

$$s \, = \, \frac{{h_{1} - \eta }}{{\varepsilon^{p} }}.$$
(37)

In new variable, Eq. (36) becomes

$$\varepsilon^{2} \left( {a^{*} + 1} \right)\left( {\left( {\,h_{1} + K - \varepsilon^{p} s} \right)\,\varepsilon^{ - 4p} \frac{{\partial^{4} \psi^{in} }}{{\partial s^{4} }} - 2\,\varepsilon^{ - 3p} \frac{{\partial^{3} \psi^{in} }}{{\partial s^{3} }} - \frac{{\varepsilon^{ - 2p} }}{{\left( {\,h_{1} + K - \varepsilon^{p} s} \right)}}\frac{{\partial^{2} \psi^{in} }}{{\partial s^{2} }} - \frac{{\varepsilon^{ - p} }}{{\left( {\,h_{1} + K - \varepsilon^{p} s} \right)^{2} }}\frac{{\partial \psi^{in} }}{\partial s}} \right.$$
$$\left. { - \frac{1}{{\left( {\,h_{1} + K - \varepsilon^{p} s} \right)^{2} }}} \right) - \frac{{\varepsilon^{ - 2p} K^{2} }}{{\left( {\,h_{1} + K - \varepsilon^{p} s} \right)}}\frac{{\partial^{2} \psi^{in} }}{{\partial s^{2} }} - \frac{{\varepsilon^{ - p} K^{2} }}{{\left( {\,h_{1} + K - \varepsilon^{p} s} \right)^{2} }}\frac{{\partial \psi^{in} }}{\partial s} - \frac{{K^{2} }}{{\left( {\,h_{1} + K - \varepsilon^{p} s} \right)^{2} }} = 0,$$
(38)

where ψ in is the solution satisfying the inner boundary condition at η = h 1.

By taking only dominant terms in Eq. (38), we can write

$$\left( {a^{*} + 1} \right)\left( {\,h_{1} + K} \right)\,\varepsilon^{2 - 4p} \frac{{\partial^{4} \psi^{in} }}{{\partial s^{4} }} - \frac{{\varepsilon^{ - 2p} K^{2} }}{{\left( {\,h_{1} + K} \right)}}\frac{{\partial^{2} \psi^{in} }}{{\partial s^{2} }} = 0.$$
(39)

From Eq. (39), p is to be determined by the principle of the least degeneracy. In order to balance the terms in Eq. (39), we require p = 1, and thus

$$\frac{{\partial^{4} \psi^{in} }}{{\partial s^{4} }} - \alpha_{1}^{2} \frac{{\partial^{2} \psi^{in} }}{{\partial s^{2} }} = 0,$$
(40)

where \(\alpha_{1} = \frac{1}{{\sqrt {a^{*} + 1} }}\left( {\frac{K}{{h_{1} + K}}} \right).\)

The inner solution ψ in is subject to the following boundary conditions at η = h 1,

$$\psi^{in} \, = \,\, - \frac{f}{2},\,\,\frac{{\partial \psi^{in} }}{\partial s} = \,\,0,\,\,\,{\text{at}}\,\,\,s\,\, = 0.$$
(41)

Now we proceed for a two terms perturbation solution of Eq. (40). To this end we write

$$\psi^{in} (s) = \psi_{0}^{in} (s) + \varepsilon \,\psi_{1}^{in} (s).$$
(42)

Substituting Eq. (42) into Eq. (40) and (41), we obtain the leading order system as follows:

$$\frac{{\partial^{4} \psi_{0}^{in} }}{{\partial s^{4} }} - \alpha_{1}^{2} \frac{{\partial^{2} \psi_{0}^{in} }}{{\partial s^{2} }} = 0,$$
(43)
$$\psi_{0}^{in} \, = \,\, - \frac{f}{2},\,\,\frac{{\partial \psi_{0}^{in} }}{\partial s} = \,\,0,{\text{ at }}s = 0.$$
(44)

The solution of above system is

$$\psi_{0}^{in} (s) = - \frac{f}{2} + C_{0} \,\left( {e^{{\alpha_{1} s}} - 1 - \alpha_{1} s} \right) + D_{0} \,\left( {e^{{ - \alpha_{1} s}} - 1 + \alpha_{1} s} \right).$$
(45)

We choose the constant \({\text{C}}_{ 0} = 0\) to avoid the exponential growth in above solution. Thus we get

$$\psi_{0}^{in} (s) = - \frac{f}{2} + D_{0} \,\left( {e^{{ - \alpha_{1} s}} - 1 + \alpha_{1} s} \right).$$
(46)

At order ε we have the following system

$$\frac{{\partial^{4} \psi_{1}^{in} }}{{\partial s^{4} }} - \alpha_{1}^{2} \frac{{\partial^{2} \psi_{1}^{in} }}{{\partial s^{2} }} = 0,$$
(47)
$$\psi_{1}^{in} \, = \,\,0,\,\,\frac{{\partial \psi_{1}^{in} }}{\partial s} = \,\, - 1,{\text{ at }}s = 0.$$
(48)

It can be easily shown that the solution of above equation is

$$\psi_{1}^{in} (s) = - s + C_{1} \,\left( {e^{{\alpha_{1} s}} - 1 - \alpha_{1} s} \right) + D_{1} \,\left( {e^{{ - \alpha_{1} s}} - 1 + \alpha_{1} s} \right).$$
(49)

Again we choose \({\text{C}}_{ 1} = 0\) and write Eq. (49) in the form

$$\psi_{1}^{in} (s) = - s + D_{1} \,\left( {e^{{ - \alpha_{1} s}} - 1 + \alpha_{1} s} \right).$$
(50)

Substitution of Eqs. (46) and (50) into Eq. (42) yield the two terms inner solution at η = h 1 as follows:

$$\psi_{{2{\text{term}}}}^{in} (s) = - \frac{f}{2} + D_{0} \,\left( {e^{{ - \alpha_{1} s}} - 1 + \alpha_{1} s} \right) + \varepsilon \left( { - s + D_{1} \,\left( {e^{{ - \alpha_{1} s}} - 1 + \alpha_{1} s} \right)} \right),$$
(51)

where D 0 and D 1 are unknown constants to be determined by the matching technique.

To find the inner solution at η = h 2, let us introduce the following stretched variable

$$\xi \, = \, \frac{{\eta - h_{2} }}{{\varepsilon^{r} }}.$$
(52)

Performing the same procedure as above, the two terms inner solution at η = h 2 is

$$\psi_{{2{\text{term}}}}^{IN} (\xi ) = \frac{f}{2} + H_{0} \,\left( {e^{{ - \alpha_{2} \xi }} - 1 + \alpha_{2} \xi } \right) + \varepsilon \left( {\xi + H_{1} \,\left( {e^{{ - \alpha_{2} \xi }} - 1 + \alpha_{2} \xi } \right)} \right),$$
(53)

with \(\alpha_{2} = \frac{1}{{\sqrt {a^{*} + 1} }}\left( {\frac{K}{{h_{2} + K}}} \right)\)

and H 0 and H 1 are unknown constants to be determined by the matching technique.

3.1.2 Outer solution

For the outer solution, we only choose terms independent of ε in Eq. (36) and write

$$- \frac{1}{{\left( {\,\eta + k} \right)}}\frac{{\partial^{2} \psi^{out} }}{{\partial \eta^{2} }} + \frac{1}{{\left( {\,\eta + k} \right)^{2} }}\frac{{\partial \psi^{out} }}{\partial \eta } - \frac{1}{{\left( {\,\eta + k} \right)^{2} }} = 0.$$
(54)

To find a two terms solution of above equation we expand

$$\psi^{out} (\eta ) = \psi_{0}^{out} (\eta ) + \varepsilon \,\psi_{1}^{out} (\eta ).$$
(55)

Substituting Eq. (55) into Eq. (54) and solving the resulting systems, we get

$$\psi^{out} (\eta ) = \eta + \left( {k\eta + \frac{{\eta^{2} }}{2}} \right)a_{0} + b_{0} + \varepsilon \left( {\left( {k\eta + \frac{{\eta^{2} }}{2}} \right)c_{1} + d_{1} } \right),$$
(56)

as two terms outer solution. In Eq. (56) a 0, b 0, c 1, and d 1 are unknown constants to be determined by higher-order matching of two inner expansions and one outer expansion.

The higher-order matching of the inner solution at η = h 1 and the outer solution is done by defining an intermediate region of O(ɛ α) and an intermediate parameter z by

$${\text{z }} = \, \frac{{h_{1} - \eta }}{{\varepsilon^{\alpha } }},$$
(57)

and then converting the inner and outer solutions given by Eqs. (51) and (56) in the intermediate parameter z and discarding the terms higher than O(ɛ α). In this way, we get

$$\left( {\psi^{out} } \right)^{\text{int}} = h_{1} + \left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)a_{0} + b_{0} + \varepsilon \left( {\left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)c_{1} + d_{1} } \right) - z\varepsilon^{\alpha } \left( {1 + \left( {K + h_{1} } \right)a_{0} } \right) + O\left( {\varepsilon^{\alpha + 1} } \right),$$
(58)
$$\left( {\psi^{in} } \right)^{\text{int}} = - \frac{f}{2} + D_{0} \,\left( { - 1 + \alpha_{1} z\varepsilon^{\alpha - 1} } \right) + z\varepsilon^{\alpha } \,\left( { - 1 + \alpha_{1} D_{1} } \right) - \varepsilon D_{1} .$$
(59)

The above two solutions are matched by comparing the various power of ε to get

$$\left. \begin{aligned} h_{1} + \left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)a_{0} + b_{0} = - \frac{f}{2} - D_{0} ,\,\,\,\,\,\,\,\,\,\,\,D_{0} = 0, \hfill \\ D_{1} = - \frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }}a_{0} ,\,\,\,\,\,\,\,\,\left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)c_{1} + d_{1} = - D_{1} . \hfill \\ \end{aligned} \right\}$$
(60)

The above matching procedure is repeated by taking inner solutions at η = h 2 and thus we write

$$w \, = \, \frac{{\eta - h_{2} }}{{\varepsilon^{\zeta } }}.$$
(61)

In the same way as done before, we convert the inner and outer solutions given by Eqs. (58) and (61) in the intermediate parameter w and discard the terms higher than O(ɛ ς).Thus we get

$$\left( {\psi^{out} } \right)^{\text{int}} = h_{2} + \left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)a_{0} + b_{0} + \varepsilon \left( {\left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)c_{1} + d_{1} } \right) + w\varepsilon^{\zeta } \left( {1 + \left( {K + h_{2} } \right)a_{0} } \right) + O\left( {\varepsilon^{\zeta + 1} } \right),$$
(62)
$$\left( {\psi^{IN} } \right)^{\text{int}} = \frac{f}{2} + H_{0} \,\left( { - 1 + \frac{{Kw\varepsilon^{\zeta - 1} }}{{K + h_{2} }}} \right) + w\varepsilon^{\zeta } \,\left( {1 + \frac{{KH_{1} }}{{K + h_{2} }}} \right) - \varepsilon H_{1} .$$
(63)

Again, the above two solutions are matched by comparing the various power of ε to get

$$\left. \begin{aligned} h_{2} + \left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)a_{0} + b_{0} = \frac{f}{2} - H_{0} ,\,\,\,\,\,\,\,\,\,\,H_{0} = 0, \hfill \\ \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{2} }}a_{0} = H_{1} ,\,\,\,\,\,\,\,\,\left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)c_{1} + d_{1} = - H_{1} . \hfill \\ \end{aligned} \right\}$$
(64)

Solving Eqs. (60) and (64), we find

$$\left. \begin{aligned} a_{0} = - \left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K},\,\,\,\,\,b_{0} = \frac{f}{2} - h_{2} + \left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K},\, \hfill \\ c_{1} = - \frac{1}{{\left( {h_{1} - h_{2} } \right)K}}\left( {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }} + \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{2} }}} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right), \hfill \\ d_{1} = \left( { - \frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }} + \left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)\frac{1}{{\left( {h_{1} - h_{2} } \right)}}\left( {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }} + \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{2} }}} \right)} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K}, \hfill \\ D_{1} = \frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }}\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K},\,\,\,\,\,\,\,\,H_{1} = - \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{2} }}\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K}. \hfill \\ \end{aligned} \right\}$$
(65)

The two terms composite solution is defined by

$$\psi_{\text{composite}} = \psi^{\text{out}} + \psi^{\text{in}} (s) - \left( {\psi^{\text{in}} } \right)^{\text{int}} +\, \psi^{\text{IN}} (\xi ) - \left( {\psi^{\text{IN}} } \right)^{\text{int}} ,$$
(66)

which is view of Eqs. (56), (51), (59), (53) and (63) becomes

$$\left. \begin{aligned} \psi_{\text{composite}} = - h_{2} + \frac{f}{2} + \eta + \left( { - \left( {K\eta + \frac{{\eta^{2} }}{2}} \right) + \left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K} + \varepsilon \left( { - \frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }}} \right. \hfill \\ - \left( {K\eta + \frac{{\eta^{2} }}{2}} \right)\frac{1}{{\left( {h_{1} - h_{2} } \right)K}}\left( {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }} + \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{2} }}} \right) + \left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)\frac{1}{{\left( {h_{1} - h_{2} } \right)K}}\left( {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }} + \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{2} }}} \right) \hfill \\ - \left. {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{1} }}e^{{ - \alpha_{1} \frac{{\left( {h_{1} - \eta } \right)}}{\varepsilon }}} - \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{2} }}e^{{ - \alpha_{2} \frac{{\left( {\eta - h_{2} } \right)}}{\varepsilon }}} } \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K}, \hfill \\ \end{aligned} \right\}$$
(67)

The presence of exponential terms in Eq. (67) clearly shows that the character of solution (67) is of boundary layer type. Equation (67) further suggests that the boundary layer growth is of \(O\left( {\left| {\sqrt {a^{*} + 1} \left( {h_{1} + k} \right)/kHa} \right|} \right)\) at the upper wall while it is of \(O\left( {\left| {\sqrt {a^{*} + 1} \left( {h_{2} + k} \right)/kHa} \right|} \right)\) at the lower wall. This indicates that boundary layer thickness is inversely proportional to Hartmann number whilst it is directly proportional to a *. This boundary layer character of solution is also confirmed through Figs. 2 and 3. In such case the variation in velocity is confined in thin layers near the walls.

Fig. 2
figure 2

Variation of velocity profile v 2(η) for K = 3, Θ = 1.5, n = 1, \(a^{*} = 1\) and x = π

Full size image
Fig. 3
figure 3

Variation of velocity profile v 2(η) for K = 2.5, Θ = 1.5, Ha = 1, n = 1 and x = π

Full size image

3.2 The case \(\varvec{n} = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\) and \(\varvec{a}^{\varvec{*}} \ne 0\)

In this subsection, we shall find the solution of governing Eq. (35) for shear-thinning fluid (n < 1) and large values of Hartmann number. To this end, we rewrite Eq. (35) as follows:

$$\begin{aligned} \frac{\partial }{\partial \eta }\left( {\frac{{\varepsilon^{2} }}{(k + \eta )}\,\,\frac{\partial }{\partial \eta }\,\left( {\left( {k + \eta } \right)^{2} \left( {a^{*} \left( { - \frac{1}{k + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) - \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right) - \left( {\frac{1}{K + \eta }\left( {1 - \frac{\partial \psi }{\partial \eta }} \right) + \frac{{\partial^{2} \psi }}{{\partial \eta^{2} }}} \right)^{n} } \right)} \right)} \right. \hfill \\ \left. { - \,\frac{{k^{2} }}{\,(k + \eta )}\,\left( {1 - \frac{\partial \psi }{\partial \eta }} \right)} \right) = \,0. \hfill \\ \end{aligned}$$
(68)

An order of magnitude analysis reveals that Eq. (68) is tractable for n < 1 which corresponds to the case of shear-thinning fluids and as a particular choice, we take \(n = {\raise0.7ex\hbox{$1$} \!\mathord{\left/ {\vphantom {1 2}}\right.\kern-0pt} \!\lower0.7ex\hbox{$2$}}\). Now following the similar procedure as given in Sect. 3.1, the two terms inner solution at η = h 1 and η = h 2 is given by

$$\psi_{{2{\text{term}}}}^{in} (s) = - \frac{f}{2} + M_{0} \,\left( {e^{{ - \alpha_{3} s}} - 1 + \alpha_{3} s} \right) + \varepsilon \left( { - s + M_{1} \,\left( {e^{{ - \alpha_{3} s}} - 1 + \alpha_{3} s} \right) + \frac{{4\sqrt {M_{0} } }}{{3a^{*} \alpha_{3} }}} \right.\left( {e^{{ - \frac{{\alpha_{3} s}}{2}}} } \right.\left. {\left. { - 1 + \frac{{\alpha_{3} s}}{2}} \right)} \right),$$
(69)
$$\psi_{{2{\text{term}}}}^{IN} (\xi ) = \frac{f}{2} + U_{0} \,\left( {e^{{ - \alpha_{4} \xi }} - 1 + \alpha_{4} \xi } \right) + \varepsilon \left( {\xi + U_{1} \,\left( {e^{{ - \alpha_{4} \xi }} - 1 + \alpha_{4} \xi } \right) + \frac{{4\sqrt {U_{0} } }}{{3a^{*} \alpha_{4} }}} \right.\left( {e^{{ - \frac{{\alpha_{4} \xi }}{2}}} } \right.\left. {\left. { - 1 + \frac{{\alpha_{4} \xi }}{2}} \right)} \right),$$
(70)

where \(\alpha_{3} = \frac{1}{{\sqrt {a^{*} } }}\left( {\frac{K}{{h_{1} + K}}} \right), \, \alpha_{4} = \frac{1}{{\sqrt {a^{*} } }}\left( {\frac{K}{{h_{2} + K}}} \right)\), M 0, M 1, U 0 and \({\text{U}}_{1}\) are unknown constants and their values are found by using the matching procedure.

The outer solution of Eq. (68) will remain same as given in (56) i.e.

$$\psi^{out} (\eta ) = \eta + \left( {K\eta + \frac{{\eta^{2} }}{2}} \right)a_{0} + b_{0} + \varepsilon \left( {\left( {K\eta + \frac{{\eta^{2} }}{2}} \right)c_{1} + d_{1} } \right),$$
(71)

In order to find unknown constants, we rewrite Eqs. (69) and (71) at η = h 1 in terms of intermediate parameter z for higher-order matching:

$$\left( {\psi^{out} } \right)^{\text{int}} = h_{1} + \left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)a_{0} + b_{0} + \varepsilon \left( {\left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)c_{1} + d_{1} } \right) - z\varepsilon^{\alpha } \left( {1 + \left( {K + h_{1} } \right)a_{0} } \right) + O\left( {\varepsilon^{\alpha + 1} } \right),$$
(72)
$$\left( {\psi^{in} } \right)^{\text{int}} = - \frac{f}{2} + M_{0} \,\left( { - 1 + \alpha_{3} z\varepsilon^{\alpha - 1} } \right) + z\varepsilon^{\alpha } \,\left( { - 1 + \alpha_{3} M_{1} + \frac{{2\sqrt {M_{0} } }}{{3a^{*} \alpha_{3} }}} \right) - \varepsilon \left( {M_{1} + \frac{{4\sqrt {M_{0} } }}{{3a^{*} \alpha_{4} }}} \right).$$
(73)

Now matching various powers ofɛin Eqs. (72) and (73), we get

$$\left. \begin{aligned} h_{1} + \left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)a_{0} + b_{0} = - \frac{f}{2} - M_{0} ,\,\,\,\,\,\,\,\,\,\,\,M_{0} = 0, \hfill \\ M_{1} = - \frac{{\left( {K + h_{1} } \right)}}{{\alpha_{3} }}a_{0} ,\,\,\,\,\,\,\,\,\left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)c_{1} + d_{1} = - M_{1} . \hfill \\ \end{aligned} \right\}$$
(74)

Similarly, we obtain some unknown constants at η = h 2 by using again higher-order matching:

$$\left. \begin{aligned} h_{2} + \left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)a_{0} + b_{0} = \frac{f}{2} - U_{0} ,\,\,\,\,\,\,\,\,\,\,U_{0} = 0, \hfill \\ \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{4} }}a_{0} = U_{1} ,\,\,\,\,\,\,\,\,\left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)c_{1} + d_{1} = - U_{1} . \hfill \\ \end{aligned} \right\}$$
(75)

From Eqs. (74) and (75), we get

$$\left. \begin{aligned} a_{0} = - \left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K},\,\,\,\,\,b_{0} = \frac{f}{2} - h_{2} + \left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K}, \hfill \\ c_{1} = - \frac{1}{{\left( {h_{1} - h_{2} } \right)K^{2} }}\left( {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{3} }} + \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{4} }}} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right), \hfill \\ d_{1} = \left( {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{3} }} + \left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)\frac{1}{{\left( {h_{1} - h_{2} } \right)K}}\left( {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{3} }} + \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{4} }}} \right)} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K}, \hfill \\ D_{1} = \frac{{\left( {K + h_{1} } \right)}}{{\alpha_{3} }}\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K},\,\,\,\,\,\,\,\,H_{1} = - \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{4} }}\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K}. \hfill \\ \end{aligned} \right\}$$
(76)

The composite solution of Eq. (68) is defined by

$$\psi_{\text{composite}} = \psi^{\text{out}} + \psi^{\text{in}} (s) - \left( {\psi^{\text{in}} } \right)^{\text{int}} + \psi^{\text{IN}} (\xi ) - \left( {\psi^{\text{IN}} } \right)^{\text{int}} ,$$
(77)

which is view of Eqs. (56), (58), (61), (64) and (69) yields

$$\left. \begin{aligned} \psi_{\text{composite}} = - h_{2} + \frac{f}{2} + \eta + \left( { - \left( {K\eta + \frac{{\eta^{2} }}{2}} \right) + \left( {Kh_{2} + \frac{{h_{2}^{2} }}{2}} \right)} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K} + \varepsilon \left( { - \frac{{\left( {K + h_{1} } \right)}}{{\alpha_{3} }}} \right. \hfill \\ + \left( {\left( { - \left( {K\eta + \frac{{\eta^{2} }}{2}} \right) + \left( {Kh_{1} + \frac{{h_{1}^{2} }}{2}} \right)} \right)\frac{1}{{\left( {h_{1} - h_{2} } \right)K}}\left( {\frac{{\left( {K + h_{1} } \right)}}{{\alpha_{3} }} + \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{4} }}} \right) + \frac{{\left( {K + h_{1} } \right)}}{{\alpha_{3} }}e^{{ - \alpha_{3} \frac{{\left( {h_{1} - \eta } \right)}}{\varepsilon }}} } \right. \hfill \\ \left. {\left. { - \frac{{\left( {K + h_{2} } \right)}}{{\alpha_{4} }}e^{{ - \alpha_{4} \frac{{\left( {\eta - h_{2} } \right)}}{\varepsilon }}} } \right)} \right)\left( {1 + \frac{f}{{h_{1} - h_{2} }}} \right)\frac{1}{K}, \hfill \\ \end{aligned} \right\}$$
(78)

It is remarked here that asymptotic solution of Eq. (68) is not possible for shear-thickening case (n > 1), in the sense that corresponding nonlinear equation can be solved but its solution does not satisfy the required boundary conditions. This fact has also been pointed out Asghar et al. [37] in their study on peristaltic flow of Sisko fluid in an asymmetric channel. The non-existence of boundary layer solution in case of shear-thickening fluid for large Hartmann number is because of the fact that in flow of such fluids the viscous force is of comparable magnitude to the magnetic force. The solution given by Eq. (78) is clearly of boundary layer type due to the presence of exponential terms. In this case Eq. (78) suggests that the boundary layer thickness at upper and lower walls is of \(O\left( {\left| {\sqrt {a^{*} } \left( {h_{1} + k} \right)/kHa} \right|} \right)\) and \(O\left( {\left| {\sqrt {a^{*} } \left( {h_{2} + k} \right)/kHa} \right|} \right),\) respectively. The qualitative behavior of solution predicted on the basis of (78) is also confirmed through graphical illustration given in Fig. 4. It is further observed through Figs. 3–5 that the structure of flow velocity in a curved channel is markedly different than that in a straight channel. As with the flow velocity structure in a straight channel [37] (where except in a thin layers near the channel walls the velocity over rest of the cross-section is uniform), the velocity in a curved channel also varies sharply in thin layers near the channel walls. However, distinct from the flow velocity in the straight channel, the velocity in a curved channel varies linearly over rest of the cross-section.

Fig. 4
figure 4

Variation of v 2(η) for K = 2.5, Θ = 1.5, a * = 1, n = 1/2 and x = π

Full size image
Fig. 5
figure 5

Variation of v 2(η) for Ha = 50, Θ = 1.5, a * = 1, n = 1/2 and x = π

Full size image

4 Conclusions

A study is performed to investigate the effect of applied magnetic field on peristaltic flow of Sisko fluid through a curved channel. The asymptotic formulae of stream function for large Hartmann number are obtained using singular perturbation method for two cases namely; n = 1, a * ≠ 0 and n = 1/2, a * ≠ 0, where n is the power-law index and a *is the generalized ratio of infinite shear rate viscosity (a) to the consistency index (b). The former case corresponds to Newtonian viscous fluid with viscosity (1 + a *) while later case describes shear-thinning fluids with viscosity \(a^{*} + \left( {\sqrt \varPi } \right)^{n - 1} ,\) where \(\sqrt \varPi\) is the magnitude of rate of deformation tensor. In the former case, the boundary layer thickness is of \(O\left( {\left| {\sqrt {a^{*} + 1} \left( {h_{1} + k} \right)/kHa} \right|} \right)\) at the upper wall whilst at lower wall it is of \(O\left( {\left| {\sqrt {a^{*} + 1} \left( {h_{2} + k} \right)/kHa} \right|} \right)\). Similarly, in the second case the layer thickness at upper and lower walls is of \(O\left( {\left| {\sqrt {a^{*} } \left( {h_{1} + k} \right)/kHa} \right|} \right)\) and \(O\left( {\left| {\sqrt {a^{*} } \left( {h_{2} + k} \right)/kHa} \right|} \right),\) respectively. The following important conclusions are drawn from this study.

  • In the first case (n = 1, a * ≠ 0), a thin boundary layer exists at the channel walls for large values of Hartmann number or small values of a *. Moreover, the thickness of the boundary layer is inversely proportional to the Hartmann number. However, it shows increasing trend with a *.

  • In the second case (n = 1/2, a * ≠ 0), the qualitative behavior of flow velocity is similar to corresponding behavior of flow velocity in case 1. However, the estimates of boundary layer thickness in either case are different.

  • The structure of flow velocity in a curved channel is quite different from that in a straight channel. In a straight channel, except in thin layers near the walls, the velocity over rest of the cross-section is uniform. The analytical estimates of boundary layer thickness reveal that in a straight channel, the thickness of boundary layers at the upper and lower walls is same. On the contrary, in a curved channel the boundary layer thickness at the upper wall is greater than that at the lower wall. This is because that in a curved channel boundary layer thickness at upper and lower walls depends upon both the curvature of channel and the axial coordinate x. For instance, the choice of parameters k = 2.5, a * = 1, Ha = 100, x = 0 yields 0.014 and 0.006, respectively as thickness of boundary layer at upper and lower walls.

  • The large values of the dimensionless radius of curvature produce velocity profile exhibiting boundary layer similar to that in a straight channel.

  • The formation of boundary layer for large values of Hartmann number is justified on the following grounds. In the present flow situation the magnetic force acts as a resistance to the flow and its magnitude is proportional to the transverse velocity [See Eq. (10)], hence amplitude of flow near the channel center is suppressed. To maintain the given flow rate, the relatively small velocity near boundaries will increase. A combination of both effects leads to the formation of boundary layer at the channel walls. Due to the symmetry of velocity about the centerline, the thickness of boundary layer at either wall is same in a straight channel. Moreover, the suppression of velocity amplitude due to magnetic force is uniform near the center in a straight channel and that is why the middle-most region out of the boundary layers moves with a uniform velocity. However, due to asymmetry of the velocity in the curved channel the suppression of velocity amplitude due to magnetic force is not uniform in the region outside boundary layers. Therefore, the velocity in this region varies linearly with radial distance. Because of asymmetry in the velocity, the boundary layer thickness at either wall is also different in a curved channel.

  • It is important to mention that boundary layer phenomenon in peristaltic flow of a Sisko fluid for large values of Hartmann number was already reported by Wang et al. [41] and Asghar et al. [37] in a straight channel. No other study is a variable in the literature highlighting the boundary layer phenomena in peristalsis. In fact, the present study extends the results reported in above investigations for a curved channel. It is worth mentioning that our results in the limit when K → ∞ are compatible with the existing results of Wang et al. [41] and Asghar et al. [37].