1 Introduction

The biological fluid flows can be generated by continual wavelike rhythmic structures of biological vessels like ureter, intestines, stomach, esophagus, and blood vessels (capillaries, veins, arteries, etc.). These rhythmic structures of smooth muscles are known as the peristaltic phenomenon. This phenomenon may be used in various applications in the physiological systems. For instance, transport of ovum and spermatozoa, fluid motion in uterine, chyme flow in the gastrointestinal tract, motion of food in the esophagus, and motion of urine. These are internal mechanisms of peristaltic phenomenon. Nowadays, external mechanisms of peristalsis exist such as motion of earthworms, finger and roller pumps operate on this mechanism, and micro and nanorobots also use the peristaltic mechanism. Utilizing these concepts, many researchers have studied many problems with peristalsis in the symmetric and asymmetric channels, which seems unrealistic, because most of the physiological and industrial systems are in curved structures. The concept of curvature in the peristalsis is investigated in only few studies. Riaz et al. [1] have investigated the electromagnetism and permeability measures in Jeffrey fluid through eccentric annuli executing peristaltic porous confines. They have produced the results that pumping rate is enhanced by magnetic field but reduced by porosity factors. Noreen [2] studied the effects of induced MHD on the peristaltic propulsion of viscous fluid in a curved configuration. In this study, the author has proved the symmetry of velocity profiles disturbs in the presence of curvature effects. Riaz et al. [3] achieved exact solutions for multiphase nonlinear fluid expressing peristaltic pumping characteristics in an annulus comprising complaint walls and magnetism is also taken into consideration. It is revealed that imposed magnetic field suppresses the fluid and particle motion. Zeeshan et al. [4] have used curved configuration to study the viscous particulate-fluid suspension in a peristaltic transport. Their observation clears that the concentration of fluid rises with the curvature parameter. Srinivas and Kothandapani [5] have published the porosity and magnetic effects on thermal and mass transfer analysis of wave type transport including compliant boundaries. Maraj et al. [6] have given the homotopy perturbation solutions for the motion of Williamson fluid under the curved peristalsis. In this study, it is noticed that mixed behavior is noticed for the velocity with the curvature parameter. Akbar and Butt [7] have described the peristaltic nanofluid propulsion in through curved walls, and studied the pressure gradient and velocity variations under the influence of curvature parameter. Some more relevant cases may be observed through various references (see [8,9,10]) and the references therein.

The study of magnetic field in fluid flow systems attracted many researchers due to its wide range of applications in industry and engineering. This study represents the interaction between the fluid flow and applied magnetic field. The applications include targeted drug delivery, imaging contrast enhancement, nanoparticle manipulation, and laser beam scanning. In view of many applications of magnetohyrodynamics, many researchers have started their research in fluid flows with magnetic field effects. Stiller et al. [11] have presented a review on the recent numerical and experimental investigations of the flow driven by rotating and traveling magnetic fields. Sucharitha et al. [12] have discussed the effect of MHD on the motion of Jeffrey fluid driven by tapered peristalsis. Meenakumari et al. [13] have used a numerical technique named RK. Fehlberg-based shooting technique to discuss the effects of inclined magnetic field on the unsteady motion of Williamson nanofluid over a stretching surface. Samrat et al. [14] have investigated the MHD flow over the paraboloid of revolution. Trivedi and Ansari [15] have performed the analytical study on the Casson nanofluid flow past a linear stretching sheet with inclined magnetic field. Nowadays, the field of biomagnetic fluid dynamics is emerging area of interest in living creatures. In general, biological cells and molecules are considered as biomagnetic materials. The use of magnetic field in the biomedicine can be captured in many ways, such as passage sealers, magnetic hyperthermia, drug delivery, imaging contrast enhancement, and nanoparticle manipulations in biomedical engineering. It is also observed from many studies that the flow patterns rapidly change under the applied magnetic field [16,17,18]. Narla et al. [19] have provided the detailed examination on the flow variables such as streamlines, pressure rise, and pressure gradient for the flow of an MHD viscoelastic fluid in a peristaltic curved configuration. Ali et al. [20] applied Generalized Differential Quadrature Method (GDQM) to suggest a numerical simulation of peristaltic Flow with changing electrical conductivity and Joule dissipation effects along with MHD. Amanullah et al. [21] have proposed the numerical magnetic field features for Carreau fluid flow numerically through an isothermal sphere.

Porous medium has many applications in engineering and industry, and it has also many applications in biomedicine and bioengineering. Generally, a porous medium is material with some pores. These pores appear in many biological systems, such as central nervous system, brain aneurysm, drug delivery, tissue replacement, and computational biology. There is a vast study present in literature in the presence of porous medium (for instance, [22,23,24]), but very few cases have been discussed the effect of porous medium under the peristaltic curved boundaries. Hayat et al. [25] have considered Ellis fluid to investigate the flow in curved peristaltic configuration under the effects of porous medium. The key observation of this study is the velocity enhances with the Darcy number. Mohammadein and Abu-Nab [26] have discussed the motion of Newtonian fluid in a curved geometry under the peristalsis and porous medium with the vapour bubble. From this study, the velocity deduction is observed with permeability. Vajravelu et al. [27] have provided the pumping type passage of Phan–Thien–Tanner fluid by taking porous medium. More literature on porous medium can be found in [28,29,30].

From the last few decades, the investigation of non-Newtonian materials has received much attention to the investigators in fluid dynamics. Rabinowitsch fluid is one of the non-Newtonian fluids (class of shear thinning liquids). This fluid model perfectly describes the diverse fluid models such as Newtonian, Dilatant, and pseudoplastic fluid in the limiting cases of the Rabinowitsch model. Some of the examples of Rabinowitsch model are blood, whipped cream, and ketchup. Based on these facts in mind, many investigators have focused in the direction of Rabinowitsch fluid flow model. Akbar and Butt [31] have discussed the motion of a Rabinowitsch fluid in the presence of metachronal wave of cilia with the exact solutions. Vaidya et al. [32] have provided the semi-analytical solutions with the help of perturbation technique for the flow of Rabinowitsch fluid under the influence of peristalsis. In this study, the authors have provided the results for the limiting cases such as Newtonian, pseudoplastic, dilatant, and fluid models. In another study, Vaidya et al. [33] have considered the same fluid model with the variable liquid and wall properties. Sadaf and Nadeem [34] have discussed the transport of a Rabinowitsch fluid under the effects of peristalsis and porous medium. Vaidya et al. [35] have focused to study the non-uniform effects of peristalsis on the motion of a Rabinowitsch liquid in the presence of wall properties. Maraj and Nadeem [36] have studied the propulsion of Rabinowitsch liquid under the considerations of peristalsis and curved configuration. Few more studies can be seen in the direction of Rabinowitsch liquid flow model in the references [37,38,39,40] and the references therein.

To the best of author’s information, no study releases the effects of magnetic field and porous medium effects on rabinowitsch model in a curved channel with a hybrid analytical technique. This study composes the peristaltic flow of Rabinowitsch model executing peristaltic waves through a curved porous channel magnetized by applied normal magnetic field. This study may be helpful in electrical conductions of many industrial for dilatant and pseudoplastic fluids and clinical issues for blood flows. The mathematical modeling has been completed by introducing the concept of low Reynolds number and long waves traveling axially. The equations of motion have been explored using wave frame to evaluate the steady incompressible flow. The obtained coupled partial differential equations are handled by two combined analytical perturbation techniques. The expressions of velocity, pressure gradient, and trapping have been dealt through graphical aspect under the variation of physically appearing parameters.

2 Mathematical modeling

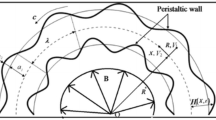
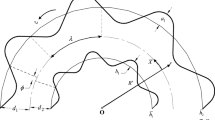
Assume a curved channel whose width is 2a which is loaded with Rabinowitsch liquid. The radius and center of curvature of the circle, where the channel is wound, are represented by \(R^{*}\) and O,  separately. There is a rearrange graph of the stream geometry in Fig. 1. We utilize a curvilinear arrange framework (\({\overline{N}} ,{\overline{S}} ,{\overline{Z}} \)) to inspect the stream in which \({\overline{N}} \) is coordinated toward the outspread course, \({\overline{S}} \) is toward the flow line, and vertical way \({\overline{Z}} \) is the representative.

Fig. 1
figure 1

Physical  structure  of  the  problem

Full size image

The Cartesian frame of reference is set at the origin O . It is related with curvilinear facilitate framework as per these changes

$$\begin{aligned} \left. {{\begin{array}{*{20}c} {{X}'=\left( R^{*}+{\overline{N}} \right) \cos \left( {\textstyle {{{\overline{S}} } \over {R^{*}}}} \right) } \\ {{Y}'=\left( R^{*}+{\overline{N}} \right) \sin \left( {\textstyle {{{\overline{S}} } \over {R^{*}}}} \right) } \\ \end{array} }} \right\} . \end{aligned}$$
(1)

The upper wall equation in \((X,\,Y)\) system is

$$\begin{aligned} X^{\prime ^{2}}+Y^{\prime ^{2}}= & {} \left( (R^{*}+a)\right. \nonumber \\&\left. +b\sin \left( {\frac{2\pi }{\lambda }\left( {R^{*}\tan ^{-1}\left( {\frac{{Y}'}{{X}'}} \right) -c{\overline{t}} } \right) } \right) \right) ^{2}.\nonumber \\ \end{aligned}$$
(2)

Putting Eq. (1) in Eq. (2), we arrive at

$$\begin{aligned} {\overline{R}} =a+b\cos \left( {\frac{2\pi }{\lambda }({\overline{S}} -c{\overline{t}} )} \right) . \end{aligned}$$
(3)

Supplanting the left-hand side of Eq. (3) by \(H_{1} \), the condition becomes

$$\begin{aligned} H_{1} ({\overline{S}} ,\,{\overline{t}} )=a+b\cos \left( {\frac{2\pi }{\lambda }({\overline{S}} -c{\overline{t}} )} \right) ,\,\quad \text{(upper }\, \text{ wall), }\nonumber \\ \end{aligned}$$
(4)

where \(\lambda \), b, and \({\overline{t}} \) are the wavelength, amplitude, and the time, separately. In the similar manner, the lower wall equation is

$$\begin{aligned} H_{2} ({\overline{S}} ,\,{\overline{t}} )=-a-b\cos \left( {\frac{2\pi }{\lambda }({\overline{S}} -c{\overline{t}} )} \right) ,\,\quad \text{(Lower }\, \text{ wall). }\nonumber \\ \end{aligned}$$
(5)

Additionally, the magnetic field \(\overline{\mathbf {B}} =\left( {0,\,B_{0} } \right) \) is applied orthogonally to the flow direction (radial) and the surfaces of geometry are assumed to be porous with voids in the layers. The MHD is playing a role of body force on the motion of the fluid whose term \(\overline{\mathbf {J}} \times \overline{\mathbf {B}} \) is inserted in the momentum equation through Maxwell’s equations and the factor of porosity is also included through Darcy’s law. The governing equations in component form for the present study have been described below [31,32,33,34,35,36]

$$\begin{aligned}&\frac{\partial }{\partial {\overline{N}} }\left( {\left( {{\overline{N}} +R^{*}} \right) \,{\overline{V}} } \right) +R^{*}\frac{\partial {\overline{U}} }{\partial {\overline{S}} }=0, \end{aligned}$$
(6)
$$\begin{aligned}&\left. {\rho \left[ {\frac{\partial {\overline{V}} }{\partial {\overline{t}} }+{\overline{V}} \frac{\partial {\overline{V}} }{\partial {\overline{N}} }+\frac{R^{*}{\overline{U}} }{{\overline{N}} +R^{*}}\frac{\partial {\overline{V}} }{\partial {\overline{S}} }-\frac{\overline{U^{2}} }{{\overline{N}} +R^{*}}} \right] =-\frac{\partial {\overline{P}} }{\partial {\overline{N}} }+} \right) \, \nonumber \\&\quad \frac{1}{{\overline{N}} +R^{*}}\frac{\partial }{\partial {\overline{N}} }\left( {\left( {{\overline{N}} +R^{*}} \right) \,{\overline{\tau }}_{\overline{N} {\overline{N}} } } \right) +\frac{R^{*}}{{\overline{N}} +R^{*}}\frac{\partial }{\partial {\overline{S}} }\left( {{\overline{\tau }}_{\overline{NS} } } \right) \nonumber \\&\quad -\frac{{\overline{\tau }}_{\overline{SS} } }{{\overline{N}} +R^{*}}-\frac{\mu }{k_{1} }{\overline{V}} ,\, \end{aligned}$$
(7)
$$\begin{aligned}&\rho _{f} \left[ {\frac{\partial {\overline{U}} }{\partial \overline{t} }+{\overline{V}} \frac{\partial {\overline{V}} }{\partial {\overline{N}} }+\frac{R^{*}{\overline{U}} }{{\overline{N}} +R^{*}}\frac{\partial {\overline{U}} }{\partial {\overline{S}} }-\frac{\overline{UV} }{{\overline{N}} +R^{*}}} \right] \nonumber \\&\qquad =-\left( {\frac{R^{*}}{{\overline{N}} +R^{*}}} \right) \,\left. \frac{\partial {\overline{P}} }{\partial {\overline{S}} }+ \right) \, \nonumber \\&\quad \frac{1}{({\overline{N}} +R^{*})^{2}}\frac{\partial }{\partial \overline{N} }\left( {\left( {{\overline{N}} +R^{*}} \right) ^{2}{\overline{\tau }} _{{\overline{N}} {\overline{S}} } } \right) \nonumber \\&\qquad +\frac{R^{*}}{{\overline{N}} +R^{*}}\frac{\partial }{\partial {\overline{S}} }\left( {{\overline{\tau }}_{\overline{SS} } } \right) -\frac{\sigma B_{o}^{2} {\overline{U}} }{({\overline{N}} +R^{*})^{2}}-\frac{\mu }{k_{1} }{\overline{U}} ,\, \end{aligned}$$
(8)

where \(\sigma \) and \(k_{1} \) are identifying the current density and porosity measures, correspondingly. In the wave frame [36], Eqs. (7) and (8) hold the subsequent form

$$\begin{aligned}&\left. {\rho \left[ {-c\frac{\partial {\overline{v}} }{\partial {\overline{s}} }+{\overline{v}} \frac{\partial {\overline{v}} }{\partial {\overline{n}} }+\frac{R^{*}({\overline{u}} +c)}{{\overline{n}} +R^{*}}\frac{\partial {\overline{v}} }{\partial {\overline{s}} }-\frac{({\overline{u}} +c)^{2}}{{\overline{n}} +R^{*}}} \right] =-\frac{\partial {\overline{p}} }{\partial {\overline{n}} }+} \right) \, \nonumber \\&\quad \frac{1}{{\overline{n}} +R^{*}}\frac{\partial }{\partial {\overline{n}} }\left( {\left( {{\overline{n}} +R^{*}} \right) \,{\overline{\tau }}_{\overline{nn} } } \right) +\frac{R^{*}}{{\overline{n}} +R^{*}}\frac{\partial {\overline{\tau }}_{\overline{ns} } }{\partial {\overline{s}} }\nonumber \\&\quad -\frac{\overline{\tau }_{\overline{ss} } }{{\overline{n}} +R^{*}}-\frac{\mu }{k_{1} }{\overline{v}} ,\, \end{aligned}$$
(9)
$$\begin{aligned}&\rho _{f} \left[ {-c\frac{\partial {\overline{u}} }{\partial {\overline{s}} }+{\overline{v}} \frac{\partial {\overline{u}} }{\partial {\overline{n}} }+\frac{R^{*}({\overline{u}} +c)}{{\overline{n}} +R^{*}}\frac{\partial {\overline{u}} }{\partial {\overline{s}} }+\frac{({\overline{u}} +c){\overline{v}} }{{\overline{n}} +R^{*}}} \right] \nonumber \\&\quad \left. =\left( {\frac{R^{*}}{{\overline{n}} +R^{*}}} \right) \,\frac{\partial {\overline{p}} }{\partial {\overline{s}} }+ \right) \, \nonumber \\&\frac{1}{({\overline{n}} +R^{*})^{2}}\frac{\partial }{\partial {\overline{n}} }\left\{ {\left( {{\overline{n}} +R^{*}} \right) \,\overline{\tau }_{\overline{ns} } } \right\} +\frac{R^{*}}{{\overline{n}} +R^{*}}\frac{\partial {\overline{\tau }}_{\overline{ss} } }{\partial {\overline{s}}}\nonumber \\&\quad \left. -\frac{\sigma B_{\circ }^{2} \left( {{\overline{u}} +c} \right) }{({\overline{n}} +R^{*})^{2}}-\frac{\mu }{k_{1} }\left( {{\overline{u}} +c} \right) \right) . \end{aligned}$$
(10)

Now, we make the above equations non-dimensional by incorporating the following dimensionless quantities:

$$\begin{aligned} s= & {} \frac{2\pi }{\lambda }{\overline{s}} ,\,\,n=\frac{{\overline{n}} }{a},\,\,u=\frac{{\overline{u}} }{c},\,\,v=\frac{{\overline{v}} }{c},\,\,\\&k=&\frac{R^{*}}{a},\,\,\tau =\frac{a}{\mu c}{\overline{\tau }} ,\,\,Re=\frac{\rho ca}{\mu },\,\varepsilon =\frac{b}{a}, \\ \delta= & {} \frac{2\pi a}{\lambda },\,\,p=\frac{2\pi a^{2}}{\lambda \mu c}{\overline{p}} ,\,\,\beta =\frac{\alpha \mu ^{2}c^{2}}{a^{2}},\,\,\\&h_{1}=&\frac{{\overline{H}}_{1} }{a},\,\,h_{2} =\frac{{\overline{H}}_{2} }{a},\,\,H^{2}=\frac{\sigma B_{0}^{2} a^{2}}{\mu },\,\,Da=\frac{k_{1} }{a^{2}}. \end{aligned}$$

After imposing above transformations, we found the dimensionless form of Eqs. (9) and (10) which can be observed

$$\begin{aligned}&\delta Re\left[ {-\delta \frac{\partial v}{\partial s}+v\frac{\partial v}{\partial n}+\delta \frac{k(u+1)}{n+k}\frac{\partial v}{\partial s}-\frac{(u+1)^{2}}{n+k}} \right] \, \nonumber \\&\quad =-\frac{\partial p}{\partial n}+\delta \left( \frac{1}{n+k}\frac{\partial }{\partial n}\left( {\left( {n+k} \right) \,\tau _{nn} } \right) \right. \nonumber \\&\quad \left. +\delta \frac{k}{n+k}\frac{\partial \tau _{ns} }{\partial s}-\frac{\tau _{ss} }{n+k}-\frac{v}{Da} \right) ,\, \end{aligned}$$
(11)
$$\begin{aligned}&Re\left[ {-\delta \frac{\partial u}{\partial s}+v\frac{\partial u}{\partial n}+\delta \frac{k(u+1)}{n+k}\frac{\partial u}{\partial s}-\frac{(u+1)v}{n+k}} \right] \nonumber \\&\quad \left. =-\left( {\frac{k}{n+k}} \right) \,\frac{\partial p}{\partial s}+ \right) \, \nonumber \\&\qquad \left. {\frac{1}{(n+k)^{2}}\frac{\partial }{\partial n}\left( {\left( {n+k} \right) ^{2}\tau _{ns} } \right) } \right) +\delta \frac{k}{n+k}\frac{\partial \tau _{ss} }{\partial s}\nonumber \\&\qquad -\frac{H^{2}}{(n+k)^{2}}\left( {u+1} \right) -\frac{\left( {u+1} \right) }{Da}. \end{aligned}$$
(12)

At this stage, we assume the lubrication approach due to waves having small wave number \(\delta \rightarrow 0\) and negligible effects of turbulence, i.e., \(Re\rightarrow 0\), and we finally receive

$$\begin{aligned}&\frac{\partial p}{\partial n}=0 \end{aligned}$$
(13)
$$\begin{aligned}&-\left( {\frac{k}{n+k}} \right) \,\frac{\partial p}{\partial s}+\frac{1}{(n+k)^{2}}\frac{\partial }{\partial n}\left( {\left( {n+k} \right) ^{2}\tau _{ns} } \right) \nonumber \\&\quad -\frac{H^{2}}{(n+k)^{2}}\left( {u+1} \right) -\frac{\left( {u+1} \right) }{Da}=0, \end{aligned}$$
(14)

where the stress component \(\tau _{ns} \) for Rabinowitsch model is calculated as [36]

$$\begin{aligned} \tau _{ns} +\beta \tau _{ns}^{3} =\frac{\partial u}{\partial n}-\frac{u+1}{n+k} \end{aligned}$$
(15)

along with the set of no-slip boundary conditions defined as [33,34,35,36]

$$\begin{aligned} u=-1\, \text{ at }\,n=\pm h(s)=\pm \left[ {1+\varepsilon \cos \left( s \right) } \right] . \end{aligned}$$
(16)

3 Solution procedure

The above achieved relations are coupled non-homogeneous differential equations with variable coefficients. Such complicated equations cannot be tackled by some exact mathematical technique. Hence, we have utilized the combined techniques of perturbation method and HPM [41] to have the series solution which is detailed as below. Let we suggest the following series for \(\tau _{ns} \) and u by assuming \(\beta \) a small parameter:

$$\begin{aligned} \tau _{ns}= & {} \tau _{0ns} +\beta \tau _{1ns} +\ldots \end{aligned}$$
(17)
$$\begin{aligned} u= & {} u_{0} +\beta u_{1} +\ldots \end{aligned}$$
(18)

Using above series in (14) and (15) and equating the terms of zeroth and first exponents of \(\beta \), we achieve the following two systems.

Coefficients of \(\beta ^{0}:\)

$$\begin{aligned}&-\left( {\frac{k}{n+k}} \right) \,\frac{\partial p}{\partial s}+\frac{1}{(n+k)^{2}}\frac{\partial }{\partial n}\left( {\left( {n+k} \right) ^{2}\tau _{0ns} } \right) \nonumber \\&\quad -\frac{H^{2}}{(n+k)^{2}}\left( {u_{0} +1} \right) -\frac{\left( {u_{0} +1} \right) }{Da}=0,\, \end{aligned}$$
(19)
$$\begin{aligned}&\tau _{0ns} =\frac{\partial u_{0} }{\partial n}-\frac{\left( {u_{0} +1} \right) }{n+k}. \end{aligned}$$
(20)

Putting Eq. (20) in Eq. (19), we approach

$$\begin{aligned}&-\left( {\frac{k}{n+k}} \right) \,\frac{\partial p}{\partial s}+\frac{1}{(n+k)^{2}}\frac{\partial }{\partial n}\nonumber \\&\qquad \left[ {\left( {n+k} \right) ^{2}\left( {\frac{\partial u_{0} }{\partial n}-\frac{\left( {u_{0} +1} \right) }{n+k}} \right) } \right] \, \nonumber \\&\qquad \left. {-\frac{H^{2}}{(n+k)^{2}}\left( {u_{0} +1} \right) -\frac{\left( {u_{0} +1} \right) }{Da}=0.} \right) \, \end{aligned}$$
(21)

with boundary conditions

$$\begin{aligned} u_{0} =-1\,\text{ at } \,n=\pm h(s)=\pm \left[ {1+\varepsilon \cos \left( s \right) } \right] . \end{aligned}$$
(22)

Coefficients of \(\beta :\)

$$\begin{aligned}&\frac{1}{(n+k)^{2}}\frac{\partial }{\partial n}\left( {\left( {n+k} \right) ^{2}\tau _{1ns} } \right) \nonumber \\&\quad -\frac{H^{2}}{(n+k)^{2}}u_{1} -\frac{u_{1} }{Da}=0,\, \end{aligned}$$
(23)
$$\begin{aligned}&\tau _{1ns} +\tau _{0ns}^{3} =\frac{\partial u_{1} }{\partial n}-\frac{u_{1} }{n+k} \end{aligned}$$
(24)

or

$$\begin{aligned} \tau _{1ns} =\frac{\partial u_{1} }{\partial n}-\frac{u_{1} }{n+k}-\left[ {\left( {\frac{\partial u_{0} }{\partial n}-\frac{\left( {u_{0} +1} \right) }{n+k}} \right) } \right] ^{3}.\nonumber \\ \end{aligned}$$
(25)

Putting Eq. (25) in Eq. (23)

$$\begin{aligned}&\frac{1}{(n+k)^{2}}\frac{\partial }{\partial n}\left[ \left( {n+k} \right) ^{2}\left( \frac{\partial u_{1} }{\partial n}-\frac{u_{1} }{n+k}-\left( \frac{\partial u_{0} }{\partial n}\right. \right. \right. \nonumber \\&\quad \left. \left. \left. -\frac{\left( {u_{0} +1} \right) }{n+k} \right) ^{3} \right) \right] \, \nonumber \\&\left. \quad {-\frac{H^{2}}{(n+k)^{2}}u_{1} -\frac{u_{1} }{Da}=0} \right) ,\, \end{aligned}$$
(26)

and boundary conditions are

$$\begin{aligned} u_{1} =0\, \text{ at } \,n=\pm h\left( s \right) . \end{aligned}$$
(27)

Solution of \(u_{0} \) by HPM

Now, we use HPM to solve the above obtained highly complicated systems of differential equations.

Let us find the solution of zeroth order system. As per policy of HPM, we first construct the deformation relation for \(u_{0} \) as follows:

(28)

where \({{\mathcal {D}}}\) is the linear differential operator of our own choice keeping in mind the order of differential equation and is selected as \({{\mathcal {D}}}=\frac{\partial ^{2}}{\partial n^{2}}, q\) is embedding parameter, and stands for the given operator applied on the unknown variable along with forcing functions of independent variable. Equation (26) takes the following form:

$$\begin{aligned}&\frac{\partial ^{2}}{\partial n^{2}}\left[ {u_{0} -} \right] +q\left[ -\left( {\frac{k}{n+k}} \right) \,\frac{\partial p}{\partial s}\right. \nonumber \\&\quad +\frac{1}{(n+k)^{2}}\frac{\partial }{\partial n}\left( {\left( {n+k} \right) ^{2}\left( {\frac{\partial u_{0} }{\partial n}-\frac{\left( {u_{0} +1} \right) }{n+k}} \right) } \right) \, \nonumber \\&\quad \left. {\left. {-\frac{H^{2}}{(n+k)^{2}}\left( {u_{0} +1} \right) -\frac{\left( {u_{0} +1} \right) }{Da}} \right] =0.} \right) \, \end{aligned}$$
(29)

Moreover, \(_{0} \) is an initial guess and it is suggested as

(30)

Now, we take the series expansion of \(u_{0} \) as increasing exponents of q, that is

$$\begin{aligned} u_{0} =u_{01} +qu_{02} +\ldots \end{aligned}$$
(31)

Zeroth-order system for \(u_{0} \)

Equating the coefficients of \(q^{0},\) we observe the following system with corresponding conditions defined on the walls:

(32)
(33)

First-order system for \(u_{0} \)

Equating the coefficients of q,  we extract the another system of equations with respective surface conditions and is elaborated as

$$\begin{aligned}&{{\mathcal {D}}}\left[ {u_{02} } \right] +\frac{\partial ^{2}u_{01} }{\partial n^{2}}\nonumber \\&\quad +\frac{2}{n+k}\frac{\partial u_{01} }{\partial n}+\frac{1}{\left( {n+k} \right) ^{2}}\frac{\partial }{\partial n}\left( {\left( {n+k} \right) \,\left( {u_{0} +1} \right) } \right) \nonumber \\&\quad -\left( {\frac{k}{n+k}} \right) \,\frac{\partial p}{\partial s}=0. \end{aligned}$$
(34)
$$\begin{aligned}&u_{02} =0\, \text{ at } \,n=\pm h(s). \end{aligned}$$
(35)

After solving above two systems, we get

(36)

and

$$\begin{aligned} u_{02}= & {} -\frac{1}{12Da^{2}h(k+n)}\nonumber \\&\quad \left( {\left. {{\begin{array}{*{20}c} {h(h-n)(h+n)(3Da(-3+H^{2})k-9Dan} \\ {-k(3k-n)(k+n)+6Da^{2}(k+n)p)} \\ {+3(k+n)(((h-k)^{2}k(h+k)} \\ {+Da(h^{2}-hH^{2}k+(-1+3H^{2})k^{2}))} \\ {(h-n)Log[-h+k]+(-(h-k)k(h+k)^{2}} \\ {+D^{2}h^{2}+hH^{2}k+(-1+3H^{2})k^{2}))} \\ {(h+n)Log[h+k]-2h(k(-h^{2}+k^{2})} \\ {(k+n)+Da(h^{2}+k(-k+3H^{2}k+H^{2}n)))} \\ {Log[k+n])} \\ \end{array} }} \right) } \right) \,\nonumber \\ \end{aligned}$$
(37)

Solution of \(u_{1} \) by HPM

Table 1 Validation of the current results by comparing with the existing literature [36]
Full size table

Let us define the homotopy equation for \(u_{1} \) as

(38)

where is an initial guess which is chosen as

(39)

Equation (38) can be replaced by the following form:

$$\begin{aligned}&\frac{\partial ^{2}}{\partial n^{2}}\left[ {u_{1} -} \right] +q\left[ \frac{1}{(n+k)^{2}}\frac{\partial }{\partial n}\left\{ \left( {n+k} \right) ^{2}\left( \frac{\partial u_{1} }{\partial n}\right. \right. \right. \nonumber \\&\quad \left. \left. -\frac{u_{1} }{n+k}-\left( {\frac{\partial u_{0} }{\partial n}-\frac{\left( {u_{0} +1} \right) }{n+k}} \right) ^{3} \right) \right\} \, \nonumber \\&\quad \left. {\left. {-\frac{H^{2}}{(n+k)^{2}}u_{1} -\frac{u_{1} }{Da}} \right] =0} \right) .\, \end{aligned}$$
(40)

Let us suppose

$$\begin{aligned} u_{1} =u_{11} +qu_{12} \ldots \, \end{aligned}$$
(41)

Inserting the above series of \(u_{1} \) into Eq. (40), we can build the two systems by equating coefficients of q.

Zeroth-order system for \(u_{1} \)

(42)

with boundary conditions

$$\begin{aligned} u_{11} \left[ {\pm h(s)} \right] =0. \end{aligned}$$
(43)

First-order system for \(u_{1} \)

$$\begin{aligned}&D\left[ {u_{12} } \right] +\frac{1}{\left( {n+k} \right) ^{2}}\frac{\partial }{\partial n}\left[ \left( {n+k} \right) ^{2}\left( \frac{\partial u_{11} }{\partial n}\right. \right. \nonumber \\&\left. \left. -\frac{u_{11} }{n+k}-\left( {\frac{\partial u_{01} }{\partial n}-\frac{\left( {u_{01} +1} \right) }{n+k}} \right) ^{3} \right) \right] \nonumber \\&\quad -\frac{H^{2}}{\left( {n+k} \right) ^{2}}u_{11} -\frac{\text{ u}_{11} }{Da}=0,\, \end{aligned}$$
(44)

with

$$\begin{aligned} u_{12} \left[ {\pm h(s)} \right] =0. \end{aligned}$$
(45)

After solving above equations simultaneously, we gather

(46)
(47)

The pressure gradient dp/dx can be evaluated as

$$\begin{aligned}&\frac{dp}{dx}=\frac{1}{2h^{3}}\nonumber \\&\quad \left( {3\left( {{\begin{array}{*{20}c} {-2h-Q-\textstyle {{h(87h^{4}-190h^{2}k^{2}+105k^{4})\beta } \over {15Da^{3}}}} \\ {+\textstyle {{h(25h^{2}k^{2}-15k^{4}+8h^{4}\beta )} \over {30Da^{2}}}} \\ {-\textstyle {{h(3k^{2}(-2+H^{2}(6-4\beta )+\beta )+h^{2}(4+(-5+8H^{2})\beta ))} \over {6Da}}} \\ {-\textstyle {1 \over {4Da^{3}k}}\left( {{\begin{array}{*{20}c} {Da(-h^{2}k+k^{3})^{2}-2(h^{2}-7k^{2})} \\ {(h^{2}-k^{2})^{2}\beta +Da^{2}(h^{4}\beta +k^{4}} \\ {(-2+H^{2}(6-4\beta )+\beta +2h^{2}k^{2}} \\ {(1-\beta +H^{2}(-1+2\beta ))))} \\ {(Log[-h+k]-Log[h+k])} \\ \end{array} }} \right) } \\ \end{array} }} \right) } \right) .\,\nonumber \\ \end{aligned}$$
(48)

4 Graphical results and discussion

This section is included to examine the tabular and graphical results of involved parameters affecting the flow characteristics. To relate the current investigation with existing literature and to enhance the validity graph of the current study, we have presented a Table 1 which clearly indicates that the study published in [36] is a limiting case of the current analysis when we overlook the effects of porosity and magnetic features. To observe the influence of emerging parameters, we have portrayed the Figs. 2, 3, 4, 5, 6, 7, 8, 9, 10, 11,1213. Figures (2, 3, 4, 5, 6, 7) contain the graphs of velocity componentsu drawn against the radial factor n under the alteration of fluid parameter \(\beta \) , Darcy number Da , the amplitude ratio \(\varepsilon \), Hartman number H, curvature k, and flow rate Q,  respectively. Figures 8, 9, 10, 11 reveal the characteristics of pressure gradient curves against the \(\beta ,Da,H\), and K,  correspondingly. We can observe the trapping analysis from Figs. 12 and 13 which are sketched under the variation of Da and H.

Fig. 2
figure 2

Alteration of velocity field u for \(\beta \) along with \(k=2,s=\pi ,Q=1,\varepsilon =0.1,Da=0.6,H=1\)

Full size image
Fig. 3
figure 3

Alteration of velocity field u for Da along with \(k=1.2,s=\pi Q=1,\varepsilon =0.1,\beta =0.05,H=2\)

Full size image
Fig. 4
figure 4

Alteration of velocity field u for \(\varepsilon \) along with \(k=1.2,s=\pi ,Q=1,\beta =0.05,Da=0.4,H=2\)

Full size image
Fig. 5
figure 5

Alteration of velocity field u for H along with \(k=1.2,s=\pi ,Q=1,\varepsilon =0.1,\,Da=0.4,\,\beta =0.05\)

Full size image
Fig. 6
figure 6

Alteration of velocity field u for k along with \(\beta =0.05,s=\pi ,Q=0.1,\varepsilon =0.2,\,Da=0.4,\,H=2\)

Full size image
Fig. 7
figure 7

Alteration of velocity field u for Q along with \(k=1.2,s=\pi ,\beta =0.05,\varepsilon =0.2,\,Da=0.4,\,H=2\)

Full size image
Fig. 8
figure 8

Alteration of pressure \(\textstyle {{\partial p} \over {\partial s}}\) for \(\beta \) along with \(k=2,Q=1,\varepsilon =0.1,\,\;Da=0.3,\,\;H=1\)

Full size image
Fig. 9
figure 9

Alteration of pressure \(\textstyle {{\partial p} \over {\partial s}}\) for Da along with \(k=1.2,Q=1,\varepsilon =0.1,\beta =0.05,\,\;H=2\)

Full size image
Fig. 10
figure 10

Alteration of pressure \(\textstyle {{\partial p} \over {\partial s}}\) for H along with \(k=1.2,Q=1,\varepsilon =0.1,\beta =0.05,Da=0.4\)

Full size image
Fig. 11
figure 11

Alteration of pressure \(\textstyle {{\partial p} \over {\partial s}}\) for k along with \(Da=0.4,Q=0.1,\varepsilon =0.2,\beta =0.05,H=2\)

Full size image

From Fig. 2, we can extract that velocity is varying directly with the increasing effect of \(\beta \) in left and middle parts of the channel, but the curves are declined in the right side. This can physically explain that the magnitude of \(\beta \) represents the elasticity of the fluid which rapids up the fluid accordingly. Figure 3 implies that velocity is lowering in the domain \([-h,\,0)\) but rising in \((0,\,h]\) by ascending variations ofDa. It reflects the physical reasoning that porosity of the medium affects the flow in lower and central regions of the channel significantly as compared to the upper half. The behavior of velocity projectile under the increments of amplitude ratio \(\varepsilon \) is quite similar to that of porosity parameterDa . It is noted from Fig 5 that Hartmann number makes the flow faster in lower area and gives reflexive behavior in the upper portion. This result is quite against the consequences found for Darcy number. It may be due to the fact that the magnetic field is applied in transverse direction to the flow which has suppressed the flow more comprehensively in the upper arrear as compared to the far away region. The readings of k on velocity profile are almost in line with that of received for Darcy number Da (Fig. 6). It means that porosity, curvature of channel, and amplitude ratio affect the flow in quite same manner. It is assumed from Fig. 7 that when we larger the numerical values of flow rate Q, the velocity increases throughout the channel. It reflects that fluid travels fast if the amount of fluid per unit time is enhanced.

Fig. 12
figure 12

Streamline for Da (a) for \(Da=5,\) (b) for \(Da=5.5,\) (c) for \(Da=6\)

Full size image
Fig. 13
figure 13

Streamline for H (a) for \(H=0.1,\) (b) for \(H=0.2,\) (c) for \(H=0.3\)

Full size image

Figures 8, 9, 10, 11 comprise the plot of pressure gradient profile \(\textstyle {{\partial p} \over {\partial s}}\) drawn against the flow rate Q for parameters \(\beta ,Da\), H, and k, correspondingly. From Fig. 8, it is concluded that \(\textstyle {{\partial p} \over {\partial s}}\) is decreasing with the large values of \(\beta \) and it becomes maximum at the center as compared the corners of the channels. This is because in the middle part of the channel, a more pressure gradient is required to maintain the flow rate, but the elasticity of the fluid decreases its magnitude. The effect of the porosity representative Da is almost same as we have examined for \(\beta \) (see Fig. 9), but in this diagram, the height of the curves is getting higher than the previous ones. It is measured from Fig. 10 that pressure gradient is getting large with the variation of applied magnetic field. Physically, it suggests that the fluid is traveling faster as observed above which may be the cause of increase in pressure profile to settle down the flow rate. The pressure curves for k can be visualized in Fig 11 and it is easily found here that \(\textstyle {{\partial p} \over {\partial s}}\) is diminishing its height when we give large magnitude to the curvature parameter k .

Figures 12 and 13 suggest the scene of flow pattern for different parameters. These graphs contain the contours of stream function \(\psi \) plotted in two-dimensional domains. Figure 12 contains the streamlines of the parameters Da; it can be obtained here that a circulating bolus is becoming large in lower part but shorter its size in upper part of the container with increasing values ofDa. It can also be seen that the flow is symmetric about the center line which is also depicting the assumption symmetric channel. It can be noticed from Fig. 13 that totally opposite scenario is observed in the sketch of streamlines for the MHD parameterH. It shows that porous medium and MHD are exerting quite different impact on flow pattern.

5 Conclusions

In this communication, we have analyzed the theoretical study of pumping characteristics of the same fluid with same circumstances along with the inclusion of two new factors, the porous medium and the MHD. After getting the analytic solution, we have seen the graphical picture of whole the analysis. The key points which we have achieved are manipulated as:

  • Porous medium is restricting the flow velocity in lower part of the channel, but in upper side, there is no hindrance to the flow.

  • It is found that the magnetic field opposes the flow speed in half side, but increases it in other region.

  • It is concluded that peristaltic pressure is increased with magnetic field, but decreased with porosity factor.

  • It is also evident from above analysis that flow pattern is showing totally opposite picture for porosity and MHD.

  • It is also measured that the current study gives the data of [36] as a limiting case of H\(=\)0 and Da\(=\)infinity.