1 Introduction

In Portugal, ore exploitation and processing has been an important economic activity, with open pit and underground structures, particularly until the early 1970s. The recent spike in metal prices and technologic developments have made extraction and processing more effective. In turn, this has led to renewed interest in previously abandoned gold mining areas, with a few experimental explorations undertaken in Alentejo, southern Portugal. A spatial approach is a suitable way to assess the potential for gold in old mining areas, as demonstrated in other countries (Darwish and Poellmann 2010).

Geochemistry is one of the most significant instruments for exploring undiscovered mineral resources (e.g., Cameron et al. 2004; Carranza et al. 2009; Carranza 2011; Hronsky 2004; Hronsky and Groves 2008; McCuaig et al. 2010; Wang et al. 2008). Geochemical cartography and the identification of associated anomalies have been a goal in mining prospection techniques since the late 1920s with multiple applications to the estimation of gold mineralized deposits (Bin 1995; Goovaerts et al. 2014; Madani 2011; Viladevall et al. 1999). Recent development of analytical methods and computational resources facilitates the implementation of geochemical mapping and its use in natural resources management (Antunes and Albuquerque 2013). In particular, multivariate data analysis has been widely applied to characterize the statistical patterns of geochemical data (Carranza 2010; El-Makky 2011; Sadeghi et al. 2013, 2014; Viladevall et al. 1999; Zuo 2011). These methods commonly aim to reduce the dimensionality of the problem through the creation of a few relevant factors that explain a large proportion of variance in a multivariate data set (Davis 2002; Reimann et al. 2008).

Stream sediment surveys remain the common geochemical approach used for regional gold exploration where slope designs distinct drainage systems (Darwish and Poellmann 2010; Fletcher 1997; Hale and Plant 1994; Goovaerts et al. 2014). The exploration of sedimentary gold (alluvial) has been conducted in distinct mineralized areas and linked up with different genetic deposits (Chapman et al. 2000; Chapman and Mortensen 2006; McInnes et al. 2008; Mortensen et al. 2004; Outridge et al. 1998; Townley et al. 2003; Viladevall et al. 1999). The alluvial gold concentrates occur downstream from the ore deposits (McInnes et al. 2008). Lithological and structural criteria are considered to be the most important exploration criteria for gold deposits (Madani 2011).

The aim of this manuscript was the development and application of a spatial statistical approach for sedimentary gold exploration, with a focus on the visualization and delineation of potential zones of low and high values for future prospections, instead of the accurate estimation of gold content. The methodology is illustrated using trace elements—Ag, As, B, Ba, Be, Cd, Co, Cr, Cu, Fe, Nb, Ni, Mn, Mo, Pb, Sb, Sn, V, Y, U, W and Zn—measured in 376 stream sediments samples that were collected in the old sedimentary gold abandoned mining region of Monfortinho (Central Portugal).

Section 2 describes the study area and the data available for modeling. The methodology is introduced in Sect. 3 and the results of its application to an old gold mine are discussed in Sect. 4. Conclusions are summarized in Sect. 5.

2 Study Area

The study area is located in Monfortinho region, about 70 km East of Castelo Branco (central Portugal), and is part of the Central Iberian Zone, in the Portuguese–Spanish border (Fig. 1). It is occupied mainly by the Cambrian schist-greywacke complex associated with Ordovician quartzites and covered by Tertiary sedimentary materials (Oliveira et al. 1992). The transboundary Portuguese-Spain border is delimited by the Erges River, one of the last wild rivers in Portugal, with a rare natural value due to its geodiversity. Agriculture is the main local activity and the thermal SPA water from Fonte Santa contributes to the economy and tourism of the region. This region is characterized by a dry climate with most streams drying up in the summer (Antunes et al. 2002).

Fig. 1
figure 1

Location of the study area in Portugal and sampling data configuration in the Tagus watershed

Full size image

The area of sampling site is approximately 140 km\(^{2}\) and surrounds the mining of sedimentary gold in the Erges River. Around mine tailing sites, the mineralogical content of the material exploited consists of inert materials from the gangue constituent’s mineralization or mineral constituents of rocks (Maroto et al. 1997). Geochemical anomalies found in the vicinity of tailings and mineralized areas indicate the action of dominant wind and transport of fine dust from the superficial layers of the heap (Santos Oliveira et al. 1998). The stream sediments, resulting from the alteration of rocks by various physical and chemical processes, are mobilized, transported and deposited along the water lines.

The geochemical composition of stream sediments and their spatial distribution in the study area were characterized using a total of 376 representative samples, collected between 1980 and 1988, in a narrow region ranging from 50 m upstream to 100 m downstream from the streams’ confluences (Instituto Geológico e Mineiro 1988) (Fig. 1). Since almost all water lines correspond to open valleys, our point-support stream sediments samples correspond to incipient instead of evolved soils. All the samples were collected on schist and their preparation included reduction, drying and grinding. Total concentration of Ag, As, Au, B, Ba, Be, Cd, Co, Cr, Cu, Fe, Nb, Ni, Mn, Mo, Pb, Sb, Sn, V, Y, U, W and Zn were analyzed by ICP-AES, with a precision of 20 % for As and 10 % for the other elements (Instituto Geológico e Mineiro 1988). Gold was measured in 12 samples collected inside the old mine area. Tin and W were analysed by X-ray fluorescence spectrometry and plasma emission with a precision of 10 % (0.05 ppb) (Antunes et al. 2002; Instituto Geológico e Mineiro 1988).

3 Methodology

The flowchart in Fig. 2 describes the different steps of the geospatial analysis which includes linear regression, indicator kriging (IK), sequential indicator simulation and local cluster analysis (LCA).

Fig. 2
figure 2

Flowchart describing the different steps of the analysis conducted on 12 gold data and 376 stream sediment metal data to delineate areas of low and high gold content

Full size image

3.1 Hard and Soft Indicator Coding

Because gold content was measured only for a small subset (\(n_{1}=12\)) of stream sediment samples, the first step was to capitalize on the relationships between gold content and four metals (Fe, As, Sn and W), which are known to be mostly associated with the local gold’s paragenesis, to predict gold content at the remaining sampled locations (\(n_{2}=364\)). Although this relationship was established from in-situ gold content it is relevant to the 364 stream sediment samples since the geochemistry of Au and the other four elements are stable during mobility and weathering (Antunes et al. 2002; Harraz et al. 2012). This prediction was here based on linear regression, resulting in an estimated value \(m_{\mathrm{LR}} ({\mathbf {u}}_\alpha )\) and associated standard error \(s_{\mathrm{LR}} ({\mathbf {u}}_\alpha )\) at all \(n_{2}\) locations with geographical coordinates \({\mathbf {u}}_\alpha \).

To account for the uncertainty attached to \(n_{2 }\) gold content estimates (soft data) relative to \(n_{1}\) measurements (hard data), each of the 12 hard data \(z( {{\mathbf {u}}_\alpha })\) and 364 soft data \(m_{\mathrm{LR}} ({\mathbf {u}}_\alpha )\) were transformed into a set of \(K=19\) indicators as follows

(1)
$$\begin{aligned} i({\mathbf {u}}_\alpha ;z_k )=G\left( {\frac{z_k -m_{\mathrm{LR}} ({\mathbf {u}}_\alpha )}{s_{\mathrm{LR}} ({\mathbf {u}}_\alpha )}}\right) , \end{aligned}$$
(2)

where \(z_{k}\) is a gold content threshold identified with 5kth percentile of the distribution of hard and soft data, and G(.) is the standard normal cumulative distribution function. The spatial connectivity of these indicators was then quantified and modeled using the indicator semivariogram defined as

$$\begin{aligned} \gamma _\mathrm{I} ({\mathbf {h}};z_k )=\frac{1}{2N(h)}\sum \limits _{\alpha =1}^{N(h)} {[i({\mathbf {u}}_\alpha ;z_k )} -i({\mathbf {u}}_\alpha +{\mathbf {h}};z_k )]^2, \end{aligned}$$
(3)

where the indicator value at location \({\varvec{u}}_{{\alpha }} \) is paired with another indicator value a lag distance \({\varvec{h}}\) away.

3.2 Indicator Kriging and Cross-Validation

The delineation of zones of low and high values required the interpolation of gold content to the nodes of a regular grid. This step was accomplished using soft indicator kriging (Goovaerts 1994) whereby the probability of being no greater than a threshold \(z_{k}\) at any node \({\mathbf {u}}_0\) was estimated as the following linear combination of indicators

$$\begin{aligned} F_{\mathrm{IK}} ({\mathbf {u}}_0 ;z_k \vert (n))=\sum \limits _{\alpha =1}^{n({\mathbf {u}}_0 )} {\lambda _{\alpha k} i({\mathbf {u}}_\alpha ;z_k )} \quad \,k=1,\ldots ,K, \end{aligned}$$
(4)

where \(\lambda _{\alpha k} \) are kriging weights that are solutions of the following system of linear equations

$$\begin{aligned} \left\{ {{\begin{array}{*{20}c} {\begin{array}{l} \sum \limits _{\alpha =1}^{n({\mathbf {u}}_0 )} {\lambda _{\alpha k} C_I } ({\mathbf {u}}_\alpha -{\mathbf {u}}_\beta ;z_k )+\mu ({\mathbf {u}}_\beta ;z_k )=C_I ({\mathbf {u}}_\beta -{\mathbf {u}}_0 ;z_k ) \\ \sum \limits _{\alpha =1}^{n({\mathbf {u}}_0 )} {\lambda _{\alpha k} =1} \\ \end{array}} \\ \end{array} }\beta =1,\ldots ,n({\mathbf {u}}_0 )} \right. . \end{aligned}$$
(5)

The indicator covariance function \(C_{\mathrm{I}}({\varvec{h}};z_{k})\) was derived by subtracting the model fitted to the experimental indicator semivariogram (Eq. 3) from the sill. Indicator kriging was conducted using the program AUTO-IK (Goovaerts 2009) which computes at each node \({\mathbf {u}}_0 \) the mean and variance of the local distributions of probability (ccdf), denoted \(\hat{z}_E ({\mathbf {u}}_0 )\) (E-type estimate) and \(s_E^2 ({\mathbf {u}}_0 )\), after correction of K probability estimates (Eq. 4) for order relation deviations and interpolation/extrapolation to complete the discrete ccdf.

The quality of the model of uncertainty provided by indicator kriging was assessed using a leave-one-out cross-validation approach whereby IK results at sampled locations \({\mathbf {u}}_\alpha \) were compared to observations (soft or hard data) that were removed one at a time. From the ccdf \(F_{\mathrm{IK}} ({\mathbf {u}}_\alpha ;z\vert ({n}))\) one can compute a series of symmetric median-centred p-probability intervals (PI) bounded by the \((1-p)/2\) and \((1+p)/2\) quantiles of that distribution: \({q}({\mathbf {u}}_\alpha ;( {1-p})/2)\) and \({q}({\mathbf {u}}_\alpha ;( {1+p})/2)\). For example, the 0.5-PI is bounded by the lower and upper quartiles of the ccdf. According to this model of local uncertainty, there is then a 0.5-probability that the actual attribute value (i.e., gold content) falls into the 0.5-PI or, equivalently, that over the study area 50 % of the 0.5-PI includes the true z values. The fraction of true values falling into the symmetric p-PI was here computed as

$$\begin{aligned} p^{*} =\frac{1}{n_1 }\sum \limits _{\alpha =1}^{n_1 } {{j}({\mathbf {u}}_\alpha ;p) } +\frac{1}{n_2 }\left[ \sum \limits _{\alpha =1}^{n_2 } {G\left( {\frac{q({\mathbf {u}}_\alpha ;(1+p)/2)-m_{\mathrm{LR}} ({\mathbf {u}}_\alpha )}{s_{\mathrm{LR}} ({\mathbf {u}}_\alpha )}}\right) }\right. \nonumber \\ \left. -G\left( \frac{q({\mathbf {u}}_\alpha ;(1-p)/2)-m_{\mathrm{LR}} ({\mathbf {u}}_\alpha )}{s_{\mathrm{LR}} ({\mathbf {u}}_\alpha )}\right) \right] , \end{aligned}$$
(6)

where \(j( {{\mathbf {u}}_\alpha ;{p}})=1\) if the hard data \({z}({\mathbf {u}}_\alpha )\) falls within the p-PI, and zero otherwise. For the \(n_{2}\) soft data, the overlap between the p-PI and the Gaussian distribution centred on the regression estimate \({m}_\mathrm{LR} ( {{\mathbf {u}}_\alpha })\) is computed using an expression similar to Eq. (2). Following Deutsch (1997), the agreement between observed,\(p_k^*\), and expected fractions, \(p_{k}\), is quantified using the following “goodness” statistic

$$\begin{aligned} G=1-\frac{1}{K'}\sum \limits _{k=1}^{K'} {w_k \vert p_k^*-p_k \vert }\quad \text{ with }\,\,\,0\le G\le 1, \end{aligned}$$
(7)

where \(w_{k}=1\) if \(p_k^*>p_k \), and 2 otherwise. \(K'\) represents the discretization level of the computation. Twice more importance is given to deviations when \(p_k^*<p_k \) (inaccurate case). The weights penalize less the accurate case, which is the case where the fraction of true values falling into the p-probability interval is larger than expected. The goodness statistic is completed by the so-called “accuracy plot” that allows one to visualize departures between observed and expected fractions as a function of the probability p.

Fig. 3
figure 3

a Scatterplot of measured gold content (\(n_{1}=12\)) versus estimates computed by linear regression from four metals (Fe, As, Sn and W). b Results of the application of this regression model to 364 stream sediment samples. Bottom scatterplot illustrates the larger uncertainty (standard error) associated to values extrapolated beyond the range (26 to 34 ppb) of the 12 gold measurements

Full size image
Fig. 4
figure 4

Location map of stream sediment samples overlaid on a topographic map of the study area. The size of yellow dots is proportional to the gold concentration estimated by linear regression

Full size image
Fig. 5
figure 5figure 5

Experimental indicator semivariograms standardized to unit sill with the isotropic model fitted automatically by AUTO-IK for each of the 19 gold content thresholds

Full size image
Fig. 6
figure 6

Results of a cross-validation of soft indicator kriging: a accuracy plot, and b scatterplot of E-type estimates (ccdf mean) versus gold data used for hard and soft indicator coding and displayed in Fig. 4

Full size image
Fig. 7
figure 7

Map of the standard deviation of the conditional cumulative distribution functions (ccdf) derived using soft indicator kriging. Black crosses denote the location of the 12 hard data (gold content) measured inside the abandoned gold mines whereas white dots are the soft data

Full size image
Fig. 8
figure 8

Results of a local cluster analysis conducted on the map of gold content estimated by soft indicator kriging: significant clusters of low (LL) and high (HH) gold content detected using local Moran’s I. Dots correspond to sampled locations

Full size image
Fig. 9
figure 9

Three simulated maps of gold content created using sequential indicator simulation (left) and the corresponding results of local cluster analysis (right)

Full size image
Fig. 10
figure 10

Map of the most frequent cluster category (LL, HH, non-significant) computed from a local cluster analysis (LCA) of one hundred simulated maps of gold content. The intensity of the shading is proportional to the likelihood of occurrence of that category

Full size image

3.3 Local Cluster Analysis

The delineation of zones of low and high contents in gold was conducted through the application of local cluster analysis (Anselin 1995; Fu et al. 2014; Goovaerts et al. 2005a, b); Goovaerts 2010)). The basic idea is to compute at each grid node a local indicator of spatial autocorrelation (LISA) and test whether this statistic is significantly positive, indicating the existence of an aggregate of grid nodes with similar gold content, either low or high. Similarity between the gold concentration E-type estimate at node \({\mathbf {u}}_0 \) (kernel value) and values estimated at \(J( {{\mathbf {u}}_0 })\) adjacent nodes \({\mathbf {u}}_{{ j}} \) (e.g., \(J( {{\mathbf {u}}_0 })=8\) nodes adjacent to \({\mathbf {u}}_0 )\) was here quantified by the local Moran’s I statistic defined as

$$\begin{aligned} I({\mathbf {u}}_0 )=\frac{\hat{z}_E ({\mathbf {u}}_0 )-m}{s}\times \frac{1}{J({\mathbf {u}}_0 )}\sum \limits _{j=1}^{J({\mathbf {u}}_0 )} {\frac{\hat{z}_E ({\mathbf {u}}_j )-m}{s}} , \end{aligned}$$
(8)

where m and s are the mean and standard deviation of the set of N grid estimates. This local statistic is simply the product of the kernel value and the average of neighboring values; it can detect both positive and negative autocorrelations. It exceeds zero if the kernel and neighborhood averaged gold content estimates jointly exceed the global mean m (High–High, HH cluster) or are jointly below m (Low–Low, LL cluster). LISA values are negative if the kernel and neighborhood mean values are on opposite sides of the global mean m, which indicates the presence of spatial outliers or anomalies: High–Low (HL outlier) or Low–High (LH outlier).

To test whether any test statistic, \(I( {{\mathbf {u}}_0 })\), is significantly greater or smaller than 0 (i.e., presence of spatial autocorrelation), one needs to know its probability distribution under the null hypothesis of spatial independence. The common way to generate such reference distribution is to shuffle the set of estimated values randomly and then to use the shuffled values to compute the neighborhood average in Eq. (8) while the kernel gold content remains the same. In other words, the LISA statistic is computed for randomly distributed gold contents in adjacent locations. This operation is repeated K times (\(K = 999\) in this article) to compute the P value of the test. Because the statistical test is repeated for each grid node, there is an increased likelihood of false positives (i.e., risk of rejecting the null hypothesis when it is true) and the test needs to be corrected for multiple testing. This correction was here accomplished using the false discovery rate (FDR) approach, which aims to control the expected proportion of true null hypotheses that will be rejected (Castro and Singer 2006); that is the objective is to limit the risk of false positives.

3.4 Propagation of Uncertainty Using Sequential Indicator Simulation

The application of local cluster analysis to E-type estimates has two main drawbacks: (i) the detection of artificial clusters resulting from the autocorrelation imparted to estimates \(\hat{z}_E ({\mathbf {u}}_0 )\) by the smoothing effect of kriging, and (ii) the failure to account for the uncertainty attached to kriging estimates (e.g., variance \(s_E^2 ({\mathbf {u}}_0 )\) of the ccdf). Goovaerts (2006) proposed a simulation-based approach to account for uncertainty in local cluster analysis and avoid the smoothing effect of kriging. First, the uncertainty attached to the spatial distribution of gold content is modeled through the generation of a set of equally-probable simulated maps, \(\{ {z^{(l)}( {{\mathbf {u}}_{{j}} }),{ j}=1,\ldots ,N;l=1,\ldots ,L} \}\), each consistent with the information available, such as histogram or a spatial correlation function. This step was here accomplished using sequential indicator simulation based on soft indicator coding (Sect. 3.1). Then, the uncertainty is propagated through the computation of the LISA statistic by replacing in Eq. (8) the E-type estimates \(\hat{z}_E ({\mathbf {u}}_0 )\) and \(\hat{z}_E ({\mathbf {u}}_j )\) by the corresponding simulated values, leading to a set of L simulated LISA values \(\{ {I^{(l)}( {{\mathbf {u}}_0 }),l=1,\ldots , L} \}\). In other words, the correlation of each node with adjacent nodes will be tested L times, enabling the computation of the probability for that node to belong to a cluster of small gold content (low value surrounded by low values) or a cluster of large gold content (high value surrounded by high values). The L classified maps are then processed to derive the most likely classification of each node and the associated likelihood (i.e., frequency of occurrence of that class over L simulations).

4 Results and Discussion

A linear regression analysis of gold content versus four metals (Fe, As, Sn and W) explained close to 80 % of the total variance (\(R^{2}=0.798\)). Although the large \(R^{2}\) is due to some extent to the small number of data available (\(n=12\)), the scatterplot in Fig. 3a indicates a good agreement between the predicted and measured gold concentrations. The application of this regression model to the remaining 364 stream sediment samples led to gold content estimates that are plotted versus their standard error in Fig. 3b. This scatterplot clearly illustrates the larger uncertainty (standard error) associated with values extrapolated beyond the range (26 to 34 ppb) of the twelve gold measurements. Such an extrapolation makes sense in the present exploratory setting where few gold samples are available and lower values are expected away from the location of the old gold mine. The larger uncertainty attached to the prediction of these lower values is incorporated into the analysis through the soft indicator coding and the subsequent simulation procedure. The gold content estimated by regression is mapped in Fig. 4. Zones of low and high gold contents could, however, not be readily delineated from this location map because of the discrete nature of the sampling and the fact that the uncertainty attached to the regression estimates was ignored.

Each of the 12 gold data and 364 regression estimates were coded into a set of 19 indicators according to Eqs. (1) and (2). This high level of discretization was justified by the fact that each soft data take the form of a Gaussian probability distribution centred on the regression estimate. The thresholds were identified from the histogram of 376 values in order to split the sample distribution into 20 classes of equal frequency. The indicator semivariograms in Fig. 5 indicate a good spatial connectivity of the indicators regardless the threshold. In particular the average relative nugget effect is 38.2 %, well within the range of 25 to 75 % commonly used to characterize a moderate spatial dependence (Cambardella et al. 1994). Interestingly the range of autocorrelation increases with the threshold: it is around 2 km for the smallest threshold’s concentrations (\(<\)17 ppb) and exceeds 6 km for the largest thresholds (\(>\)23 ppb). In other words, the highest gold values are better connected in space than the lowest gold values, which is unlike most environmental datasets where high concentrations are often isolated hotspots (e.g., Goovaerts et al. 2005a, b).

Indicator semivariogram models were used with ordinary kriging to interpolate hard and soft indicator data to the nodes of a grid with 100 m spacing. A small percentage (1.9 %) of kriged probabilities had to be slightly corrected (average correction \(=\) 0.0015) in order to create valid cumulative probability distributions at each of the 11,286 grid nodes. The resolution of the discrete ccdf was then increased by performing a linear interpolation between tabulated bounds provided by the sample histogram (Deutsch and Journel 1998). The accuracy of the resulting model of uncertainty was first quantified using cross-validation. The accuracy plot indicates a very good agreement between observed and expected proportions of true values falling into probability intervals, leading to a goodness statistics close to 1 (Fig. 6a). The mean absolute prediction error was 3.6 ppb and the scatterplot in Fig. 6b illustrates the good correlation between E-type estimates and the original 376 data (\(r=0.73\)). As for all least-squares interpolation methods (Goovaerts 1997), results display a conditional bias whereby the large concentrations are underestimated while the small concentrations are overestimated.

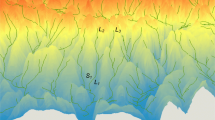
Figure 7 shows the map of the standard deviation of the local distributions of probability (ccdf) which can be interpreted as a measure of local uncertainty. As expected, the uncertainty is the lowest within the gold mines (upper right corner) where actual gold content was measured at 12 locations denoted by black crosses. At other locations the uncertainty combines the standard error of regression estimates where gold was not recorded (white dots) with the uncertainty caused by spatial interpolation. The uncertainty is particularly large in sparsely sampled areas (zones A and B) and in zones of greater spatial variability which border between areas of low and high gold content displayed in the map of E-type estimates at the top of Fig. 8. A local cluster analysis was conducted using a significance level \(\alpha =0.05\) and the false discovery rate (FDR) approach for multiple testing correction. Two significant clusters of low gold content (LL) and two significant clusters of high gold content (HH) were identified within the study area (Fig. 8, bottom). Of particular interest are the higher gold content estimates found along the Erges River and downstream from the old abandoned sedimentary mineralization.

A better alternative to the smooth map of E-type estimates is an ensemble of simulated maps which reproduce the variability displayed by hard and soft data and model the uncertainty attached to their spatial distribution. One hundred maps were generated by sequential indicator simulation and each underwent a local cluster analysis similar to the one conducted for the single map of E-type estimates. Figure 9 shows the results for the first three simulated maps, which illustrates the uncertainty attached to the spatial distribution of gold content and how it impacts the definition of the LL and HH clusters. One obvious difference with kriging results (Fig. 8, bottom) is the much smaller size and spatial compactness of the clusters of low and high gold content; in particular, the cluster of high gold content immediately downstream from the gold mines vanished almost completely on some simulations. The remaining HH cluster is, however, bigger and more spatially compact than LL clusters, which agrees with the longer range of autocorrelation displayed by the indicator semivariograms corresponding to higher thresholds (Fig. 5). This difference in size between LL and HH clusters was less apparent on the classification map based on E-type estimates because the smoothing effect of kriging artificially inflated the size of these clusters.

The local Moran’s I was also found significantly lower than zero at multiple locations, which indicates the presence of spatial outliers or anomalies. The set of 100 LCA results was summarized by assigning each grid node to the most frequent category (ML classification) and reporting that maximum frequency. Figure 10 confirms the conclusions drawn from the first three realizations regarding the severe shrinking of the cluster of high gold content located immediately downstream from the gold mines: only one node has a likelihood of belonging to that cluster above 0.75 and even for a 0.5 likelihood the cluster is pretty small with a size less than 5 % the size of the same cluster delineated on the basis of E-type estimates (Fig. 8, bottom). In comparison, the HH cluster in the Southern part of the study area represents 35 % of the counterpart kriging HH cluster and is now split into two parts. For both HH and LL clusters, the centres of the cluster are typically associated with the highest likelihood (i.e., more intense shading). Note that none of the nodes in the ML classification is flagged as a significant outlier.

5 Conclusions

This paper presented a multivariate geostatistical methodology to delineate areas of potential interest for future sedimentary gold exploration. The challenge was the existence of only a dozen of gold measurements confined to the grounds of the old gold mines, which precluded the application of traditional interpolation techniques, such as cokriging. The spatial characterization of the study area could, however, rely on the availability of a large set of stream sediment samples and the relationship between concentrations of several metals and gold content that was modeled using linear regression. This information translated into a set of prior distributions of probability that were discretized into indicator vectors and their semivariograms revealed the stronger spatial connectivity of larger gold concentration estimates (\(>\)23 ppb) relative to smaller concentrations (\(<\)17 ppb).

Soft indicator kriging allowed the derivation of the distributions of probability for gold content at the nodes of a regular grid, accounting for the uncertainty caused by the initial linear regression, in particular when extrapolating beyond the range of the twelve gold data, and the uncertainty resulting from the spatial interpolation. The use of the public-domain program AUTO-IK (Goovaerts 2009) greatly facilitated the application of indicator kriging with 19 thresholds as all the computation, including the modeling of 19 indicator semivariograms, was done automatically. Cross-validation demonstrated the accuracy of these models of uncertainty. The delineation of aggregates of low and high gold content was accomplished using local cluster analysis (LCA), which is commonly used to detect cancer clusters (Goovaerts and Jacquez 2005), yet has been seldom used in earth sciences (Zhang et al. 2008). Unlike a simple visual interpretation of a map of kriging estimates, LCA is based on statistical testing of the strength of spatial autocorrelation and allows the delineation of zones of significant clustering. One main difference between the applications of LCA in earth sciences relative to epidemiology is the sheer size of the dataset (e.g., large interpolation grid versus a few hundred administrative units), which increased the risk of false detection through multiple testing. This issue was here addressed using the false discovery rate (FDR) approach.

Because it is a least-square interpolator, kriging tends to create smooth maps which display greater spatial continuity than the original data and a conditional bias. This was a shortcoming for the application of local cluster analysis since it led to artificially large clusters. In addition, the model of local uncertainty provided by the ccdf, which captures the uncertainty attached to applying regression outside the range of the data, was useless to characterize the uncertainty of a multi-point statistic like the local Moran’s I. Both drawbacks were overcome by implementing the approach within a stochastic simulation framework. Sequential indicator simulation generated maps that reproduce the variability displayed by gold data, resulting in the identification of clusters of smaller size and the detection of spatial anomalies or outliers corresponding to significant negative spatial auto correlation. On the other end, the ensemble of 100 realizations provided a model of spatial uncertainty that could be propagated through the local cluster analysis to compute the likelihood of the clusters of high gold concentrations. In the current application, we found a clear Au enrichment along the Erges River downstream from the old abandoned sedimentary mineralization. The likelihood of this cluster of higher gold content would justify the future sampling of this area to validate the findings of the present study. The local likelihood could also help prioritizing which locations should be explored first, information that would be unavailable from a simple visual interpretation of maps of E-type estimates.