Predictive modeling and comparative evaluation of geostatistical models for geochemical exploration through stream sediments

Abstract

Geochemical exploration of stream sediments is an important step for the identification of areas of interest with potential mineralization, particularly in the early stages of mineral exploration. A total of 407 sample points for 15 different geochemical traces were collected from Central Wales and classified into two groups: a training group consisting of 285 samples and a testing group consisting of 122 samples. Geospatial characterization of each parameter at stream level was performed using two different prediction models; the inverse distance weighting and the geostatistical kriging. Several variations of the IDW model was applied based on the power function and the number of the sample points, and the best one selected based on “root mean square prediction error” statistic. The same statistic was also used in the best-fitted semivariogram models including the circular, spherical, exponential and Gaussian for each geochemical parameter in Kriging. Finally, the mineral prospectivity map of the area was developed based on the geochemical accumulation index (GAI) using multivariate overlay analysis. The experimental results show that there is no single method that can be used independently to predict the spatial distribution of geochemical elements in streams. Instead, a combinatory approach of IDW and kriging is advised in order to generate more accurate predictions. The mineral prospectivity map based on GAI showed that most of the mineral-enriched streams were found in northwest, northeast, and south part of the study area which was also confirmed with the existing mining activities in the region.

Introduction

Stream sediments usually result from the erosion and transportation of soil and rock remnant, and other materials present upstream of the sampling locations within a basin (Merritt et al. 2003). Thus, stream sediments are considered to be representative of the geochemistry of the rocks present in the upstream drainage basin. Usually, stream sediments are the primary sampling source for geochemical exploration, primarily in areas where distinct drainage systems exist due to the local topography (Fletcher 1997; Salminen and Gregorauskien 2000; Zuluaga et al. 2017). Geochemical exploration sampling from stream sediments is a suitable technique for identification of areas of interest with significant mineralization content, particularly in the early stages of mining for undiscovered minerals (Arndt et al. 2017; Carranza 2017; Cheng 2007, 2012; de Mulder et al. 2016; Khalajmasoumi et al. 2017; Nieto et al. 2014). For the best results, it is always preferred to get as many samples as possible to work with a dense and large sampling dataset. However, high-density sampling of stream sediments is challenging due to the cost involved in getting geographical accessibility. Therefore, a limited number of samples are usually collected from the field and after analyzing in the lab used for estimation for larger areas using geostatistical interpolation models (Ottesen et al. 1989).

Geostatistical models have been extensively used as a powerful tool for providing accurate estimates of any spatial/temporal phenomena at unsampled locations using sampled data along with a quantification of the related uncertainty (Cai et al. 2018; Dagdelen and Vega 1997; Goovaerts 2000; Liu et al. 2006, 2018; Lu and Wong 2008; Moral 2010; Piel et al. 2013; Ssempiira et al. 2017). Several spatial interpolation methods, including geostatistics, have been developed in the past to better predict spatial distributions based on limited samples. However, the accuracy of the interpolated surface varied widely between models (Robinson and Metternicht 2006). In general spatial interpolation methods can be divided into three main categories, i.e., with respect to the number of points used for prediction (global/local), with respect to the surface smoothness (exact/approximate), and with respect to the error estimation (deterministic/stochastic) (Li and Heap 2014).

The most common interpolation methods used for geospatial characterization of geochemical data from streams are Nearest Neighbor (NN) (Li and Heap 2014; Yang et al. 2004), Triangular Irregular Network (TIN) (Li and Heap 2014; Wu et al. 2011; Yang et al. 2004), Inverse Distance Weighting (IDW) (Li and Heap 2014; Lu and Wong 2008), Radial Based Functions (RBF) (Ding et al. 2017) and Kriging (Kleinschmidt et al. 2000; Panahi et al. 2004; Wu et al. 2011). In general, kriging is the most applied, tested, and validated geostatistical model in the field of spatial interpolation. The most significant advantage of this model over several other spatial and statistical models is that kriging considers the spatial correlation of the data for the predictions. Several types of kriging have evolved over the time, but the most commonly used are ordinary kriging (OK), simple kriging (SK), universal kriging (UK), indicator kriging (IK), and co-kriging (Panahi et al. 2004). Among all these techniques, the predictions are highly dependent not only on the location of the data but also on the accurate development of the semivariogram model. But the development of the required semivariogram model is time taking and subjective. In addition to that, the transformation of the data may also be required in non-stationary conditions and directional trends needed to be considered (Nieto and Toffait 2007). Hence different geospatial characterization methods have been used in the past to characterize geochemical mineralization which tends to overextend predictions to areas not really influenced by the original stream mineralization condition. As it is not required that a stream sediment sample (S₁) be collected at a particular location (L₁) on a stream which represents the geochemical value at L₁, it is quite possible that it is a representative of the upstream location L₂ or L₃, i.e., the potential source of the mineralized zone (Fig. 1).

Fig. 1

3D topographical representation of streams along with geochemical sampling and value locations

Therefore this research focuses on the development of a new approach for geospatial characterization based on a continuous geochemical prediction surface up to the extent of sampling streams. Hence geochemically spatial predictions of continuous streams will provide improved estimations in streams considering the source of the mineralization.

Geochemical data are usually geospatial data as it can be expressed as x, y, and z, where x and y are location coordinates (latitude, longitude or easting, northing) and z represents the recorded value (i.e., elements concentration) at those coordinates. Geochemical data are usually stored in a spatial format as point data with location and value, hence can be processed in geoinformatics (Zuo et al. 2016). With the advancement in computer technology, several geographic information system (GIS)-based numerical codes are available with a strong component of geostatistics embedded in them. Surface interpolations through geostatistical modelling in GIS are very powerful for estimating geochemical values (Johnston et al. 2012; Li and Heap 2014). This research study has also incorporated a very strong GIS numerical package ESRI’s ArcGIS Geostatistical Analyst, which is equipped with advanced spatial geostatistical predictive models for predictive modelling. The two widely used interpolation methods, including the geostatistical (IDW and Kriging), were selected and applied to test their efficiency for geochemical characterization and prediction along the unsampled streams. Also these, models have been extensively used in the past, but none of them has been applied and tested for the prediction of geochemical values at individual stream levels, which is a new proposed methodology of this research study. Furthermore, the geochemical accumulation index (GAI) has been developed in this research to identify the mineral enriched streams and for identification of potential mineral prospects in the study area.

Materials and methods

Study area

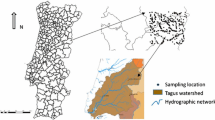
The study area for this research is located in Central Wales of Great Britain (Fig. 2) and has a prolonged history of gold mining, with the main center of activity being the “Dolgellau Gold Belt” where the Clogau and Gwynfynydd mines were very active gold mines, particularly towards South, in the Welsh Basin, where gold has been mined since the Roman times. Besides gold, several other secondary products such as lead, copper, zinc, iron, nickel sulfides and others are present throughout the Wales area.

Fig. 2

Study area map highlighting the location of major towns, roads, and stream sediment sample points

The dataset used in this study (WF/MR/93/013) was obtained from the British Geological Survey (BGS) (Brown 1993). The stream sediment baseline geochemistry data was estimated from samples collected across the central Wales region by BGS as shown in Fig. 2. Sampling was based on the collection of heavy minerals accumulated from the first- and second-order streams. Active stream sediment was moved through a 2-mm sieve, collected in a wooden pan (about 3–4 kg) and condensed by panning to about 60 g. This process was repeated using additional sediment from the same site and the two concentrates combined together were inspected on-site for heavy minerals and collected in a Kraft bag. A total of 407 samples were collected and analyzed for 15 different elements, including titanium (Ti), manganese (Mn), iron (Fe), vanadium (V), nickel (Ni), copper (Cu), zinc (Zn), zirconium (Zr), tin (Sn), antimony (Sb), barium (Ba), cerium (Ce), lead (Pb), arsenic (As), and gold (Au). Gold was estimated on 60 g of the sample by atomic absorption spectrometry after grinding and dissolution in aqua regia (a yellow-orange fuming liquid), with a lower confidence limit of detection as 10 parts per billion (ppb) Au. All other elements (Ti, Mn, Fe, V, Ni, Cu, Zn, Zr, Sn, Sb, Ba, Ce, Pb, and As) were determined by X-ray fluorescence analysis of milled sub-samples in parts per million (ppm). The descriptive statistic of the 15 elements is given in Table 1.

Table 1 Summary statistics of geochemical elements in the study area (N = 407)

From Table 1, it can be observed that the distributions of most geochemical parameters are positively skewed and their frequency diagrams do not follow a normal distribution (Bai and Ng 2005; Beedles and Simkowitz 1978). Coefficient of variation (CV) values < 10 and > 90% indicate low and high variability, respectively, in the data (Reed et al. 2002), and in this dataset, Ti and Au have the lowest and the highest variability, respectively. It can be observed through summary statistics that the data need to be transformed to a normal distribution and as all the variables have variability so spatial and geostatistical modelling can be applied for further predictions (Komnitsas et al. 2010). Further, the correlation coefficient (Pearson coefficient) matrix, as shown in Fig. 3 was developed to highlight the statistical relationship between geochemical variables (Facchinelli et al. 2001). The correlation coefficient matrix reveals that the correlation coefficient value r ranges from negative 0.66 (between Ti and Pb) to positive 0.69 (between Fe and V). The r values are statistically significant at a 0.05 (5%) confidence level.

Fig. 3

The correlation matrix between different geochemical variables highlighting the positive and negative associations

Directional distributional trend of geochemical data

Usually, the standard deviational ellipse (SDE) is used to capture the spatial trend for a set of measured observations (Lefever 1926). The SDE is based on standard deviations computed on spatial coordinates (x, y) of the observations and has been applied to describe bivariate features. Most commonly, it is applied to assess the geographical distribution trend of the features concerned by analyzing both of their dispersion and direction. For a given set of n samples $\mathcal{M}={\left\{\left({x}_i,{y}_i,{z}_i\right)\right\}}_{i=1}^n$, the corresponding SDE is defined by three parameters: spatial mean (or average spatial location) ($\overline{x},\overline{y}$), spatial dispersion (or concentration) (σ_x, σ_y), and orientation of the geochemical data θ. In addition to the traditional spatial mean center (gravity on the distribution), weighted spatial mean or median of the data could also be used as other options (Wang et al. 2015). The average spatial location of the SDE is computed using the following equation:

$$ \overline{x}=\frac{1}{n}{\sum}_{i=1}^n{x}_i,\overline{y}=\frac{1}{n}{\sum}_{i=1}^n{y}_i $$

(1)

the average spatial location is subtracted from each sample to center the observed samples at the origin, i.e.,

$$ \tilde{x}_{i}={x}_i-\overline{x},\tilde{y}_{i}={y}_i-\overline{y} $$

(2)

the centered samples are then used to compute the orientation of the SDE as follows

$$ \theta =\arctan \frac{A+\sqrt{A^2+4{B}^2}}{2B} $$

(3)

where

$$ A=\left({\sum}_{i=1}^n{\tilde{x}}_i^2-{\sum}_{i=1}^n{\tilde{y}}_i^2\right),\kern1em B={\sum}_{i=1}^n{\tilde{x}}_i{\tilde{y}}_i $$

and finally, the spatial dispersion of the SDE is computed using the shifted and oriented samples based on

$$ {\displaystyle \begin{array}{ccc}{\sigma}_x& =& \sqrt{\frac{1}{n}{\sum}_{i=1}^n{\left({\tilde{y}}_i\sin \theta +{\tilde{x}}_i\cos \theta \right)}^2}\\ {}{\sigma}_y& =& \sqrt{\frac{1}{n}{\sum}_{i=1}^n{\left({\tilde{y}}_i\cos \theta -{\tilde{x}}_i\sin \theta \right)}^2}\end{array}} $$

(4)

A rule-of-thumb drawn from the Rayleigh distribution recommends that a first, second, and third standard deviational ellipse will cover approximately 63, 98, and 99.99% of the features (geochemical data) in two dimensions (x and y) (Wang et al. 2015). In this research, the directional distributional trend of all the 15 elements was assessed with one standard deviation, which covers 63% of the data in ArcGIS software.

Streams delineation using digital elevation model

Global Digital Elevation Map (GDEM) derived from the Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER) was used to extract the streams present in the study area. The GDEM was re-projected from Geographical Coordinate Systems to Projected Coordinates Systems for spatial referencing. The pre-processing of GDEM is always required and recommended before the extraction of any spatial information. Usually, a raw DEM often has a large number of “sinks” (or false depressions), i.e., single or multiple pixels with extreme low elevation and are completely enclosed by immediate higher elevation pixels (Jones 2002). The sinks, if present in the DEM, then must be removed using the fill operation available in any raster GIS packages. In this research study FILL operation of ArcHydro model of ESRI’s ArcGIS was applied as shown in Fig. 4. The FILL operation eliminates the sinks by either (a) raising the elevation on the sink cell to that of its lowest neighbor or (b) lowering the elevation of the lowest neighbor adjacent to the sink (Jones 2002).

Fig. 4

The effect of FILL operation on the GDEM as on left side false depressions were filled after applying the operation

After pre-processing of the GDEM, the next step is to determine the flow direction, which is the ability to control the direction of water from every pixel in the raster to its downslope neighbor. Several algorithms can be used to determine the direction of flow, including the Multi-Flow Direction (MFD), D-Infinity (DINF), and D8 (Płaczkowska et al. 2015). Among all these, the D8 (eight flow direction) method is the simplest and the most effective. D8 assigns the flow (in terms of coding) from individual pixel to one of its eight connecting cells, either adjacent or diagonal, in the direction with the steepest downward slope.

Once the flow direction raster is created, the next step is to calculate areas where water may accumulate as a result of rainfall, known as the Flow Accumulation raster. Mainly, the value to each cell in the resulting raster contains the sum of the amount of water that has fallen on all the raster cells upstream from it. The objective is to simulate the flow, or possible flow, of water to form creeks, streams, and/or rivers. A threshold value is required to determine the minimum number of cells that can generate the flow, i.e., in this study a threshold of 150 was set, which means that a minimum of 150 cells should contribute to generating a flow into a cell (Wei et al. 2016). The threshold value is selected from a range [100, 359] according to the number of connected pixels which fall on the stream to generate an adequate amount of flow. After highlighting the streams in the area, the next step is to convert them from raster to vector by using the Streams to Feature utility of ArcHydro. The mineral prediction at stream level will provide more realistic information and help to mark the mineral-enriched zones as compared with a classical square regional predicted surface.

Spatial interpolation methods

Inverse distance weighting (IDW)

IDW is a local, exact, and deterministic interpolation model, which means it predicts a value at unsampled locations using a subset of sampled values, and then it will be the same, i.e., the line passes through the points and gives no error assessment. Due to its simplicity and computationally non-intensiveness, several researchers, without having much knowledge in spatial statistics and geostatistics, will use IDW as a default method to produce a surface when data values exist only at sampled locations. This model assumes that data values that are nearby to one another are more similar than those that are at far distances (Wong 2016). To calculate a value for any unsampled location, IDW uses the measured values close to the unsampled location.

The IDW model predicts the unknown geochemical value ${\hat{g}}^{(e)}\left({\mathbf{r}}_u\right)$ of element e at location r_u, using the observed (or known) element values g^(e)(r_i) at sampled locations r_i as follows:

$$ \hat{g}\left({\mathbf{r}}_u\right)={\sum}_{i,{\mathbf{r}}_i\in {\mathcal{N}}_u^k}{w}_ig\left({\mathbf{r}}_i\right), $$

(5)

where w_i is the weight for the observed value g^(e)(r_i) for geochemical element e and ${\mathcal{N}}_u^k$ is the set of k nearest sample locations around the spatial location r_u. In other words, the predicted value ${\hat{g}}^{(e)}\left({\mathbf{r}}_u\right)$ at r_u is a weighted sum of observed values g^(e)(r_i) with

$$ {\sum}_{i=1}^k{w}_i=1 $$

The weight w_i is inversely proportional to the α^th power of Euclidean distance between r_u and r_i and defined as follows:

$$ {w}_i=\frac{{\left\Vert {\mathbf{r}}_i-{\mathbf{r}}_u\right\Vert}^{-\alpha }}{\sum_{j=1}^k{\left\Vert {\mathbf{r}}_j-{\mathbf{r}}_u\right\Vert}^{-\alpha }}, $$

(6)

where ‖r_i − r_u‖ is defined as Euclidean distance between r_u and r_i.

The α parameter is quantified as a geometric form for the weight while other conditions are possible. This condition indicates that if α is more significant than 1, then the distance-decay influence will be more as compared with an increase in distance and vice versa. Therefore, a small α tend to give predicted values as averages of g^(e)(r_i) in the neighborhood, while large α assign more weights to the nearest points and gradually decrease for points far away. As a result, when α → 0

$$ {\displaystyle \begin{array}{r}\underset{\alpha \to 0}{\mathrm{Lim}}\hat{g}\left({\mathbf{r}}_u\right)\kern0.5em =\kern0.5em \underset{\alpha \to 0}{\mathrm{Lim}}{\sum}_{i=1}^k{w}_ig\left({\mathbf{r}}_i\right);\\ {}\begin{array}{cc}=& \underset{\alpha \to 0}{\mathrm{Lim}}{\sum}_{i=1}^k\frac{{\left\Vert {\mathbf{r}}_i-{\mathbf{r}}_u\right\Vert}^{-\alpha }}{\sum_{j=1}^k{\left\Vert {\mathbf{r}}_j-{\mathbf{r}}_u\right\Vert}^{-\alpha }}g\left({\mathbf{r}}_i\right);\end{array}\\ {}\begin{array}{c}\begin{array}{cc}=& \underset{\alpha \to 0}{\mathrm{Lim}}{\sum}_{i=1}^k\frac{1}{\sum_{j=1}^k1}g\left({\mathbf{r}}_i\right);\end{array}\\ {}\begin{array}{cc}=& \frac{1}{k}{\sum}_{i=1}^kg\left({\mathbf{r}}_i\right),\end{array}\end{array}\end{array}} $$

(7)

and w_i → 1/k. Then, the predicted value is the average of all sampled values. Similarly when α → ∞, $\hat{g}\left({\mathbf{r}}_u\right)=g\left({\mathbf{r}}_c\right)$ where r_c is the closest sample location.

Usually, the geoscientists and mineralogists use the power α = 2, which is known as the inverse distance squared weighted model. In this research, three different IDW power values α = 1, α = 2, and α = 3 had been tested to generate the geochemical prediction surfaces. There is no theoretical reasoning in the selection of a particular value over others, however, the influence of changing power should be examined by visualizing the output and observing the validation statistics. The measured values near to the unsampled location have more impact on the predicted value than those farther apart. IDW considers that each sampled point has a local impact that reduces with distance. So this model uses weights assigned to the sample values as it gives more weights to points nearby to the unsampled location, and the weights reduce as a function of distance; therefore, the name inverse distance weighting.

Kriging

Kriging predicts the structure of spatial variability through a variogram and incorporates the spatial autocorrelation (Hattis et al. 2012). The kriging prediction is modeled as the summation of a global trend λ (which is the general trend in the entire data) and a local stochastic variation ε (Matheron 1963):

$$ \hat{g}\left({\mathbf{r}}_i\right)=\lambda \left({\mathbf{r}}_i\right)+\varepsilon \left({\mathbf{r}}_i\right), $$

(8)

where r_i represents the spatial coordinates. Depending on the global trend λ, several types of Kriging models have been established. For example, simple kriging (SK) assumes λ = 0; ordinary kriging (OK) assumes λ as an unknown constant mean; and universal kriging (UK) assumes λ a general polynomial trend as z = ax + by + c, where x, y are the variables for the latitude and longitude respectively and z can be statistically analyzed from the past data. In this research study OK is used because it provides more realistic and reliable predictions based on mean squared errors; is an unbiased predictor for sparsely sampled regions (Cressie 1993); and minimizes the influence of spatial outliers (Triantafilis et al. 2001), if present in the data. The OK method predicts the $\hat{g}\left({\mathbf{r}}_u\right)$ at r_u using the weighted sum of the data as follows:

$$ \hat{g}\left({\mathbf{r}}_u\right)={\sum}_{i,{\mathbf{r}}_i\in {\mathcal{N}}_u^k}{w}_i{\mathbf{g}}_i\left({\mathbf{r}}_i\right). $$

(9)

The choice of weight in Eq. (9) should be made in such a way that w_i yields the lowest mean square estimation error (Cressie 1993). Besides this the selection of w_i also depends on the type of semivariogram model as suggested by Deutsch and Journel (1992). The experimental semivariogram $\hat{\gamma}(r)$ can be defined as the average square difference of the geochemical data values between the samples, parted by the lag vector r. If there are no explicit directional dependencies present among the data values, then Matheron method-of-moments estimator can be used to develop unidirectional experimental semivariogram as follows:

$$ \hat{\gamma}(r)=\frac{1}{2k(r)}{\sum}_{i=1}^{k(r)}\left\{{\left[g\left({\mathbf{r}}_i\right)-g\left({\mathbf{r}}_i+r\right)\right]}^2\right\} $$

(10)

where k(r) is the number of sample pairs at lag distance r, (Deutsch and Journel 1992) after which $\hat{\gamma}(r)$ is then fitted to the model function γ_g(r). The weights w_i for ordinary kriging can be given by the (k + 1) × (k + 1) linear systems of equations as follows:

$$ {\sum}_{i,{\mathbf{r}}_i\in {\mathcal{N}}_u^k}{w}_i{\gamma}_g\left({\mathbf{r}}_i,{\mathbf{r}}_j\right)+\mu ={\gamma}_g\left({\mathbf{r}}_j,{\mathbf{r}}_u\right),\kern1em j=1,\dots, k $$

(11)

$$ {\sum}_{i,{\mathbf{r}}_i\in {\mathcal{N}}_u^k}{w}_i=1 $$

(12)

where k is the number of geochemical samples within the proximity of $\hat{g}\left({\mathbf{r}}_u\right)$; γ_g(r_i, r_j) is the semivariogram between two geochemical samples r_i and r_j; γ_g(r_j, r_u) is the semivariogram between r_j and predicted r_u; and μ is a linear external parameter called the Lagrange factor. The variance of OK prediction is given by Eq. (12), whereas the Lagrange factor compensates the uncertainty related to the mean value.

$$ {\sigma}_{\mathrm{E}}^2\hat{g}\left({\mathbf{r}}_u\right)={\sum}_{i,{\mathbf{r}}_i\in {\mathcal{N}}_u^k}{w}_i{\gamma}_g\left({\mathbf{r}}_i,{\mathbf{r}}_u\right)+\mu $$

(13)

Semivariogram estimation

In literature, there are several types of semivariogram models (Olea 2006; Varouchakis and Hristopulos 2013), but the most commonly used are Gaussian and circular, and these are also tested in this study along with exponential and spherical. The general equation for all these semivariogram models are given as follows:

$$ {\gamma}_g\left(\mathbf{r}\right)={\sigma}_g^2\ \left[1-\exp \left(-\frac{\left|\mathbf{r}\right|}{\xi}\right)\right] $$

(14)

$$ {\gamma}_g\left(\mathbf{r}\right)={\sigma}_g^2\ \left[1-\exp \left(-\frac{{\left|\mathbf{r}\right|}^2}{\xi^2}\right)\right] $$

(15)

$$ {\gamma}_g\left(\mathbf{r}\right)={\sigma}_g^2\ \left[1.5\kern0.5em \left|\mathbf{r}\right|/\xi -0.5\ {\left(\left|\mathbf{r}\right|/\xi \right)}^3\right]\ \theta \left(\xi -\left|\mathbf{r}\right|\right) $$

(16)

where

$$ \theta \left(\xi -\left|\mathbf{r}\right|\right)=\left\{\begin{array}{cc}0& \mathrm{if}\xi -\left|\mathbf{r}\right|<0;\\ {}1& \mathrm{if}\xi -\left|\mathbf{r}\right|\ge 0,\end{array}\right. $$

and

$$ {\gamma}_g\left(\mathbf{r}\right)={\sigma}_g^2\ \left\{1-\frac{2}{\pi}\mathrm{co}{\mathrm{s}}^{-1}\left(\frac{\mathbf{r}}{\xi}\right)+\frac{2r}{\pi}\sqrt{1-\frac{\mathbf{r}}{\xi^2}}\right\}. $$

(17)

in the above equations ${\sigma}_g^2$ is the variance; ∣r∣ is the Euclidean norm of the lag vector r, and ξ is the characteristics length. After the development of semivariogram models, the most appropriate one is selected by comparing the root mean square prediction error statistics between the observed and predicted geochemical values. Depending on the semivariogram model, the prediction error at location S₀ can be computed in terms of the standard deviation as follows:

$$ \overline{E}\left({\mathbf{r}}_u\right)={\sum}_{i=1}^k{w}_i\gamma \left(\left\Vert {\mathbf{r}}_i-{\mathbf{r}}_u\right\Vert \right) $$

(18)

where ‖r_i − r_u‖ is the distance among the locations r_i and r_u.

Sample size requirements for variogram computation

As per recommended in the literature, a minimum of 100– 150 data points are required to achieve a steady variogram (Voltz and Webster 1990). This requirement is fulfilled in this research, with 407 geochemical points available for each element. Because the number of sample points was more than the minimum number as recommended in literature, so anisotropy (directional trend) can also be determined if present in the data. The ArcGIS Geostatistical Analyst can compute the optimum parameters, such as Major Axis (Range), Minor Axis (Range), and Angle of Rotation (Direction) to constitute the anisotropic effect.

Potential mineral prospects

The potential mineral prospectivity was done by developing the geochemical accumulation index (GAI) using the multivariate overlay analysis to map the high, medium, and low-mineral enriched streams. Multivariate overlay analysis has been used by several research studies (Correia and Waitzberg 2003; Hou et al. 2017) to classify the regions in different classes of underlying physical phenomenon. All the predicted surfaces of both IDW and Kriging were classified into three main classes based on Jenks Natural Breaks (JNB) algorithm (Khamis et al. 2018). With JNB, classes were made for each geochemical predicted map based on features similarity and relatively significant data value differences in classes. The standardized classes were combined through linear combination by adding them together to obtain the final high, medium, and low mineralized streams.

Results and discussion

The directional distributions (standard deviational ellipse) were used to map the geographical trend of different geochemical elements, as shown in Fig. 5. The ellipses were developed using the first standard deviation (almost 63% of the data) as it is recommended by several research studies (Kent and Leitner 2007; Seidl et al. 2015) to avoid the effects of any potential spatial outlier if present in the data.

Fig. 5

Directional distribution through standard deviational ellipses of all the geochemical elements (N = 407)

In general, all the elements are distributed north to south except the gold, which showed the directional trend in northeast to southwest. For a detailed analysis, these 15 geotechnical elements were grouped in five different classes of direction and geographical concentration, as shown in Fig. 5.

The results showed that nine geochemical elements (As, Ba, Ce, Fe, Mn, Ni, Ti, V, Zr) have north to south distribution, whereas Mn and As are concentrated more towards the north and south, respectively. The main regions of As mineralization may be due to metasedimentary rocks and form post-orogenic granites in the southeast area of the study. Cohen et al. (1999) also found similar results in Wales and associated the variability of As with the geological rocks located within the area. The three elements Pb, Sb, and Zn can be grouped because of the same directional trend, i.e., northwest to southeast with Zn as a bigger ellipse as it has more variability. The Sn also has north-south concentration but the largest deviational ellipse, which means it has the highest variability and 63% of the values distributed all over the study area. Cu has the most concentrated values, i.e., smaller standard deviational ellipse and is mainly distributed north-south but at west of the study area. The gold has an altogether different distribution, which is northeast to southwest, but 63% of the data values are geographically concentrated in the lower part of the study area.

Streams delineation

Stream delineation was performed from the ASTER global digital elevation model with 30-m spatial resolution using the D8- algorithm. The flow direction raster shows that the majority of the flow in the basin was from north and northeast to southwest and west which can be due to the presence of the Irish Sea on the West of Wales. The flow accumulation raster shows the major flow lines (streams) in the area based on the directional raster. Finally, the streams were extracted using that flow accumulation raster with a threshold value of 150, as discussed in the methodology section of this paper.

Figure 6 showed that all the sample locations were correctly overlaid on the streams, which can be taken as the verification of the accuracy of extracted streams and the used threshold value. These streams were further converted into a vector data format, and a buffer of 100 m was applied to them, to be further used in the prediction models, as shown in Fig. 7.

Fig. 6

Extracted streams (solid blue lines) from the digital elevation model and overlaid on the sample locations (solid green dots)

Fig. 7

The extracted streams in the study area

Criteria for comparison

The geochemical sample points were split into two groups named as the training and the test group with 70% and 30 of the points, respectively. The criterion to split data was that the sample points located in the homogenous geological group and on the same streams were selected and separated from the training data as test data.

Out of the total 407 geochemical sample points, 285 were used to train the model, and the remaining 122 points were used to test the accuracy of the predicted surfaces. The root means square prediction error (RMSPE) statistics were used to select to assess the difference between predicted and the actual geochemical values (Robinson and Metternicht 2006). The formula for RMSPE is given as the following equation:

$$ \mathrm{RMSPE}=\kern0.5em \sqrt{\frac{1}{N}{\sum}_{i=1}^N{\left\{Z\left({x}_i\right)-\kern0.5em \hat{Z}\left({x}_i\right)\right\}}^2} $$

(19)

where $\hat{Z}\left({x}_i\right)\kern0.5em$ is the predicted geochemical value, Z(x_i) is the geochemical observed (known) value, and N is the total number of samples. Ideally, the value of RMSPE should be zero if there is no error in prediction; however, the low RMSPE suggests less error in the predicted surface and vice-versa.

Spatial interpolation and interpretation

The predicted/interpolated geochemical surfaces developed by IDW were controlled and changed by varying the two IDW parameters, i.e. the power function and the number of sample points used in the prediction. Starting with the lower power (α) as 1 to a higher power of 3 were tested, whereas the number of the nearest sample points were varied from 5 to 15 with increments of 5 at each step. The other parameters, like sector type, which is the directional search for the inclusion of several points, were kept fixed, i.e., four sectors with a 45° offset, angle 0, and auto-calculation of semi-major and minor axis.

For an initial prediction, the model was set with low power (α) as 1 and a maximum of 5 neighbor points were selected. The number of neighbor points was increased up to a maximum of 15 with the same power. The same procedure was repeated for powers 2 and 3. The results showed that a single power factor and number of neighbors could not be used for all the geochemical variables; all the three power value and a different number of neighbors produced best geochemical prediction surfaces for different elements. The lowest root mean square prediction error (RMSPE) statistics (Table 2) were used to select the most appropriate combination model parameters for the geochemical elements.

Table 2 RMSPE of all the geochemical elements against different IDW models

To discuss the effects of power and the number of neighbors Sn is taken as a case study, the prediction surfaces with all the variation of powers and neighbors are shown in Fig. 8.

Fig. 8

Prediction maps of Tin (Sn) for different power and sample points used in the IDW model

The comparison of Sn-predicted surface, as shown in Fig. 8, revealed that areas with a low (near to zero) concentration remain almost the same in all the model types, but the area of medium and high concentration varies with different models. The change is quite significant at the edges and in the middle, particularly the southern part of the map. The maps of all the predicted streams geochemical properties through the IDW models based on the lowest RMSPE are given in Fig. 9.

Fig. 9

Predicted stream surfaces of all the geochemical elements based on the lowest RMSPE of IDW model

The results of geochemical properties of stream sediments showed that Au was present in the lower streams of the study area towards the south and southwest, whereas no or very low gold concentration was found in the northern part of the study area. There were only traces of Gold present in the study area, and distinct anomalies in the area could be associated with the dominated alluvium (containing several significant placer deposits) or metasedimentary rocks (Cohen et al. 1999). As, Fe, Ti, V, and Zr had variable concentration and could be found throughout the streams present in the study area. The highest and above-average concentration of Ba was observed in the eastern and western streams to the north, respectively. The high concentrations of Cu were mainly in the middle streams towards the north of the study area, whereas average values were found in the middle. The Ce was significant in the lower streams of the study area towards the south with a little higher amount in the northwest region of the study area. Mn showed less variability and is mainly concentrated in the upper streams more towards the north. Ni and Pb were found in high concentration near the eastern streams of the study area. Sb followed the same trend of concentration as Ni and Pb but in more streams. Sn was mainly dominated in the lower streams towards the south with medium and a few high quantities in the northwest and northeast of the study area. The highest concentration of Zn was observed in the northeastern and middle streams with average values in the lower streams of the study area. For kriging, interpolation is the first and the most important thing to develop an empirical semivariogram model and then fitting that model as structural analysis in Kriging; this process is usually known as variography. The four most commonly applied theoretical semivariogram models circular, spherical, exponential, and Gaussian were tested against the streams’ sediment geochemical data. The semivariogram models were tried to fit the average of the binned data; also the directional variations were incorporated for micro-tuning of the models.

The selection of the most appropriate semivariogram model for a particular geochemical element was made based on the lowest yielded RMSPE by each model. The semivariogram of all the models, along with their RMSPE, is given in Fig. 10.

Fig. 10

Semivariogram models of all the geochemical elements along with different RMSPE

The analysis showed that out of the 15 streams’ sediment geochemical elements, only two can be better predicted with the circular semivariogram model, which is V and Ba. The spherical semivariogram model can be used for Mn, Ni, Cu, Zr, Sn, Ce, As, and Au, whereas the exponential semivariogram model is suited best for Ti, Fe, Sb, and Pb. Only one geochemical element Zn can be best predicted by the Gaussian semivariogram model. To discuss the effects of the semivariogram model on stream sediments, Sn was taken as a case study, the prediction surfaces with all the circular, spherical, exponential, and Gaussian semivariogram models are shown in Fig. 11.

Fig. 11

Prediction maps of Tin (Sn) for different semivariogram models used in kriging interpolation

The comparison of Sn predicted surface through four semivariogram models, as given in Fig. 11, showed that the spherical model is more accurate than the others as it produced more continues geochemical values in streams. The same is supported by the semivariogram model of Sn, as mentioned in the Fig.10. The circular model also showed some continuity but is not as accurate as of the spherical. This continuity might be due to the circular semivariogram model, which shows a little variation in the start and then levels off. The exponential semivariogram model of Sn suggested abrupt changes in the geochemical values, and the same is highlighted in the predicted surface. The Gaussian model showed some variability but is unable to depict appropriately because most of the geochemical sample points were not fitted through the model. The change is quite significant at the edges in the north and the middle, particularly the southern part of the map. The maps of all the predicted streams geochemical properties through the kriging model based on the lowest RMSPE of the best-fitted semivariogram model is given in Fig. 12. The trend of prediction surfaces by kriging is in line with the IDW results but significantly more realistic and continues.

Fig. 12

Predicted stream surfaces of all the geochemical elements based on the lowest RMSPE of semivariogram models using kriging

Potential mineral prospects

The multivariate overlay analysis for both IDW and kriging predicted surfaces were carried out in order to develop the geochemical accumulation index (GAI) of the study area, as shown in Fig. 13.

Fig. 13

Mineral-enriched streams extracted through geochemical accumulation index (GAI)

The higher values of GAI in a stream represent the higher chances of mineralization at the origin and surrounding regions and vice versa. The results showed that most of the mineral enriched streams were found in the northwest, northeast, and southern parts of the study area. By tracing these mineral-enriched streams, the potential mineral prospects can also be mapped accordingly and with less time and cost. The potential mineral prospects, as identified in this research area, were also confirmed with the existing mining activities in the regions, as shown in Fig. 14. This showed that the methodology adopted in this research study could successfully be applied to identify the potential mineral prospects in a region using stream sedimentation.

Fig. 14

Existing mining activities overlaid on the GAI based mineral enriched streams

Comparison of prediction models

In order to choose the best prediction surfaces, the root means square prediction error (RMSPE) of each geochemical element for both IDW and Kriging models were compared (Table 3).

Table 3 Semivariogram models of all the geochemical elements along with different RMSPE

The highest and the lowest difference between IDW and Kriging model were found among Ce and As, respectively. For Ce and As, the IDW model with power as 1 and number of nearest sample points as 5 gives the better prediction surface with the lowest RMSPE, whereas as per kriging, the spherical model generates the lowest RMSPE which is also lower than the IDW model. Overall, the kriging model yields a low RMSPE because it incorporates the spatial correlation (autocorrelation) of the sample streams’ geochemical values along with their locations. Several researchers also concluded that the kriging model is better for spatial predictions than the IDW model. For example, Shahbeik et al. (2014) applied IDW and kriging for mineral ore prediction, and it was concluded that the kriging performs much better, and the results were reliable. Similarly, another study conducted by Mueller et al. (2004) showed that kriging is more efficient in the prediction of soil fertility than IDW. Also, Goovaerts (2000) stated that Kriging yields more accurate rainfall predictions with the lowest root mean square error.

Conclusion

This study has shown a novel approach for prediction of geochemical properties of stream sediments using geostatistical interpolation models, including IDW and kriging. Instead of generating over-extended predicted surface models that most likely are outside the mineralization range from the stream samples, the new proposed geospatial characterizations were modelled strictly based on the geo-profile of each stream using digital elevation 3D models. The predicted geochemical value distribution at each stream showed an overall improved spatial characterization that can be used to accurately trace back the key minerals within each of the streams. The study showed that the two spatial prediction models used, IDW and kriging methods, should be used under a combinatory approach in order to predict the spatial distribution of geochemical elements better. Overall, spatial realizations using IDW with a low power function tended to produce more accurate results probably due to the relatively high variability among the geochemical sample data (Robinson and Metternicht 2006) (Kravchenko and Bullock 1999). The kriging method also showed accurate results as well, specifically when using the spherical semivariogram model and then exponential models. The mineral prospectivity map based on the geochemical accumulation index (GAI) showed that most of the mineral-enriched streams were located in the northwest, northeast, and southern parts of Central Wales; the same was also confirmed with the existing mining activities in the region.

The statistics ‘root mean square prediction error’ (RMSPE) was used as the primary indicator to assess the estimation accuracy of both methods. The resulting models with the lower RMSPE values were considered for further analysis. One of the critical conclusions resulting from this study is that IDW and kriging results should not be considered independently; instead, a combinatory model should be produced in the prediction of the geochemical elements for stream sediments. Further research should investigate if other geo-environmental factors such as proximity to the sea, structural geology, geophysical conditions, and terrain slope angle can be incorporated into the characterization model.