Thermal analysis of the flow of the Maxwell nanofluid through the cone and disk system space with dual diffusion and multiple rotations

Abstract

Among various non-Newtonian models, the current study considers Maxwell fluid flow between cone and disk devices in conjunction with dual diffusion. In this scenario, the combination of Fourier’s and Fick’s law assumptions, including the Cattaneo–Christov heat and mass flux terminologies, is used for describing heat and mass transfer, respectively. The flow is analyzed in four different cases including: (i) rotation of the disk and cone in the reverse direction, (ii) rotation of both cone and disk in one direction, (iii) rotation of the cone and stationary status of the disk, and (iv) rotating disk with the stationary cone. The primary governing model consists of partial differential equations, which are tackled through the control volume finite element method (CVFEM). This system is reduced into a set of nonlinear ordinary differential equations with the help of similarity variables, which is solved using the Runge–Kutta fourth-order (RK-4) technique. In order to understand heat transfer and mass diffusion, the performance of the physical parameters is analyzed for the potential applications of heat exchange devices. It is observed that the increasing Maxwell parameter has inauspicious effects on fluid motion and thermal state. The radial component of velocity is noted to dwindle with higher magnetic parameter. Meanwhile, the case of a swirling disk and a still cone improves the transverse velocity. Despite that, the thermal boundary layer is observed to be an increasing function of thermophoretic and Brownian motion parameters. Moreover, higher thermal relaxation time and Prandtl number fasten the convection process. Furthermore, the thermophoretic parameter, concentration relaxation parameter, and Schmidt number have apparently favorable effects on relative mass diffusion regions compared to the Brownian parameter.

Introduction

In nature, most of the fluids are non-Newtonian and they have numerous applications in the field of science and engineering. The printing materials, drag-decreasing agents, food atoms, polymer products, and biofluids are examples of non-Newtonian fluids. In the literature, most of the researchers are using simple energy equations having linear structures and are not compatible with non-Newtonian fluids having a parabolic nature. The phenomenon is described by the researchers in terms of the diffusion of thermal and concentration gradients to describe the natural behavior of the non-Newtonian fluids. Aifantis [1] first introduced the double-diffusive model in 1976. The phenomenon is characterized as the diffusion of thermal and concentration gradients that cause fluid motion. When the temperature difference is retained, thermal diffusion in amalgam gives rise to the concentration gradient. Similarly, the phenomenon of double-diffusive convection is widely used in engineering, manufacturing, and the biotech industry. The phenomenon is of specific interest to researchers due to its utility in biomedicine. Hence, many researchers have studied the concept of double diffusion with low Reynolds numbers. Ganesan et al. [2] also observed the phenomenon for non-Newtonian fluids. Raju et al. [3] have taken thermophoresis, inclined Brownian motion, and magnetic flux together to analyze the impact of double diffusion. The double-diffusive convective flow under peristalsis has numerous applications in biomedicine. Mabood et al. [4] have used the double diffusion idea considering Maxwell fluid flow over a rotating disk. Similarly, some other relevant studies of the likewise subject can be seen in the articles [5,6,7,8,9,10,11] and references within. Fourier’s law yields a parabolic energy equation and is naturally very appropriate for non-Newtonian fluids. In non-Newtonian fluids, the deformation rate and shear stress exhibit parabolic structure. Therefore, the non-Newtonian fluid flow in combination with dual diffusion including Fourier's and Fick's law is naturally very appropriate. The combination of a cone and a disk system has many potential applications in various technical and industrial areas, for instance, conical diffusers for fluid distribution in the desired direction, a viscometer used for viscosity measure, medical devices, and many more. In the field of medical and commercial sciences, cone–disk devices have multiple kinds of functions including outcomes of fluid viscosity with the help of a viscometer have been discussed by Mooney et al. [12]. Phan-Thien [13] later discussed the non-Newtonian behavior and instability of an Oldroyd-B fluid within a cone–plate geometry. Viscometry [14] has studied the calculation of viscosity for various fluids. Through thermal analysis, the flow of fluid passes from a rotating cone and disk has been discussed by Wang [15]. Pressing air for gas turbines within the cooling system in a conical diffuser has been discussed by [16]. In biomedical research, the joint form of the cone disk devices is used on a large scale. Turkyilmazoglu [17] used the cone disk system to analyze the heat transfer and summarized the importance of the large gap angle in the case of the heat transfer rate. A theoretical study of Buongiorno nanofluid flow between a cone–disk system has been discussed by Basavarajappa and Bhatta [18]. Gul et al. [19] have discussed the combined investigations of heat and mass transfer analysis in the system of rotation through cone and disk devices. The solidity analysis of the edge layer of Casson nanofluid, due to the rotating cone attached to the complete attitude of instability, has been discussed by Moatimid et al. [20]. Recently, the heat transfer rate enhancement, heat mass transfer investigation, nanofluids, and stability analysis for the flows confined to the canonical gap of the cone–disk system have remained in the limelight among many researchers. Shevchuk [21] explained how the angle between the cone and disk of the framework affects fluid motion, thermal transport, and mass transfer. A particular consideration was given to solar radiation-related heat transport through the preceding geometry by Srilatha et al. [22], allowing both cone disks to be stationary or rotating at varying angular speeds. Turkyilmazoglu [23] elaborated on the flow and thermal transfer rates through a fluid flowing within the gap of a swirling cone and stretchable disk. Some of other recent studies regarding the subject can be found in the citations [24,25,26,27,28] and references within. All these authors have elaborated on various fluid flows, other than Maxwell fluid, under the possible situations of cone–disk apparatus. Maxwell fluids are suitable for polymer applications due to their low complexity; however, when the Maxwell fluid is combined with MHD influences, its thermal, mechanical, and electrical properties can be enhanced, opening up various potential applications, including commercial heat exchange devices, nuclear power plants, hydroelectric power plants, and more [29]. Further advancement in nanoscience introduced Maxwell nanofluid, which is a suspension of a nanostructure in viscoelastic non-Newtonian fluid. Based on their tendencies to significantly enhance heat transfer efficiency, increase thermal conductivity, improve lubrication properties, and provide other functional characteristics, Maxwell nanofluid has gained a lot of appreciation in the fields of thermal engineering, microelectronics, nanofluidics, biomedicines, fiber technology, and many more.

In view of the above discussion and literature study, it is clear from the above discussion that the aspect of double diffusion in the Maxwell nanofluid flow between disk and cone devices has not been studied till now. Henceforth, the current analysis’s goal is to examine the impact of the model parameters for the Maxwell nanofluid model taking into consideration the double diffusion on flow. To understand the heat and mass transfer phenomena, the combination of Fourier's and Fick's law assumptions include the Cattaneo–Christov heat and mass flux terminologies, respectively [30, 31]. Mathematically, the differential equations are first time modeled for the present analysis. Here, the major change in Fourier's law is that it turns the energy equation into the parabolic form, which shows that the entire medium is instantaneously caused by the initial disruption [30, 31]. Moreover, in non-Newtonian fluids, since the deformation rate and shear stress exhibit parabolic structure, therefore, the combination of Fourier’s and Fick’s laws is very suitable due to their parabolic structure. Furthermore, the solution to the problem is obtained through the control volume finite element method (CVFEM) [26,27,28,29,30,31,32] and Runge–Kutta fourth-order method (RK-4) [33,34,35,36,37] techniques, and the results are validated. By using CVFEM, the governing partial differential equations are solved. Using similarity variables, this system is reduced into a set of nonlinear ordinary differential equations, which are solved using RK-4. All the obtained results are validated and evaluated in graphs and tables. The study's objectives are as follows:

• The Maxwell fluid flow is considered in three-dimensional space in the disk and cone system including the magnetic field. The MHD effect on the Maxwell fluid flow for the cone disk system is the objective of this study.

• Conduction of heat through Fourier's Law and diffusion of mass through Fick's Law are used effectively to understand the heat and mass transfer phenomena and are not considered for the cone and disk systems before.

• Tangential and radial stress calculation, including torque in the case of the Maxwell nanofluid, of the system, is not available in the literature.

• The two approaches of RK-4 and CVFEM are also the objective of this study.

Flow description

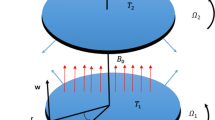
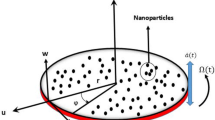
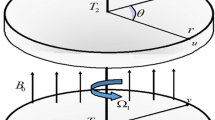
This work determines to investigate Maxwell (non-Newtonian) nanofluid flow in a conical gap between cone and disk devices that are at an angle “$\gamma$”. Cylindrical coordinates $(r,\theta ,z)$ are used to formulate our problem, where “r” represents the horizontal radial direction, “$\theta$” shows the azimuthal axis, and “$z$” is taken as the axial axis perpendicular to the disk. Both devices (i.e. cone and disk) are stationary or allowed to rotate in either the same or reverse directions. Generally, the symbols $`\Omega \text{'}$ and $`\omega \text{'}$ are used to distinguish between the angular velocity of the cone and disk, respectively. Furthermore, along the z-direction, a magnetic field $`B_{0} \text{'}$ with equal strength is used. Illustratively, the flow of Maxwell nanofluid between cone–disk apparatus is shown in Fig. 1a and b.

Fig. 1

(a) Geometry of the problem (b) Grid representation of the problem

The constitutive relation governing the Maxwell nanofluid is given as [29]:

$$\left( {1 + \lambda_{1} \frac{D}{Dt}} \right)S = \mu \left( {1 + \lambda_{2} \frac{D}{Dt}} \right)A_{1} ,$$

(1)

where $`\lambda_{1} \text{'}$, $`\lambda_{2} \text{'}$, $`\mu \text{'}$, $`S\text{'}$, and $`A_{1} \text{'}$ represent the relaxation time, retardation time, dynamic viscosity, additional stress tensor, and Rivlin–Ericksen tensor of order one, respectively, while $\frac{D}{Dt} \equiv \frac{\partial }{\partial t} + V \cdot\nabla$ characterizes the substantial/material derivative. Note that Eq. (1) represents the Newtonian fluid behavior if $\lambda_{1} = \lambda_{2}$ = 0. The expressions that represent the generalized form of Fourier’s and Fick’s laws, in the structure of the well-known Cattaneo–Christov model, follow so [28,29,30,31]:

$$q + \varepsilon_{0} \left( {\frac{\partial q}{{\partial t}} + V \cdot \nabla q + (\nabla \cdot V)q - q \cdot \nabla V} \right) = - k\nabla T,$$

(2)

$$J + \varepsilon_{1} \left( {\frac{\partial J}{{\partial t}} + V \cdot \nabla J + (\nabla \cdot V)J - J \cdot \nabla V} \right) = - D_{{\text{B}}} \nabla C,$$

(3)

where q and J represent heat flux, mass flux, $\varepsilon_{0} ,\varepsilon_{1}$ represents thermal time, and mass relaxation time, and D_B and k represent the Brownian diffusion coefficient and thermal conductivity. If $\varepsilon_{0} = \varepsilon_{1} = 0$, then we obtain the classical Fick’s and Fourier’s laws from Cattaneo–Christov's theory. The above equations are converted to the following equations for the incompressible and steady flow of fluid.

$$q + \varepsilon_{0} (V\cdot (\nabla q) - q\cdot (\nabla V)) = - k\nabla T,$$

(4)

$${\mathbf{J}} + \varepsilon_{1} (V\cdot (\nabla {\mathbf{J}}) - {\mathbf{J}}\cdot (\nabla V)) = - D_{\text{B}} \nabla C,$$

(5)

The governing nonlinear equations are [30,31,32]

$$\frac{\partial u}{{\partial r}} + \frac{\partial w}{{\partial z}} + \frac{u}{r} = 0,$$

(6)

$$\begin{aligned}& u\frac{\partial u}{{\partial r}} - \frac{1}{r}v^{2} + w\frac{\partial u}{{\partial z}} = v_{\text{f}} \frac{{\partial^{2} u}}{{\partial z^{2} }} - \frac{{\sigma_{\mathrm f} }}{{\rho_{\text f} }}B_{0}^{2} \left( {u + \lambda_{1} w\frac{\partial u}{{\partial z}}} \right) - \hfill \\ &\lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial r^{2} }} + w^{2} \frac{{\partial^{2} u}}{{\partial z^{2} }} + 2uw\frac{{\partial^{2} u}}{\partial r\partial z} - \frac{2}{r}uv\frac{\partial v}{{\partial r}} - \frac{2}{r}vw\frac{\partial v}{{\partial z}} + \frac{1}{{r^{2} }}uv^{2} + \frac{1}{r}v^{2} \frac{\partial u}{{\partial r}}} \right), \, \hfill \\ \end{aligned}$$

(7)

$$\begin{aligned}& u\frac{\partial u}{{\partial r}} - \frac{1}{r}uv + w\frac{\partial v}{{\partial z}} = v_{f} \frac{{\partial^{2} v}}{{\partial z^{2} }} - \frac{{\sigma_{f} }}{{\rho_{f} }}B_{0}^{2} \left( {u + \lambda_{1} w\frac{\partial u}{{\partial z}}} \right) \hfill \\ & \quad - \lambda_{1} \left( {u^{2} \frac{{\partial^{2} u}}{{\partial r^{2} }} + w^{2} \frac{{\partial^{2} v}}{{\partial z^{2} }} + 2uw\frac{{\partial^{2} v}}{\partial r\partial z} + \frac{2}{r}uv\frac{\partial u}{{\partial r}} + \frac{2}{r}vw\frac{\partial u}{{\partial z}} - \frac{2}{{r^{2} }}u^{2} v - \frac{1}{{r^{2} }}v^{3} + \frac{1}{r}v^{2} \frac{\partial v}{{\partial r}}} \right), \, \hfill \\ \end{aligned}$$

(8)

$$\begin{aligned} &u\frac{\partial T}{{\partial r}} + w\frac{\partial T}{{\partial z}} = \alpha_{\text{f}} \frac{{\partial^{2} T}}{{\partial z^{2} }} + 2\varepsilon_{0} \tau \frac{{D_\text{T} }}{{T_{\infty } }}\left( {u\frac{\partial T}{{\partial z}}\frac{{\partial^{2} T}}{\partial r\partial z} + w\frac{\partial T}{{\partial z}}\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) + \tau \left( {D_{\text B} \left( {\frac{\partial C}{{\partial z}}\frac{\partial T}{{\partial z}}} \right) + \frac{{D_\text{T} }}{{T_{\infty } }}\left( {\frac{\partial T}{{\partial z}}} \right)^{2} } \right) \hfill \\&\quad + \varepsilon_{0} \tau D_{\text B} \left( {u\frac{{\partial^{2} C}}{\partial r\partial z}\frac{\partial T}{{\partial z}} + u\frac{\partial C}{{\partial z}}\frac{{\partial^{2} T}}{\partial r\partial z} + w\frac{{\partial^{2} C}}{{\partial z^{2} }}\frac{\partial T}{{\partial z}} + w\frac{\partial C}{{\partial z}}\frac{{\partial^{2} T}}{{\partial z^{2} }}} \right) \hfill \\&\quad - \varepsilon_{0} \left( {u^{2} \frac{{\partial^{2} T}}{{\partial r^{2} }} + 2uw\frac{{\partial^{2} T}}{\partial r\partial z} + w^{2} \frac{{\partial^{2} T}}{{\partial z^{2} }} + u\frac{\partial w}{{\partial r}}\frac{\partial T}{{\partial z}} + u\frac{\partial u}{{\partial r}}\frac{\partial T}{{\partial r}} + w\frac{\partial u}{{\partial z}}\frac{\partial T}{{\partial r}} + w\frac{\partial w}{{\partial z}}\frac{\partial T}{{\partial z}}} \right), \, \hfill \\ \end{aligned}$$

(9)

$$\begin{aligned} & u\frac{\partial C}{{\partial r}} + w\frac{\partial C}{{\partial z}} = D_{\text{B}} \frac{{\partial^{2} C}}{{\partial z^{2} }} + \varepsilon_{1} \frac{{D_\text{T} }}{{T_{\infty } }}\left( {u\frac{{\partial^{3} T}}{{\partial r\partial z^{2} }} + w\frac{{\partial^{3} T}}{{\partial z^{3} }}} \right) + \frac{{D_{{\text{T}}} }}{{T_{\infty } }}\frac{{\partial^{2} T}}{{\partial z^{2} }} \hfill \\&\quad - \varepsilon_{1} \frac{{D_\text{T} }}{{T_{\infty } }}\left( {u^{2} \frac{{\partial^{2} C}}{{\partial r^{2} }} + 2uw\frac{{\partial^{2} C}}{\partial r\partial z} + w^{2} \frac{{\partial^{2} C}}{{\partial z^{2} }} + u\frac{\partial w}{{\partial r}}\frac{\partial C}{{\partial z}} + u\frac{\partial u}{{\partial r}}\frac{\partial C}{{\partial r}} + w\frac{\partial u}{{\partial z}}\frac{\partial C}{{\partial r}} + w\frac{\partial w}{{\partial z}}\frac{\partial C}{{\partial z}}} \right). \hfill \\ \end{aligned}$$

(10)

In accordance with the Cattaneo–Christov theory of heat and mass diffusion [30, 31], Eqs. (6)–(10) are subject to the following boundary conditions.

$$\begin{aligned}& \begin{array}{*{20}c} {u = 0,} &{v = \omega r,} &{w = 0,} &{\begin{array}{*{20}c} {T = T_{{\text{w}}},} &{C = C_{{\text{w}}} ,} & {({\text{at }}z = 0)} \\ \end{array} } \\ \end{array} \hfill \\ &\begin{array}{*{20}c} {u = 0,} &{v = \Omega z,} & {w = 0,} &{\begin{array}{*{20}c} {T = T_{\infty },\,} & {C = C_{\infty } ,} & {{\text{(at }}\,z = r\tan \gamma )} \\ \end{array} } \\ \end{array} \hfill \\ \end{aligned}$$

(11)

where the subscripts $`\infty \text{'}$, $`w\text{'}$, and $`f\text{'}$ are written for corresponding superficial conditions, ambient constraints, and Maxwell nanofluid, while $`\gamma \text{'}$ represents the angle between cone and disk. Here, $u,v,w$ are the velocity components in the $r,\theta ,z$ directions. Similarly, $\nu , \, \lambda_{1} ,\rho , \, k,{\text{ C}}_{\text{p}} , \, \sigma , \, \lambda_{2} , \, T$, and C are the kinematic viscosity, the relaxation time, the density of the fluid, the thermal conductivity, the specific heat, the electrical conductivity, the retardation time, the temperature, and the fluid concentration, respectively. Besides, $`\upsilon = {\mu \mathord{\left/ {\vphantom {\mu \rho }} \right. \kern-0pt} \rho }\text{'}$, $`\alpha = {k \mathord{\left/ {\vphantom {k {\left( {\rho c_{\text{p}} } \right)}}} \right. \kern-0pt} {\left( {\rho c_{\text{p}} } \right)}}\text{'}$, and $`D_{\text{B}} \text{'}$ manifest momentum diffusivity, thermal diffusivity, and mass diffusivity, relatively. The transformation used in the given model is as follows [20].

$$\begin{aligned}& u = \frac{{\upsilon_{{\text{f}}} f(\eta )}}{r} = {\text{U}}_{{\text{w}}} f(\eta ){,}\,\,v = \frac{{\upsilon_{{\text{f}}} g(\eta )}}{r} = {\text{U}}_{{\text{w}}} g(\eta ),\,\,w = \frac{{\upsilon_{{\text{f}}} h(\eta )}}{r} = {\text{U}}_{{\text{w}}} h(\eta ), \hfill \\ & {\text{p}}(\eta {) = }\frac{{\rho \upsilon_{{\text{f}}}^{2} P}}{{r^{2} }} = {\text{U}}_{{\text{w}}}^{2} \rho P,\,\,\eta = \frac{z}{r},\,\,\Theta = \frac{{T - T_{\infty } }}{{T_{{\text{w}}} - T_{\infty } }},\,\,\phi = \frac{{C - C_{\infty } }}{{C_{{\text{w}}} - C_{\infty } }}. \hfill \\ \end{aligned}$$

(12)

where ‘$U_{w}$’ is used for respective surface velocity. Transformed equations are:

$$h^{\prime} - \eta f^{\prime} = 0,$$

(13)

$$\begin{aligned} &(1 + \eta^{2} )f^{\prime\prime} + 3\eta f^{\prime} + \left( {\eta ff^{\prime} - f^{\prime}{\text{ h}} + f^{2} + g^{2} } \right) - Mf + M\lambda f^{\prime}{\text{ h }} -\lambda (2f^{3} + 4\eta f^{\prime} \, f^{2} + \eta^{2} f^{2} f^{\prime\prime} + h^{2} f^{\prime\prime} \hfill \\ &- g^{2} f - \eta g^{2} f^{\prime} - 4ff^{\prime}{\text{ h}} - 2\eta ff^{\prime\prime}{h + 2fg}^{2} + 2\eta fgg^{\prime} - 2gg^{\prime}h + fg^{2} ) = 0, \hfill \\ \end{aligned}$$

(14)

$$\begin{aligned}& (1 + \eta )g^{\prime\prime} + 3\eta g^{\prime} - \left( {\eta fg^{\prime} + g^{\prime}h + 2fg - Mg + M\lambda g^{\prime}h} \right) - \lambda (4\eta f^{2} g^{\prime} + \eta^{2} f^{2} g^{\prime\prime} \hfill \\ &- 4gg^{\prime}h - 2\eta gg^{\prime\prime}h + g^{2} g^{\prime\prime} - 2f^{2} g + 2\eta fgf^{\prime} - \eta g^{2} g^{\prime}) = 0, \hfill \\ \hfill \\ \end{aligned}$$

(15)

$$\begin{aligned}& (1 + \eta^{2} )h^{\prime\prime} + 3\eta fh^{\prime} + \eta fh^{\prime} - hh^{\prime} + h + fh{ - }\lambda (2f^{2} h + \eta^{2} \, f^{2} h + \eta^{2} f^{2} h^{\prime\prime} - h^{2} h^{\prime\prime} \hfill \\& - 4fhh^{\prime} - 2\eta fhh^{\prime\prime} - g^{2} h - \eta g^{2} h) = 0, \hfill \\ \end{aligned}$$

(16)

$$\begin{aligned} &(1 + \eta^{2} )\Theta^{\prime\prime} + \eta \Theta^{\prime}\, - \Pr \left( {h\Theta^{\prime} - \eta f\Theta^{\prime}} \right) + \Pr N_{\text b} \left( {\eta^{2} + 1} \right)\Theta^{\prime}\Phi^{\prime} + N_\text{t} \Pr \left( {1 + \eta^{2} } \right)\Theta^{{\prime}{2}} \hfill \\& - \Pr \varepsilon_\text{t} (2\eta f^{2} \Theta^{\prime} + hh^{\prime}\Theta^{\prime} - \eta hf^{\prime}\Theta^{\prime} + 2fh\Theta^{\prime} + 2\eta fh\theta^{\prime\prime} + \eta^{2} f^{2} \Theta^{\prime\prime} + h^{2} \Theta^{\prime\prime}) = 0, \hfill \\ \end{aligned}$$

(17)

$$\begin{aligned}& (1 + \eta^{2} )\phi^{\prime\prime} + \eta \,\phi^{\prime} - Sc\left( {h\phi^{\prime} - \eta f\phi^{\prime}} \right) + \frac{{N_{\text b} }}{{N_\text{t} }}\left( {(\eta^{2} + 1)\phi^{\prime\prime} + \eta \phi^{\prime}} \right) \hfill \\& - \varepsilon_\text{c} Sc(2\eta f^{2} \phi^{\prime} + hh^{\prime}\phi^{\prime} - \eta fh\phi^{\prime} + 2fh\phi^{\prime} + 2\eta fh\phi^{\prime\prime} + \eta^{2} f^{2} \phi^{\prime\prime} - h^{2} \phi^{2} ) = 0, \hfill \\ \end{aligned}$$

(18)

whereas the transformed boundary conditions are:

$$\begin{aligned} &f(0) = 0,h(0) = 0,\,\,g(0) = {\text{Re}}_{\upomega } ,\Theta (0) = 1,\phi (0) = 1, \hfill \\& f(\eta_{0} ) = 0,h(\eta_{0} ) = 0,g(\eta_{0} ) = {\text{Re}}_{\Omega } ,\Theta (\eta_{0} ) = 0,\phi (\eta_{0} ) = 0. \hfill \\ \end{aligned}$$

(19)

Meanwhile, in Eqs. (13)–(18) the symbols $\lambda ,M,{\text{ Nt}},{\text{ Nb}}, \text{Sc},{\text{ Pr}},\varepsilon_\text{t}$ and $\varepsilon_\text{c}$ are the dimensionless parameters that symbolize the Maxwell nanofluid parameter, magnetic parameter, thermophoretic parameter, Brownian motion parameter, Schmidt number, Prandtl number, thermal relaxation time, and concentration relaxation time, respectively, while $`{\text{Re}}_{\upomega } \text{'}$ and $`{\text{Re}}_{\Omega } \text{'}$ are the local Reynolds numbers at the surface of the disk and cone, accordingly. These obtained non-dimensional quantities are defined as:

$$\left\{ \begin{aligned}& \lambda = \frac{{\lambda_{1} U_{{\text{w}}}^{2} }}{{\upsilon_{f} }},M = \frac{{\upsilon_{{\text{f}}} \sigma_{{\text{f}}} B_{0}^{2} }}{{\rho_{{\text{f}}} U_{{\text{w}}}^{2} }},{\text{ Nt}} = \frac{{\tau D_{{\text{T}}} }}{{\upsilon_{{\text{f}}} T_{\infty } }}(T_{{\text{w}}} - T_{\infty } ),{\text{ Nb}} = \frac{{\tau D_{{\text{B}}} }}{{\upsilon_{{\text{f}}} }}(C_{{\text{w}}} - C_{\infty } ), \hfill \\& \text{Sc} = \frac{{\upsilon_{{\text{f}}} }}{{D_{{\text{B}}} }},{\text{ Pr}} = \frac{{\mu_{{\text{f}}} (c_\text{p} )_{{\text{f}}} }}{{k_{{\text{f}}} }},\varepsilon_{{\text{t}}} = \frac{{\varepsilon_{0} U_{{\text{w}}}^{2} }}{{\upsilon_{{\text{f}}} }},\varepsilon_\text{c} = \frac{{\varepsilon_{1} U_{{\text{w}}}^{2} }}{{\upsilon_{{\text{f}}} }},{\text{Re}}_{\upomega } = \frac{{r^{2} \omega }}{{\upsilon_{{\text{f}}} }}, \, {\text{Re}}_{\Omega } = \frac{{r^{2} \Omega }}{{\upsilon_{{\text{f}}} }}. \hfill \\ \end{aligned} \right.$$

(20)

Physical quantities of interest

In the view of the obtained self-similar system, the physical quantities of prime interest at the surface of both cone and disk are the radial skin friction coefficient $(C_{{\text{f}}} )$, tangential skin friction coefficient $(C_{{\text{g}}} )$, Nusselt number (${\text{Nu}}$), and Sherwood number $({\text{Sh}})$, respectively. Mathematically, as elaborated in references [17,18,19], the-said substantial parameters are given as:

$$\left\{ \begin{aligned}& C_{{\text{f}}} = \frac{{\tau_{r} }}{{\rho_{{\text{f}}} U_{{\text{w}}}^{2} }}, \, \;\;{\text{ where }}\;\; \, \tau_{{\text{r}}} = \left[ {\mu_{{\text{f}}} \left( {\frac{\partial u}{{\partial z}} + \frac{\partial w}{{\partial r}}} \right)} \right]_{z = 0, \, r\tan \lambda } \hfill \\& C_{{\text{g}}} = \frac{{\tau_{\theta } }}{{\rho_{{\text{f}}} U_{{\text{w}}}^{2} }}, \, \;\;{\text{where }}\;\; \, \tau_{\theta } = \left[ {\mu_{{\text{f}}} \left( {\frac{\partial v}{{\partial z}} + \frac{1}{r}\frac{\partial w}{{\partial \theta }}} \right)} \right]_{z = 0, \, r\tan \lambda } \hfill \\ \end{aligned} \right.$$

(21)

$$\left\{ \begin{aligned}& {\text{Nu}} = \frac{{rq_{{\text{w}}} }}{{k_{{\text{f}}} (T_{{\text{w}}} - T_{\infty } )}},\;\;{\text{ where }}\;\;{\text{ q}}_{{\text{w}}} = - k_{{\text{f}}} \left( {\frac{\partial T}{{\partial z}}} \right)_{z = 0, \, r\tan \gamma } \hfill \\ &{\text{Sh}} = \frac{{rJ_{{\text{w}}} }}{{D_{{\text{B}}} (T_{{\text{w}}} - T_{\infty } )}}, \, \;\;{\text{ where }}\;\;{\text{ J}}_{{\text{w}}} = - D_{{\text{B}}} \left( {\frac{\partial C}{{\partial z}}} \right)_{z = 0, \, r\tan \gamma } \hfill \\ \end{aligned} \right.$$

(22)

Here in (20), $`\tau_{{\text{r}}} \text{'}$ and $`\tau_{\theta } \text{'}$ are the shear stresses in radial and tangential directions, accordingly. Likewise, in Eq. (21), $`q_{{\text{w}}} \text{'}\, \;{\text{and}}\; \, `J_{{\text{w}}} \text{'}$ symbolizes the heat and mass transfer rates, providing a measure of how much heat and mass sources are transported along the surfaces, correspondingly. With the use of Eq. (12), Eqs. (20) and (21) become:

$$\left\{ \begin{aligned}& {\text{Re}}^{2}_{{\upomega }} \cdot C_{{{\text{fd}}}} = f^{\prime}(0),\quad {\text{Re}}^{2}_{\Omega } \cdot C_{{{\text{fc}}}} = f^{\prime}(\eta_{0} ), \hfill \\& {\text{Re}}^{2}_{{\upomega }} \cdot C_{{{\text{gd}}}} = g^{\prime}(0),\quad {\text{Re}}^{2}_{\Omega } \cdot C_{{{\text{gc}}}} = g^{\prime}(\eta_{0} ), \hfill \\ &{\text{Nu}}_{{\text{d}}} = - \Theta^{\prime}(0),\quad \quad \;{\text{Nu}}_{{\text{c}}} = - \Theta^{\prime}(\eta_{0} ), \hfill \\ &{\text{Sh}}_{{\text{d}}} = - \phi^{\prime}(0),\quad \quad \;\;{\text{Sh}}_{{\text{c}}} = - \phi^{\prime}(\eta_{0} ), \hfill \\ \end{aligned} \right.$$

(23)

where ‘d’ and ‘c’ stand for disk and cone, respectively.

Solution methodologies

The governing model of the proposed flow problem includes either a set of partial differential equations (PDEs) or substantial boundary conditions, Eqs. (6)–(11), or a similarity system of ordinary differential equations (ODEs), Eqs. (13)–(19). To numerically tackle the supervising models, two solution methodologies are adopted, i.e., the control volume finite element method (CVFEM) for PDEs and the Runge–Kutta fourth-order method (RK-4) for ODEs.

Control volume finite element method (CVFEM)

The highly nonlinear PDE solutions are not possible through commonly used numerical techniques. High-performance machines and advanced techniques are required to solve such models. Therefore, the governing system of PDEs in Eqs. (6)–(11) is solved with the recently established control volume finite element method (CVFEM). CVFEM is a powerful mathematical technique widely used in computational fluid dynamics (CFD) and heat transfer simulations to provide higher-order accurate and robust solutions to complex multi-phase flows, involving irregular geometries, strong gradients, complicated patterns, and irregular layouts [38]. CVFEM offers several advantages over traditional schemes, like finite difference method (FDM), finite volume method (FVM), and finite element method (FEM). It provides flexibility in handling complex geometries and an accurate representation of the solution within each control volume (CV). One of the key characteristics of CVFEM is that it preserves the local conservation properties of the underlying partial differential equations (PDEs) and can be directly applied to them. Thus, many researchers have employed CVFEM to get efficient solutions to nonlinear differential systems, such as [32, 39,40,41,42] and references within the manuscripts. The CVFEM approach is used through the new FEATool Multiphysics Software. The standard Navier–Stokes equations already exist in this software just editing is required to set the Navier–Stokes equations according to the model problem. Also, the physical conditions of editing exist in the software.

Runge–Kutta fourth-order method

The system of the nonlinear PDEs is converted into a set of nonlinear ODEs to solve through common numerical methods. The Runge–Kutta fourth-order method (RK-4) is one of the widely used methods for the solution of nonlinear ODEs. Also, this scheme is affordable for the common machine. The system of ODEs in Eqs. (13)–(19) is transformed into the first-order ODEs. The Runge–Kutta fourth-order method (RK-4) is one of the most widely used and well-known methods for numerically integrating ODEs [43]. It strikes a good balance between accuracy, stability, and simplicity, making it a reliable and popular choice for solving ODEs in various scientific and engineering applications [33,34,35,36,37].

Results and discussion

This section is assigned to the significant impressions of sundry dimensionless parameters on non-dimensional velocity components (radial ‘$f(\eta )$’ and transverse ‘$g(\eta )$’), temperature field ‘$\theta (\eta )$’ and concentration profile ‘$\phi (\eta )$’. These outcomes are illustrated graphically in Figs. 2–7, accordingly. First and foremost, Table 1 is generated to validate the implemented numerical schemes. It shows the comparison of the present results with previously published results of Turkyilmazoglu [17], Basavarajappa and Bhatta [18] considering common parameters. From the obtained results, we see that our results are in great agreement with those available results. Thus, we can conclude that our model is valid for the present investigation.

Fig. 2

a Impact of ‘M’ and ‘$\lambda$’ on ‘$f\left( \eta \right)$’. b Impact of ‘M’ and ‘${\text{Re}}_{\upomega } ,{\text{Re}}_{\Omega }$’ on ‘$g\left( \eta \right)$’

Fig. 3

a–d Impact of ‘M’ and ‘$\lambda$’ on ‘$g(\eta )$’ for specific values of ‘${\text{Re}}_{\upomega } {\text{,Re}}_{{\Omega }}$’

Fig. 4

a, b Impacts of ‘$\varepsilon_{{\text{t}}} ,\Pr$’ and ‘${\text{Nb}},{\text{Nt}}$’ on the temperature field $\Theta (\eta )$

Fig. 5

a, b Impacts of ‘${\text{Nb}},{\text{Nt}}$’ and ‘${\text{Sc}},\varepsilon_{{\text{c}}}$’ on concentration field $\phi (\eta )$

Fig. 6

a, b The contour figures for the fluid flow between the gap of the cone and disk system

Fig. 7

a, b The streamlines for the fluid flow between the gap of the cone and disk system

Table 1 Four models comparison with the existing literature considering common parameters ${\text{M}} = \lambda = \varepsilon_\text{t} = 0.0$, ${\text{Pr}} = 0.7$, and ${\text{Re}}_{\upomega } = {\text{Re}}_{\Omega } = 10$

Figure 2a demonstrates the decreasing behaviors of ‘$f(\eta )$’ against increasing estimations for ‘$M$’ and ‘$\lambda$’, represented by dashed and solid lines, respectively. A higher magnetic field parameter retards fluid motion. This is because the Lorentz force generated by the magnetic field opposes fluids’ motion. Thus, increments in the value of ‘$M$’ cause a reduction in the radial component of the velocity, as can be seen in the graph. However, it should be noted that near the disk and cone, ‘$M$’ is not much influential in comparison with the influences in the canonical gap between them. Besides, Fig. 2a also illustrates the adverse consequences associated with the radial velocity that is caused by rising values of the Maxwell parameter ‘$\lambda$’. In contrast to ‘$M$’, the downward patterns in ‘$f(\eta )$’ due to ‘$\lambda$’ are more significant and visible. On the other hand, Fig. 2b shows the fluctuations that occur in $`g\left( \eta \right)\text{'}$ as a result of $`M\text{'}$ (dashed lines), and $`{\text{Re}}_{\upomega } ,{\text{Re}}_{\Omega } \text{'}$ (solid lines), considering four cases $`{\text{Re}}_{\upomega } = 0,{\text{Re}}_{\Omega } = 1\text{'}$, $`{\text{Re}}_{\upomega } = 1,{\text{Re}}_{\Omega } = 0\text{'}$, $`{\text{Re}}_{\upomega } = 1,{\text{Re}}_{\Omega } = - 1\text{'}$, and $`{\text{Re}}_{\upomega } = - 1,{\text{Re}}_{\Omega } = 1\text{'}$. It is worth noting that the Reynolds numbers ‘$\text{Re}_{\upomega }, \text{Re}_{{\Omega }}$’ stand for the disk and cone devices' rotation whose values are selected depending on the flow model and the fluidic media under consideration. Here, their values are specifically held as either $`0\text{'}$ (a stationary case) or $`1\text{'}$ (a spinning case, with equal inertial and viscous forces). ${\text{Re}}_{\upomega } = 0$ means the disk is static, and ${\text{Re}}_{\Omega } = 0,$ means the cone is static. In all four cases, the transverse velocity field declines with the augmentation of the magnetic field. Conforming to the physical consequences associated with magnetic sources, ' $g(\eta )$' diminishes gradually against increasing '$M$'. However, from Fig. 2a and b, it is clear that the transverse velocity component is significantly more affected as compared to the motion along the radial direction.

In Fig. 3a–d, four models (1,2,3,4) are discussed that explain the influence of the Maxwell parameter $(\lambda )$ and magnetic parameter $(M)$ on '$g(\eta )$' for four specific scenarios of ‘${\text{Re}}_{\upomega }, {\text{Re}}_{{\Omega }}$’. Model (1) represents the combination of a static disk and a rotating cone $\left( {{\text{Re}}_{\upomega } = 0, \, {\text{Re}}_{\Omega } = 1} \right)$, Model (2) represents the combination of a rotating disk and a static cone $\left( {{\text{Re}}_{\upomega } = 1, \, {\text{Re}}_{\Omega } = 0} \right)$, Model (3) represents the combination of both a rotating disk and cone in the same direction $\left( {{\text{Re}}_{\upomega } = 1, \, {\text{Re}}_{\Omega } = 2} \right)$, whereas Model (4) represents the combination of both rotating disk and cone in opposite directions $\left( {{\text{Re}}_{\upomega } = - 1, \, {\text{Re}}_{\Omega } = 1} \right)$, respectively. It is evident that the flow of Maxwell nanofluid, which happens between the conical gap, is wholly induced by the swirling motion of the rotating component. In all cases, the transverse velocity field of the Maxwell nanofluid declines with the increasing valves of ‘$M$’ and ‘$\lambda$’. This is because the augmentation in ‘$M$’ corresponds to enhanced Lorentz effects, while the increasing values of ‘$\lambda$’ reduce the momentum diffusivity. Thus, opposite natures have been observed for the parameters ‘$M$’ and ‘$\lambda$’. From a physical point of view, the results seem to be very encouraging for the flow control applications. Besides, note that in Model (4), the larger values of ‘${\text{Re}}_{\upomega }, {\text{Re}}_{{\Omega }}$’ evolving turbulence and stability can happen to study the flow behavior. This model is quite interesting and useful for the paint industry to shake the thicker fluids and sustain uniformity.

Figure 4a, b displays the behaviors of dimensionless temperature against increasing values of $`\varepsilon_\text{t} ,\Pr \text{'}$ and $`{\text{Nb}},{\text{Nt}}\text{'}$, respectively. Thermal relaxation time $`\varepsilon_\text{t} \text{'}$ is a measure of how long an object takes to return to its ambient temperature after heating. In Fig. 4a, it is showed that the temporal measure of fluid is a decreasing function of $`\varepsilon_\text{t} \text{'}$. The Prandtl number is an intrinsic dimensionless parameter that characterizes the dominance of the momentum boundary layer (MBL) over the thermal boundary layer (TBL). In terms of diffusive measures, it represents the ratio of momentum diffusivity to thermal diffusivity. Generally, liquids with small Prandtl numbers are free-flowing and excellent heat conductors. Nevertheless, an increase in the Prandtl number is associated with a high momentum diffusivity or rapid thermal transport. This fact can be visualized in Fig. 4a, which plots decreasing patterns in '$\Theta (\eta )$' for varying the as $\Pr = 10,11,12.$ Figure 4b shows that '$\Theta (\eta )$' enhances when the estimations for $`\text{Nb}\text{'}$ and $`Nt\text{'}$ are upsurge. From a thermodynamic perspective, thermophoresis occurs when a significant temperature gradient exists. For example, the radiant units of industrial boilers and excessive heat reservoirs of nuclear plants are susceptible to thermophoresis. Therefore, higher values of ‘$Nt$’ result in an abrupt gain of thermal energy within TBL and cause temperature gradients to expand on a comparatively larger region. On the other hand, the Brownian motion parameter is associated with random agitations of micro or nanoparticles in the fluid, which arise due to their collisions with each other. In a fluid dynamic, Brownian motion gives rise to the continual motion of the particles by preventing them from settling down, stabilizing the colloidal solution. However, the stronger Brownian effect, or higher value of ‘$\text{Nb}$’, intensified caloric states are reported throughout TBL. It is worth mentioning that ‘$Nt$’ has more evident influences on ‘$\Theta (\eta )$’ than ‘$\text{Nb}$’. Moreover, in comparison between Fig. 4a, b, it is observed that the conviction rate is improved for higher $`\varepsilon_\text{t} \text{'}$ and '$\Pr$', while dwindling results are associated with ‘$\text{Nt}$’ and ‘$\text{Nb}$’, accordingly.

Figure 5a, b displays the impacts on concentration profile associated with $`\text{Nb}, \text{Nt}\text{'}$ and $`\text{Sc},\varepsilon_\text{c} \text{'}$ , respectively. Figure 5a illustrates that ‘$\phi (\eta )$’ is an increasing function of ‘$Nt$’. Brownian motion is referred to as the random motion of suspended particles. Therefore, with an increase in Brownian parameter ‘$\text{Nb}$’, ‘$\phi (\eta )$’ ultimately reduces. Although, in contrast to ‘$Nt$’, the fluctuations as a result of enhanced 'Nb' are minor, as can be seen in Fig. 6. On the other hand, Fig. 5b plots the concentration fluxes related to $`\varepsilon_\text{c} \text{'}$ and ‘$Sc$’. The graph shows that ‘$\phi (\eta )$’ encounters down-fall with an increase in $`\varepsilon_\text{c} \text{'}$. From a physical point of view, the concentration relaxation time provides insights into the temporal behavior of concentration gradients to achieve equilibrium or relaxes to a steady state. Figure 5b shows that a rise in $`\varepsilon_\text{c} \text{'}$ suggests a down-surge in ‘$\phi (\eta )$’ and a higher rate of mass convection. In the study of mass transfer phenomena, Schmidt's number relates the rates of momentum to the mass transport of particles through a fluidic medium. It plays a crucial role in various applications, including the design of chemical reactors, analysis of pollutant dispersion in the environment, and modeling of heat and mass transfer processes in engineering systems. By definition, a lower value of ‘$\text{Sc}$’ implies that the fluid under consideration has rapid transportation of solid particles, while a high 'Sc ' indicates the opposite. This fact is clear from Fig. 5b, where ‘$\phi (\eta )$’ is decreasing within the diffusion layer when the Schmidt number is increased as $\text{Sc}$ = 0.1, 0.3, and 0.5. Moreover, it is evident that ‘$\text{Nt}$’, $`\varepsilon_\text{c} \text{'}$, and ‘$Sc$’ has relatively favorable impacts on the relative mass diffusion regions as compared to that of ‘$\text{Nb}$’.

Figure 6a, b describes the contour representation of the flow scenario between the gap of the cone and the disk system. The vorticity near the gap is quite visible, and high intensity is shown by the variation of the grids. Figure 7(a, b) describes the streamlined representation of the flow scenario between the gap of the cone and the disk system. The streamlines vary with the variation of the grids.

Tables 2–5 portray the impacts of distinct factors on ${\text{Re}}_{\upomega }^{2} \cdot C_{{{\text{gd}}}}$ and ${\text{Re}}^{2}_{\Omega } .C_{\text{gc}}$ using four different models. The consequence of $\lambda$ and $M$ on ${\text{Re}}^{2}_{\upomega } \cdot C_{{{\text{gd}}}} \;\& \;{\text{Re}}^{2}_{\Omega } \cdot C_{{{\text{gc}}}}$ is shown in Table 2 using static disk and rotating cone (${\text{Re}}_{\upomega } = 0,{\text{Re}}_{\Omega } = 10$). The augmented values of $\lambda ,M$ heightens ${\text{Re}}_{\upomega }^{2} \cdot C_{{{\text{gd}}}}$ and ${\text{Re}}^{2}_{\Omega } \cdot C_{{{\text{gc}}}}$. Physically, the larger values of $\lambda ,M$ indicate that the resistive force and fluid particles collide and decline the fluid's velocity, and consequently, the skin friction increases. Table 3 displays the consequence of the rotating disk and static cone $({\text{Re}}_{\upomega } = 100,{\text{Re}}_{\Omega } = 0),$ versus the skin friction using the increasing values of $\lambda ,M$. The augmented values of '$\lambda ,M$' heighten ${\text{Re}}^{2}_{\upomega } \cdot C_{\text{gd}} \;{\text{and}}\;{\text{Re}}^{2}_{\Omega } \cdot C_{\text{gc}}$. From the obtained results, it is observed that the drag force is more prominent in the model (2). Tables 4 and 5 show the rotation of both devices in the same direction and opposite direction. When the cone and disk apparatus are rotating in the same direction, then the skin friction enhances with the increasing values of $\lambda ,M$ in both models (3,4). But, the effect of the resistive force is more prominent in the case of the opposite rotations. Physically, the turbulence effect generates when both devices rotate in the opposite direction. Therefore, skin friction is more prominent in the model (4).

Table 2 Model (1): The static disk and rotating cone in case of skin friction versus ‘$M$’ and ‘$\lambda$’

Table 3 Model (2): The rotating disk and static cone in case of the skin friction versus '$\lambda$' and '$M$'

Table 4 Model (2): The rotating disk and cone in case of skin friction versus '$\lambda$' and '$M$'

Table 5 Model (2): The opposite rotating disk and cone in case of the skin friction versus '$\lambda$' and '$M$'

Table 6 displays the impacts of ${\text{Nt}},{\text{Nb}}$ and $\varepsilon_\text{t}$ on the Nusselt numbers at the disk and cone surfaces, respectively. The mounting is in $\text{Nt, Nb}$ heightened $\Theta^{\prime}(0),\Theta^{\prime}(\eta_{0} )$ , while it declines with mounting in $\varepsilon_\text{t}$. Substantially, greater values of ${\text{Nt}},{\text{Nb}}$ increase the thermophoretic force and Brownian effect, which causes to boost the heat transfer rate. The heat transfer rate declined versus the thermal relaxation time parameter $\varepsilon_\text{t}$. Physically, in the case of the higher values of $\varepsilon_\text{t}$, the fluid particles take additional time to convey heat into the attached particles and consequently decline the heat transfer rate. Table 7 shows the effect of the Schmitt number and solutal relaxation time parameter $({\text{Sc}},\varepsilon_{{\text{c}}} )$ on the mass transfer rate in the disk/cone disk system. The larger values of the parameters ${\text{(Sc}},\varepsilon_{{\text{c}}} )$ decline in the mass transfer rate. It reveals that the mass transfer rate and the thickness of the boundary layer decline with the increase of $\varepsilon_\text{c}$. Furthermore, it is concluded that all the obtained results by CVFEM, illustrated in Figs. 2–7, and RK-4, listed in Tables 2–7, are found to be in excellent agreement with each other.

Table 6 Heat transfer rates $\Theta^{\prime}(0)$ and $\Theta^{\prime}\left( {\eta_{0} } \right)$ versus different values of parameters $Nt$, $\text{Nb}$, and $\varepsilon_\text{t}$

Table 7 Mass transfer rates $\phi^{\prime}\left( 0 \right)$ and $\phi^{\prime}\left( {\eta_{0} } \right)$ versus different values of parameters Sc, and $\varepsilon_\text{c}$

Conclusions

A major aim of this study is to examine the three-dimensional flow dynamics of Maxwell nanofluid flow within the gap of a cone–disk apparatus (CDA), incorporated with the double diffusion mechanism. Fourier's law of heat conduction in combination with the generalized Fick's law of diffusion is effectively used to describe the heat and mass transfer, respectively. The current flow analysis covers four different situations: rotating cone and disk in the counter direction, rotating cone and disk in the counter direction, rotating cone with static disk, and rotating disk with stationary cone. The present work examined the exciting flow, heat, and mass transfer properties of a disk-cone apparatus, and the outcomes may have applications in targeted drug delivery and other mechanical systems. In the existing literature, the focus has been given to Newtonian fluids. Here we have targeted the non-Newtonian Maxwell fluids, which are more reliable for the types of blood, medication, paint, and so on. The basic governing equations of nonlinear PDEs are reduced into nonlinear ODEs through similarity variables. The ODE system obtained is handled numerically using the Runge–Kutta fourth-order (RK-4) technique, while the PDE system is handled using the recently developed control volume finite element method (CVFEM). Heat convection and mass diffusion are explained by elaborating the imperative effects of physical parameters in graphical and tabular notions. As a result of this study, the following observations have been made:

• An increase in the Maxwell parameter decelerates the fluid, while temperature gradually lessens.

• The radial component of velocity dwindles for escalated magnetic sources.

• The transverse velocity is improved when the disk is swirling while the cone is held still.

• With higher values of thermophoretic and Brownian motion parameters, the temperature enhances and, consequently, the thermal boundary layer expands.

• It appears that the conviction rate is improved for higher thermal relaxation time and Prandtl number.

• Moreover, the thermophoretic parameter, concentration relaxation parameter, and Schmidt number show relatively favorable effects on relative mass diffusion regions as compared to the Brownian parameter.

• A turbulence effect is generated when both cone and disk rotate oppositely, which implies that frictional measures dominate in this case.

• In contrast to the thermal relaxation time parameter, the thermophoretic force and Brownian effect boost the heat transfer rate.

• With increasing concentration relation time, the mass transfer rate and the thickness of the boundary layer are found to decline.