Introduction

The heat transfer mechanisms are important due to the efficiency of many technological and industrial applications. Over the decade, the scientists and engineers are taking advantages of nanofluid technology, to achieve the required goal. The term “nanofluid” was first proposed by Choi and Eastman (1995). Recently, the practical applications of nanofluid in heat transfer equipment include radiators, heat exchanger, solar collectors, electronic cooling system, detergency, automobile, and medical applications. Temperature plays an important role in increasing the effect of thermal conductivity of nanofluid. However, the performance of the thermal conductivity depends on size, shape, and material of nanofluid. For example, metallic nanofluid have higher thermal conductivity than non-metallic nanofluid and the small-sized nanoparticle has higher thermal conductivity as compared to the large-sized nanoparticles. The temperature effects on the thermal conductivity have been studied in Refs. Das et al. (2003), Chon and Kihm (2005), and Li and Peterson (2006). The features of two slip mechanisms called Brownian diffusion and thermophoresis were studied by Buongiorno (2006). These two features of nanofluid create enhanced heat transfer effects which were presented by Sheikholeslami et al. (2014). Heat transfer in nanofluid flow over a flat plate with the help of self-similar transformations was given by Avramenko et al. (2014). The three-dimensional flow of nanofluid due to stationary or moving surface was presented by Khan et al. (2014). Hayat et al. (2015) proposed the model for magnetohydrodynamic (MHD) three-dimensional flow over a couple of stress nanofluid in the presence of nonlinear thermal radiation over a stretchable surface. The stagnation point of the rotating nanofluid in boundary layer flow on the external surface was given by Anwar et al. (2015). The nanofluid flow between two parallel plates in the presence of a magnetic field was studied by Sheikholeslami et al. (2016). Mustafa (2017) studied the Buongiorno model of nanofluid flow due to a rough rotating disk. Khan et al. (2018) discussed the nanofluid flow over a rotating disk under the influence of magnetic field and dissipation effects. The effects of chemically reaction, magnetic field and heat source on Sutterby nanofluid flow due to rotating stretchable disk were examined by Hayat et al. (2018). The motion of nanofluid thin film on a rotating disk under the influence of non-linear thermal radiation was studied by Ahmed et al. (2019). Some recent articles on nanofluids are given in Refs. Turkyilmazoglu (2016), Turkyilmazoglu (2019a, b), Ahmed et al. (2019a, b, c), and Turkyilmazoglu (2020).

The heat transfer flow problem over a rotating disk has numerous practical applications in various engineering applications such as rotating machinery, gas turbine rotator, air cleaning machines, thermal power generating systems, computer storage devices, and electronic devices. The current problem also discusses the heat transfer flow over rotating disk in the presence of nanofluid, which is a quite interesting topic in recent literature. At very first in 1920, Karman (1921) presented the problem for rotating disk to the case of flow impulsively starting from rest. Following the pioneering work of Karman, many new problems have been introduced to the rotating disk flow problem, e.g., the surface of rotating disk having suction/injection properties was studied in Stuart (1954) and Kuiken (1971). The transfer of heat from an air-cooled rotating disk was proposed by Owen et al. (1974). Hall (1986) and Jarre et al. (1996) have studied the aspects of rotating disk problem theoretically, numerically and experimentally. The characteristics of flow and heat transfer due to rotating disk was presented by Turkyilmazoglu (2014). Khan et al. (2020a, b) presented the Maxwell fluid model for rotating and vertically moving disk by analyzing flow features, MHD and non-linear thermal radiation over a rotating disk.

Fluids such as water, oil, and air are classified as Newtonian fluids, while the non-Newtonian fluids are honey, blood, paint polymer solution, corn starch in water, ketchup, motor oil, lubricant spray, coffee in water and hydraulics fluids. However, in many industrial process of fluid motion, we have to deal with non-Newtonian fluids, due to the fact that various assumptions of Newtonian behavior are not valid. In general terms “non-Newtonian” is related as viscoelastic. Non-Newtonian can be defined as the dependence of its viscosity to the stress applied but this does not mean that all non-Newtonian fluids need to have elastic properties. There are some examples of inelastic behavior, i.e. shear stress dependence on viscosity in Bird et al. (1977). Ezzat (2010) investigated the conducting thermoelectric materials for a new class of thermoelectric non-Newtonian fluids. The applications and perspective of non-Newtonian fluids in industries were given by Peng et al. (2014). Nadeem et al. (2014) investigated a model of non-Newtonian nanofluid over a stretchable sheet. The characteristic connection of non-Newtonian nanofluid between two vertical plates is investigated analytically and numerically by Hatami and Ganji (2014).

Radiative effects are important during the heat transfer process because they have many applications in engineering, industries, and material science, for instance, gas for a cooled reactor, glass production, furnace design, polymer preparing, in space technology, etc. Furthermore, electromagnetic waves are responsible for transfer heat and energy via radiations. However, there is no attempt in the literature to consider the radiation effects on flow and heat transfer of Maxwell nanofluid over a vertically moving rotating disk. Radiation effects on free convection viscous incompressible flow past a vertical porous plate with uniform temperature and suction were analyzed by Hossain et al. (1999). Some investigations regarding the effects of thermal radiation using linearized Rosseland approximation are given in Refs. Ellahi et al. (2016), Akbar et al. (2016), Alebraheem and Ramzan (2019), Ellahi et al. (2019), Alamri et al. (2019), Sarafraz et al. (2020), and Ellahi et al. (2020). Effects of thermal radiation in the peristaltic flow of Jeffrey nanofluid and MHD nanofluid flow are discussed by Hayat et al. (2016, 2015).

The aim of the present work is to investigate the effects of non-linear thermal radiation on the flow and temperature fields across an unsteady MHD nanofluid over a vertically moving disk. Buongiorno’s model is implemented for the current analysis to show the impact of Brownian motion and thermophoresis due to nanoparticles. Using Karman transformation variables, the motion equations are integrated numerically for solution through the built-in scheme, namely bvp4c in MATLAB. Graphical behavior is presented to describe the role of physical parameters. Such as wall motion, magnetic parameter, Deborah number, and Schmidt number.

Mathematical modeling

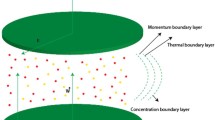
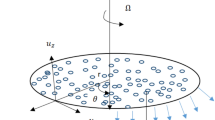
The graphical view of rotating and vertically moving disk geometry is shown in Fig. 1. We consider an incompressible Maxwell nanofluid over a rotating and vertically moving disk. The physical problem is associated with the cylindrical coordinates \(\left( r,\ \varphi ,\ z\right) \) with the directions of radial, azimuthal and axial as \(\left( u,\ v,\ w\right) \), respectively. A uniform beam of magnetic field is thrown along the z-axis. A well-known Buongiorno’s model is implemented to trace the features of thermophoresis and Brownian diffusion. Furthermore, the disk is rotating as well as vertically moving so we have an ambient temperature \(T_{\infty }\) and concentration \(C_{\infty }\) of fluid, whereas the disk is subjected to the time-dependent wall temperature \(T_{w}(t)\) and time-dependent wall concentration \(C_{w}(t)\). So this will make the difference in temperature and concentration. Temperature and concentration difference are given as

$$\begin{aligned} \Delta T=T_{w}(t)-T_{\infty },\ \Delta C=C_{w}(t)-C_{\infty }. \end{aligned}$$
(1)

The expressions for wall temperature (Turkyilmazoglu 2018) and concentration are given as

$$\begin{aligned} T_{w}(t)=\hbox {ca}(t)^{-2\alpha _{1}}+T_{\infty },\ C_{w}\left( t\right) =\hbox {ca}(t)^{-2\alpha _{2}}+C_{\infty }, \end{aligned}$$
(2)

where c is the arbitrary constant and \(\alpha _{1}\) and \(\alpha _{2}\) are the wall temperature and wall concentration parameters, respectively. When \(\alpha _{1}=\alpha _{2}=0,\) then the wall is sustained a constant wall temperature and constant wall concentration.

Fig. 1
figure 1

Flow configuration

Full size image

These assumptions lead to the following flow problem (Ahmed et al. 2019b):

$$\begin{aligned}&u_{r}+\frac{u}{r}+w_{z}=0, \end{aligned}$$
(3)
$$\begin{aligned}&u_{t}+uu_{r}+wu_{z}-\frac{v^{2}}{r}+\lambda _{1} \nonumber \\&\quad \left( \begin{array}{c} u^{2}u_{rr}+u_{tt}+2uu_{rt}+2wu_{zt}-2\frac{v}{r}v_{t}-\frac{2vu}{r}v_{r}+ \frac{v^{2}u}{r^{2}}-\frac{2wv}{r}v_{z} \\ +2wuu_{rz}+w^{2}u_{zz}+\frac{v^{2}}{r}u_{r} \end{array} \right) \nonumber \\&\quad =\nu \left\{ u_{zz}\right\} -\frac{\sigma B_{o}^{2}}{\rho f} \left( u+\lambda _{1}\left( u_{t}+wu_{z}\right) \right) , \end{aligned}$$
(4)
$$\begin{aligned}&v_{t}+wv_{z}+uv_{r}+\frac{vu}{r}+\lambda _{1} \nonumber \\&\quad \left( \begin{array}{c} u^{2}v_{rr}+w^{2}v_{zz}+v_{tt}+2uv_{rt}+2\frac{v}{r}u_{t}+2wv_{zt}-\frac{ 2vu^{2}}{r^{2}}+\frac{2vu}{r}u_{r}-\frac{v^{3}}{r^{2}} \\ +2uwv_{rz}+\frac{2wv}{r}u_{z}+\frac{v^{2}}{r}v_{r} \end{array} \right) \nonumber \\&\quad =\nu \left\{ v_{zz}\right\} -\frac{\sigma B_{o}^{2}}{\rho f}\left( v+\lambda _{1}\left( v_{t}+wv_{z}\right) \right) , \end{aligned}$$
(5)
$$\begin{aligned}&T_{t}+uT_{r}+wT_{z}+\frac{1}{\rho c_{p}}(q_{rad})_{z} \nonumber \\&\quad =\alpha \left\{ T_{zz}\right\} +\tau \left( D_{B}T_{z}C_{z}+\frac{D_{T}}{T_{\infty }}\left( T_{z}\right) ^{2}\right) , \end{aligned}$$
(6)
$$\begin{aligned}&C_{t}+uC_{r}+wC_{z}=\frac{D_{T}}{T_{\infty }}\left( T_{zz}\right) +D_{B}\left( C_{zz}\right) , \end{aligned}$$
(7)

where the subscripts involving either of the variables \(r,\ z\), and t represent the partial derivatives. Further (u, v, w) show the velocity components, \(\left( C,T\right) \) concentration and temperature, respectively, \(\tau \) shows the heat capacities of ratio. \((D_{B},D_{T})\) denote the Brownian diffusion and thermophoresis diffusion coefficients. With the help of Rosseland approximation, the radiative heat flux \(q_{\hbox {rad}}\) in Eq. (6) can be written as Ahmed et al. (2019b)

$$\begin{aligned} q_{\hbox {rad}}=-\frac{4\sigma ^{*}}{3k^{*}}\left( T_{z}^{4}\right) =-\frac{ 16\sigma ^{*}T^{3}}{3k^{*}}T_{z}. \end{aligned}$$
(8)

In the above expressions, \(k^{*}\) and \(\sigma ^{*}\) are denoted as mean absorption coefficient and Stefan–Boltzmann constant. Using Eq. (8) in Eq. (6), we get

$$\begin{aligned}&T_{t}+uT_{r}+wT_{z}-\frac{16\sigma ^{*}}{3\rho c_{p}k^{*}}\left( T^{3}T_{z}\right) ,_{z} \nonumber \\&\quad =\alpha \left( T_{zz}\right) +\tau \left( D_{B}T_{z}C_{z}+\frac{D_{T}}{T_{\infty }}\left( T_{z} \right) ^{2}\right) . \end{aligned}$$
(9)

Boundary conditions

The physical problem is modeled under the following conditions (Turkyilmazoglu 2018):

$$\begin{aligned} u&= {} 0, \, v=\Omega (t)r,\ w=\beta \overset{\cdot }{a}(t),\ C=C_{w}(t), \nonumber \\ T&= {} T_{w}(t)\ \text {at}\ z=a(t), \nonumber \\ u&= {} v=0,\ C=C_{\infty }, \, T=T_{\infty }\ \text {as }z\rightarrow \infty , \end{aligned}$$
(10)

where \(\beta \) is the strength of wall porosity. The constant value of \(\beta =1\) implies \(w=\overset{\centerdot }{a}(t)\) which means the moving surface is impermeable having no heat and mass transfer workout. As we are discussing the action of wall motion, the strength of wall porosity is either wall suction or wall injection. Here we classified the wall injection for the value \(\beta >1\) and for the wall suction \(\beta <1\). In the current study, the wall strength is set to be fixed with \(\beta =2\).

Similarity hypothesis

We define the following transformations (Hayat et al. 2015):

$$\begin{aligned} \begin{aligned}&\left( u,\ v,\ w,\ T,\ C\right) \\&\quad =\left( F\frac{r\nu }{a^{2}(t)},\ \ G\frac{ r\nu }{a^{2}(t)},\ \ H\frac{\nu }{a(t)},\ T_{\infty }+\Delta T\theta ,\ C_{\infty }+\Delta C\phi \right) , \\&\left( \eta ,\ \eta _{t},\ \eta _{z}\right) =\left( \frac{z}{a(t)}-1,\ - \frac{\overset{\centerdot }{a}(t)}{a(t)}\left( \eta +1\right) ,\ \frac{1}{ a(t)}\right) , \end{aligned} \end{aligned}$$
(11)

where \(\eta \) is the non-dimensional distance measured along the axis of rotation, \(F,\ G\) and H are the radial velocity, tangential velocity and axial velocity, respectively, and these are the functions of \(\eta \). Using Eq. (11) in Eqs. (3–5), (7), (9) and (10), we obtain

$$\begin{aligned}&2F+H^{\prime }=0, \end{aligned}$$
(12)
$$\begin{aligned}&F^{\prime \prime }-F^{2}+G^{2}-HF^{\prime }+S(1-S\beta _{1}) \left( F+\frac{ \eta +1}{2}F^{\prime }\right) \nonumber \\&\qquad -\frac{3}{2}S^{2}\beta _{1} \left( F+\left( \eta +1\right) F^{\prime }+\frac{\left( \eta +1\right) ^{2}}{6}F^{\prime \prime }\right) \nonumber \\&\qquad +2\beta _{1}(2HGG^{\prime }-2HFF^{\prime }+H^{2}F^{\prime \prime }) \nonumber \\&\qquad -M\left( F-S\beta _{1}(F+\frac{\eta +1}{2}F^{\prime })+\beta _{1}HF^{\prime }\right) +2S\beta 1 \nonumber \\&\qquad \left( HF+F^{2}-G^{2}+\frac{\left( \eta +1\right) }{2}\left( FF^{\prime }+GG^{\prime }+HF^{\prime \prime }\right) \right) \nonumber \\&\quad =0, \end{aligned}$$
(13)
$$\begin{aligned}&G^{\prime \prime }-2FG-HG^{\prime }+S\left( 1-S\beta _{1}\right) \left( \frac{\eta +1}{2}G^{\prime }\ +G\right) \nonumber \\&\qquad -\frac{3}{2}S^{2}\beta _{1}\left( G+\left( \eta +1\right) G^{\prime }+\frac{\left( \eta +1\right) ^{2}}{6} G^{\prime \prime }\right) \nonumber \\&\qquad -2\beta _{1}\left( 2FHG^{\prime }+2HGF^{\prime }+H^{2}G^{\prime \prime }\right) \nonumber \\&\qquad -M\left( G-S\beta _{1}\left( G+\frac{\eta +1}{2}G^{\prime }\right) +\beta _{1}HG^{\prime }\right) \nonumber \\&\qquad +2S\beta _{1}\left( 2FG^{\prime }+HG^{\prime }+\frac{\left( \eta +1\right) }{2}\left( GF^{\prime }+FG^{\prime }+HG^{\prime \prime }\right) \right) \nonumber \\&\quad =0, \end{aligned}$$
(14)
$$\begin{aligned}&\left( 1+\frac{4}{3}\hbox {Rd}\right) \theta ^{\prime \prime }\nonumber \\&\qquad +\frac{4}{3}\hbox {Rd}\left[ \begin{array}{c} \left( \theta _{w}-1\right) ^{3}\left( 3\theta ^{2}\theta ^{\prime 2}+ \theta ^{3}\theta ^{\prime \prime }\right) +3\left( \theta _{w}-1\right) ^{2}\left( 2\theta \theta ^{\prime 2}+\theta ^{2}\theta ^{\prime \prime }\right) \\ +3\left( \theta _{w}-1\right) \left( \theta ^{\prime 2}+\theta \theta ^{\prime \prime }\right) \end{array} \right] \nonumber \\&\qquad +\Pr S\left( \alpha _{1}\theta +\frac{\eta +1}{2} \theta ^{\prime }\right) \nonumber \\&\quad +\Pr \left( \hbox {Nb}\theta \phi ^{\prime }+\hbox {Nt} \theta ^{\prime 2}-H\theta ^{\prime }\right) =0, \end{aligned}$$
(15)
$$\begin{aligned}&\phi ^{\prime \prime }-\hbox {Sc}H\phi ^{\prime }+\frac{\hbox {Nt}}{\hbox {Nb}}\theta ^{\prime \prime }+\hbox {Sc}\ S\left[ \alpha _{2}\phi +\frac{\eta +1}{2}\phi \right] =0, \end{aligned}$$
(16)
$$\begin{aligned}&F\left( 0\right) =0, \, G\left( 0\right) =\omega \text {, }H(0)=\beta \frac{S}{2},\ \theta (0)=1=\phi (0), \nonumber \\&F\left( \infty \right) = \, G\left( \infty \right) =\ \theta (\infty )=\phi (\infty )=0. \end{aligned}$$
(17)

In the above equations, \(F,\ G,\ H,\ \theta ,\) and \(\phi \) are the dimensionless radial, azimuthal and axial velocities, temperature and concentration parameter, respectively. From Eqs. (12–17), there are some parameters that influence the flow motion, temperature and concentration fields of Maxwell nanofluid. These are \(S,\ \beta _{1},\ \hbox {Nt},\ \hbox {Nb},\ \beta ,\ \hbox {Rd},\ \theta _{w},\ M,\ \omega ,\ \Pr ,\ \alpha _{1},\ \alpha _{2}\), and \(\hbox {Sc}\), respectively, called wall motion up and down, Deborah number, thermophoresis, Brownian motion, wall permeability, radiation parameter, temperature ratio parameter, magnetics field, rotation parameter, Prandtl number, wall temperature parameter, wall concentration parameter, and Schmidt numbers. The mathematical forms of these parameters are

$$\begin{aligned} S & = {} \frac{2a(t)\overset{\cdot }{a}(t)}{\nu },\ a(t)=h\sqrt{\frac{S\nu }{h^{2}} t+1},\ \ \beta _{1}= \frac{\lambda _{1}\nu }{a^{2}(t)}, \nonumber \\ \hbox {Nt} & = {} \frac{\tau D_{B}ca(t)^{-2\alpha _{1}}}{\tau _{0}\nu },\ \hbox {Nb}=\frac{\tau D_{B}ca(t)^{-2\alpha _{2}}}{\nu }, \nonumber \\ R_{d} & = {} \frac{4\sigma ^{*}T_{\infty }^{3}}{3kk^{*}},\ M=\frac{\sigma B_{0}^{2}a^{2}(t)}{\nu \rho _{f}},\ \omega =\frac{\Omega (t)\ a^{2}(t)}{\nu }, \nonumber \\ \Pr & = {} \frac{\nu }{\alpha },\ S_{c}=\frac{\nu }{D_{B}}. \end{aligned}$$
(18)

Here \(\Omega (t)=\frac{\omega \nu }{h^{2}+\nu St}\) implies the rotation of disk. The value \(S>0\) reduces the rotation of disk and thus causing disk decelerating rotation. Contrarily, \(S<0\) enhances the rotation of disk which accelerates the rotation of disk.

Nusselt number

From the engineering perspective, the quantity local Nusselt number \(\hbox {Nu}_{r}\) is very important. Physically, \(Nu_{r}\) is the wall heat transfer. This is expressed by the following expression:

$$\begin{aligned} \hbox {Nu}_{r}=-\left[ 1+\frac{16\sigma ^{*}T_{\infty }^{3}}{3\rho c_{p}k^{*} }\right] \frac{r}{\left( T_{w}-T_{\infty }\right) }\left( \frac{\partial T}{ \partial z}\right) \mid _{z=0}. \end{aligned}$$
(19)

In dimensionless notation, one can write

$$\begin{aligned}&{\text {Re}}^{-1/2}\ Nu_{r} \nonumber \\&\quad =-\theta ^{\prime }(0)\left( 1+\frac{4}{3}\hbox {Rd}\left\{ 1+\theta (0)(\theta _{w}-1)\right\} ^{3}\right) , \end{aligned}$$
(20)

where \({\text {Re}}^{1/2}=\frac{r}{a(t)}\) is the local Reynolds number.

Sherwood number

Mass transfer rate at the disk surface can be defined through Sherwood number as follows:

$$\begin{aligned} \hbox {Sh}_{r}=-\frac{r}{\left( C_{w}-C_{\infty }\right) }\left( \frac{\partial C}{ \partial z}\right) \ |_{z=0,} \end{aligned}$$
(21)

and dimensionless form is

$$\begin{aligned} \hbox {Sh}_{r}{\text {Re}}^{-\frac{1}{2}}=-\phi ^{\prime }(0). \end{aligned}$$
(22)

Numerical solution procedure

The numerical solution of the dimensionless nonlinear momentum, temperature, and concentration Eqs. (12–16) with the boundary conditions (17) are computed numerically with the bvp4c technique, one of the collection methods which uses the Lobatto formula. This technique requires initial guesses which satisfy the boundary conditions. Once initial guesses are provided by user then another built-in method, namely finite difference method is used to modify the guesses for further iterations. The order of accuracy in the numerical calculation is controlled with error tolerance less \(10^{-6}\). By default, this collocation method uses 61 grid points with CPU time of 12 s. In this process, we convert higher order system of ordinary differential equations into a system of first-order ordinary differential equations by introducing some new variables defined as

$$\begin{aligned} H& = {} X_{1},\ H^{\prime }=X_{1}^{\prime },\ F=X_{2},\ F^{\prime }=X_{3},\ F^{\prime \prime }=X_{3}^{\prime }, \nonumber \\ G & = {} X_{4},\ G^{\prime }=X_{5}, \nonumber \\ G^{\prime \prime } &= {} X_{5}^{\prime },\ \theta =X_{6},\ \theta ^{\prime }=X_{7},\ \theta ^{\prime \prime }=X_{7}^{\prime },\ \phi =X_{8}, \nonumber \\ \phi ^{\prime } &= {} X_{9},\ \phi ^{\prime \prime }=X_{9}^{\prime }. \end{aligned}$$
(23)
$$\begin{aligned} X_{1}^{\prime } & = {} -2X_{2}, \end{aligned}$$
(24)
$$\begin{aligned} X_{3}^{\prime } & = {} \frac{ \begin{array}{c} X_{2}^{2}-X_{4}^{2}+X_{1}X_{3}+S\left( S\beta _{1}-1\right) \left( X_{2}+ \frac{\eta +1}{2}X_{3}\right) +\frac{3}{2}S^{2}\beta _{1}\left( X_{2}+\left( \eta +1\right) X_{3}\right) \\ -2S\beta _{1}\left( X_{2}^{2}-X_{4}^{2}+X_{1}X_{2}+\frac{\eta +1}{2}\left( X_{2}X_{3}+X_{4}X_{5}\right) \right) -4\beta _{1}\left( X_{1}X_{4}X_{5}-X_{1}X_{2}X_{3}\right) \\ +M\left( X_{2}-S\beta _{1}\left( X_{2}+\frac{\eta +1}{2}X_{3}\right) +\beta _{1}X_{1}X_{3}\right) \end{array} }{1-\frac{S^{2}\beta _{1}}{4}\left( \eta +1\right) ^{2}+S\beta _{1}X_{1}\left( \eta +1\right) +2\beta _{1}X_{1}^{2}}, \end{aligned}$$
(25)
$$\begin{aligned} X_{5}^{\prime } & = {} \frac{ \begin{array}{c} 2X_{2}X_{4}+X_{1}X_{5}+S\left( S\beta _{1}-1\right) \left( X_{4}+\frac{\eta +1}{2}X_{5}\right) +\frac{3}{2}S^{2}\beta _{1}\left( X_{4}+\left( \eta +1\right) X_{5}\right) \\ -2S\beta _{1}\left( 2X_{2}X_{5}+X_{1}X_{5}+\frac{\eta +1}{2}\left( X_{2}X_{5}+X_{4}X_{3}\right) \right) +4\beta _{1}\left( X_{1}X_{2}X_{5}-X_{1}X_{3}X_{4}\right) \\ +M\left( X_{4}-S\beta _{1}\left( X_{4}+\frac{\eta +1}{2}X_{5}\right) +\beta _{1}X_{1}X_{5}\right) \end{array} }{1-\frac{S^{2}\beta _{1}}{4}\left( \eta +1\right) ^{2} +S\beta _{1}X_{1}\left( \eta +1\right) +2\beta _{1}X_{1}^{2}}, \end{aligned}$$
(26)
$$\begin{aligned} X_{7}^{\prime } & = {} \frac{ \begin{array}{c} \Pr \ \left( X_{1}X_{7}-\ S\left( \frac{\eta +1}{2}X_{7}+\alpha _{1}X_{6}\right) \right) -4\hbox {Rd}\left( \theta _{w}-1\right) ^{3}X_{6}^{2}X_{7}^{2}-8\hbox {Rd}\left( \theta _{w}-1\right) ^{2}X_{6}X_{7}^{2} \\ -4\left( \theta _{w}-1\right) X_{7}^{2}-\Pr \left( NtX_{7}^{2}+NbX_{7}X_{9}\right) \end{array} }{1+\frac{4}{3}\hbox {Rd}+\frac{4}{3}\hbox {Rd}\left( \theta _{w}- 1\right) ^{3}X_{6}^{3}+4\hbox {Rd}\left( \theta _{w}-1\right) ^{2} X_{6}^{2}+4\hbox {Rd}\left( \theta _{w}-1\right) X_{6}} \end{aligned}$$
(27)
$$\begin{aligned} X_{9}^{\prime } & = {} Sc\left( X_{1}X_{9}-S\left( \frac{\eta +1}{2}X_{9}+ \alpha _{2}X_{8}\right) \right) -\frac{\hbox {Nt}}{\hbox {Nb}}X_{7}^{\prime } \end{aligned}$$
(28)

with conditions

$$\begin{aligned} X_{1}(0) & = {} \beta \frac{S}{2},\ X_{2}(0)=0,\ X_{4}(0)=\omega , \nonumber \\ X_{6}(0) & = {} 1=X_{8}(0), \nonumber \\ X_{2}(\infty ) & = {} X_{4}(\infty )=X_{6}(\infty )=X_{8}(\infty )=0. \end{aligned}$$
(29)

Code validation

The validation of numerical outcomes for local skin friction and Nusselt number is shown in Tables 1 and 2. Table 1 shows the comparison with Turkyilmazoglu (2018) for the effects of wall motion parameter S on local skin friction and Nusselt number by keeping other parameters \(\omega =1.0,\ \hbox {Pr}=1.0,\ \beta =2\) and \(\alpha _{1}=0.5\) fixed and rest of parameters zero. In Table 2, we have fixed the values \(\omega =2.0,\ \hbox {Pr}=1.0,\ \beta =2\) and \(\alpha _{1}=0.5\) and other parameters are zero. These tables show an excellent comparison and correlation with Turkyilmazoglu (2018).

Graphical discussion

In this section, we present the physical description and numerical simulation for the velocity, temperature and concentration fields, local Nusselt and Sherwood numbers for an unsteady Maxwell nanofluid flow. Heat transfer analysis is done with the consideration of Buongiorno’s model. The graphical and numerical results are discussed with the parameters in the following ranges:

$$\begin{aligned}&S\in \left[ -0.6,\ 0.4\right] ,\ M\in [0,\ 3.0],\ \hbox {Nb}\in [0.3,\ 2.0],\\&\hbox {Nt}\in [0.0,\ 1.2],\ \Pr \in \left[ 0.5,\ 2.5\right] ,\\&\beta _{1}\in [0.0,\ 2.8],\ \hbox {Rd}\in \left[ 0,\ 0.8\right] ,\ \theta _{w}\in \left[ 1,2.2\right] ,\\&\alpha _{1}\in \left[ -3,\ 1\right] ,\ \alpha _{2}\in \left[ 1,\ 1.8\right] \end{aligned}$$

and fixing the values

$$\begin{aligned}&\beta =\omega =2.0,\ S=M=\hbox {Rd}=\beta _{1}=0.2,\ \theta _{w}=1.2,\\&\hbox {Sc}=\alpha _{1}=\alpha _{2}=1.0,\ \hbox {Nt}=0.4,\ \hbox {Nb}=0.6. \end{aligned}$$
Fig. 2
figure 2

Variation of S on \(\mathbf{a} \) radial velocity, \(\mathbf{b} \) azimuthal velocity, \(\mathbf{c} \) axial velocity, \(\mathbf{d} \) temperature profile and \(\mathbf{e} \) concentration profile

Full size image

Figure 2a shows the variation of radial velocity with the variation of wall motion S. It clearly shows that an upward wall motion reduces the rotational features of radial velocity. These effects on the rotating disk are blowing like for an upward action of wall motion. It is noted an enhancement in radial velocity with the action of wall motion. Similarly, Fig. 2b demonstrates the tangential velocity of nanofluid with varying values of wall motion parameter S. The influence of wall motion is to enhance the tangential velocity of nanofluid. The effects of wall motion parameter on the axial velocity show the blowing which increases the axial velocity of nanofluid as shown in Fig. 2c. In Fig. 2d, e, the effects of wall motion parameter on the temperature \(\theta \) and concentration \(\phi \) fields of the nanofluids are shown. It is obvious from these figures that both temperature and concentration profiles are increasing function of S.

Fig. 3
figure 3

Variation of \(\beta _{1}\) on \(\mathbf{a} \) radial velocity, \(\mathbf{b} \) azimuthal velocity, \(\mathbf{c} \) axial velocity, and \(\mathbf{d} \) temperature profile

Full size image

Figure 3a–d illustrates the graphical behavior of fluid velocity and temperature field with the effects of Deborah number \(\beta _{1}\). Deborah number is defined as the ratio of time relaxation to observation time. So progressing value of \(\beta _{1}\) increases the relaxation time which indicates the more solid-like characteristics. \(\beta _{1}=0\) implies the Maxwell fluid reduces into case of viscous fluid. Figure 3a, c shows the increase in quantity \(\beta _{1}\), for which the reduction in radial and axial velocities of nanofluids is observed. In Fig. 3b–d, it is noted the effects of Deborah number is to increase the azimuthal velocity and temperature field of Maxwell nanofluid over vertically moving disk.

Fig. 4
figure 4

Variation of M on \(\mathbf{a} \) radial velocity, \(\mathbf{b} \) azimuthal velocity, \(\mathbf{c} \) axial velocity, and \(\mathbf{d} \) temperature profile

Full size image

Figure 4a–d shows the effects of magnetic field parameter M. The features of magnetic field are tested on velocity field of nanofluid over vertically moving disk. It is observed that the higher magnetic field has the tendency to slow down the motion of nanofluid. Physically, the magnetic parameter M is ratio of the electromagnetic force to viscous force, so an increasing value of M implies the viscous force is dominant and as a result it decreases the radial and tangential velocity components. On the contrary it is noted that the axial velocity and temperature distribution enhance with the increase of magnetic field effects.

Fig. 5
figure 5

Variation of \(\hbox {Nt}\) and \(\hbox {Nb}\) on (a, b) temperature profile and (c, d) concentration profile

Full size image

Figure 5a, b shows the variation of temperature field of nanofluids with the increasing effects of Brownian motion and thermophoresis parameter over vertically moving disk. Here both parameters \(\hbox {Nt}\) and \(\hbox {Nb}\) are showing a significant increase in temperature profile. This trend is expected because the properties of Brownian motion create the random motion in fluid that causes an increase in temperature field of nanofluid. Figure 5c, d demonstrates the behavior of concentration field of Maxwell nanofluid with the variation of Brownian motion and thermophoresis. It is obvious that the Brownian motion creates random motion in fluid that creates resistance and consequently the concentration of fluids decreases with the Brownian motion effects. On the contrary, variation of concentration profile against the thermophoresis effect is shown in Fig. 5d. Physically, thermophoresis effects simply repel the particles away from a hot surface to cold surface due to which the concentration profile increases. The features of Nt are to enhance the concentration field.

Fig. 6
figure 6

Variation of \(\mathbf{a} \, \hbox {Rd}\), \(\mathbf{b} \, \Pr , \mathbf{c} \alpha _{1}\) and \(\mathbf{d} \theta _{w}\) on temperature profile

Full size image

Figure 6a, b shows the effects of radiation parameter \(\hbox {Rd}\) and Prandtl number \(\hbox {Pr}\) on temperature field of nanofluids. An increase in temperature as well as thermal boundary layer thickness of nanofluid with the gradual enhancement in \(\hbox {Rd}\) is observed. However, the trends of temperature field for \(\hbox {Pr}\) are quite opposite. Figure 6c, d displays the variation of temperature field \(\theta \) with the effects of temperature ratio parameter \(\theta _{w}\) and wall temperature parameter \(\alpha _{1}\). The temperature field of nanofluid enhances with both temperature ratio parameter \(\theta _{w}\) and wall temperature parameter \(\alpha _{1}\). Figure 7a displays the variation of Schmidt number in the concentration profile. Concentration of fluid decreases due to decrease in mass diffusivity. Figure 7b shows the variation of wall concentration parameter in a concentration profile. It is seen that \(\phi \) is an increasing function of \(\alpha _{2}\).

Fig. 7
figure 7

Variation of concentration profile \(\phi \) with \(\mathbf{a} \ \hbox {Sc}\), \(\mathbf{b} \alpha _{2}\)

Full size image

Figure 8a, b shows the heat transfer rate with variation of parameters \((\hbox {Nt} ,S)\) and \((\omega ,\hbox {Rd})\). Figure 8a shows the decreasing behavior with increasing \((\hbox {Nt},S)\). Figure 8b illustrates an increase in heat transfer with increasing \((\omega ,\hbox {Rd})\). Figure 8c displays an increase in mass transfer with increasing wall motion parameter S. Figure 8d presents an increase in mass transfer rate with increasing the fluid thermophoresis \(\hbox {Nt}\) and Brownian motion \(\hbox {Nb}\).

Fig. 8
figure 8

Nusselt number for \(\mathbf{a} \ \hbox {Nt},\ \hbox {Nb} \, \mathbf{b} \hbox {Rd},\ \omega \), and Sherwood number for \(\mathbf{c} \, S\), \(\hbox {Nb} \, \mathbf{d} \, \hbox {Nt}\), \(\hbox {Nb}\)

Full size image
Table 1 A comparison of \(F^{\prime }(0)\), \(G^{\prime }(0)\) and \(-\theta ^{\prime }(0)\) for various values of S when \(\omega =1.0\)
Full size table
Table 2 A comparison of \(F^{\prime }(0)\), \(G^{\prime }(0)\) and \(-\theta ^{\prime }(0)\) for various values of S when \(\omega =2.0\)
Full size table

Concluding remarks

In this study, we have investigated the flow behavior during an unsteady motion of Maxwell nanofluid over vertically moving as well as rotating disk in the presence of magnetic field effects. The Buongiorno model is implemented to reveal the effects of Brownian motion and thermophoresis due to nanofluids. The impacts of some leading parameters on the flow behavior, temperature and concentration fields of nanofluids via graphical and tabular forms are discussed. The following significant features of this study can be summarized a

  • The behavior of wall upward and downward motion parameter is observed similarly to that of injection and suction parameters.

  • Overall the impact of wall motion parameter on radial, azimuthal, axial velocities, temperature and concentration profiles is to enhanced, these.

  • Temperature profile of nanofluid is enhanced, while concentration field reduces with higher values of Brownian motion.

  • Boundary layer of both thermal and concentration profiles is enhanced due to increasing thermophoresis effects.

  • Magnetic field effects are observed to reduce the radial and azimuthal velocity of nanofluid.

  • Nusselt number is increased by decreasing the values of wall motion parameter.