Introduction

In the twenty-first century, electro-magnetically supported transport has been gaining popularity in biomedical sciences, electromechanical systems, and bio-electrochemical engineering. It develops due to the interaction of electromagnetic fields and electrolytic fluids and generates interesting dynamical characteristics. When a charged solid surface gets into interaction with electrolyte or aqueous solutions, the positively indicted ions in the electrolytic fluids are attracted to it while the negatively charged ions repel it. As a response, an electric double layer (EDL) is produced across the charged solid area. The EDL is made up of two layers: a stationary stern layer generated near the charged solid surface and a diffusive layer formed by moving positively charged ions. The positively charged EDL will migrate along imposed electric field if it is employed parallel to the solid–fluid layer. Subsequently, the viscous drag causes the bulk liquid to be mobilized. An electro-osmotic flow (EOF) is an import of electrokinetic phenomena. It has potential biomedical and technological applications in micro- and nano-fluidic devices/systems, for example, electro-osmotic liquid pumps, pectoral fin-inspired wave energy conversion devices, medication delivery pumps, cell culture, DNA testing, tissue scaffolding, cooling chips, minimally invasive medical procedures, cellular micro-injection, bio-chip fabrication, photosynthetic-based fuel systems, corrosion mitigation, non-absorbent polymer injection systems, blood and urine diagnosis, and microbial fuel cells in carbon capture. Reuss [1] was the first to explore and report the EOF in 1809. Wiedemann [2] later proposed a mathematical framework for EOF. Because of the rigorous requirements and benefits of EOF mechanisms, numerous scientists have concentrated their efforts over the EOF subject to various flow constraints and liquid models. The dual consequence of electro-osmosis and peristalsis is significant in several biological, industrial and engineering assessments. An analytical investigation to explore electro-osmosis phenomenon in bio-rheological micropolar fluid flow via sinusoidal wavy micro-channels was presented by Chaube et al. [3]. Their results exposed that the pumping characteristic can be altered by modifying externally imposed electric field. Jayavel et al. [4] uncovered the electro-osmotic phenomena in the peristaltic flow of pseudo-plastic nanofluid via a micro-channel. In this research, it was recorded that the axial velocity of nanofluid declines near the left wall but a contrarily trend is witnessed in the zone close to the right wall for booster values of electro-osmotic term. A theoretical analysis for the EOF of double-layered fluids inside a flexible peristaltic tube was presented by Ali et al. [5]. Their outcomes revealed that both trapping and reflux can be circumvented by augmenting electrokinetic slip velocity. Noreen et al. [6] discovered the electro-osmotic phenomena in biofluid flow via a peristaltic micro-channel. They disclosed that the pressure gradient gets a declination for enhanced electro-osmotic parameter. For more recent researches, the readers are referred to Refs. [7,8,9,10].

The study of mobility of ionized fluid under the interaction of electromagnetic fields is termed electro-magneto-hydrodynamic (EMHD). In this phenomenon, body forces on the stream are generated as a result of several interactions between magnetic field, electrical charges in EDL, electric field, and electrical currents. EMHD plays an incredible role in technological, biotechnological, biomedical, and bio-clinical fields such as biochemical engineering, developing micro-fabrication technology, targeting medications delivery system, and micro-electromechanical systems (MEMS). EMHD phenomena in peristaltic propagation have gained an amazing concern of researcher due to prospective submissions in bioengineering, bio-rheological, and medical domains. Noreen et al. [11] exposed the electro-osmosis regulated peristaltic propagation of magneto-nanofluid via a flexible micro-channel considering Joule heating. Their outputs revealed that the pressure gradient firstly attenuates and then amends with growing estimations of electro-osmotic parameter or Hartmann number. The electro-magneto-osmosis in peristaltic propagation of dusty viscoelastic biofluids via micro-channel was inspected by Ramesh et al. [12]. They disclosed that both magnetic field and electro-osmotic parameter markedly suppress the velocity profile for both fluids and particles phase. Recently, Ramesh et al. [13] have disclosed the electro-osmotic events in the peristaltic flow of magneto-nanofluid with couple stress fluid model via a micro-channel considering the slip and convective wall conditions. Results of this paper claimed that entrapped bolus is expanded by mounted Hartmann number but compressed by elevated electro-osmotic parameter. The peristaltic transportation of a third-order non-Newtonian liquid via a micro-channel under joint action of magneto-hydrodynamics, and electro-osmosis has been examined by Tanveer et al. [14]. The fluid velocity profile is significantly amended by the electro-osmotic term, while it is decremented in the core domain of the conduit but incremented nearby the walls due to an augmentation in magnetic field. Additional related research works are found in Refs. [15,16,17,18].

Researchers and modelers have recently shown an eagerness in peristaltic phenomena, which has a wide variety of deployments in the bio-mechanical, bioengineering, as well as biomedical fields. Continual contractions and relaxations of tube/channel/duct walls drive the fluid elements through it. This phenomenon is frequently realized in blood motion in arteries/vessels, saliva movement, spermatic material propagation and cerebrospinal fluids movement, food swallowing down the esophagus, chyme motion, and so on. This process has been smartly utilized in multi-ways, such as finger and roller pumps, electro-pneumatics, bio-mimetic devices, embryo-cardiovascular pumps, corrosive fluid propelling, blood pump and oxygenator device, blood filtration, heart–lung machine, dialysis machine, ventilator machine, diabetic pumps delivery schemes of insulin, bio-mimetic capillary designs and glucose sensing. In order to understand the peristaltic action of non-Newtonian bio-rheological liquids, researchers have conducted several theoretical and computational investigations under a wide range of different assumptions. The peristaltic activity was initially examined by Latham [19]. After his path-breaking work, Shapiro et al. [20] scrutinized the peristaltic mechanism in order to transport the liquids through a channel/duct subject to lubrication estimates. The electro-osmosis-assisted peristaltic stream of non-Newtonian blood via micro-vascular tube was explored by Tripathi et al. [21]. The MHD peristaltic pumping of non-Newtonian blood was simulated by Rashidi et al. [22]. They pointed out that the pressure rise per wavelength gets an augmentation for higher magnetic parameter. An inspection into the streaming of Rabinowitsch liquid inside an inclined non-uniform pipe with wall characteristics and wall slippage was made by Manjunatha et al. [23]. In this research, they tracked out that the entrapped bolus shape inflates with an elevation in rigidity and stiffness parameters. Some other considerable research studies on the peristaltic drive of physiological liquids were descripted in refs. [24,25,26,27].

Almost all physiological materials, including mucus, synovium fluid, blood, cerebrospinal fluid, retinal humor, endobronchial discharges, and tear film liquid, exhibit non-Newtonian viscoelastic attributes. A non-Newtonian viscoelastic fluid model called the Jeffrey liquid is one of the simplest liquid models evaluated to others for understanding physio-rheological properties of physiological fluids. Many scholars have conducted substantial research on peristaltic propulsion of physiological liquids using the Jeffrey liquid model. The cilia driven MHD stream of Jeffrey fluid in a tube was theoretically studied by Maqbool et al. [28]. They recorded that the fluid velocity field upsurges by incrementing the Jeffrey parameter. Tripathi et al. [29] designed a mathematical simulation to study electro-osmosis modulated viscoelastic physiological fluid stream in a peristaltic cylindrical tube with Jeffrey fluid model. Their results exposed that blood flow rate gets an enhancement with viscoelastic nature of blood and electric effects. Yasmeen et al. [30] implemented an analytical approach to examine viscoelastic attributes in the peristalsis of magnetized Jeffrey fluid through a sinusoidal tube. They exposed that the dynamic flow profiles (velocity and pressure gradients) exhibit little dependency on the Jeffrey parameter. Shaheen et al. [31] conducted an inspection on the micro-rheological attributes of mucus propagation in a ciliary domain with the aid of Jeffrey nanoliquid model. They evaluated the velocity fields for recovery and effective strokes and discovered that the efficient stroke velocity is larger than the recovery stroke velocity. Vaidya et al. [32] presented the peristaltic movement of magnetized Jeffrey liquid with varying viscosity through an asymmetric wavy conduit. They noted that viscosity parameter uplifts the velocity profile in the core domain of the wavy channel. The MHD peristaltic propulsion of a reactive Jeffrey liquid via a penetrable wavy conduit was researched by Abbas et al. [33]. Their outcomes have exposed that pumping rate improves for higher Jeffrey term in the co-pumping domain. Some additional researches on peristalsis of viscoelastic Jeffrey liquid are recorded in refs. [34,35,36,37].

Motile cilia-regulated peristaltic transport appears significantly during cells’ motion or adjacent materials flowing over cell surface. This phenomenon can be observed in vast physiological transit mechanisms such as feeding, breathing, reproduction, locomotion, circulation and respiration. In our body, cilia are very minuscule hair-like appendages that are usually existing on the eukaryotic cell surfaces, for example, kidneys, eye retina, ears, etc., and some physiological vessel/tube/tract like respiratory tract, digestive tract, reproductive and nervous systems. Like oars, they smash back and forth strikes in synchronism to generate a commensurate patterns of traveling wave along the area, recognized as metachronal wave. Cilia-generated metachronal waves are primarily utilized to control flow continuity and improve fluid propulsion. Dust and mucus are dispelled from the airways by ciliary motion in the respiratory tract surface [38]. The cilia in our kidneys operate as a sensory-antenna for our body. They collect signals from the adjacent urinary bladder and respond to cell warnings about the flow of urine in the surrounding area. As food moves via the digestive tract, the cilia beating helps to keep it moving [39]. Ghazal et al. [40] have recorded the movement of egg and sperm swimming in the oviduct liquids via the oviducts. Cilia in male efferent ductules [41] are liable for mixing and dispersing sperms so that they can easily reach their ultimate destination without aggregation and blockage. Farooq et al. [42] addressed a cilia-endorsed MHD transport of viscoelastic Jeffrey liquid through a porous channel considering the cumulative impact pf chemical reaction, and external heat source. They exhibited that semen is a viscoelastic liquid with a lower volumetric flow rate than Newtonian liquid under related conditions. Sadaf et al. [43] analyzed the cilia-aided convection of a viscoelastic Jeffrey liquid in a tube with ciliated sinusoidal wall. Shaheen et al. [44] reproduced a mathematical model for viscoelastic mucus flow in an axisymmetric ciliated duct. They considered the upper convected Maxwell (UCM) fluid model to explain the rheology of mucus which attributes a relaxation time, and precisely describes normal stress production in shear flows. Their outcomes explored that pressure rise is evidenced to boost significantly by increasing cilia length and relaxation time, while axial velocity is remarkably declined. The two-layered cilia-generated propulsion of Phan–Thien–Tanner (PTT) liquid in attendance of thermal and concentration impact has been investigated by Maqbool et al. [45]. In this search, the two-layered design approach is attributed to the prevalence of the airway ciliary layer (ACL) and peri-ciliary liquid layer (PCL) on the epithelial tissue in the inner wall of trachea. Maqbool et al. [46] have explored the impact of buoyancy force in mixed convective ciliary movement of magnetized mucus with Carreau fluid model inside a channel. The cilia-assisted magneto-electro-osmotic transport of non-Newtonian liquid via a ciliated conduit with wall slip have been explored by Munawar [47]. According to his findings, as cilia length and cilia structure eccentricity improve, the shear stress of the ciliary wall uplifts. Shaheen et al. [48] have reported the electro-osmosis endorsed transport of radiated viscoelastic Jeffrey fluids via a ciliary channel with heat generation/ absorption. In order to emphasize ciliary transport importance in physiology and biomedicine disciplines, several significant findings were explored for engaged readers [49,50,51,52].

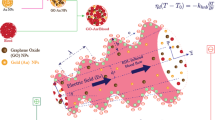
Nanotechnology has recently gained great attention. Scientists examined the efficiency of this research area in various applications such as heat exchangers, photovoltaic, photocatalysts, and biomedical engineering. Nanomaterials perform an important function in industry by controlling the heat mechanism and improving system efficiency. Recent development in bio-nanotechnology has disclosed a large array of benefits for nanomaterials (nanoparticles (NPs), nanofibers, nanotubes, etc.) in medical science. According to the new mechanism advanced by nanofluid dynamics, drugs can be delivered to various organs in human bodies in a uniform manner. Nanofluids are made by scattering nano-sized particles (dimension \(< 100\) nm) in conventional liquids like water, lubricants, engine oil, emulsions, ethylene glycol, biofluids, and blood. This concept was first presented by Choi [53] to upsurge the thermal efficiency of working base fluids. The inspection of operating nanofluids in diverse geometrical aspects is carried out in many researches [54,55,56,57,58,59,60,61,62,63]. Hybrid nanofluids refer to the dispersion of two or more different nanomaterials in the same operating fluids. There are numerous applications for these nanofluids in the fields of medical and bioengineering, for instance, disease diagnostics, preventive medicine, orthopedic lubrications, therapeutics, arthritis, antibacterial and anticancer drugs, versatile vaccines, etc. Almost all of the drugs are composed in the form of hybrid nano-liquids, and blood is utilized as a base liquid for testing the chemical reactions of these materials in the blood stream. Due to various applications in medical science, blood-based hybrid nanofluids have been extensively scrutinized via numerous researchers. The physical significance of hybrid nano-blood (CuO-Cu/blood) in a narrow stenosed artery was examined by Ijaz et al. [64]. They recorded that hybrid NPs are more suitable as compared to mono nano-blood to reduce hemodynamic effect of stenosed artery. Saleem et al. [65] demonstrated peristaltic streaming of blood infused with hybridized nanoparticles via a curved tube with ciliated wall. They revealed that a rapid increment in pressure gradient in hybrid nano-blood (Ag–Cu/blood) is recorded as evaluated to Cu-blood. Das et al. [66] presented an electromagnetic flow of blood suspended with hybridized nanoparticles inside an endoscopic conduit with peristaltic wave. They recorded that the concentration of nanoparticles in hybrid nano-blood (Ag-Al2O3/blood) has a potential to modulate heat-conducting behaviors in flow conduit. The cilia-assisted flow of non-Newtonian blood diffused with copper and gold nanoparticle in a ciliary tube under consideration of entropy and heat generation has been anatomized by Ali et al. [67]. The entropy generation for hybrid nano-blood is higher than for nano-blood. With an electromagnetic field along through Hall currents, Das et al. [68] have studied the hemodynamical properties of blood suspended with copper and gold nanoparticles in a non-uniform endoscopic annulus through wall slip. According to their findings, the inclusion of gold and copper nanoparticles in blood possesses higher temperature than copper nanoparticles. Ali et al. [69] recently explored electromagnetic phenomena in a cilia-modulated hybridized nano-blood flow. In this research, they found that the blood is emphasized on being cooled by enlarging hybrid NPs volume fractions. Some more related articles on peristalsis of blood via the suspension of hybridized NPs are loaded in Refs. [70,71,72].

After a critical literary review, it is believed that no mathematical model has been documented yet in order to simulate the electro-magneto-hydrodynamic flow of ionized blood suspended with nanoparticles via ciliated arterial/vessel systems. In the current era, nanomaterials are extremely utilized in advanced medical science, such as bio-nano-polymer coatings for medical devices, administration of nano-drug in cardiovascular healing, smart bio-mimetic electro-osmotic nanofluid pumps in ocular analysis, etc. Inspired by the aforementioned new things, here we plan to develop a new mathematical model for EOF of ionized non-Newtonian blood carrying dissimilar copper and gold nanoparticles via a vertical ciliated peristaltic micro-vessel under an electromagnetic field environment. The Jeffrey viscoelastic liquid model is invoked to mimic non-Newtonian features of blood mixed with hybridized copper and gold nanoparticles (Au-Cu/blood). The modeled formulae are shortened based on lubrication and Debye–Hückel linearization estimations. The sophisticated homotopy perturbation technique is opted to track out the optimal series solution for outcoming coupled nonlinear equations. A comparison between the hybrid nano-blood (Au-Cu/blood) model and the Cu-blood model is executed. The novelty of the proposed research work is the exploration of EDL’s phenomena and its critical role in streaming ionized blood infused with magnetized copper and gold nanoparticles via ciliated micro-vessel with peristaltic wall.

For further clarification, the novel objectivities of this simulation are itemized in the following bullets:

  • Exploration of electric double-layer (EDL) phenomena and its impact on the electro-magneto-hydrodynamic flow of non-Newtonian blood suspended with hybridized nanoparticles (copper and gold) due to the metachronal beating of cilia tips inside micro-vessel

  • Fitting of Jeffrey liquid model in order to explain the non-Newtonian rheology of blood

  • Integration of ionic blood (electrolyte solution), magnetic hybridized nanoparticles, electromagnetic force (Lorentz force), and buoyancy force

  • Derivation of optimal series solutions by opting the homotopy perturbation method (HPM).

Modeling

Physical scheme

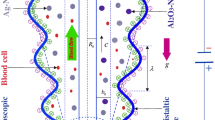
Consider the two-dimensional laminar electro-magneto-hydrodynamic (EMHD) of ionized non-Newtonian blood via a vertical micro-vessel with a ciliated wall. The wall of the micro-vessel wall is furnished with cilia and outer wall is negatively charged. The blood motion is induced by the cilia beating as well as electro-osmotic body force. The hybrid nano-blood is prepared as a homogeneous scattering of Cu-Au nano-powders into the blood. A cylindrical coordinate system \((\tilde{R},\tilde{Z})\) is considered to devise the current modeled problem, where \(\tilde{Z}\) is the axial coordinate, and \(\tilde{R}\) radial coordinate. The geometry of the modeled problem is displayed in Fig. 1. A magnetic field is anticipated along the \(\tilde{R}\) direction. An external electric field is applied along the \(\tilde{Z}\) direction, which induces the EMHD inside the ciliated micro-vessel. The electrokinetic body force is \(\rho_{{\text{e}}} E = \rho_{{\text{e}}} (E_{{{\tilde{\text{R}}}}} ,E_{{{\tilde{\text{Z}}}}} )\). The micro-vessel wall is sustained with the uniform temperature \(T_{0}\).

Fig. 1
figure 1

Geometrical structure of the problem

Full size image

The envelopes of the cilia tips can be defined mathematically as [64]:

$$ \tilde{R} = \tilde{H} = \tilde{F}(\tilde{Z},\tilde{t}) = \tilde{a} + \delta \tilde{a}\cos \frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t}), $$
(1)
$$ \tilde{Z} = \tilde{G}(\tilde{Z},\tilde{Z}_{0} ,\tilde{t}) = \tilde{a} + \delta \tilde{a}\alpha \;\sin \;\frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t}), $$
(2)

where \(\delta\) represents the dimensionless the cilia length, \(\tilde{a}\) the mean radius of the ciliated pipe, \(c\) metachronal wave speed, \(\alpha\) the eccentricity due to elliptical motion, \(\lambda\) the metachronal wavelength, and \(\tilde{Z}_{0}\) the reference particle position. The large number of cilia merges and exhibits a beating model over the inner wall of the ciliated pipe. This beating pattern produces a continuous chain of waves that acts similar to a sinusoidal or peristaltic wave at the wall of the pipe. Equations (1–2) describe the geometry of cilia movement in the form of elliptical shape.

The velocity constituents of the blood flow incited due to the cilia tips are [64]:

$$ \tilde{W} = \left( {\frac{{\partial \tilde{Z}}}{{\partial \tilde{t}}}} \right)_{{\tilde{Z}_{0} }} = \frac{{\partial \tilde{G}}}{{\partial \tilde{t}}} + \frac{{\partial \tilde{G}}}{{\partial \tilde{Z}}}\frac{{\partial \tilde{Z}}}{{\partial \tilde{t}}} = \frac{{\partial \tilde{G}}}{{\partial \tilde{t}}} + \frac{{\partial \tilde{G}}}{{\partial \tilde{Z}}}\tilde{W} $$
(3)
$$ \tilde{U} = \left( {\frac{{\partial \tilde{R}}}{{\partial \tilde{t}}}} \right)_{{\tilde{Z}_{0} }} = \frac{{\partial \tilde{F}}}{{\partial \tilde{t}}} + \frac{{\partial \tilde{F}}}{{\partial \tilde{Z}}}\frac{{\partial \tilde{Z}}}{{\partial \tilde{t}}} = \frac{{\partial \tilde{F}}}{{\partial \tilde{t}}} + \frac{{\partial \tilde{F}}}{{\partial \tilde{Z}}}\tilde{W} $$
(4)

Through Eqs. (1–2), Eqs. (3–4) can be rewritten as:

$$ \tilde{W} = - \frac{{\frac{2\pi }{\lambda }\delta \alpha \tilde{a}c\;\cos \;\frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t})}}{{1 - \frac{2\pi }{\lambda }\delta \alpha \tilde{a}\;\cos \;\frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t})}} $$
(5)
$$ \tilde{U} = \frac{{\frac{2\pi }{\lambda }\delta \alpha \tilde{a}c\;\sin \;\frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t})}}{{1 - \frac{2\pi }{\lambda }\delta \alpha \tilde{a}\;\cos \;\frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t})}} $$
(6)

Jeffrey liquid scheme

To study viscoelastic attributes of hybrid nano-blood, Jeffrey fluid model is taken into consideration. In this regard, the corresponding constitutive relation for the extra-stress tensor \(\tilde{S}\) can be expressed as [37]:

$$ \tilde{S} = \frac{1}{{1 + \lambda_{1}^{ * } }}(\dot{\gamma } + \lambda_{2} \ddot{\gamma }), $$
(7)

where \(\lambda_{1}^{ * }\) assigns the ratio of relaxation time to retardation time, \(\lambda_{2}\) the retardation time, \(\dot{\gamma }\) the shear rate, and dots (\(\cdot\)) the differentiation with respect to time.

Electro-hydrodynamics

In electrostatics theory, the electric potential function in an electrolyte solution satisfies the Poisson–Boltzmann equation. According to it, the electric potential \(\tilde{\Phi }\) across the EDL is expressed as follows [15, 73]:

$$ \nabla^{2} \tilde{\Phi } = - \frac{{\rho_{\text{e}} }}{{\varepsilon_{0} }}, $$
(8)

where \(\varepsilon_{0}\) is the dielectric permittivity of the ionic blood (electrolyte) and \(\rho_{{\text{e}}}\) the net charge density of the ionic blood in a unit volume due to the EDL, which is given as follows [15]:

$$ \rho_{{\text{e}}} = e\overline{z}(n^{ + } - n^{ - } ), $$
(9)

\(e\) represents the net electronic charge (\(1.6 \times 10^{ - 19}\) C), \(\overline{z}\) is the valency for both the ions (cations and anions), and \(n^{ - }\) and \(n^{ + }\) are the ionic concentrations of anions and cations in the ionic blood, respectively. The Boltzmann distribution function for local ionic density is as follows [59]:

$$ n^{ \pm } = n_{0} e^{{ \pm \frac{{\text{e}\overline{z}\tilde{\Phi }}}{{K_{B} T_{a} }}}} , $$
(10)

where \(n_{0}\) is the bulk density of anions and cations in the ionic blood, \(K_{{\text{B}}}\) the Boltzmann constant, and \(T_{{\text{a}}}\) the average temperature of the ionic blood. In the endoscopic conduit, there is no gradient of ionic concentration in the axial direction and hence the distribution of ionic concentration is appropriate [15, 73, 74]. In a unit volume of the ionic blood, the electric charge density is rewritten as:

$$ \rho_{{\text{e}}} = - 2n_{0} e\overline{z}\sinh \left( {\frac{{e\overline{z}\tilde{\Phi }}}{{K_{{\text{B}}} T_{{\text{a}}} }}} \right). $$
(11)

In view of (8) and (11), the simplified Poisson–Boltzmann equation is as:

$$ \nabla^{2} \tilde{\Phi } = \frac{{2n_{0} e\overline{z}}}{{\varepsilon_{0} }}\sinh \left( {\frac{{e\overline{z}\tilde{\Phi }}}{{K_{{\text{B}}} T_{{\text{a}}} }}} \right). $$
(12)

For very low zeta potential \(( < 25mV)\) for a wide range of PH of the electrolytic blood solutions across EDL, the Poisson–Boltzmann Eq. (12) can be simplified by adopting \(\sinh \left( {\frac{{e\overline{z}\tilde{\Phi }}}{{K_{{\text{B}}} T_{{\text{a}}} }}} \right) \approx \frac{{e\overline{z}\tilde{\Phi }}}{{K_{{\text{B}}} T_{{\text{a}}} }}\) under the \(Debye - H\ddot{u}ckel\) linearization approximation and takes the form:

$$ \nabla^{2} \tilde{\Phi } = \frac{{2n_{0} \left( {e\overline{z}} \right)^{2} }}{{\varepsilon_{0} K_{{\text{B}}} T_{{\text{a}}} }}\tilde{\Phi }. $$
(13)

Governing equations

The governing equations in the laboratory frame for the proposed EMHD of ionized blood with hybridized nanoparticles’ suspension via a ciliated micro-vessel with peristaltic wall under the above-mentioned suppositions and employing Boussinesq approximation are [75, 76]:

$$ \frac{{\partial \tilde{U}}}{{\partial \tilde{R}}} + \frac{{\tilde{U}}}{{\tilde{R}}} + \frac{{\partial \tilde{W}}}{{\partial \tilde{Z}}} = 0, $$
(14)
$$ \rho_{{{\text{hnf}}}} \left( {\frac{{\partial \tilde{U}}}{{\partial \tilde{t}}} + \tilde{U}\frac{{\partial \tilde{U}}}{{\partial \tilde{R}}} + \tilde{W}\frac{{\partial \tilde{U}}}{{\partial \tilde{Z}}}} \right) = - \frac{{\partial \tilde{P}}}{{\partial \tilde{R}}} + \frac{1}{{\tilde{R}}}\frac{\partial }{{\partial \tilde{R}}}(\tilde{R}\tilde{S}_{{\tilde{\text{R}}\tilde{\text{R}}}} ) + \frac{\partial }{{\partial \tilde{Z}}}(\tilde{S}_{{\tilde{\text{R}}\tilde{\text{Z}}}} ), $$
(15)
$$ \rho_{{{\text{hnf}}}} \left( {\frac{{\partial \tilde{W}}}{{\partial \tilde{t}}} + \tilde{U}\frac{{\partial \tilde{W}}}{{\partial \tilde{R}}} + \tilde{W}\frac{{\partial \tilde{W}}}{{\partial \tilde{Z}}}} \right) = - \frac{{\partial \tilde{P}}}{{\partial \tilde{Z}}} + \frac{1}{{\tilde{R}}}\frac{\partial }{{\partial \tilde{R}}}(\tilde{R}\tilde{S}_{{\tilde{\text{R}}\tilde{\text{Z}}}} ) + \frac{\partial }{{\partial \tilde{Z}}}(\tilde{S}_{{\tilde{Z}\tilde{Z}}} ) + (\rho \beta_{{\tilde{T}}} )_{{{\text{hnf}}}} g(\tilde{T} - \tilde{T}_{0} ) $$
$$ - \sigma_{{{\text{hnf}}}} B_{0}^{2} \tilde{W} + \rho_{{\text{e}}} E_{{{\tilde{\text{Z}}}}} , $$
(16)
$$ \begin{gathered} (\rho c_{\text{p}} )_{{{\text{hnf}}}} \left( {\frac{{\partial \tilde{T}}}{{\partial \tilde{t}}} + \tilde{U}\frac{{\partial \tilde{T}}}{{\partial \tilde{R}}} + \tilde{W}\frac{{\partial \tilde{T}}}{{\partial \tilde{Z}}}} \right) = \tilde{S}_{{\tilde{\text{R}}\tilde{\text{R}}}} \frac{{\partial \tilde{U}}}{{\partial \tilde{R}}} + \tilde{S}_{{\tilde{\text{R}}\tilde{\text{Z}}}} \frac{{\partial \tilde{W}}}{{\partial \tilde{R}}} + \tilde{S}_{{\tilde{\text{Z}}\tilde{\text{R}}}} \frac{{\partial \tilde{U}}}{{\partial \tilde{Z}}} + \tilde{S}_{{\tilde{\text{Z}}\tilde{\text{Z}}}} \frac{{\partial \tilde{W}}}{{\partial \tilde{Z}}} \hfill \\ \quad \quad \quad + k_{{{\text{hnf}}}} \left( {\frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{R}^{2} }} + \frac{1}{{\tilde{R}}}\frac{{\partial \tilde{T}}}{{\partial \tilde{R}}} + \frac{{\partial^{2} \tilde{T}}}{{\partial \tilde{Z}^{2} }}} \right) + Q_{0} , \hfill \\ \end{gathered} $$
(17)

where \(\tilde{P}\) denotes the blood pressure, \(\tilde{W}\), \(\tilde{U}\) the respective axially and radially velocity components of Cu-Au /blood in the fixed frame, \(E_{{{\tilde{\text{Z}}}}}\) the axially applied electric field, \(\tilde{T}\) the Cu-Au/blood temperature, \(k_{{{\text{hnf}}}}\) the thermal conductivity of Cu-Au/blood, \(\rho_{{{\text{hnf}}}}\) the density of Cu-Au/blood, \((c_{p} )_{{{\text{hnf}}}}\) the specific heat of Cu-Au/blood at constant pressure, and \(Q_{0}\) the internal heat source coefficient.

In the fixed (laboratory) frame, the worthy boundary conditions for the flow configuration are proposed as [64]:

$$ \frac{{\partial \tilde{W}}}{{\partial \tilde{R}}} = 0,{\kern 1pt} \,\,\frac{{\partial \tilde{T}}}{{\partial \tilde{R}}} = 0,{\kern 1pt} \,\,\frac{{\partial \tilde{\Phi }}}{{\partial \tilde{R}}} = 0\,\,{\text{at}}\;\tilde{R} = 0, $$
$$ \tilde{W} = - \frac{{\frac{2\pi }{\lambda }\delta \alpha \tilde{a}c\;\cos \;\left( {\frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t})} \right)}}{{1 - \frac{2\pi }{\lambda }\delta \alpha \tilde{a}\;\cos \;\left( {\frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t})} \right)}},{\kern 1pt} \tilde{T} = \tilde{T}_{0} ,{\kern 1pt} \tilde{\Phi } = \tilde{\Phi }_{0} \;{\text{at}}\;\tilde{R} = \tilde{H} = \tilde{a} + \delta \tilde{a}\cos \;\left( {\frac{2\pi }{\lambda }(\tilde{Z} - c\tilde{t})} \right), $$
(18)

Empirical relations and thermophysical properties

The empirical relations and thermophysical properties of Au NPs, blood, and Cu NPs are provided in Tables 1 and 2.where \(\phi_{1}\) and \(\phi_{2}\) denote the solid volume fractions of Cu and gold NPs, respectively. The suffices \(s_{1}\), \(s_{2}\), \(f\), \(hnf\), and \(nf\) signify solid Cu NPs, solid Au NPs, base liquid (blood), hybrid nano-blood (Cu-Au/blood), and nano-blood (Cu-blood), respectively. The case \(\phi_{1} = \phi_{2} = 0\) (with no suspension of NPs) corresponds to the pure-blood. The thermophysical properties are specified in Table 2.

Table 1 Hybrid nano-blood and nano-blood models [68]
Full size table
Table 2 Thermophysical properties of blood, copper, and gold NPs [68]
Full size table

Flow scrutiny in moving frame of reference

Here flow problem is considered unsteady. For this in the fixed frame into the steady state in the wave frame \((\tilde{r},\tilde{z})\), developing via the same wave speed c, the linear transformations are established as [64, 73]:

$$ \begin{aligned} \tilde{r} = & \tilde{R},\;{\mkern 1mu} \tilde{z} = \tilde{Z} - c\tilde{t},\;\tilde{u} = \tilde{U},{\mkern 1mu} \;\tilde{w} = \tilde{W} - c,\;{\mkern 1mu} \tilde{h}(\tilde{z},\tilde{t}) \\ &\quad= \tilde{H}(\tilde{Z},\tilde{t}),\;{\mkern 1mu} \tilde{p}(\tilde{z},\tilde{r},\tilde{t}) \\ & \tilde{P}(\tilde{Z},\tilde{R},\tilde{t}),{\text{ }}\tilde{T}(\tilde{z},\tilde{r},\tilde{t}) = \tilde{T}(\tilde{Z},\tilde{R},\tilde{t}), \\ \end{aligned}$$
(19)

Using these dimensionless variables:

$$ \begin{gathered} r = \frac{{\tilde{r}}}{{\tilde{a}}},{\kern 1pt} \,z = \frac{{\tilde{z}}}{\lambda },{\kern 1pt} \,w = \frac{{\tilde{w}}}{c},{\kern 1pt} \,u = \frac{{\lambda \tilde{u}}}{{\tilde{a}c}},{\kern 1pt} \,p = \frac{{\tilde{a}^{2} \tilde{p}}}{{c\lambda \mu_{{\text{f}}} }},{\kern 1pt} \,\theta = \frac{{\tilde{T} - \tilde{T}_{0} }}{{\tilde{T}_{0} }},{\kern 1pt} \,\Phi = \frac{{\tilde{\Phi }}}{{\Phi_{0} }},{\kern 1pt} {\kern 1pt} \,\Phi_{0} = \frac{{K_{\text{B}} T_{\text{a}} }}{{e\tilde{z}}},{\kern 1pt} \,{\kern 1pt} t = \frac{{c\tilde{t}}}{\lambda }, \hfill \\ \beta = \frac{{\tilde{a}}}{\lambda },{\kern 1pt} \,\lambda_{1} = \frac{{c\lambda_{1}^{ * } }}{{\tilde{a}}},{\kern 1pt} \,Re = \frac{{c\tilde{a}\rho_{{\text{f}}} }}{{\mu_{{\text{f}}} }},{\kern 1pt} \,M^{2} = \frac{{\sigma_{\text{f}} B_{0}^{2} \tilde{a}^{2} }}{{\mu_{\text{f}} }},{\kern 1pt} \,\kappa = b_{0} e\tilde{z}\sqrt {\frac{{2n_{0} }}{{\varepsilon_{0} K_{{\text{B}}} T_{{\text{a}}} }}} = \frac{{b_{0} }}{{\lambda_{\text{D}} }},{\kern 1pt} \,U_{{{\text{hs}}}} = - \frac{{\varepsilon_{0} \zeta E_{{{\tilde{\text{z}}}}} }}{{c\mu_{{\text{f}}} }}, \hfill \\ Gr = \frac{{g\tilde{a}^{2} \tilde{T}_{0} \rho_{{\text{f}}} (\beta_{\text{T}} )_{{\text{f}}} }}{{c\mu_{{\text{f}}} }},{\kern 1pt} \,Br = \frac{{c^{2} \mu_{{\text{f}}} }}{{(c_{{\text{p}}} )_{{\text{f}}} \tilde{T}_{0} }},{\kern 1pt} \,S_{\text{ij}} = \frac{{\tilde{a}\tilde{S}_{{{\text{ij}}}} }}{{c\mu_{{\text{f}}} }},{\kern 1pt} \,h = \frac{{\tilde{h}}}{{\tilde{a}}},{\kern 1pt} \,\xi = \frac{{Q_{0} \tilde{a}^{2} }}{{k_{{\text{f}}} \tilde{T}_{0} }}, \hfill \\ \end{gathered} $$
(20)

where \(Re\) is the Reynolds number, \(M^{2}\) the magnetic field term, \(\lambda_{1}\) the Jeffrey parameter, \(U_{\text{hs}}\) the Helmholtz–Smoluchowski velocity (maximum electro-osmotic velocity, \(\kappa\) the electro-osmotic term, \(Gr\) the thermal Grashof number, \(Br\) the Brinkman number, and \(\xi\) the internal heat source term.

In pursuance of (7), (19–20), and the lubrication estimations, Eqs. (13–17) related to the viscoelastic hybrid nano-blood can be put in the dimensionless form as:

$$ \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \Phi }{{\partial r}}} \right) = \kappa^{2} \Phi , $$
(21)
$$ \frac{\partial p}{{\partial r}} = 0, $$
(22)
$$ - \frac{\partial p}{{\partial z}} + \frac{{x_{1} }}{{1 + \lambda_{1} }}\frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial w}{{\partial r}}} \right) + x_{2} Gr\theta + \kappa^{2} U_{{{\text{hs}}}} \Phi - x_{3} M^{2} (w + 1) = 0, $$
(23)
$$ \frac{{x_{4} }}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \theta }{{\partial r}}} \right) + \frac{{x_{1} Br}}{{1 + \lambda_{1} }}\left( {\frac{\partial w}{{\partial r}}} \right)^{2} + \xi = 0, $$
(24)

where \(x_{1} = \frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{{\text{f}}} }}\), \(x_{2} = \frac{{(\rho \beta )_{{{\text{hnf}}}} }}{{(\rho \beta )_{{\text{f}}} }}\), \(x_{3} = \frac{{\sigma_{{{\text{hnf}}}} }}{{\sigma_{{\text{f}}} }}\), \(x_{4} = \frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }}\).

The non-dimensional form of the physical boundary conditions (BCs) becomes

$$ \frac{\partial w}{{\partial r}} = 0,{\kern 1pt} \,\frac{\partial \theta }{{\partial r}} = 0,{\kern 1pt} \,\frac{\partial \Phi }{{\partial r}} = 0\;\,{\text{at}}\;\,r = 0, $$
$$ \begin{gathered} \frac{\partial w}{{\partial r}} = 0,{\kern 1pt} \,\frac{\partial \theta }{{\partial r}} = 0,{\kern 1pt} \,\frac{\partial \Phi }{{\partial r}} = 0\;\,{\text{at}}\;\,r = 0, \hfill \\ w = - 1 - \frac{2\pi \delta \alpha \beta \cos 2\pi z}{{1 - 2\pi \delta \alpha \beta \cos 2\pi z}},{\kern 1pt} \,\theta = 0,{\kern 1pt} \,\Phi = 1\;{\text{at}}\;r = h(z) = 1 + \delta \cos 2\pi z, \hfill \\ \end{gathered} $$
(25)

where \(\beta\) is the wave number.

Solution of Poisson–Boltzmann Eq. (21) subject to boundary conditions (25) can be easily derived by using Mathematica software and given by

$$ \Phi (r,z) = \frac{{I_{0} (\kappa r)}}{{I_{0} (\kappa h)}}, $$
(26)

where \(I_{0}\) designates the zeroth order modified Bessel function of first kind.

HPM solution

Equations (23–24) are highly coupled nonlinear, and it is complex to resolve it analytically. Thus, series solution or numerical scheme is the only one opportunity to handle this coupled nonlinear equations. Recently, He [74] proposed the homotopy perturbation method (HPM). In several engineering, mechanical and liquid dynamical branches, HPM has been employed to extort more precise solution or estimation in series scheme through high convergence precision of linear and nonlinear modeled equations. A homotopy is selected and built through \(\hat{q} \in [0,1][0,1]\) embedding term considered to be small quantity [75] in this technique.

After inserting (26) in (23), Eqs. (23–24) become:

$$ \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial w}{{\partial r}}} \right) + a_{0} I_{0} (\kappa r) + a_{1} \theta - a_{2} (w + 1) - a_{3} = 0, $$
(27)
$$ \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial \theta }{{\partial r}}} \right) + a_{4} \left( {\frac{\partial w}{{\partial r}}} \right)^{2} + a_{5} = 0, $$
(28)

where

$$ \begin{gathered} a_{0} = \frac{{\kappa^{2} (1 + \lambda_{1} )U_{\text{hs}} }}{{x_{1} I_{0} (\kappa h)}},\;\;a_{1} = \frac{{x_{2} }}{{x_{1} }}(1 + \lambda_{1} ){\kern 1pt} Gr,\;\;a_{2} = \frac{{x_{3} }}{{x_{1} }}(1 + \lambda_{1} )M^{2} ,\;\; \hfill \\ a_{3} = \frac{{1 + \lambda_{1} }}{{x_{1} }}\frac{dp}{{dz}},\;\;a_{4} = \frac{{x_{1} Br}}{{x_{4} (1 + \lambda_{1} )}},\;\;a_{5} = \frac{\xi }{{x_{4} }}. \hfill \\ \end{gathered} $$
(29)

In order to solve Eqs. (27–28), we construct a homotopy \(\hat{h}(r,\hat{q}):\Omega \times [0,1] \to \Re\) which assures

$$ \begin{gathered} (1 - \hat{q})[\hat{L}(\hat{w}) - \hat{L}(\hat{w}_{0} )] + \hat{q}[\hat{L}(\hat{w}) \hfill \\ \quad + a_{0} I_{0} (\kappa r) + a_{1} \hat{\theta } - a_{2} (\hat{w} + 1) - a_{3} ] = 0 \hfill \\ \end{gathered} $$
(30)
$$ (1 - \hat{q})[\hat{L}(\hat{\theta }) - \hat{L}(\hat{\theta }_{0} )] + \hat{q}[\hat{L}(\hat{\theta }) + a_{4} \left( {\frac{{\partial \hat{w}}}{\partial r}} \right)^{2} + a_{5} ] = 0, $$
(31)

where \(\hat{L} = \frac{1}{r}\frac{\partial }{\partial r}\left( {r\frac{\partial }{\partial r}} \right)\).Supposing the initial guess for the linear operator has the form

$$ \hat{w}_{0} (r,z) = X + \frac{1}{4}(1 + \lambda_{1} )(r^{2} - h^{2} )\frac{\text{d}p}{{\text{d}z}},\;\;\hat{\theta }_{0} (r,z) = \frac{1}{4}(r^{2} - h^{2} ). $$
(32)

In view of HPM, the estimated solutions \(\hat{w}(r,z)\) and \(\hat{\theta }(r,z)\) have been supposed in the these forms of power series:

$$ \begin{gathered} \hat{w}(r,z) = \hat{w}_{0} + \hat{w}_{1} \hat{q} + \hat{w}_{2} \hat{q}^{2} + \cdots , \hfill \\ \hat{\theta }(r,z) = \hat{\theta }_{0} + \hat{\theta }_{1} \hat{q} + \hat{\theta }_{2} \hat{q}^{2} + \cdots \hfill \\ \end{gathered} $$
(33)

Presently, including Eqs. (30–31) in Eqs. (28–29) and comparing the powers of \(\hat{q}\), the linear equations scheme can be achieved. On view of homotopy perturbation scheme, taking \(\hat{q} = 1\), one has

$$ w(r,z) = \hat{w}(r,z) = \hat{w}_{0} + \hat{w}_{1} + \hat{w}_{2} + \cdots $$
(34)
$$ \theta (r,z) = \hat{\theta }(r,z) = \hat{\theta }_{0} + \hat{\theta }_{1} + \hat{\theta }_{2} + \cdots $$
(35)

The final expressions for blood temperature and velocity field are:

$$ w(r,z) = A_{1} + A_{2} (r^{2} - h^{2} ) + A_{3} (r^{4} - h^{4} ) + A_{4} (r^{6} - h^{6} ) + A_{5} I_{0} (\kappa r), $$
(36)
$$ \begin{gathered} \theta (r,z) = A_{6} (r^{2} - h^{2} ) + A_{7} (r^{4} - h^{4} ) + A_{8} (r^{6} - h^{6} ) + A_{9} [2I_{0} (h\kappa ) - h\kappa I_{1} (h\kappa ) \hfill \\ - 2I_{0} (\kappa r) + \kappa rI_{1} (\kappa r)], \hfill \\ \end{gathered} $$
(37)

where \(I_{1}\) designates the first order modified Bessel function of first kind and the constants \(A_{1}\), \(A_{2}\), \(A_{3}\), \(A_{4}\), \(A_{5}\), \(A_{6}\), \(A_{7}\), \(A_{8}\) and \(A_{9}\) are given in Appendix A.

Stream function, flow rate, wall shear stress and heat transport coefficient

The volume flow rate \(Q\) is computed as

$$ Q = 2\pi \int_{0}^{h} r{\kern 1pt} w(z,r){\text{d}}r, $$
(38)

with this, the pressure gradient is

$$ \frac{\text{d}p}{{\text{d}z}} = \frac{1}{{2B_{1} }}\{ B_{2} - (B_{2}^{2} - 4B_{1} B_{3} )^{1/2} \} , $$
(39)

where \(B_{1} ,\;B_{2} ,\) and \(B_{3}\) are given in Appendix A.

The mean volume flow rate via one period of the peristaltic wave is:

$$ F = Q + \frac{1}{2}\left( {\frac{{\delta^{2} }}{2} + 1} \right), $$
(40)

The non-dimensional pressure rise \(\Delta p\) toward one period of wavelength can be articulated as

$$ \Delta p = \int_{0}^{1} \frac{\text{d}p}{{\text{d}z}}{\kern 1pt} {\text{d}}z, $$
(41)

To assess the numerical estimations of the pressure rise \(\Delta p\), \({\text{Mathematica}}\) built-in function \({\text{N}}\;{\text{Integrate}}\) is deployed.

The speed components are articulated in terms of the stream function and are defined as

$$ u = - \frac{1}{r}\frac{\partial \psi }{{\partial r}},\;w = \frac{1}{r}\frac{\partial \psi }{{\partial r}} $$
(42)

To acquire the stream function \(\psi\), we integrate \(w = \frac{1}{r}\frac{\partial \psi }{{\partial r}}\) through \(\psi = 0\) at \(r = 0\), and then the stream function is specified as

$$ \psi = r^{2} \left[ {\frac{{A_{1} }}{2} - \frac{1}{2}h^{2} (A_{2} + A_{3} h^{2} + A_{4} h^{4} )} \right] + \frac{{A_{2} }}{4}r^{4} + \frac{{A_{3} }}{6}r^{6} + \frac{{A_{4} }}{8}r^{8} + \frac{{A_{5} }}{\kappa }rI_{1} (\kappa r), $$
(43)

The stream function denotes the volumetric flow rate via the cross section bounded through the ciliated tube wall.

The wall shear at the tube wall is estimated by utilizing the following equation:

$$ \begin{aligned} S_{\text{rz}} \,=\,& \frac{{\mu_{{{\text{hnf}}}} }}{{\mu_{{\text{f}}} }}\left( {\frac{\partial w}{{\partial r}}} \right)_{{{\text{r}} = {\text{h}}}} \\\,=\,& x_{1} [2A_{2} h + 4A_{3} h^{3} + 6A_{4} h^{5} + A_{5} \kappa I_{1} (h\kappa )]. \\ \end{aligned} $$
(44)

The heat transport coefficient at the wall of ciliated pipe is calculated as:

$$ \begin{aligned} Z^{ * } = \frac{{k_{{{\text{hnf}}}} }}{{k_{{\text{f}}} }}\frac{{\text{d}}h}{{{\text{d}}z}}\left( {\frac{\partial \theta }{{\partial r}}} \right)_{{{\text{r}} = {\text{h}}}} \\ = - 2\pi \delta hx_{4} [2A_{6} + 4A_{7} h^{2} + 6A_{8} h^{4} + A_{9} \kappa^{2} I_{2} (h\kappa )]\sin 2\pi z, \\ \end{aligned} $$
(45)

where \(I_{2}\) designates the second-order modified Bessel function of first kind.

Code validation

To testify the authenticity of our semi-analytical resolutions, we have supposed a particular cases. The current model moderates to the model studied via [76] by deputizing \(\kappa = \xi = \phi_{1} = \phi_{2} = 0\). Furthermore, in Fig. 2a-b, the graphical comparison of the present model in the absence of viscous dissipation have been carried out for exact solution and semi-analytical homotopic perturbation approach. These figures affirm that our computed homotopic solution for the limiting case is very close to the results of exact solution. Furthermore, a numeric contrast in Table 3 is performed in the constraining case and reported excellent correlation with Nadeem and Sadaf [79]. These establish the authenticity of the present solutions.

Fig. 2
figure 2

Profiles of velocity and temperature through \(Br = 0\), \(\alpha = 0.1\), \(\beta = 0.2\), \(M^{2} = 1\), \(\xi = 1\), \(\delta = 0.1\), \(F = 0.5\), \(Gr = 2\), \(\kappa = 1\), \(\lambda_{1} = 0.6\), \(U_{{{\text{hs}}}} = - 2\), \(z = 0.75\), \(\phi_{1} = \phi_{2} = 0.02\)

Full size image
Table 3 Comparison of velocity profile for when varying \(\phi_{1} = 0.02\), \(\alpha = 0.02\), \(\beta = 0.11\), \(z = 0.08\), \(\xi = 0.17\), \(\delta = 0.05\), \(F = 0.16\), \(\lambda_{1} = M^{2} = Br = \phi_{2} = \kappa = 0\)
Full size table

Outcomes and discussion

In this segment, the physical explorations of graphical demonstration for various relevant terms over the pertinent hybrid nano-blood flow characteristics are explicated. The significant fluctuation in the dimensionless velocity and temperature evolutions, pumping characteristics (Axial pressure gradient and pressure rise per wavelength), mean flow rate \(F\), wall shear stress (WSS), heat transport coefficient (HTC), and streamlines for magnetic term \(M^{2}\), Jeffrey term \(\lambda_{1}\), electro-osmotic term \(\kappa\), cilia length \(\delta\), Helmholtz–Smoluchowski velocity (maximum electro-osmotic speed) \(U_{\text{hs}}\), Brinkman number \(Br\), thermal Grashof number \(Gr\), heat source term \(\xi\), and NPs volume fractions \(\phi_{1}\), \(\phi_{2}\) is demonstrated in Figs. 3–9. The graphical demonstrations are executed by taking default values/ranges of parameters and flow constants [15, 64, 73]: \(M^{2} = 0 - 2\), \(\kappa = 2 - 4\), \(U_{hs} = - 4 - - 2\), \(\lambda_{1} = 0 - 0.9\), \(\alpha = 0.1 - 0.4\), \(\beta = 0.1 - 0.4\), \(\delta = 0.1 - 0.7\), \(F = 0.1 - 0.5\), \(Br = 0.1 - 0.5\), \(z = 0 - 2\), \(\xi = 0 - 2\), \(\phi_{1} = 0 - 0.1\), \(\phi_{2} = 0 - 0.1\). In addition, \(\phi_{1} = \phi_{2} = 0\) corresponds to pure blood, \(\phi_{1} = 0.02\), \(\phi_{2} = 0\) for Cu-blood, and \(\phi_{1} = 0.02\), \(\phi_{2} = 0.02\) for Cu-Au/blood. The graphical and numerical outcomes are assessed by implementing computational software Mathematica.

Fig. 3
figure 3

Evolution of \(w(r,z)\) for various physical terms \(\alpha = 0.1\), \(\beta = 0.2\), \(z = 0.75\), \(Br = 0.1\), \(\xi = 1.0\), and a \(\lambda_{1} = 0.6\), \(\kappa = 2.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(\delta = 0.1\), \(F = 0.5\), \(Gr = 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), b \(M^{2} = 1.0\), \(\kappa = 3.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(\delta = 0.1\), \(F = 0.5\), \(Gr = 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), c \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(U_{{{\text{hs}}}} = - 2.0\), \(\delta = 0.1\), \(F = 0.5\), \(Gr = 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), d \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 2.0\), \(\delta = 0.1\), \(F = 0.5\), \(Gr = 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), e \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 2.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(F = 0.5\), \(Gr = 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), f \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 2.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(\delta = 0.1\), \(Gr = 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), g \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 3.0\), \(U_{hs} = - 2.0\), \(\delta = 0.1\), \(F = 0.5\), \(\phi_{1} = \phi_{2} = 0.02\), h \(M^{2} = 3.0\), \(\lambda_{1} = 0.6\), \(\kappa = 2.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(\delta = 0.1\), \(F = 0.5\), \(Gr = 1.0\)

Full size image

Axial velocity profile

The ascendancy of different elevating dynamical quantities, namely magnetic parameter \(M^{2}\), Jeffrey parameter \(\lambda_{1}\), cilia length \(\delta\), thermal Grashof number \(Gr\), electro-osmotic term \(\kappa\), Helmholtz–Smoluchowski velocity (maximum electro-osmotic speed) \(U_{\text{hs}}\), and NPs volume fractions \(\phi_{1}\) and \(\phi_{2}\) on the dimensionless axial velocity evolution \(w(r,z)\), is explicated in Fig. 3a-h. The alternation of magnetic parameter \(M^{2}\) via axial velocity field is verified in Fig. 3a. It is evident from these curves that the axial velocity is substantially decremented at the core region of the ciliary vessel for growing \(M^{2}\) for both hybrid Au-Cu/blood and Cu-blood flow. The red blood cell contains hemoglobin molecules which are formed by iron oxide. Those red cells are attracted by the strong Lorentz forces which are generated by intensifying \(M^{2}\). Hence, blood circulation is disrupted by an implication of a strong magnetic field. Therefore, the blood flow can be influentially controlled through choosing suitable strength of applied magnetic field during various kinds of complex surgeries. Figure 3b is designed to disclose how Jeffrey parameter \(\lambda_{1}\) affects the axial velocity. The plotted figures explore that by boosting the Jeffrey parameter \(\lambda_{1}\), the axial velocity rises in the core domain of the ciliary vessel, but the overturn trend is evident in the peripheral domain. Jeffrey parameter \(\lambda_{1}\) designates the proportion of relaxation time to retardation time. In the scenario of physiological fluids (such as blood, mucus, semen, etc.), the retardation time is longer than the relaxation time (\(\lambda_{1} < 1\)). This suggests that when stress is relieved, the physiological fluids respond more quickly and get back to their normal state, which has a significant consequence through the pressure gradient, resulting in an increment in axial flow at the core domain of the ciliary blood vessel. The consequence of electro-osmotic term \(\kappa\) via the axially varying speed distribution is directed in Fig. 3c. The axial velocity exposes an elevating trend in the core domain of ciliary blood vessels for larger \(\kappa\), while an inverse trend is witnessed in the peripheral domain. Debye length or EDL (electric double layer) thickness is inversely linked to the electro-osmotic term, which characterizes the electro-osmosis phenomenon. An upsurge in \(\kappa\) (thinning the EDL) amplifies the electrical potential distribution which accelerates the blood pumping in the core domain of the micro-vessel and suppresses it in the peripheral domain of the vessel wall. In the EOF regime, a thin EDL plays as a stabilizing factor. It can be perceived that the electro-osmotic parameter \(\kappa\) (essential factor in electro-osmosis) synchronizes electric potential in the EDL and is useful for designing and developing micro-blood pumps and mixing physiological fluids (blood, mucus, saliva, semen, etc.) with reagents (medications, nutrients, enzyme, etc.).

Figure 3d portends the alteration of axial velocity for Helmholtz–Smoluchowski speed (maximum electro-osmotic speed) \(U_{{{\text{hs}}}}\). The respective figure designates that there is a suppressing behavior in the blood flow in the core area of the blood vessel and an inverse trend is manifested nearby the blood vessel wall toward changing values (from \(- 4\) to \(- 1\)) of \(U_{{{\text{hs}}}}\). Physically, \(U_{\text{hs}} < 0\) corresponds to the axial electric field orientated in the peristaltic wave way, which assists the electro-osmotic body force \(- \kappa^{2} U_{{{\text{hs}}}} \Phi\). A decrement in negative \(U_{{{\text{hs}}}}\) physically means that the strength of the axially applied electric field is weakened which produces a slow movement of ionic species in the liquid medium. Therefore, the lowering electro-osmotic velocity exhibits declining behavior in the overall axial speed. The fluctuation in axial velocity for multiple values of cilia length \(\delta\) is delineated in Fig. 3e. It is evident that the speed in the streaming domain is deteriorating as \(\delta\) increases. A longer \(\delta\) generates more resistive forces in the streaming region, leading to a declination in velocity distribution. Figure 3f is pervaded to disclose the alteration of axial speed for multiple values of flow rate term \(F\). It is noted that an elevation in \(F\) reveals a mounting trend in the axial speed throughout the streaming area. For larger \(F\), less resistive force is produced throughout the ciliary vessel, and as a outcome, the velocity field gets an escalation.

The impact of enlarging thermal \(Gr\) over the velocity field is manifested in Fig. 3g. A higher \(Gr\) boosts up the buoyancy force which improves the axial speed profile in the main domain, but an inverse outcome is found at the peripheral area of the ciliary vessel. Figure 3h descripts the consequences of \(\phi_{1}\) and \(\phi_{2}\) over the axial velocity profile. An improvement in \(\phi_{1}\) and \(\phi_{2}\) corresponds to a denunciation in the axial speed in the principal domain of the ciliary blood vessel, and a slight augmentation nearby the ciliary micro-vessel wall. From Fig. 3a–g the axial velocity for Cu-Au/blood accomplishes higher estimations than Cu-blood at the core domain but an inverse trend is found at the peripheral domain of the ciliary micro-vessel.

Temperature distribution

In this subpart, Fig. 4a–h is configured to elucidate the contribution of different emerging physical terms such as magnetic term \(M^{2}\), Jeffrey term \(\lambda_{1}\), Brinkman number \(Br\), heat source parameter \(\xi\), electro-osmotic term \(\kappa\), Helmholtz–Smoluchowski speed \(U_{{{\text{hs}}}}\), and nanoparticles (NPs) volume fractions (\(\phi_{1} ,\;\phi_{2}\)) over the non-dimensional temperature field. In Fig. 4a, the fluctuation of Cu-Au/blood and Cu-blood temperature for intensifying magnetic parameter \(M^{2}\) is manifested. It is worthy to note that both Cu-Au/blood and Cu-blood temperature elevates for when \(M^{2}\) enlarges. It is witnessed that the peak of the temperature distribution is found at the center (\(r = 0\)) of the ciliary tube. Blood flow under a magnetic field dissipates thermal energy and as a result, the temperature for both hybrid and nano-blood upsurges. An augmentation of hybrid and nano-blood temperature due to increasing strength of magnetic field has tremendous application in hyperthermic treatment for cancerous cells. The sway of mounting Jeffrey parameter \(\lambda_{1}\) on both Cu-Au/blood and Cu-blood temperature is disclosed in Fig. 4b. For \(\lambda_{1} < 1\) (physiological fluids), the retardation time is higher than the relaxation time. An enhancement in \(\lambda_{1}\) enlarges the relaxation time which enriches the visco-elasticity of blood, and as an outcome, the temperature for both Cu-Au/blood and Cu-blood gets a diminution. The upshot due to an enhancement in Brinkman number \(Br\) on hybrid Cu-Au/blood and Cu-blood temperature is explored in Fig. 4c. An upliftment in \(Br\) receives a remarked attenuation in the temperature of blood. The Brinkman number is a physical function of the proportion of thermal energy yielded by viscous debauchery and heat transport by molecular colliding. For \(Br < 1\), heat transport by molecular colliding is higher than heat produced via viscous dissipation. Therefore, incrementing \(Br\) reduces the impact of heat transit by molecular colliding and abates the temperature of blood. Figure 4d is divulged to outline the consequence of heat source term \(\xi\) on both Cu-Au/blood and Cu-blood temperature. It is evident from these graphs that an upliftment in \(\xi\) yields more heat energy, which dramatically raises the blood temperature. To outline the upshot of \(U_{{{\text{hs}}}}\) over temperature, Fig. 4e is presented. It is remarked that both Cu-Au/blood and Cu-blood temperature tends to a declination for changing values from \(- 3.5\) to \(- 2.0\) of \(U_{{{\text{hs}}}}\). A higher negative \(U_{\text{hs}}\) strongly assists the electro-osmotic body force which develops temperature profile. In Fig. 4f, the iteration of both Cu-Au/blood and Cu-blood temperature for multiple values of electro-osmotic parameter \(\kappa\) is exposed. It infers that a higher value of \(\kappa\) attenuates the thickness of EDL which has a flourishing role in the enhancement of the temperature profile. According to the kinetic theory of molecules, kinetic energy and temperature are directly related. An inhomogeneous dispersion of electric potential within the hybrid nano-blood produces kinetic energy in the blood cells and nanoparticles, which tends to uplift the temperature profile when \(\kappa\) enlarges.

Fig. 4
figure 4

Evolution of \(\theta (r,z)\) for various physical terms \(\alpha = 0.1\), \(\beta = 0.2\), \(z = 0.75\), \(\delta = 0.1\), \(F = 0.5\), \(Gr = 2.0\), and a \(\lambda_{1} = 0.6\), \(Br = 0.1\), \(\xi = 1.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(\kappa = 3.0\), \(\phi_{1} = \phi_{2} = 0.02\), b \(M^{2} = 1.0\), \(Br = 0.1\), \(\xi = 1.0\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(\phi_{1} = \phi_{2} = 0.02\), c \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\xi = 1.0\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(\phi_{1} = \phi_{2} = 0.02\), d \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Br = 0.1\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(\phi_{1} = \phi_{2} = 0.02\), e \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Br = 0.1\), \(\xi = 1.0\), \(\kappa = 3.0\), \(\phi_{1} = \phi_{2} = 0.02\), f \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Br = 0.1\), \(\xi = 1.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), g \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Br = 0.1\), \(\xi = 1.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(\kappa = 3.0\), h \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Br = 0.1\), \(\xi = 1.0\), \(U_{{{\text{hs}}}} = - 2.0\), \(\kappa = 3.0\)

Full size image

The fluctuation of temperature profile for multiple values of NPs volume fractions (\(\phi_{1}\) and \(\phi_{2}\)) is designed in Fig. 4g. It is worthy to record that improvement in \(\phi_{1}\) and \(\phi_{2}\) leads to an attenuation in the temperature of hybrid nano-blood. It is mechanically justified since the scattering of dissimilar NPs is related directly to the thermal diffusivity, which is the main reason for fast heat migration from the flow regime, resulting in a crucial reduction in the blood temperature. Due to a significant advancement in the thermophysical behavior of blood, the hybrid NPs concentration is preferred over the mono NPs concentration. As blood goes away from the ciliated vessel wall, NPs at the peripheral domain of the ciliated vessel heated up, the blood circulation enriches in the central domain of the ciliary blood vessel, and the temperature of blood subsequently diminishes. The alteration in the temperature for Cu-Au/blood, Cu-blood, Au-blood, and pure blood is interpreted via Fig. 4h. It is remarked that Cu-Au/blood depicts supremacy toward other nano or pure blood. Furthermore, Au NPs have a significantly bigger atomic number, which causes a subsequent drop in blood temperature. So, Au NPs have higher thermal efficiency than Cu NPs. In case of hyperthermic therapy for cancerous cells, this output is extremely beneficial (Au NPs as a drug carrier).

Pumping features

Axial pressure gradient

Figure 5a–h is suggested to demystify the consequences of magnetic term \(M^{2}\), Jeffrey term \(\lambda_{1}\), thermal \(Gr\), electro-osmosis parameter \(\kappa\), \(U_{{{\text{hs}}}}\), cilia length \(\delta\), and NPs volume fractions (\(\phi_{1}\) and \(\phi_{2}\)) on the fluctuation of the pressure gradient \({\text{d}}p/{\text{d}}z\). The upshot of magnetic parameter \(M^{2}\) via \({\text{d}}p/{\text{d}}z\) is revealed in Fig. 5a. An intensifying \(M^{2}\) leads to boost up the drag force which tends to suppress the pressure gradient. In Fig. 5b, the alteration of the pressure gradient \({\text{d}}p/{\text{d}}z\) for increasing Jeffrey parameter \(\lambda_{1}\) is exposed. An upsurge in \(\lambda_{1}\) decreases the retardation time which attenuates the elastic property of blood and consequently, \({\text{d}}p/{\text{d}}z\) gets an improvement. The variation of pressure gradient \(dp/dz\) for increasing \(Gr\) is demonstrated in Fig. 5c. For growing \(Gr\), a strong buoyancy force is expanded in the flow domain and consequently, thriving behavior is noted in \({\text{d}}p/{\text{d}}z\).

Fig. 5
figure 5

Evolution of pressure gradient \(\frac{dp}{{dz}}\) for various physical terms \(\alpha = 0.1\), \(\beta = 0.2\), F = 0.5, \(Br = 0.1\), \(\xi = 1.0\), and a \(\lambda_{1} = 0.6\), \(Gr = 2.0\), \(\kappa = 2.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), b \(M^{2} = 1.0\), \(Gr = 2.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), c \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), d \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 2.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), e \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 2.0\), \(\kappa = 3.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), f \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), g \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), h \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\)

Full size image

Figure 5d is divulged to perceive the sway of electro-osmotic term \(\kappa\) on \({\text{d}}p/{\text{d}}z\). It discloses that \(\kappa\) has a diminutive impact on \({\text{d}}p/{\text{d}}z\). For an upliftment in \(\kappa\) (thin EDL), the electro-osmotic force (EOF) is mounted, which generates a substantial deterioration in the pressure gradient. This entails that ion diffusion from the charged surface has a substantial impact on pumping characteristics. Graphs of Fig. 5e disclose that mounted \(U_{{{\text{hs}}}}\) amplifies the pressure gradient \({\text{d}}p/{\text{d}}z\). It is inferred that more pressure gradient is perceived for weaker the axial electric field in flow direction. Figure 5f is illustrated to explore the impression of cilia length \(\delta\) over \({\text{d}}p/{\text{d}}z\). It is noteworthy to record that cilia length \(\delta\) has a subsequent accentuation in \({\text{d}}p/{\text{d}}z\). The growth of NPs volume fractions (\(\phi_{1}\) and \(\phi_{2}\)) outcomes in a dramatic enhancement of \({\text{d}}p/{\text{d}}z\), as shown in Fig. 5g. This suggests that the abundance of hybrid NPs can significantly alter the pressure gradient. The pressure gradients of Cu-Au/blood, Cu-blood, Au-blood, and pure blood are compared in Fig. 5h. These visualizations demonstrate that the pressure gradient for Cu-Au/blood is greater than Cu-blood, Au-blood, and pure blood.

Pressure rise per wavelength

One of the most significant physiological features in the peristaltic pumping process is the pressure rise \(\Delta P\). Figure 6a–h is portrayed to manifest the alteration of \(\Delta P\) against the mean volumetric flow rate \(F\) for multiple values of \(M^{2}\), \(\lambda_{1}\), \(Gr\), \(\kappa\), Helmholtz–Smoluchowski velocity \(U_{\text{hs}}\), cilia length \(\delta\), and NPs volume fractions (\(\phi_{1}\) and \(\phi_{2}\)). Figure 6a reveals that pressure rise \(\Delta P\) has a waning nature with amplifying \(M^{2}\). An intensified magnetic field can offer a surprising response to low blood viscosity, and consequently, a commensurate decrement in \(\Delta P\) also affirms good agreement with the existing literature [80]. Figure 6b is outlined for exploring the influence of \(\lambda_{1}\) over \(\Delta P\). An augmentation in \(\lambda_{1}\) leads to an improvement in viscosity of hybrid and nano-blood in the axial direction, which encourages the pressure rise \(\Delta P\). The variation of the pressure rise \(\Delta P\) for multiple values of \(Gr\) is designed in Fig. 6c. Physically, an enlargement in \(Gr\) induces a strong buoyancy force in the flow area, which elevates the pressure rise. Figure 6d discloses the alteration of pressure rise \(\Delta P\) due to increasing electro-osmotic parameter \(\kappa\). Higher \(\kappa\) improves the electrical potential which attenuates the pressure rise. Figure 6e exhibits the thriving behavior in \(\Delta P\) for changing values \(- 3.5\) to \(- 2\) of \(U_{{{\text{hs}}}}\). For an ascent in \(U_{{{\text{hs}}}}\), the axial electric field is remarkably boosted and as a result, \(\Delta P\) evolves. Thus, the Helmholtz–Smoluchowski velocity \(U_{{{\text{hs}}}}\) can be designed to control the pumping features of EOFs. Figure 6f explores the depleting trends in \(\Delta P\) in the region (\(0 < F \le\) 1) and it evolves in the rest with enlarging \(\delta\). Figure 6g delineates that \(\delta\) strongly elevates with larger values of NPs volume fractions (\(\phi_{1}\) and \(\phi_{2}\)). From the physical point of view, to pump the hybrid nano-blood with a higher concentration, more effort is required. A higher concentration of hybrid NPs leads to a higher increment in the pressure rise. Furthermore, Fig. 6h exposes the comparative studies of pressure rise \(\Delta P\) for Cu-Au/blood, Cu-blood, Au-blood, and pure blood. Outcomes communicate that \(\Delta p_{{{\text{Cu}} - {\text{Au}}/{\text{blood}}}} > \Delta p_{{{\text{Au}} - {\text{blood}}}} > \Delta p_{{{\text{Cu}} - {\text{blood}}}} > \Delta p_{{{\text{Pure}}{\kern 1pt} - {\text{blood}}}}\). There is an inversely linear relationship between \(\Delta p\) and mean flow rate \(F\). These findings are consistent with the physical predictions of the relevant parameters.

Fig. 6
figure 6

\(\Delta P\) evolution for various physical terms \(\alpha = 0.1\), \(\beta = 0.2\), \(Br = 0.1\), \(\xi = 1.0\), and a \(\lambda_{1} = 0.6\), \(Gr = 2.0\), \(\kappa = 2.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), b \(M^{2} = 1.0\), \(Gr = 2.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), c \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), d \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 2.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), e \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 2.0\), \(\kappa = 3.0\), \(\delta = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), f \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), g \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\), h \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\delta = 0.1\)

Full size image

Wall share stress (WSS)

Figure 7a–f is sketched to demystify the consequence of \(M^{2}\), \(\lambda_{1}\), \(Gr\), \(\kappa\), \(U_{{{\text{hs}}}}\), and (\(\phi_{1}\), \(\phi_{2}\)) via \(S_{{{\text{rz}}}}\) at the ciliary micro-vessel wall. From these figures, it is clear that WSS \(S_{{{\text{rz}}}}\) has an inverse deportment as compared to the pressure rise. WSS \(S_{{{\text{rz}}}}\) on the micro-vessel tube wall is significantly enhanced for greater values of \(M^{2}\), \(U_{{{\text{hs}}}}\), \(\phi_{1}\), and \(\phi_{2}\); however, an inverse outcome is tracked out for increasing \(\lambda_{1}\), \(Gr\), and \(\kappa\), as shown in Fig. 7a–f. Higher \(M^{2}\) generates larger Lorentzian drag force which retards ciliary flow pressure rise and results in boosting WSS. It is detected that WSS exhibits monotonically increasing behavior with the mean flow rate \(F\). The hybrid Cu-Au/blood flow accomplishes comparatively higher WSS as compared to Cu-blood.

Fig. 7
figure 7

Evolution of \(S_{rz}\) for \(\alpha = 0.1\), \(\beta = 0.2\), \(\delta = 0.1\), \(Br = 0.1\), \(\xi = 0.5\), and (a) \(\lambda_{1} = 0.6\), \(Gr = 2.0\), \(\kappa = 2.0\), \(U_{\text{hs}} = - 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), (b) \(M^{2} = 1.0\), \(Gr = 1.0\), \(\kappa = 3.0\), \(U_{\text{hs}} = - 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), (c) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 2.0\), \(U_{\text{hs}} = - 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), (d) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(U_ {\text{hs}} = - 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), (e) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), (f) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 2.0\), \(U_{\text{hs}} = - 2.0\)

Full size image

Heat transport coefficient

The fluctuation of the heat transport coefficient \(Z^{ * }\) at the ciliary micro-vessel wall for varying values of \(M^{2}\), \(\lambda_{1}\), \(U_{{{\text{hs}}}}\), \(\kappa\), \(Br\), \(\xi\), \(\delta\), \(\phi_{1}\), and \(\phi_{2}\) is depicted in Fig. 8a–j. The heat transfer coefficient \(Z^{ * }\) exposes a depleting nature for escalating estimation of \(M^{2}\), \(\lambda_{1}\), \(U_{\text{hs}}\), \(\kappa\), and a reverse trend is tracked out for elevating \(Br\), \(\xi\), \(\delta\), \(\phi_{1}\), and \(\phi_{2}\), as sketched in Fig. 8a–i. The magnetic field reduces the intensity of ciliary movement at the vessel wall which decreases heat transfer coefficient \(Z^{ * }\) 3.7% for hybrid nano-blood and 12.4% for Cu nano-blood. From the physical point of view, higher negative \(U_{{{\text{hs}}}}\) strengthens the EOFs which compensate the frictional kinetic energy loss and boost the heat transfer coefficient \(Z^{ * }\). On another side, a thinner EDL (higher value of \(\kappa\)) infers a lower velocity of blood pumping near the micro-vessel wall and as a result, it possesses a lower rate of heat transport. It is also depicted that due to changes of \(\kappa\) from 2.0 to 3.5, \(Z^{ * }\) decreases 8.2% for Cu-Au/blood and 19.8% Cu-blood, respectively. A elevated Br uplifts the kinetic energy of NPs which upsurge the heat transfer coefficient \(Z^{ * }\) 65.7% for Cu-Au/blood and 45.6% for Cu nano-blood. The ionic hybrid or nano-blood in the micro-vessel is energized with upswing heat source parameter \(\xi\), due to which \(Z^{ * }\) surges 26.9% for Cu-Au/blood and 28.8% Cu-blood, respectively. This propensity of heat generation could be efficient in the treatment of thermal therapy. The process of heat transfer is accentuated due to higher alteration in pressure gradient by larger \(\delta\). The NPs volume fractions are directly related to the thermal diffusion of the hybrid or nano-blood, which assists the quick transfer process of heat from the flow domain. Consequently, an enlargement in \(\phi_{1}\) or \(\phi_{2}\) leads to upliftment in the process of heat transport. The outcomes of Fig. 8j conclude that \(Z_{{{\text{Pure}}{\kern 1pt} \;{\text{blood}}}}^{ * } < Z_{{{\text{Cu}} - {\text{blood}}}}^{ * } < Z_{{{\text{Au}} - {\text{blood}}}}^{ * } < Z_{{{\text{Cu}} - {\text{Au}}/{\text{blood}}}}^{ * }\). Due to the higher atomic number of Au NPs as compared to Cu NPs, Au-blood possesses relatively more heat migration than Cu-blood or pure blood, whereas the supreme heat transport process is observed for hybrid Cu-Au/blood.

Fig. 8
figure 8

Evolution of heat transport coefficient \(Z^{ * }\) for various physical terms \(\alpha = 0.1\), \(\beta = 0.2\), \(F = 0.5\), \(Gr = 2.0\), and (a) \(\lambda_{1} = 0.6\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(Br = 0.1\), \(\xi = 1.0\), \(\delta = 0.1\), \(z = 0.3\), \(\phi_{1} = \phi_{2} = 0.02\), (b) \(M^{2} = 1.0\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(Br = 0.1\), \(\xi = 1.0\), \(\delta = 0.1\), \(z = 0.3\), \(\phi_{1} = \phi_{2} = 0.02\), (c) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 3.0\), \(Br = 0.1\), \(\xi = 0.1\), \(\delta = 0.1\), \(z = 0.7\), \(\phi_{1} = \phi_{2} = 0.02\), (d) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(U_{\text{hs}} = - 2.0\), \(Br = 0.1\), \(\xi = 1.5\), \(\delta = 0.1\), \(z = 0.3\), \(\phi_{1} = \phi_{2} = 0.02\), (e) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(U_{hs} = - 2.0\), \(\kappa = 2.0\), \(\xi = 0.5\), \(\delta = 0.1\), \(z = 0.3\), \(\phi_{1} = \phi_{2} = 0.02\), (f) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(Br = 0.1\), \(\delta = 0.1\), \(z = 0.3\), \(\phi_{1} = \phi_{2} = 0.02\), (g) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(Br = 0.1\), \(\xi = 1.0\), \(z = 0.3\), \(\phi_{1} = \phi_{2} = 0.02\), (h) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(Br = 0.1\), \(\xi = 1.0\), \(\delta = 0.1\), \(z = 0.35\), \(\phi_{2} = 0.02\), (i) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(Br = 0.1\), \(\xi = 1.0\), \(\delta = 0.1\), \(z = 0.35\), \(\phi_{1} = 0.02\), (j) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(U_{\text{hs}} = - 2.0\), \(\kappa = 3.0\), \(Br = 0.1\), \(\xi = 2.0\), \(\delta = 0.1\), \(z = 0.35\)

Full size image

Streamlines pattern

The velocity vectors in a flow domain are mechanically coupled via streamlines. Indeed, the existence of a stagnation point causes streamlines to separate and construct an enveloping bolus of fluid. In a metachronal wave propagation, the development of bolus and the split-up of streamlines are known as trapping phenomena. Figure 9a–o explores the insight into the modification in the development of bolus and streamline configurations under the variations of \(M^{2}\), \(\lambda_{1}\), \(Gr\), \(\kappa\), \(U_{{{\text{hs}}}}\), \(\delta\), \(\phi_{1}\), and \(\phi_{2}\). Figure 9a–b is demonstrated to unveil the streamlines pattern for \(M^{2}\). With changing \(M^{2}\), there is a slight change in bolus structure. To explore the impressions of Jeffrey parameter \(\lambda_{1}\) on streamline structures, Fig. 9c–d is manifested. There is a major modification in size and number of entrapped boluses for a higher estimation of \(\lambda_{1}\). It is attributed that a higher Jeffrey parameter enlarges the size and number of trapped boluses. The impact of \(Gr\) on streamlines is presented in Fig. 9e–f. It is noteworthy here that with an elevation in \(Gr\), the entrapped bolus is amended in size and number. The upshot of \(\kappa\) over streamlines is delineated in Fig. 9g–h. An amendment in \(\kappa\) expands the entrapped bolus in size as well as in number. Figure 9i–j is designed to assess the variation in streamline modification with Helmholtz–Smoluchowski velocity \(U_{{{\text{hs}}}}\). There is a contraction in size and number of streamlines under the changes of \(U_{\text{hs}}\) from \(- 3\) to \(- 2\). The alternation of the entrapped bolus is significantly attenuated by increasing cilia length \(\delta\), as shown in Fig. 9k–l. Figure 9m–o portends the comparison of captured streamlines for Cu-Au/blood, Cu-blood, and pure blood. It is perceived that there is no significant alteration in streamlines for hybrid or nano-blood but a contraction in size and number of the entrapped bolus is exposed in the case of pure blood.

Fig. 9
figure 9figure 9

Streamlines for different physical parameters \(\alpha = 0.1\), \(\beta = 0.2\), \(F = 0.5\), \(Br = 0.1\), \(\xi = 0.5\), and (a)\(\&\)(b) \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 2.0\), \(U_{hs} = - 2.0\), \(\delta = 0.1\), \(\xi = 0.5\), \(\phi_{1} = \phi_{2} = 0.02\), (c)\(\&\)(d) \(M^{2} = 1.0\), \(Gr = 1.0\), \(\kappa = 2.0\), \(U_{hs} = - 2.0\), \(\delta = 0.1\), \(\xi = 0.5\), \(\phi_{1} = \phi_{2} = 0.02\), (e)\(\&\)(f) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(\kappa = 2.0\), \(U_{hs} = - 2.0\), \(\delta = 0.1\), \(\xi = 0.5\), \(\phi_{1} = \phi_{2} = 0.02\), (g)\(\&\)(h) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(U_{hs} = - 2.0\), \(\delta = 0.1\), \(\xi = 0.1\), \(\phi_{1} = \phi_{2} = 0.02\), (i)\(\&\)(j) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 3.0\), \(\delta = 0.1\), \(\xi = 0.5\), \(\phi_{1} = \phi_{2} = 0.02\), (k)\(\&\)(l) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 2.0\), \(U_{hs} = - 2.0\), \(\phi_{1} = \phi_{2} = 0.02\), (m)\(\&\)(n) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 2.0\), \(U_{hs} = - 2.0\), \(\delta = 0.1\), \(\xi = 0.5\)(o) \(M^{2} = 1.0\), \(\lambda_{1} = 0.6\), \(Gr = 1.0\), \(\kappa = 2.0\), \(U_{hs} = - 2.0\), \(\delta = 0.1\), \(\xi = 0.5\), \(\phi_{1} = \phi_{2} = 0.0\)\(\phi_{1} = \phi_{2} = 0.0\)

Full size image

Conclusions

In this research article, a new mathematical scheme is prepared for the electro-magneto-hydrodynamic flow of ionized non-Newtonian blood injected through Cu–Au NPs via a vertical ciliated micro-vessel with peristaltic waves. To capture the non-Newtonian rheological attributes of the hybrid nano-blood, Jeffrey liquid model is fitted. The mathematical representations are simplified via Debye–H\(\ddot{u}\)ckel linearization and lubrication postulates. The analytic estimation for electric potential is tracked out in terms of Bessels functions. The estimated power series solutions of the associated nonlinear coupled flow equations are computed employing homotopy perturbation method. The significant influences of evolving physical terms toward the axial distribution of the blood temperature and velocity, WSS, axial pressure gradient, pressure rise per wavelength, heat transport coefficient, and streamlines pattern have been evidenced and anatomized. The noteworthy outcomes turned out from this graphical illustration are epitomized as:

  • A higher assisting the electro-osmotic force and thin EDL significantly hinder the blood motion nearby the ciliary micro-vessel wall.

  • Enhancement in Jeffrey parameter or Grashof number boosts up the blood velocity, whereas magnetic field or cilia length yields a perceptible attenuation in the central area of the micro-vessel.

  • The blood in the flow conduit is remarkably energized due to an elevation in heat source parameter, while reverse propensity is tracked out due to Jeffrey parameter, Brinkman number, and NPs’ volume fractions.

  • The temperature of hybrid nano-blood is greater than nano-blood or pure blood.

  • The pressure gradient is abated for the assisting electro-osmotic force and thin EDL, while it is important through higher values of Jeffrey term or cilia length.

  • The heat transfer coefficient surges 26.9% for Cu-Au/blood and 28.8% Cu-blood with changing estimation of heat source term from 0.5 to 2.0.

  • The heat exchange rate for hybrid nano-blood (26% for Cu-Au/blood) is greatly evaluated to nano-blood (20% for Au-blood and 11.4% for Cu-blood).

Outcomes obtained in this hemodynamic investigation are very productive for deeper insights into EDL phenomena in the EMHD flow of ionized blood doped with copper and gold nanoparticles via a ciliated micro-vessel. This novel model can be applicable in muco-ciliary clearance processes of respiratory systems, bio-micro-electro-mechanical systems, hemodynamic therapies, simulations of chirurgical treatments, and medical engineering.