A Mirror Inertial Forward–Reflected–Backward Splitting: Convergence Analysis Beyond Convexity and Lipschitz Smoothness

Abstract

This work investigates a Bregman and inertial extension of the forward–reflected–backward algorithm (Malitsky and Tam in SIAM J Optim 30:1451–1472, 2020) applied to structured nonconvex minimization problems under relative smoothness. To this end, the proposed algorithm hinges on two key features: taking inertial steps in the dual space, and allowing for possibly negative inertial values. The interpretation of relative smoothness as a two-sided weak convexity condition proves beneficial in providing tighter stepsize ranges. Our analysis begins with studying an envelope function associated with the algorithm that takes inertial terms into account through a novel product space formulation. Such construction substantially differs from similar objects in the literature and could offer new insights for extensions of splitting algorithms. Global convergence and rates are obtained by appealing to the Kurdyka–Łojasiewicz property.

1 Introduction

Consider the following composite minimization problem

$$\begin{aligned} \mathop {{{\,\textrm{minimize}\,}}}\limits _{x\in \overline{C}}\varphi (x)\mathrel {{:}{=}}f(x)+g(x), \end{aligned}$$

(P)

where $C\subseteq \mathbb {R}^n$ is a nonempty open and convex set with closure $\overline{C}$, $f:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}\mathrel {{:}{=}}\mathbb {R}\cup \{\pm \infty \}}$ is proper, lower semicontinuous (lsc), and differentiable on $C$, and $g:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ is proper and lsc (we refer to Sect. 2 for a precise statement of the assumptions on the problem). For notational brevity, we denote $\varphi _{\overline{C}}\mathrel {{:}{=}}\varphi +{{\,\mathrm{\delta }\,}}_{\overline{C}}$ where ${{\,\mathrm{\delta }\,}}_X$ is the indicator function of set $X\subseteq \mathbb {R}^n$, namely such that ${{\,\mathrm{\delta }\,}}_X(x)=0$ if $x\in X$ and $+\infty$ otherwise. By doing so, problem (P) can equivalently be cast as the “unconstrained” minimization

$$\begin{aligned} \mathop {{{\,\textrm{minimize}\,}}}\limits _{x\in \mathbb {R}^n}\varphi _{\overline{C}}(x). \end{aligned}$$

Note that (P) is beyond the scope of traditional first-order methods that require global Lipschitz continuity of $\nabla f$ and the consequential descent lemma [11, Prop. A.24]; see, e.g., [3, 23,24,25, 28, 35] for such algorithms. To resolve this issue, Lipschitz-like convexity was introduced in the seminal work [5], furnishing a descent lemma beyond the aforementioned setting. This notion was then referred to as relative smoothness (see Definition 3.2) and has played a central role in extending splitting algorithm to the setting of (P); see, e.g., [13, 17, 20, 27, 34, 39].

The goal of this paper is to propose a Bregman inertial forward–reflected–backward method $i^*$FRB (Algorithm 1) for solving (P), which, roughly speaking, iterates

$$\begin{aligned}{} & {} x^{k+1} \in (\nabla h+\gamma \partial g)^{-1}(\nabla h(x^k)+\beta (\nabla h(x^k)-\nabla h(x^{k-1})-\gamma (2\nabla f(x^k)\\ {}{} & {} \quad -\nabla f(x^{k-1})), \end{aligned}$$

where $\gamma >0$ is the stepsize, $\beta$ is an inertial parameter, and h is the kernel. In the convex case, the above scheme reduces to the inertial forward–reflected–backward (FRB) method proposed in [29] when $h=(1/2)\Vert {}\cdot {}\Vert ^2$, which is not applicable to (P) due to its assumption on Lipschitz continuity of $\nabla f$.

A fundamental tool in our analysis is the $i^*$FRB-envelope (see Definition 4.4), which is the value function associated with the parametric minimization of a “model” of (P); see Sect. 4.1. The term “envelope” is borrowed from the celebrated Moreau envelope [31] and its relation with the proximal operator. Indeed, there has been a re-emerged interest of employing an associated envelope function to study convergence of splitting methods, such as forward–backward splitting [1, 43], Douglas–Rachford splitting and ADMM [42, 44], alternating minimization algorithm [38], as well as the splitting scheme of Davis and Yin [26]. The aforementioned works share one common theme: regularity properties of the associated envelope function are used for further enhancement and deeper algorithmic insights. Similar conclusions remain valid for the case of $i^*$FRB, but this direction will not be pursued here and the discussion limited to Remark 5.2.

In this work, we consider an envelope function with two independent variables, allowing us to take inertial terms into account. Although merit functions with two variables have been applied in the literature, see, for instance, [14, 47], to the best of our knowledge envelopes, that is, the result of parametric minimizations that enjoy more regularity properties, have only been analyzed and employed as single-variable functions. Continuity properties resulting from marginalization are at the base of linesearch extensions such as the one in [1], which also studies Bregman-type proximal algorithms but cannot account for inertial terms. In this regard, we believe that our methodology is appealing in its own right, as it can be instrumental for deriving inertial extensions of other splitting methods. In fact, in accounting for inertial terms, as one shall see in Sect. 4.4 a nonpositive inertial parameter is required for the sake of convergence under relative smoothness. This result, although more pessimistic, aligns with the recent work [18] regarding the impossibility of accelerated Bregman forward–backward method under the same assumption; see Remark 4.7 for a detailed discussion. We also note that recent research has shown that negative inertia could contribute to convergence of algorithms; see, for instance, [19, 22]. Another notable feature is that we express (relative) smoothness of function $f$ equivalently in terms of (relative) weak convexity of both $f$ and $-f$; see Lemma 3.4. Our motivation stems from the fact that the relative smoothness modulus is a two-sided condition for both $f$ and $-f$, resulting in possibly loose results that fail to capture special structure of these functions. In contrast, treating $f$ and $-f$ separately through their (relative) weak convexity furnishes tight stepsize results that better reflect the geometry of the problem; see Sect. 4.4. A similar approach was considered in [41], but to the best of our knowledge the Bregman extension investigated here is novel.

Equipped with the aforementioned novel techniques, we conduct a case study on the forward–reflected–backward splitting. Our work differs from the analysis carried out in [45], which also deals with an inertial forward–reflected–backward algorithm using Bregman metrics but is still limited to the Lipschitz smoothness assumption. The game changer that enables us to cope with the relative smoothness is taking the inertial step in the dual space, that is, interpolating application of $\nabla h$ (cf. step 2 of Algorithm 1), whence the name, inspired by [10], mirror inertial forward–reflected–backward splitting ($i^*$FRB). Despite the fact that there are simpler algorithms for solving (P), the novelty of this work emphasizes on the aforementioned theoretical contribution. Furthermore, we note that the FRB scheme demonstrates its full power when applied to minimax problems (see, e.g., [12]), in which case one shall encounter similar subproblems. In turn, we hope that the $i^*$FRB-envelope and the operator developed in this work, which are associated with the FRB subproblems, shall again shed light on the convergence analysis.

The rest of the paper is structured as follows. In the next section, we formally define the problem setting and the proposed mirror inertial forward–reflected–backward algorithm ($i^*$FRB), after providing some preliminary material and notational conventions. In Sect. 3, we revisit the notion of relative smoothness and interpret it as a two-sided relative weak convexity. After introducing the $i^*$FRB-envelope, these findings are used to construct a merit function for the proposed $i^*$FRB; the proof of the main result therein is deferred to Appendix A. The convergence analysis of $i^*$FRB is carried out in Sect. 5. Section 6 draws some concluding remarks.

2 Problem Setting and Proposed Algorithm

2.1 Preliminaries and Notation

We let $\mathbb {R}^n$ be the Euclidean space with norm given by $\Vert x\Vert =\sqrt{\langle x,x\rangle }$ for $x\in \mathbb {R}^n$, and ${\mathcal {j}}\mathrel {{:}{=}}(1/2 )\Vert {}\cdot {}\Vert ^2$. The extended real line is denoted by $\overline{\mathbb {R}}\mathrel {{:}{=}}\mathbb {R}\cup \{\pm \infty \}$. The positive and negative part of $r\in \mathbb {R}$ are, respectively, defined as $[r]_+\mathrel {{:}{=}}\max \{0,r\}$ and $[r]_-\mathrel {{:}{=}}\max \{0,-r\}$, so that $r=[r]_+-[r]_-$.

The distance of a point $x\in \mathbb {R}^n$ to a nonempty set $S\subseteq \mathbb {R}^n$ is given by ${{\,\textrm{dist}\,}}(x,S)=\inf _{z\in S} \Vert z-x\Vert$. The interior, closure, and boundary of $S$ are, respectively, denoted as ${{\,\textrm{int}\,}}S$, $\overline{S}$, and ${{\,\textrm{bdry}\,}}S=\overline{S}{\setminus }{{\,\textrm{int}\,}}S$. The indicator function of $S$ is ${{\,\mathrm{\delta }\,}}_S:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ defined as ${{\,\mathrm{\delta }\,}}_S(x)=0$ if $x\in S$ and $+\infty$ otherwise.

A function $f:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ is proper if $f\not \equiv +\infty$ and $f>-\infty$, in which case its domain is defined as the set ${{\,\textrm{dom}\,}}f\mathrel {{:}{=}}\{x\in \mathbb {R}^n:f(x)<+\infty \}$. For $\alpha \in \mathbb {R}$, $[f\le \alpha ]\mathrel {{:}{=}}\{x\in \mathbb {R}^n:f(x)\le \alpha \}$ denotes the $\alpha$-sublevel set of $f$; $[\alpha \le f\le \beta ]$ with $\alpha ,\beta \in \mathbb {R}$ is defined accordingly. We say that $f$ is level bounded (or coercive) if $\liminf _{\Vert x\Vert \rightarrow +\infty }f(x)=+\infty$, and $1$-coercive if $\lim _{\Vert x\Vert \rightarrow +\infty }f(x)/\Vert x\Vert =+\infty$. The Fenchel conjugate of $f$ is denoted as $f^*\mathrel {{:}{=}}\sup _{z\in \mathbb {R}^n}\{\langle {}\cdot {},z\rangle -f(z)\}$. Given $x\in {{\,\textrm{dom}\,}}f$, $\partial f(x)$ denotes the Mordukhovich (limiting) subdifferential of $f$ at $x$, given by

$$\begin{aligned} \partial f(x) \mathrel {{:}{=}}\{v\in \mathbb {R}^n: \exists (x^k,v^k)_{k\in \mathbb {N}}~\text {s.t.}~ x^k\rightarrow x,~f(x^k)\rightarrow f(x),~ {\hat{\partial }} f(x^k)\ni v^k\rightarrow v \}, \end{aligned}$$

and ${\hat{\partial }} f(x)$ is the set of regular subgradients of $f$ at $x$, namely vectors $v\in \mathbb {R}^n$ such that $\liminf _{\begin{array}{c} z\rightarrow x\\ z\ne x \end{array}}{ \frac{ f(z)-f(x)-\langle v,z-x\rangle }{ \Vert z-x\Vert } } \ge 0.$ The notation $\partial ^\infty f(x)$ denotes the horizon subdifferential of $f$ at $x$, defined as $\partial f(x)$ up to replacing $v^k\rightarrow v$ with $\lambda _kv^k\rightarrow v$ for some sequence $\lambda _k\searrow 0$. For $x\notin {{\,\textrm{dom}\,}}f$, we set $\partial f(x)=\partial ^\infty f(x)=\emptyset$; see, e.g., [30, 37]. ${\mathcal {C}^k({\mathcal {U}})}$ is the set of functions ${{\mathcal {U}}\rightarrow \mathbb {R}}$ which are $k$ times continuously differentiable, where $\mathcal {U}$ is a nonempty open set. We write ${\mathcal {C}^k}$ if ${{\mathcal {U}}}$ is clear from context. The notation $T:\mathbb {R}^n\rightrightarrows \mathbb {R}^{m}$ indicates a set-valued mapping, whose domain and graph are defined as ${{\,\textrm{dom}\,}}T=\{x\in \mathbb {R}^n:T(x)\ne \emptyset \}$ and ${{\,\textrm{gph}\,}}T=\{(x,y)\in \mathbb {R}^n\times \mathbb {R}^{m}:y\in T(x)\}$, respectively. $T$ is said to be outer semicontinuous (osc) if ${{\,\textrm{gph}\,}}T$ is a closed subset of $\mathbb {R}^n\times \mathbb {R}^m$, and locally bounded if every ${\bar{x}}\in \mathbb {R}^n$ admits a neighborhood ${\mathcal N_{{\bar{x}}}}$ such that ${\bigcup _{x\in {\mathcal {N}}_{{\bar{x}}}}T(x)}$ is a bounded subset of $\mathbb {R}^m$.

Following the terminology of [37, Def. 1.16], we say that a function $F:X\times U\subseteq \mathbb {R}^n\times \mathbb {R}^m\rightarrow {\overline{\mathbb {R}}}$ with values $F(x,u)$ is level bounded in $x$ locally uniformly in $u$ if for any $\alpha \in \mathbb {R}$ and ${\bar{u}}\in U$ there exists a neighborhood ${{\mathcal {N}}_{{\bar{u}}}}$ of ${\bar{u}}$ in $U$ such that the set ${\{(x,u)\in X\times {\mathcal {N}}_{\bar{u}}:F(x,u)\le \alpha \}}$ is bounded.

2.2 The Mirror Inertial Forward–Reflected–Backward algorithm

Throughout, we fix a 1-coercive Legendre kernel $h:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ with ${{\,\textrm{dom}\,}}\nabla h={{\,\textrm{int}\,}}{{\,\textrm{dom}\,}}h=C$. Recall that a proper, convex, and lsc function is said to be Legendre if it is essentially strictly convex and essentially smooth, i.e., such that $h$ is strictly convex on $C$ and $\Vert \nabla h(x_k)\Vert \rightarrow +\infty$ for every sequence $(x_k)_{k\in \mathbb {N}}\subset C$ converging to a boundary point of $C$. We will consider the following iterative scheme for addressing problem (P), where ${{\,\textrm{D}\,}}_h:\mathbb {R}^n\times \mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ denotes the Bregman distance induced by $h$, defined as

$$\begin{aligned} {{\,\textrm{D}\,}}_h(x,y) \mathrel {{:}{=}}{\left\{ \begin{array}{ll} h(x)-h(y)-\langle \nabla h(y),x-y\rangle &{} \quad \text {if }y\in C, \\ +\infty &{} \quad \text {otherwise}. \end{array}\right. } \end{aligned}$$

(2.1)

Note that Algorithm 1 takes inertial step in the dual space, hence the abbreviation $i^*$FRB. We will work under the following assumptions.

Assumption 1

The following hold in problem (P):

• A1 $f:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ is smooth relative to $h$ (see Sect. 3).

• A2 $g:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ is proper and lsc.

• A3 $\inf \varphi _{\overline{C}}>-\infty$.

• A4 For any $v\in \mathbb {R}^n$ and $\gamma >0$, ${{\,\textrm{argmin}\,}}\{\gamma g+h-\langle v,{}\cdot {}\rangle \}\subseteq C$.

• A5 For any $\gamma >0$, $\lim _{\Vert x\Vert \rightarrow \infty } \frac{\gamma g(x)+h(x)}{\Vert x\Vert }=\infty$.

Some remarks are in order.

Remark 2.1

(constraint qualifications for Assumption 1.A4) As will be made explicit in Lemma 4.2, Assumptions 1.A4 and 1.A5 are requirements ensuring that Algorithm 1 is well defined. Note that, in general, the minimizers therein are a (possibly empty) subset of ${{\,\textrm{dom}\,}}h\cap {{\,\textrm{dom}\,}}g$; Assumption 1.A4 thus only excludes points on the boundary of ${{\,\textrm{dom}\,}}h$. This standard requirement is trivially satisfied when ${{\,\textrm{dom}\,}}h$ is open, or more generally when constraint qualifications enabling a subdifferential calculus rule on the boundary are met, as is the case when $g$ is convex. If $g$ is proper and lsc, Assumption 1.A4 is satisfied if $\partial ^\infty g\cap \bigl (-\partial ^\infty h\bigr )\subseteq \{0\}$ holds everywhere (this condition being automatically guaranteed at all point outside the boundary of $C$, having $\partial ^\infty h$ empty outside ${{\,\textrm{dom}\,}}h$ and $\{0\}$ in its interior). Indeed, optimality of ${\bar{x}}\in {{\,\textrm{argmin}\,}}\{\gamma g+h-\langle v,{}\cdot {}\rangle \}$ implies that $v\in \partial [\gamma g+h](\bar{x})\subseteq \gamma \partial g({\bar{x}})+\partial h({\bar{x}})$, with inclusion holding by [37, Cor. 10.9] and implying nonemptiness of $\partial h({\bar{x}})$; see Sect. 2.1 for definitions of subdifferentials.

Remark 2.2

(Assumption 1.A5 and prox-boundedness) Apparently, Assumption 1.A5 together with lower semicontinuity ensures that minimizers of $\gamma g+h-\langle v,{}\cdot {}\rangle$ do exist for any $\gamma$ and $v$. (Relative) prox-boundedness [21, Def. 2.3], which amounts to the same condition but only required for $\gamma$ small enough, would also suffice to our purposes as long as parameters exceeding such “threshold” are excluded from the analysis. Assumption 1.A5 is nevertheless a very mild and standard requirement [13] that enables a simpler exposition at virtually no expense of generality. We additionally remark that this requirement is superfluous whenever $f$ and $h$ are continuous relative to ${{\,\textrm{dom}\,}}h$, or when ${{\,\textrm{dom}\,}}h$ has bounded intersection with its boundary. We postpone the discussion to Lemma 3.6 for the details.

3 Relative Smoothness and Weak Convexity

Throughout the paper, we will adopt the convention that $1/0=+\infty$ and $+\infty \cdot 0=0$. In order to resolve possible ill definitions of difference of extended real-valued functions, we adopt the extended arithmetics $\mathbin {\dot{+}}$ and $\mathbin {\dot{-}}$ of [32, §2], defined as the respective $+$ and − whenever the operation makes sense and otherwise evaluating to $+\infty$, namely

$$\begin{aligned} -\infty \mathbin {\dot{-}}(-\infty ) = -\infty \mathbin {\dot{+}}\infty = +\infty \mathbin {\dot{-}}\infty = +\infty \mathbin {\dot{+}}(-\infty ) = \infty . \end{aligned}$$

Furthermore, we denote by $\mathbin {{\dot{\pm }}}$ and $\mathbin {{\dot{{\mp }}}}$ the extended arithmetic equivalents of ± and ${\mp }$, respectively. Notice in particular that

$$\begin{aligned} a\mathbin {\dot{-}}b = (-b)\mathbin {\dot{-}}(-a) \end{aligned}$$

(3.1)

holds for any extended-real pair $(a,b)\in \overline{\mathbb {R}}\times \overline{\mathbb {R}}$.

The following lemma collects other properties of extended arithmetics that will be frequently used throughout.

Lemma 3.1

Let $\psi :\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ be proper, and $a,b\in \mathbb {R}$ be fixed. Then, the following hold:

• (i) $a\psi \mathbin {{\dot{\pm }}}b\psi \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_E = (a\pm b)\psi \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_E$ for any $E\subseteq {{\,\textrm{dom}\,}}\psi$.

• (ii) If $a>0$, then $a\psi \mathbin {{\dot{\pm }}}b\psi = (a\pm b)\psi \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_{{{\,\textrm{dom}\,}}\psi }$.

Proof

In both cases, we shall verify the equivalences pointwise at any $x\in \mathbb {R}^n$, analyzing the cases $x\in {{\,\textrm{dom}\,}}\psi$ and $x\notin {{\,\textrm{dom}\,}}\psi$ separately.

If $x\in {{\,\textrm{dom}\,}}\psi$, one has that $\psi (x)\in \mathbb {R}$ by properness of $\psi$; hence, the extended arithmetic notation is superfluous in both assertions and the claims are trivially true. If $x\notin {{\,\textrm{dom}\,}}\psi$, then ${{\,\mathrm{\delta }\,}}_E(x)=+\infty$ in assertion 3.1.(i) and similarly $a\psi (x)=\infty$ in assertion 3.1.(ii). Therefore, the extended arithmetic convention ensures that all expressions evaluate to $+\infty$ in this case, and thus coincide. $\square$

Definition 3.2

(relative smoothness) We say that a function $f:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ is smooth relative to $h$ if ${{\,\textrm{dom}\,}}f\supseteq {{\,\textrm{dom}\,}}h$ and there exists a constant $L_{f,h}\ge 0$ such that

$$\begin{aligned} L_{f,h}h \mathbin {\dot{+}}f \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C\quad \text {and}\quad L_{f,h}h\mathbin {\dot{-}}f\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C\end{aligned}$$

(3.2)

are proper convex functions. We may alternatively say that $f$ is $L_{f,h}$-smooth relative to $h$ to make the smoothness modulus $L_{f,h}$ explicit.

The addition of ${{\,\mathrm{\delta }\,}}_C$ in (3.2) serves the purpose of assessing convexity of $L_{f,h}\mathbin {{\dot{\pm }}}f$ only on set $C$, in line with the original “Lipschitz-like convexity” notion of [5, §2.2] as well as the subsequent nonconvex generalization in [13, Def. 2.2], referred to as “$L_{f,h}$-smooth adaptability” of the pair $(f,h)$. Differently from those works, however, we do not impose (continuous) differentiability of $f$ on $C$ in the definition, for this property is automatically guaranteed; see Proposition 3.7 for the details.

Notice further that the constant $L_{f,h}$ may be loose. For instance, if $f$ is convex, then $Lh\mathbin {\dot{+}}f$ is convex for any $L\ge 0$, indicating that it is only convexity of $L_{f,h}h\mathbin {\dot{-}}f\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C$ that dictates the value of $L_{f,h}$. This motivates us to consider one-sided conditions and treat $f$ and $-f$ separately.

Definition 3.3

(relative weak convexity) We say that a function $f:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ is weakly convex relative to $h$ if $f\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_{{{\,\textrm{dom}\,}}h}$ is proper and there exists a (possibly negative) constant $\sigma _{f,h}\in \mathbb {R}$ such that $f \mathbin {\dot{-}}\sigma _{f,h}h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C$ is a convex function. We may alternatively say that $f$ is $\sigma _{f,h}$-weakly convex relative to $h$ to make the weak convexity modulus $\sigma _{f,h}$ explicit.

In accordance with the Euclidean case, having $\sigma _{f,h}\ge 0$ implies convexity while $\sigma _{f,h}> 0$ relative strong convexity. Considering possibly improper functions in Definition 3.3 allows us to identify relative smoothness as a two-sided relative weak convexity, as we are about to show, regardless of whether a function has full domain or not. This fact extends the well-known equivalence between Lipschitz differentiability and the combination of weak convexity and weak concavity in the Euclidean setting; see Lemma 3.8 for the details.

Lemma 3.4

(relative smoothness and relative weak convexity) Let $f:\mathbb {R}^n\rightarrow \overline{\mathbb {R}}$ be proper. Then, $f$ is smooth relative to $h$ iff both $f$ and $-f$ are weakly convex relative to $h$. More precisely, if $f$ is $L_{f,h}$-smooth relative to $h$, then both $f$ and $-f$ are $(-L_{f,h})$-relatively weakly convex. Conversely, if $f$ and $-f$ are $\sigma _{f,h}$- and $\sigma _{-f,h}$-weakly convex relative to $h$, respectively, then $f$ (as well as $-f$) is $L_{f,h}$-smooth relative to $h$ with

$$\begin{aligned} L_{f,h}=\max \{|\sigma _{f,h}|,|\sigma _{-f,h}|\} \end{aligned}$$

(3.3)

(see (3.6) for a simplified expression without absolute values).

Proof

That relative smoothness implies relative weak convexity with the given moduli is straightforward (properness of $\pm f\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_{{{\,\textrm{dom}\,}}h}$ follows from the inclusion ${{\,\textrm{dom}\,}}f\supseteq {{\,\textrm{dom}\,}}h$). Suppose that $\pm f$ are $\sigma _{\pm f,h}$-relatively weakly convex. First, observe that properness of $\pm f\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_{{{\,\textrm{dom}\,}}h}$ implies the inclusion ${{\,\textrm{dom}\,}}f\supseteq {{\,\textrm{dom}\,}}h$. Then, the convexity of $\pm f\mathbin {\dot{-}}\sigma _{\pm f,h}h{}\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C$ implies that

$$\begin{aligned} L_{f,h}h\mathbin {{\dot{\pm }}}f \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C={}&(-\sigma _{\pm f,h}+\sigma _{\pm f,h}+L_{f,h})h \mathbin {{\dot{\pm }}}f \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C\\ ={}&-\sigma _{\pm f,h}h \mathbin {\dot{+}}\sigma _{\pm f,h}h \mathbin {\dot{+}}L_{f,h}h \mathbin {{\dot{\pm }}}f \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C\\ ={}&\bigl [ \pm f\mathbin {\dot{-}}\sigma _{\pm f,h}h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C\bigr ] + \bigl [ (L_{f,h}+\sigma _{\pm f,h})h \bigr ] \end{aligned}$$

are proper and convex (since $L_{f,h}+\sigma _{\pm f,h}\ge 0$, cf. (3.3)), where the second identity uses Lemma 3.1.(i) to distribute the coefficients of $h$. Appealing to Definition 3.2, $f$ is $L_{f,h}$-smooth relative to $h$. $\square$

The relative weak convexity moduli $\sigma _{\pm f,h}$ will be henceforth adopted when referring to Assumption 1.A1. It will be convenient to normalize these quantities into pure numbers

$$\begin{aligned} p_{\pm f,h} \mathrel {{:}{=}}\tfrac{\sigma _{\pm f,h}}{L_{f,h}} \in [-1,1]. \end{aligned}$$

(3.4)

Notice that $L_{f,h}=0$ only when $f$ is affine on $C$, and in this case, we conventionally set $p_{\pm f,h}=0$. The comment below will be instrumental in Sect. 4.4.

Remark 3.5

If $f$ and $-f$ are $\sigma _{f,h}$- and $\sigma _{-f,h}$-weakly convex relative to $h$, respectively, then invoking (3.3) and (3.4) yields that

$$\begin{aligned} -2\le p_{f,h}+p_{-f,h}\le 0 \quad \text {and}\quad -1\in \{p_{f,h},p_{-f,h}\}, \end{aligned}$$

(3.5)

where the inclusion holds provided $L_{f,h}\ne 0$. (As said above, the case $L_{f,h}=0$ amounts to $f$ being affine on $C$.) The second inequality owes to the fact that, by definition, both $f-\sigma _{f,h}h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C$ and $-f-\sigma _{-f,h}h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C$ are convex functions, and therefore so is their sum

$$\begin{aligned} \bigl [f\mathbin {\dot{-}}\sigma _{f,h}h\bigr ] \mathbin {\dot{+}}\bigl [-f\mathbin {\dot{-}}\sigma _{-f,h}h\bigr ] \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C={}&(-{}\sigma _{f,h}-\sigma _{-f,h})h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_{C}&\\ ={}&L_{f,h}(-{}p_{f,h}-p_{-f,h})h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C, \end{aligned}$$

where we used Lemma 3.1.(i) together with the fact that $f\mathbin {\dot{-}}f={{\,\mathrm{\delta }\,}}_{{{\,\textrm{dom}\,}}f}$ and that ${{\,\textrm{dom}\,}}f\supseteq {{\,\textrm{dom}\,}}h\supseteq C$. In turn, the inclusion in (3.5) follows from (3.3) and the definition (3.4): indeed, as long as $L_{f,h}\ne 0$, (3.4) implies that at least one among $p_{f,h}$ and $p_{-f,h}$ must attain absolute value of one. If the value is 1, then combining inequalities (3.4) and (3.5) entails the desired inclusion. Thus, whenever $f$ is convex (resp. concave), since one can take $p_{f,h}=0$ (resp. $p_{-f,h}=0$), by virtue of the inclusion in (3.5) it directly follows that $p_{-f,h}=-1$ (resp. $p_{f,h}=-1$) must hold.

Notice that the condition $\sigma _{f,h}+\sigma _{-f,h}\le 0$ shown in the above remark yields a simplification in the expression (3.3), for the absolute values can be resolved to

$$\begin{aligned} L_{f,h}=\max \{|\sigma _{f,h}|,|\sigma _{-f,h}|\} = \max \{-\sigma _{f,h},-\sigma _{-f,h}\}. \end{aligned}$$

(3.6)

We now turn to a lemma that guarantees well definedness of Algorithm 1.

Lemma 3.6

(relative   prox-boundedness) suppose that Assumption 1 holds. Then, the set ${{\,\textrm{argmin}\,}}\{\gamma g+h-\langle v,{}\cdot {}\rangle \}$ as in Assumption 1.A4 is nonempty for any $v\in \mathbb {R}^n$ and $0<\gamma <1/[\sigma _{-f,h}]_-$. In other words, $g$ is prox-bounded relative to $h$ with threshold $\gamma _{g,h}\ge 1/[\sigma _{-f,h}]_-$ [21, Def. 2.3].

In fact, the claim still holds with Assumption 1.A5 being replaced by continuity of $f$ and $h$ relative to ${{\,\textrm{dom}\,}}h$, or by the weaker condition

$$\begin{aligned} \lim _{\begin{array}{c} \Vert x\Vert \rightarrow \infty \\ {x\in {{\,\textrm{bdry}\,}}{{\,\textrm{dom}\,}}h} \end{array}}\frac{\gamma g(x)+h(x)}{\Vert x\Vert }=\infty \end{aligned}$$

(3.7)

for any $v\in \mathbb {R}^n$ and $\gamma <1/[\sigma _{-f,h}]_-$.

Proof

The claim is obvious if Assumption 1 holds in its entirety, and in fact, the restrictions on $\gamma$ are superfluous in this case; see the commentary within Remark 2.2 and [13, Lem. 3.1] for a formal proof. We now show the sufficiency of the claimed alternatives to Assumption 1.A5. Recall that a proper convex function admits an affine minorant; see, e.g., [9, Cor. 16.18]. By observing that

it follows that $\gamma g+h{}+{{\,\mathrm{\delta }\,}}_C$ is 1-coercive. Therefore, for any $v\in \mathbb {R}^n$ the function $\gamma g+h+{{\,\mathrm{\delta }\,}}_C-\langle v,{}\cdot {}\rangle$ is level bounded. Observe that ${{\,\textrm{argmin}\,}}\{\gamma g+h-\langle v,{}\cdot {}\rangle \} = {{\,\textrm{argmin}\,}}\{\gamma g+h+{{\,\mathrm{\delta }\,}}_C-\langle v,{}\cdot {}\rangle \}$ provided that the left-hand side is nonempty, which owes to Assumption 1.A4. To fix a notation, let

$$\begin{aligned} \psi \mathrel {{:}{=}}\gamma g+h-\langle v,{}\cdot {}\rangle \quad \text {and}\quad \mathring{\psi }\mathrel {{:}{=}}\psi +{{\,\mathrm{\delta }\,}}_C. \end{aligned}$$

Since $\psi$ is lsc and $\mathring{\psi }$ is 1-coercive, the sets of minimizers are (nonempty and) compact provided that ${{\,\textrm{argmin}\,}}\psi \ne \emptyset$. It thus suffices to show that indeed ${{\,\textrm{argmin}\,}}\psi$ is nonempty. Let $(x^k)_{k\in \mathbb {N}}$ be a minimizing sequence for $\psi$, namely such that $\psi (x^k)\rightarrow \inf \psi$. Since $\psi$ is lsc, it suffices to show that $(x^k)_{k\in \mathbb {N}}$ is bounded.

If $(x^k)_{k\in \mathbb {N}}$ is unbounded, then coercivity of $\mathring{\psi }$ implies that $x^k\in {{\,\textrm{bdry}\,}}C$ for $k$ large enough. This clearly cannot happen under condition (3.7). Suppose instead that $h$ and $f$ are continuous on ${{\,\textrm{dom}\,}}h$. Then,

is both 1-coercive (and convex) on $C={{\,\textrm{int}\,}}{{\,\textrm{dom}\,}}h$, in the sense that $h\mathbin {\dot{-}}\gamma f+{{\,\mathrm{\delta }\,}}_C$ is 1-coercive, and continuous on its domain ${{\,\textrm{dom}\,}}h$, and consequently, it is 1-coercive on the entire space.¹ Therefore, also

$$\begin{aligned} \psi = \gamma \varphi _{\overline{C}}- \langle v,{}\cdot {}\rangle + (h\mathbin {\dot{-}}\gamma f) \ge \gamma \inf \varphi _{\overline{C}}- \langle v,{}\cdot {}\rangle + (h\mathbin {\dot{-}}\gamma f) \end{aligned}$$

is 1-coercive, which shows that also in this case the minimizing sequence $(x^k)_{k\in \mathbb {N}}$ cannot be unbounded. $\square$

We now discuss “transitivity” properties of relative smoothness, beginning from continuous differentiability. We point out that the following result is well known; however, the proof is included for completeness.

Proposition 3.7

Suppose that $f$ is $L_{f,h}$-smooth relative to $h$. Then $f$ is continuously differentiable on C.

Proof

By assumption, ${\hat{\partial }} (L_{f,h}h\mathbin {{\dot{\pm }}}f)$ are nonempty on $C$. (In particular, on $C$ the extended arithmetic notation is redundant.) The subdifferential sum rule yields that $(\forall x\in C)~ {\hat{\partial }} (L_{f,h}h\pm f)(x) = L_{f,h} \nabla h(x) + {\hat{\partial }}(\pm f)(x)$, implying that ${\hat{\partial }}(\pm f)(x)$ must be nonempty. The smoothness of $h$ implies that $\pm f$ are regular through [37, Ex. 8.20]. The proof then follows by invoking [37, Thm. 9.18(a)–(d) and Cor. 9.19(a)–(b)]. $\square$

Next we turn to Lipschitz differentiability. The result below is a (well-known) generalization of the (well-known) equivalence between smoothness relative to the Euclidean kernel ${\mathcal {j}}$ and Lipschitz differentiability, a fact that will be invoked in Sect. 4 and whose proof is given next for the sake of completeness.

Lemma 3.8

(Lipschitz smoothness from weak convexity) For any $F:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$, the following are equivalent:

• (a) There exist $\sigma _{\pm F}\in \mathbb {R}$ such that both $F-\sigma _F{\mathcal {j}}$ and $-F-\sigma _{-F}{\mathcal {j}}$ are proper, convex, and lsc;

• (b) ${{\,\textrm{dom}\,}}\partial F=\mathbb {R}^n$, and there exist $\sigma _{\pm F}\in \mathbb {R}$ such that for all $(x_i,v_i)\in {{\,\textrm{gph}\,}}\partial F$, $i=1,2$, it holds that $\sigma _F\Vert x_1-x_2\Vert ^2 \le \langle v_1-v_2,x_1-x_2\rangle \le -\sigma _{-F}\Vert x_1-x_2\Vert ^2$;

• (c) There exists $L_F\ge 0$ such that $F$ is $L_F$-smooth relative to ${\mathcal {j}}$;

• (d) There exists $L_F\ge 0$ such that $\nabla F$ is $L_F$-Lipschitz differentiable.

In particular, assertions 3.8.(a) and/or 3.8.(b) imply assertions 3.8.(c) and 3.8.(d) with $L_F = \max \{-\sigma _F,-\sigma _{-F}\}$, and conversely, 3.8.(c) and/or 3.8.(d) imply 3.8.(a) and 3.8.(b) with $\sigma _{\pm F}=-L_F$.

Proof

3.8.(a) $\Leftrightarrow$3.8.(c)  The equivalence between the statements as well as the relation between the constants follows from Lemma 3.4 and (3.6).

3.8.(a) $\Rightarrow$3.8.(b)  Function $\psi \mathrel {{:}{=}}F-\sigma _F{\mathcal {j}}$ is convex, and therefore, its subgradient $\partial \psi =\partial F-\sigma _F{{\,\textrm{id}\,}}$ is monotone. This readily shows the first inequality in assertion 3.8.(b). The second inequality will follow from the same argument applied to the convex function $-F-\sigma _{-F}{\mathcal {j}}$ once we show that $\partial (-F)=-\partial F$. Indeed, it follows from [37, Ex. 12.28(b),(c)] that both $F$ and $-F$ are lower-, in the sense of [37, Def. 10.29], hence continuously differentiable by [37, Prop. 10.30]. Thus, invoking [37, Thm. 9.18] (which applies by virtue of [37, Cor. 9.19(a)–(b)]) one has that $\partial F=\{\nabla F\}=\{-\nabla (-F)\}=-\partial (-F)$, as claimed.

3.8.(b) $\Rightarrow$3.8.(d)  It follows from [42, Lem. 2.1] that $F$ is continuously differentiable and satisfies $|\langle \nabla F(x)-\nabla F(y),x-y\rangle | \le L_F\Vert x-y\Vert ^2$ with $L_F\mathrel {{:}{=}}\max \{|\sigma _F|,|\sigma _{-F}|\}$. In turn, simple algebra yields

$$\begin{aligned} 0 \le \langle \nabla (F+L_F{\mathcal {j}})(x)-\nabla (F+L_F{\mathcal {j}})(y),x-y\rangle \le 2L_{F}\Vert x-y\Vert ^2. \end{aligned}$$

By virtue of [33, Thm. 2.1.5], function $F+L_F{\mathcal {j}}$ is convex with $(1/2L_F )$-cocoercive gradient, namely such that

$$\begin{aligned} \langle \nabla (F+L_F{\mathcal {j}})(x)-\nabla (F+L_F{\mathcal {j}})(y),x-y\rangle \\ \ge \tfrac{1}{2L_F}\Vert \nabla (F+L_F{\mathcal {j}})(x)-\nabla (F+L_F{\mathcal {j}})(y)\Vert ^2 \end{aligned}$$

for all $x,y\in \mathbb {R}^n$. Expanding the square and rearranging yields the sought Lipschitz inequality $\Vert \nabla F(x)-\nabla F(y)\Vert ^2\le L_F^2\Vert x-y\Vert ^2$.

3.8.(d) $\Rightarrow$3.8.(a)  From the quadratic upper bound [11, Prop. A.24], it follows that

$$\begin{aligned} \pm F(x_2) \ge \pm F(x_1) {}\pm {} \langle \nabla F(x_1),x_2-x_1\rangle {}-{} \tfrac{L_F}{2}\Vert x_2-x_1\Vert ^2, \end{aligned}$$

or, equivalently,

$$\begin{aligned} (L_F{\mathcal {j}}\pm F)(x_2) \ge (L_F{\mathcal {j}}\pm F)(x_1) + \langle \nabla (L_F{\mathcal {j}}\pm F)(x_1),x_2-x_1\rangle . \end{aligned}$$

This proves convexity of $L_F{\mathcal {j}}\pm F$, whence the claim by taking $\sigma _{\pm F}=-L_F$. $\square$

The above lemma can be used to show that a function which is smooth relative to $h$ is Lipschitz differentiable whenever $h$ is, as shown next. The proof hinges on the following more general “transitivity” property of relative smoothness.

Lemma 3.9

Let $h_1,h_2:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ be Legendre kernels, and let $f:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$. If $f$ is $L_{f,h_1}$-smooth relative to $h_1$ and $h_1$ is $L_{h_1,h_2}$-smooth relative to $h_2$, then $f$ is $L_{f,h_2}$-smooth relative to $h_2$ with $L_{f,h_2}=L_{f,h_1}L_{h_1,h_2}$.

Proof

By definition, ${{\,\textrm{dom}\,}}h_2\subseteq {{\,\textrm{dom}\,}}h_1\subseteq {{\,\textrm{dom}\,}}f$, and $L_{f,h_1}h_1\mathbin {{\dot{\pm }}}f{}+{{\,\mathrm{\delta }\,}}_{C_1}$ and $L_{h_1,h_2}h_2\mathbin {{\dot{\pm }}}h_1{}+{{\,\mathrm{\delta }\,}}_{C_2}$ are all proper convex functions, where $C_i\mathrel {{:}{=}}{{\,\textrm{int}\,}}{{\,\textrm{dom}\,}}h_1$, $i=1,2$. If $L_{f,h_1}=0$, then $f$ is affine on $C_1$ as discussed in Lemma 3.4, and the claim is trivially true. Suppose that $L_{f,h_1}>0$, and notice that necessarily $L_{h_1,h_2}>0$ too holds since $h_1$ is strictly convex. Thus,

$$\begin{aligned} L_{f,h_1}L_{h_1,h_2}h_2\mathbin {{\dot{\pm }}}f \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_{C_2} ={}&L_{f,h_1}L_{h_1,h_2}h_2\mathbin {{\dot{\pm }}}f+{{\,\mathrm{\delta }\,}}_{C_2} \\ ={}&L_{f,h_1}(L_{h_1,h_2}h_2-h_1)+(L_{f,h_1}h_1\pm f) + {{\,\mathrm{\delta }\,}}_{C_2} \end{aligned}$$

are also convex functions, where the second identity uses Lemma 3.1.(i) together with the fact that ${{\,\textrm{dom}\,}}h_2\subseteq {{\,\textrm{dom}\,}}h_1$. In fact, they are also proper since the domains include ${{\,\textrm{dom}\,}}h_2\ne \emptyset$. By Definition 3.2, this means that $f$ is $L_{f,h_1}L_{h_1,h_2}$-smooth relative to $h_2$. $\square$

When $h_2={\mathcal {j}}$, and by appealing to the equivalence between Lipschitz differentiability and smoothness relative to $h_2$ asserted in Lemma 3.8, the following special case is obtained.

Corollary 3.10

Suppose that $f$ is $L_{f,h}$-smooth relative to $h$, and that $h$ is $L_h$-Lipschitz differentiable. Then $f$ is Lipschitz differentiable with modulus $L_f=L_{f,h}L_h$.

We conclude the section with a result regarding relative weak convexity and smoothness of linear combinations that will be useful in the next section.

Lemma 3.11

Suppose that $f$ is smooth relative to $h$, and let $\sigma _{\pm f,h}$ be the weak hypoconvexity moduli of $\pm f$ relative to $h$. Then, for every $\alpha ,\beta \in \mathbb {R}$ the function $\psi \mathrel {{:}{=}}\alpha f\mathbin {\dot{+}}\beta h$ is smooth relative to $h$ with

$$\begin{aligned} \sigma _{\psi ,h} ={}&{\left\{ \begin{array}{ll} |\alpha |\sigma _{f,h}+\beta &{} \quad \text {if }\alpha \ge 0, \\ |\alpha |\sigma _{-f,h}+\beta &{} \quad \text {if }\alpha <0, \end{array}\right. } \end{aligned}$$

(3.8a)

$$\begin{aligned} \sigma _{-\psi ,h} ={}&{\left\{ \begin{array}{ll} |\alpha |\sigma _{-f,h}-\beta &{} \quad \text {if }\alpha \ge 0, \\ |\alpha |\sigma _{f,h}-\beta &{} \quad \text {if }\alpha <0, \end{array}\right. } \end{aligned}$$

(3.8b)

and

$$\begin{aligned} |\alpha |L_{f,h}+|\beta | \ge {} L_{\psi ,h}\nonumber \\ ={}&{\left\{ \begin{array}{ll} \max \{ -\beta -\alpha \sigma _{f,h}, \beta -\alpha \sigma _{-f,h} \} &{} \quad \text {if }\alpha \ge 0, \\ \max \{ \beta +\alpha \sigma _{f,h}, -\beta +\alpha \sigma _{-f,h} \} &{} \quad \text {if }\alpha <0. \end{array}\right. } \end{aligned}$$

(3.8c)

Proof

If $\alpha =0$ the claim is trivial. If $\alpha >0$, then for every $\sigma \in \mathbb {R}$ we have

$$\begin{aligned} \psi \mathbin {\dot{-}}\sigma h\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C= \alpha \bigl [ ( f\mathbin {\dot{-}}\sigma _{f,h}h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C) \mathbin {\dot{+}}\tfrac{\beta -\sigma +\alpha \sigma _{f,h}}{\alpha }h \bigr ], \end{aligned}$$

where Lemma 3.1.(i) was used to distribute the coefficients of $h$. Since the term in round brackets is (proper and) convex, for any $\sigma \le \alpha \sigma _{f,h}+\beta$ one has that $\psi \mathbin {\dot{-}}\sigma h\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C$ is convex. Clearly, it is also proper, with domain agreeing with ${{\,\textrm{dom}\,}}h$. If $\alpha <0$, the same arguments can be used via the identity

$$\begin{aligned} \psi \mathbin {\dot{-}}\sigma h\mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C= -\alpha \bigl [ ( -f\mathbin {\dot{-}}\sigma _{-f,h}h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_C) \mathbin {\dot{+}}\tfrac{\beta -\sigma -\alpha \sigma _{-f,h}}{-\alpha }h \bigr ]. \end{aligned}$$

The expression for $\sigma _{-\psi ,h}$ follows by replacing $\alpha$ and $\beta$ with $-\alpha$ and $-\beta$; in turn, the expression for $L_{\psi ,h}$ follows from (3.6). $\square$

4 Algorithmic Analysis Toolbox

In the literature, convergence analysis for nonconvex splitting algorithms typically revolves around the identification of a “Lyapunov potential,” namely a lower bounded function that decreases its value along the iterates. In this section, we will pursue this direction. To simplify the discussion, we introduce

$$\begin{aligned} \hat{h}\mathrel {{:}{=}}\tfrac{1}{\gamma }h\mathbin {\dot{-}}f \quad \text {and}\quad \hat{f}_{\!\beta }\mathrel {{:}{=}}f\mathbin {\dot{-}}\tfrac{\beta }{\gamma }h \mathbin {\dot{+}}{{\,\mathrm{\delta }\,}}_{{{\,\textrm{dom}\,}}h}. \end{aligned}$$

(4.1)

Notice that $\hat{f}_{\!\beta }$ is a proper function with ${{\,\textrm{dom}\,}}\hat{f}_{\!\beta }={{\,\textrm{dom}\,}}h$ for any $\beta \in \mathbb {R}$, but for strictly positive values of $\beta$ it may fail to be lsc at some boundary points of $C$. This will nevertheless cause no concern in the analysis of Algorithm 1, since, as will be showcased in Lemma 4.2.(iii), its iterates remain confined within the open set $C$ onto which $\hat{f}_{\!\beta }$ is continuously differentiable. On the other hand, not only is $\hat{h}$ lsc on the whole $\mathbb {R}^n$, but it is actually a Legendre kernel, for $\gamma$ small enough.

Lemma 4.1

([1, Thm. 4.1]) Suppose that Assumption 1.A1 holds. Then, for every $\gamma <1/[\sigma _{-f,h}]_-$ the function $\hat{h}$ is a Legendre kernel with ${{\,\textrm{dom}\,}}\hat{h}={{\,\textrm{dom}\,}}h$.²

Notice further that, as a linear combination of $f$ and $h$, we may invoke Lemma 3.11 to infer that $\hat{f}_{\!\beta }$ is smooth relative to $h$ with

$$\begin{aligned} \sigma _{\pm \hat{f}_{\!\beta },h} = \tfrac{\gamma \sigma _{\pm f,h}{\mp }\beta }{\gamma } \quad \text {and}\quad L_{\hat{f}_{\!\beta },h} = \tfrac{1}{\gamma }\max \{ \beta -\gamma \sigma _{f,h},\, -\beta -\gamma \sigma _{-f,h} \}. \end{aligned}$$

(4.2)

We will also (ab)use the notation ${{\,\textrm{D}\,}}_\psi$ of the Bregman distance for functions $\psi :\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ differentiable on $C$ that are not necessarily convex. This notational abuse is justified by the fact that all algebraic identities of the Bregman distance used in the manuscript (e.g., the three-point identity [16, Lem. 3.1]) are valid regardless of whether $\psi$ is convex or not, and will overall yield a major simplification of the math. In particular, for any $\psi _1,\psi _2$ that are continuously differentiable on $C$ and for any $\lambda \in \mathbb {R}$ we may exploit the identities ${{\,\textrm{D}\,}}_{\psi _1\mathbin {\dot{+}}\psi _2}={{\,\textrm{D}\,}}_{\psi _1}\mathbin {\dot{+}}{{\,\textrm{D}\,}}_{\psi _2}$, ${{\,\textrm{D}\,}}_{\psi _1\mathbin {\dot{-}}\psi _2}={{\,\textrm{D}\,}}_{\psi _1}\mathbin {\dot{-}}{{\,\textrm{D}\,}}_{\psi _2}$, and ${{\,\textrm{D}\,}}_{\lambda \psi _1}=\lambda {{\,\textrm{D}\,}}_{\psi _1}$, holding on $\mathbb {R}^n\times C$, with no concern about the sign of $\lambda$ or whether either function is convex or not.

4.1 Parametric Minimization Model

As a first step toward the desired goals, as well as to considerably simplify the discussion, we begin by observing that the $i^*$FRB-update is the result of a parametric minimization. To this end, we introduce the “model” defined by

(4.3a)

(4.3b)

where the last equality holds due to the well-known three-point identity (see [16, Lem. 3.1]). Notice that no extended arithmetics are necessary in the above formulae due to the restriction $(w,x,x^-)\in {{\,\textrm{dom}\,}}h\times C\times C$ which guarantees the finiteness of all quantities involved, except possibly $\varphi (w)$. Then, adding constant terms from the $x$-update in $i^*$FRB yields

where the second last equality owes to the relation $\nabla h(y^k) = \nabla h(x^k)-\gamma \bigl (\nabla f(x^k)-\nabla f(x^{k-1})\bigr )$ (recall step 1 of $i^*$FRB). It follows that the $x$-update in $i^*$FRB can be compactly expressed as

$$\begin{aligned} x^{k+1} \in {}&{\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x^k,x^{k-1}), \end{aligned}$$

(4.4a)

where ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}:C\times C\rightrightarrows C$ defined by

(4.4b)

is the $i^*$FRB-operator with stepsize $\gamma$ and inertial parameter $\beta$. The fact that ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}$ maps pairs in $C\times C$ to subsets of $C$ is a consequence of Assumption 1.A4, as we are about to formalize in Lemma 4.2.(iii). Note that many models can be defined whose marginal minimization with respect to the first variable results in the same ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}$, and all these differ by additive terms which are constant with respect to $w$. Among these, the one given in (4.3b) reflects the tangency condition for every $x,x^-\in C$. A consequence of this fact and other basic properties are summarized next.

Lemma 4.2

(basic properties of the model and the operator ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}$) Suppose that Assumption 1 holds, and let $\gamma <1/[\sigma _{-f,h}]_-$ and $\beta \in \mathbb {R}$ be fixed. The following hold:

• (i) 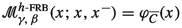for all $x,x^-\in C$.

• (ii) is level bounded in $w$ locally uniformly in $(x,x^-)$.

• (iii) ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}$ is locally bounded and osc,³ and ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$ is a nonempty and compact subset of $C$ for any $x,x^-\in C$.

• (iv) $\nabla \hat{h}(x)-\nabla \hat{h}(\bar{x})-\nabla \hat{f}_{\!\beta }(x)+\nabla \hat{f}_{\!\beta }(x^-)\in {\hat{\partial }} {\varphi }({\bar{x}})$ for any $x,x^-\in C$ and ${\bar{x}}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$.

• (v) If $x\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x)$, then $0\in {\hat{\partial }} {\varphi }(x)$ and ${\text {T}}_{\gamma '\!,\,\beta }^{h\text {-frb}}(x,x)=\{x\}$ for every $\gamma '\in (0,\gamma )$.

Proof

We start by observing that Lemma 3.6 ensures that ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$ is nonempty for any $x,x^-\in C$; this follows by considering the expression (4.3a) of the model, by observing that, for any $x\in C$, $\varphi +{{\,\textrm{D}\,}}_{\hat{h}}({}\cdot {},x) = g+\tfrac{1}{\gamma }h-\hat{h}(x)-\langle \nabla \hat{h}(x),{}\cdot {}-x\rangle$. For the same reason, it then follows from Assumption 1.A4 that ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)\subset C$.

4.2.(i)  Apparent, by considering $w=x$ in (4.3b).

4.2.(ii) & 4.2.(iii)  The first assertion owes to the fact that $\hat{h}$ is 1-coercive by Lemma 4.1 and that both $\hat{h}$ and $\nabla \hat{f}_{\!\beta }$ are continuous on $C$, so that for any compact set one has that

as is apparent from (4.3a). In turn, the second assertion follows from [37, Thm. 1.17].

4.2.(iv)  Follows from the optimality conditions of , having $\bar{x}\in C$ by assertion 4.2.(iii) so that the calculus rule of [37, Ex. 8.8(c)] applies (having $\hat{h}$ smooth around ${\bar{x}}\in C$).

4.2.(v)  That $0\in {\hat{\partial }} {\varphi }(x)$ follows from assertion 4.2.(iv), and the other claim from [1, Lem. 3.6] by observing that ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x)={{\,\textrm{argmin}\,}}\{\varphi +{{\,\textrm{D}\,}}_{\hat{h}}({}\cdot {},x)\}$ for any $\gamma >0$ and $\beta \in \mathbb {R}$. $\square$

Remark 4.3

(inertial effect) Letting ${\tilde{f}}=f\mathbin {\dot{+}}ch$ and ${\tilde{g}}=g\mathbin {\dot{-}}ch$ for some $c\in \mathbb {R}$, ${\tilde{f}}+{\tilde{g}}$ gives an alternative decomposition of $\varphi$ which still complies with Assumption 1, having $\sigma _{\pm {\tilde{f}},h}=\sigma _{\pm f,h}\pm c$ by Lemma 3.11. Relative to this decomposition, for any stepsize ${{\tilde{\gamma }}}$ and inertial parameter ${{\tilde{\beta }}}$, the corresponding model is given by

Thus,

and in particular $i^*$FRB steps with the respective parameters coincide. The effect of inertia can then be explained as a redistribution of multiples of $h$ among $f$ and $g$ in the problem formulation, having for any $\gamma >0$ and $\beta <1$.

4.2 The $i^*$FRB-envelope

Having defined model and its solution mapping ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}$ resulted from parametric minimization, we now introduce the associated value function, which we name $i^*$FRB-envelope.

Definition 4.4

($i^*$FRB-envelope) The envelope associated with $i^*$FRB with stepsize $\gamma <1/[\sigma _{f,h}]_-$ and inertia $\beta \in \mathbb {R}$ is the function $\phi _{\gamma \!,\,\beta }^{h\text {-frb}}:C\times C\rightarrow {\mathbb {R}}$ defined as

(4.5)

Lemma 4.5

(basic properties of $\phi _{\gamma \!,\,\beta }^{h\text {-frb}}$) Suppose that Assumption 1 holds. Then, for any $\gamma <1/[\sigma _{f,h}]_-$ and $\beta \in \mathbb {R}$ the following hold:

• (i) $\phi _{\gamma \!,\,\beta }^{h\text {-frb}}$ is (real-valued and) continuous on $C\times C$; in fact, it is locally Lipschitz provided that .

• (ii) For any $x,x^-\in C$ and ${\bar{x}}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$

  

• (iii) $\phi _{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-) {}\le {} \varphi (x)$ for any $x,x^-\in C$.

Proof

4.5.(i)  In light of the uniform level boundedness asserted in Lemma 4.2.(ii), continuity of $\phi _{\gamma \!,\,\beta }^{h\text {-frb}}$ follows from [37, Thm. 1.17(c)] by observing that the mapping is continuous for every $w$; in fact, when $f$ and $h$ are both on $C$, the gradient $\nabla _{(x,x^-)}{\mathcal {M}}_{\gamma \!,\,\beta }^{h\text {-frb}}(w,x,x^-) = ( \nabla \hat{f}_{\!\beta }(x^-)-\nabla \hat{f}_{\!\beta }(x)+ \bigl (\nabla ^2\hat{f}_{\!\beta }-\nabla ^2\hat{h}\bigr )(x)(w-x),\,\nabla ^2\hat{f}_{\!\beta }(x^-)(x-w))$ exists and is continuous with respect to all its arguments, which together with local boundedness of ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}$, cf. Lemma 4.2.(iii), gives that $-\phi _{\gamma \!,\,\beta }^{h\text {-frb}}$ is a lower- function in the sense of [37, Def. 10.29], and in particular locally Lipschitz continuous by virtue of [37, Thm.s 10.31 and 9.2].

4.5.(ii) & 4.5.(iii)  The identity follows by definition, cf. (4.5) and (4.4b). The inequality follows by considering $w=x$ in (4.5) and (4.3b). $\square$

4.3 Establishing a Merit Function

We now work toward establishing a merit function for $i^*$FRB, starting from comparing the values of $\phi _{\gamma \!,\,\beta }^{h\text {-frb}}({\bar{x}},x)$ and $\phi _{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$, with ${\bar{x}}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$. Owing to Lemma 4.5.(iii), we have

(4.6)

From here two separate cases can be considered, each yielding surprisingly different results. The watershed lies in whether the “complicating” term is positive or not: one case will result in a very straightforward convergence analysis in the full generality of Assumption 1, while the other will necessitate an additional Lipschitz differentiability requirement. The convergence analysis in both cases revolves around the identification of a constant $c>0$ determining a lower bounded merit function

(4.7)

The difference between the two cases is determined by function $\xi$ appearing in the last Bregman operator ${{\,\textrm{D}\,}}_\xi$, having $\xi =\hat{f}_{\!\beta }$ in the former case and $\xi =L_{\hat{f}_{\!\beta }}{\mathcal {j}}$ in the latter, where $L_{\hat{f}_{\!\beta }}$ is a Lipschitz constant for $\nabla \hat{f}_{\!\beta }$ and we remind that

$$\begin{aligned} {\mathcal {j}}\mathrel {{:}{=}}\tfrac{1}{2}\Vert {}\cdot {}\Vert ^2 \end{aligned}$$

(4.8)

is the squared Euclidean norm. The two cases are stated in the next theorem, which constitutes the main result of this section. Special and worst-case scenarios leading to simplified statements will be given in Sect. 4.4. In what follows, patterning the normalization of $\sigma _{\pm f,h}$ into $p_{\pm f,h}$ detailed in Sect. 3, we also introduce the scaled stepsize

$$\begin{aligned} \alpha \mathrel {{:}{=}}\gamma L_{f,h}, \end{aligned}$$

(4.9)

which as a result of the convergence analysis will be confined in the interval $(0,1)$.

Theorem 4.6

Let $\alpha$ be given by (4.9). Suppose that Assumption 1 holds and consider one of the following scenarios:

• (A) either $\hat{f}_{\!\beta }$ is convex (e.g., when $\alpha p_{f,h}-\beta \ge 0$) and $\beta > -(1+3\alpha p_{-f,h})/2$, in which case

  $$\begin{aligned} \xi \mathrel {{:}{=}}\hat{f}_{\!\beta }\quad \text {and}\quad c \mathrel {{:}{=}}1+2\beta +3\alpha p_{-f,h}>0, \end{aligned}$$

• (B) or $\hat{f}_{\!\beta }$ is $L_{\hat{f}_{\!\beta }}$-Lipschitz differentiable, $h$ is $\sigma _h$-strongly convex, and

  $$\begin{aligned} c \mathrel {{:}{=}}(1+\alpha p_{-f,h}) - \tfrac{2\gamma L_{\hat{f}_{\!\beta }}}{\sigma _h} > 0, \end{aligned}$$

  in which case $\xi \mathrel {{:}{=}}L_{\hat{f}_{\!\beta }}{\mathcal {j}}$.

Then, for as in (4.7) the following assertions hold:

• (i) For every $x,x^-\in C$ and ${\bar{x}}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$,

  

  (4.10a)

  and

  

  (4.10b)

• (ii) .

• (iii) If either $h$ is strongly convex or ${{\,\textrm{dom}\,}}h=\mathbb {R}^n$, then is level bounded provided that $\varphi _{\overline{C}}$ is.

The proof of this result is detailed in the dedicated Appendix A; before that, let us draw some comments. As clarified in the statement of Theorem 4.6.(A), convexity of $\hat{f}_{\!\beta }$ can be enforced by suitably choosing $\gamma$ and $\beta$ without imposing additional requirements on the problem. However, an unusual yet reasonable condition on inertial parameter $\beta$ may be necessary.

Remark 4.7

In order to furnish Theorem 4.6.(A), we shall see soon that $\beta \le 0$ may be required; see Sect. 4.4. Such assumption, although more pessimistic, coincides with a recent conjecture by Dragomir et al. [18, §4.5.3], which states that inertial methods with nonadaptive coefficients fail to converge in the relative smoothness setting, and provides an alternative perspective to the same matter through the lens of the convexity of $\hat{f}_{\!\beta }$.

Unlike Theorem 4.6.(A), however, additional assumptions are needed for the Lipschitz differentiable case of Theorem 4.6.(B). This is because the requirement is equivalent to smoothness relative to the Euclidean Bregman kernel ${\mathcal {j}}$, while Assumption 1 prescribes bounds only relative to $h$.

Remark 4.8

Under Assumption 1, one has that $\hat{f}_{\!\beta }$ is Lipschitz differentiable with modulus $L_{\hat{f}_{\!\beta }}$ under either one of the following conditions:

• (B1) either $\nabla h$ is $L_h$-Lipschitz, and $L_{\hat{f}_{\!\beta }} = \tfrac{L_h}{\gamma }\max \{ \beta -\alpha p_{f,h}, -\beta -\alpha p_{-f,h} \}$,

• (B2) or $\beta =0$ and $\nabla f$ is $L_f$-Lipschitz, in which case $L_{\hat{f}_{\!\beta }}=L_f$.

Recalling that $\hat{f}_{\!\beta }=f-\frac{\beta }{\gamma }h$, the second condition is tautological. In case $\nabla h$ is $L_h$-Lipschitz, the claim follows from (4.2) together with Corollary 3.10.

4.4 Simplified Bounds

In this section, we provide bounds that only discern whether $f$ is convex, concave, or neither of the above. As discussed in Remark 3.5, these cases can be recovered by suitable combinations of the coefficients $p_{\pm f,h}\in \{0,\pm 1\}$ and thus lead to easier, though possibly looser, bounds compared to those in Theorem 4.6. We will also avail ourselves of the estimates of $L_{\hat{f}_{\!\beta }}$ in Remark 4.8 to discuss the cases in which $\hat{f}_{\!\beta }$ is Lipschitz differentiable. To simplify the exposition, we may provide smaller estimates of the coefficient $c$ in Theorem 4.6, owing to the fact that replacing $c$ with any $c'\in (0,c]$ does not affect the validity of the statement and only causes the inequalities (4.10) to be possibly looser.

Without distinguishing between upper and lower relative bounds, whenever $f$ is $L_{f,h}$-smooth relative to $h$ as in Assumption 1 one can consider $\sigma _{\pm f,h}=-L_{f,h}$ or, equivalently, $p_{f,h}=p_{-f,h}=-1$. Plugging these values into Theorem 4.6 yields the following.

Corollary 4.9

(worst-case bounds) Suppose that Assumption 1 holds. All the claims of Theorem 4.6 hold when $\gamma >0$, $\beta \in \mathbb {R}$ and $c>0$ are such that

• (A) either $-1/2<\beta <0$ and $\gamma \le (1/L_{f,h}) \min \{-\beta ,(1+2\beta -c)/3 \},$ in which case $\xi =\hat{f}_{\!\beta }$;

• (B1) or $h$ is $\sigma _h$-strongly convex and $L_h$-Lipschitz differentiable, $|\beta |<\sigma _h/2L_h$ and $\gamma \le (1/L_{f,h})[(\sigma _h(1-c)-2L_h|\beta |)/(\sigma _h+2L_h) ],$ in which case $\xi =(L_h/\gamma )(\alpha +|\beta |){\mathcal {j}}$;

• (B2) or $h$ is $\sigma _h$-strongly convex, $\nabla f$ is $L_f$-Lipschitz continuous, $\beta =0$ and $\gamma \le \sigma _h(1-c)/(\sigma _hL_{f,h}+2L_{f,h})$, in which case $\xi =L_f{\mathcal {j}}$.

Proof

Setting $p_{\pm f,h}=-1$ in Theorem 4.6, one has:

4.9.(A)  The bounds in the statement of Theorem 4.6.(A) read $0 < c = 1+2\beta -3\alpha$ and $\beta \le -\alpha$. Expressed in terms of $\alpha =\gamma L_{f,h}$, the claimed bounds on $\gamma$ are obtained. In turn, imposing $\alpha >0$ results in the claimed bounds on $\beta$.

4.9.(B1) & 4.9.B2  The two subcases refer to the corresponding items in Remark 4.8. We shall show only the first one, as the second one is a trivial adaptation after observing that $L_f=L_{f,h}L_h$ by virtue of Corollary 3.10. The value of $L_{\hat{f}_{\!\beta }}$ as in Remark (B1) reduces to $L_{\hat{f}_{\!\beta }}=(L_h/\gamma )(\alpha +|\beta |)$. Plugged into Theorem 4.6.(B) yields $0 < c = 1-\alpha - 2(\alpha +|\beta |)L_h/\sigma _h$, implying that $\gamma =\alpha /L_{f,h}$ is bounded as in assertion 4.9.(B1). Imposing $\alpha >0$ yields also the claimed bounds on $\beta$. $\square$

When $f$ is convex on $C$, $\sigma _{f,h}=0$ can be considered resulting in $p_{f,h}=0$ and $p_{-f,h}=-1$.⁴

Corollary 4.10

(bounds when $f$ is convex) Suppose that Assumption 1 holds and that $f$ is convex. All the claims of Theorem 4.6 remain valid if $\gamma >0$, $\beta \in \mathbb {R}$ and $c>0$ are such that

• (A) either $-1/2<\beta \le 0$ and $\gamma \le (1/L_{f,h})[(1+2\beta -c)/3 ]$, in which case $\xi =\hat{f}_{\!\beta }$;

• (B1) or $h$ is $\sigma _h$-strongly convex and $L_h$-Lipschitz differentiable,

  $$\begin{aligned} |\beta |<\tfrac{\sigma _h}{2L_h} \quad \text {and}\quad \gamma \le \tfrac{1}{L_{f,h}}\min \{ \tfrac{\sigma _h(1-c)+2L_h\beta }{\sigma _h+2L_h},\, \tfrac{\sigma _h(1-c)-2L_h\beta }{\sigma _h} \}, \end{aligned}$$

  in which case $\xi =(L_h/\gamma )\max \{\beta ,\alpha -\beta \}{\mathcal {j}}$;

• (B2) or $h$ is $\sigma _h$-strongly convex, $\nabla f$ is $L_f$-Lipschitz, $\beta =0$, and $\gamma \le (1-c)\sigma _h/(\sigma _hL_{f,h}+2L_f)$, in which case $\xi =L_f{\mathcal {j}}$.

Proof

We will pattern the proof of Corollary 4.9, and omit the proof of assertion 4.10.(B2) which is an easy adaptation of that of assertion 4.10.(B1). Setting $p_{f,h}=0$ and $p_{-f,h}=-1$ in Theorem 4.6, one has:

4.10.(A)  The bounds in the statement of Theorem 4.6.(A) read $0 < c = 1+2\beta -3\alpha$ and $\beta \le 0$. This readily yields the bound $\gamma L_{f,h}=\alpha \le \frac{1+2\beta -c}{3}$ after replacing $c = 1+2\beta -3\alpha$ by $c\le 1+2\beta -3\alpha$ with an abuse of notation on $c$, under which inequalities in the desired Theorem 4.6.(i) hold with possibly looser bounds. In turn, the condition $\alpha >0$ then constrains $\beta \in (-1/2,0]$, as claimed.

4.10.(B1)  The value of $L_{\hat{f}_{\!\beta }}$ in Remark (B1) reduces to $\frac{L_h}{\gamma }\max \{\beta ,\alpha -\beta \}$. Plugged into Theorem 4.6.(B) yields $0 < c = (1-\alpha ) - 2L_h/\sigma _h\max \{\beta ,\alpha -\beta \}$, and in particular

$$\begin{aligned} \begin{array}{lll} c \le (1-\alpha ) - 2\beta L_h/\sigma _h, \\ c \le (1-\alpha ) - 2(\alpha -\beta )L_h/\sigma _h. \end{array} \end{aligned}$$

In terms of $\gamma =\alpha /L_{f,h}$, this results in the bound for $\gamma$ as in assertion 4.10.(B1). In turn, imposing $\alpha >0$ results in the claimed bounds on $\beta$. $\square$

Similarly, when $f$ is concave (that is, $-f$ is convex) on $C$, then $\sigma _{-f,h}=0$ can be considered, resulting in $p_{f,h}=-1$ and $p_{-f,h}=0$.

Corollary 4.11

(bounds when $f$ is concave) Suppose that Assumption 1 holds and that $f$ is concave. All the claims of Theorem 4.6 remain valid if $\gamma >0$, $\beta \in \mathbb {R}$ and $c>0$ are such that

• (A) either $(c-1)/2 \le \beta <0$ and $\gamma \le -\beta /L_{f,h},$ in which case $\xi =\hat{f}_{\!\beta }$;

• (B1) or $h$ is $\sigma _h$-strongly convex and $L_h$-Lipschitz differentiable,

  $$\begin{aligned} -\tfrac{(1-c)\sigma _h}{2L_h}\le \beta <\tfrac{\sigma _h}{2L_h} \quad \text {and}\quad \gamma \le \tfrac{1}{L_{f,h}}\tfrac{\sigma _h(1-c)-2L_h\beta }{2L_h}, \end{aligned}$$

  in which case $\xi =\frac{L_h}{\gamma }\max \{\alpha +\beta ,-\beta \}{\mathcal {j}}$;

• (B2) or $h$ is $\sigma _h$-strongly convex, $f$ is $L_f$-Lipschitz differentiable, $\beta =0$ and $\gamma \le \sigma _h(1-c)/(2L_f),$ in which case $\xi =L_f{\mathcal {j}}$.

Proof

Set $p_{f,h}=-1$ and $p_{-f,h}=0$ in Theorem 4.6. A similar argument as in Corollary 4.10 completes the proof:

4.11.(A)  From Theorem 4.6.(A), we obtain $-\alpha -\beta \ge 0$ and $c = 1+2\beta > 0$. Recalling that $\alpha =\gamma L_{f,h}$ must be strictly positive, the bound on $\gamma$ and on $\beta$ as in the statement are obtained.

4.11.(B1)  Remark (B1) yields the estimate $L_{\hat{f}_{\!\beta }}=L_h/\gamma \max \{\alpha +\beta ,-\beta \}$, which plugged into the statement of Theorem 4.6.(B) gives $0 < c = 1 - 2L_h/\sigma _h\max \{\alpha +\beta ,-\beta \}$. Therefore,

$$\begin{aligned}{} & {} c \le 1 + 2\beta L_h/\sigma _h, \\{} & {} c \le 1 - 2(\alpha +\beta )L_h/\sigma _h, \end{aligned}$$

which in terms of $\gamma =\alpha /L_{f,h}$ results in the bound on $\gamma$ and lower bound on $\beta$ as in assertion 4.11.(B1). The upper bound on $\beta$ follows from ensuring $\sigma _h-2L_h\beta >0$, which is necessary for the bound $\gamma >0$.

Once again, the case 4.11.(B2) is an easy adaptation of 4.11.(B1). $\square$

5 Convergence Analysis

In this section, we study the behavior of sequences generated by $i^*$FRB. Although some basic convergence results can be derived in the full generality of Assumption 1, establishing local optimality guarantees of the limit point(s) will ultimately require an additional full domain assumption.

Assumption 2

Function $h$ has full domain, that is, $C=\mathbb {R}^n$.

Assumption 2 is standard for nonconvex splitting algorithms in a relative smooth setting. To the best of our knowledge, the question regarding whether this requirement can be removed remains open; see, e.g., [39] and the references therein.

5.1 Function Value Convergence

We begin with the convergence of merit function value.

Theorem 5.1

(function value convergence of $i^*$FRB) Let $(x^k)_{k\in \mathbb {N}}$ be a sequence generated by $i^*$FRB (Algorithm 1) in the setting of Theorem 4.6. Then,

• (i) It holds that

  

  (5.1)

  In particular, $\sum _{k=0}^{\infty }{{\,\textrm{D}\,}}_h\left( x^k,x^{k-1}\right) <+\infty$ and as $k\rightarrow +\infty$ for some $\varphi ^\star \ge \inf \varphi _{\overline{C}}$.

If Assumption 2 also holds, then:

• (ii) If $\varphi _{\overline{C}}$ is level bounded, then $(x^k)_{k\in \mathbb {N}}$ is bounded.

• (iii) Let $\Omega$ be the set of limit points of $(x^k)_{k\in \mathbb {N}}$. Then, $\varphi$ is constant on $\Omega$ with value $\varphi ^\star$, and for every $x^\star \in \Omega$ it holds that $x^\star \in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x^\star ,x^\star )$ and $0\in {\hat{\partial }} {\varphi }(x^\star )$.

Proof

5.1.(i)  Recall from Theorem 4.6 that the inequality (5.1) holds and that , from which convergence of readily follows. In turn, telescoping (5.1) shows that $\sum _{k\in \mathbb {N}}{{\,\textrm{D}\,}}_h(x^k,x^{k-1})$ is finite.

5.1.(ii)  From Theorem 5.1.(i), holds for every $k$. Then boundedness of $(x^k)_{k\in \mathbb {N}}$ is implied by level boundedness of ; see Theorem 4.6.(iii).

5.1.(iii)  Suppose that a subsequence $(x^{k_j})_{j\in \mathbb {N}}$ converges to a point $x^\star$, then so do the subsequences $(x^{k_j\pm 1})_{j\in \mathbb {N}}$ by Theorem 5.1.(i) and [8, Prop. 2.2(iii)].⁵ Since $x^{k_j+1}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x^{k_j},x^{k_j-1})$, by passing to the limit, osc of ${\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}$ (Lemma 4.2.(iii)) implies that $x^\star \in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x^\star ,x^\star )$. Invoking Lemma 4.2.(v) yields the stationarity condition $0\in {\hat{\partial }} {\varphi }(x^\star )$. Moreover, by continuity of one has

where the last equality follows from Lemma 4.5.(ii), owing to the inclusion $x^\star \in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x^\star ,x^\star )$ (and the fact that ${{\,\textrm{D}\,}}_\psi (x,x)=0$ for any differentiable function $\psi$). From the arbitrarity of $x^\star \in \Omega$, we conclude that $\varphi \equiv \varphi ^\star$ on $\Omega$. $\square$

The full domain assumption on $h$ in Theorem 5.1.(ii) is stronger than necessary, but suffices to our purposes. The proof invokes the level bounedness of via Theorem 4.6.(iii), which hinges on the property that whenever $(x_k)_{k\in \mathbb {N}}\subset C$ is bounded and $(x_k^-)_{k\in \mathbb {N}}\subset C$ is unbounded, $({{\,\textrm{D}\,}}_h(x_k,x_k^-))_{k\in \mathbb {N}}$ too is unbounded. As such, Theorem 5.1.(ii) remains valid for any $h$, possibly without full domain, as long as the induced Bregman distance ${{\,\textrm{D}\,}}_h(w,x)$ is level bounded in $x$ locally uniformly in $w$.

Remark 5.2

($i^*$FRB as a globalization framework) The “sufficient” decrease property over the merit function assessed in Theorem 5.1.(i) together with the continuity of makes $i^*$FRB a suitable candidate for the continuous-Lyapunov descent (CLyD) framework [40, §4], enabling the globalization of fast local methods $x^+=x+d$ by using only $i^*$FRB operations, with no change of metrics. Indeed, because of continuity, not only is smaller than at $(x^{k+1},x^k)$, but also at sufficiently close points. This means that the $i^*$FRB update can be replaced by $(1-\tau _k)(x^{k+1},x^k)+\tau _k(x^k+d^k,x^{k-1}+d_-^k)$, where $(d^k,d_-^k)$ is the sought update direction at the current iterate pair $(x^k,x^{k-1})$ and $\tau _k$ is a stepsize to be backtracked until a sufficient decrease on is achieved. Under assumptions, suitable choices of $(d^k,d_-^k)$ can yield fast asymptotic rates. We refer the interested reader to the analysis of the Bella algorithm [1, Alg. 5.1], based on Bregman proximal gradient but otherwise very closely related.

It is now possible to demonstrate the necessity of some of the bounds on the stepsize that were discussed in Sect. 4.4, by showing that ${{\,\textrm{D}\,}}_h(x^{k+1},x^k)$ may otherwise fail to vanish. Note that, for $\beta =0$, the following counterexample constitutes a tightness certificate for the bound $\gamma <1/3L_f$ derived in [47] in the noninertial Euclidean case.

Example 5.3

The bound $\alpha =\gamma L_{f,h}<(1+2\beta )/3$ is tight even in the Euclidean case. To see this, consider $g={{\,\mathrm{\delta }\,}}_{\{\pm 1\}}$ and for a fixed $L>0$ let $f(x)=Lh(x)=\frac{L}{2}x^2$. Then, one has $L_{f,h}=\sigma _{f,h}=L$ and $\sigma _{-f,h}=-L$. For $\gamma <1/L =1/[\sigma _{-f,h}]_-$, it is easy to see that

$$\begin{aligned} {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-) ={}&-{{\,\textrm{sgn}\,}}\bigl ( \nabla \hat{f}_{\!\beta }(x)-\nabla \hat{f}_{\!\beta }(x^-)-\nabla \hat{h}(x) \bigr ) \\ ={}&{{\,\textrm{sgn}\,}}\bigl ( (1-2\alpha +\beta )x+(\alpha -\beta )x^- \bigr ) \end{aligned}$$

(with ${{\,\textrm{sgn}\,}}0\mathrel {{:}{=}}\{\pm 1\}$), where the first equality follows from (4.3a) and (4.4b). Let $x^{-1}=-1$, $x^0=1$. Suppose that $\alpha \ge (1+2\beta )/3$, then $((-1)^k)_{k\in \mathbb {N}}$ is a sequence generated by $i^*$FRB for which ${{\,\textrm{D}\,}}_h(x^{k+1},x^k)\equiv 2\not \rightarrow 0$.

As a consequence of Theorem 5.1.(i), the condition ${{\,\textrm{D}\,}}_h(x^{k+1},x^k)\le \varepsilon$ is satisfied in finitely many iterations for any tolerance $\varepsilon >0$. While this could be used as termination criterion, in the generality of Assumptions 1 and 2 there is no guarantee on the relaxed stationarity measure ${{\,\textrm{dist}\,}}(0,{\hat{\partial }} {\varphi }(x^{k+1}))$, which through Lemma 4.2.(iv) can only be estimated as

$$\begin{aligned} \begin{aligned}&{{\,\textrm{dist}\,}}(0,{\hat{\partial }} {\varphi }(x^{k+1})) \le \Vert v^{k+1}\Vert \\&~~\text {with}~~ v^{k+1}\mathrel {{:}{=}}\nabla \hat{h}(x^k)-\nabla \hat{h}(x^{k+1})-\nabla \hat{f}_{\!\beta }(x^k)+\nabla \hat{f}_{\!\beta }(x^{k-1}), \end{aligned} \end{aligned}$$

(5.2)

where $\hat{h}$ and $\hat{f}_{\!\beta }$ are as in (4.1). On the other hand, in accounting for possibly unbounded sequences, additional assumptions are needed for the condition $\Vert v^{k+1}\Vert \le \varepsilon$ to be met in finitely many iterations. One such is the so-called uniform smoothness of $h$, which by [4, Thm. 3.8(1)–(2)] can be defined in terms of an inequality

$$\begin{aligned} {{\,\textrm{D}\,}}_h(x,y) \le \varrho (\Vert x-y\Vert ) \end{aligned}$$

(5.3)

holding for every $x,y\in \mathbb {R}^n$, where $\varrho :\mathbb {R}_+\rightarrow {\mathbb {R}_+}$ is a nondecreasing function such that $\rho (0)=0$ and $\rho (s)/s \rightarrow 0$ as $s\searrow 0$. As shown in [4, Thm. 3.8(1)–(2)], the dual counterpart is given by uniform convexity, which amounts to $h^*$ being uniformly smooth.

Lemma 5.4

(termination criteria) Suppose that Assumption 2 holds, and let $(x^k)_{k\in \mathbb {N}}$ be a sequence generated by $i^*$FRB (Algorithm 1) in the setting of Theorem 4.6. If

• (A) either $\varphi$ is level bounded,

• (B) or $h^*$ is uniformly convex (equivalently, $h$ is uniformly smooth),

then, for $v^{k+1}$ as in (5.2) it holds that $v^{k+1}\rightarrow 0$. Thus, for any $\varepsilon >0$ the condition $\Vert v^{k+1}\Vert \le \varepsilon$ is satisfied for all $k$ large enough and guarantees ${{\,\textrm{dist}\,}}(0,{\hat{\partial }} {\varphi }(x^{k+1}))\le \varepsilon$.

Proof

The implication of $\Vert v^{k+1}\Vert \le \varepsilon$ and $\varepsilon$-stationarity of $x^{k+1}$ has already been discussed. If $\varphi$ is level bounded, then Theorem 5.1 implies that $(x^k)_{k\in \mathbb {N}}$ is contained in a compact subset of $C=\mathbb {R}^n$. Recall from Theorem 5.1.(i) that ${{\,\textrm{D}\,}}_h(x^{k+1},x^k)\rightarrow 0$, which implies through [7, Ex. 4.10(ii)], Assumption 2, and the boundedness of $(x^k)_{k\in \mathbb {N}}$ that $x^{k+1}-x^k\rightarrow 0$. In turn, $v^{k+1}\rightarrow 0$ holds by uniform continuity of $\nabla \hat{h}$ and $\nabla \hat{f}_{\!\beta }$ on the aforementioned compact set. In case $h^*$ is uniformly convex, this being equivalent to uniform smoothness of $h$ by [4, Thm. 3.8(1)–(2)], the vanishing of ${{\,\textrm{D}\,}}_{h^*}(\nabla h(x^k),\nabla h(x^{k+1}))={{\,\textrm{D}\,}}_h(x^{k+1},x^k)$ implies through [36, Prop. 4.13(IV)] that $\Vert \nabla h(x^k)-\nabla h(x^{k+1})\Vert \rightarrow 0$. Since ${{\,\textrm{D}\,}}_{L_{f,h}h+f}\le 2L_{f,h}{{\,\textrm{D}\,}}_h$ holds by convexity of $L_{f,h}h-f$, from the characterization (5.3) it is apparent that $L_{f,h}h+f$ too is uniformly smooth. Arguing as above, the vanishing of ${{\,\textrm{D}\,}}_{L_{f,h}h+f}(x^{k+1},x^k)$ implies that of $\Vert \nabla [L_{f,h}h+f](x^{k+1})-\nabla [L_{f,h}h+f](x^k)\Vert$. Note that

$$\begin{aligned} \hat{f}_{\!\beta }{\mathop {=}\limits ^{\text {(def)}}} f - \tfrac{\beta }{\gamma }h = L_{f,h}h+f - \left[ L_{f,h}+\tfrac{\beta }{\gamma } \right] h \quad \text {and}\quad \hat{h}{\mathop {=}\limits ^{\text {(def)}}} \tfrac{1}{\gamma }h-f = \tfrac{1-\beta }{\gamma }h - \hat{f}_{\!\beta }. \end{aligned}$$

Then the vanishing of $\Vert \nabla [L_{f,h}h+f](x^{k+1})-\nabla [L_{f,h}h+f](x^k)\Vert$ and $\Vert \nabla h(x^k)-\nabla h(x^{k+1})\Vert$ implies that

$$\begin{aligned} v^{k+1}{\mathop {=}\limits ^{\text {(def)}}}\nabla \hat{h}(x^k)-\nabla \hat{h}(x^{k+1})-\nabla \hat{f}_{\!\beta }(x^k)+\nabla \hat{f}_{\!\beta }(x^{k-1})\rightarrow 0, \end{aligned}$$

as desired. $\square$

5.2 Global Convergence

In this subsection, we work toward the global sequential convergence of $i^*$FRB. To this end, we introduce a key concept which will be useful soon. For $\eta \in (0,+\infty ]$, denote by $\Psi _\eta$ the class of functions $\psi :[0,\eta )\rightarrow \mathbb {R}_+$ satisfying the following: (i) $\psi (t)$ is right-continuous at $t=0$ with $\psi (0)=0$; (ii) $\psi$ is strictly increasing on $[0,\eta )$; (iii) $\psi$ is continuously differentiable on $(0,\eta )$.

Definition 5.5

([2, Def. 3.1]) Let $F:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ be proper and lsc, and let $\partial F$ be its Mordukhovich limiting subdifferential. We say that F has the Kurdyka–Łojasiewicz (KL) property at ${\bar{x}}\in {{\,\textrm{dom}\,}}\partial F$, if there exist a neighborhood $U\ni {\bar{x}}$, $\eta \in (0,+\infty ]$ and a concave $\psi \in \Psi _\eta$, such that for all $x\in U\cap [0<F-F(\bar{x})<\eta ]$,

$$\begin{aligned} \psi '\bigl (F(x)-F({\bar{x}})\bigr )\cdot {{\,\textrm{dist}\,}}\bigl (0,\partial F(x)\bigr )\ge 1. \end{aligned}$$

Moreover, F is a KL function if it has the KL property at every $x\in {{\,\textrm{dom}\,}}\partial F$.

Now we present our main result on global convergence. As the proof is standard, we defer it to Appendix B for the sake of completeness.

Theorem 5.6

(sequential convergence of $i^*$FRB) Suppose that Assumption 2 holds, and let $(x^k)_{k\in \mathbb {N}}$ be a sequence generated by $i^*$FRB (Algorithm 1) in the setting of Theorem 4.6. Assume in addition the following:

• A1 $\varphi$ is level bounded.

• A2 f, h are twice continuously differentiable and $\nabla ^2h$ is positive definite everywhere.

• A3 $\varphi ,h$ are semialgebraic functions (see, e.g., [2, §4.3]).

Then $\sum _{k=0}^\infty \Vert x^{k+1}-x^k\Vert <+\infty$ and there exists $x^\star$ with $0\in {\hat{\partial }} {\varphi }(x^{\star })$ such that $x^k\rightarrow x^\star$ as $k\rightarrow +\infty$.

Remark 5.7

We note that a sharp estimation on $\sum _{k=0}^\infty \Vert x^{k+1}-x^k\Vert$ can be obtained by replacing Assumption 5.6.A3 in Theorem 5.6 with the notion introduced in [46].

Remark 5.8

Compared to the Lipschitz smooth case considered in [47], the twice continuous differentiability assumption in Theorem 5.6 is a technicality for finding an upper bound on $\Vert (u^k,v^k)\Vert$, which consists of difference of gradients, as a multiple of $\Vert x^k-x^{k-1}\Vert$; see also [1, Thm. 5.7] for a similar assumption. We delay its relaxation for future research.

5.3 Convergence Rates

Having established convergence of $i^*$FRB, we now turn to its rate. Recall that a function is said to have KL exponent $\theta \in [0,1)$ if it satisfies the KL property (recall Definition 5.5) and there exists a desingularizing function of the form $\psi (t)=ct^{1-\theta }$ for some $c>0$.

Theorem 5.9

(function value and sequential convergence rate) Suppose that all the assumptions in Theorem 5.6 are satisfied, and follow the notation therein. Define $(\forall k\in \mathbb {N})$ and

for all $\omega ,x,x^-\in \mathbb {R}^n$. Assume in addition that has KL exponent $\theta \in [0,1)$ at $(x^\star ,x^\star ,x^\star )$. Then the following hold:

• (i) If $\theta =0$, then $e_k\rightarrow 0$ and $x^k\rightarrow x^\star$ after finite steps.

• (ii) If $\theta \in (0,1/2 ]$, then there exist $c_1,{\hat{c}}_1>0$ and $Q_1,{\hat{Q}}_1\in [0,1)$ such that for k sufficiently large,

  $$\begin{aligned} e_k\le {\hat{c}}_1{\hat{Q}}_1^k\text { and }\Vert x^k-x^\star \Vert \le c_1Q_1^k. \end{aligned}$$

• (iii) If $\theta \in (1/2,1)$, then there exist $c_2,{\hat{c}}_2>0$ such that for k sufficiently large,

  $$\begin{aligned} e_k\le {\hat{c}}_2k^{-\frac{1}{2\theta -1}} \text { and } \Vert x^k-x^\star \Vert \le c_2k^{-\frac{1-\theta }{2\theta -1}}. \end{aligned}$$

Proof

See Appendix C. $\square$

6 Conclusions

This work contributes a mirror inertial forward–reflected–backward splitting algorithm ($i^*$FRB), extending the forward–reflected–backward method proposed in [29] to the nonconvex and relative smooth setting. We have shown that the proposed algorithms enjoy pleasant properties akin to other splitting methods in the same setting. However, our methodology deviates from tradition through the $i^*$FRB-envelope, an envelope function defined on a product space that takes inertial terms into account, which, to the best of our knowledge, is the first of its kind and thus could be instrumental for future research. This approach also requires the inertial parameter to be negative, which coincides with a recent result [18] regarding the impossibility of accelerated non-Euclidean algorithms under relative smoothness. Thus, it is interesting to see whether an explicit example can be constructed to prove the sharpness of such restrictive assumption. It is also worth applying our technique to other two-stage splitting methods, such as Tseng’s method, to obtain similar extensions.

Appendices

Proof of Theorem 4.6

Throughout this appendix, we remind that the adoption of extended arithmetics is not necessary, since, as a result of Lemma 4.2.(iii), all variables are confined in the open set $C$ onto which both $h$ and $f$ (and consequently $\hat{h}$ and $\hat{f}_{\!\beta }$ as well, for any $\beta \in \mathbb {R}$) are finite-valued.

1.1 Proof of Theorem 4.6.(i) and 4.6.(ii)

We begin by proving a technical lemma in the setting of Theorem 4.6.(A).

Lemma A.1

Suppose that Assumption 1 holds and let $\gamma >0$ and $\beta \in \mathbb {R}$ be such that $\hat{f}_{\!\beta }\mathrel {{=}}f\mathbin {\dot{-}}\frac{\beta }{\gamma }h{}+{{\,\mathrm{\delta }\,}}_{{{\,\textrm{dom}\,}}h}$ is a convex function. Then, for every $x,x^-\in C$ and $\bar{x}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$

$$\begin{aligned} \left( \phi _{\gamma \!,\,\beta }^{h\text {-frb}}+{{\,\textrm{D}\,}}_{\hat{f}_{\!\beta }}\right) ({\bar{x}},x) \le \left( \phi _{\gamma \!,\,\beta }^{h\text {-frb}}+{{\,\textrm{D}\,}}_{\hat{f}_{\!\beta }}\right) (x,x^-) {}-{} {{\,\textrm{D}\,}}_{\hat{h}-2\hat{f}_{\!\beta }}({\bar{x}},x). \end{aligned}$$

(A.1)

Proof

The claimed inequality follows from (4.6) together with the fact that ${{\,\textrm{D}\,}}_{\hat{f}_{\!\beta }}\ge 0$. $\square$

In the setting of Theorem 4.6.(A), recall that we set $c\mathrel {{:}{=}}1+2\beta +3\alpha p_{-f,h}>0$. Then, inequality (A.1) can equivalently be written in terms of as

where the second inequality owes to the fact that ${{\,\textrm{D}\,}}_{\hat{h}-2\hat{f}_{\!\beta }-\frac{c}{\gamma }h}\ge 0$, since $\hat{h}-2\hat{f}_{\!\beta }-\frac{c}{\gamma }h$ is convex, having

the coefficient of $h$ being null by definition of $c$, and $-f-\sigma _{-f,h}h$ being convex by definition of the relative weak convexity modulus $\sigma _{-f,h}$, cf. Definition 3.3. This proves (4.10a); inequality (4.10b) follows similarly by observing that

$$\begin{aligned} 0 \le {{\,\textrm{D}\,}}_{\hat{h}-2\hat{f}_{\!\beta }-\frac{c}{\gamma }h} = {{\,\textrm{D}\,}}_{\hat{h}-\hat{f}_{\!\beta }}-{{\,\textrm{D}\,}}_{\hat{f}_{\!\beta }}-\tfrac{c}{\gamma }{{\,\textrm{D}\,}}\le {{\,\textrm{D}\,}}_{\hat{h}-\hat{f}_{\!\beta }}-\tfrac{c}{\gamma }{{\,\textrm{D}\,}}_h, \end{aligned}$$

so that

This concludes the proof of Theorem 4.6.(i) and 4.6.(ii) in the setting of Theorem 4.6.(A).

Now we work under the setting of Theorem 4.6.(B), in which case the following lemma will be useful.

Lemma A.2

Additionally to Assumption 1, suppose that $\hat{f}_{\!\beta }$ is $L_{\hat{f}_{\!\beta }}$-Lipschitz differentiable for some $L_{\hat{f}_{\!\beta }}\ge 0$. Then, for every $x,x^-\in C$ and ${\bar{x}}\in {\text {T}}_{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-)$ we have

$$\begin{aligned} \left( \phi _{\gamma \!,\,\beta }^{h\text {-frb}}+{{\,\textrm{D}\,}}_{L_{\hat{f}_{\!\beta }}{\mathcal {j}}}\right) ({\bar{x}},x) \le \left( \phi _{\gamma \!,\,\beta }^{h\text {-frb}}+{{\,\textrm{D}\,}}_{L_{\hat{f}_{\!\beta }}{\mathcal {j}}}\right) (x,x^-) - {{\,\textrm{D}\,}}_{\hat{h}-2L_{\hat{f}_{\!\beta }}{\mathcal {j}}}(\bar{x},x). \end{aligned}$$

(A.2)

Proof

By means of the three-point identity, that is, by using (4.3a) in place of (4.3b), inequality (4.6) can equivalently be written as

$$\begin{aligned} \phi _{\gamma \!,\,\beta }^{h\text {-frb}}({\bar{x}},x) \le \varphi _{\overline{C}}({\bar{x}}) ={}&\phi _{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-) - {{\,\textrm{D}\,}}_{\hat{h}}(\bar{x},x) - \langle {\bar{x}}-x,\nabla \hat{f}_{\!\beta }(x)-\nabla \hat{f}_{\!\beta }(x^-)\rangle \end{aligned}$$

which by using Young’s inequality on the inner product and $L_{\hat{f}_{\!\beta }}$-Lipschitz differentiability yields

$$\begin{aligned} \le {}&\phi _{\gamma \!,\,\beta }^{h\text {-frb}}(x,x^-) - {{\,\textrm{D}\,}}_{\hat{h}}({\bar{x}},x) + \tfrac{L_{\hat{f}_{\!\beta }}}{2}\Vert \bar{x}-x\Vert ^2 + \tfrac{L_{\hat{f}_{\!\beta }}}{2}\Vert x-x^-\Vert ^2. \end{aligned}$$

(A.3)

Rearranging and using the fact that ${{\,\textrm{D}\,}}_{{\mathcal {j}}}(x,y)=\frac{1}{2}\Vert x-y\Vert ^2$ yields the claimed inequality. $\square$

Under Theorem 4.6.(B), recall that we define

$$\begin{aligned} c \mathrel {{:}{=}}(1+\alpha p_{-f,h}) {}-{} \tfrac{2\gamma L_{\hat{f}_{\!\beta }}}{\sigma _h} > 0. \end{aligned}$$

We will pattern the arguments of the previous case, and observe that inequality (A.2) can equivalently be written in terms of as

Once again, the fact that ${{\,\textrm{D}\,}}_{\hat{h}-2L_{\hat{f}_{\!\beta }}{\mathcal {j}}-\frac{c}{\gamma }h}\ge 0$ owes to the convexity of $\hat{h}-2L_{\hat{f}_{\!\beta }}{\mathcal {j}}-\frac{c}{\gamma }h$ on ${{\,\textrm{dom}\,}}h$, having

altogether proving (4.10a). Similarly, inequality (4.10b) follows from (A.3) together with the fact that ${{\,\textrm{D}\,}}_{\hat{h}-L_{\hat{f}_{\!\beta }}{\mathcal {j}}}\ge {{\,\textrm{D}\,}}_{\hat{h}-2L_{\hat{f}_{\!\beta }}{\mathcal {j}}}\ge \frac{c}{\gamma }{{\,\textrm{D}\,}}_h$, as shown above, having

This concludes the proof of Theorems 4.6.(i) and 4.6.(ii).

1.2 Proof of Theorem 4.6.(iii)

We first state a property of the Bregman distance ${{\,\textrm{D}\,}}_h$ that holds when $h$ is as in the assertion of the theorem. The proof is provided for completeness, though part of it is straightforward and the rest is an easy adaptation of [6, Lem. 7.3(viii)].

Lemma A.3

Let $h:\mathbb {R}^n\rightarrow {\overline{\mathbb {R}}}$ be a 1-coercive Legendre kernel. If either $h$ is strongly convex or ${{\,\textrm{dom}\,}}h=\mathbb {R}^n$, then ${{\,\textrm{D}\,}}_h(x,y)$ is level bounded in $y$ locally uniformly in $x$.

Proof

Let $(x^k)_{k\in \mathbb {N}}$ and $(y^k)_{k\in \mathbb {N}}$ be sequences in $\mathbb {R}^n$ such that ${{\,\textrm{D}\,}}_h(x^k,y^k)\le \ell$ for some $\ell \in \mathbb {R}$. Suppose that $(x^k)_{k\in \mathbb {N}}$ is bounded; then the proof reduces to showing that also $(y^k)_{k\in \mathbb {N}}$ is. If $h$ is, say, $\sigma _h$-strongly convex for some $\sigma _h>0$, the claim trivially follows from the fact that ${{\,\textrm{D}\,}}_h(x,y)\ge (\sigma _h/2)\Vert x-y\Vert ^2$ in this case.

Suppose that ${{\,\textrm{dom}\,}}h=\mathbb {R}^n$, then it follows from [6, Thm. 3.4] that $h^*$ is 1-coercive. Furthermore, observe that

$$\begin{aligned} \ell \ge {{\,\textrm{D}\,}}_h(x^k,y^k) ={}&h(x^k)-h(y^k)-\langle \nabla h(y^k),x^k-y^k\rangle \\ ={}&h(x^k)+h^*(\nabla h(y^k))-\langle \nabla h(y^k),x^k\rangle \\ \ge {}&c+h^*(\nabla h(y^k))-\Vert \nabla h(y^k)\Vert c', \end{aligned}$$

where $c\mathrel {{:}{=}}\inf h(x^k)$ and $c'\mathrel {{:}{=}}\sup \Vert x^k\Vert$ are finite. Since $h^*$ is 1-coercive, it follows that $(\nabla h(y^k))_{k\in \mathbb {N}}$ is bounded, and therefore so is $(y^k)_{k\in \mathbb {N}}$ by virtue of [6, Thm. 3.3]. $\square$

We now turn to the proof of Theorem 4.6.(iii). By contraposition, suppose that is not level bounded, and consider an unbounded sequence $(x_k,x_k^-)_{k\in \mathbb {N}}$ such that

for some $\ell \in \mathbb {R}$. Then, it follows from (4.10b) that

$$\begin{aligned} \inf \varphi _{\overline{C}}+ \tfrac{c}{\gamma }{{\,\textrm{D}\,}}_h({\bar{x}}_k,x_k) + \tfrac{c}{2\gamma }{{\,\textrm{D}\,}}_h(x_k,x_k^-) \le \varphi _{\overline{C}}({\bar{x}}_k) + \tfrac{c}{\gamma }{{\,\textrm{D}\,}}_h({\bar{x}}_k,x_k) \\+ \tfrac{c}{2\gamma }{{\,\textrm{D}\,}}_h(x_k,x_k^-) \le \ell , \end{aligned}$$

and in particular both $({{\,\textrm{D}\,}}_h({\bar{x}}_k,x_k))_{k\in \mathbb {N}}$ and $({{\,\textrm{D}\,}}_h(x_k,x_k^-))_{k\in \mathbb {N}}$ are bounded. Moreover, it follows from Lemma A.3 that if $(x_k^-)_{k\in \mathbb {N}}$ is unbounded then so is $(x_k)_{k\in \mathbb {N}}$, and similarly unboundedness of $(x_k)_{k\in \mathbb {N}}$ implies that of $({\bar{x}}_k)_{k\in \mathbb {N}}$. Since at least one among $(x_k)_{k\in \mathbb {N}}$ and $(x_k^-)_{k\in \mathbb {N}}$ is unbounded, it follows that $({\bar{x}}_k)_{k\in \mathbb {N}}$ is unbounded. Noticing that this sequence is contained in $[\varphi _{\overline{C}}\le \ell ]$, we conclude that $\varphi _{\overline{C}}$ is not level bounded.

Proof of Theorem 5.6

In the remainder of this section, we will make use of the norm on the product space $\mathbb {R}^n\times \mathbb {R}^n$ defined as . For a set $E\subseteq \mathbb {R}^n$, define $(\forall \varepsilon >0)$ $E_\varepsilon =\{x\in \mathbb {R}^n:{{\,\textrm{dist}\,}}(x,E)<\varepsilon \}$.

Let $(\forall k\in \mathbb {N})$ $z^k=(x^{k+1},x^k,x^{k-1})$, and let $\Omega$ be the set of limit points of $(z_k)_{k\in \mathbb {N}}$. Define

Set $(\forall k\in \mathbb {N})$ for simplicity. Then , $\delta _{k}\rightarrow \varphi ^\star$ decreasingly and ${{\,\textrm{dist}\,}}(x^k,\Omega )\rightarrow 0$ as $k\rightarrow +\infty$ by invoking Theorem 5.1. Assume without loss of generality that $(\forall k\in \mathbb {N})$ $\delta _{k}>\varphi ^\star$, otherwise we would have $(\exists k_0\in \mathbb {N})$ $x^{k_0}=x^{k_0+1}$ due to Theorem 5.1.(i), from which the desired result readily follows by simple induction. Thus, $(\exists k_0\in \mathbb {N})$ $(\forall k\ge k_0)$ . Appealing to Theorem 5.1.(iii) and Lemma 4.2.(i) yields that is constantly equal to $\varphi ^\star$ on the compact set $\Omega$. Note that satisfies the KL property under Assumption 5.6.A3; see, e.g., [2, §4.3]. In turn, appealing to Assumption 5.6.A3 and a standard uniformizing technique of the KL property, see, e.g., [13, Lem. 6.2], implies that there exists a concave $\psi \in \Psi _\eta$ such that for $k\ge k_0$

(B.1)

Define $(\forall k\in \mathbb {N})$

$$\begin{aligned} u^k ={}&\nabla ^2\hat{h}(x^k)(x^k-x^{k+1})+\nabla ^2\hat{f}_{\!\beta }(x^k)(x^{k+1}-x^k)+\tfrac{c}{2\gamma }\bigl (\nabla h(x^k)-\nabla h(x^{k-1})\bigr ) \\&+\nabla \hat{f}_{\!\beta }(x^{k-1})-\nabla \hat{f}_{\!\beta }(x^k)+\nabla \xi (x^k)-\nabla \xi (x^{k-1}), \\ v^k ={}&\nabla ^2\hat{f}_{\!\beta }(x^{k-1})(x^k-x^{k+1}) \\ {}&+\tfrac{c}{2\gamma }\nabla ^2h(x^{k-1})(x^{k-1}-x^k)+\nabla ^2\xi (x^{k-1})(x^{k-1}-x^k). \end{aligned}$$

Applying subdifferential calculus to yields that

which together with Lemma 4.2.(iv) entails that . In turn, Assumption 5.6.A2 implies that there exists $M>0$ such that

(B.2)

Finally, we show that $(x^k)_{k\in \mathbb {N}}$ is convergent. For simplicity, define $(\forall k,l\in \mathbb {N})$ $\Delta _{k,l}=\psi \left( \delta _{k}-\varphi ^\star \right) -\psi \left( \delta _{l}-\varphi ^\star \right)$. Then, combining (B.1) and (B.2) yields

where the second inequality is implied by concavity of $\psi$, the third one follows from (5.1), and the fourth one holds because $\sigma >0$ is the strong convexity modulus of h on a convex compact set that contains all the iterates. Hence,

(B.3)

Summing (B.3) from $k=k_0$ to an arbitrary $l\ge k_0+1$ yields that

where the second inequality holds as $\psi \ge 0$, from which one sees that $\sum _{k=0}^\infty \Vert x^{k+1}-x^k\Vert$ is finite as l is arbitrary. A similar procedure shows that $(x^k)_{k\in \mathbb {N}}$ is Cauchy, which together with Theorem 5.1.(iii) entails the rest of the statement.

Proof of Theorem 5.9

Assume without loss of generality that has desingularizing function $\psi (t)=t^{1-\theta }/(1-\theta )$ and let $(\forall k\in \mathbb {N})$ $\delta _{k}=\sum _{i=k}^\infty \Vert x^{i+1}-x^i\Vert$. We claim that

$$\begin{aligned} (\forall k\ge k_0+1) ~\delta _k\le \tfrac{4\gamma M}{(1-\theta )c\sigma }e_{k}^{1-\theta }. \end{aligned}$$

(C.1)

Indeed, summing (B.3) from every $k\ge k_0$ to $l\ge k+1$ and passing l to infinity give

from which the desired claim readily follows. It is routine to see that the desired sequential rate can be implied by those of $(e_k)_{k\in \mathbb {N}}$ through (C.1); see, e.g., [45, Thm. 5.3]; therefore, it suffices to prove convergence rate of $(e_k)_{k\in \mathbb {N}}$.

Recall from Theorem 5.1.(i) that $(e_k)_{k\in \mathbb {N}}$ is a decreasing sequence converging to 0. Then invoking the KL exponent assumption yields

where the first equality holds due to Lemma 4.5.(ii), which together with (B.2) implies that

(C.2)

Appealing again to Theorem 5.1.(i) gives

where the last inequality is implied by (C.2). Then [15, Lem. 10] justifies the desired rate of $(e_k)_{k\in \mathbb {N}}$.