Energy Dissipative Local Discontinuous Galerkin Methods for Keller–Segel Chemotaxis Model

Abstract

In this paper, we apply the local discontinuous Galerkin (LDG) method to solve the classical Keller–Segel (KS) chemotaxis model. The exact solution of the KS chemotaxis model may exhibit blow-up patterns with certain initial conditions, and is not easy to approximate numerically. Moreover, it has been proved that there exists a definition of free energy of the KS system which dissipates with respect to time. We will construct a consistent numerical energy and prove the energy dissipation with the LDG discretization. Several numerical experiments in one and two space dimensions will be given. Especially, for solutions with blow-up (converge to Dirac delta functions), the densities of KS model are computed to be strictly positive in the numerical experiments and the energies are also numerically observed to be strictly positive and decreasing as are seen in the figures. Therefore, the scheme is stable for the KS model with blow-up solutions.

1 Introduction

In this paper, we study the classical Keller–Segel (KS) chemotaxis model [29, 36]. Let $\Omega$ be a convex, bounded and open set in $\mathbb {R}^2$, then we focus on the following common formulation [7],

$$\begin{aligned}&\rho _t=\Delta \rho -\nabla \cdot (\chi \rho \nabla c),\quad \pmb {x}\in \Omega ,t>0,\end{aligned}$$

(1.1a)

$$\begin{aligned}&c_t=\Delta c+\rho -c,\quad \pmb {x}\in \Omega ,t>0, \end{aligned}$$

(1.1b)

as well as its one dimensional version. Chemotaxis is the nonlinear movement of cell in reaction to a chemical substance, where cell approaches chemically favorable environments and avoids unpleasant ones. In (1.1) $\rho$ represents the densities of cells and c denotes the chemical concentration. The chemotactic sensitivity function $\chi$ is supposed to be a positive constant. For simplicity, we take $\chi \equiv 1$ in this paper. However, this assumption is not essential. The initial conditions are given as

$$\begin{aligned} \rho (\pmb {x},0)=\rho ^0(\pmb {x}),~\text{ and }~c(\pmb {x},0)=c^0(\pmb {x}),\quad \pmb {x}\in \Omega . \end{aligned}$$

(1.2)

In addition, the boundary conditions are set to be homogeneous Neumann boundary condition

$$\begin{aligned} \nabla \rho \cdot \mathbf{n}=\nabla c \cdot \mathbf{n}=0, \end{aligned}$$

(1.3)

where $\mathbf{n}$ is the outer normal of the boundary $\partial \Omega$. With this boundary condition, $\int _\Omega \rho d \pmb {x}= \int _{\Omega }\rho ^0 d\pmb {x}$ is a constant during the time evolution and the system is thus isolated.

It is not easy to obtain the existence and uniqueness of the weak solutions to (1.1). In [19, 20], the initial densities $\rho ^0$ and $c^0$ are assumed to be strictly positive and satisfy

$$\begin{aligned} \rho ^0(x,y)\in L^2(\Omega ),\;\; \rho ^0\ge a^0>0 \text { and }c^{0}(x,y)\in W^{1,p}(\Omega ), \;\;p>2,\quad \forall \ (x,y)\in \Omega , \end{aligned}$$

(1.4)

where $W^{1,p}(\Omega )$ denote the Sobolev space of functions on $\Omega$ with the usual norm $\Vert \cdot \Vert _{1,p}$.

Moreover, ${\rho }^0$ is assumed to satisfy a smallness condition [19], that is, there exists a constant $C_{\Omega }^{\text {GNS}}>0$, such that

$$\begin{aligned} C^{\text {GNS}}_{\Omega } \,\chi \Vert \rho ^0\Vert _{L^1(\Omega )}<1, \end{aligned}$$

where $C_{\Omega }^{\text {GNS}}$ denotes the best constant in the Gagliardo–Nirenberg–Sobolev inequality. Then for appropriate $T>0$, there exists a unique weak solution $(\rho , c)$ (see details in [20]) such that

$$\begin{aligned} \rho \in C\left( [0,T]; L^2(\Omega )\cap L^2(0,T; H^1(\Omega ))\right) , \quad c\in L^2(0,T; H^1(\Omega )). \end{aligned}$$

(1.5)

The exact solutions of the KS chemotaxis model are always non-negative. Moreover, the model exhibits blow-up patterns with certain initial conditions [19, 20, 24, 25, 34]. Biologically, finite-time blow up for solutions is expected to describe chemotactic collapse, that is the tendency of cells to concentrate to form spora, which can be explained mathematically as concentration of $\rho (x,t)$ towards a Dirac delta mass in finite time [25, 34] in the sense of distribution. When the blow-up patterns occur, the density $\rho$ of cells will strengthen in the vicinity of isolated points, and these regions become sharper and eventually result in finite time point-wise blow-ups. It was well known that blow-up never occurs in problems in one space dimension [34], whereas blow-up occurs within finite time in 2D and 3D cases. In 2D space, mathematical proofs for spherically symmetric solutions in a ball have been given in [24, 34]. When the initial mass is greater than a certain threshold

$$\begin{aligned} \chi \Vert \rho ^0\Vert _{L^1(\Omega )}>8\pi , \end{aligned}$$

the exact solution will blow up at the center of the ball, and this is proved to be the only possible singularity. For nonsymmetric cases, if $4\pi<\chi \Vert \rho ^0\Vert _{L^1(\Omega )}<8\pi$ and the corresponding solution of (1.1) blows up at finite time, then the blow-up happens at the boundary of $\Omega$ [26, 27]. However, no such restriction in mass appears for the 3D case [24]. More theoretical work can be found in [20, 24,25,26].

It is difficult to construct numerical schemes for (1.1), and most of the previous works are for the following simplified system

$$\begin{aligned} \begin{array}{ll} \rho _t-\nabla \cdot (\nabla \rho -\chi \rho \nabla c)=0,\quad &{}x\in \Omega , t>0,\\ -\triangle c=\rho -c,\quad &{}x\in \Omega , t>0, \end{array} \end{aligned}$$

(see, for example, [19, 23, 33, 41] and the references therein). Recently, there are some significant works designed to solve (1.1) directly [17, 35, 39, 40]. In [35], the semigroup methods were used to obtain the stability and error estimates of the finite element methods. Later, In [39], the author constructed conservative upwind finite-element method to yield positive numerical approximations under mild assumptions of the meshes. Subsequently, in [40], the authors constructed implicit second-order positivity preserving finite-volume schemes in three-dimensional space, and their technique requires solving a large dense linear system of equations coupling together all grid points at each stage of the two stage TR-BDF2 method when updating the diffusion terms at each time step. In [17], the interior penalty discontinuous Galerkin (IPDG) method was applied to rectangular meshes to obtain suboptimal rate of convergence, and the finite element space is assumed to be piecewise polynomials of degree $k\ge 2$. Other related works in this direction include [14,15,16]. Besides the above, in [38] the authors applied the conservative upwind finite volume method for the simplified system. Later in [6], the authors constructed a second order positivity-preserving scheme to a revised system by differentiating (1.1) with respect to x and y, hence the schemes were not designed to solve (1.1) directly. Subsequently, in [18], the author developed a composite particle-grid numerical method with adaptive time stepping to resolve and propagate singular solutions of (1.1). In [31], the authors applied finite difference method to the 2D problem and investigated the problem in the transient regime. The scheme is proved to be stable as long as the initial condition does not exceed certain threshold. Recently, in [30], the local discontinuous Galerkin methods were considered and the optimal rates of convergence were proved under some special finite element spaces. Moreover, following [44], the positivity-preserving technique was also introduced to obtain physically relevant numerical approximations and defined the numerical blow-up time which was verified to be convergent to the exact value by numerical benchmarks. Besides the above, for the KS chemotaxis model (1.1), one can define a free energy

$$\begin{aligned} E(t)=\int _{\Omega }\left( \rho \ln (\rho )-\rho c+\frac{1}{2}c^2+\frac{1}{2}|\nabla c|^2\right) d\Omega . \end{aligned}$$

(1.6)

In most of the previous works the energy (1.6), which was proved to be decreasing during time evolution, has been used to prove the existence of the global solutions of the system (1.1), see [2, 3, 5, 13, 20, 28, 32] as an incomplete list. Numerical method based on a hybrid variational principle was introduced in [4]. The implementation utilizes the steepest descent of free energy under a special distance metric. In this paper, we will apply a special LDG scheme and construct a numerical energy which is consistent with (1.6). It is well known that in LDG methods, the axillary variables must be introduced, and in general we can obtain the $L^2$ stability. However, for the (1.1), such a stability cannot be obtained since the exact solution may yield blow-up patten. Therefore, one of the most significant difficulty is how to introduce the axillary variables. In this paper, we will rewrite (1.1) into several special first-order equations and construct consistent and dissipating numerical energy accordingly.

The DG method was first introduced in 1973 by Reed and Hill [37] in the framework of neutron linear transport. Subsequently, Cockburn et al. developed Runge–Kutta discontinuous Galerkin (RKDG) methods for hyperbolic conservation laws in a series of papers [8,9,10,11]. In [12], Cockburn and Shu introduced the LDG method to solve the convection-diffusion equations. Their idea was motivated by Bassi and Rebay [1], where the compressible Navier-Stokes equations were successfully solved. Recently, the DG methods were applied to linear hyperbolic equations with $\delta$-singularities [42] to obtain high-order approximations under suitable negative-order norms. Subsequently, the methods have also been applied to nonlinear hyperbolic equations with $\delta$-singularities [43, 45]. Recently, the idea has been extended to parabolic equations with blow-up solutions by using the LDG method [22]. In this paper, we follow the same direction and employ the LDG method to capture the blow-up phenomenon. For the KS chemotaxis model (1.1), the exact solution may exhibits blow-up patten. Therefore, the $L^2$ stability of the LDG method is missing. However, this leads another way to define the numerical blow-up time. In [30], we introduced a new idea to capture the numerical blow-up time by using the $L^2$ norm of the numerical approximations under different resolutions. In this paper, we will continue this approach and compute the numerical approximations up to the blow-up appears. Moreover, we construct the numerical energy, consistent with (1.6), that is decreasing during time evolution. Even though the energy can be negative, numerical experiments for blow-up solutions demonstrate the positivity of the energy. Therefore, this approach provides the stability of the LDG scheme for problems with blow-up solutions. Before we finish the introduction, we would like to demonstrate the main differences between the LDG method in this paper and the one introduced in [30]. In [30], we basically followed the idea introduced in [12] and define $\mathbf{p}=\nabla \rho$, $\mathbf{q}=\nabla c$ to rewrite (1.1) as

$$\begin{aligned}&\rho _t=\nabla \cdot \mathbf{p}-\nabla \cdot (\chi \rho \mathbf{q}),\quad \quad \mathbf{p}=\nabla \rho ,\\&c_t=\nabla \cdot \mathbf{q} +\rho -c,\quad \quad \quad \quad \mathbf{q}=\nabla c, \end{aligned}$$

However, we cannot anticipate the numerical energy to be dissipative. Moreover, the numerical approximation contains severe oscillations near the concentration of the $\delta$-singularities. In this paper, we will apply the new idea to decompose (1.1) and prove that the numerical energy is dissipative during time evolution. Numerical experiments also demonstrate the same conclusion.

The organization of this paper is as follows. In Sect. 2, we construct the energy stable LDG scheme for the KS chemotaxis model. In Sect. 3, we construct the numerical energy and prove the energy dissipation for the semi-discrete LDG scheme. Numerical experiments in one and two space dimensions will be given in Sect. 4 to demonstrate the stability of the LDG scheme for problems with blow-up solutions. Finally, we will end in Sect. 5 with concluding remarks and remarks for future work.

2 The LDG Scheme

In this section, we define the finite element spaces and proceed to construct the LDG scheme for the KS chemotaxis model (1.1).

Let $\Omega _h=\{K\}$ be a partition of the domain $\Omega$ with rectangular or triangular element K. Denote $h_K$ to be the diameter of element K, and $h=\max _Kh_K$. Moreover, assume the partition is quasi-uniform, i.e. there exists a number $\tau >0$ such that every $K\in \Omega _h$ contains a circle of radius $r_K$ with $r_K\ge h_K/\tau$. We define the finite element space $V_h^k$ as

$$\begin{aligned} V_h^k=\left\{ z: z\big |_{K}\in P^{k}(K),\forall K\in \Omega _h\right\} , \end{aligned}$$

where $P^{k}(K)$ is the set of polynomials of degree up to k in cell K.

We choose ${{\varvec{\beta }}}$ to be a fixed vector that is not parallel to any normals of element interfaces. Moreover, we denote $\Gamma _h$ to be the set of all element interfaces and $\Gamma _0=\Gamma _h{\setminus }\partial \Omega .$ Let $e\in \Gamma _0$ be an interior edge shared by elements $K_\ell$ and $K_r$, where ${{\varvec{\beta }}}\cdot \mathbf{n}_\ell >0$, and ${{\varvec{\beta }}}\cdot \mathbf{n}_r<0$, respectively, with $\mathbf{n}_\ell$ and $\mathbf{n}_r$ being the outward normals of $K_\ell$ and $K_r$, respectively. For any $z\in V_h^k$, we define $z^-=z|_{\partial K_\ell }$ and $z^+=z|_{\partial K_r}$, respectively. The jump and average of z across the cell interface are given as $[z]=z^+-z^-$ and $\{z\}=\frac{z^++z^-}{2},$ respectively. Moreover, for $\mathbf{s}\in \mathbf{V}_h^k=V_h^k\times V_h^k,$ we define $\mathbf{s}^+$, $\mathbf{s}^-$, $[\mathbf{s}]$ and $\{\mathbf{s }\}$ analogously. Furthermore, we also define $\partial \Omega _-=\{e\in \partial \Omega |{\varvec{\beta }}\cdot \mathbf{n}<0,\mathbf{n} {\text { is the outer normal of }}e\},$ and $\partial \Omega _+=\partial \Omega {\setminus }\partial \Omega _-$.

To construct the LDG method scheme, we introduce the axillary variables $\mathbf{w}$, $\mathbf{s}$, $\mathbf{q}\in \mathbf{V}_h^k$ and $r\in V_h^k$, then the chemotaxis model (1.1) can be written as

$$\begin{aligned}&\rho _t=\nabla \cdot \mathbf{w},\\&\mathbf{w}=\rho \mathbf{s},\\&\mathbf{s}=\nabla (r-c),\\&r=\ln (\rho ),\\&c_t=\nabla \cdot \mathbf{q}+\rho -c,\\&\mathbf{q}=\nabla c. \end{aligned}$$

The formulation of the LDG scheme is to find $\rho _h$, $r_h$, $c_h\in V_h^k$ and $\mathbf{w}_h,$$\mathbf{s}_h,$$\mathbf{q}_h\in \mathbf{V}_h^k$, such that for any test functions v, u,  $\theta \in V_h^k$ and ${{\varvec{\phi }}}$, ${{\varvec{\psi }}}$, ${{\varvec{\xi }}}\in \mathbf{V}_h^k$, we have

$$\begin{aligned}&({\rho _h}_t,v)_{K}=-(\mathbf{w}_h,\nabla v)_K+\langle \widehat{\mathbf{w}_h}\cdot \mathbf{n},v\rangle _{\partial K}, \end{aligned}$$

(2.1a)

$$\begin{aligned}&(\mathbf{w}_h,{{\varvec{\phi }}})_K=(\rho _h\mathbf{s}_h,{{\varvec{\phi }}})_K,\end{aligned}$$

(2.1b)

$$\begin{aligned}&(\mathbf{s}_h,{{\varvec{\psi }}})_K=-(r_h-c_h,\nabla \cdot {{\varvec{\psi }}})_K+\langle \widehat{r_h}-\widehat{c_h},{{\varvec{\psi }}}\cdot \mathbf{n}\rangle _{\partial K},\end{aligned}$$

(2.1c)

$$\begin{aligned}&(r_h,u)_K=(\ln (\rho _h) ,u)_K,\end{aligned}$$

(2.1d)

$$\begin{aligned}&({c_h}_t,\theta )_{K}=-(\mathbf{q}_h,\nabla \theta )_K+\langle \widehat{\mathbf{q}_h}\cdot \mathbf{n},\theta \rangle _{\partial K}+(\rho _h-c_h,\theta )_K,\end{aligned}$$

(2.1e)

$$\begin{aligned}&(\mathbf{q}_h,{{\varvec{\xi }}})_K=-(c_h,\nabla \cdot {{\varvec{\xi }}})_K+\langle \widehat{c_h},{{\varvec{\xi }}}\cdot \mathbf{n}\rangle _{\partial K}, \end{aligned}$$

(2.1f)

where $(u,v)_K:=\int _K uv dxdy$, $({{\varvec{\phi }}},{{\varvec{\psi }}})_K:=\int _K {{\varvec{\phi }}}\cdot {{\varvec{\psi }}}dxdy$ and $\langle u,v\rangle _{\partial K}:=\int _{\partial K} uv ds$. $\mathbf{n}$ is the outward normal vector of cell K. The “hat” terms in (2.1) at the cell interfaces are numerical fluxes. In this paper, we choose

$$\begin{aligned} \widehat{\mathbf{w}_h}=\{\mathbf{w}_h\}+\alpha [\mathbf{w}_h],\quad \widehat{r_h}=\{r_h\}-\alpha [r_h],\quad \widehat{c_h}=\{c_h\}-\alpha [c_h]\quad \widehat{\mathbf{q}_h}=\{\mathbf{q}_h\}+\alpha [\mathbf{q}_h]. \end{aligned}$$

(2.2)

If we take $\alpha =\pm 1$, then the fluxes (2.2) turn out to be the alternating fluxes. Moreover, due to the Neumann boundary condition, we take

$$\begin{aligned} \widehat{\mathbf{w}_h}\cdot \mathbf{n}|_e=0,\quad \widehat{r_h}|_e=r_h^+,\quad \widehat{c_h}|_e=c_h^+,\quad \widehat{\mathbf{q}_h}\cdot \mathbf{n}|_e=0, \end{aligned}$$

if $e\in \partial \Omega _-$, and

$$\begin{aligned} \widehat{\mathbf{w}_h}\cdot \mathbf{n}|_e=0,\quad \widehat{r_h}|_e=r_h^-,\quad \widehat{c_h}|_e=c_h^-,\quad \widehat{\mathbf{q}_h}\cdot \mathbf{n}|_e=0, \end{aligned}$$

if $e\in \partial \Omega _+$.

We also denote

$$\begin{aligned} (u,v)=\sum _{K\in \Omega _h}(u,v)_K,\quad ({{\varvec{\phi }}},{{\varvec{\psi }}})=\sum _{K\in \Omega _h}({{\varvec{\phi }}},{{\varvec{\psi }}})_K, \end{aligned}$$

then (2.1) can be written as

$$\begin{aligned}&({\rho _h}_t,v)=-\mathcal {L}^d(\mathbf{w}_h,v),\end{aligned}$$

(2.3a)

$$\begin{aligned}&(\mathbf{w}_h,{{\varvec{\phi }}})=(\rho _h\mathbf{s}_h,{{\varvec{\phi }}}),\end{aligned}$$

(2.3b)

$$\begin{aligned}&(\mathbf{s}_h,{{\varvec{\psi }}})=-\mathcal {Q}(r_h-c_h,{{\varvec{\psi }}}),\end{aligned}$$

(2.3c)

$$\begin{aligned}&(r_h,u)=(\ln (\rho _h) ,u),\end{aligned}$$

(2.3d)

$$\begin{aligned}&({c_h}_t,\theta )=-\mathcal {L}^d(\mathbf{q}_h,\theta )+(\rho _h-c_h,\theta ),\end{aligned}$$

(2.3e)

$$\begin{aligned}&(\mathbf{q}_h,{{\varvec{\xi }}})=-\mathcal {Q}(c_h,{{\varvec{\xi }}}), \end{aligned}$$

(2.3f)

where

$$\begin{aligned} \mathcal {L}^d(\mathbf{p},w):= & {} (\mathbf{p},\nabla w)-\sum _{K\in \Omega _h}\langle \widehat{\mathbf{p}}\cdot \mathbf{n}_K,w\rangle _{\partial K},\\ \mathcal {Q}(u,\mathbf{w}):= & {} (u,\nabla \cdot \mathbf{w})-\sum _{K\in \Omega _h}\langle \hat{u}, \mathbf{w}\cdot \mathbf{n}_K\rangle _{\partial K}. \end{aligned}$$

It is easy to check the following identities by integration by parts on each cell, with the given choice of the numerical fluxes, for any functions u and $\mathbf{w}$,

$$\begin{aligned} \mathcal {L}^d(\mathbf{w},u)+\mathcal {Q}(u,\mathbf{w})=0. \end{aligned}$$

(2.4)

Remark 2.1

It is not easy to derive the a priori error estimates for the new LDG method proposed above. The main difficulty is the numerical energy $E_h$ given in (3.1) may not be positive. However, numerical experiments in Sect. 4 demonstrate optimal convergence rates if $P^k$ polynomials are applied for problems in two space dimensions. We will discuss the error estimates in the future.

3 Energy Dissipation

In this section, we will construct a suitable numerical energy $E_h(t)$ obtained from the semi-discretized LDG scheme (2.1) and prove the energy dissipation.

3.1 Free Energy of the LDG Scheme

In this subsection, we proceed to construct the numerical energy $E_h(t)$, which is consistent with the free energy E(t) given in (1.6) and prove that it is decreasing with respect to t.

The numerical energy $E_h(t)$ is defined as follows

$$\begin{aligned} E_h(t)=\int _{\Omega }\rho _h \ln (\rho _h)-\rho _hc_h+\frac{1}{2}c_h^2+\frac{1}{2}|\pmb {q}_h|^2d\Omega . \end{aligned}$$

(3.1)

The numerical energy given above is similar to that in (1.6). However, $E_h$ is used for the numerical approximations while (1.6) is for the exact solution.

Theorem 3.1

The numerical energy given in (3.1) satisfies the following identity

$$\begin{aligned} \frac{d}{dt}E_h(t)=-({c_h}_t,{c_h}_t)-(\rho _h\mathbf{s}_h,\mathbf{s}_h). \end{aligned}$$

(3.2)

Proof

Firstly, we take the derivative of (2.3f) with respect to time and choose ${{\varvec{\xi }}}=\mathbf{q}_h$ to obtain

$$\begin{aligned} ({\mathbf{q}_h}_t,\mathbf{q}_h)=-\mathcal {Q}({c_h}_t,\mathbf{q}_h). \end{aligned}$$

(3.3)

Next, take $\theta ={c_h}_t$ in (2.3e), one can obtain

$$\begin{aligned} ({c_h}_t,{c_h}_t)=-\mathcal {L}^d(\mathbf{q}_h,{c_h}_t)+(\rho _h-c_h,{c_h}_t). \end{aligned}$$

(3.4)

We add (3.3) and (3.4) and use (2.4) to get

$$\begin{aligned} ({\mathbf{q}_h}_t,\mathbf{q}_h)+({c_h}_t,{c_h}_t)=(\rho _h-c_h,{c_h}_t). \end{aligned}$$

(3.5)

Secondly, we choose the test functions $v=r_h-c_h$ in (2.3a) and ${{\varvec{\psi }}}=\mathbf{w}_h$ in (2.3c) to obtain

$$\begin{aligned}&({\rho _h}_t,r_h-c_h)=-\mathcal {L}^d(\mathbf{w}_h,(r_h-c_h)),\\&(\mathbf{s}_h,\mathbf{w}_h)=-\mathcal {Q}(r_h-c_h,\mathbf{w}_h). \end{aligned}$$

Adding up the above two equations and using (2.4), we have

$$\begin{aligned} ({\rho _h}_t,r_h-c_h)+(\mathbf{s}_h,\mathbf{w}_h)=0. \end{aligned}$$

(3.6)

Then let ${{\varvec{\phi }}}=\mathbf{s}_h$ in (2.3b) and $u={\rho _h}_t$ in (2.3d), Eq. (3.6) becomes

$$\begin{aligned} (\ln (\rho _h),{\rho _h}_t)-({\rho _h}_t,c_h)+(\rho _h\mathbf{s}_h,\mathbf{s}_h)=0. \end{aligned}$$

(3.7)

Thirdly, take $v=1$ in (2.3a) to obtain

$$\begin{aligned} ({\rho _h}_t,1)=-\mathcal {L}^d(\mathbf{w}_h,1)=0. \end{aligned}$$

(3.8)

Finally, we can obtain

$$\begin{aligned} \frac{d}{dt}E_h(t)&=(\ln (\rho _h)+1,{\rho _h}_t)-({\rho _h}_t,c_h)-(\rho _h,{c_h}_t)+(c_{h},{c_h}_t)+({\mathbf{q}_h}_t,\mathbf{q}_h)\\&=-({c_h}_t,{c_h}_t)-(\rho _h\mathbf{s}_h,\mathbf{s}_h) \end{aligned}$$

where in the second step, we use (3.5), (3.7) and (3.8). Now we complete the proof. $\square$

Remark 3.1

We proved the dissipation of the free energy with the LDG discretization. Also to the best of our knowledge, we did not see any references claimed that the violation of the initial threshold will make the energy to be negative infinity. On the other hand, the free energy of the 2D test examples are numerically observed to be strictly positive provided the exact solutions blow up (see Examples 4.6 and 4.7). Therefore, we numerically obtain the stability of our scheme due to the monotonicity and boundedness of the free energy for problems with blow-up solutions.

Remark 3.2

When $\rho _h$ attains negative values, $E_h$ in (3.1) is not well-defined and may not decrease in (3.2). Hence the energy dissipation relies heavily on the positivity of $\rho _h$. However, the positivity-preserving technique in [30] cannot be applied since we cannot obtain positive numerical approximations for the first-order scheme. Moreover, the positivity-preserving technique require a special slope limiter. However, with the limiter, the energy equality in Theorem 3.1 will be violated. In (3.2), it is possible to redefine the numerical energy as

$$\begin{aligned} E_h(t)=\int _{\Omega }\rho _h \ln (|\rho _h|)-\rho _hc_h+\frac{1}{2}c_h^2+\frac{1}{2}|\pmb {q}_h|^2d\Omega , \end{aligned}$$

and the numerical energy is well defined. With the new definition, it is easy to check that Theorem 3.1 is still valid.

4 Numerical Experiments

In this section, we provide numerical experiments in one and two space dimensions to verify the energy stability. We consider uniform meshes in this section for simplicity and apply third-order strong-stability-preserving (SSP) time discretization [21] to solve the ODE system $\mathbf{u}_t=\mathbf{L}(\mathbf{u})$

$$\begin{aligned} \mathbf{u}^{(1)}= & {} \mathbf{u}^n+\Delta t\mathbf{L}(\mathbf{u}^n),\\ \mathbf{u}^{(2)}= & {} \frac{3}{4}\mathbf{u}^n+\frac{1}{4}\left( \mathbf{u}^{(1)}+\Delta t\mathbf{L}(\mathbf{u}^{(1)})\right) ,\\ \mathbf{u}^{n+1}= & {} \frac{1}{3}\mathbf{u}^n+\frac{2}{3}\left( \mathbf{u}^{(2)}+\Delta t\mathbf{L}(\mathbf{u}^{(2)})\right) . \end{aligned}$$

The time step $\Delta t$ is chosen to be $\Delta t=cfl*h^2$, with $cfl=0.1,0.01,0.001,0.0001$ for $P^0$, $P^1$, $P^2$ and $P^3$ finite element spaces, respectively. For simplicity, if not otherwise stated, we choose $\alpha =1$ and use alternating fluxes [see (2.2)].

In each of the following experiments, the numerical energy $E_h(t)$ is decreasing during time evolution. Especially, for problems with blow-up solutions, the energy is also positive. Following [30], we compute the $L^2$ norm of numerical approximations at time t with $N\times N$ cells (N cells for the 1D case), defined as S(N, t) and define the numerical blow-up time as

$$\begin{aligned} t_b(N)=\inf \{t:~S(2N,t)\ge S(N,t)*1.05\}. \end{aligned}$$

(4.1)

In [30], the authors used numerical experiments to verify the convergence of the numerical blow-up time during mesh refinements. We will continue this approach and take the final time to be the blow-up time if the blow-up appears.

4.1 One Dimensional Space

In this subsection, numerical experiments in one space dimension are presented. The problem in one space dimension does not exist blow-up patterns for any initial conditions. We first check the accuracy of the algorithm.

Example 4.1

We consider 1D KS chemotaxis model with source terms.

$$\begin{aligned}&\rho _t=\rho _{xx}-(\rho c_x)_x- \frac{2\rho }{2+\sin (x)}+\frac{(\cos (2x)-2\sin (x))\rho ^2}{(2+\sin (x))^2},\quad x\in [0,2\pi ],\\&c_t=c_xx+\rho -c-\frac{2c}{2+\sin (x)},\quad x\in [0,2\pi ], \end{aligned}$$

with the exact solution $\rho =c=(2+\sin (x))\exp (-t)$ and periodic boundary conditions.

Table 1 Example 4.1, accuracy test at time $=0.1$

Example 4.1 aims to verify the accuracy of the LDG scheme with $\alpha =1$ and $\alpha =0$ respectively. The results can be found in Table 1. We list the $L^2$ and $L^\infty$ errors of $\rho$ at final time $T=0.1$. From the table, we can observe optimal rates of convergence with $\alpha =1$. For $\alpha =0$, we can see that the rates of convergence have optimal and suboptimal accuracy for odd orders and even orders respectively.

Example 4.2

Consider 1D KS chemotaxis model (1.1) on the domain $[0,\pi ]$ with smooth initial condition and homogeneous Neumann boundary conditions

$$\begin{aligned} \rho (x,0)=c(x,0)=2+\cos (x),\text { and }\nabla \rho \cdot \mathbf{n}=\nabla c \cdot \mathbf{n}=0. \end{aligned}$$

Fig. 1

Example 4.2: the energy (left) and $\rho$ (right) with $N=80$ and $N=160$ by using $P^2$ piecewise polynomials

In this example, the exact solution is smooth and the energy $E_h(t)$ is negative. We choose the final time to be $T=0.1.$ From Fig. 1, we can see that the energy is decreasing during time evolution and the numerical approximations of densities are positive in this example.

Example 4.3

Finally, we consider 1D KS chemotaxis model (1.1) on the computational domain $[-2,2]$ with initial and Neumann boundary conditions given as

$$\begin{aligned} \rho (x,0)=\frac{400}{1+40x^2},\quad c(x,0)=\frac{200}{1+20x^2},\quad \text { and }\quad \rho _x=c_x=0, \end{aligned}$$

respectively.

In this example, the initial condition is symmetric and the derivative is large. Therefore, the exact solution might be approximately singular at $x=0$. Moreover, to preserve the symmetry, we choose $\alpha =0$ in the numerical fluxes. We use $P^3$ polynomials and take $N=320$ and $N=640$ to check the convergence of the numerical approximations at $T=0.001$, and the results are given in Fig. 2.

Fig. 2

Example 4.3: the numerical approximations of $\rho$ with $N=320$ (left) and $N=640$ (right) by using $P^3$ polynomials

From the figure, we can see that the numerical approximations under different resolutions agree with each other, and the exact solution does not blow up. To demonstrate this point, we also compute the $L^2$ norm of the numerical approximations with $N=160,320,640$ at $T=0.001$, and the results are given in Fig. 3.

Fig. 3

Example 4.3: the $L^2$ norm of the numerical approximations with $N=160, 320, 640$ with $P^3$ polynomials at $T=0.001$

Moreover, we compute the numerical free energy (3.1) and the $L^2$ norm of the numerical approximations by using $P^3$ polynomials with $N=160,320,640$ at $T=0.001$. The results are plotted in Fig. 3, 4. We can see that, the $L^2$ norms of the numerical approximations are almost identical, and the exact solution does not blow up at $T=0.001$. Though the exact solution contains a cusp at x=0 and looks like a delta-singularity shape, the numerical energy is still positive and the solution is not a blow-up as in 1D. Figure 4 contains the numerical energy with $N=160$, $N=320$ and $N=640$.

Fig. 4

Example 4.3: the numerical energy with $N=160$, $N=320$ and $N=640$ with $P^3$ polynomials at $T=0.001$

From the figure, we can observe that the numerical energy is positive and decreasing during time evolution, which further implies the energy stability of the scheme. The result is consistent with Theorem 3.1.

4.2 Two Dimensional Space

In this subsection, we will present numerical examples in two space dimensions to show the performance of our algorithm. For simplicity, we take $N_x=N_y=N.$

Example 4.4

We study the following KS chemotaxis model on the computational domain $[0,2\pi ]\times [0,2\pi ]$ with source terms to check the accuracy

$$\begin{aligned}&\rho _t=\Delta \rho -\nabla \cdot (\rho \nabla c)-\frac{4\rho }{2+\sin (x+y)}+\frac{2\rho ^2(\cos (2(x+y))-2\sin (x+y))}{(2+\sin (x+y))^2},\\&c_t=\Delta c+\rho -c-\frac{4c}{2+\sin (x+y)}, \end{aligned}$$

with the exact solution $\rho =c=(2+\sin (x+y))\exp (-2t)$ and periodic boundary conditions.

Table 2 Example 4.4, accuracy test at time $=0.1$

In Table 2, we present the $L^2$ and $L^\infty$ errors of $\rho$ at the final time $T=0.1$ of Example 4.4 to test the accuracy of the LDG scheme. From the table, we can observe optimal rates of convergence.

Example 4.5

Consider 2D KS chemotaxis model (1.1) on the computational domain $[0,\pi ]\times [0,\pi ]$ with initial and Neumann boundary conditions given as

$$\begin{aligned} \rho (x,y,0)=c(x,y,0)=2+\cos (x)\cos (y),\quad \text { and }\quad \nabla \rho \cdot \mathbf{n}=\nabla c \cdot \mathbf{n}=0, \end{aligned}$$

respectively.

Fig. 5

Example 4.5: the numerical approximations of $\rho$ with $N=40$ (left) and $N=80$ (right) and $P^1$ polynomials

In this example, the exact solution is smooth and the energy E(t) is negative at $t=0$. We use $P^1$ polynomials and compute the numerical solutions at $T=0.1$ with $N=40$ and 80. The numerical approximations of $\rho$ are given in Fig. 5. From the figure, we can see that the numerical approximations of $\rho$ are strictly positive. Moreover, Fig. 6 shows the numerical energy. We can see that the energy is decreasing during time evolution.

Fig. 6

Example 4.5: the numerical energy with $N=40$ and $N=80$ with $P^1$ piecewise polynomials

Now, we proceed to problems with blow-up solutions.

Example 4.6

Let us consider 2D KS chemotaxis model (1.1) on the computational domain $[-2,2]\times [-2,2]$ with homogeneous Neumann boundary conditions and the initial conditions are given as

$$\begin{aligned}&\rho (x,y,0)=\frac{400}{1+40(x^2+y^2)},\\&c(x,y,0)=\frac{200}{1+20(x^2+y^2)}. \end{aligned}$$

The exact solution is symmetric and will blow up if t is large. To preserve the symmetry, we choose $\alpha =0$ in (2.2). We use both $P^1$ and $P^2$ polynomials and the schemes are first and third order accurate, respectively, according to the error table in Example 4.4. Moreover, we take $N=80$ and 160 in this example. The $L^2$ norms of the numerical approximations of $\rho$ are given in Fig. 7.

Fig. 7

Example 4.6: the $L^2$ norm of the numerical approximations of $\rho$ with $N=80$ and $N=160$ by using $P^1$ (left) and $P^2$ (right) polynomials

Following the notations given in (4.1), the red line and green line are for S(80, t) and S(160, t), respectively and the numerical blow-up time $t_b(80)$ is approximately $t=0.00032$ for both $P^1$ and $P^2$ polynomials. Moreover, we plot the contour and the cross section at $x=0$ of $\rho$ at $T=6\times 10^{-4}$ for $P^2$ polynomials in Fig. 8. From the figure, we cannot observe undershoots, and the numerical approximations remain positive in this example.

Fig. 8

Example 4.6: the contour (left) and cross section at $x=0$ (right) of $\rho$ with $N=160$ by using $P^2$ at $T=6\times 10^{-4}$ polynomials

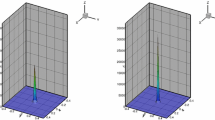
Moreover, we also plot the contours of $\rho$ at $T=6\times 10^{-4}$ for $P^1$ polynomials with $N=80$ and $N=160$ in Fig. 9 and we can observe significant differences. Especially, the maximum value of $\rho$ for $N=160$ is almost four times of that for $N=80$. This clearly demonstrate the appearance of the blow-up.

Fig. 9

Example 4.6: the contour plots of $\rho$ with $N=80$ (left) and $N=160$ (right) by using $P^1$ at $T=6\times 10^{-4}$ polynomials

We plot the numerical energy for $N=80$ and $N=160$ in Fig. 10. From the figure, we can observe that the energy is decreasing and strictly positive during time evolution, which clearly demonstrated the stability of the algorithm.

Fig. 10

Example 4.6: the numerical energy with $N=80$ and $N=160$ by using $P^2$ polynomials

Finally, we repeat the example given in [30] and demonstrate the energy stability of the algorithm.

Example 4.7

We consider 2D KS chemotaxis model (1.1) on the computational domain $[-0.5,0.5]\times [-0.5,0.5]$ with homogeneous Neumann boundary conditions and the initial conditions are given as

$$\begin{aligned}&\rho (x,y,0)=840\exp (-84(x^2+y^2)),\\&c(x,y,0)=420\exp (-42(x^2+y^2)). \end{aligned}$$

The exact solution is symmetric and will blow up if t is large. To preserve the symmetry, we also choose $\alpha =0$ in (2.2).

Fig. 11

Example 4.7: the $L^2$ norms of the numerical approximations of $\rho$ with $N=50$ and $N=100$ by using $P^1$ (left) and $P^2$ (right) polynomials

In Fig. 11, we plot the $L^2$ norm of the numerical approximations of $\rho$ with $N=50$ and $N=100$ by using $P^1$ and $P^2$ polynomials, and based on the numerical experiments in Example 4.4, the schemes are first and third order accurate, respectively. We cannot observe significant difference between the two panels. Following (4.1), we can see that the numerical blow-up appears at about $t_b=8.2\times 10^{-5}.$

In [14], the authors computed the same example for $P^2$ polynomials with $h=\frac{1}{50}\,(N=50)$. For comparison, we present the contour and the cross section at $x=0$ of $\rho$ at $t=1.21\times 10^{-4}$ in Fig. 12 for $P^2$ polynomials. We can obtain similar results given in [14].

Fig. 12

Example 4.7: the contour (left) and cross section at $\hbox {x} = 0$ (right) of $\rho$ with $P^2$ polynomials. We take $h=\frac{1}{50}$

Finally, to demonstrate the energy stability, we plot the numerical energy in Fig. 13. We can see that the energy is strictly positive and decreasing during time evolution. Therefore, our algorithm is stable.

Fig. 13

Example 4.7: the free energy with $N=50$ and $N=100$

5 Conclusion

In this paper, we construct a numerical energy for the LDG method for Keller–Segel chemotaxis model. The energy is proved to the decreasing during time evolution. For solutions with blow-up, the energy is also strictly positive which further implies the stability of the numerical algorithm.