Direct Discontinuous Galerkin Method with Interface Correction for the Keller-Segel Chemotaxis Model

Abstract

The Keller-Segel (KS) chemotaxis equation is a widely studied mathematical model for understanding the collective behavior of cells in response to chemical gradients. This paper investigates the direct discontinuous Galerkin method with interface correction (DDGIC) for one-dimensional and two-dimensional KS equations governing the cell density and chemoattractant concentration. We establish error estimates for the proposed scheme under suitable smoothness assumptions of the exact solutions. Numerical experiments are conducted to validate the theoretical results. We explore the impact of different coefficient settings in the numerical fluxes on the error of the DDGIC method on uniform and nonuniform meshes. Our findings reveal that the DDGIC method achieves optimal convergence rates with any admissible coefficients for polynomials of odd degrees, while the accuracy of the cell density is sensitive to the numerical flux coefficient in the chemoattractant concentration for polynomials of even degrees. These results hold regardless of whether the mesh is uniform or nonuniform.

1 Introduction

The Keller-Segel (KS) model is a widely used mathematical model for studying chemotaxis, which involves the movement of biological cells and microorganisms in response to chemical gradients. The model consists of two nonlinear equations: a convection-diffusion equation for the cell density and a reaction-diffusion equation for the chemoattractant concentration. It describes the dynamics of cell density and chemoattractant concentration, where cells both move in response to the gradient of the chemoattractant and produce the chemoattractant. The KS model’s intuitive simplicity, analytical tractability, and ability to replicate key behavior of chemotactic populations have made it successful in studying various biological systems, including bacterial colonies, immune cell migration, and tumor invasion.

The existence and uniqueness of weak solutions to the KS model heavily depend on the initial conditions. For certain initial conditions, these solutions may exhibit blow-up or singular, spiky behaviors [6, 14, 19,20,21,22,23, 31]. Additionally, the exact solutions are always positive. These facts pose challenges in designing accurate and computationally efficient numerical methods for KS models. Previous works are primarily focused on the simplified parabolic-elliptic system; see, for example, [9, 13, 18, 29, 38] and the references therein.

In recent years, a few numerical techniques have been developed to deal with the parabolic-parabolic system of the KS model. Semi-group methods were proposed in [32] to obtain stability and error estimates of finite element methods. Conservative upwind finite element methods were designed in [34] and analyzed in [35] to obtain positive numerical approximations with suitable meshes. An implicit finite element method was presented in [37] to maintain mass conservation and guarantee the positivity of the cell density in three-dimensional models. The second-order central-upwind finite volume method was introduced in [5] to preserve the positivity of the solution. Later, a fourth-order hybrid finite-volume-finite-difference scheme was developed in [4]. In [12], a composite particle-grid numerical method with adaptive time stepping was studied to resolve singular solutions. Other works include the positivity-preserving and asymptotic preserving method of [27], the moving mesh method of [2] to precisely compute the collapse time, and the convergence of numerical blow-up time calculation in [15]. We refer to the recent review article [1] for a comprehensive summary of analytical and numerical developments for the KS equations.

Discontinuous Galerkin (DG) methods are another popular approach for KS models. They were investigated in [8], and error estimates for fully discrete schemes with forward Euler or second-order explicit strong-stability-preserving (SSP) Runge–Kutta (RK) methods were analyzed in [10]. The interior penalty DG (IPDG) methods were investigated in [11] to obtain suboptimal convergence rates and numerical fluxes were constructed for the nonlinear convection term to obtain positive approximations. The local DG (LDG) method was applied in [24] to obtain optimal error estimates, and a positivity-preserving limiter was added to construct second-order positivity-preserving LDG schemes. The constructed LDG method was proposed in [16] and was proven energy dissipative and numerically positive with a third order of accuracy.

This paper investigates the KS models in the direct DG (DDG) methods framework. The DDG methods are a class of DG methods specifically designed for solving diffusion equations. Unlike the LDG method, which introduces auxiliary variables for the derivatives of the solution and rewrites the original equation into a first-order system, the DDG method is based on the direct weak formulation of the diffusion equations with a numerical flux formula designed at the cell interfaces to approximate the spatial derivatives of the solution. The original DDG method was introduced in [25], and the DDGIC method [26] is a variation of the original DDG method by adding interface correction terms to balance the solution and test function in the bilinear form. This guarantees optimal convergence and improves the capability of the DDG method. Compared to other DDG variations, the DDGIC method is the most suitable solver for time-dependent parabolic equations. The DDGIC method explores fewer degrees of freedom and thus is more efficient than the LDG method. Unlike the DG methods listed above, the DDGIC method does not introduce auxiliary variables to separately approximate the solution’s gradient. While it is standard to introduce gradient approximations to maintain the overall convergence orders, such methods are expensive. Moreover, the DDGIC method possesses the superconvergence property of approximating the solution’s gradient [39]. Such a property leads to the capability of the DDGIC method to solve the KS equations optimally and directly without auxiliary variables. Furthermore, it was proved in [33] to preserve positivity with a third order of accuracy for the KS models.

This paper applies the DDGIC method to one- and two-dimensional KS equations. We aim to establish the estimate for the bilinear and nonlinear terms of the DDGIC operators and prove the error estimates under suitable smoothness assumptions of the exact solutions before blow-up occurs. The numerical solutions are proved to achieve k-th order of accuracy under $L^{\infty }(L^2)$ norm for the DDGIC scheme with $P^k$ polynomial approximations. Numerical experiments are conducted to validate the theoretical results. We further investigate whether the convergence of the DDGIC method is affected by different coefficient settings in the numerical flux on both uniform and nonuniform meshes. Numerical tests show that, for the DDGIC method with odd-degree polynomial approximations, optimal $(k+1)$th convergence rates are achieved with any admissible numerical flux coefficients, while for polynomials of even-degree, the errors of the cell density are sensitive to the numerical flux coefficient in the chemoattractant concentration. This phenomenon holds regardless of whether the mesh is uniform or nonuniform.

The paper is organized as follows. In Sect. 2, we introduce the KS chemotaxis equations and present the DDGIC method for one-dimensional and two-dimensional models. In Sect. 3, we establish error estimates for the proposed scheme for two-dimensional models. Section 4 is devoted to numerical tests to validate the proposed DDGIC scheme. Concluding remarks are given in Sect. 5.

2 DDGIC Method for Keller-Segel Equations

In this section, we introduce the KS chemotaxis models and present the algorithm formulation of the DDGIC method for solving the model equations.

2.1 Model Equations

The KS chemotaxis model consists of two governing equations: one equation represents the concentration of cells, and the other equation represents the diffusion and production of the chemoattractant. The one-dimensional version of the KS model is given by

$$\begin{aligned}&\rho _t+(\chi c_x \rho )_x=\rho _{xx}, \quad x\in (a,b), \,t>0, \end{aligned}$$

(2.1a)

$$\begin{aligned}&c_t=c_{xx}-c+\rho , \quad x\in (a,b), \,t>0. \end{aligned}$$

(2.1b)

The two-dimensional version of the KS model [6] is given by

$$\begin{aligned}&\rho _t+ \nabla \cdot (\chi \rho \nabla c)=\triangle \rho , \quad (x,y)\in \Omega ,\; t>0, \end{aligned}$$

(2.2a)

$$\begin{aligned}&c_t=\triangle c-c+\rho , \quad (x,y)\in \Omega ,\; t>0, \end{aligned}$$

(2.2b)

where $\Omega$ is a convex, bounded, and open set ${\mathbb {R}}^2$. In these equations, $\rho$ is the cell density, c is the chemoattractant concentration, and $\chi$ is the chemotactic sensitivity. For simplicity, we set $\chi =1$ in our study.

The boundary conditions are set as homogeneous Neumann boundary conditions. For the one-dimensional case, we have $\rho _x=c_x=0$ at the boundaries $x=a$ and $x=b$. For the two-dimensional case, the boundary conditions are given by

$$\begin{aligned} \nabla \rho \cdot {\textbf{n}}=\nabla c\cdot {\textbf{n}}=0, \qquad (x,y)\in \partial \Omega , \end{aligned}$$

(2.3)

where ${\textbf{n}}$ is the outward unit normal vector of the boundary $\partial \Omega$.

Initial conditions are crucial for the existence and uniqueness of the weak solution to (2.1) and (2.2). Specifically, assume that the initial conditions $\rho _0(x,y)$ and $c_0(x,y)$ for two-dimensional equations satisfy the following conditions

$$\begin{aligned} \rho _0\in L^2(\Omega ),\;\; C^{GNS}\Vert \rho _0\Vert _{L^1(\Omega )}<1,\;\;\rho _0(x,y) \ge a_0>0, \;\text {and } c_0\in H^1_p(\Omega ), \,p>2, \end{aligned}$$

(2.4)

where $a_0$ is some positive constant and $C^{GNS}$ is the best constant in the Gagliardo-Nirenbuerg-Sobolev inequality. Then, for a suitable time $T>0$, there exists a unique weak solution with

$$\begin{aligned} \rho \in C([0,T];L^2(\Omega )\cap L^2(0,T;H^1(\Omega )), \quad c\in L^2(0,T;H^1(\Omega )). \end{aligned}$$

(2.5)

More details can be found in [13, 14]. It is worth mentioning that the solutions to the KS model can exhibit blow-up pattern with certain initial conditions. This phenomenon is known as chemotactic collapse, which describes the tendency of cells to concentrate to form spore-like structures. Mathematically, the blow-up corresponds to the concentration of the cell density $\rho$ towards a Dirac delta function in the sense of distribution in finite time. We refer interested readers to [6, 13, 14, 17, 19,20,21,22,23, 31].

2.2 DDGIC Method: One-Dimensional Case

In this section, we present the algorithm formulation of the DDGIC method for the one-dimensional KS equation (2.1).

We start by making a partition of the spatial domain [a, b] into N computational cells, denoting each cell as $I_j=[x_{j-\frac{1}{2}},x_{j+\frac{1}{2}}]$ with

$$\begin{aligned} a=x_{\frac{1}{2}}<x_{\frac{3}{2}}<\cdots <x_{N+\frac{1}{2}}=b. \end{aligned}$$

We further denote the cell size as $h_j=x_{j+\frac{1}{2}}-x_{j-\frac{1}{2}}$ and let $h=\max _{1\le j\le N} h_j.$ The mesh is assumed to be regular, namely there exists a constant $\gamma >0$ independent of h such that

$$\begin{aligned} h_j\ge \gamma h, \; 1\le j\le N. \end{aligned}$$

The finite element space is defined by

$$\begin{aligned} {\mathbb {V}}^k_h:=\left\{ v_h\in L^2[a,b]:\quad v_h|_{I_j}\in P^k(I_j), \quad j=1, \dots , N\right\} , \end{aligned}$$

where $P^k(I_j)$ denotes the space of polynomials of degree up to k defined in the cell $I_j$. For $v_h\in {\mathbb {V}}^k_h$, we define the jump and average of $v_h$ across the cell interface as

$$\begin{aligned} \llbracket v_h\rrbracket =v_h^+ - v_h^-, \quad \quad \{ \{\!\{ v_h \}\!\} \}=\frac{1}{2}(v_h^+ + v_h^-), \end{aligned}$$

where $v_h^+,\;v_h^-$ denote the left and right limits of the function v at the cell interface, respectively.

For simplicity, let $f(\rho )=c_x\rho$ denote the convection term. The semi-discrete DDGIC scheme for solving the one-dimensional KS equation (2.1) is defined as follows: find the unique functions $\rho _h,\, c_h\in {\mathbb {V}}^k_h$ such that, for all test functions $v_h,\,w_h\in {\mathbb {V}}_h^k$, we have

$$\begin{aligned} \int _{I_j} (\rho _h)_tv_h&dx+\left. \left( \widehat{f(\rho _h)}-\widehat{(\rho _h)_x}\right) v_h \right| ^{j+\frac{1}{2}}_{j-\frac{1}{2}} -\int _{I_j}(f(\rho _h)-(\rho _h)_x)(v_h)_x dx\nonumber \\&\quad +\frac{(v_h)^-_x}{2}\llbracket \rho _h\rrbracket _{j+\frac{1}{2}}+\frac{(v_h)^+_x}{2} \llbracket \rho _h\rrbracket _{j-\frac{1}{2}}=0, \end{aligned}$$

(2.6a)

$$\begin{aligned} \int _{I_j} (c_h)_tw_h&dx-\left. \widehat{(c_h)_x} w_h\right| ^{j+\frac{1}{2}}_{j-\frac{1}{2}} +\int _{I_j}(c_h)_x(w_h)_x dx +\int _{I_j}(c_h-\rho _h)w_h dx\nonumber \\&\quad +\frac{(w_h)^-_x}{2} \llbracket c_h\rrbracket _{j+\frac{1}{2}}+\frac{(w_h)^+_x}{2}\llbracket c_h\rrbracket _{j-\frac{1}{2}} =0, \end{aligned}$$

(2.6b)

where we adopt the following short notations

$$\begin{aligned}&\left. \left( \widehat{f(\rho _h)}-\widehat{(\rho _h)_x}\right) v_h \right| ^{j+\frac{1}{2}}_{j-\frac{1}{2}}:=\left( \widehat{f(\rho _h)}-\widehat{(\rho _h)_x}\right) (v_h)^-_{j+\frac{1}{2}}-\left( \widehat{f(\rho _h)}-\widehat{(\rho _h)_x}\right) (v_h)^+_{j-\frac{1}{2}}, \\&\quad \left. \widehat{(c_h)_x} w_h\right| ^{j+\frac{1}{2}}_{j-\frac{1}{2}}:=\widehat{(c_h)_x} (w_h)^-_{j+\frac{1}{2}}-\widehat{(c_h)_x} (w_h)^+_{j-\frac{1}{2}}. \end{aligned}$$

The above weak formulation is obtained by directly multiplying both sides of the system (2.1) by test functions and performing integration by parts in the cell $I_j$. $\widehat{f(\rho _h)}$, $\widehat{(\rho _h)_x}$, and $\widehat{(c_h)_x}$ are the so-called numerical fluxes, since $\rho _h, c_h\in {\mathbb {V}}_h^k$ are discontinuous at the cell interfaces.

For the DDGIC method, numerical fluxes $\widehat{(c_h)_x}$ and $\widehat{(\rho _h)_x}$ directly approximate the derivatives $(c_h)_x$ and $(\rho _h)_x$ of the solutions at the cell interfaces. They are uniquely defined at the cell interface by

$$\begin{aligned} \widehat{(\rho _h)_x}&=\beta _{0}\frac{\llbracket \rho _h\rrbracket }{h}+ \{\!\{ (\rho _h)_x \}\!\} +\beta _{1}h \llbracket (\rho _h)_{xx}\rrbracket , \end{aligned}$$

(2.7a)

$$\begin{aligned} \widehat{(c_h)_x}&=\beta _0\frac{\llbracket c_h \rrbracket }{h}+ \{\!\{ (c_h)_x \}\!\} +\beta _{1}h \llbracket (c_h)_{xx}\rrbracket , \end{aligned}$$

(2.7b)

where, with a slight abuse of notation, h is taken as the average of the mesh sizes $h_j$ and $h_{j+1}$ when evaluating the numerical fluxes at the cell interface $x_{j+\frac{1}{2}}$. The numerical fluxes $\widehat{(c_h)_x}$ and $\widehat{(\rho _h)_x}$ involve the jump of the solutions, jump, the average of the first derivative, and the jump of the second-order derivative. They are consistent to the spatial derivatives $c_x$ and $\rho _x$ of the solutions. It is worth noting that there exists a large group of admissible coefficients pair $(\beta _0, \beta _{1})$ that ensures the stability and optimal accuracy of the DDGIC method [26].

For the numerical flux $\widehat{f(\rho _h)}$ associated with the convection term $f(\rho )=c_x\rho$, we employ the Lax-Friedrichs (LF) flux

$$\begin{aligned} \widehat{f(\rho _h)}=\frac{1}{2}\left( (f(\rho ^+_h)+f(\rho ^-_h))-\alpha (\rho ^+_h-\rho ^-_h) \right) , \end{aligned}$$

(2.8)

where $f(\rho ^{\pm }_h)=(\widehat{(c_h)_x})(\rho _h)^{\pm }$ with $\widehat{(c_h)_x}$ defined in (2.7b). For the local LF fluxes, $\alpha$ is taken as $\alpha =|(\widehat{(c_h)_x})_{j+\frac{1}{2}}|$. For the global LF flux, $\alpha$ is taken as $\alpha =\max _{1\le j\le N}|(\widehat{(c_h)_x})_{j+\frac{1}{2}}|$. Regarding the Neumann boundary conditions, we simply set $\widehat{(\rho _h)_x}=\widehat{(c_h)_x}=0$ at the boundaries $x=a$ and $x=b$.

2.3 DDGIC Method: Two-Dimensional Case

In this section, we present the algorithm formulation of the DDGIC method for the two-dimensional KS equation (2.2).

Let ${\mathcal {T}}_h$ be a shape-regular partition of the domain $\Omega$ consisting of rectangular or triangular elements K. Denote ${\mathcal {E}}_h$ as the set of all edges, ${\mathcal {E}}_h^I$ as the set of all internal edges, and ${\mathcal {E}}_h^D$ as the set of all boundary edges of ${\mathcal {T}}_h$. Clearly, ${\mathcal {E}}_h={\mathcal {E}}_h^I \cup {\mathcal {E}}_h^D$. We denote $h_K$ as the diameter of the element K and $h_e$ as the length of the edge $e\in {\mathcal {E}}_h$. The element K is regular in the sense that there exists a positive constant $\gamma$ independent of h such that

$$\begin{aligned} h_K\ge \gamma h,\quad k\in {\mathcal {T}}_h. \end{aligned}$$

The finite element space is defined as

$$\begin{aligned} {\mathbb {V}}_h^k:=\{v_h\in L^2(\Omega ): v_h|_K\in P^k(K), \forall K\in {\mathcal {T}}_h\}, \end{aligned}$$

where $P^k(K)$ denotes the set of polynomials of total degree at most k in the element K.

For $v_h\in {\mathbb {V}}_h^k$, we further introduce the concepts of jumps and averages. For any edge $e\in \partial K \cap {\mathcal {E}}_h^I$ sharing with the element $K'$, the jump and average of $v_h$ over e are defined as

$$\begin{aligned} \llbracket v_h\rrbracket =v_h|_{K'}-v_h|_{K}, \quad \{\!\{ v_h \}\!\} =\frac{1}{2}\left( v_h|_{K}+v_h|_{K'}\right) . \end{aligned}$$

(2.9)

In the two-dimensional case, denote the nonlinear convection term as ${\textbf{F}}(\rho )=(c_x\rho ,c_y\rho )$ for simplicity. The semi-discrete DDGIC scheme for solving (2.2) is defined as follows: find the unique solutions $\rho _h, \ c_h\in {\mathbb {V}}^k_h$ such that, for any test functions $v_h, \ w_h \in {\mathbb {V}}^k_h$, we have

$$\begin{aligned}&\int _{K} (\rho _h)_t v_h dxdy +\int _{\partial K}\left( \widehat{{\textbf{F}}(\rho _h)\cdot {\textbf {n}}}-\widehat{(\rho _h)_{\textbf {n}}}\right) v_hds \nonumber \\&\quad +\int _{K}\left( \nabla \rho _h-{\textbf{F}}(\rho _h)\right) \cdot \nabla v_h dxdy +\int _{\partial K}\llbracket \rho _h\rrbracket \frac{(v_h)_{{\textbf {n}}}}{2} ds=0, \end{aligned}$$

(2.10a)

$$\begin{aligned}&\int _{K} (c_h)_t w_h dxdy -\int _{\partial K}\widehat{(c_h)_{\textbf {n}}} w_hds +\int _{K} \nabla c_h\cdot \nabla w_hdxdy \nonumber \\&\quad +\int _{K} (c_h-\rho _h ) w_hdxdy+\int _{\partial K}\llbracket c_h\rrbracket \frac{(w_h)_{{\textbf {n}}}}{2} ds=0, \end{aligned}$$

(2.10b)

where $(\phi )_{{\textbf {n}}}=\nabla \phi \cdot {\textbf {n}}$ represents the normal derivative of any function $\phi$, and ${\textbf{n}}$ denotes the outward unit normal vector to $\partial K$.

Similarly to the one-dimensional case, numerical fluxes $\widehat{(\rho _h)_{{\textbf {n}}}}$ and $\widehat{(c_h)_{{\textbf {n}}}}$ are introduced to directly approximate the normal derivatives $(\rho _h)_{{\textbf {n}}}$ and $(c_h)_{{\textbf {n}}}$ across the edges. These fluxes involve the solution jump, the average of the normal derivative, and the jump of the second order normal derivative, given by

$$\begin{aligned} \widehat{(\rho _h)_{{\textbf {n}}}}&=\beta _{0}\frac{\llbracket \rho _h\rrbracket }{h_e}+ \{\!\{ (\rho _h)_{{\textbf {n}}} \}\!\} +\beta _{1}h_e \llbracket (\rho _h)_{{\textbf {nn}}}\rrbracket , \end{aligned}$$

(2.11a)

$$\begin{aligned} \widehat{(c_h)_{{\textbf {n}}}}&=\beta _0\frac{\llbracket c_h \rrbracket }{h_e}+ \{\!\{ (c_h)_{{\textbf {n}}} \}\!\} +\beta _{1}h_e \llbracket (c_h)_{{\textbf {nn}}}\rrbracket , \end{aligned}$$

(2.11b)

where $(\rho _h)_{{\textbf {nn}}}=\nabla (\nabla \rho _h \cdot {\textbf {n}})\cdot {\textbf {n}}$. According to [26], the admissible coefficients pair $(\beta _0, \beta _{1})$ can be chosen to ensure the stability and optimal accuracy of the DDGIC method.

For the numerical flux $\widehat{{\textbf{F}}(\rho _h)\cdot {\textbf {n}}}$ associated with the nonlinear convection term ${\textbf{F}}(\rho _h)=\rho _h \nabla c_h$, again we use the LF flux to approximate ${\textbf{F}}(\rho )\cdot {\textbf {n}}$ on the edge e of the element K sharing with the element $K'$. The LF flux is defined as

$$\begin{aligned} \widehat{{\textbf{F}}(\rho _h)\cdot {\textbf {n}}}=\frac{1}{2}\left( \widehat{(c_h)_{{\textbf {n}}}} \left( \rho _h|_{K'}+\rho _h|_K \right) -\alpha \left( \rho _h|_{K'}-\rho _h|_K \right) \right) , \end{aligned}$$

(2.12)

where $\widehat{(c_h)_{{\textbf {n}}}}$ is given in (2.11b). For the local LF flux, we set $\alpha$ as $\alpha =\big |\widehat{(c_h)_{{\textbf {n}}}}|_e\big |$. For the global LF flux, we set $\alpha$ as $\alpha =\max _{e \in {\mathcal {E}}_h^I}\big |\widehat{(c_h)_{{\textbf {n}}}}|_e\big |$. Due to the Neumann boundary condition, for $e\in \partial \Omega$, we set

$$\begin{aligned} \widehat{(\rho _h)_{{\textbf {n}}}}=\widehat{(c_h)_{{\textbf {n}}}} =\widehat{{\textbf{F}}(\rho _h)\cdot {\textbf {n}}}=0. \end{aligned}$$

(2.13)

For the convenience of analysis, by summing up (2.10a)–(2.10b) over all elements $K\in {\mathcal {T}}_h$, together with the boundary conditions (2.13), we obtain the semi-discrete DDGIC scheme in the global form, given by

$$\begin{aligned}&\int _{\Omega } (\rho _h)_t v_h ~dxdy -{\mathbb {A}}_h(\rho _h,c_h,v_h)+{\mathbb {B}}_h(\rho _h,v_h)=0, \end{aligned}$$

(2.14a)

$$\begin{aligned}&\int _{\Omega } (c_h)_t w_h ~dxdy + {\mathbb {B}}_h(c_h,w_h) +\int _{\Omega } (c_h-\rho _h ) w_h ~dxdy =0, \end{aligned}$$

(2.14b)

with the nonlinear functional ${\mathbb {A}}_h(\rho _h,c_h,v_h)$ defined as

$$\begin{aligned} {\mathbb {A}}_h(\rho _h,c_h,v_h):=\displaystyle \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K}\rho _h \nabla c_h\cdot \nabla v_h ~dxdy + \displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \widehat{{\textbf{F}}(\rho _h)\cdot {\textbf {n}}} \llbracket v_h\rrbracket ~ds, \end{aligned}$$

(2.15)

and the bilinear form ${\mathbb {B}}_h(u_h,v_h)$ defined as

$$\begin{aligned} {\mathbb {B}}_h(u_h,v_h):=\displaystyle \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K}\nabla u_h\cdot \nabla v_h ~dxdy +\displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e\left( \widehat{(u_h)_{{\textbf {n}}}}\llbracket v_h\rrbracket + \{\!\{ (v_h)_{{\textbf {n}}} \}\!\} \llbracket u_h\rrbracket \right) ~ds. \nonumber \\ \end{aligned}$$

(2.16)

3 Error Estimates

In this section, we carry out the error estimate for the DDGIC method solving the two-dimensional KS chemotaxis model (2.2). The analysis can also be conducted in a similar and easier way for one-dimensional case. We first introduce the norms and some inequalities used in the proof in Sect. 3.1, and present the main result and its proof in Sect. 3.2.

3.1 Preliminaries

In this subsection, we present the notations and norms used in this paper. We adopt the standard norms and seminorms in the Sobolev space. Let $H^{\ell }(K)$ denote the space equipped with the norm $\Vert \cdot \Vert _{H^{\ell }(K)}$, in which the function itself and the derivatives up to the $\ell$-th order are all in $L^2(\Omega )$. Clearly, $H^0(K)=L^2(K)$. We further define the stand $L^\infty$ norm in K as $\Vert \cdot \Vert _{\infty ,K}$ and define the $L^\infty$ norm on the whole domain as $\Vert \cdot \Vert _{\infty }=\max _{K\in {\mathcal {T}}_h}\Vert \cdot \Vert _{\infty ,K}$. We further introduce the energy norm for piecewise polynomial function $v_h\in {\mathbb {V}}^k_h$ as

$$\begin{aligned} |\!|\!| v_h |\!|\!| _h:=\left( \sum _{K\in {\mathcal {T}}_h}\int _{K}\nabla v_h\cdot \nabla v_h d {\textbf{x}}+\sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e\frac{\llbracket v_h\rrbracket ^2}{h_e}ds\right) ^{1/2}. \end{aligned}$$

(3.1)

We also define the standard $L^2$ projection $\Pi$ as

$$\begin{aligned} (\Pi \rho ,\,v_h)_K=(\rho ,\,v_h)_K, \quad \forall v_h\in P^k(K). \end{aligned}$$

(3.2)

The following two lemmas are to show the approximation property of the $L^2$ projection and the classical trace inequalities, which can be obtained by standard arguments in [7].

Lemma 3.1

(projection property) For any function $v\in H^{k}(\Omega )$, the project error satisfies

$$\begin{aligned} \Vert v-\Pi v\Vert _{H^{m}(K)}+h\Vert v-\Pi v\Vert _{\infty ,K}\le C_k h_K^{k-m} \Vert v\Vert _{H^{k}(K)}, \quad \forall \;\; 0\le m \le k, \; K\in {\mathcal {T}}_h, \end{aligned}$$

where m and k are non-negative integers, and the constant $C_k$ is independent of $h_K$ and v.

Lemma 3.2

(trace theorem with scaling) For $K\in {\mathcal {T}}_h$ and $e\subset \partial K$, there exists a positive constant $C_g$ independent of K such that

$$\begin{aligned} \Vert v\Vert _{L^2(e)}\le & {} C_g h_K^{-1/2}(\Vert v\Vert _{L^2(K)}+h_K\Vert \nabla v\Vert _{{\textbf{L}}^2(K)}), \; \text {for } v\in H^s(K) \text { with } s\ge 1,\\ \Vert v_{{\textbf{n}}}\Vert _{L^2(e)}\le & {} C_g h_K^{-1/2}(\Vert \nabla v\Vert _{{\textbf{L}}^2(K)}+h_K\Vert \nabla ^2 v\Vert _{{\textbf{L}}^2(K)}), \; \text {for } v\in H^s(K) \text { with } s\ge 2. \end{aligned}$$

For the finite element space ${\mathbb {V}}^k_h$, we state the classical inverse properties in the following lemma, the proof of which can be found in [7].

Lemma 3.3

(inverse inequality) For any function $v_h\in {\mathbb {V}}_h^k$, there exist positive constants $C_t$ and $C_i$ independent of $v_h,\,K$, and $h_k$ such that

$$\begin{aligned} \Vert \nabla v_h\Vert _{{\textbf{L}}^2(K)}&\le C_i h_K^{-1}\Vert v_h\Vert _{L^2(K)},\\ \Vert v_h\Vert _{L^2(e)}&\le C_th_K^{-1/2}\Vert v_h\Vert _{L^2(K)},\\ \Vert (v_h)_{{\textbf{n}}}\Vert _{L^2(e)}&\le C_th_K^{-1/2}\Vert \nabla v_h\Vert _{{\textbf{L}}^2(K)}. \end{aligned}$$

We end this subsection by establishing the coercivity of the bilinear form (2.16).

Lemma 3.4

(coercivity) There exists a positive constant $C_s$ for the DDGIC scheme (2.14) such that, for any $v_h\in {\mathbb {V}}_h^k$, we have

$$\begin{aligned} {\mathbb {B}}_h(v_h,v_h)\ge C_s |\!|\!| v_h |\!|\!| _h^2. \end{aligned}$$

(3.3)

Proof

It follows from the definition of the numerical flux in (2.11) that the bilinear form (2.16) can be rewritten as

$$\begin{aligned} {\mathbb {B}}(v_h,v_h)=\displaystyle \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K}\nabla v_h\cdot \nabla v_h ~dxdy +\displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e\left( \beta _{0}\frac{\llbracket v_h\rrbracket }{h_e}+ 2 \{\!\{ (v_h)_{{\textbf {n}}} \}\!\} +\beta _{1}h_e \llbracket (v_h)_{{\textbf {nn}}}\rrbracket \right) \llbracket v_h\rrbracket ~ds. \end{aligned}$$

(3.4)

We first estimate the term involving $\{\!\{ (v_h)_{{\textbf {n}}} \}\!\}$. Let $e\in {\mathcal {E}}_h^I$ be an edge shared by elements $K_1$ and $K_2$. Then according to the definition of average $\{\!\{ \cdot \}\!\}$ in (2.9) and Lemma 3.3, we have

$$\begin{aligned} \begin{aligned} \Vert \{\!\{ (v_h)_{{\textbf {n}}} \}\!\} \Vert _{L^2(e)}&\le \frac{1}{2}\left\| ((v_h)_{{\textbf {n}}})|_{K_1} \right\| _{L^2(e)}+\frac{1}{2}\left\| ((v_h)_{{\textbf {n}}})|_{K_2}\right\| _{L^2(e)}\\&\le \frac{C_t}{2} h_{K_1}^{-1/2}\Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_1)}+ \frac{C_t}{2} h_{K_2}^{-1/2}\Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_2)}\\&\le \frac{C_t}{2} h_{e}^{-1/2}\left( \Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_1)}+\Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_2)}\right) , \end{aligned} \end{aligned}$$

(3.5)

where the last inequality is based on the fact that $h_e\le h_{K_1}$ and $h_e\le h_{K_2}$, when $h_K$ represents the longest edge of element K. It is important to note that this inequality also holds with a slight modification of a constant when $h_K$ denotes the general diameter of K. This is because for any regular element K and $e\subset \partial K$, there exists a positive constant $\mu$ independent of K such that $h_e\le \mu h_{K}$.

Combining the estimate (3.5) with the Cauchy-Schwarz inequality and Young’s inequality leads to

$$\begin{aligned} \displaystyle \left| \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e 2 \{\!\{ (v_h)_{{\textbf {n}}} \}\!\} \llbracket v_h\rrbracket ~ds \right|&\le 2\sum _{e\in {\mathcal {E}}_h^I}\Vert \{\!\{ (v_h)_{{\textbf {n}}} \}\!\} \Vert _{L^2(e)}\Vert \llbracket v_h\rrbracket \Vert _{L^2(e)}\\&\le \displaystyle {C_t}\sum _{e\in {\mathcal {E}}_h^I}\left( \Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_1)} +\Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_2)}\right) h_{e}^{-1/2}\Vert \llbracket v_h\rrbracket \Vert _{L^2(e)}\\&\le \sqrt{2}C_t\sum _{e\in {\mathcal {E}}_h^I}\left( \Vert \nabla v_h\Vert ^2_{{\textbf{L}}^2(K_1)} +\Vert \nabla v_h\Vert ^2_{{\textbf{L}}^2(K_2)}\right) ^{1/2} h_{e}^{-1/2}\Vert \llbracket v_h\rrbracket \Vert _{L^2(e)}\\&\le \sqrt{6} C_t\left( \sum _{K\in {\mathcal {T}}_h}\Vert \nabla v_h\Vert ^2_{{\textbf{L}}^2(K)}\right) ^{1/2}\left( \sum _{e\in {\mathcal {E}}_h^I} h_{e} ^{-1}\Vert \llbracket v_h\rrbracket \Vert ^2_{L^2(e)}\right) ^{1/2}\\&\le \frac{1}{\epsilon }\sum _{K\in {\mathcal {T}}_h}\Vert \nabla v_h\Vert ^2_{{\textbf{L}}^2(K)} +\frac{3}{2}\epsilon \displaystyle C_t^2 \sum _{e\in {\mathcal {E}}_h^I} h_{e}^{-1}\Vert \llbracket v_h\rrbracket \Vert ^2_{L^2(e)}, \end{aligned}$$

where $\epsilon$ is a small positive constant independent of $h_e$ and $v_h$. It is worth mentioning that the coefficient $\sqrt{6}$ in the fourth inequality is specific to the use of a triangular mesh. In the case of a rectangular mesh, this coefficient should be adjusted to $2\sqrt{2}$. However, it is important to emphasize that adjusting this coefficient does not impact the results of the lemma or the main theorem. Hence, for the sake of simplicity and clarity, we will continue using the triangular mesh as an illustrative example to demonstrate the analysis procedure.

For the term involving $\llbracket (v_h)_{{\textbf {nn}}}\rrbracket$, similar estimates can be conducted to obtain

$$\begin{aligned} \begin{aligned} \Vert \llbracket (v_h)_{{\textbf {nn}}}\rrbracket \Vert _{L^2(e)}&\le \Vert (v_h)_{{\textbf {nn}}}|_{K_1}\Vert _{L^2(e)} +\Vert (v_h)_{{\textbf {nn}}}|_{K_2}\Vert _{L^2(e)}\\&\le C_t h_{K_1}^{-1/2}\Vert \nabla (v_h)_{{\textbf {n}}} \Vert _{{\textbf{L}}^2(K_1)}+C_t h_{K_2}^{-1/2}\Vert \nabla (v_h)_{{\textbf {n}}}\Vert _{{\textbf{L}}^2(K_2)}\\&\le C_t C_i h_{K_1}^{-3/2}\Vert (v_h)_{{\textbf {n}}}\Vert _{{L}^2(K_1)}+C_t C_i h_{K_2}^{-3/2}\Vert (v_h)_{{\textbf {n}}}\Vert _{{L}^2(K_2)}\\&\le \sqrt{2}C_tC_ih_e^{-3/2}\left( \Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_1)}+\Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_2)}\right) , \end{aligned} \end{aligned}$$

(3.6)

where the third inequality is due to Lemma 3.3. And

$$\begin{aligned} \displaystyle \left| \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e\beta _{1}h_e \llbracket (v_h)_{{\textbf {nn}}}\rrbracket \llbracket v_h\rrbracket ~ds\right|&\le \displaystyle \sum _{e\in {\mathcal {E}}_h^I} \beta _1 h_e\Vert \llbracket (v_h)_{{\textbf {nn}}}\rrbracket \Vert _{L^2(e)}\Vert \llbracket v_h\rrbracket \Vert _{L^2(e)}\\&\le \sqrt{2}\displaystyle \beta _1C_tC_i \displaystyle \sum _{e\in {\mathcal {E}}_ h^I}\left( \Vert \nabla v_h\Vert _{{\textbf{L}}^2(K_1)}+\Vert \nabla v_h\Vert _{{\textbf{L}}^ 2(K_2)}\right) h_{e}^{-1/2}\Vert \llbracket v_h\rrbracket \Vert _{L^2(e)}\\&\le 2\sqrt{3} \beta _1C_tC_i\left( \sum _{K\in {\mathcal {T}}_h}\Vert \nabla v_h\Vert ^2_{{\textbf{L}}^2(K)}\right) ^{1/2}\left( \sum _{e\in {\mathcal {E}}_h^I} h_{e}^{-1}\Vert \llbracket v_h\rrbracket \Vert ^2_{L^2(e)}\right) ^{1/2}\\&\le \frac{1}{\delta }\sum _{K\in {\mathcal {T}}_h}\Vert \nabla v_h\Vert ^2_{{\textbf{L}}^2(K)} +12\delta \beta _1^2 C_t^2C_i^2 \sum _{e\in {\mathcal {E}}_h^I} h_{e}^{-1}\Vert \llbracket v_h\rrbracket \Vert ^2_{L^2(e)}, \end{aligned}$$

where $\delta$ is a small positive constant independent of $h_e$ and $v_h$.

By substituting the above two terms into (3.4), we have

$$\begin{aligned} {\mathbb {B}}(v_h,v_h)&\ge \left( 1-\frac{1}{\epsilon }-\frac{1}{\delta }\right) \sum _{K\in {\mathcal {T}}_h}\Vert \nabla v_h\Vert ^2_{{\textbf{L}}^2(K)} \\&\quad +\left( \beta _0-\frac{3}{4}\epsilon C_t^2 -12\delta \beta _1^2C_t^2C_i^2\right) \sum _{e\in {\mathcal {E}}_h^I}h_{e}^{-1}\Vert \llbracket v_h\rrbracket \Vert ^2_{L^2(e)}. \end{aligned}$$

After choosing $\epsilon ,\,\delta$ such that $1-\frac{1}{\epsilon }-\frac{1}{\delta }>0$ and $\frac{3}{4}\epsilon C_t^2+12\delta \beta _1^2C_t^2C_i^2<\beta _0$, and setting $C_s=\min \left( 1-\frac{1}{\epsilon }-\frac{1}{\delta }, \beta _0-\frac{3}{4}\epsilon C_t^2 -12\delta \beta _1^2C_t^2C_i^2 \right)$, we complete the proof. $\square$

3.2 Error Estimates

In this subsection, we show the main result and the proof of the error estimates of the DDGIC scheme (2.14).

We state the main result in the following theorem.

Theorem 3.1

(Main result) Let $\rho ,\,c\in L^\infty (0,T; H^{k+1}(\Omega )\cap C^{2}(\Omega ))$ ($k>1$) be the exact solution of (2.2). Let $\rho _h,\,c_h\in V_h^k$ be the numerical solutions of the DDGIC scheme (2.14). The initial discretization is taken as the standard $L^2$ projection (3.2). Then there exists a positive constant C independent of h such that

$$\begin{aligned} \Vert (\rho -\rho _h)(t)\Vert _{L^2(\Omega )}+\Vert (c-c_h)(t)\Vert _{L^2(\Omega )}\le Ch^k,\quad t\in [0,T]. \end{aligned}$$

(3.7)

Here and below, C is a generic positive constant that does not depend on h, k, K, or the solutions $\rho$ and c. It may have different values at different occurrences.

To prove this theorem, it follows from the standard treatment in finite element analysis that the error between the exact solution and numerical solution can be divided as

$$\begin{aligned} e_{\rho }&=\rho -\rho _h=\xi _\rho -\eta _\rho , \text { with } \xi _\rho =\Pi \rho -\rho _h,\;\eta _\rho =\Pi \rho -\rho , \end{aligned}$$

(3.8a)

$$\begin{aligned} e_{c}&=c-c_h=\xi _c-\eta _c, \;\text { with } \xi _c=\Pi c-c_h,\;\;\eta _c=\Pi c-c. \end{aligned}$$

(3.8b)

Estimates of the projection errors $\eta _\rho$ and $\eta _c$ can be obtained according to Lemma 3.1. Then by triangle inequality, Theorem 3.1 can be proved by obtaining the error estimates for $\xi _\rho$ and $\xi _c$, which will be discussed in the following two subsections.

3.2.1 Error Equations

We first show that the exact solutions under suitable smooth conditions satisfy the DDGIC scheme (2.14) in the following lemma.

Lemma 3.5

Let $\rho ,\,c\in L^\infty (0,T; H^{k+1}(\Omega )\cap C^{2}(\Omega ))$ be the exact solution of (2.2). Then, for any $v_h,\ w_h\in {\mathbb {V}}^k_h$, we have

$$\begin{aligned}&\int _{\Omega } \rho _t v_h ~dxdy -{\mathbb {A}}_h(\rho ,c,v_h)+{\mathbb {B}}_h(\rho ,v_h)=0, \end{aligned}$$

(3.9a)

$$\begin{aligned}&\int _{\Omega } c_t w_h ~dxdy + {\mathbb {B}}_h(c,w_h) +\int _{\Omega } (c-\rho ) w_h ~dxdy =0, \end{aligned}$$

(3.9b)

with the nonlinear functional ${\mathbb {A}}_h$ and the bilinear form ${\mathbb {B}}_h$ defined in (2.15) and (2.16), respectively.

Proof

By multiplying the system (2.2) with test functions $v_h, w_h \in {\mathbb {V}}^k_h$, and performing integration by parts in the element K, we obtain the weak formulation of (2.2)

$$\begin{aligned}&\int _{K} \rho _t v_h ~dxdy +\int _{\partial K}\left( {{\textbf{F}}(\rho )\cdot {\textbf {n}}}-{\rho _{\textbf {n}}}\right) v_h~ds +\int _{K}\left( \nabla \rho -{\textbf{F}}(\rho )\right) \cdot \nabla v_h ~dxdy=0, \end{aligned}$$

(3.10a)

$$\begin{aligned}&\int _{K} c_t w_h ~dxdy -\int _{\partial K} {c_{\textbf {n}}} w_h~ds +\int _{K} \nabla c\cdot \nabla w_h ~dxdy+\int _{K} (c-\rho ) w_h ~dxdy =0, \end{aligned}$$

(3.10b)

with ${\textbf{F}}(\rho )=\rho \nabla c$. The smoothness of the exact solutions implies that $\llbracket \rho \rrbracket =0$, $\llbracket c\rrbracket =0$, $\llbracket \rho _{{\textbf {nn}}}\rrbracket =0$, and $\llbracket c_{{\textbf {nn}}} \rrbracket =0$ at the element interfaces. Together with the definition of the numerical fluxes in (2.11), we have

$$\begin{aligned} \widehat{\rho _{\textbf {n}}}=\nabla \rho \cdot {\textbf {n}}=\rho _{\textbf {n}}, \quad \widehat{c_{\textbf {n}}}=c_{\textbf {n}}, \quad \widehat{{\textbf{F}}(\rho )\cdot {\textbf {n}}}={\textbf{F}}(\rho )\cdot {\textbf {n}}=\rho c_{\textbf {n}}. \end{aligned}$$

(3.11)

Therefore, the weak formulation (3.10) can be rewritten as

$$\begin{aligned}&\int _{K} \rho _t v_h ~dxdy +\int _{\partial K}\left( \widehat{{\textbf{F}}(\rho )\cdot {\textbf {n}}}-\widehat{\rho _{\textbf {n}}}\right) v_h~ds +\int _{K}\left( \nabla \rho -{\textbf{F}}(\rho )\right) \cdot \nabla v_h ~dxdy\\&\quad +\int _{\partial K}\llbracket \rho \rrbracket \frac{(v_h)_{{\textbf {n}}}}{2} ~ds=0,\\&\int _{K} c_t w_h ~dxdy -\int _{\partial K} \widehat{c_{\textbf {n}}} w_h~ds +\int _{K} \nabla c\cdot \nabla w_h ~dxdy++\int _{\partial K}\llbracket c\rrbracket \frac{(w_h)_{{\textbf {n}}}}{2} ~ds\\&\quad +\int _{K} (c-\rho ) w_h ~dxdy =0, \end{aligned}$$

which means that the exact solutions $\rho$ and c satisfy the DDGIC scheme (2.10). By summing up the above equations over all elements $K\in {\mathcal {T}}_h$, the exact solutions also satisfy the DDGIC scheme in the global form (2.14). Thus, the proof is complete. $\square$

By subtracting (3.9) from (2.14), together with the definition of $\Pi$ in (3.2) and the linearity of the bilinear form (2.16), we obtain the error equations

$$\begin{aligned} \int _{\Omega } (\xi _\rho )_t v_h ~dxdy + {\mathbb {B}}_h(\xi _\rho ,v_h)&={\mathbb {A}}_h(\rho ,c,v_h)-{\mathbb {A}}_h(\rho _h,c_h,v_h)+{\mathbb {B}}_h(\eta _{\rho },v_h), \end{aligned}$$

(3.12a)

$$\begin{aligned} \int _{\Omega } (\xi _c)_t w_h ~dxdy + {\mathbb {B}}_h(\xi _c,w_h)&= {\mathbb {B}}_h(\eta _c,w_h) +\int _{\Omega } \left( \xi _\rho -\xi _c\right) w_h ~dxdy. \end{aligned}$$

(3.12b)

3.2.2 Error Estimate for $\xi _\rho$ and $\xi _c$

To investigate the errors of $\xi _\rho$ and $\xi _c$, we make the following a priori assumption

$$\begin{aligned} \Vert \rho _h(t)\Vert _{\infty }\le C,\quad t\in [0,T], \end{aligned}$$

(3.13)

to deal with nonlinear terms. The rationale behind adopting such an assumption can be verified as follows. Let $t^*=\sup \{{\tilde{t}}|\Vert \rho _h(t)\Vert _{\infty }\le C,\; t\in [0,{\tilde{t}}]\}$. It can be confirmed that (3.13) holds at $t=0$. Note that $\rho _h(0)=\Pi \rho (0)$. Based on the smoothness of the exact solutions and Lemma 3.1, we deduce that $\Vert \rho (0)\Vert _\infty <C$ and $\Vert (\rho -\rho _h)(0)\Vert _\infty <C$. By applying the triangle inequality, we have $\Vert \rho _h(0)\Vert _\infty =\Vert \rho (0)-(\rho -\rho _h)(0)\Vert _\infty \le C$. Hence, the set $\{{\tilde{t}}|\Vert \rho _h(t)\Vert _{\infty }\le C,\; t\in [0,{\tilde{t}}]\}$ is not empty, and $t^*$ exists. Suppose (3.13) fails and $t^*<T$. It follows from the fact that $\Vert {\rho _h(t)}\Vert _{\infty }$ is a continuous function of t that there exists a positive constant $\varepsilon$ such that $\Vert \rho _h(t)\Vert _{\infty }\le C$ for $t\in [0,t^*+\varepsilon ]$. However, this contradicts the definition of $t^*$. Thus, the verification of the a priori assumption is complete.

Lemma 3.6

Under the a priori assumption (3.13), the DDGIC scheme 2.14 satisfies

$$\begin{aligned} \Vert \xi _\rho \Vert _{L^2(\Omega )}+\Vert \xi _c\Vert _{L^2(\Omega )}\le Ch^k. \end{aligned}$$

Proof

By taking test functions $v_h=\xi _\rho$ in (3.12a) and $w_h=\xi _c$ in (3.12b), and applying the coercivity of the bilinear form in Lemma 3.4, we can rewrite the error equations as

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert \xi _\rho \Vert ^2_{L^2(\Omega )}+C_s |\!|\!| \xi _\rho |\!|\!| ^2_h&\le {\mathbb {B}}_h(\eta _\rho ,\xi _\rho )+{\mathbb {A}}_h(\rho ,c,\xi _\rho )-{\mathbb {A}}_h(\rho _h,c_h,\xi _\rho ), \end{aligned}$$

(3.14a)

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert \xi _c\Vert ^2_{L^2(\Omega )}+C_s |\!|\!| \xi _c |\!|\!| ^2_h&\le {\mathbb {B}}_h(\eta _c,\xi _c) + \int _{\Omega } \left( \xi _\rho -\xi _c\right) \xi _c ~dxdy. \end{aligned}$$

(3.14b)

We estimate the terms in the right hand side in the following three steps.

$\underline{\textbf{Step}\,\mathbf{1:}\, \textbf{estimate}\, \textbf{of}\, \textbf{the}\, \textbf{bilinear}\, \textbf{terms}\, {\mathbb {B}}_h(\eta _\rho ,\xi _\rho )\, \textbf{and} {\mathbb {B}}_h(\eta _c,\xi _c)}$

According to the definition of the bilinear form in (2.16), the term ${\mathbb {B}}_h(\eta _\rho ,\xi _\rho )$ can be rewritten into three terms

$$\begin{aligned} {\mathbb {B}}_h(\eta _\rho ,\xi _\rho ) =O_1+O_2+O_3, \end{aligned}$$

(3.15)

where

$$\begin{aligned} O_1&=\displaystyle \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K}\nabla \eta _\rho \cdot \nabla \xi _\rho ~dxdy,\\ O_2&=\displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e\widehat{(\eta _\rho )_{{\textbf {n}}}}\llbracket \xi _\rho \rrbracket ~ds,\\ O_3&=\displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \{\!\{ (\xi _\rho )_{{\textbf {n}}} \}\!\} \llbracket \eta _\rho \rrbracket ~ds, \end{aligned}$$

with $\widehat{(\eta _\rho )_{{\textbf {n}}}}$ defined the same as the flux in (2.11).

For the term $O_1$, a simple use of Young’s inequality, together with Lemma 3.1 and the definition of the energy norm $|\!|\!| \cdot |\!|\!|$ in (3.1), leads to

$$\begin{aligned} \begin{aligned} O_1&\le \frac{1}{C_s} \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K} |\nabla \eta _\rho |^2 ~dxdy + \frac{C_s}{4} \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K} |\nabla \xi _\rho |^2 ~dxdy\\&\le Ch^{2k} \Vert \rho \Vert ^2_{H^{k+1}(\Omega )}+\frac{C_s}{4} |\!|\!| \xi _\rho |\!|\!| ^2_h. \end{aligned} \end{aligned}$$

(3.16)

For the term $O_2$, by Young’s inequality and the definition (2.11), we have

$$\begin{aligned} \begin{aligned} O_2&\le \frac{h}{C_s} \displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \left( \widehat{(\eta _\rho )_{{\textbf {n}}}}\right) ^2 ~ds+\frac{C_s}{4} \displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \frac{\llbracket \xi _\rho \rrbracket ^2 }{h} ~ds\\&\le \frac{3h}{C_s} \displaystyle \sum _{e\in {\mathcal {E}}_h^I}\int _e \left( \beta ^2_{0}\frac{\llbracket \eta _\rho \rrbracket ^2}{h_e^2}+ \{\!\{ (\eta _\rho )_{{\textbf {n}}} \}\!\} ^2+\beta _{1}^2h_e^2 \llbracket (\eta _\rho )_{{\textbf {nn}}}\rrbracket ^2\right) ~ds+\frac{C_s}{4} |\!|\!| \xi _\rho |\!|\!| ^2_h. \end{aligned} \end{aligned}$$

(3.17)

We estimate these terms on element boundaries one by one in the following. Let $e\in {\mathcal {E}}_h^I$ be an edge shared by elements $K_1$ and $K_2$. It follows from the definition of average and jump in (2.9), Lemma 3.1 and Lemma 3.2 that

$$\begin{aligned} \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \frac{\llbracket \eta _\rho \rrbracket ^2}{h_e^2} ~ds\le & {} 2\sum _{e\in {\mathcal {E}}_h^I} h_e^{-2} \left( \Vert \eta _\rho |_{K_1}\Vert ^2_{L^2(e)} +\Vert \eta _\rho |_{K_2}\Vert ^2_{L^2(e)}\right) \nonumber \\\le & {} 2\sum _{e\in {\mathcal {E}}_h^I} h_e^{-2}C_g^2\left( h_{K_1}^{-1}\left( \Vert \eta _\rho \Vert _{L^2(K_1)}+h_{K_1}\Vert \nabla \eta _\rho \Vert _{{\textbf{L}}^2(K_1)}\right) ^2 \right. \nonumber \\{} & {} +\left. h_{K_2}^{-1}\left( \Vert \eta _\rho \Vert _{L^2(K_2)}+h_{K_2}\Vert \nabla \eta _\rho \Vert _{{\textbf{L}}^2(K_2)}\right) ^2\right) \nonumber \\\le & {} \displaystyle 2\sum _{e\in {\mathcal {E}}_h^I} h_e^{-2}C_g^2C_k^2\left( h_{K_1}^{2k+1}\Vert \rho \Vert ^2_{H^{k+1}(K_1)} +h_{K_2}^{2k+1}\Vert \rho \Vert ^2_{H^{k+1}(K_2)}\right) \nonumber \\\le & {} \;C \sum _{K\in {\mathcal {T}}_h} h_{K}^{2k-1} \Vert \rho \Vert ^2_{H^{k+1}(K)}\nonumber \\\le & {} C h^{2k-1} \Vert \rho \Vert ^2_{H^{k+1}(\Omega )}. \end{aligned}$$

(3.18)

$$\begin{aligned} \sum _{e\in {\mathcal {E}}_h^I}\int _e \{\!\{ (\eta _\rho )_{{\textbf {n}}} \}\!\} ^2 ~ds\le & {} \frac{1}{2}\sum _{e\in {\mathcal {E}}_h^I} \left( \Vert (\eta _\rho )_{{\textbf {n}}}|_{K_1}\Vert ^2_{L^2(e)} +\Vert (\eta _\rho )_{{\textbf {n}}}|_{K_2}\Vert ^2_{L^2(e)}\right) \nonumber \\\le & {} \frac{1}{2}\sum _{e\in {\mathcal {E}}_h^I}C_g^2\left( h_{K_1}^{-1}\left( \Vert \nabla \eta _\rho \Vert _{{\textbf{L}}^2(K_1)}+h_{K_1}\Vert \nabla ^2\eta _\rho \Vert _{{\textbf{L}}^2(K_1)}\right) ^2\right. \nonumber \\{} & {} +\left. h_{K_2}^{-1}\left( \Vert \nabla \eta _\rho \Vert _{{\textbf{L}}^2(K_2)}+h_{K_2}\Vert \nabla ^2 \eta _\rho \Vert _{{\textbf{L}}^2(K_2)}\right) ^2\right) \nonumber \\\le & {} \;C \sum _{K\in {\mathcal {T}}_h} h_{K}^{2k-1} \Vert \rho \Vert ^2_{H^{k+1}(K)}\nonumber \\\le & {} C h^{2k-1} \Vert \rho \Vert ^2_{H^{k+1}(\Omega )}. \end{aligned}$$

(3.19)

$$\begin{aligned} \sum _{e\in {\mathcal {E}}_h^I} \int _e h_e^2 \llbracket (\eta _\rho )_{{\textbf {nn}}}\rrbracket ^2~ds\le & {} 2\sum _{e\in {\mathcal {E}}_h^I}h_e^2 \left( \Vert (\eta _\rho )_{{\textbf {nn}}}|_{K_1}\Vert ^2_{L^2(e)} +\Vert (\eta _\rho )_{{\textbf {nn}}}|_{K_2}\Vert ^2_{L^2(e)}\right) \nonumber \\\le & {} 2\sum _{e\in {\mathcal {E}}_h^I}h_e^2C_g^2 \left( h_{K_1}^{-1}\left( \Vert \nabla (\eta _\rho )_{{\textbf {n}}}\Vert _{{\textbf{L}}^2(K_1)} +h_{K_1}\Vert \nabla ^2(\eta _\rho )_{{\textbf {n}}}\Vert _{{\textbf{L}}^2(K_1)}\right) ^2\right. \nonumber \\{} & {} +\left. h_{K_2}^{-1}\left( \Vert \nabla (\eta _\rho )_{{\textbf {n}}}\Vert _{{\textbf{L}}^2(K_2)} +h_{K_2}\Vert \nabla ^2(\eta _\rho )_{{\textbf {n}}}\Vert _{{\textbf{L}}^2(K_2)}\right) ^2\right) \nonumber \\\le & {} \displaystyle 4\sum _{e\in {\mathcal {E}}_h^I}h_e^2C_g^2 \left( h_{K_1}^{-1}\left( \Vert \nabla ^2\eta _\rho \Vert _{{\textbf{L}}^2(K_1)}+h_{K_1}\Vert \nabla ^3\eta _ \rho \Vert _{{\textbf{L}}^2(K_1)}\right) ^2\right. \nonumber \\{} & {} +\left. h_{K_2}^{-1}\left( \Vert \nabla ^2\eta _\rho \Vert _{{\textbf{L}}^2(K_2)}+h_{K_2}\Vert \nabla ^3\eta _ \rho \Vert _{{\textbf{L}}^2(K_2)}\right) ^2\right) \nonumber \\\le & {} C h^{2k-1} \Vert \rho \Vert ^2_{H^{k+1}(\Omega )}. \end{aligned}$$

(3.20)

By substituting (3.18)–(3.20) into (3.17), we obtain

$$\begin{aligned} \begin{aligned} O_2\le Ch^{2k} \Vert \rho \Vert ^2_{H^{k+1}(\Omega )}+\frac{C_s}{4} |\!|\!| \xi _\rho |\!|\!| ^2_h. \end{aligned} \end{aligned}$$

(3.21)

For the term $O_3$, we can use Young’s inequality to obtain

$$\begin{aligned} \begin{aligned} O_3 \le \frac{C_s }{6C^2_t} \displaystyle \sum _{e\in {\mathcal {E}}_h^I} h_e\displaystyle \int _e \{\!\{ (\xi _\rho )_{{\textbf {n}}} \}\!\} ^2 ~ds+\frac{3C^2_t}{2C_s} \displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \frac{\llbracket \eta _\rho \rrbracket ^2 }{h_e} ~ds, \end{aligned} \end{aligned}$$

(3.22)

which follows a similar estimate as in (3.5) for the term involving $(\xi _\rho )_{{\textbf {n}}}$ and a similar estimate as in (3.18) for the term involving $\llbracket \eta _\rho \rrbracket$, yielding

$$\begin{aligned} \begin{aligned} O_3&\le \frac{C_s }{6C^2_t}\sum _{e\in {\mathcal {E}}_h^I} \frac{C_t^2}{4}\left( \Vert \nabla \xi _\rho \Vert _{{\textbf{L}}^2(K_1)}+\Vert \nabla \xi _\rho \Vert _{{\textbf{L}}^2(K_2)}\right) ^2+C h^{2k}\Vert \rho \Vert ^2_{H^{k+1}(\Omega )} \\&\le \frac{C_s }{4} \sum _{K\in {\mathcal {T}}_h}\Vert \nabla \xi _\rho \Vert _{{\textbf{L}}^2(K)}^2+C h^{2k} \Vert \rho \Vert ^2_{H^{k+1}(\Omega )} \\&\le \frac{C_s}{4} |\!|\!| \xi _\rho |\!|\!| ^2_h+C h^{2k} \Vert \rho \Vert ^2_{H^{k+1}(\Omega )}. \end{aligned} \end{aligned}$$

(3.23)

It follows from substituting the estimates in (3.16), (3.17), and (3.22) into (3.15) that we get t the estimate for the bilinear term ${\mathbb {B}}_h(\eta _\rho ,\xi _\rho )$ as

$$\begin{aligned} {\mathbb {B}}_h(\eta _\rho ,\xi _\rho )\le \frac{3C_s}{4} |\!|\!| \xi _\rho |\!|\!| ^2_h+C h^{2k} \Vert \rho \Vert ^2_{H^{k+1}(\Omega )}. \end{aligned}$$

(3.24)

Similar estimates can be conducted for the term ${\mathbb {B}}_h(\eta _c,\xi _c)$, leading to

$$\begin{aligned} {\mathbb {B}}_h(\eta _c,\xi _c)\le \frac{3C_s}{4} |\!|\!| \xi _c |\!|\!| ^2_h+C h^{2k} \Vert c\Vert ^2_{H^{k+1}(\Omega )}. \end{aligned}$$

(3.25)

$\underline{\textbf{Step}\,\mathbf{2:}\,\textbf{estimate}\, \textbf{of}\, \textbf{the}\, \textbf{nonlinear}\, \textbf{term}\, {\mathbb {A}}_h(\rho ,c,\xi _\rho )-{\mathbb {A}}_h(\rho _h,c_h,\xi _\rho )}$

Based on the definition of the nonlinear functional ${\mathbb {A}}_h(\rho _h,c_h,v_h)$ in (2.15), this nonlinear term can be rewritten as

$$\begin{aligned} {\mathbb {A}}_h(\rho ,c,\xi _\rho )-{\mathbb {A}}_h(\rho _h,c_h,\xi _\rho ) = Z_{1}+Z_2, \end{aligned}$$

(3.26)

where

$$\begin{aligned} Z_1&=\displaystyle \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K}\rho \nabla c\cdot \nabla (\xi _\rho ) ~dxdy -\displaystyle \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K}\rho _h \nabla c_h\cdot \nabla (\xi _\rho ) ~dxdy,\\ Z_2&=\displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \widehat{{\textbf{F}}(\rho )\cdot {\textbf {n}}} \llbracket \xi _\rho \rrbracket ~ds-\displaystyle \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \widehat{{\textbf{F}}(\rho _h)\cdot {\textbf {n}}} \llbracket \xi _\rho \rrbracket ~ds. \end{aligned}$$

For the term $Z_1$, it can be rewritten as

$$\begin{aligned} Z_1=\sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K}(\xi _\rho -\eta _\rho ) \nabla c\cdot \nabla \xi _\rho ~dxdy +\displaystyle \sum _{K\in {\mathcal {T}}_h}\displaystyle \int _{K}\rho _h \nabla (\xi _c-\eta _c)\cdot \nabla \xi _\rho ~dxdy, \end{aligned}$$

which, combining with Lemma 3.1 and Lemma 3.3, the a priori assumption (3.13), the fact that $\Vert \nabla c\Vert _{{\textbf{L}}^\infty (\Omega )} \le C$ due to the smoothness of the exact solution, the Cauchy-Schwarz inequality, and Young’s inequality yields

$$\begin{aligned} Z_1\le & {} C \sum _{K\in {\mathcal {T}}_h}\Vert \xi _\rho -\eta _\rho \Vert _{L^2(K)} \Vert \nabla \xi _\rho \Vert _{{\textbf{L}}^2(K)} +C\sum _{K\in {\mathcal {T}}_h}\Vert \nabla (\xi _c-\eta _c)\Vert _{{\textbf{L}}^2(K)}\Vert \nabla \xi _\rho \Vert _{{\textbf{L}}^2(K)} \nonumber \\\le & {} C \sum _{K\in {\mathcal {T}}_h}\left( \Vert \xi _\rho \Vert _{L^2(K)}+\Vert \eta _\rho \Vert _{L^2(K)} +\Vert \nabla \xi _c\Vert _{{\textbf{L}}^2(K)}+\Vert \nabla \eta _c\Vert _{{\textbf{L}}^2(K)} \right) \Vert \nabla \xi _\rho \Vert _{{\textbf{L}}^2(K)} \nonumber \\\le & {} C\left( h^{2k+2}\Vert \rho \Vert _{H^{k+1}(\Omega )}^2 +\Vert \xi _\rho \Vert ^2_{L^2(\Omega )}+h^{2k}\Vert c\Vert _{H^{k+1}(\Omega )}^2 + |\!|\!| \xi _c |\!|\!| _h^2\right) +\frac{C_s}{8} |\!|\!| \xi _\rho |\!|\!| _h^2.\nonumber \\ \end{aligned}$$

(3.27)

For the term $Z_2$ involving fluxes at the element interface, we follow (3.11) and the definition of average and jump in (2.9), and rewrite the fluxes defined in (2.12) as

$$\begin{aligned} \widehat{{\textbf{F}}(\rho _h)\cdot {\textbf {n}}}=\widehat{(c_h)_{{\textbf {n}}}} \{\!\{ \rho _h \}\!\} - \frac{\alpha }{2} \llbracket \rho _h\rrbracket , \qquad \widehat{{\textbf{F}}(\rho )\cdot {\textbf {n}}}= \widehat{c_{{\textbf {n}}}} \{\!\{ \rho \}\!\} -\frac{\alpha }{2} \llbracket \rho \rrbracket \end{aligned}$$

Then the term $Z_2$ can be split as

$$\begin{aligned} Z_2=Z_{21}+Z_{22}, \end{aligned}$$

(3.28)

where

$$\begin{aligned} Z_{21}&=\sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \left( \widehat{c_{{\textbf {n}}}} \{\!\{ \rho \}\!\} -\widehat{(c_h)_{{\textbf {n}}}} \{\!\{ \rho _h \}\!\} \right) \llbracket \xi _\rho \rrbracket ~ds,\\ Z_{22}&=- \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \frac{\alpha }{2} \llbracket \rho -\rho _h\rrbracket \llbracket \xi _\rho \rrbracket ~ds. \end{aligned}$$

The estimate of $Z_{21}$ follows the similar line as the estimate for $Z_1$, yielding

$$\begin{aligned} \begin{aligned} Z_{21}&= \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \left( \widehat{c_{{\textbf {n}}}} \{\!\{ \xi _\rho -\eta _\rho \}\!\} -\Vert \widehat{(\xi _c-\eta _c)_{{\textbf {n}}}} \{\!\{ \rho _h \}\!\} \right) \llbracket \xi _\rho \rrbracket ~ds\\&\le C \sum _{e\in {\mathcal {E}}_h^I}h_e^{1/2}\left( \Vert \{\!\{ \xi _\rho -\eta _\rho \}\!\} \Vert _{L^2(e)}+\Vert \widehat{(\xi _c-\eta _c)_{{\textbf {n}}}}\Vert _{L^2(e)}\right) h_e^{-1/2}\Vert \llbracket \xi _\rho \rrbracket \Vert _{L^2(e)}\\&\le C \sum _{e\in {\mathcal {E}}_h^I}h_e\left( \Vert \{\!\{ \xi _\rho \}\!\} \Vert _{L^2(e)}^2+\Vert \{\!\{ \eta _\rho \}\!\} \Vert ^2_{L^2(e)}+\Vert \widehat{( \xi _c)_{{\textbf {n}}}}\Vert ^2_{L^2(e)^2}+\Vert \widehat{(\eta _c)_{{\textbf {n}}}}\Vert ^2_{L^2(e)}\right) +\frac{C_s}{16} |\!|\!| \xi _\rho |\!|\!| _h^2, \end{aligned} \end{aligned}$$

where we have used the fact that $\widehat{c_{{\textbf {n}}}}={c_{{\textbf {n}}}}$ in (3.11) and $\nabla c$ is uniformly bounded due to the smoothness assumption of the exact solution. Then the term involving $\{\!\{ \xi _\rho \}\!\}$ can be handled in a similar fashion as the estimates in (3.5), the term involving $\{\!\{ \eta _\rho \}\!\}$ can be estimated by Lemma 3.2, the term involving the fluxes $\widehat{( \xi _c)_{{\textbf {n}}}}$ can be similarly handed as in (3.23), and the term $\widehat{(\eta _c)_{{\textbf {n}}}}$ can be handled in a similar fashion as the estimates in (3.17), yielding

$$\begin{aligned} Z_{21}\le & {} C \sum _{K\in {\mathcal {T}}_h}\left( \Vert \xi _\rho \Vert _{{L}^2(K)}^2+\Vert \eta _\rho \Vert _{{L}^2(K)}^2+h_K^2\Vert \nabla \eta _\rho \Vert _{{\textbf{L}}^2(K)}^2\right) \\{} & {} +C\left( h^{2k}\Vert c\Vert _{H^{k+1}(\Omega )}^2+ |\!|\!| \xi _c |\!|\!| _h^2\right) +\frac{C_s}{16} |\!|\!| \xi _\rho |\!|\!| _h^2, \end{aligned}$$

which, together with Lemma 3.1, leads to

$$\begin{aligned} Z_{21} \le C\left( h^{2k+2}\Vert \rho \Vert _{H^{k+1}(\Omega )}+h^{2k}\Vert c\Vert _{H^{k+1}(\Omega )}+\Vert \xi _\rho \Vert _{L^2(\Omega )}^2 + |\!|\!| \xi _c |\!|\!| _h^2\right) +\frac{C_s}{16} |\!|\!| \xi _\rho |\!|\!| _h^2. \nonumber \\ \end{aligned}$$

(3.29)

The estimate of $Z_{22}$ can be conducted in a similar way as

$$\begin{aligned} \begin{aligned} Z_{22}&=- \sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e \frac{\alpha }{2} \llbracket \xi _\rho -\eta _\rho \rrbracket \llbracket \xi _\rho \rrbracket ~ds\\&\le \frac{\alpha }{2}\sum _{e\in {\mathcal {E}}_h^I}\displaystyle \int _e\Vert \llbracket \xi _\rho -\eta _\rho \rrbracket \Vert _{L^2(e)}\Vert \llbracket \xi _\rho \rrbracket \Vert _{L^2(e)}~ds\\&\le C\left( h^{2k+2}\Vert \rho \Vert _{H^{k+1}(\Omega )}+\Vert \xi _\rho \Vert _{L^2(\Omega )}^2 \right) +\frac{C_s}{16} |\!|\!| \xi _\rho |\!|\!| _h^2. \end{aligned} \end{aligned}$$

(3.30)

It follows from substituting (3.29) and in (3.30) into (3.28) that we obtain the estimate for the term $Z_2$ as

$$\begin{aligned} Z_2 \le C\left( h^{2k+2}\Vert \rho \Vert _{H^{k+1}(\Omega )}+h^{2k}\Vert c\Vert _{H^{k+1}(\Omega )}+\Vert \xi _\rho \Vert _{L^2(\Omega )}^2 + |\!|\!| \xi _c |\!|\!| _h^2\right) +\frac{C_s}{8} |\!|\!| \xi _\rho |\!|\!| _h^2. \end{aligned}$$

(3.31)

Then by collecting the estimates in (3.27) and (3.31) for the terms $Z_1$ and $Z_2$ in (3.26), we have

$$\begin{aligned} \begin{aligned}&{\mathbb {A}}_h(\rho ,c,\xi _\rho )-{\mathbb {A}}_h(\rho _h,c_h,\xi _\rho )\\&\quad \le C\left( h^{2k+2}\Vert \rho \Vert _{H^{k+1}(\Omega )}+h^{2k}\Vert c\Vert _{H^{k+1}(\Omega )}+\Vert \xi _\rho \Vert _{L^2(\Omega )}^2 + |\!|\!| \xi _c |\!|\!| _h^2\right) +\frac{C_s}{4} |\!|\!| \xi _\rho |\!|\!| _h^2. \end{aligned} \end{aligned}$$

(3.32)

$\underline{\textbf{Step}\,\mathbf{3:} \textbf{estimate}\, \textbf{of}\,\textbf{the}\,\textbf{term}\, \int _{\Omega } \left( \xi _\rho -\xi _c\right) \xi _c ~dxdy\, \textbf{and}\,\textbf{final}\,\textbf{estimate}}$

For the term $\int _{\Omega } \left( \xi _\rho -\xi _c\right) \xi _c ~dxdy$, a simply use of Young’s inequality leads to

$$\begin{aligned} \int _{\Omega } \left( \xi _\rho -\xi _c\right) \xi _c ~dxdy \le \frac{1}{2}\Vert \xi _\rho \Vert ^2_{L^2(\Omega )}-\frac{1}{2}\Vert \xi _c\Vert ^2_{L^2(\Omega )}\le \frac{1}{2}\Vert \xi _\rho \Vert ^2_{L^2(\Omega )}. \end{aligned}$$

(3.33)

By substituting (3.24) and (3.32) into (3.14a), we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert \xi _\rho \Vert ^2_{L^2(\Omega )} \le C\left( h^{2k}\Vert \rho \Vert _{H^{k+1}(\Omega )}+h^{2k}\Vert c\Vert _{H^{k+1}(\Omega )}+\Vert \xi _\rho \Vert _{L^2(\Omega )}^2 + |\!|\!| \xi _c |\!|\!| _h^2\right) . \end{aligned}$$

(3.34)

By substituting (3.25) and (3.33) into (3.14b), we obtain

$$\begin{aligned} \frac{1}{2}\frac{d}{dt} \Vert \xi _c\Vert ^2_{L^2(\Omega )}+\frac{C_s}{4} |\!|\!| \xi _c |\!|\!| ^2_h \le Ch^{2k}\Vert c\Vert ^2_{H^{k+1}(\Omega )}+ \frac{1}{2}\Vert \xi _\rho \Vert ^2_{L^2(\Omega )}. \end{aligned}$$

(3.35)

Combining (3.34) and (3.35), for a positive constant $\delta$, we have

$$\begin{aligned}&\frac{1}{2}\frac{d}{dt} \Vert \xi _\rho \Vert ^2_{L^2(\Omega )} +\delta \left( \frac{1}{2}\frac{d}{dt} \Vert \xi _c\Vert ^2_{L^2(\Omega )}+\frac{C_s}{4} |\!|\!| \xi _c |\!|\!| ^2_h\right) \\&\quad \le C\left( h^{2k}\Vert \rho \Vert _{H^{k+1}(\Omega )}+h^{2k}\Vert c\Vert _{H^{k+1}(\Omega )}+\Vert \xi _\rho \Vert _{L^2(\Omega )}^2 + |\!|\!| \xi _c |\!|\!| _h^2\right) \\&\qquad +\delta ( Ch^{2k}\Vert c\Vert ^2_{H^{k+1}(\Omega )}+ \frac{1}{2}\Vert \xi _\rho \Vert ^2_{L^2(\Omega )}). \end{aligned}$$

For sufficiently large $\delta$ such as $\delta =\frac{4C}{C_s}$, we have

$$\begin{aligned} \frac{d}{dt} \Vert \xi _\rho \Vert ^2_{L^2(\Omega )} +\delta \frac{d}{dt} \Vert \xi _c\Vert ^2_{L^2(\Omega )}&\le C\left( h^{2k}\Vert \rho \Vert _{H^{k+1}(\Omega )}+h^{2k}\Vert c\Vert _{H^{k+1}(\Omega )}+\Vert \xi _\rho \Vert _{L^2(\Omega )}^2)\right) . \end{aligned}$$

Thus, with the $L^2$ projection as the initial discretization, the proof is complete by applying the Gronwall’s inequality. $\square$

4 Numerical Results

In this section, we provide numerical experiments to demonstrate the accuracy of the DDGIC method. For temporal discretization, we apply the third-order SSPRK method [36]. A collection of admissible coefficients $(\beta _0,\beta _1)$ is available to guarantee the optimal convergence of the DDGIC method for diffusion equations. On the other hand, it was proved in [39] that, when the coefficient $\beta _1$ coefficient taken as

$$\begin{aligned} \beta _1=\frac{1}{2k(k+1)}, \end{aligned}$$

for $P^2$ polynomial approximations on uniform mesh, the numerical solution of the DDGIC method is superconvergent to the solution’s spatial derivative under the following momentum norm

$$\begin{aligned} ME_m[c_x-(c_h)_x] = \max _{1\le j\le N} \left|\frac{\int _{I_j}(c_x-(c_h)_x) w_h(x)~\text {d}x}{\Vert w_h\Vert _{L^1}}\right|,\quad \text{ where }\,\, w_h\in P^m(I_J), \end{aligned}$$

which measures the error of the approximation of $(c_h)_x$ to the solution’s spatial derivative $c_x$. The superconvergence of the chemoattractant variable c is required to maintain the optimal convergence for the cell density. Thus, in this section, we explore both the setting of $\beta _1=\frac{1}{2k(k+1)}$ and $\beta _1\ne \frac{1}{2k(k+1)}$ in the numerical flux (2.7b or 2.11b) for $P^k$ approximations, and further investigate the influence of $\beta _1$ on convergence orders on both uniform and nonuniform meshes. Specifically, we denote the coefficient $\beta _1$ for the cell density $\rho _h$ and chemoattractant $c_h$ by $\beta _{1\rho }$ and $\beta _{1c}$, respectively.

For the settings of the coefficient $\beta _0$, it was demonstrated in [3, 28, 30, 39] that the errors of the DDG methods stay almost the same for different choices of admissible coefficient $\beta _0$. Thus, in our numerical experiments, we fix $\beta _0=1$ for $P^0$, $\beta _0=2$ for $P^1$, $\beta _0=6$ for $P^2$ and $P^3$, and $\beta _0=10$ for $P^4$ and $P^5$ polynomials.

Example 4.1

(one-dimensional accuracy test) In this example, we follow [16] and consider the following one-dimensional KS equations

$$\begin{aligned} \rho _t+(c_x \rho )_x&=\rho _{xx}-\frac{2\rho }{2+\cos (x)}-\frac{(\cos (2x)+2\cos (x))\rho ^2}{(2+\cos (x))^2}, \quad x\in [0,2\pi ], \end{aligned}$$

(4.1a)

$$\begin{aligned} c_t&=c_{xx}-c+\rho -\frac{2c}{2+\cos (x)}, \qquad \qquad x\in [0,2\pi ], \end{aligned}$$

(4.1b)

with initial conditions $\rho (x,0)=c(x,0)=2+\cos x$ and Neumann boundary conditions. The exact solutions is

$$\begin{aligned} \rho (x,t)=c(x,t)=e^{-t}(2+\cos x). \end{aligned}$$

We apply the DDGIC scheme (2.6) to perform numerical simulations with $P^k (k=0,1,\dots ,5)$ polynomials up to $T=0.2$. The time step is set as

$$\begin{aligned} \Delta t = \frac{1}{\frac{1}{\text {cflc}\cdot \Delta x} + \frac{1}{\text {cfld}\cdot \Delta x^2}}, \end{aligned}$$

where $\text {cflc}$ and $\text {cfld}$ are the CFL numbers associated for the convection and diffusion terms, respectively. Specifically, we set $\text {cflc}=0.3$ and $\text {cfld}=0.1$ for $k=0, 1$, $\text {cflc}=0.2$ and $\text {cfld}=0.01$ for $k=2$, $\text {cflc}=0.1$ and $\text {cfld}=0.01$ for $k=3$, and $\text {cflc}=0.05$ and $\text {cfld}=0.001$ for $k=4, 5$.

For $k=0$ and $k=1$, the coefficient $\beta _1$ before the solution’s second derivative jump term does not contribute to the numerical flux calculation. Optimal first and second convergence orders are obtained for the DDGIC method. For $k=3$ and $k=5$ odd-degree approximations, different settings of $\beta _1$ achieve the same optimal order of accuracy. The $L^2$ and $L^\infty$ errors and orders are listed in Table 1 for uniform mesh and in Table 2 for nonuniform mesh, corresponding to the case of $\beta _1\ne \frac{1}{2k(k+1)}$. In particular, we take $\beta _1=\frac{1}{12}$ for $k=3$, and $\beta _1=\frac{1}{40}$ for $k=5$. The nonuniform mesh is generated from a 40% random perturbation of the uniform mesh. In particular, the right end of the cell $I_j$ is modified to be $x_{j+\frac{1}{2}}+40\%(r_{j+\frac{1}{2}}-0.5)\Delta x$, where $x_{j+\frac{1}{2}}$ is the uniform mesh cell right end with mesh size $\Delta x$. The random number $r_{j+\frac{1}{2}}$ is generated from the uniform distribution over the range of (0,1). It can be observed that both $\rho _h$ and $c_h$ achieve the optimal convergence order of $(k+1)$ regardless of whether the mesh is uniform or nonuniform.

For even-degree polynomial approximations on uniform mesh, we list the $L^2$ and $L^\infty$ errors and orders in Table 3 for $P^2$ approximation and in Table 4 for $P^4$ approximation, corresponding to different setting of $\beta _1$ chosen in the numerical fluxes for $\rho _h$ and $c_h$. We also list the errors and orders on nonuniform mesh in Tables 5 and 6. It can be observed that all the settings of $\beta _{1c}$ and $\beta _{1\rho }$ leads to the optimal convergence of order $(k+1)$ for $c_h$, while the choice of $\beta _{1c}=\frac{1}{2k(k+1)}$ leads to the optimal order convergence of $(k+1)$ for $\rho _h$. For $\beta _{1c}\ne \frac{1}{2k(k+1)}$, the convergence order gradually decreases to k. The optimal convergence of the DDGIC method to KS equations may relate to the superconvergence property of the method on its approximation to the solution’s derivative or gradient, i.e., $(c_h)_x$.

Table 1 One-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.1 at $t=0.2$ on uniform mesh

Table 2 One-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.1 at $t=0.2$ on nonuniform mesh

Table 3 One-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.1 at $t=0.2$ on uniform mesh

Table 4 One-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.1 at $t=0.2$ on uniform mesh

Table 5 One-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.1 at $t=0.2$ on nonuniform mesh

Table 6 One-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.1 at $t=0.2$ on nonuniform mesh

Example 4.2

(one-dimensional delta-shape approximation) In this example, we consider the one-dimensional KS equation (2.1) over the computational domain [-2, 2] with initial conditions

$$\begin{aligned} \rho (x,0)=\frac{400}{1+40x^2},~~~ c(x,0)=\frac{200}{1+20x^2}, \end{aligned}$$

(4.2)

and zero Neumann boundary conditions $\rho _x=c_x=0$. The initial condition for the cell density $\rho$ is symmetric and involves a sharp transition solution profile. The exact solution is close to a Dirac delta function at $x=0$.

We apply the DDGIC method with $P^3$ polynomials to simulate the evolution of the solutions up to $t=6\times 10^{-3}$. In Fig 1, we output the approximations of the cell density $\rho _h$ with $N=160$ and $N=320$.

The solution ensembles a Dirac delta function, even though it does not blow up in the one-dimensional case. The DDGIC method can sharply capture the spiky solution without oscillations. The result agree well with those in the literature.

Fig. 1

One-dimensional delta-shape approximation: cell density $\rho _h$ simulation for Example 4.2 at $t=6\times 10^{-3}$ with $P^3$ polynomials on $N=160$ (left) and $N=320$ (right)

Example 4.3

(two-dimensional accuracy test) In this example, we follow [16] and consider the following two-dimensional KS equations

$$\begin{aligned} \rho _t+ \nabla \cdot (\rho \nabla c)&=\triangle \rho -\frac{4\rho }{2+\cos (x+y)}-\frac{2\rho ^2(\cos (2(x+y))+2\cos (x+y))}{(2+\cos (x+y))^2}, \end{aligned}$$

(4.3a)

$$\begin{aligned} c_t&=\triangle c-c+\rho -\frac{4c}{2+\cos (x+y)}, \qquad ~~ (x,y)\in [0, 2\pi ]\times [0, 2\pi ], \end{aligned}$$

(4.3b)

with initial conditions $\rho (x,y,0)=c(x,y,0)=2+\cos (x+y)$ and Neumann boundary conditions. The exact solutions are

$$\begin{aligned} \rho _h(x,y,t)=c_h(x,y,t)=e^{-2t}{(2+\cos (x+y))}. \end{aligned}$$

We conduct accuracy tests of the DDGIC method (2.10) on rectangular meshes using $P^k (k=0,1,\dots ,4)$ polynomial approximations. The time step size is set as

$$\begin{aligned} \Delta t = \frac{1}{\frac{\max |c_x|}{\text {cflc}\cdot \Delta x} + \frac{\max |c_y|}{\text {cflc}\cdot \Delta y}+\frac{1}{\text {cfld}\cdot \Delta x^2}+\frac{1}{\text {cfld}\cdot \Delta y^2}}. \end{aligned}$$

Here, $\text {cflc}$ and $\text {cfld}$ are the CFL numbers for the convection and diffusion terms, respectively. We apply $\text {cflc}=0.3$ and $\text {cfld}=0.1$ for $k=0, 1$ piece wise constant and linear polynomials, $\text {cflc}=0.1$ and $\text {cfld}=0.01$ for $k=2,3$ piece wise quadratic and cubic polynomials, and $\text {cflc}=0.01$ and $\text {cfld}=0.001$ for $k=4$ the $P^4$ polynomials.

We investigate whether the accuracy of the DDGIC method is affected by the choice of $\beta _1$ in the numerical flux, especially $\beta _{1c}$ for the chemoattractant variable $c_h(x,y,t)$. First and second optimal convergence orders are achieved for low order approximations of $k=0$ and $k=1$. For high order odd-degree polynomial approximations, i.e., $k=3$, different $\beta _1$ all lead to the fourth order optimal convergence. The $L^2$ and $L^\infty$ errors and orders for $k=0,1,3$ are listed in Table 7. For $k=3$, we choose $\beta _1=\frac{1}{12}$ for which $\beta _1\ne \frac{1}{2k(k+1)}$.

The convergence orders of the DDGIC method are impacted by the choice of $\beta _{1c}$ for the chemoattractant variable, particularly for $k=2,4$ even-degree polynomial approximations. The $L^2$ and $L^\infty$ errors and orders with different settings of $\beta _1$ in the numerical fluxes for $\rho _h$ and $c_h$ are presented in Table 8 for $P^2$ approximations and in Table 9 for $P^4$ approximations. We observe again that all the settings of $\beta _{1c}$ and $\beta _{1\rho }$ result in optimal convergence orders for the chemical variable $c_h$, while the setting of $\beta _{1c}=\frac{1}{2k(k+1)}$ leads to the optimal order convergence of $(k+1)$. When $\beta _{1c} \ne \frac{1}{2k(k+1)}$, the convergence order gradually decreases to k-th order. The phenomena relate to the superconvergence property of the DDGIC method in its approximation to the solution’s gradient, specifically $(c_h)_x$ and $(c_h)_y$.

We also perform accuracy tests on nonuniform mesh generated from a 40% random perturbation to the uniform mesh, similar to the one-dimensional nonuniform mesh partitioning. We list the $L^2$ and $L^\infty$ errors and orders for $k=0,1,3$ in Table 10 ($\beta _1=\frac{1}{12}$ for $k=3$). Errors and orders for $k=2$ with different $\beta _1$ are presented in Table 11. Errors and orders for $k=4$ with different $\beta _1$ are listed in Table 12. The DDGIC method achieves the same convergence orders on nonuniform mesh as on uniform mesh.

Table 7 Two-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.3 at $t=0.2$ on uniform mesh

Table 8 Two-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.3 at $t=0.2$ on uniform mesh, and $P^2$ polynomial approximations

Table 9 Two-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.3 at $t=0.2$ on uniform mesh

Table 10 Two-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.3 at $t=0.2$ on nonuniform mesh

Table 11 Two-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.3 at $t=0.2$ on nonuniform mesh

Table 12 Two-dimensional accuracy test: $L^2$ and $L^\infty$ errors and orders of $\rho _h$ and $c_h$ for Example 4.3 at $t=0.2$ on nonuniform mesh

Example 4.4

(two-dimensional blow up case) In this example, we consider the two-dimensional KS equations (2.2) on the computational domain $[-2, 2]\times [-2, 2]$ with the following initial conditions

$$\begin{aligned} \rho (x,y,0)=\frac{400}{1+40(x^2+y^2)}, ~~~c(x,y,0)=\frac{200}{1+20(x^2+y^2)}, \end{aligned}$$

and homogeneous Neumann boundary conditions. The cell density corresponding to such a large initial will blow up in a finite time.

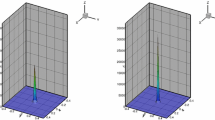
We apply $P^2$ polynomials to approximate the evolution of the solutions up to $t=6\times 10^{-4}$, at which a delta-shape or close to blow-up solution profile is present. The cell density $\rho _h$ approximation with $N=160$ is demonstrated in Fig. 2, in which twelve contour lines and the cross-section at $y=0$ are exported. The high order polynomial solutions are maintained positive at all time levels. The DDGIC method can capture the delta-shape solution evolution with high resolution and no oscillations. The DDGIC method simulations are similar to those in [16].

Fig. 2

Two-dimensional blow up case: cell density $\rho _h$ approximation with $P^2$ polynomials for Example 4.4. The contour (left) and the cross-section at $y=0$ (right) of $\rho _h$ at $t=6\times 10^{-4}$ corresponding to $N=160$ are exported

5 Conclusion

In this paper, we apply the DDGIC method to solve one-dimensional and two-dimensional KS chemotaxis models, which govern the evolution of cell density and chemoattractant concentration. Error estimates are established under suitable smoothness assumptions of the exact solutions. Numerical experiments are provided for both one-dimensional and two-dimensional examples using the DDGIC method with polynomials of degree k. The impact of different coefficient settings ($\beta _{1c},\beta _{1\rho }$) in the numerical fluxes are explored on uniform and nonuniform meshes. It is observed that for odd degrees k, the optimal convergence rates of order $(k+1)$ are achieved for both the cell density $\rho _h$ and the chemoattractant concentration $c_h$ with any admissible coefficients. For even degrees k, the optimal convergence rate of order $(k+1)$ is obtained for the cell density $\rho _h$ only with $\beta _{1c}=\frac{1}{2k(k+1)}$. The convergence rates decrease to k with $\beta _{1c}\ne \frac{1}{2k(k+1)}$. These insights contribute to developing more accurate and efficient numerical techniques for simulating chemotaxis phenomena.