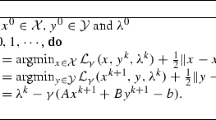1 Introduction

We consider the following separable convex minimization problem with linear constraints and its objective function is the sum of more than one functionn without coupled variables:

$$\begin{aligned} \min \, \left\{ \sum _{i=1}^m \theta _i(x_i) \,\bigg |\, \sum _{i=1}^m A_i x_i =b, \; x_i\in \mathcal {X}_i, \; i=1,\ldots , m \right\} , \end{aligned}$$
(1.1)

where \(\theta _i: {\mathfrak {R}}^{n_i}\rightarrow {\mathfrak {R}} \;(i=1,\ldots , m)\) are convex (not necessarily smooth) closed functions; \(A_i\in \mathfrak {R}^{l\times n_i}, b \in \mathfrak {R}^l\), and \(\mathcal {X}_i \subseteq \mathfrak {R}^{n_i}\;(i=1,\ldots ,m)\) are convex sets. The solution set of (1.1) is assumed to be nonempty throughout our discussions in this paper.

We are interested in the scenario where each function \(\theta _i\) may have some special properties; consequently, it is not suitable to treat (1.1) as a generic convex minimization model and ignore the individual properties of the functions in its objective when attempting to design an efficient algorithm for (1.1). Therefore, instead of applying the benchmark augmented Lagrangian method (ALM) in [14, 17] directly to (1.1), we are more interested in its splitting versions which embed the Jacobian (i.e., parallel) or Gauss–Seidel (i.e., serial) decomposition into the ALM partially or fully, depending on the speciality of (1.1). These splitting versions can treat the functions \(\theta _i\)’s individually; take advantage of their properties more effectively; and thus generate significantly easier subproblems.

Let \(\lambda \in \mathfrak {R}^l\) be the Lagrange multiplier associated with the linear equality constraint in (1.1) and the Lagrangian function of (1.1) be

$$\begin{aligned} L(x_1,x_2, \ldots , x_m,\lambda ) = \sum _{i=1}^m \theta _i(x_i) -\lambda ^T\left( \sum _{i=1}^m A_i x_i -b\right) , \end{aligned}$$
(1.2)

defined on \(\Omega := \mathcal {X}_1\times \mathcal {X}_2 \times \cdots \times \mathcal {X}_m \times \mathfrak {R}^l\). Then, the augmented Lagrangian function of (1.1) is

$$\begin{aligned} \mathcal {L}_{\beta }(x_1,x_2, \ldots , x_m,\lambda ) = \sum _{i=1}^m \theta _i(x_i) -\lambda ^T\left( \sum _{i=1}^m A_i x_i -b\right) + \frac{\beta }{2} \left\| \sum _{i=1}^m A_i x_i -b \right\| ^2, \end{aligned}$$
(1.3)

where \(\beta >0\) is a penalty parameter. The application of ALM to (1.1) with a Gauss–Seidel decomposition results in the scheme

$$\begin{aligned} \left\{ \! \begin{array}{l} x_1^{k+1} =\arg \min \left\{ \mathcal {L}_\beta \left( x_1,x_2^k,x_3^k,\ldots ,x_{m-1}^k, x_m^k,\lambda ^k\right) \;\big |\; x_1\in \mathcal {X}_1 \right\} ; \\ x_2^{k+1} =\arg \min \left\{ \mathcal {L}_\beta \left( x_1^{k+1},x_2,x_3^k \ldots ,x_{m-1}^k, x_m^k,\lambda ^k\right) \; \big | x_2\in \mathcal {X}_2 \right\} ;\\ \qquad \quad \ldots \\ x_i^{k+1} =\arg \min \left\{ \mathcal {L}_\beta \left( x_1^{k+1},x_2^{k+1},\ldots ,x_{i-1}^{k+1},x_i,x_{i+1}^k,\ldots ,x_m^k,\lambda ^k\right) \;\big | x_i\in \mathcal {X}_i \right\} ;\\ \qquad \quad \ldots \\ x_m^{k+1}= \arg \min \left\{ \mathcal {L}_\beta \left( x_1^{k+1},x_2^{k+1}, \ldots ,x_{m-1}^{k+1}, x_m,\lambda ^k\right) \; \big | x_m\in \mathcal {X}_m\right\} ; \\ {\lambda }^{k+1} = \lambda ^k - \beta \left( \sum _{j=1}^{m}A_j x_j^{k+1}-b\right) . \end{array} \right. \end{aligned}$$
(1.4)

When the special case where \(m=2\) in (1.1) is considered, the scheme (1.4) reduces to the alternating direction method of multipliers (ADMM), a method originally proposed in [5] and now a very popular method in various fields (see, e.g. [1, 3, 4] for review papers). Recently, it was shown in [2] that the scheme (1.4) is not necessarily convergent when \(m\ge 3\) if no further assumptions are made for (1.1). An efficient remedy is to correct the output of (1.4) by some correction steps; some prediction–correction methods based on (1.4) were thus proposed, see e.g. [11, 13]. Notice that the variables \(x_i\)’s are not treated equally in (1.4), because they are updated in serial order. The correction steps in [11, 13] can be regarded as a re-weighting among the variables; and thus compensate the asymmetry of variables appearing in (1.4). As a result, this type of prediction–correction methods can preserve the simplicity of subproblems by using (1.4) as the predictor, and simultaneously guarantee the convergence by adopting an appropriate correction step.

The resulting subproblems by applying the ALM to (1.1) can also be decomposed in the Jacobian fashion, and the scheme is

$$\begin{aligned} \left\{ \! \begin{array}{l} x_1^{k+1} =\arg \min \left\{ \mathcal {L}_\beta \left( x_1,x_2^k,x_3^k,\ldots ,x_{m-1}^k, x_m^k,\lambda ^k\right) \;\big |\; x_1\in \mathcal {X}_1 \right\} ; \\ x_2^{k+1} =\arg \min \left\{ \mathcal {L}_\beta \left( x_1^{k},x_2,x_3^k \ldots ,x_{m-1}^k, x_m^k,\lambda ^k\right) \; \big | x_2\in \mathcal {X}_2 \right\} ;\\ \qquad \quad \ldots \\ x_i^{k+1} =\arg \min \left\{ \mathcal {L}_\beta \left( x_1^{k},x_2^{k},\ldots ,x_{i-1}^{k},x_i,x_{i+1}^k,\ldots ,x_m^k,\lambda ^k\right) \; \big | x_i\in \mathcal {X}_i \right\} ;\\ \qquad \quad \ldots \\ x_m^{k+1}= \arg \min \left\{ \mathcal {L}_\beta \left( x_1^{k},x_2^{k}, \ldots ,x_{m-1}^{k}, x_m,\lambda ^k\right) \; \big | x_m\in \mathcal {X}_m\right\} ; \\ {\lambda }^{k+1} = \lambda ^k - \beta \left( \sum _{j=1}^{m}A_j x_j^{k+1}-b\right) . \end{array} \right. \end{aligned}$$
(1.5)

One advantage of (1.5) is that the decomposed subproblems are eligible for parallel computation; it thus has potential applications for large-scale or big-data scenarios of the model (1.1). The subproblems in (1.4) must be solved sequentially while those in (1.5) could be solved in parallel; but these subproblems are of the same level of difficulty as the objective function of each of them consists of one \(\theta _i(x_i)\) and a quadratic term of \(x_i\). Despite the eligibility of parallel computation, the scheme (1.5), however, might be divergent even for the special case of \(m=2\), as shown in [10]. This can be understood easily: the Jacobian decomposition of ALM does not use the latest iterative information and it is a loose approximation to the real objective function of the ALM. This can also explain intuitively why the Gauss–Seidel decomposition of ALM for the special case of (1.1) with \(m=2\) (which is exactly the ADMM) is convergent, while the Jacobian decomposition of ALM is not.

In the literature, e.g., [8–10], it was also suggested to correct the output of (1.5) by some correction steps so as to ensure the convergence. Some prediction–correction methods based on (1.5) were thus proposed; and their efficiency has been verified in various contexts. For prediction–correction methods based on (1.5), simple correction steps are preferred. For example, for some special cases of (1.1) such as some low-rank optimization models, if the correction steps are too complicated, then they may not be able to preserve well the low-rank structure of the iterates. Some numerical results of this kind of applications can be found in [12, 16, 19]. It is thus interesting to know if it is possible to ensure the convergence of (1.5) without any correction step. Again, by the intuition that the scheme (1.5) is divergent due to the fact that the Jacobian decomposition in the augmented Lagrangian function sacrifices too much accuracy to approximate the real ALM subproblem at each iteration, we consider it too loose or aggressive to take the output (1.5) directly as a new iterate. Instead, we want to keep the new iterate “close” to the last iterate to some extent. One way to do so is to apply the very classical proximal point algorithm in [15, 18] and regularize each subproblem in (1.5) proximally. We thus propose the following proximal version of the Jacobian decomposition of ALM for (1.1):

(1.6)

The proximal coefficient \(s>0\) in (1.6) plays the role of controlling the proximity of the new iterate to the last one. We refer to [15, 18] and many others in the PPA literature for deep discussions on the proximal coefficient. In fact, how to choose the proximal coefficient s is very tricky. An obvious fact is that the proximally regularized objective function reduces to the original one when \(s=0\). Thus, given the divergence of (1.5) which corresponds to (1.6) with \(s=0\), the value of s should not be too small; or it must be “sufficiently large” in order to ensure the convergence of (1.6).

Later, we will show that the scheme (1.6) is just an application of the PPA to the model (1.1) with a customized proximal coefficient in metric form. Therefore, from the PPA literature, we can easily show that the convergence of (1.6) can be ensured if the proximal coefficient s satisfies \(s\ge m-1\). Moreover, the PPA illustration of (1.6) immediately implies the convergence of (1.6) and its worst-case convergence rate measured by the iteration complexity in both the ergodic and nonergodice senses, by existing results in the literature (e.g. [6, 7, 15, 18]). Thus theoretical analysis for its convergence can be skipped. Studying the scheme (1.6) in optimization form, its close relationship to the PPA is not clear. But we will show that their close relationship can be very easily demonstrated via the variational inequality context; or equivalently, via the first-order optimality conditions of the minimization problems in (1.6). Therefore, our analysis will be essentially conducted in the variational inequality context.

Moreover, we will show that the proximal Jacobian decomposition of ALM (1.6) is closely related to the interesting application of the ADMM in [20]. In [20], it was suggested to reformulate the model (1.1) as a convex minimization problem with two blocks of functions and variables first, and then apply the original ADMM to the two-block reformulation. We will show that the ADMM application in [20] differs from the special case of (1.6) with \(s=m-1\) only in that its penalty parameter \(\beta \) is m time larger than that of (1.6).

2 Preliminaries

In this section, we review some preliminaries that are useful in our analysis.

2.1 The Variational Inequality Reformulation of (1.1)

Let \(\bigl (x_1^*,x_2^*,\ldots , x_m^*,\lambda ^*\bigr )\) be a saddle point of the Lagrange function (1.2). Then we have the following saddle-point inequalities

$$\begin{aligned} {{\displaystyle {L_{\lambda \in \mathfrak {R}^l}}}}\left( x_1^*,x_2^*,\ldots ,x_m^*,\lambda \right)\le & {} L\left( x_1^*,x_2^*,\ldots , x_m^*,\lambda ^*\right) \nonumber \\\le & {} L_{\Bigl (\!\!\!\begin{array}{c} x_i\in \mathcal {X}_i \\ i=1,\ldots , m \end{array}\!\!\!\Bigr )}\left( x_1,x_2, \ldots ,x_m,\lambda ^*\right) . \end{aligned}$$
(2.1)

Setting \((x_1, \ldots , x_{i-1}, x_i,x_{i+1}, \ldots , x_m,\lambda ^*) = (x_1^*, \ldots , x_{i-1}^*, x_i,x_{i+1}^*, \ldots , x_m^*,\lambda ^*)\) in the second inequality in (2.1) for \(i=1,2,\ldots ,m\), we get

$$\begin{aligned} x_i^*\in \mathcal {X}_i, \quad \theta _i(x_i) - \theta _i\left( x_i^*\right) + \left( x_i-x_i^*\right) ^T\left( -A_i^T\lambda ^*\right) \ge 0, \quad \forall x_i\in \mathcal {X}_i, \quad i=1, \ldots , m. \end{aligned}$$

On the other hand, the first inequality in (2.1) means

$$\begin{aligned} \lambda ^*\in \mathfrak {R}^l, \quad (\lambda - \lambda ^*)^T\left( \sum _{i=1}^m A_ix_i^*-b\right) \ge 0, \quad \forall \quad \lambda \in \mathfrak {R}^l. \end{aligned}$$

Recall \(\Omega = \mathcal {X}_1\times \mathcal {X}_2 \times \cdots \times \mathcal {X}_m \times \mathfrak {R}^l\). Thus, finding a saddle point of \(L(x_1,x_2, \ldots , x_m,\lambda )\) is equivalent to finding a vector \(w^*=(x_1^*,x_2^*,\ldots ,x_m^*,\lambda ^*) \in \Omega \) such that

$$\begin{aligned} \begin{array}{ll} \left\{ \begin{array}{rl} \theta _1(x_1) -\theta _1\left( x_1^*\right) + \left( x_1- x_1^*\right) ^T \left( - A_1^T\lambda ^*\right) &{}\ge 0, \quad \forall \, x_1\in \mathcal {X}_1,\\ \theta _2(x_2) -\theta _2\left( x_2^*\right) + \left( x_2- x_2^*\right) ^T \left( - A_2^T\lambda ^*\right) &{}\ge 0, \quad \forall \, x_2\in \mathcal {X}_2, \\ \qquad \ldots \ldots \\ \theta _i(x_i) -\theta _i \left( x_i^*\right) + \left( x_i- x_i^*\right) ^T \left( -A_i^T\lambda ^*\right) &{}\ge 0, \quad \forall \, x_i\in \mathcal {X}_i, \\ \qquad \ldots \ldots \\ \theta _m(x_m) -\theta _m\left( x_m^*\right) + \left( x_m- x_m^*\right) ^T \left( - A_m^T\lambda ^*\right) &{}\ge 0, \quad \forall \, x_m\in \mathcal {X}_m, \\ \left( \lambda -\lambda ^*\right) ^T\left( \sum _{i=1}^m A_ix_i^* - b\right) &{}\ge 0, \quad \forall \lambda \in \mathfrak {R}^l. \end{array} \right. \end{array} \end{aligned}$$
(2.2)

More compactly, the inequalities in (2.2) can be written into the following mixed variational inequality (MVI):

$$\begin{aligned} \hbox {MVI}\,(\theta ,F,\Omega )\quad \theta (x) - \theta (x^*) + (w-w^*)^T F(w^*) \ge 0, \quad \forall \, w\in \Omega , \end{aligned}$$
(2.3)

with

$$\begin{aligned} x=\left( \begin{array}{c} x_1 \\ x_2 \\ \vdots \\ x_m \end{array}\right) , \quad \theta (x) =\sum _{i=1}^m\theta _i(x_i), \quad w=\left( \begin{array}{c} x_1 \\ x_2\\ \vdots \\ x_m \\ \lambda \end{array} \right) , \quad F(w)=\left( \begin{array}{c}-A_1^T\lambda \\ -A_2^T\lambda \\ \vdots \\ -A_m^T\lambda \\ \sum \nolimits _{i=1}^m A_ix_i - b \end{array} \right) . \end{aligned}$$
(2.4)

It is trivial to verify that the mapping F(w) given in (2.4) is monotone under our assumptions onto (1.1).

As we have mentioned, our analysis will be conducted in the variational inequality context. So, the MVI reformulation (2.3) is the starting point for further analysis.

2.2 Proximal Point Algorithm

Applying the classical proximal point algorithm (PPA) in [15, 18] to the MVI (2.3), we obtain the scheme

$$\begin{aligned}&w^{k+1} \in \Omega , \quad \theta (x) -\theta (x^{k+1}) + (w-w^{k+1})^T \big ( F(w^{k+1}) + G(w^{k+1} -w^k) \big ) \ge 0,\nonumber \\&\quad \forall \, w\in \Omega , \end{aligned}$$
(2.5)

where \(G \in \mathfrak {R}^{(\sum _{i=1}^m n_i+l)\times (\sum _{i=1}^m n_i+l)}\) is the proximal coefficient in metric form and it is required to be positive semi-definite. The most usual choice is to choose G as a diagonal matrix with the same or different entries. In [6], some customized block-wise choices of the matrix G were suggested in accordance with the special structure of the function \(\theta (x)\) and the mapping F(w) in (2.4) to yield some efficient splitting methods for convex minimization and saddle-point models.

3 The Scheme (1.6) is a Customized Application of the PPA

Now, we show that the proximal Jacobian decomposition of ALM (1.6) is a special case of the PPA (2.5) with a particular matrix G. The positive semi-definiteness condition of G thus provides us a sufficient condition to ensure the convergence of (1.6).

We first observe the first-order optimality conditions of the minimization problems in (1.6). More specifically, the solution \(x_i^{k+1}\in \mathcal {X}_i\) of the \(x_i\)-subproblem in (1.6) can be expressed as

$$\begin{aligned} x_i^{k+1}= & {} \arg \min \left\{ \theta _i(x_i) -(\lambda ^k)^TA_ix_i + \frac{\beta }{2}\left\| A_i\left( x_i-x_i^k\right) +\left( \sum _{j=1}^mA_jx_j^k -b\right) \right\| ^2\right. \nonumber \\&\left. +\,\frac{s\beta }{2}\left\| A_i\left( x_i-x_i^k\right) \right\| ^2 \, \big |\, x_i\in \mathcal {X}_i \right\} , \end{aligned}$$
(3.1)

and the inequality

$$\begin{aligned}&\theta _i(x_i) -\theta _i\left( x_i^{k+1}\right) + \left( x_i-x_i^{k+1}\right) ^T \left\{ -A_i^T\left[ \lambda ^k -\beta \left( \sum _{j=1}^mA_jx_j^k -b\right) \right] \right. \nonumber \\&\left. \quad +\, (s+1) \beta A_i^TA_i\left( x_i^{k+1} -x_i^k\right) \right\} \ge 0 \end{aligned}$$
(3.2)

holds for all \(x_i\in \mathcal {X}_i\). Note that it follows from (1.6) that

$$\begin{aligned} \lambda ^k ={\lambda }^{k+1} + \beta \left( \sum _{j=1}^mA_jx_j^{k+1} -b\right) . \end{aligned}$$
(3.3)

Substituting (3.3) into (3.2), we have

$$\begin{aligned}&\theta _i(x_i) -\theta _i\left( x_i^{k+1}\right) + \left( x_i-x_i^{k+1}\right) ^T \left\{ -A_i^T{\lambda }^{k+1} + (s+1) \beta A_i^TA_i\left( x_i^{k+1} -x_i^k\right) \right. \nonumber \\&\quad \left. -\,\beta A_i^T \left( \sum _{j=1}^m A_j\left( x_j^{k+1} - x_j^k\right) \right) \right\} \ge 0. \end{aligned}$$
(3.4)

Moreover, the Eq. (3.3) can be written as

$$\begin{aligned} \left( \sum _{j=1}^mA_jx_j^{k+1} -b\right) + \frac{1}{\beta }({\lambda }^{k+1} -\lambda ^k) =0, \end{aligned}$$

or further as

$$\begin{aligned} {\lambda }^{k+1}\in {\mathfrak {R}^l}, \quad (\lambda - {\lambda }^{k+1})^T\left\{ \left( \sum _{j=1}^mA_jx_j^{k+1} -b\right) + \frac{1}{\beta }({\lambda }^{k+1} -\lambda ^k)\right\} \ge 0, \quad \forall \, \lambda \in {\mathfrak {R}^l}.\nonumber \\ \end{aligned}$$
(3.5)

Combining (3.4) and (3.5) together, we get \(w^{k+1}=(x_1^{k+1},\ldots ,x_m^{k+1},{\lambda }^{k+1})\in \Omega \) such that

$$\begin{aligned}&\theta (x) -\theta (x^{k+1}) + \left( \begin{array}{c} x_1-x_1^{k+1} \\ \vdots \\ x_m-x_m^{k+1} \\ \lambda - {\lambda }^{k+1} \end{array}\right) ^T \left\{ \left( \begin{array}{c} - A_1^T{\lambda }^{k+1} \\ \vdots \\ - A_m{\lambda }^{k+1} \\ \sum _{j=1}^m A_j x_j^{k+1} -b \end{array} \right) \qquad \qquad \right. \nonumber \\&\quad + \left. \left( \begin{array}{c} (s+1) \beta A_1^TA_1\left( x_1^{k+1}-x_1^k\right) -\beta A_1^T\sum _{j=1}^m A_j\left( x_j^{k+1}-x_j^k\right) \\ \vdots \\ (s+1) \beta A_m^TA_m \left( x_m^{k+1}-x_m^k\right) -\beta A_m^T\sum _{j=1}^m A_j\left( x_j^{k+1}-x_j^k\right) \\ \frac{1}{\beta }({\lambda }^{k+1} -\lambda ^k) \end{array} \right) \right\} \ge 0,\quad \forall \, w\in \Omega .\nonumber \\ \end{aligned}$$
(3.6)

Therefore, recalling the notation in (2.4), the inequality (3.6) shows that the scheme (1.6) can be written as the PPA scheme (2.5) where the matrix G is given by

$$\begin{aligned} G=\left( \begin{array}{cccc} (s+1)\beta A_1^TA_1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} (s+1)\beta A_m^TA_m &{} 0 \\ 0 &{} \cdots &{} 0 &{} \frac{1}{\beta }I_l \end{array} \right) - \beta \left( \begin{array}{cccc} A_1^TA_1 &{} \cdots &{} A_1^T A_m &{} 0\\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ A_m^TA_1 &{} \cdots &{} A_m^TA_m &{} 0 \\ 0 &{} \cdots &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$
(3.7)

Thus, proving the convergence of the scheme (1.6) reduces to ensuring the convergence of the PPA (2.5) with the specific matrix G given in (3.7). As analyzed in [6], the convergence of the PPA (2.5) is ensured if the proximal coefficient G is positive semi-definite. Note that the matrix G given in (3.7) can be written as

$$\begin{aligned} G = \mathcal {P}^T \left( \begin{array}{ccccc} sI &{} -I &{} \cdots &{} -I &{} 0 \\ -I &{} sI &{} \ddots &{} \vdots &{} \vdots \\ \vdots &{} \ddots &{} \ddots &{} -I &{} 0\\ -I &{} \cdots &{} -I &{} sI &{} 0 \\ 0 &{} \cdots &{} 0 &{} 0 &{} I \end{array} \right) \mathcal {P} \end{aligned}$$

with

$$\begin{aligned} \mathcal {P}= \hbox {diag}\left( \sqrt{\beta } A_1,\ldots , \sqrt{\beta }A_m,\sqrt{\frac{1}{\beta }}I_l\right) . \end{aligned}$$

Therefore, G is positive semi-definite if \(s\ge m-1\). We thus have the following theorem immediately.

Theorem 3.1

The proximal Jacobian decomposition of ALM (1.6) is convergent if \(s\ge m-1\).

Remark 3.2

As long as the convergence of (1.6) can be ensured, we prefer smaller values of s in order to render “larger” step sizes to accelerate its convergence (see more explanation in the conclusions). Hence, we recommend to take \(s=m-1\) to implement the scheme (1.6). When \(s=m-1\), the matrix G in (3.7) becomes

$$\begin{aligned} G=\left( \begin{array}{cccc} m\beta A_1^TA_1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} m\beta A_m^TA_m &{} 0 \\ 0 &{} \cdots &{} 0 &{} \frac{1}{\beta }I_l \end{array} \right) - \beta \left( \begin{array}{cccc} A_1^TA_1 &{} \cdots &{} A_1^T A_m &{} 0\\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ A_m^TA_1 &{} \cdots &{} A_m^TA_m &{} 0 \\ 0 &{} \cdots &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$
(3.8)

In addition, the \(x_i\)-subproblem in (1.6) is reduced to [see the optimal condition of (3.2)]

$$\begin{aligned} x_i^{k+1} = \arg \min \left\{ \theta _i(x_i) + \frac{\beta }{2m} \left\| m A_i\left( x_i-x_i^k\right) + \left[ \left( \sum _{j=1}^mA_jx_j^k -b\right) -\frac{1}{\beta }\lambda ^k \right] \right\| ^2 \, \big |\, x_i\in \mathcal {X}_i \right\} . \end{aligned}$$

Then, it is easy to see that scheme (1.6) with \(s=m-1\) is just a special case of Algorithm 8.1 in [6].

Remark 3.3

For the special case of (1.1) where \(m=1\), it follows from \(s=m-1\) that \(s=0\). Then, the scheme (1.6) recovers the original ALM in [14, 17]. In this sense, the scheme (1.6) can also be regarded as a generalized version of the ALM for the multiple-block separable convex minimization model (1.1).

4 The Relationship of (1.6) to the ADMM in [20]

In [20], by introducing the notations:

$$\begin{aligned} \theta (x)= & {} \sum _{i=1}^m\theta _i(x_i), \qquad \mathcal {A}= \hbox {diag}(A_1, A_2, \ldots , A_m),\\ x= & {} \left( \begin{array}{c} x_1\\ x_2\\ \vdots \\ x_m \end{array} \right) \; (x_i\in \mathcal {X}_i, i=1,\ldots , m),\;\; y=\left( \begin{array}{c} y_1\\ y_2\\ \vdots \\ y_m \end{array} \right) \; (y_i\in \mathfrak {R}^l, i=1,\ldots , m),\\ \mathcal {X}= & {} \mathcal {X}_1\times \mathcal {X}_2\times \ldots \mathcal {X}_m,\;\;\;\hbox {and} \;\; \mathcal {Y}= \left\{ y=(y_1,\ldots , y_m) \, \big |\, \sum _{i=1}^m y_i=b\right\} , \end{aligned}$$

the model (1.1) is reformulated as the following two-block separable convex minimization model:

$$\begin{aligned} \begin{array}{rl} \min &{} \theta (x) \\ &{} \mathcal {A} x -y = 0, \\ &{} x\in \mathcal {X}, \; y\in \mathcal {Y}. \end{array} \end{aligned}$$
(4.1)

Thus, the original ADMM is applicable.

For the reformulation (4.1), we denote by \(z=(z_1, z_2,\ldots , z_m)\) the Lagrangian multiplier (each \(z_i\in \mathfrak {R}^l\) is associated with the linear constraint \(A_ix_i-y_i=0\)); and by \(\alpha >0\) the penalty parameter. Then the augmented Lagrangian function of (4.1) is

$$\begin{aligned} \mathcal {L}_{\alpha }(x,y, z) = \theta (x) -z^T(\mathcal {A}x-y) +\frac{\alpha }{2}\Vert \mathcal {A}x-y\Vert ^2, \end{aligned}$$

which is defined on \(\mathcal {X}\times \mathcal {Y} \times \mathcal {R}^{ml}\). Applying the original ADMM to (4.1), we obtain the scheme

figure a

In the next, we will show that the ADMM application (4.2) is closely related to the scheme (1.6) with \(s=m-1\). The bridge connecting these two schemes which seem completely different is again the MVI (2.2). More specifically, we will show the ADMM application (4.2) is also a special case of the PPA (2.5); and by comparing it with the PPA illustration of (1.6), we find that it coincides with the scheme (1.6) with \(s=m-1\) if we take \(\alpha =m\beta \) in (4.2).

4.1 A Simpler Representation of (4.2)

Let us take a deeper look at the subproblems in (4.2) and derive a simpler representation of (4.2). First, using the structure of the matrix \(\mathcal {A}\), the variables \(x^{k+1}=(x_1^{k+1}, x_2^{k+1},\ldots , x_m^{k+1})\) are obtained by solving the following subproblems which are eligible for parallel computation:

$$\begin{aligned}&x_i^{k+1} = \arg \min \left\{ \theta _i(x_i) -(z_i^k)^T\left( A_ix_i - y_i^k\right) + \frac{\alpha }{2} \left\| A_ix_i - y_i^k\right\| ^2 \, \big |\, x_i\in \mathcal {X}_i \right\} ,\nonumber \\&\quad i=1,\ldots ,m. \end{aligned}$$
(4.3)

Note that the first-order optimality condition of (4.3) is characterized by

$$\begin{aligned}&x_i^{k+1}\in \mathcal {X}_i, \quad \theta _i(x_i) - \theta _i\left( x_i^{k+1}\right) + \left( x_i - x_i^{k+1}\right) ^T \left( - A_i^T z_i^k + \alpha A_i^T\left( A_i x_i^{k+1} -y_i^k\right) \right) \ge 0, \nonumber \\&\quad \forall \,x_i\in \mathcal {X}_i. \end{aligned}$$
(4.4)

Second, for the y-subproblem in (4.2), we have

$$\begin{aligned} y^{k+1}= & {} \arg \min \left\{ -(z^k)^T(\mathcal {A}x^{k+1}-y) + \frac{\alpha }{2} \Vert \mathcal {A}x^{k+1} - y\Vert ^2 \, \big |\, y\in \mathcal {Y} \right\} \nonumber \\= & {} \arg \min \left\{ \frac{\alpha }{2} \left\| \mathcal {A}x^{k+1} -y - \frac{1}{\alpha } z^k \right\| ^2 \, \big |\, y\in \mathcal {Y} \right\} \nonumber \\= & {} \arg \min \left\{ \frac{\alpha }{2} \left\| y- \left( \mathcal {A}x^{k+1} - \frac{1}{\alpha } z^k\right) \right\| ^2 \,\big |\, y\in \mathcal {Y} \right\} . \end{aligned}$$
(4.5)

Let \(\eta \in {\mathfrak {R}^l}\) be the Lagrangian multiplier for the linear constraint \(\sum _{i=1}^m y_i=b\) in the minimization problem

$$\begin{aligned} \min \left\{ \frac{1}{2} \Vert y- \left( \mathcal {A}x^{k+1} - \frac{1}{\alpha } z^k\right) \Vert ^2\, \big |\, \sum _{i=1}^m y_i=b\right\} . \end{aligned}$$

Based on the optimality condition of the above subproblem, we have

$$\begin{aligned} \left\{ \begin{array}{l} \left( \begin{array}{c} y^{k+1}_1\\ y^{k+1}_2\\ \vdots \\ y^{k+1}_m \end{array} \right) - \left( \begin{array}{c} A_1x^{k+1}_1 - z_1^k/\alpha \\ A_2x^{k+1}_2 - z_2^k/\alpha \\ \vdots \\ A_my^{k+1}_m - z_m^k/\alpha \end{array} \right) - \left( \begin{array}{c} \eta \\ \eta \\ \vdots \\ \eta \end{array} \right) = \left( \begin{array}{c} 0\\ 0\\ \vdots \\ 0 \end{array} \right) , \\ \\ \quad y_1^{k+1} + y_2^{k+1} + \cdots + y_m^{k+1} =b. \end{array} \right. \end{aligned}$$
(4.6)

From the above system of linear equations, we get

$$\begin{aligned} \left\{ \begin{array}{l} \sum _{i=1}^m y_i^{k+1} -\sum _{i=1}^m A_ix_i^{k+1} + \frac{1}{\alpha } \sum _{i=1}^m z_i^k =m\eta , \\ \sum _{i=1}^m y_i^{k+1} =b. \end{array} \right. \end{aligned}$$

and thus

$$\begin{aligned} \eta = \frac{1}{m\alpha } \sum _{j=1}^m z_j^k - \frac{1}{m} \left( \sum _{j=1}^m A_jx_j^{k+1} -b \right) . \end{aligned}$$

Substituting it into (4.6), we obtain

figure b

Last, for the updating formula for the multiplier \(z^{k+1}\) in (4.2), by using the structure of \(\mathcal {A}\), it can be written as

$$\begin{aligned} z_i^{k+1} = z_i^k - \alpha \bigl ( A_ix_i^{k+1} - y_i^{k+1}\bigr ), \quad i=1,\ldots , m. \end{aligned}$$
(4.8)

It follows from (4.7a) that

$$\begin{aligned} A_ix_i^{k+1} - y_i^{k+1} = \frac{1}{\alpha } z_i^k -\eta , \quad i=1,\ldots , m. \end{aligned}$$

Substituting it into (4.8), we obtain

$$\begin{aligned} z_i^{k+1} = z_i^k - \alpha \left( \frac{1}{\alpha } z_i^k -\eta \right) = \alpha \eta , \quad i=1,\ldots , m. \end{aligned}$$
(4.9)

Thus, for \(k >0\), every entry of the vector \(z^k\) is equal, i. e.,

$$\begin{aligned} z_1^k =z_2^k =\cdots = z_m^k. \end{aligned}$$
(4.10)

Using this fact in (4.7), we get

$$\begin{aligned} y_i^{k+1} = A_ix_i^{k+1} - \frac{1}{m} \left( \sum _{j=1}^m A_jx_j^{k+1} -b \right) , \quad i=1,\ldots , m. \end{aligned}$$
(4.11)

Substituting it into (4.8), it becomes

$$\begin{aligned} z_i^{k+1} = z_i^k - \frac{\alpha }{m} \left( \sum _{j=1}^m A_jx_j^{k+1} -b \right) , \quad i=1,\ldots , m. \end{aligned}$$
(4.12)

Using (4.3), (4.11) and (4.12), the procedure (4.2) becomes

figure c

Recall (4.11), we have

$$\begin{aligned} y_i^k = A_ix_i^k - \frac{1}{m} \left( \sum _{j=1}^m A_jx_j^k -b \right) . \end{aligned}$$

Substituting it into (4.13a), and each \(z_i\in \mathfrak {R}^l\) in (4.13) by \(\lambda \in \mathfrak {R}^l\) (because each \(z_i^k\) is equal), the scheme (4.2) can be written as the following simpler form:

figure d

4.2 The ADMM (4.2) is an Application of PPA

Now, we show that the scheme (4.14) is also an application of the PPA (2.5). Hence, we show the close relationship between the ADMM scheme (4.2) and the proximal Jacobian decomposition scheme (1.6).

The solution of the \(x_i\)-subproblem in (4.14a) is characterized by

$$\begin{aligned}&\theta _i(x_i) - \theta _i(x_i^{k+1}) + \left( x_i - x_i^{k+1}\right) ^T \left\{ - A_i^T \lambda ^k + \alpha A_i^T\left[ A_i\left( x_i^{k+1}-x_i^k\right) \right. \right. \\&\left. \left. \quad +\frac{1}{m}\left( \sum _{j=1}^m A_jx_j^k -b \right) \right] \right\} \ge 0, \; \forall \, x_i\in \mathcal {X}_i. \end{aligned}$$

By using (4.14b), the above inequality can be rewritten as

$$\begin{aligned}&\theta _i(x_i) - \theta _i\left( x_i^{k+1}\right) + \left( x_i - x_i^{k+1}\right) ^T\left\{ - A_i^T \lambda ^{k+1} + \alpha A_i^T\left[ A_i\left( x_i^{k+1}-x_i^k\right) \right. \right. \nonumber \\&\quad \left. \left. - \frac{1}{m}\sum _{j=1}^m A_j\left( x_j^{k+1} -x_j^k\right) \right] \right\} \ge 0. \end{aligned}$$
(4.15)

In addition, (4.14b) can be written as

$$\begin{aligned}&\lambda ^{k+1}\in \mathfrak {R}^l, \quad (\lambda - \lambda ^{k+1})^T \left\{ \left( \sum _{j=1}^m A_jx_j^{k+1} -b \right) + \frac{m}{\alpha }(\lambda ^{k+1} - \lambda ^k) \right\} \ge 0,\nonumber \\&\quad \forall \lambda \in \mathfrak {R}^l. \end{aligned}$$
(4.16)

Combining (4.15) and (4.16) yields

$$\begin{aligned}&w^{k+1}\in \Omega , \quad \theta (x) -\theta (x^{k+1}) + \left( \begin{array}{c} x_1-x_1^{k+1}\\ \vdots \\ x_m-x_m^{k+1}\\ \lambda - {\lambda }^{k+1} \end{array}\right) ^T \left\{ \left( \begin{array}{c} - A_1^T{\lambda }^{k+1} \\ \vdots \\ - A_m^T{\lambda }^{k+1} \\ \sum _{j=1}^m A_j {x}_j^{k+1} -b \end{array} \right) \right. \nonumber \\&\quad +\, \left. \left( \begin{array}{c} \alpha A_1^TA_1\left( x_1^{k+1}-x_1^k\right) - \frac{\alpha }{m} A_1^T\sum _{j=1}^m A_j\left( x_j^{k+1}-x_j^k\right) \\ \vdots \\ \alpha A_m^TA_m\left( x_m^{k+1}-x_m^k\right) - \frac{\alpha }{m} A_m^T\sum _{j=1}^m A_j\left( x_j^{k+1}-x_j^k\right) \\ \frac{m}{\alpha }({\lambda }^{k+1} -\lambda ^k) \end{array} \right) \right\} \ge 0, \quad \forall \, w\in \Omega .\nonumber \\ \end{aligned}$$
(4.17)

Recall the notations in (2.4). The following theorem follows from the inequality (4.17) immediately.

Theorem 4.1

The scheme (4.14) is an application of the PPA (2.5) with the matrix G given by

$$\begin{aligned} G=\left( \begin{array}{cccc} \alpha A_1^TA_1 &{} 0 &{} \cdots &{} 0 \\ 0 &{} \ddots &{} \ddots &{} \vdots \\ \vdots &{} \ddots &{} \alpha A_m^TA_m &{} 0 \\ 0 &{} \cdots &{} 0 &{} \frac{m}{\alpha }I_l \end{array} \right) - \frac{\alpha }{m} \left( \begin{array}{cccc} A_1^TA_1 &{} \cdots &{} A_1^T A_m &{} 0\\ \vdots &{} \ddots &{} \vdots &{} \vdots \\ A_m^TA_1 &{} \cdots &{} A_m^TA_m &{} 0 \\ 0 &{} \cdots &{} 0 &{} 0 \end{array} \right) . \end{aligned}$$
(4.18)

4.3 The Relationship of (1.6) to the ADMM (4.2)

Based on our previous analysis, it is clear to see that the matrix G in (4.18) with \(\alpha =\beta m\) coincides with that defined in (3.8). We summarize the relationship between the schemes (1.6) and (4.2) in the following theorem.

Theorem 4.2

The ADMM scheme (4.2) proposed in [20] for solving the model (1.1) with \(\alpha =m\beta \) is the same as the proximal Jacobian decomposition of ALM scheme (1.6) with \(s=m-1\).

5 Conclusions

In this paper, we further studied the convergence when a full Jacobian decomposition is implemented to the augmented Lagrangian method (ALM) for solving a multiple-block separable convex minimization model with linear constraints; and showed that the full Jacobian decomposition of ALM without any correction step can be convergent if each decomposed subproblem is regularized by a proximal term. It was shown via the variational inequality context that the proximal version of the Jacobian decomposition of ALM is an application of the proximal point algorithm (PPA); and this fact easily indicates its convergence under the condition that the proximal coefficient is greater than or equal to \(m-1\) where m is the number of function blocks used in the decomposition. We also showed that an interesting application of the alternating direction of multipliers (ADMM) in [20] is closely related to the proximal version of the Jacobian decomposition of ALM where the proximal coefficient is taken as \(m-1\).

In the PPA literature, it is commonly known that the proximal coefficient can not be too large. For the specific application of PPA (1.6), if s is too large, the quadratic term \(\frac{s\beta }{2}\Vert A_i(x_i-x_i^k)\Vert ^2\) plays a too heavy weight in the objective of the \(x_i\)-subproblem and thus the new iterate \(x_i^{k+1}\) is forced to be too “close” to \(x_i^k\)—as a result the “too-small-step-size” phenomenon which is doomed to lead to slow convergence will occur. Therefore, under the condition that the convergence of (1.6) is ensured, smaller values of s are preferred. Since we have shown that the condition \(s\ge m-1\) is sufficient to ensure the convergence of (1.6) and the ADMM in [20] can be regarded as an application of (1.6) with \(s=m-1\), in this sense the ADMM in [20] is the best choice when implementing the scheme (1.6) to solve the model (1.1).

On the other hand, for the cases of (1.1) where the value of m is large, the value \(m-1\) still might be too large to be the proximal coefficient for (1.6). Slower convergence is inevitable due to the resulting small or even tiny step sizes. It thus deserves an intensive research to investigate whether it is possible to ensure the convergence of the scheme (1.6) while the proximal coefficient can be much smaller than \(m-1\). Meanwhile, for such a case of (1.1) where m is large, we may still need to resort to prediction–correction type methods that take the output of the decomposed ALM scheme (1.4) or (1.5) as a predictor and then correct the predictor appropriately. The reason is that for such a prediction–correction method, the decomposed subproblems via either the Jacobian or Gauss–Seidel decomposition do not need to be proximally regularized, because of the “make-up” of the correction steps; thus too small step sizes could be avoided. Of course, the correction steps should be as simple as possible to yield satisfactory numerical performance, as we have mentioned. Some numerical results showing the superiority of prediction–correction type methods based on (1.5) for (1.1) with large values of m can be found in [10]. Moreover, the numerical results in [11, 13, 16, 20] have shown the efficiency of prediction–correction type methods based on (1.4) for (1.1) even for the case where m is very small, e.g. \(m=3\).